水力空化现象是指液体内局部压力降低时,液体内部或液固交界面上蒸汽或气体。空泡的形成、发展和溃灭的过程[1-2]。利用空泡溃灭时释放的大量能量,水力空化可以应用在废水处理、强化工业过程及空化水射流等领域。同时在螺旋桨空化噪声,超空泡减阻技术的研究目前也很多[3-4]。空化发生器原理是当水流流过收缩装置时,过流断面急剧变化,水流被增速降压,当压强降到水的气化压强下时发生空化[5]。空化效果的强弱影响空化发生器的效率,确定出最优化的复合空化器的结构参数来强化空化的效果,设计出高效率的空化发生器装置对生产应用具有重要的意义。
目前,国内外很多学者都对水力空化装置进行了探讨研究。例如:王智勇等[6]针对不同压力、不同喉部直径和扩散段长度对文丘里管内部空化现象的影响进行数值模拟;章昱等采用标准k-ω模型对孔板的水力空化装置进行数值模拟,探讨空化效应强度的影响因素问题;曾章美等[9]对孔板位置一定时,不同的文丘里管喉部的组合情况进行数值模拟,得出急型的复合结构的空化器空化效果更强。但这些研究一般集中于组合空化发生器中的文丘里管结构的研究,其空化效果还有待于提高。
本文结合文丘里管和孔板各自的优点,设计了一种把孔板嵌套在文丘里管喉部位置组成复合结构的两级空化发生器,在管内流量和过流截面积一定时,通过用多个小管径的孔道代替大直径的单文丘里管管道,分别在孔板孔道和文丘里管渐扩段发生2次空化过程,两级空化发生器中液流经过了2次加速,从而能够产生更多的空化泡,空化泡不断地产生和溃灭,大大提高了空化效应,以此来提高空化发生器整体的空化效果。两级空化发生器的空化面积和空化维持时间都要更长,从整体上来看,更有利于长时间的作业和强化。且此设计是一体式复合结构空化发生器,制造成本低,结构紧凑,更易运输和节省材料。且本文在所设计的复合空化发生器形式的基础上,分别针对3组孔不同排布方式孔板与文丘里管喉部进行复合的装置,利用Fluent软件分别对3种空化发生器的气液两相流场进行数值计算,对比分析不同形式流场的空化效果,以获得相对较高效率的两级空化发生器结构的优化设计,此数值模拟的结果可为研究多级空化发生器结构设计提供参考信息。
1 数值理论计算本文装置中的液流视为不可压缩的稳定流动,利用Fluent软件采用标准K-ε湍流模型和混合模型(misture mordel),压力梯度采用Standard格式离散,动量方程和湍流输运方程采用绝对稳定的一阶迎风格式,压力速度耦合采用Simple方式,在低压区引入空化模型的混合多项流模式对流场进行计算。
1.1 湍流模型本文计算中,空化发生器中的水流为不可压缩的稳定流动,湍流模型选择应用较广泛的k-ε两方程模型。标准k-ε模型基于Wilcoxk-ε,在加入Reynolds数以及各种流体特性的条件下改善得到的,所以本文求解采用标准k-ε模型。标准k-ε模型的连续性方程为:
| $\frac{{\partial {{u}}}}{{\partial {{x}}}} + \frac{{\partial {{v}}}}{{\partial {{y}}}} = 0;$ | (1) |
动量方程为:
| $\begin{split} &\frac{{\partial {{y}}}}{{\partial {{{x}}_{{j}}}}}{\rm{\rho }}{{\rm{\mu }}_{{i}}}{{\rm{\mu }}_{{j}}} = \\ & - \frac{{\partial {{p}}}}{{\partial {{{x}}_{m{i}}}}} + \frac{{\partial \left( {{\rm{\eta }}\partial {\rm{\mu }}{/_{{i}}}\partial {{\rm{\mu }}_{\rm{j}}} - {\rm{\rho }}\overline {{\rm{\mu }}_{{i}}^{\rm{'}}{\rm{\mu }}_{{j}}^{\rm{'}}} } \right)}}{{\partial {{\rm{x}}_{{j}}}}},\;\;\;\;{{i}},{{j}} = 1,2,3; \end{split}$ | (2) |
式中:ρ 为流体密度;μ为时均速度;p为流体压力;η为流体动力粘度,
湍流动能方程为:
| $ \begin{split} &\frac{{\partial \left( {{{\rho k}}} \right)}}{{\partial {{t}}}} + \frac{{\partial \left( {{\rm{\rho k}}{{\rm{\mu }}_{{i}}}} \right)}}{{\partial {{{x}}_{\rm{i}}}}} = \frac{\partial }{{\partial {{{x}}_{{j}}}}}\left[ {\left( {{\rm{\mu }} + \frac{{{{\rm{\mu }}_{{j}}}}}{{{{\rm{\sigma }}_{\rm{k}}}}}} \right)\frac{{\partial {{k}}}}{{\partial {{{x}}_{{j}}}}}} \right] + \\ &{{{G}}_{{k}}} + {{{G}}_{{b}}} - {\rm{\rho \varepsilon }} - {{{Y}}_{{M}}} + {{{S}}_{{k}}}; \end{split} $ | (3) |
式中:Gb为由浮力产生的湍动能;YM为可压缩湍流中阶梯的散布所生成的波动;Gk为由层流的速率差生成的湍动能。
湍流耗散方程为:
| $\begin{split} &\frac{\partial }{{\partial {{t}}}}{\rm{\rho \varepsilon }} + \frac{\partial }{{\partial {{{x}}_{\rm{i}}}}}\left( {{\rm{\rho \varepsilon }}{{\rm{\mu }}_{\rm{i}}}} \right) = \frac{\partial }{{\partial {{{x}}_{\rm{j}}}}}\left[ {\left( {{\rm{\mu }} + \frac{{{{\rm{\mu }}_{{j}}}}}{{{{\rm{\sigma }}_{{k}}}}}} \right)\frac{{\partial {\rm{\varepsilon }}}}{{\partial {{{x}}_{{j}}}}}} \right] + \\ &{{{C}}_{1{\rm{\varepsilon }}}}\frac{{\rm{\varepsilon }}}{{{k}}}\left( {{{{G}}_{{k}}} + {{{C}}_{3{\rm{\varepsilon }}}}{{{G}}_{{b}}}} \right) - {{{C}}_{2{\rm{\varepsilon }}}}{\rm{\rho }}\frac{{{{\rm{\varepsilon }}^2}}}{{{k}}} + {{m{S}}_{\rm{\varepsilon }}}{\text{。}} \end{split}$ | (4) |
式中:C1ε,C2ε,C3ε为常数;σk,σε为两方程的Prandtll数。
1.2 空化模型考虑到本文研究的对象和体系,综合分析选择Schnerr and Sauer空化模型。其空化模型表达式为:
| ${\text{当}}{{p}} < {{{p}}_{\rm{v}}}\;\;{{{R}}_{{e}}} = \frac{{{{\rm{\rho }}_{\rm{v}}}{{\rm{\rho }}_{\rm{l}}}}}{{\rm{\rho }}}{\rm{\alpha }}\left( {1 - {\rm{\alpha }}} \right)\frac{3}{{{{{R}}_{\rm{B}}}}}\sqrt {\frac{2}{3}\frac{{{{{p}}_{{v}}} - {{p}}}}{{{{\rm{\rho }}_{\rm{l}}}}}}, $ | (5) |
| ${\text{当}}{{p}} < {{{p}}_{\rm{v}}}\;\;{{{R}}_{{c}}} = \frac{{{{\rm{\rho }}_{\rm{v}}}{{\rm{\rho }}_{\rm{l}}}}}{{\rm{\rho }}}{\rm{\alpha }}\left( {1 - {\rm{\alpha }}} \right)\frac{3}{{{{{R}}_{{B}}}}}\sqrt {\frac{2}{3}\frac{{{{p}} - {{{p}}_{\rm{v}}}}}{{{{\rm{\rho }}_{\rm{l}}}}}}{\text{。}} $ | (6) |
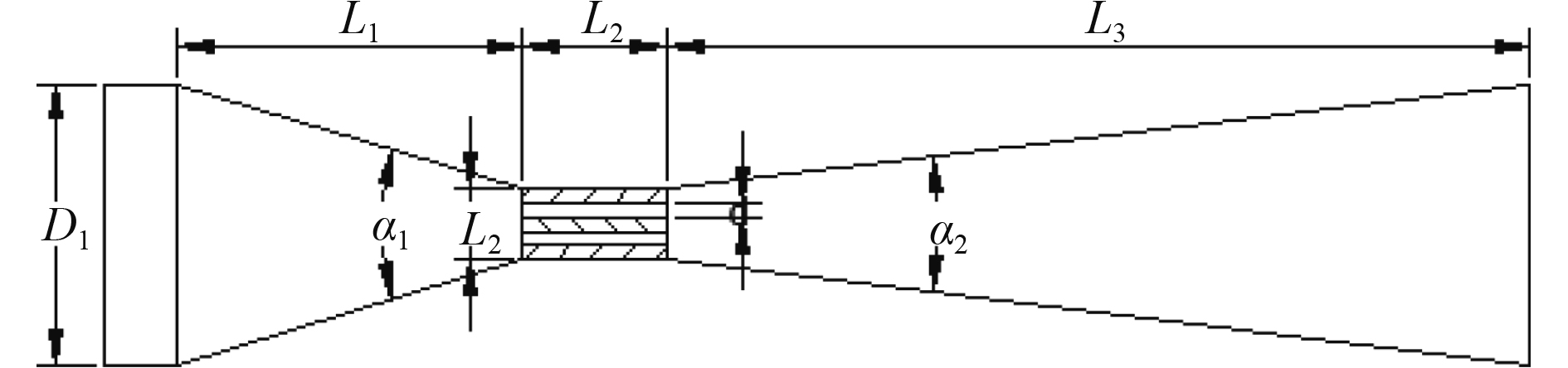
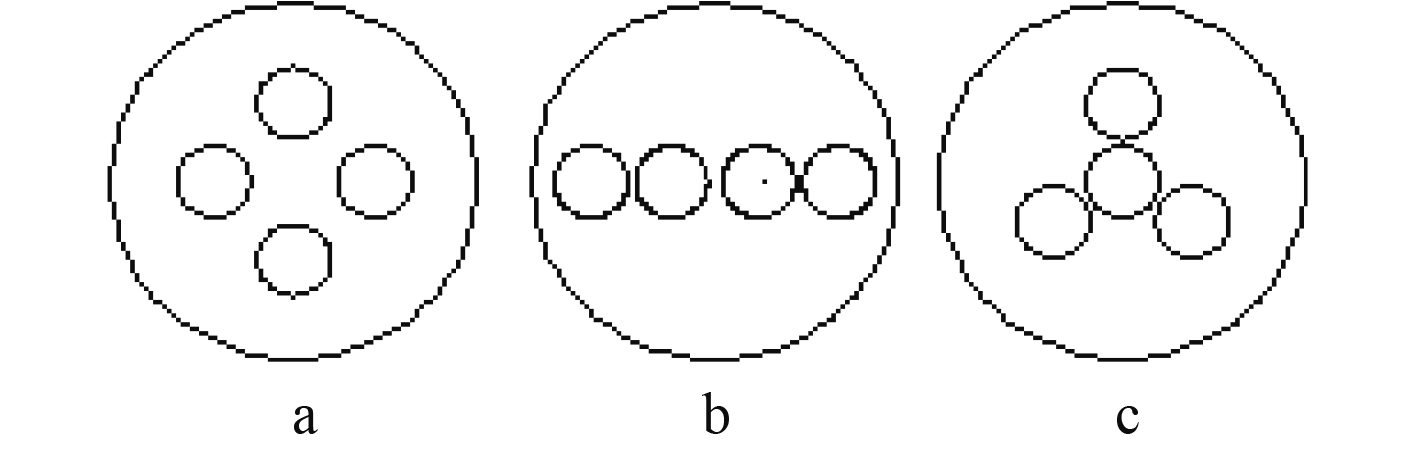
图1为设计的复合两级空化发生器结构示意图。图中,入口和出口直径D1=20 mm,孔板直径D2=5 mm,孔板小孔直径d=1 mm,渐缩段长度L1=24 mm,孔板长度L2=10 mm,渐扩段长度L3=63 mm,入口锥角α1为40°,出口锥角α2为18°。图2为设计的3种不同的孔板孔的排布方式,分别为a环状排布、b直线排布、c中心孔辐射状排布。
|
图 1 复合结构空化发生器结构示意图 Fig. 1 Schematic diagram of composite structure cavitation generator |
|
图 2 孔板孔的排布方式 Fig. 2 Arrangement of orifice holes |
本文利用CFD对三维模型进行网格划分,如图3所示。采用非结构性网格进行计算,对孔板孔道部分进行加密处理,通过网格检查,确保网格质量满足要求。本文选取25 ℃水和25 ℃的水蒸气为对象进行数值模拟,设置进口条件为速度等于0.5 m/s,出口条件为压力0 Pa,无滑移标准壁面函数边界条件。水的密度为998 kg/m3,表面张力为0.717 N/m,设定不可压缩相为水。

|
图 3 空化发生器的网格示意图 Fig. 3 Schematic diagram of the cavitation generators |
通过使用Fluent软件对流场进行数值计算,使用Tecplot软件进行后处理。
3.1 速度分布图4为3种不同复合结构空化发生器的速度分布云图。由图可知,3种空化发生器的速率都是先增大,在孔板孔口处速率达到最大。由于流体惯性,通过孔板孔道后流体依然具有较高的流速,从而形成射流,整个过程表现为速度分布由中心轴线向管壁转移的过程。而在文丘里管渐扩段的锥角影响下,水流的流动区域变大,使水的流动速率逐渐变小,在管道表面周围水流受到摩擦力作用流体流速开始逐渐降低。不同的孔板排布对空化发生器的速度场分布有显著的影响。3种装置的核心区的平均速度是c>a>b,这是由于中心孔辐射状排布的空化发生器c有中心孔,总体的速度更容易叠加,使流体受到的阻力较小,从而可以将更多地能量转化为空化效应的势能,所以核心区的速度相对最高,径向范围的速度场也最大;而复合结构空化发生器b和发生器c相比没有中心孔,所以整体的速度场分布范围和整体核心区的平均速度相对于c范围略微减小;直线分布的空化发生器b由于沿直线均匀分布,孔间隔较大,水流在流出孔道后的射流不集中,相对于其他两种装置核心区的水流速度相对较小。轴向方向速度矢量存在负值,说明有回流区,这是因为高速水流在文丘里管壁面阻挡所致。

|
图 4 空化发生器的速度云图 Fig. 4 Cavitation generator speed cloud |
图5为3种复合结构空化发生器的湍动能云图分布。从图中可以观察到,水流在进入孔板孔道前的流场湍动能很小,在流进孔道后迅速增大后又减小,在文丘里管渐扩段部分,湍动能再次增大。空化产生期间空泡的生成和破灭导致了流场的振荡,湍动能也同时进一步改变,在此过程中湍动能有2次幅值的变化,即发生了2次空化过程。由图可知,不同的孔板排布方式对空化发生器的整体湍动能散布有显著的影响,其中空化发生器c的湍动能相对于其他2种空化发生的散布区域更广和湍动能更强。这和前面的速度场分布有类似的规律。

|
图 5 空化发生器的湍动能云图 Fig. 5 The kinetic energy cloud diagram of the cavitation generator |
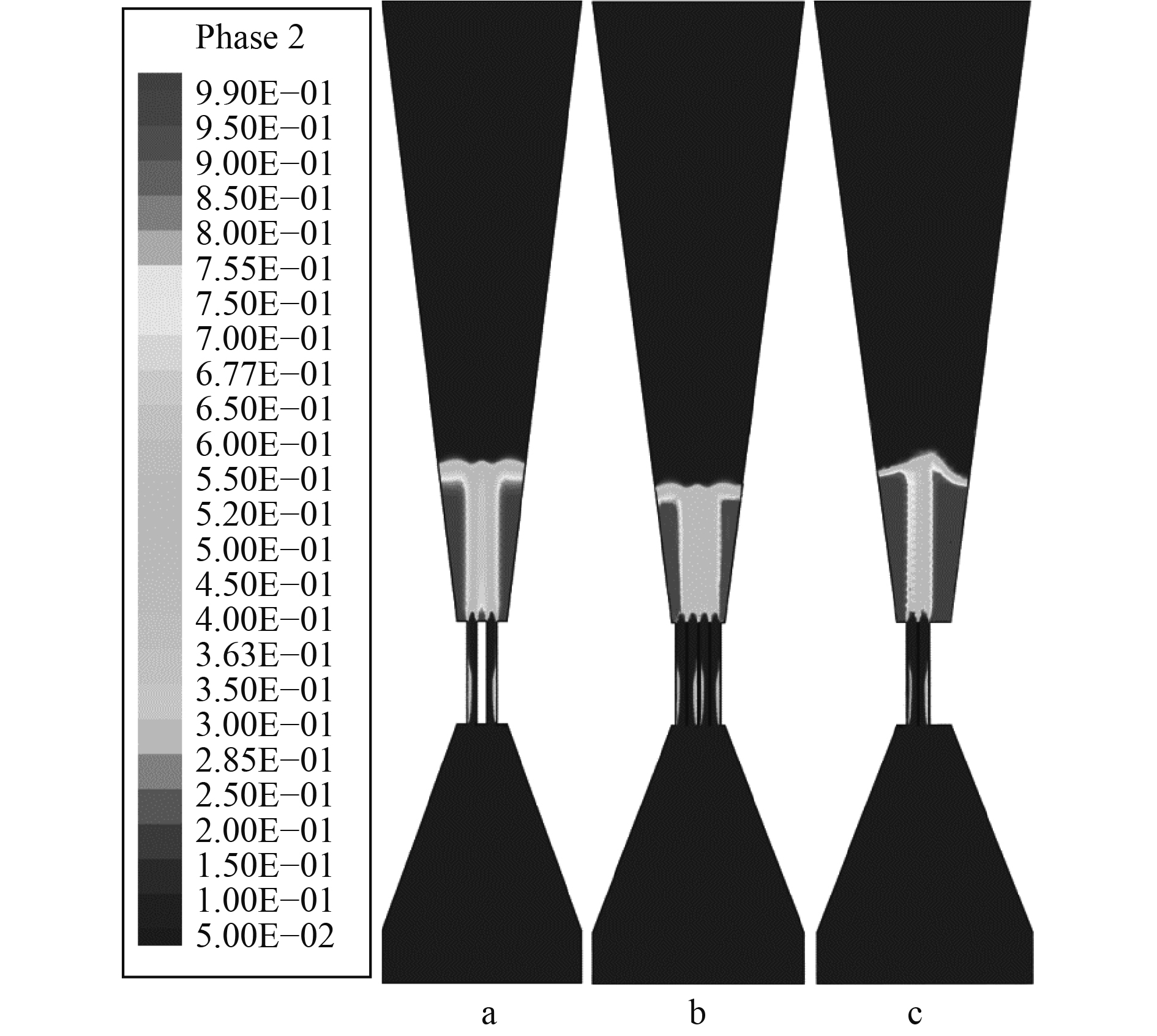
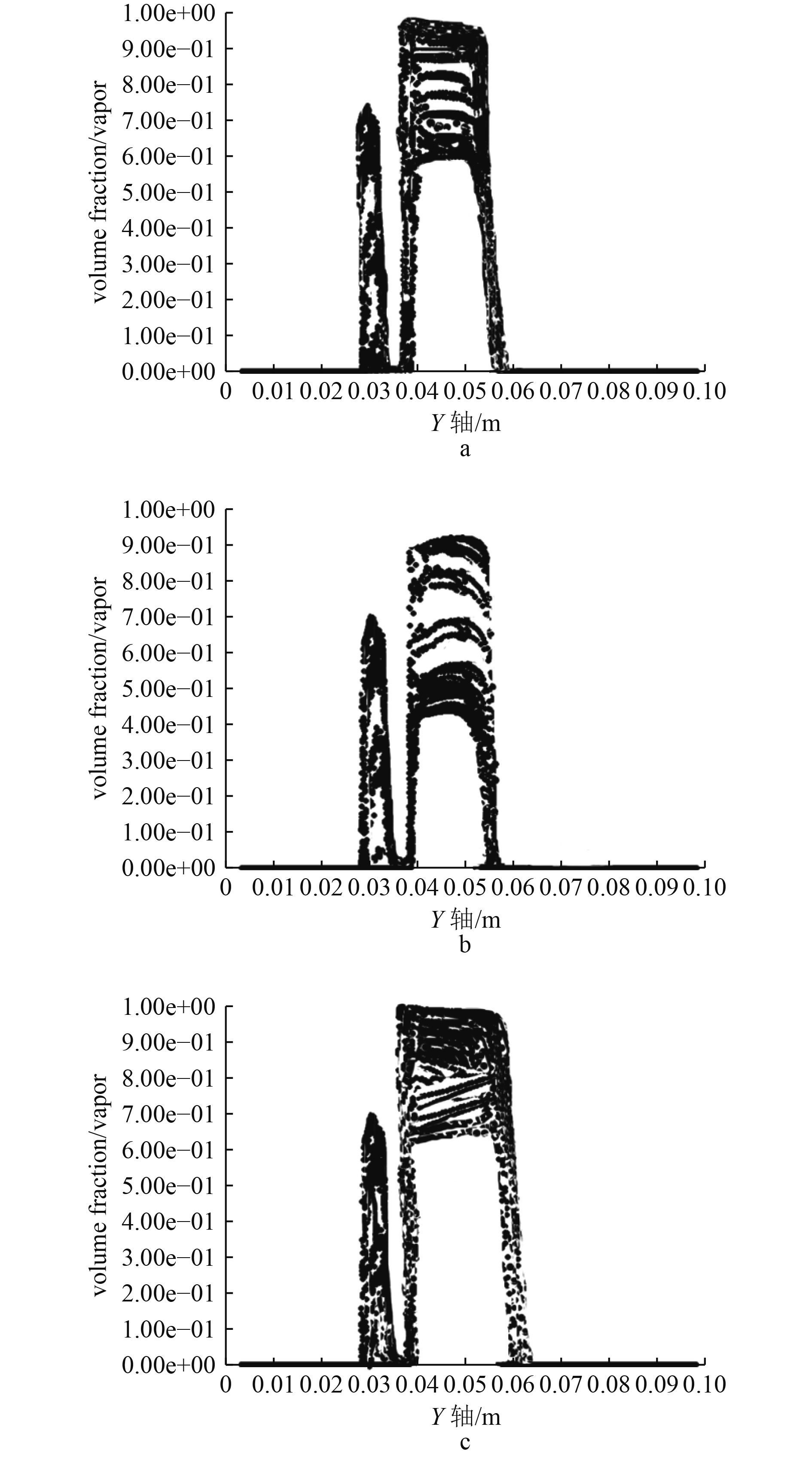
图6和图7分别为3种空化发生器的汽含率云图和分布散点图。可以清晰地看出汽含率的分布情况,其中图7的横坐标是沿管轴的距离,孔板位于28~38 mm范围内。可知,3种两级复合空化发生器的汽含率分布形状基本相似,3种复合结构空化器在Y轴坐标上汽含率都呈现出2次最高值,说明产生了2次空化。汽含率较高点主要产生在孔道区域(28~35 mm)和文丘里管锥角扩散段范围内(38~64 mm),表明空化大部分是产生在这些区域中,这与前面分析过的速度场和湍动能分布规律相似,汽含率的最高点都产生在文丘里管锥形段的流场中,主要集中在50%~97%左右。从图6和图7可以看出,空化发生器c的最高汽含率大概是99%,说明核心区的部分区域几乎完全空化,核心区的平均汽含率明显高于其他2种空化发生器。而且对比3种空化发生器的空化区域,很明显的空化发生器c的空化区域范围最长,在28~35 mm和38~64 mm之间。说明不同的孔板分布结构对于复合式空化发生器的空化场有较显著的影响,3种两级空化的复合空化发生器中带中心孔的辐射状排布的孔板复合结构空化发发生器的空化效果最好,这也和前面的速度场和湍动能的分析结果一致。
|
图 6 空化发生器的汽含率云图 Fig. 6 Cavitation rate of the cavitation generator |
|
图 7 空化发生器汽含率分布散点图 Fig. 7 Scatter plot of vapor content distribution of cavitation generator |
本文在复合结构空化发生器装置基础上,在相同的边界条件下,基于CFD数值模拟软件结合S-S空化模型分析所设计的3种不同孔板分布的复合结构空化发生器的性能,得到了3种空化发生器的速度云图、湍动能云图、汽含率云图和分布散点图进行对比分析,得到如下结论:
1)本文中所设计的孔板孔道嵌套在文丘里管喉部组成的复合结构两级空化发生器可以发生2次空化,最高汽含率可以达到99%。该装置经历2次速度、湍动能的变化,可以产生更多的空化气泡,一定程度上大大提高了空化发生器的整体空化效果。
2)不同的孔板孔道排布方式影响了空化发生器内流场分布情况和大小,对速度场和湍动能产生的位置和大小范围也有影响,同时空化发生器核心区的平均汽含率也有影响。
3)本文对比分析了3种不同的两级复合结构空化发生器,在相同边界条件下,带中心孔的辐射状排布的孔板与文丘里管喉部完全嵌套所组成的复合结构空化发生器速度场和湍动能分布范围最大,汽含率最高可达99%,空化发生器范围也最大,综合对比可知,此空化发生器装置的空化性能最好。
| [1] |
HAN B, JU D Y. Compressive residual stress induced by water cavitation peening: A finite element analysis[J]. Material and Design, 2009, 30(8): 3325-3332. DOI:10.1016/j.matdes.2008.11.029 |
| [2] |
管金发, 邓松圣, 张攀峰. 文丘里管空化装置设计与数值模拟[J]. 后勤工程学院学报, 2012, 28(3): 30-34. DOI:10.3969/j.issn.1672-7843.2012.03.007 |
| [3] |
启军, 邱家兴, 程玉胜, 等. 船舶螺旋桨空化噪声非均匀调制特性及其应用[J]. 舰船科学技术, 2017, 39(6): 18-22. DOI:10.3404/j.issn.1672-7619.2017.06.004 |
| [4] |
王超, 林杨, 胡志强, 等. 空化模型中的相变系数对不同头型的适用性研究[J]. 舰船科学技术, 2018, 40(2): 39-45. DOI:10.3404/j.issn.1672-7649.2018.02.007 |
| [5] |
王永广, 赵连玉, 邓橙, 等. 基于孔板和文丘里管复合结构空化器的空化效果数值模拟[J]. 环境工程, 2012, 30: 458-460. |
| [6] |
王杰阳. 多孔板水力空化发生器空化过程的数值模拟研究[D]. 天津: 天津科技大学, 2015.
|
| [7] |
章昱, 李育敏, 计建炳. 孔板水力空化装置的数值模拟[J]. 化学反应工程与工艺, 2011, 27(3): 219-223. DOI:10.3969/j.issn.1001-7631.2011.03.005 |
| [8] |
张建峰, 卢晓江, 余冬梅. 孔板为发生器的水力空化装置的实验研究[J]. 轻工机械, 2008, 26(2): 15-18. DOI:10.3969/j.issn.1005-2895.2008.02.005 |
| [9] |
曾章美, 刘小兵, 兰巍, 等. 孔板和文丘里管复合结构空化器的优化设计[J]. 西华大学学报(自然科学版), 2015, 34(6): 92-95. DOI:10.3969/j.issn.1673-159X.2015.06.019 |
 2020, Vol. 42
2020, Vol. 42
