当流体在近壁面流动时,近壁区域各物理变量的变化梯度非常大,因此该区域在采用CFD进行数值计算时需要着重考虑。对于近壁区域的处理目前主要有2种方法:一种是壁面函数法,该方法无需对过渡层和粘性底层进行直接求解,而是通过半经验公式将湍流核心区域的求解变量与壁面上的物理量联系起来;另一种方法是近壁模型法,使用该方法时需要在壁面附近划分足够细的网格,使之可以求解粘性影响的区域[1]。
对于k-ε两方程高雷诺数湍流模型与壁面函数相结合的模式,边界层网格尺度对计算结果有较大影响,即需要保证y+值在一个合理的范围[2]。资丹等[3]提出3种具有不同边界层网格尺度的网格划分方案,分析了不同初始y+值对泵站流场数值计算结果的影响。杜云龙等[4]确定出船舶阻力数值计算中对结果影响最大的因素为边界层网格尺度。Jialun Liu等[5]系统研究了网格类型、计算域形状、网格大小以及网格增长率对船舶舵系水动力计算结果的影响。Nguyen Van Trieu[6]采用SST k-w壁面模型法研究鱼尾舵随边宽度对水动力性能的影响。赖晨光等[7]研究了不同湍流模型在匹配不同边界层网格策略时对汽车外流场数值计算精确性的影响。
本文所进行的高效舵水动力数值计算属于高雷诺数粘性绕流问题,采用壁面函数法就可以有效地模拟流体的流动。为了研究边界层网格尺度在高效舵水动力计算中的影响,在网格数量无关性检查的基础上,针对几种典型的初始壁面y+值,应用Standard k-ε湍流模型对一种新型随边扭曲高效舵进行水动力计算,并将模拟结果与模型试验结果进行对比分析,从而为高效舵水动力计算提供参考。
1 模型试验舵的敞水模型试验在上海船舶运输科学研究所的拖曳水池中进行。水池长192 m,深4.2 m,宽10 m,设置在水池上的拖车系统运行速度为0.01~10 m/s。采用六分力传感器测量作用在舵上的升力FL、阻力Fd和扭矩M。
试验工况和缩尺比如表1所示。
|
|
表 1 随边扭曲高效舵缩尺比试验 Tab.1 Scale model test of high effectiveness twisted rudder |
本试验需测量在不同舵角下舵的受力情况,力的测量从0°~30°范围每隔5°进行一次。试验时,首先需调整舵角至相应角度,再将拖车开至工况要求的速度,最后拖车保持匀速行驶至试验结束。舵的尾流场如图1所示。

|
图 1 舵的尾流场 Fig. 1 The wake field of the rudder |
本文在数值计算时假定流体为密度不变,不可压缩的粘性流,其连续性方程和动量方程可以简化如下:
| $ \frac{{\partial {{u}}}}{{\partial {{x}}}} + \frac{{\partial {{v}}}}{{\partial {{y}}}} + \frac{{\partial {{w}}}}{{\partial {{z}}}} = 0{\text{,}} $ | (1) |
| $ \left. \begin{aligned} & \rho \frac{{\partial u}}{{\partial {{t}}}} + \rho u\frac{{\partial u}}{{\partial {{x}}}} + \rho v\frac{{\partial u}}{{\partial {{y}}}} + \rho w\frac{{\partial u}}{{\partial {{z}}}} =\\ & \mu \left( {\frac{{{\partial ^2}u}}{{\partial {{{x}}^2}}} + \frac{{{\partial ^2}u}}{{\partial {{{y}}^2}}} + \frac{{{\partial ^2}u}}{{\partial {{{z}}^2}}}} \right) - \frac{{\partial P}}{{\partial {{x}}}} + {S_x} \\ & \rho \frac{{\partial v}}{{\partial {{t}}}} + \rho u\frac{{\partial v}}{{\partial {{x}}}} + \rho v\frac{{\partial v}}{{\partial {{y}}}} + \rho w\frac{{\partial v}}{{\partial {{z}}}} =\\ & \mu \left( {\frac{{{\partial ^2}v}}{{\partial {{{x}}^2}}} + \frac{{{\partial ^2}v}}{{\partial {{{y}}^2}}} + \frac{{{\partial ^2}v}}{{\partial {{{z}}^2}}}} \right) - \frac{{\partial P}}{{\partial {{y}}}} + {S_y} \\ & \rho \frac{{\partial w}}{{\partial {{t}}}} + \rho u\frac{{\partial w}}{{\partial {{x}}}} + \rho v\frac{{\partial w}}{{\partial {{y}}}} + \rho w\frac{{\partial w}}{{\partial {\rm{z}}}} =\\ & \mu \left( {\frac{{{\partial ^2}w}}{{\partial {{{x}}^2}}} + \frac{{{\partial ^2}w}}{{\partial {{{y}}^2}}} + \frac{{{\partial ^2}w}}{{\partial {{{z}}^2}}}} \right) - \rho g - \frac{{\partial P}}{{\partial {{z}}}} + {S_z} \end{aligned} \right\}{\text{。}} $ | (2) |
式中:u,v,w分别为在x,y,z方向上的速度分量;g为重力加速度;ρ为流体密度;
Standard k-ε湍流模型[8]是较为常用的两方程湍流模型,其输运方程如下:
| $ \begin{split} & \frac{\partial }{{\partial t}}\left( {\rho k} \right) + \frac{\partial }{{\partial {x_i}}}\left( {\rho k{u_i}} \right) = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\delta _k}}}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right] + \\ &{G_k} + {G_b} - \rho \varepsilon - {Y_M} + {S_k} {\text{,}} \\ & \frac{\partial }{{\partial t}}\left( {\rho \varepsilon } \right) + \frac{\partial }{{\partial {x_i}}}\left( {\rho \varepsilon {u_i}} \right) = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\delta _k}}}} \right)\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right] +\\ & {C_{1\varepsilon }}\frac{\varepsilon }{k}\left( {{G_k} + {C_{3\varepsilon }}{G_b}} \right) - {C_{2\varepsilon }}\rho \frac{{{\varepsilon ^2}}}{k} + {S_\varepsilon } {\text{。}} \end{split} $ | (3) |
其中:Gk为平均速度引起的湍动能产生项;Gb为浮力引起的湍动能产生项;涡黏系数为ut,Ym表示湍动耗散率;C1ε,C2ε,C3ε,σε和σk为经验常数(取值参考文献[8])。
3 计算域的建立舵的几何模型与模型试验保持一致,模型的建立在Rhinoceros中完成。舵的外流场为一个单独的长方体计算域,如图2所示。舵前端距速度入口边界4倍弦长,来流速度与模型试验拖车速度一致;舵随边距压力出口边界7倍弦长;计算域宽度方向取6倍弦长,左右侧面设定为壁面边界;舵顶和舵底分别距流场底部和顶部4倍舵高,为壁面边界;舵表面设为无滑移壁面边界。模型试验时,测得的水温为19.2 Cº,因此数值模拟时水的动力粘度为0.001 029 9 Pa∙s,密度取为998.26 kg/m3。
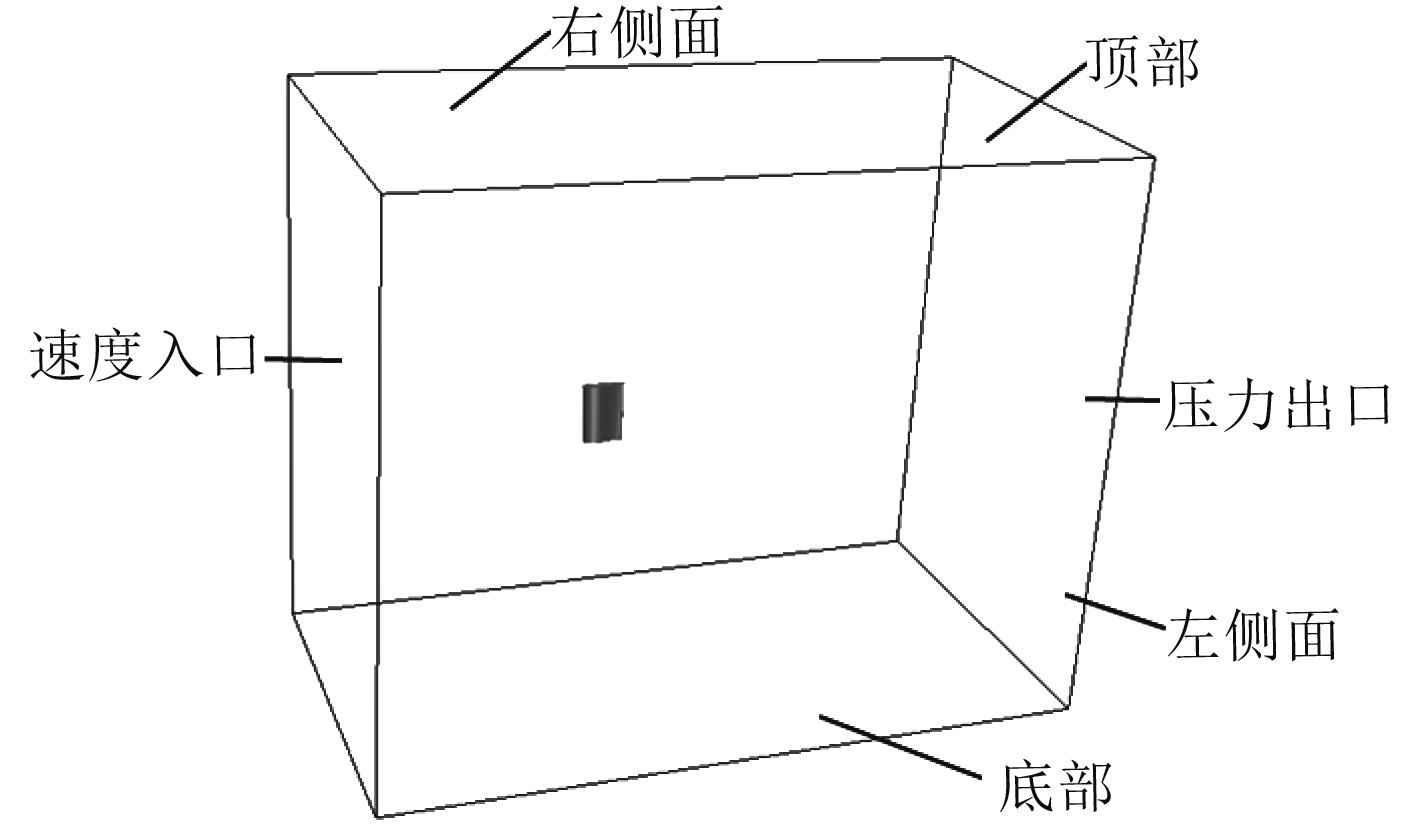
|
图 2 计算域及边界面 Fig. 2 Computational domain and the boundary condition |
网格的划分情况对流体的运动以及数值计算的精度和收敛情况具有重要的影响[9-10],因此在探讨边界层网格尺度对高效舵水动力数值计算影响前,对边界层外的网格进行无关性验证。本次验证对计算域采用4种不同的网格尺度,分别对应4种不同数量的网格mesh1,mesh2,mesh3,mesh4和mesh5。计算时采用Standard k-ε湍流模型和相同的边界层网格尺度。网格无关性验证结果如表2和图3所示。
|
|
表 2 四种不同网格数量下的升力系数对比 Tab.2 Comparison of lift coefficient with different mesh scale |
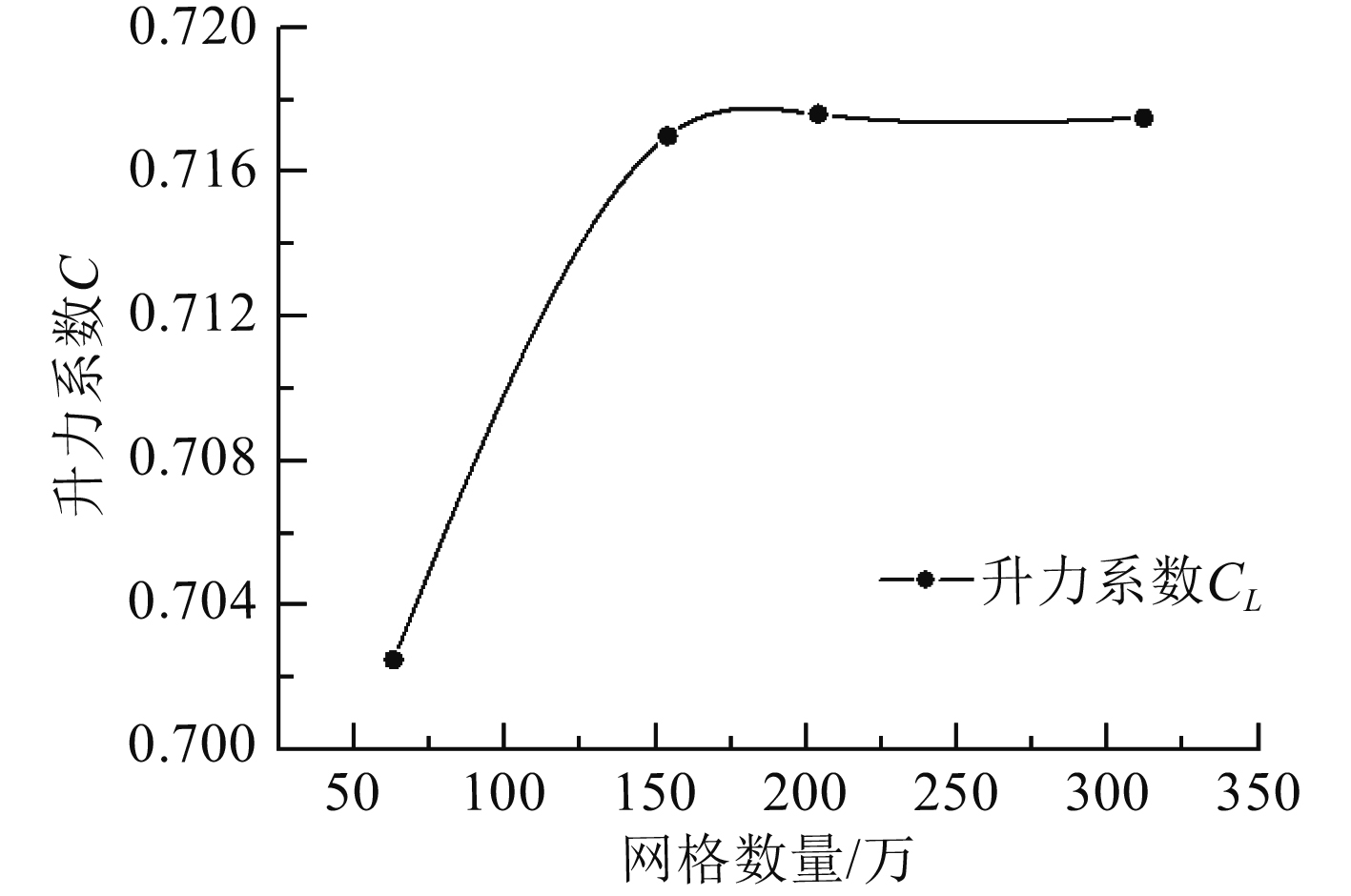
|
图 3 不同网格数量下的升力系数对比 Fig. 3 Comparison of lift coefficient with different mesh scale |
从表2和图3可以看出,随着网格数量的增加数值计算结果变化不大,同时由mesh2和mesh4对比可以看出,当网格数量达到152万后,增加网格数量对计算结果没有明显的影响,不过较为细密的网格对舵周围流场细节的捕捉更为精确,因此最终选择mesh3为后续数值计算的网格划分方案。
4.2 边界层网格尺度影响舵在流场中运动时,由于水具有粘性,流体在近壁区域的流动大致可以分为内、中、外3层:贴近壁面的一层称为粘性底层,该层的流动几乎是层流;过渡层处于粘性底层的外面,流体的流动状态介于层流与湍流之间;最外层是完全湍流层也称为对数层,湍流处于充分发展状态。为了合理描述边界层内的流动,引入体现边界层网格尺度的无量纲参数y+,其表达式如公式4所示[11]。通常认为,当y+<5的区域为粘性底层,5<y+<30的区域为过渡层,y+>30的区域为对数层。
| $ {{y}^{+}}=0.172\cdot \left( \frac{\Delta {{y}_{p}}}{L} \right)\cdot R{{e}^{0.9}}{\text{。}} $ | (4) |
其中:L为特征长度,Re为雷诺数,△yp为第1层网格高度。
为了研究边界层网格尺度对数值模拟结果产生的影响,选用典型的初始壁面y+值3,15,30,60和150对15°攻角下的高效舵进行水动力计算,其中边界层内的网格增长率取1.2。不同初始壁面y+值下数值计算结果与模型试验结果对比如表3所示。
|
|
表 3 不同初始壁面y+值下数值计算结果与模型试验结果对比 Tab.3 Comparison of model test with numerical calculations at different y+ |
从表3和图4的对比可以看出,随着初始壁面y+值的增加,升力系数与模型试验误差从–0.807%变化到2.033%,阻力系数从4.622%变化到–4.507%,从而说明初始壁面y+值对高效舵水动力计算精度有着较为明显的影响;阻力系数对初始壁面y+值的敏感性较升力系数更为明显,这是由于初始壁面y+值直接反应了边界层内网格尺度,边界层内的网格尺度直接影响舵近壁区速度梯度的变化,从而影响作用在舵上的阻力,但由于壁面函数的应用第1层边界层厚度不宜过薄,即y+不宜过小。从图4还可以看出,随着y+值的增加,舵尾静流区的范围逐渐减小,舵周围流场速度分布也略有不同,这也能说明初始壁面y+值对舵水动力计算会产生影响。综合来看当初始壁面y+值取30时,数值计算结果与模型试验结果误差最小。
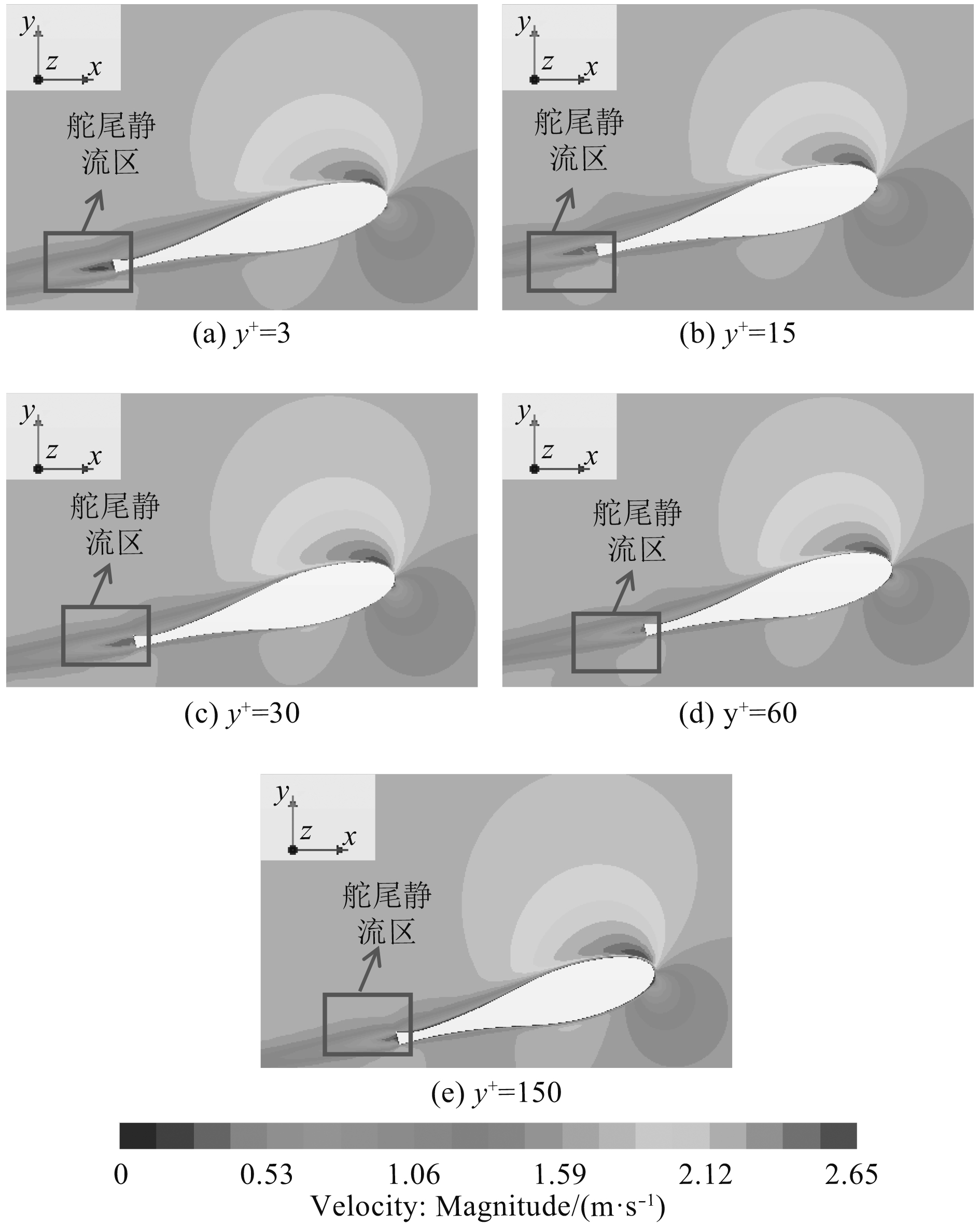
|
图 4 舵周围速度分布云图 Fig. 4 Velocity distribution around the rudder |
基于前文的网格划分方案和壁面初始y+值,对随边扭曲高效舵进行攻角从0°~30°(间隔为5°)下数值模拟,并将模型试验与模拟结果进行了对比,如图5所示。可以看出,数值模拟与模型试验结果吻合度较高,尤其在失速角以前。

|
图 5 数值模拟与模型试验结果对比 Fig. 5 Comparison of numerical calculations with model test |
为了研究边界层网格尺度在高效舵水动力计算中的影响,在网格数量无关性检查的基础上,针对几种典型的y+值,应用Standard k-ε湍流模型对一种新型随边扭曲高效舵进行水动力计算,并与模型试验结果进行对比。
可以看出,初始壁面y+值对高效舵水动力计算精度有明显的影响;阻力系数对初始壁面y+值的敏感性较升力系数更为显著;当初始壁面y+值取30时,数值计算结果与模型试验结果误差最小,因此建议进行高效舵水动力数值计算时初始壁面y+值取在30左右。
| [1] |
朱旭东. 湍流模型的比较、改进和应用[D]. 南京: 南京航空航天大学, 2005.
|
| [2] |
资丹, 王福军, 陶然, 等. 边界层网格尺度对泵站流场计算结果影响研究[J]. 水利学报, 2016, 47(2): 139-149. |
| [3] |
杜云龙, 陈伟民, 董国祥. 典型油船船模静水阻力CFD计算策略探讨[J]. 江苏科技大学学报(自然科学版), 2017, 31(5): 661-665. |
| [4] |
熊超强. 低阻力汽车外流场的数值模拟及其误差分析[D]. 广州: 华南理工大学, 2012.
|
| [5] |
JIALUN Liu1, ROBERT Hekkenberg et al. Mesh properties for RANS Simulations of aerofoil-shape rudder hydrodynamics[C]// 10th International Workshop on Ship and Marine Hydrodynamics, 2017,.
|
| [6] |
VAN Nguyen, T., IKEDA, Y.. Hydrodynamic characteristic of rudder sections with high lift force[J]. Journal of the Japan Society of Naval Architects and Ocean Engineers, 2013(19): 403-406. |
| [7] |
赖晨光, 王擎宇, 付中正. 基于湍流模型与边界层网格策略的汽车外流场数值计算精度分析[C]// 中国汽车工程学会汽车空气动力学分会, 2017.
|
| [8] |
LAUNDER B E, SPALDING D B. Lectures in Mathematical Models of Turbulence[M]. London: Academic Press, 1972.
|
| [9] |
罗天, 万德成. 基于CFD的船舶横摇数值模拟与粘性效应分析[J]. 中国舰船研究, 2017, 12(2): 1-11, 48. DOI:10.3969/j.issn.1673-3185.2017.02.001 |
| [10] |
苏绍娟, 介推, 王天霖, 等. 基于CFD与三因次法结合的低速多用途船的阻力预报[J]. 舰船科学技术, 2017, 39(4): 59-63. DOI:10.3404/j.issn.1672-7619.2017.04.012 |
| [11] |
丁江明, 江佳炳, 秦江涛, 等. 高速滑行艇阻力性能RANS计算中网格影响因素[J/OL]. 哈尔滨工程大学学报, 2019(6): 1-7[2019-01-21].
|
 2020, Vol. 42
2020, Vol. 42
