2. 武汉理工大学 船舶动力工程技术交通行业重点实验室,湖北 武汉 430063;
3. 武汉理工大学 国家水运安全工程技术研究中心可靠性工程研究所,湖北 武汉 430063
2. Key Laboratory of Marine Power Engineering and Technology (Ministry of Transport), Wuhan University of Technology, Wuhan 430063, China;
3. Reliability Engineering Institute, National Engineering Research Center for Water Transport Safety (WTS Center), Wuhan University of Technology, Wuhan 430063, China
作为一种利用流体冲击叶轮转动的动力机械结构体,涡轮机已被广泛用于发电、航空、航海等领域。从适用流体工质的角度而言,涡轮机一般被分为汽轮机、燃气轮机和水轮机等不同类型。受其结构特点和运行原理的制约,传统涡轮机(如叶片式涡轮机)在设计制造和应用过程中有诸多技术问题需予特别考虑,如涡轮叶片具有复杂形状,叶片和活塞膨胀装置容易在固定外壳和旋转动力装置之间发生空气泄漏,在流体为高粘度、强研磨性、含有固体颗粒或两相流的流体的情况下,存在许多不兼容的问题(如涡轮机工质为纳米流体时会对叶片造成侵蚀和污染)[1]。
无叶片、由流体剪切力驱动的特斯拉涡轮机具有结构简单、制造公差要求相对较低、密封性能突出等特点,在运转时流体会产生压力梯度(与流速的平方呈正相关)与圆盘的离心力相互平衡,以防止轴承等部件因超速运转而发生损坏[2]。同时由于运转过程中产生离心力场,使得机体具有自洁性,保证了涡轮机在工质为非常规燃料(如生物质)产生固体颗粒的情况下也可以正常运转[3],所以在利用研磨液、含有固体颗粒流体以及其他特殊物化特性流体工质方面具有独特的适应性。现阶段,由于超临界蒸汽朗肯循环、超临界二氧化碳布雷顿循环等多种循环系统处于探索阶段,使得特斯拉涡轮机因其特性在生产实践中具有替代传统涡轮机的显著潜力。与目前仍在使用的传统叶片式涡轮机相比,特斯拉涡轮机的能量转换效率相对较低,主要原因是其结构体特点所导致的进口和喷嘴压力损失、轴承能量损失、端盖表面流体粘性损失以及增压室中的流体耗散损失等。如通过针对性研究解决上述能量损失问题,则能够通过提升特斯拉涡轮机的实际能量转换效率而极大地拓展其在工业领域的应用范围[4]。
本文进行综述现阶段特斯拉涡轮机的开发和应用前景以及研究方法的进展,介绍特斯拉涡轮机的组成及特性,总结国内外特斯拉涡轮机的研究现状,讨论有待深入研究和突破的关键技术,以期为推进特斯拉涡轮机技术的基础研究提供理论指导。
1 特斯拉涡轮机的应用领域在高负荷功率运行情况下,叶片式涡轮机运行效率数倍于特斯拉涡轮机,而低负荷时两者的运行效率则相反[5]。基于这项发现,国内外学者就特斯拉涡轮机在低负荷功率运行条件下的应用进行了探索,并取得了一定的成果。Lampart等[5]讨论了在一个联合发电的微型动力装置中使用特斯拉涡轮机的可能性。Carey[6]将特斯拉涡轮机用作太阳能有机朗肯循环加热和电力系统的膨胀器,通过验证建立的一维理想化的动量转移模型,发现在最佳设计条件下,其可以实现75%的熵效率,证明了特斯拉涡轮机的高效性。Choon等[7]开发了一种水力发电特斯拉涡轮机,以实现家庭供水中潜在能量的循环发电利用,在供水时将自来水进入储水罐过程中产生的势能转化为电能,避免水流到达储水罐后造成能量浪费。Hasan等[8]从改变采用皮带或链条连接压缩机转子与汽车发动机曲轴实现能量传递的传统方法入手,探讨了在车辆中使用特斯拉涡轮替代空调压缩机驱动单元的可能性。清华大学燃气轮机研究所的顾春伟等[9]针对低品位能的利用问题,采用一种无量纲公式,改进了使用特斯拉涡轮机作为膨胀器的有机朗肯循环系统的一维模型,确认特斯拉涡轮机是小型有机朗肯循环系统的潜在选择。Damodhar等[10]针对边远地区电力短缺或没有电力供应的问题,结合特斯拉涡轮机在低水压的情况下拥有更高的运行效率的特性,设计制造了一种便携式水轮机,该水轮机可以在任何有水源的地方使用,为边远地区电力供应问题提供了有效的解决方案。
2 特斯拉涡轮机的研究方法 2.1 特斯拉涡轮机数学建模方法确认圆盘内部的流动属性是特斯拉涡轮机数学建模的基础,Murata等[11]发现圆盘内部的流动是层流而外部的流动是湍流,为假定圆盘之间是层流的分析模型建立提供了理论基础。Harwood[12]还发现,峰值效率是在低雷诺数的情况下实现的,进一步验证了在实验分析中应该使用圆盘之间是层流流动的假设,为特斯拉涡轮机的操作提供了可行的控制条件。
随着对于特斯拉涡轮机的研究逐渐深入,研究方法逐步系统化,数学模型的建立及计算方法的优化将节省特斯拉涡轮机设计所消耗的时间成本。诸多研究者在特斯拉涡轮机的研究分支开展了研究,并得出了相应的结论,为后来的研究者提供了理论基础和可供参考使用的数学模型。
1)数学模型
Deam等[13]开发了一种简单的特斯拉涡轮机的分析模型,用来考虑不可压缩性和一维流动问题。
| $ \begin{array}{*{20}{c}} {{\rm{F}} = {\rm{A\chi }}{P_{res}}f\left( \theta \right)}\text{,}\\ {{\eta _{1D}} = \sqrt {\left( {1 - \chi f\left( \theta \right)} \right)} {\rm{\chi }}f\left( \theta \right)\theta }\text{。} \end{array} $ |
| $ \begin{aligned} & {\text{求导后}},{\text{得}}\\ & \frac{\partial {{\eta }_{1D}}}{\partial \chi }={{f\left( 1-\chi f \right)}^{{}^{1}\!\!\diagup\!\!{}_{2}\;}}\theta -\frac{1}{2}{f^{2}}\chi {{\left( 1-\chi f\right)}^{{}^{-1}\!\!\diagup\!\!{}_{2}\;}}\theta \text{。} \end{aligned} $ |
式中:F为皮带拉力,N;A为涡轮机流道截面面积,mm2;Pres涡轮机的储层压力,Pa;
在给定的速度比θ下,通过参数χ求出最优的几何形状,从而得到转子的最大值。但是径向流特性的缺失限制了该理论继续开展可能性,此外该理论旨在预测无能量损失时的最大效率,而这个情况只有当转子速度与流体流动速度相等时才能达到。然而,如果在转子和流体之间没有相对运动,粘性阻力将会因此变为零,此时没有能量输出。
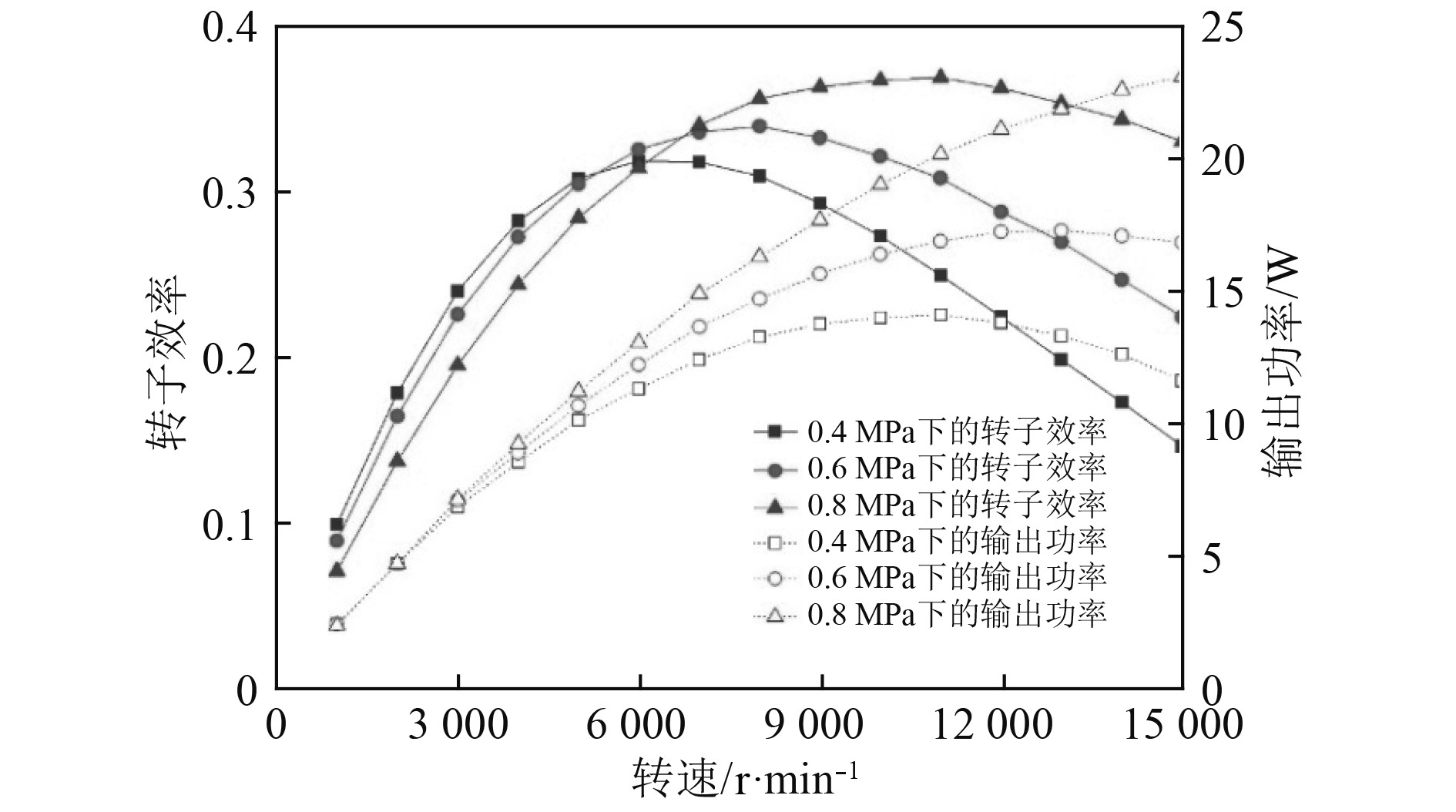
针对市场对小型发电系统的需求日益增长的现象,Talluri等[14]通过EES软件中的专用自制程序,开发了若干个用于解决转子流场的创新模型,用以评估能量在定子、转子、扩散器等各个部件的损耗,在使用正己烷作为工质的低质量流率条件下,将不同压力和转速参数输入这些模型中进行计算,得出结论如图1所示,在低质量流率的条件下,可以得到较高的转子效率,但会导致较低的功率输出。
2)计算方法
针对特斯拉涡轮机测试装置灵敏度不高的问题,Hoya等[15]研制了一种特斯拉涡轮机和柔性试验台,并完整地描述了一种简单而有效的计算净输出功率、整体能量损失以及轴承和其他能量损失的方法,即“角加速度法”,实现了在高速旋转下确定极低的扭矩,为特斯拉涡轮机提供了详细的测量和操作经验。
Couto等[16]提出了一项简单的计算程序,用于估计特斯拉涡轮机内部所需的圆盘数量,以达到确认最佳圆盘数量的要求。该计算是基于旋转圆盘上旋转流体的边界层厚度进行的估算,计算结果为层流边界层厚度δ,但是该程序在计算过程中使用了绝对切向速度来确认相对旋转参考系的边界层厚度,会造成较大的偏差。此外,该计算也没有进行实验或数值验证。
| $ {\rm{\delta }} \approx 5\sqrt {\frac{{v \cdot \left( {{r_1} - {r_2}} \right)}}{U}} \text{。} $ |
式中:v为流体的运动粘度,m2/s;r1为圆盘的内径,mm;r2为圆盘的外径,mm;U为流体在进口处的流速,m/s
Guha等[17]提出了一种系统的计算流体动力学研究设计方法,以满足实际的约束条件,并提供了计算功率和效率最高值的方法。通过追踪动态相似数、入口切向速度和入口进气角三个无量纲参数,确认了与传统涡轮机中的流体摩擦只会产生负面作用不同,特斯拉涡轮机中的流体摩擦虽然增加了径向压降但是同时提高了发电效率。通过对这一双重作用进行全面的分析和量化,可以得到两者之间的平衡动态相似数的最优值和入口切向速度比,实现效率最大化。
2.2 特斯拉涡轮机几何建模仿真方法随着计算机配置的不断提升以及计算机技术的不断突破,学者可以利用仿真软件进行几何模型的建立及仿真,也可以通过计算机辅助二维分析完成模型的优化,并完成实验结果的预测和实验条件的调整,以优化各部分的设计参数和提高实物实验的成功率。
为研究转子圆盘间隙宽度和转速对设计和非设计体积流量的影响,Engin等[18]根据角动量守恒原理设计了一种特斯拉涡轮机并进行了二维分析和测试。但由于低粘度、切向性和吸排气截面较大导致机械能损失与输入功率相当,该涡轮机表现出极低的性能特性,需要对喷嘴和内部机械结构进行进一步的优化设计以减小机械能的损失。
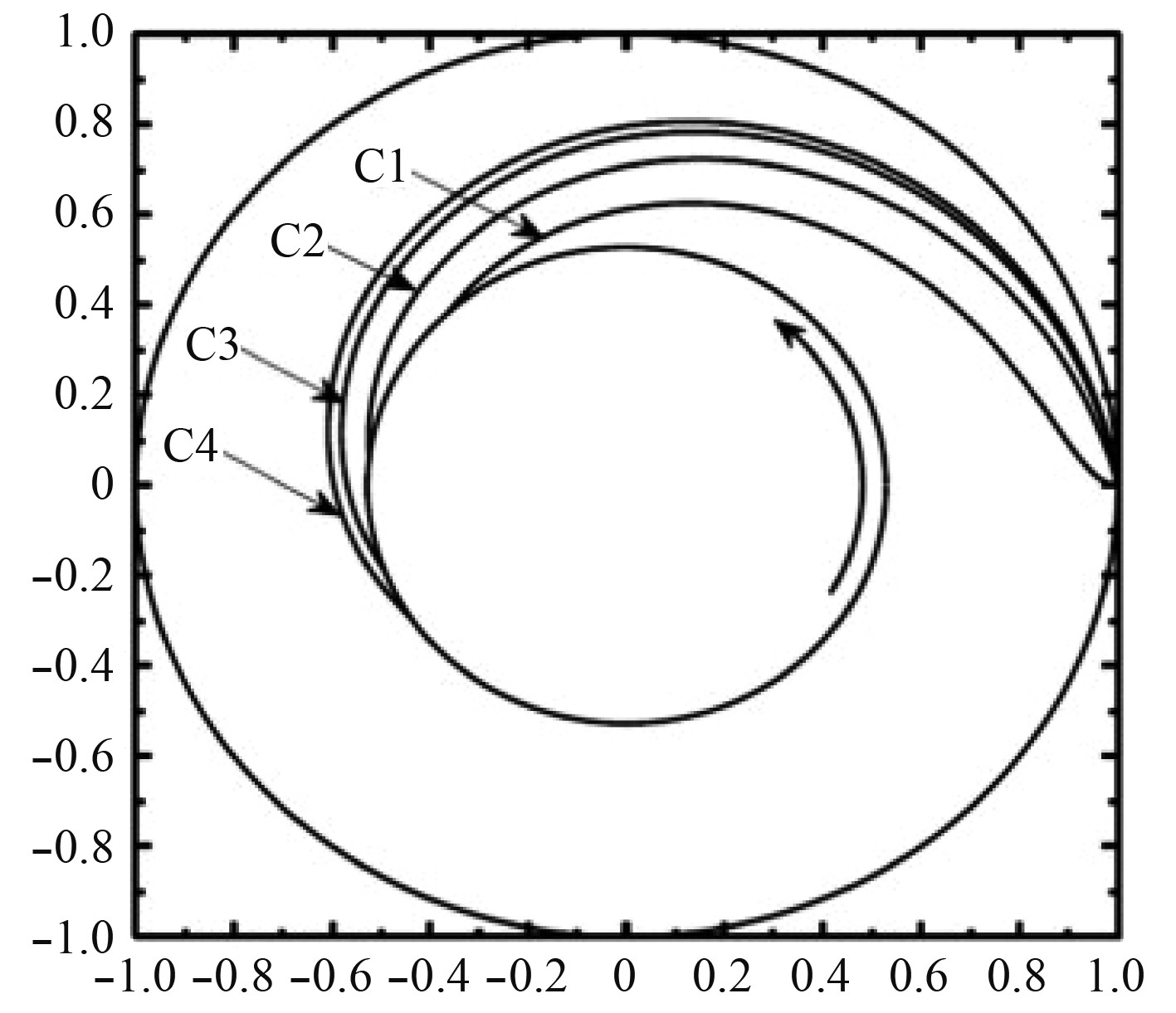
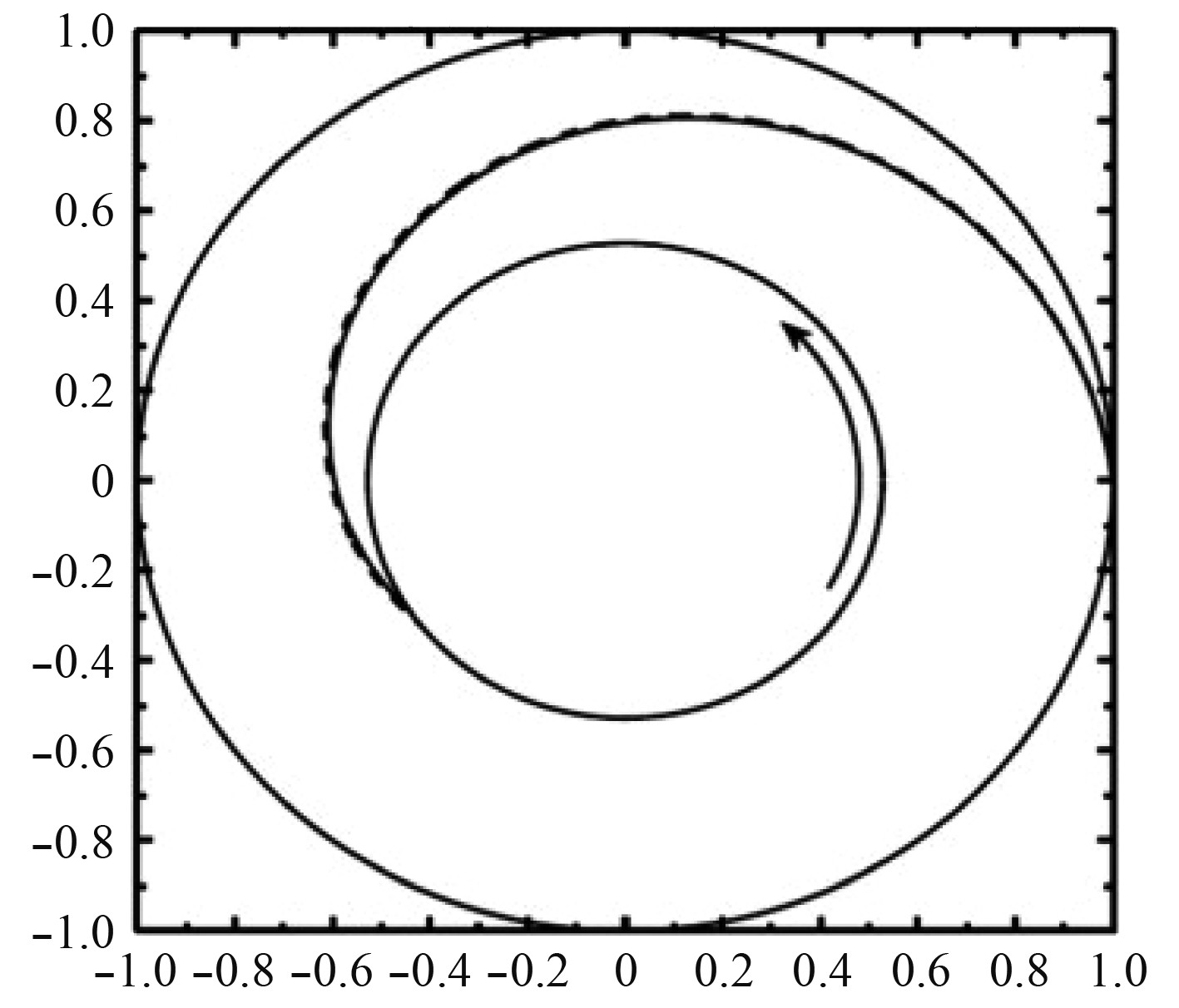
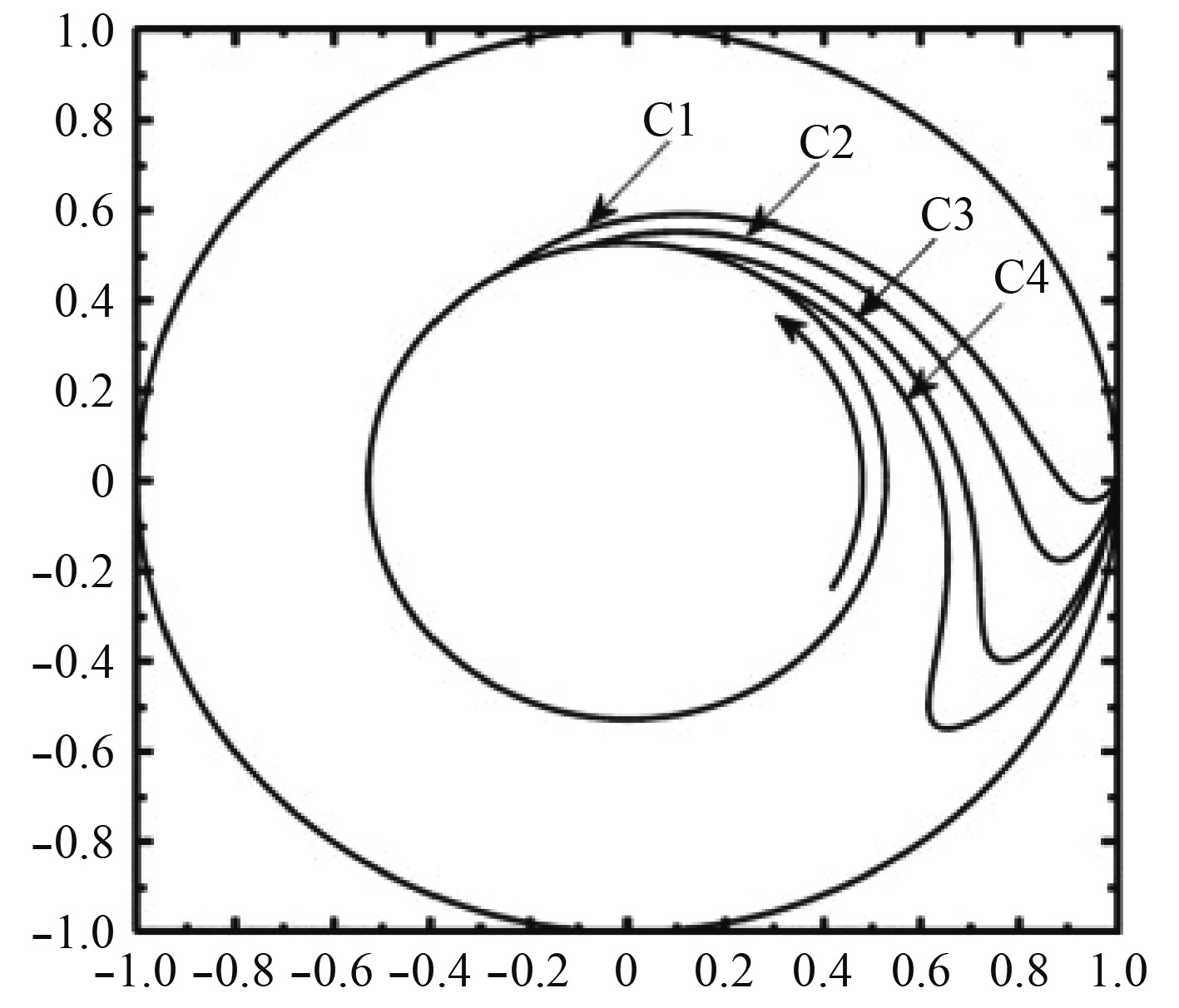
为确认影响特斯拉涡轮机内流体流动路径的因素,Sengupta等[19]采用三维CFD仿真的方法,使用Fluent研究了特斯拉涡轮机内部的三维流场和流动路径,对其进行了精细的流体动力学分析,并用纳维叶-斯托克斯方程验证简化的分析模型,得到结果如图2 ~ 图4所示。当切向速度比γ(转子入口流体的平均绝对切向速度与圆盘旋转速度的比值)大于1时,长度、形状和速度方向对相对流动路径的影响很小,甚至当切向速度比γ大于10时,相对流动路径几乎不再受到这些因素的影响,而当切向速度比γ小于1时,这些因素对相对流动路径的影响将十分显著。
为解决特斯拉涡轮机中流体能量在喷嘴处的过度损失问题,Neckel等[20]针对喷嘴的优化问题,采用Ansys-CFX的剪切应力传递模型设计并制造了一种新型喷嘴,以提高流体的喷射效率,并得出结论,平面喷嘴发散区域内的内部通量会因不对称的分离而扩大,为特斯拉涡轮机的几何聚合型喷嘴参数设计提供了有价值的参考。
为研究特斯拉涡轮机受工质影响的程度,Sengupta等[21]使用Fluent将纳米流体(最大体积分数为0.05的铁颗粒水溶液)作为特斯拉涡轮机的工质,并对特斯拉涡轮机圆盘间隙间流动的流体进行了流场仿真,在保持其他影响因素不变的条件下,从0开始逐渐增加铁颗粒的体积分数,通过计算速度场、压力场和流体路径得到相应的输出功率的增益,结果如图5所示。当纳米颗粒的体积分数增加到0.05时,输出功率的增益超过了30%,而涡轮机的效率没有发生显著变化,为在不影响涡轮机效率的情况下实现输出功率的增益提供了可行方案。
2.3 特斯拉涡轮机运行效率分析方法1)截断级数代换法[22],即通过开发一种扰动流解和迭代方案的程序,提高雷诺数的解决方案。程序的运行结果取决于雷诺数和质量流率这2个参数,其得到的结果通常是渐近解。为得到进一步准确结果,需要补充圆盘外径、切向速度等其他参数。使用截断级数代换法的问题通常只需要少量参数就能解决,但同时也造成精确度不高的后果;
2)批量参数分析法[23 – 24],即针对转子内流动过程和多盘泵的极限性能和效率的一种“先近似”分析法。在无量纲参数的基础上,给出了大量的几何和流量参数,通过数值计算得到方程的解。但由于摩擦因素概念的缺失,批量参数分析法在绝大多数情况下用处不大[25]。
3 特斯拉涡轮机的关键问题 3.1 特斯拉涡轮机的层流边界层稳定性问题层流边界层稳定性的降低会影响到涡轮机的运行效率,理论上,通常假定特斯拉涡轮盘之间流动的流体是层流,然而,当转子高速旋转导致压力下降时,这种假设就不成立了。为了找出层流理论的适用性及在转子高速运转情况下圆盘之间的流动情况,需要进行详细的稳定性研究。
有诸多文献描述了2个旋转圆盘之间流动的各种情况,Gregory[26],Faller和Kaylor[27]等描述了高速旋转圆盘边界层的2种不稳定类型。第1种类型是由于粘性不稳定而产生的,第2种类型是因为屈曲失稳而产生的。尽管两者在流向、相速度和波长上都不同,但是其表征的不稳定性都是以漩涡的常规系统形式出现在边界层中的。Savas[28 – 29]在Bödewadt层中观察到这2种不稳定类型的不稳定形式[30],即具有分离边界层的圆盘之间的流动不稳定形式(对应第1种不稳定类型)通常以内部传播圆波的形式出现,而随着雷诺数的增加,将产生漩涡,并与圆波同时存在[31 – 32];具有合并边界层的圆盘之间的流动不稳定形式(对应第2种不稳定类型)通常以局部点或孤立波的形式出现[33],而随着雷诺数的增加,若干湍流结构将叠加产生短波漩涡。
为了区分在不同旋转流动过程中可能出现的不稳定模式,Gauthier等[34]研究了共旋流动、弱反向旋转流动和高反向旋转流动过程,并在共旋流动和弱反向旋转流动中都观察到了轴对称传播螺旋和正向螺旋2种不稳定模式,而只有在高反向旋转流动过程中,才观察到了第3种类型不稳定模式,表现为负向螺旋。分析结果表明,与转子-定子系统相比,共旋流动和弱反向旋转流动情况下的2种不稳定模式在性质上是相同的,但是负向螺旋只会在高度反向旋转流动中产生。
研究者确认了层流及湍流可能出现的区域,并将圆盘之间的流动作了进一步的划分,Murata等[11]在实验中观察到,除了在进口处和出口处的一些小区域会出现湍流外,特斯拉涡轮机的圆盘间隙内的流动一般为层流。Rice[23]通过实验进一步将特斯拉涡轮机圆盘之间流动分为层流、回流区层流、湍流、过渡流和反向过渡流等5种状态。Wu[35]经过实验计算验证了Nendl所提出的理论[36 – 37],并认为粘几何数Δ(visco-geometric number)最充分地描述了流动体系,通过集合所有可用的实验和分析证据后界定:如果根据粘几何数计算出结果小于10时,流体为层流;在10 ~ 20之间时,流体为过渡流;大于20时,流体为湍流。虽然上述方案都能在一定程度上确定在不同工质和不同转速情况下圆盘之间的流动情况,但是目前特斯拉涡轮机的圆盘之间的流体稳定性分析还没有彻底完成,计算的精度不高,需要进行进一步的定量分析,以精确地判断在不同的工况下,特斯拉涡轮机的圆盘之间的流动的类型。
| $ \Delta = \frac{{{v_r} \cdot {b^2}}}{{v \cdot r}}\text{。} $ |
式中:vr为流体的动力粘度,Pa·s;b为圆盘间的间距,mm;v为流体的运动粘度,m2/s;r为圆盘间空间的一般径向坐标,mm
3.2 特斯拉涡轮机的整机运行效率问题材料设计和成型技术的进步为解决此前制约特斯拉涡轮机应用发展的圆盘耐受性问题(即圆盘在高负荷运转下容易发生翘曲的问题)提供了完善的应对方案,现阶段制约特斯拉涡轮机运行效率的因素主要包括:涡轮机中的各项具体设计参数(如流量、压力等)的影响;能量和压力在喷嘴和进口等其他部件及结构上的损失。
根据Rice[25]实验的结果分析,流体为层流状态时的运行效率可以达到95%以上,以水为工作介质可以达到10.7%的效率[7],而想要达到较高的转子效率,则必须降低流体的流量。根据不同喷嘴—转子仿真系统在使用不同设计参数时的转子效率(见表1),通过数值分析可以总结出转子的最高效率是在低流速和低压力的情况下实现的[38]。
|
|
表 1 使用不同流体输出最大功率时的具体参数[38] Tab.1 Specific parameters for maximum power output using different fluids[38] |
Rice[23]对特斯拉涡轮机进行了进一步的实验和分析,通过用9个圆盘组成了一个转子,其外半径为88.9 mm,圆盘间隙间距为1.59 mm,圆盘之间的各个间隙通过单个喷嘴单独供应空气,空气进入温度约为37.8 ℃,该喷嘴指向与圆盘的切向方向成15°的角度,从该涡轮机的测试中得到了如表2所示的一组数据。
|
|
表 2 优化参数前涡轮机的代表性性能数据[23] Tab.2 Representative performance data of turbine before optimizing parameters[23] |
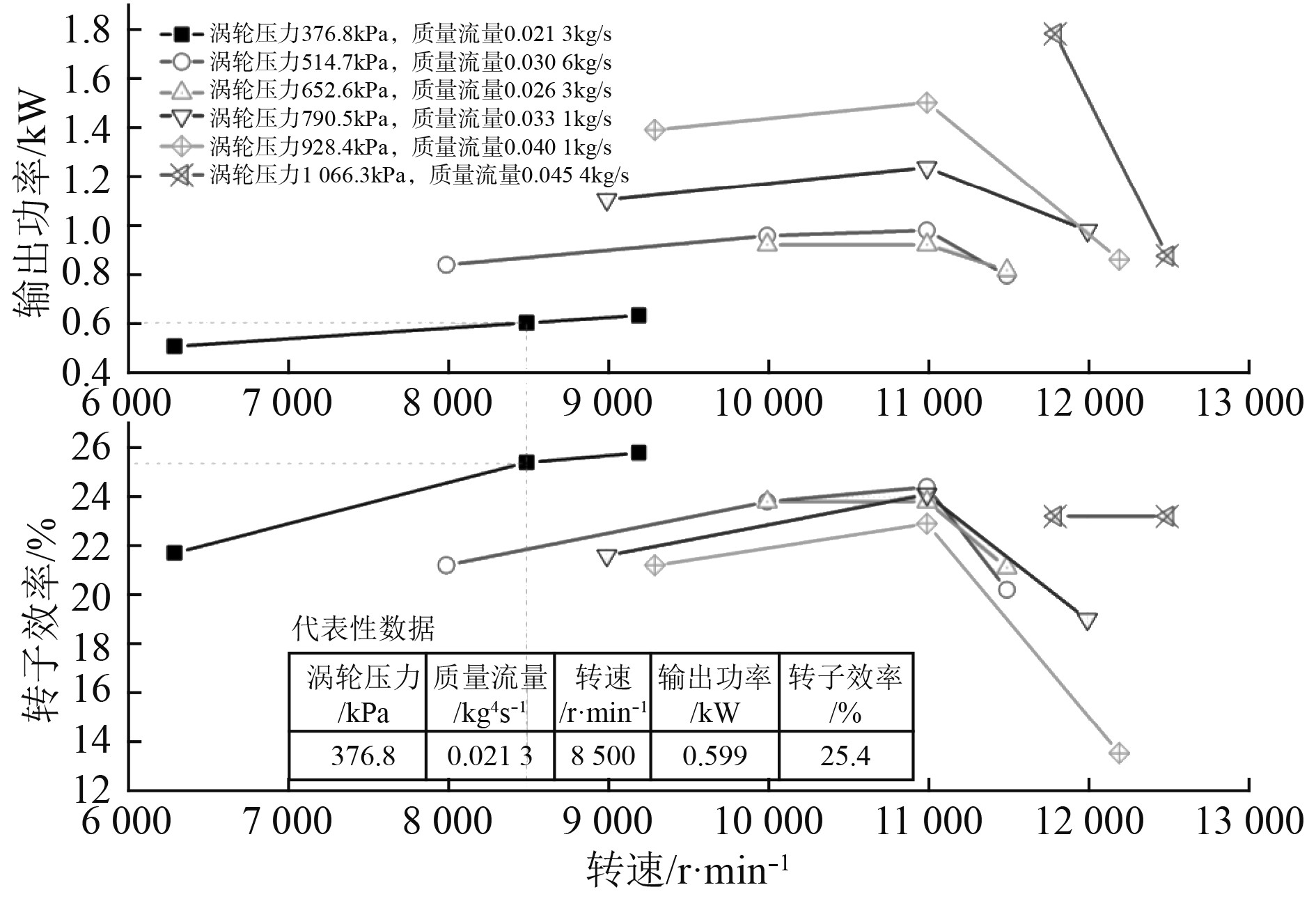
根据上一组实验数据分析,通过将圆盘的数量增加到11,并且将圆盘之间的间隙间距减小到1.02 mm来进一步修改相同的涡轮机,保持整个转子宽度基本上与原始护罩中的相同。喷嘴角度重新排列为10°,以便产生更高的喷嘴出口速度,从而改善涡轮机性能,对比数据如图6所示。
|
图 6 优化参数后涡轮机的代表性性能数据[23] Fig. 6 Representative performance data of turbine after optimization parameters[23] |
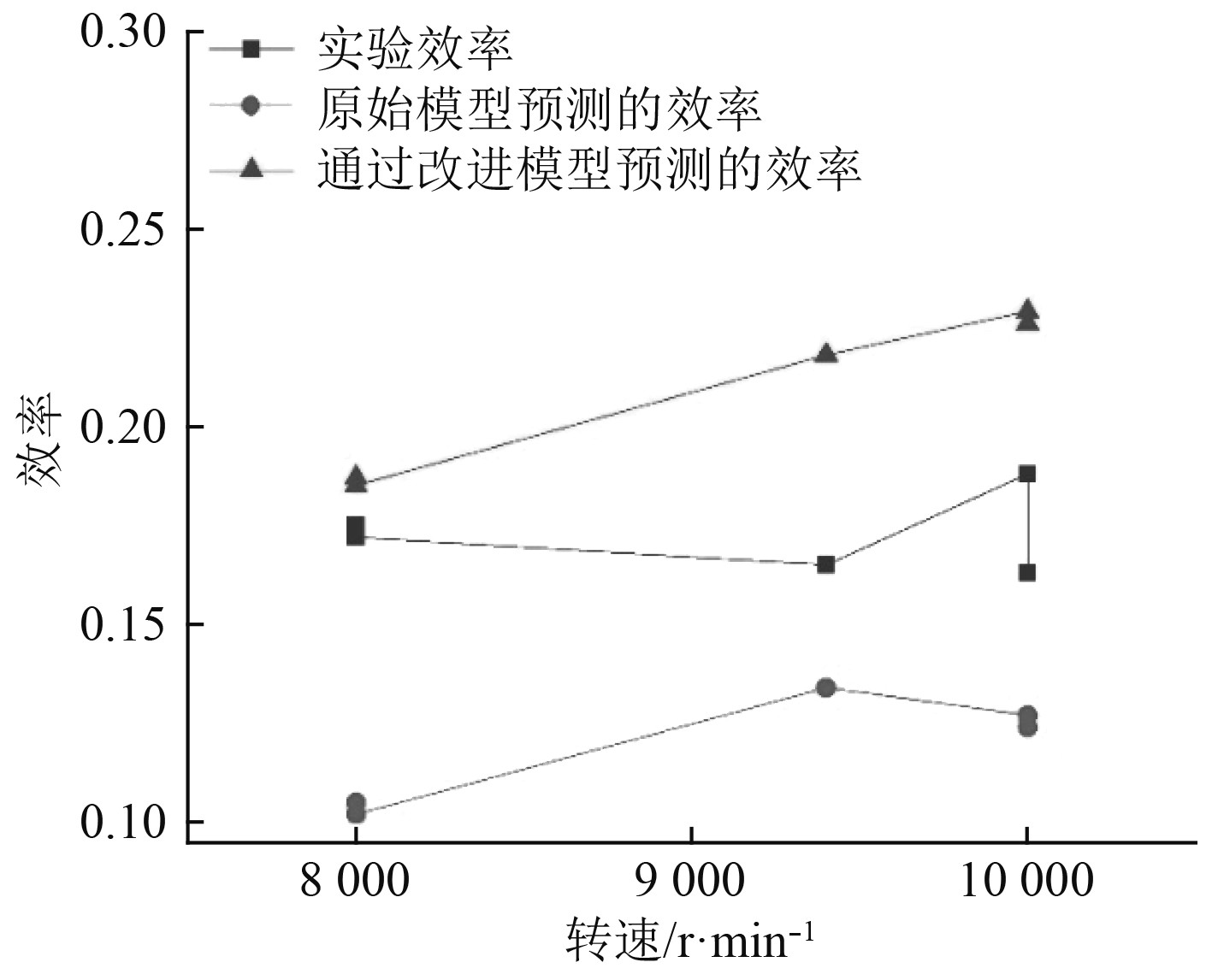
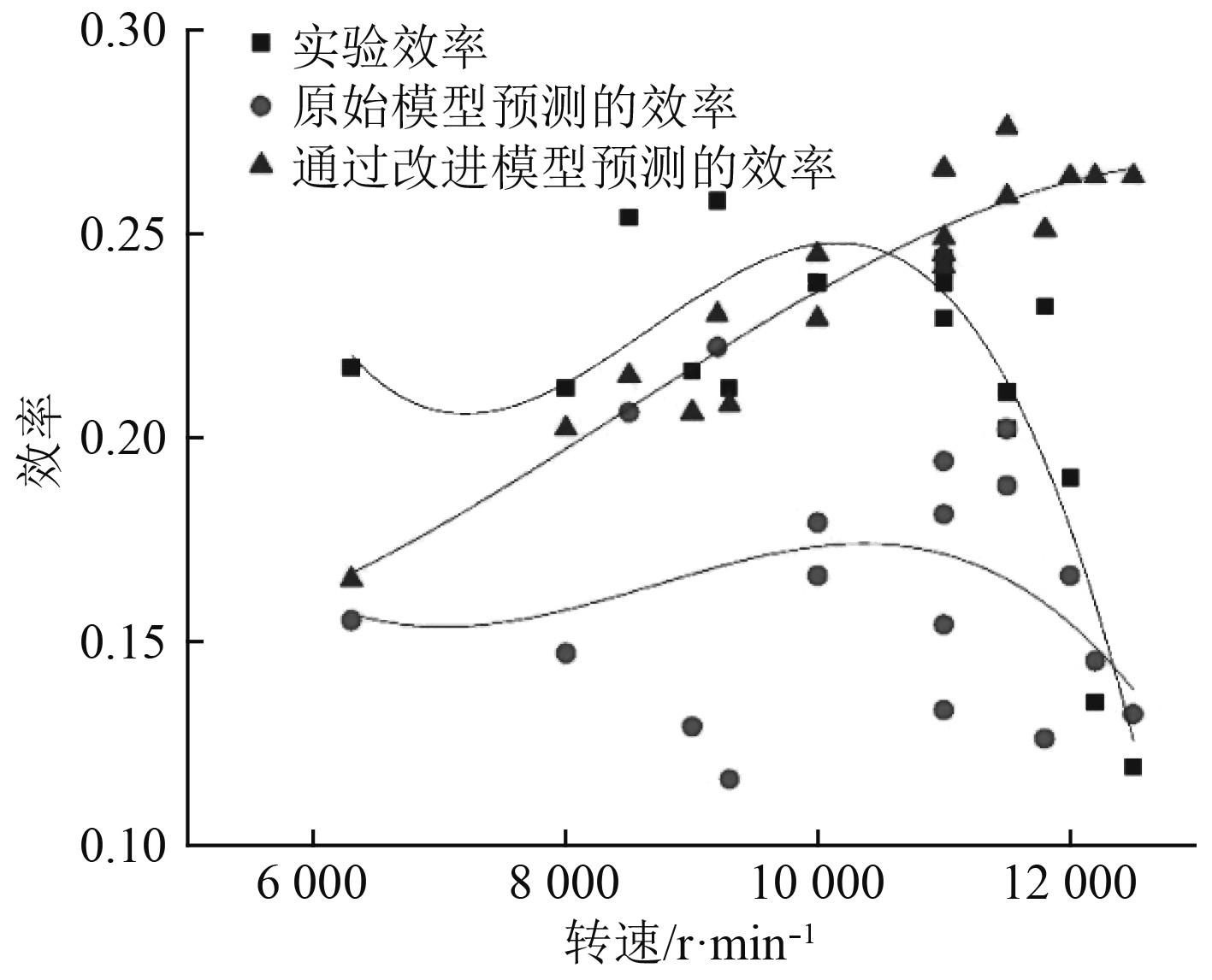
在Rice完成工作的基础上,顾春伟等[39]对Rice的一维模型进行了改进,并得到了如图7和图8所示的2组对照数据。结果表明在Rice的模型中,喷嘴出口速度受限于声速,流速会在喷嘴喉部降低。而在改进模型中,改进的喷嘴可以允许超音速流动并引入极限膨胀比来改进模型,使得喷嘴出口流速更合理,对涡轮机性能有显着影响。
|
图 7 优化参数前实验效率预测对比[49] Fig. 7 Prediction of experimental efficiency before optimization of parameters[49] |
|
图 8 优化参数后实验效率预测对比[49] Fig. 8 Prediction of experimental efficiency after optimization of parameters[49] |
由图8中数据可以判断出,对于中低转速范围,改进模型预测的特斯拉涡轮效率与实验结果吻合良好。然而,在高转速范围(高于11 500 r/min)内,实验结果表明特斯拉涡轮机效率显着下降。通过在改进模型中采用正常冲击波相关性来评估冲击损失效应并确定转子入口处的切向参数,将多组数据通过计算机仿真。得到的结果表明,在高转速条件下,切向冲击波引起的流量损失是突然降低效率的原因,证实了在一维模型也需要考虑流体工质的压缩性。
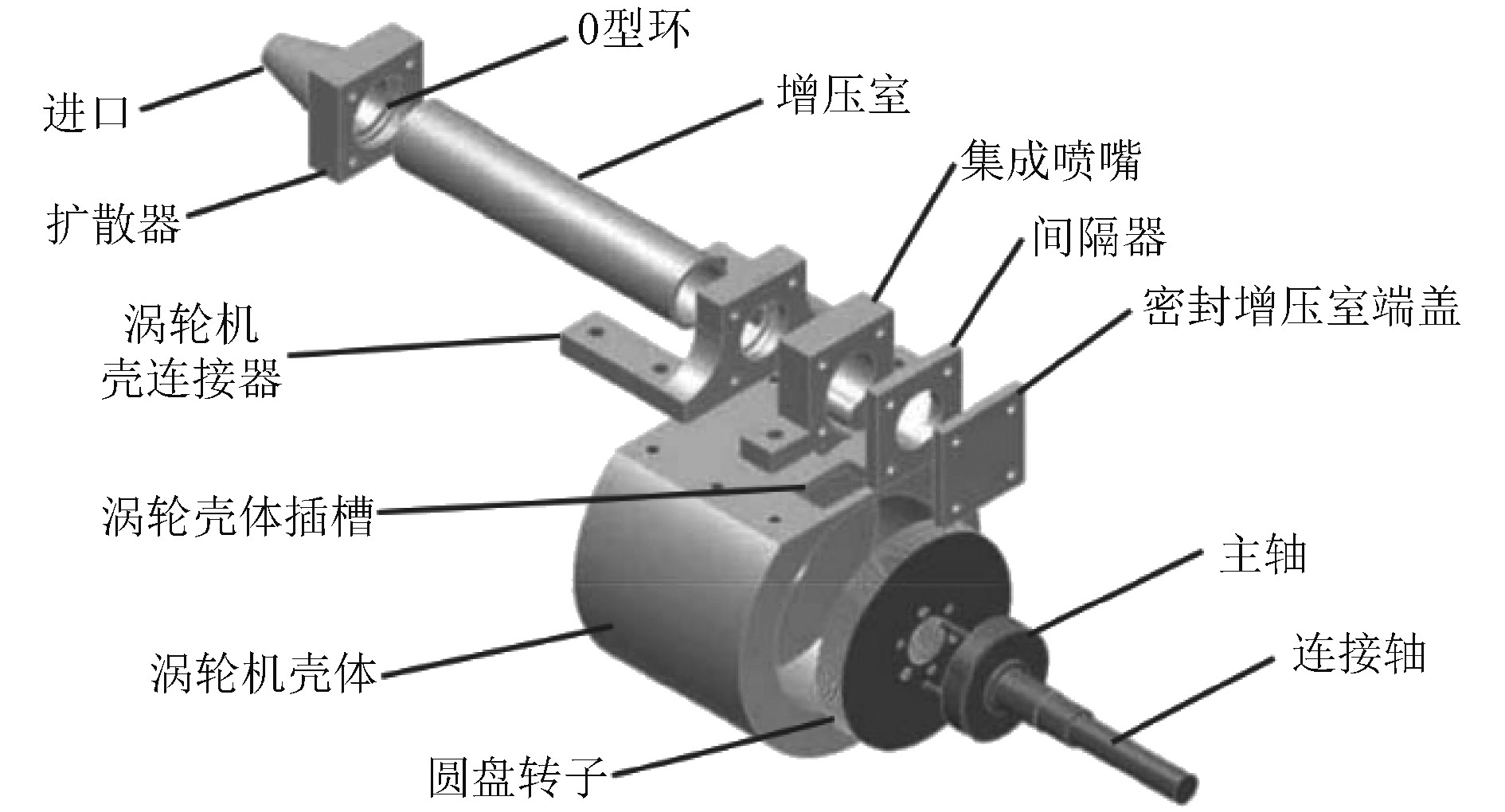
Guha[40]通过对特斯拉涡轮机效率损失主要来源的系统研究,发现喷嘴和进口的性能是特斯拉涡轮机整体效率的一个限制因素(损失约占13% ~ 34%),为了优化特斯拉涡轮机的进气性能,设计并测试了一种利用增压室完成进气的新型喷嘴(见图9),实验测定的喷嘴和入口压力损失小于1%。该设计仅需要对套管进行微小改变,就能实现将增压室和喷嘴集成到特斯拉涡轮机上,并可以通过将喷嘴设计成其他几何形状,以研究流体喷射到转子中的方式整体机器效率的影响,为研究转子效率提供了可行方案。
|
图 9 利用气室完成进气的新型喷嘴[40] Fig. 9 A new type of nozzle that uses the air chamber to complete the air intake[40] |
本文综述了特斯拉涡轮机的发展现状,列举了国内外学者在各个领域进行的特斯拉涡轮机取代传统涡轮机的探索性实验,总结了逐步完善的研究方法理论体系,综述了特斯拉涡轮机研究需要解决的关键问题,即层流边界层的稳定性问题和运行效率问题,建议对特斯拉涡轮机进一步进行以下研究:
1)特斯拉涡轮的工质为纳米流体时,只有当流量参数的选择合适时,才能够保证在实现最高效率值的同时,提供足够高的输出功率,因此流量参数的优化设计有待开展。
2)特斯拉涡轮机的喷嘴实现增压并保障流体均匀平稳喷出,将进一步提升机体运行效率。
3)特斯拉涡轮机的圆盘之间的流体稳定性分析还没有彻底完成,计算的精度不高,需要完成进一步的定量分析。
4)特斯拉涡轮机的进口处产生的湍流会严重影响机体运行的平稳性,需要对涡轮机进口进行优化设计以降低湍流出现的频率。
| [1] |
KAUFUI V WONG, OMAR De Leon. Applications of nanofluids: current and future[J]. Advances in Mechanical Engineering, 2010, 2010(2): 519659-519670. |
| [2] |
AGRAWAL S K, Gardner G, Pledgie S. Design and fabrication of an active gravity balanced planar mechanism using auxiliary parallelograms[J]. Journal of Mechanical Design, 2001, 123(4): 525-528. DOI:10.1115/1.1413771 |
| [3] |
STEIDEL R, WEISS H. Performance test of a bladeless turbine for geothermal applications: UCID-17068[R]. Lawrence Livermore Laboratory, 1974.
|
| [4] |
ALOIS P, ROLF V, VOLKER M K. Performance analysis of a miniature turbine generator for intracorporeal energy harvesting[J]. ASME, 2014, 136(8): 81101-81110. |
| [5] |
LAMPART P, KOSOWSKI K, PIWOWARSKI M, et al. Design analysis of tesla micro-turbine operating on a low-boiling medium[J]. Polish Maritime Research, 2009, 16(Special): 28-33. |
| [6] |
CAREY V P. Assessment of Tesla turbine performance for small scale solar rankine combined heat and power systems[J]. Journal of Engineering for Gas turbines and Power, 2010, 132(12): 122301-122309. DOI:10.1115/1.4001356 |
| [7] |
CHOON T W, RAHMAN A A, JER F S, et al. Optimization of Tesla turbine using computational fluid dynamics approach, 12442761[R]. Langkawi: Industrial Electronics and Applications (ISIEA), IEEE Symposium, 2011.
|
| [8] |
HASAN, ALI M. Investigating the possibility of using a tesla turbine as a drive unit for an automotive air-conditioning compressor using CFD modeling[J]. ASHRAE Transactions, 2016, 122(1): 146-158. |
| [9] |
SONG Jian, GU Chun-wei, LI Xue-song. Performance estimation of Tesla turbine applied in small scale organic rankine cycle (ORC) system[J]. Applied Thermal Engineering, 2017, 110(1): 318-326. |
| [10] |
DAMODHAR R, MRUTHYUNJAYA K N, NAVEEN, et al. Design and fabrication of portable water turbine[J]. International Research Journal of Engineering and Technology, 2017, 4(6): 56-72. |
| [11] |
MURATA S, YUKATA M, YOSHIYUKI. A study on a disk friction pump[N], Bulletin of the Japanese Society of Mechanical Engineers, 1976-02-25(354).
|
| [12] |
HARWOOD P. Further investigation into Tesla turbomachinery[R]. Senior Project Report, Mechanical Engineering Department, University of Newcastle, United Kingdom, 2008.
|
| [13] |
DEAM R T, LEMMA E, MACE B, et al. On scaling down turbines to millimeter size[J]. Journal of Engineering for Gas Turbines & Power, 2008, 130(5): 819-825. |
| [14] |
TALLURI L, FIASCHI D, NERI G, at el. Design and optimization of a Tesla turbine for ORC applications[J]. Applied Energy, 2018, 226: 300-319. DOI:10.1016/j.apenergy.2018.05.057 |
| [15] |
HOYA G P, GUHA A. The design of a test rig and study of the performance and efficiency of a Tesla disc turbine[J]. Proceedings of the Institution of Mechanical Engineers, Part A: Journal of Power and Energy, 2009, 223(4): 451-465. DOI:10.1243/09576509JPE664 |
| [16] |
COUTO H S, DUARTE J B F, BASTOS-NETTO D. The Tesla turbine revisited[R]. Sochi: 8thAsia-Pacific International Symposium on Combustion and Energy Utilization, 2006.
|
| [17] |
GUHA A, SENGUPTA S. A non-dimensional study of the flow through co-rotating discs and performance optimization of a Tesla disc turbine[J]. Proceedings of the Institution of Mechanical Engineers, Part A: Journal of Power and Energy, 2017, 231(8): 721-738. DOI:10.1177/0957650917715148 |
| [18] |
ENGIN T, ÖZDEMIR M, ÇEMECI S. Design, testing and two-dimensional flow modeling of a multiple-disk fan[J]. Experimental Thermal & Fluid Science, 2009, 33(8): 1180-1187. |
| [19] |
SENGUPTA S, GUHA A. Analytical and computational solutions for three-dimensional flow-field and relative pathlines for the rotating flow in a Tesla disc turbine[J]. Computers & Fluids, 2013, 88(11): 344-353. |
| [20] |
NECKEL A L, GODINHO M. Influence of geometry on the efficiency of convergent-divergent nozzles applied to Tesla turbines[J]. Experimental Thermal & Fluid Science, 2015, 62(62): 131-140. |
| [21] |
SENGUPTA S, GUHA A. Flow of a nanofluid in the microspacing within co-rotating discs of a Tesla turbine[J]. Applied Mathematical Modelling, 2016, 40(1): 285-499. |
| [22] |
MATSCH L, RICE W. An asymptotic solution for laminar flow of an incompressible fluid between rotating disks[J]. Journal of Applied Mechanics, 1968, 35(2): 155-159. |
| [23] |
RICE W. An analytical and experimental investigation of multiple-disk turbines[J]. Journal of Engineering for Gas Turbines & Powe, 2014, 87(1): 29-36. |
| [24] |
SCHROEDER H B. An investigation of viscosity force in air by means of a viscosity turbine[R]. BAE Thesis, Rensselaer Polytechnic Institute, 1950.
|
| [25] |
RICE W. Tesla turbomachinery[M]. Handbook of Turbomachinery, 2003: 861-874
|
| [26] |
GREGORY N, STUART J T, WALKER W S. On the stability of three dimensional boundary layers with application to the flow due to a rotating disk[J]. Philosophical Transactions of the Royal Society B Biological Sciences, 1955, 248(943): 155-199. DOI:10.1098/rsta.1955.0013 |
| [27] |
FALLER A J, KAYLOR R E. Numerical study of the instability of the laminar ekman boundary layer[J]. Journal of the Atmospheric Sciences, 1966, 23(4): 466-480. |
| [28] |
SAVAS Ö. On flow visualization using reflective flakes[J]. Journal of Fluid Mechanics, 1985, 152(152): 235-248. |
| [29] |
SAVAS Ö. Stability of bödewadt flow[J]. Journal of Fluid Mechanics, 1987, 183(183): 77-94. |
| [30] |
PIKHTOV S V, Smirnov E M. Boundary layer stability on a rotating disk with corotation of the surrounding fluid[J]. Fluid Dynamics, 1992, 27(5): 657-663. |
| [31] |
SCHOUVEILER L, GAL P L, CHAUVE M P. Stability of a traveling roll system in a rotating disk flow[J]. Physics of Fluids, 1998, 10(11): 2695-2697. DOI:10.1063/1.869793 |
| [32] |
SERRE E, CRESPO DAE, BONTOUX P. Annular and spiral patterns in flows between rotating and stationary discs[J]. Journal of Fluid Mechanics, 2001, 434(434): 65-100. |
| [33] |
SANK′OV P I, SMIRNOV E M. Bifurcation and transition to turbulence in the gap between rotating and stationary parallel disks[J]. Fluid Dynamics, 1984, 19(5): 695-703. |
| [34] |
GAUTHIER G. GONDRET P, MOISY F, et al. Instabilities in the flow between co- and counter-rotating disks[J]. Journal of Fluid Mechanics, 2002, 473(473): 1-21. |
| [35] |
WU P S. Evaluation of analytical models for multiple-disk pump rotor calculations[D]. M.S. Thesis, Department of Mechanical and Aerospace Engineering, Arizona State University, 1986.
|
| [36] |
NENDL D. Dreidimensionale laminare instabilitäten bei ebenen wänden[J]. Z. Angew. Math. Mech, 1973, 56(56): 211-213. |
| [37] |
NENDL D. Reibungsturbine[J]. VDI-Berichte, 1973, 193(193): 287-293. |
| [38] |
KRISHNAN V G, IQBAL Z, MAHARBIZ M M. A micro Tesla turbine for power generation from low pressure heads and evaporation driven flows[C]. China: The 16th International Conference on Solid-State Sensors, Actuators and Microsystems, 2011: 1851-1854.
|
| [39] |
SONG Jian, REN Xiao-dong, LI Xuesong, et al. One-Dimensional model analysis and performance assessment of Tesla turbine[J]. Applied Thermal Engineering, 2018, 134: 546-554. DOI:10.1016/j.applthermaleng.2018.02.019 |
| [40] |
GUHA A, SMILEY B. Experiment and analysis for an improved design of the inlet and nozzle in Tesla disc turbines[J]. Proceedings of the Institution of Mechanical Engineers Part A Journal of Power & Energy, 2010, 224(2): 261-277. |
 2020, Vol. 42
2020, Vol. 42