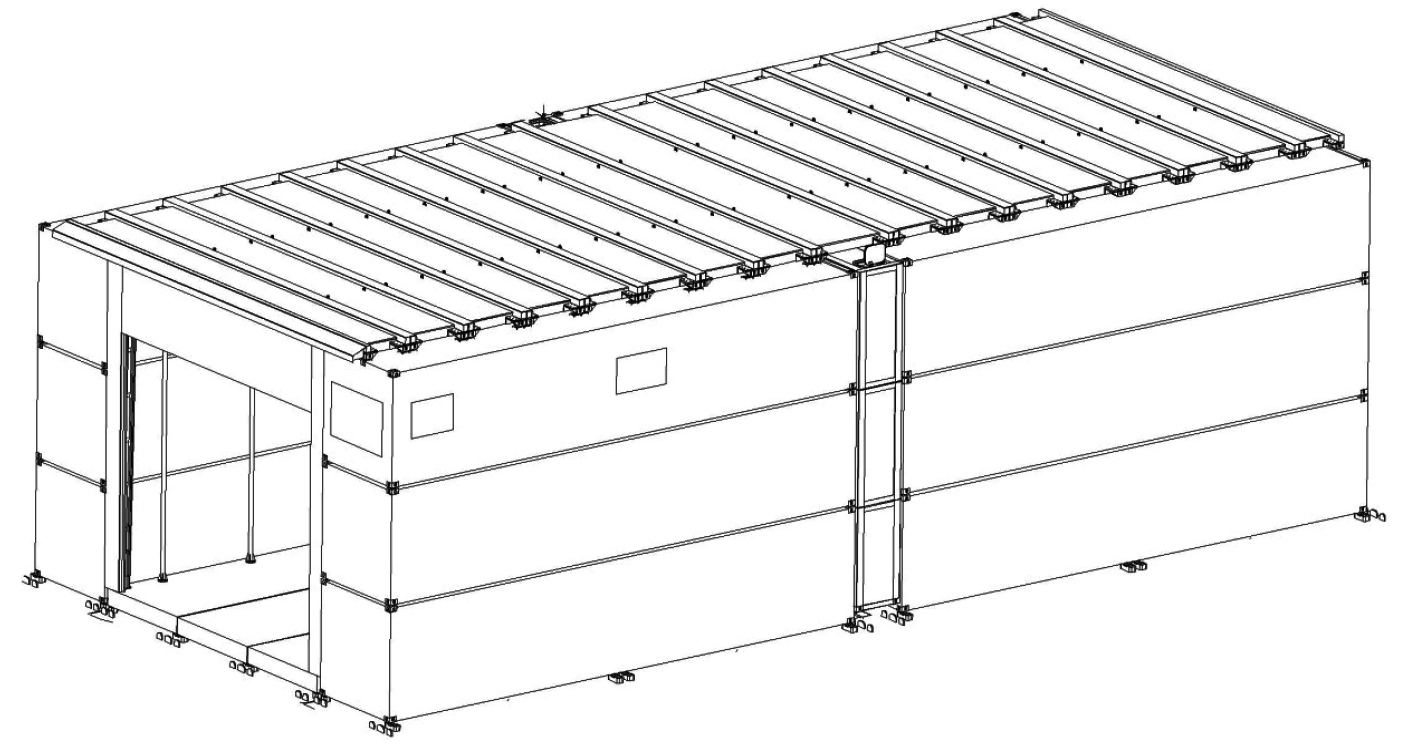
拼装式直升机机库用于加装在战时被动员征用的集装箱船等民用船舶上,在动员民船搭载舰载直升机出海执行任务时,为直升机提供船上的安全停放场所。机库主体由上下3层、前后2列集装箱垒成的机库侧壁、固定在侧壁上的机库顶板,以及机库门、后墙、梯道等组成,机库结构示意图如图1所示。侧壁上下层集装箱之间,侧壁集装箱与机库顶板之间用船用连接件拼装在一起,在机库外侧利用花篮拉杆进行斜拉绑扎,同时在集装箱端面处增加垂直绑扎,以增加抗摇、抗风能力。该机库的设计难点在于既要采用集装箱拼装式结构[1],以满足在商用状态的民船上快速加装和拆卸的要求,又要满足远海恶劣海况下的结构强度要求和风雨密要求[2]。
|
图 1 机库主体结构 Fig. 1 Main structure of hangar |
舰船上一般较少应用拼装式结构,常规的舰船机库主要是固定式机库,其结构为船体上层建筑的一部分,在舰船建造时一并完成机库建造,其结构设计和强度分析计算主要依据舰船结构设计计算方法[3],而目前采用集装箱拼装技术形式的结构物主要是陆上集装箱建筑,国外已进行了一些集装箱模块化建筑的力学性能研究[4-6],但都针对陆地上使用环境,受力情况较简单,其抗摇、抗风等标准远低于海上使用要求,目前针对船用临时拼装式机库结构特点和应用海况的可参考的强度分析计算方法较少。经过论证分析,研究提出拼装式机库结构特点和海上要求的机库整体强度分析计算方法。
1 机库受力分析 1.1 分析思路机库强度设计要求能够在海上经受长期横摇22.5°、纵摇7.5°,能够承受12级风和强度0.96 kPa,密度95.8 kg/m3,积深102 cm的雪载荷。分析计算思路为通过计算求出横、纵摇产生的横向、纵向及垂向加速度值,叠加风、雪等多种外力作用,采用有限元软件建立结构有限元模型并进行分析,选择极端工况加载边界条件和载荷进行计算,得到机库结构的应力值及位移,最终依据相关规范及所用材料强度评估机库的强度与变形。依据的规范包括:
1)CCS《钢制海船入级规范(2018版)》第2篇第7章:集装箱船结构强度及集装箱系固直接计算方法;
2)ISO 1496-1:2013《货运集装箱系列:规范和试验第1部分:一般用途货物集装箱》。
1.2 受力分析1)机库所受的力包括由于船舶的横摇、纵摇和垂荡运动所产生的惯性力,机库结构的重力,以及风压、雪载荷、系固力。
2)机库侧壁集装箱近似于空箱,集装箱上所受的力可分为Fx,Fy及Fz三个分力,如图2所示。其中ox为横摇中心轴,Fx,Fy及Fz均作用在集装箱的中心,即认为集装箱的重心位于箱的中心处,在系固计算中可接受集装箱的重心位置位于箱高的45%处。

|
图 2 机库侧壁集装箱受力 Fig. 2 Force on side-wall container of hangar |
1)船只在横摇纵摇运动状态下惯性力计算
根据已知数据,船在波浪中的运动状态如表1所示。
|
|
表 1 船只在波浪中的运动状态 Tab.1 The state of motion of the ship in waves |
最大横摇共振时候,扰动力的周期与船舶的摇摆周期一致[7]。船舶的横摇方程式为:
| ${\varphi _m} = \varphi \sin \left( {\frac{{2{\text{π}} }}{{{T_\varphi }}} + {\varepsilon _\varphi }} \right)\text{,}$ |
式中:φ为船舶最大横倾角度;Tφ为船舶横摇周期;εφ为相位差。
船舶横摇角加速度最大值为:
最大纵摇发生在共振时候,扰动力的周期与船舶的摇摆周期一致。船舶的纵摇方程式为:
| ${\theta _m} = \theta \sin \left( {\frac{{2{\text{π}} }}{{{T_\theta }}} + {\varepsilon _\theta }} \right)\text{,}$ |
式中:
船舶纵摇角加速度最大值为:
故纵摇引起的垂向加速度
2)集装箱系固计算
横向加速度at计算如下:
| $ \begin{split}{a_t} =& \left( {g + {b_v}} \right) \cdot \sin {\varphi _m} + {b_h} \cdot \cos {\varphi _m} +\\ &{\left( {\frac{{2{\text{π}} }}{{{T_\varphi }}}} \right)^2} \cdot {\varphi _m} \cdot \left( {z - {z_{ROLL}}} \right)\text{。}\end{split}$ |
式中:g为重力加速度,取9.81 m/s;bv为由纵摇和升沉引起的垂向运动的加速度,m/s;bh为由艏摇和横荡引起的横向运动的加速度,m/s;φm为船舶最大横摇角,°;z为集装箱重心位置距基线高度,m;zROLL为船舶横摇中心线距基线高度,m;z-zROLL为取10.7 m。
故at=6.19 m/s2。
垂向加速度av计算如下:
| ${a_v} = \left( {g + {b_v}} \right) \cdot \cos {\varphi _m},\;{\rm{m}}/{{\rm{s}}^2}\text{。}$ |
故av=12.168 0 m/s2。
纵向加速度al计算如下:
| ${a_l} = g \cdot \left( {0.4 - 0.001{L_{BP}}} \right)\text{。}$ |
式中:g为重力加速度,取9.81 m/s;LBP为垂线间长,m,为177 m。
故al=2.187 6 m/s2。
3)集装箱所受风载荷
强度满足12级风后不破坏,12级风风速取35 m/s,空气密度取1.25 kg/m3,风压由贝努利方程计算[8]:
| $p = \frac{1}{{2\rho {v^2}}} = 0.766\;{\rm{kN}}/{{\rm{m}}^2}\text{。}$ |
采用船舶与海洋工程专业常用MSC.Patran有限元软件建立结构有限元模型[9]。由于梯道、机库门、后墙均采用轻质材料,相对机库的总质量占比很小,且不作为承力构件,因此在建模时予以忽略。机库前后部结构和荷载相同,为简化计算对机库采取一半建模[10],分别建立了机库侧壁集装箱、机库顶板的有限元模型,其中机库侧壁由3层集装箱连接组成,机库顶板由铝合金型材框架和表面铝板组成。集装箱面板、库顶板面板等板材均采用四边形和少量的三角形板壳元模拟,集装箱框架以及库顶板框架采用梁单元模拟,整个模型共113 024个单元,有限元模型如图3所示。其中组成机库侧壁的上下层集装箱以4个角件通过连接件相固定,形成分析计算模型。

|
图 3 机库有限元模型 Fig. 3 Finite element model of the hangar |
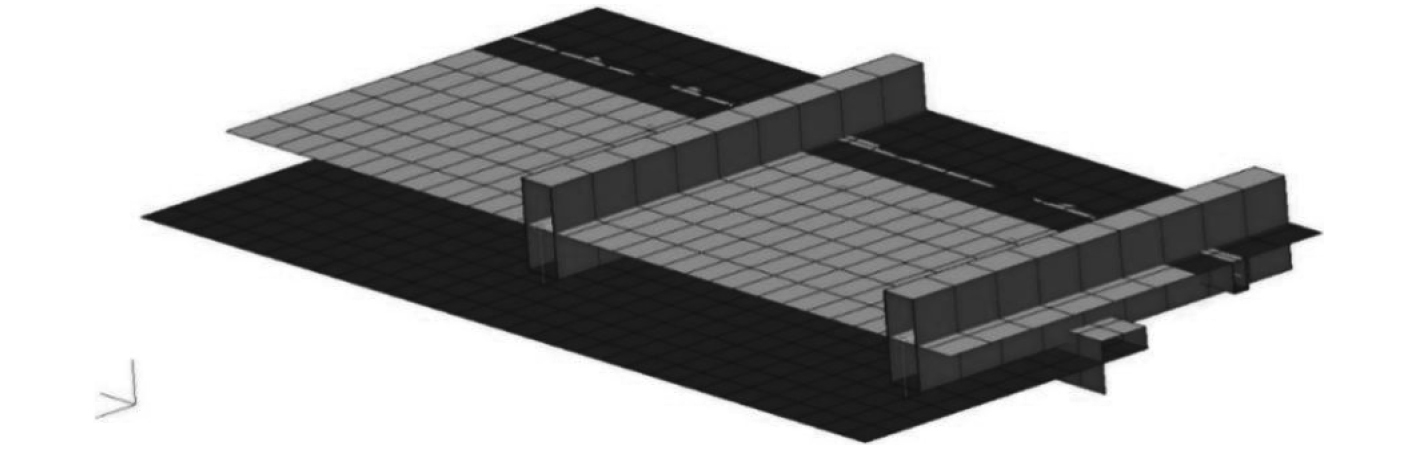
机库顶板与集装箱顶通过连接进行紧固连接,在建模中通过MPC节点连接[11],设置为位移与转角关联[12],如图4所示。
|
图 4 机库顶板有限元模型 Fig. 4 Finite element model of the hangar roof |
1)材料参数
机库侧壁集装箱材料为耐候钢,基本参数如下:
密度7 850 kg/m3;
屈服强度235 MPa;
弹性模量206 E/GPa;
泊松比0.3;
剪切模量80 E/GPa。
机库顶板材料为铝合金,基本参数如下:
密度2 700 kg/m3;
屈服强度195 MPa;
弹性模量45 E/GPa;
泊松比0.33;
剪切模量16.917 E/GPa。
绑扎器材弹性模量:
拉杆(绑扎到1层箱顶或2层箱底)14 000 kN/cm2;
拉杆(绑扎到2层箱顶或3层箱底)17 500 kN/cm2。
2)边界条件
边界条件设置如图5所示。其中受力一侧的拉杆以预应拉力的方式加载在角件上,拉力0.8 t;风压以均布力加在右侧集装箱侧壁上,如图中右侧部分,强度为0.766 kN/m2,方向垂直于集装箱侧壁;雪载以均布压力加在机库顶板表面上以及最上层集装箱的顶面上,垂直向下,强度为0.98 kN/m2。

|
图 5 模型边界条件 Fig. 5 The boundary conditions of the model |
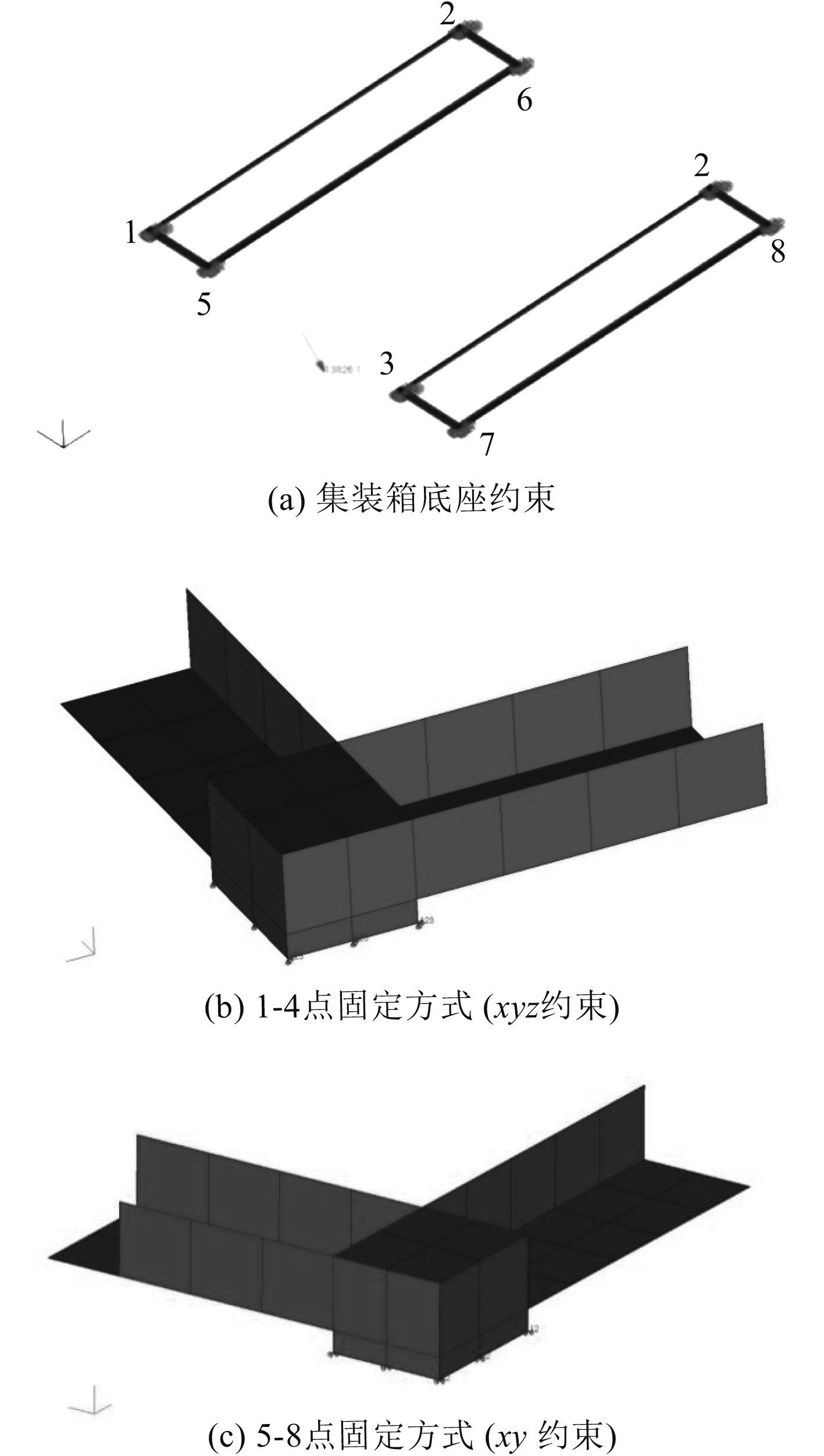
集装箱底座约束如图6(a)所示,1-4点3个方向位移约束如图6(b)所示,底座5-8点垂向位移放松,仅约束纵向和横向的位移如图6(c)所示;受拉一侧的拉杆在软件计算中未加预紧力,在强度校核时再将其加上,拉杆连接方式为铰接。
|
图 6 集装箱底座约束和固定方式 Fig. 6 Base constraints and fixing methods of container |
3)结果分析
对于板壳单元,通常以四边形单元或三角形单元应力中心点表面的最大合成应力值(中面膜应力和局部弯曲应力的叠加后计算)作为判断对象[13];对于梁单元,则以梁单元剖面上最大合成应力值作为判断对象[14]。合成应力值为按下式[15]计算所得的合成应力(Von Mises合成应力):
| $ {\sigma _0} = \sqrt {\sigma _x^2 + \sigma _y^2 - {\sigma _x}{\sigma _y} + 3\tau _{xy}^2} \text{。} $ |
式中:
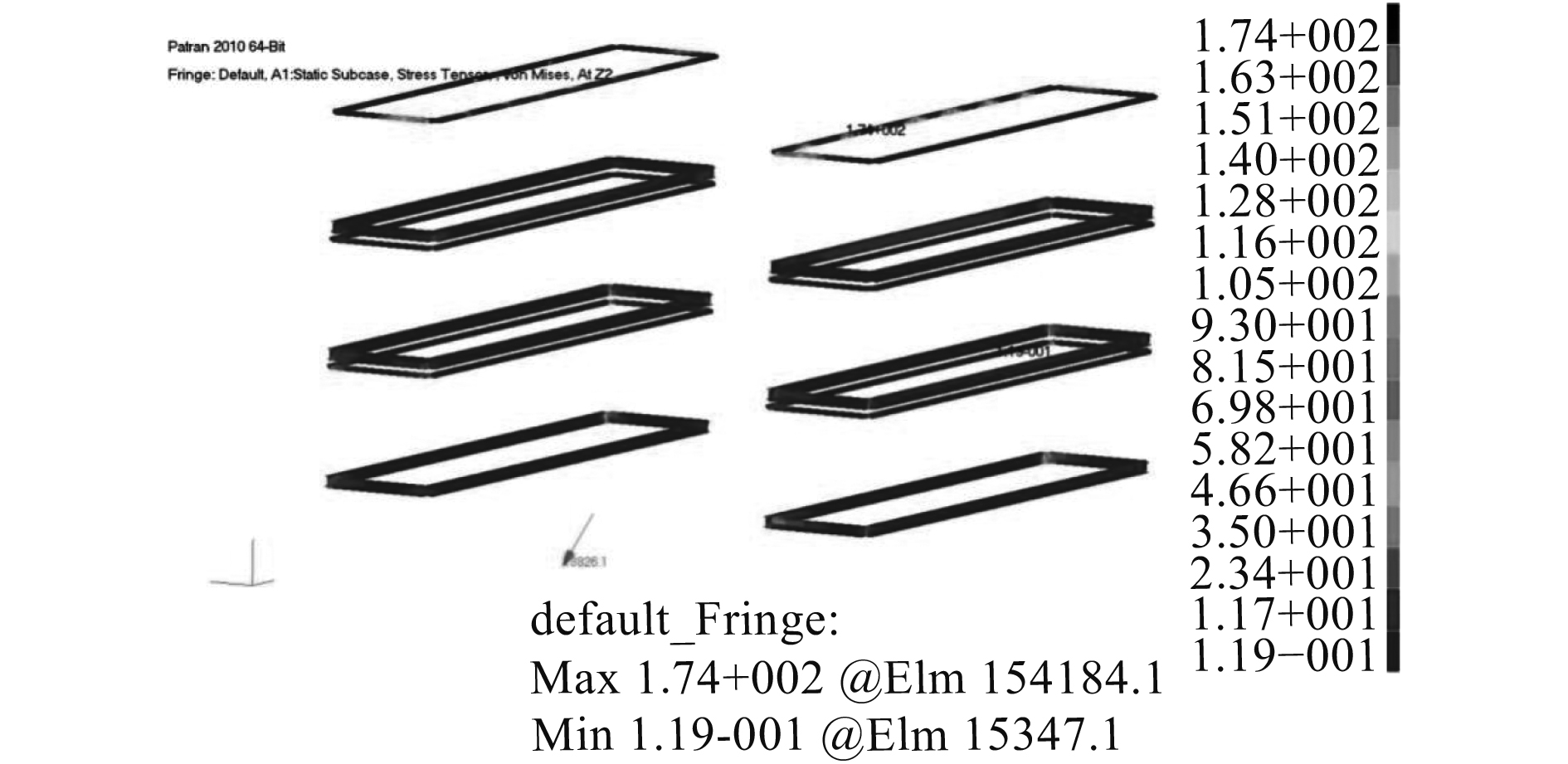
采用MSC.Patran有限元软件计算结构应力,并进行强度校核,分析计算应力云图如图7所示。其中最大应力出现在侧壁集装箱顶部的纵框架上,如图8所示。最大应力为174 MPa。侧壁集装箱材料屈服强度为235 MPa,机库侧壁结构满足强度要求。

|
图 7 机库应力云图 Fig. 7 Stress nephogram of the the hangar |
|
图 8 机库应力最大处 Fig. 8 Location of maximum stress in hangar |
机库顶板与侧壁顶部的连接通过MPC节点关联,主要受机库顶板与侧壁节点连接集中力的影响,机库顶板的应力云图如图9所示。最大应力为12.6 MPa,顶板铝合金材料屈服强度为240 MPa,机库顶板满足结构强度要求。

|
图 9 机库顶板应力云图 Fig. 9 Stress nephogram of the hangar roof |
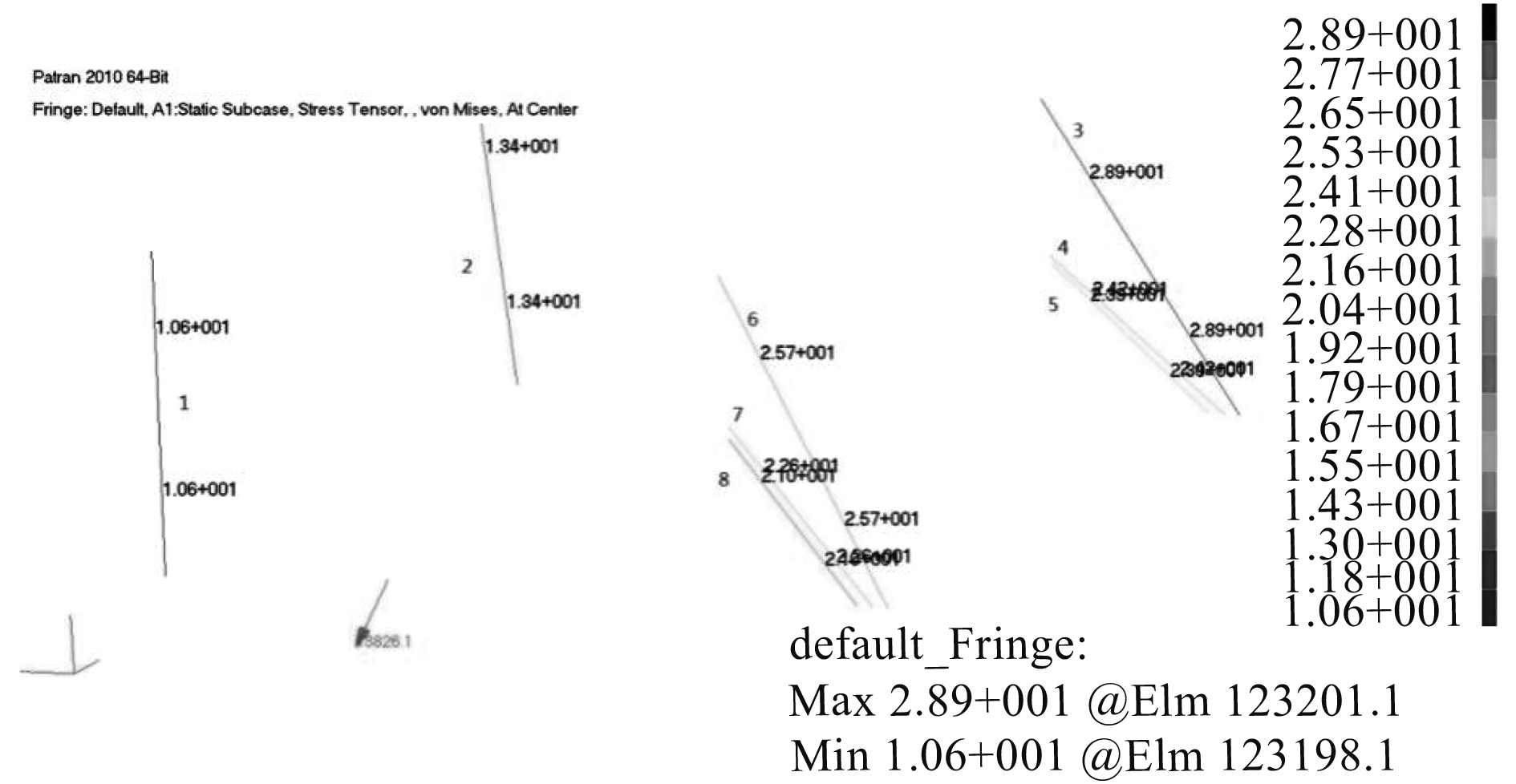
拉杆的应力仿真计算结果如图10和表2所示,最大应力为28.9 MPa。拉杆的预紧力为0.8 t,拉杆直径为25 mm,横截面积为490.625 mm2,故拉杆最大拉力为22.02 kN。
|
|
表 2 拉杆应力值 |
|
图 10 绑扎杆应力云图 Fig. 10 Stress nephogram of the lashing bars |
根据《钢制海船入级规范》,对集装箱无论采用何种系固方式,作用在集装箱上的力均应不超过集装箱的许用负荷。符合国际标准组织(ISO)标准系列的集装箱许用负荷如下:
1)作用于角件上的绑扎力:端壁或侧壁上的水平分力应不超过150 kN;
2)端壁或侧壁上的垂直分力:应不超过300 kN;
3)角件上水平分力和垂直分力的合力:应不超过300 kN。
机库集装箱拉杆总拉力最大值为22.02 kN,故角件满足绑扎力强度要求。
采用有限元软件分析计算机库结构的整体变形图,结果如图11所示。

|
图 11 机库位移云图 Fig. 11 Displace nephogram of the hangar |
机库最大变形出现在机库顶板上平面中心处,变形量为33.0 mm,此变形为弹性变形,不影响其机库整体结构强度及风雨密性。
机库侧壁顶部位移云图如图12所示。由风载荷及横向惯性力产生最大位移为4.52 mm,位于左侧集装箱角柱顶部,不影响其机库整体结构强度及风雨密性。

|
图 12 侧壁顶部位移云图 Fig. 12 Displace nephogram of the top of lateral wall |
机库侧壁框架位移云图,如图13所示。最大位移为5.51 mm。

|
图 13 侧壁框架位移云图 Fig. 13 Displacement nephogram of the frame of side-wall |
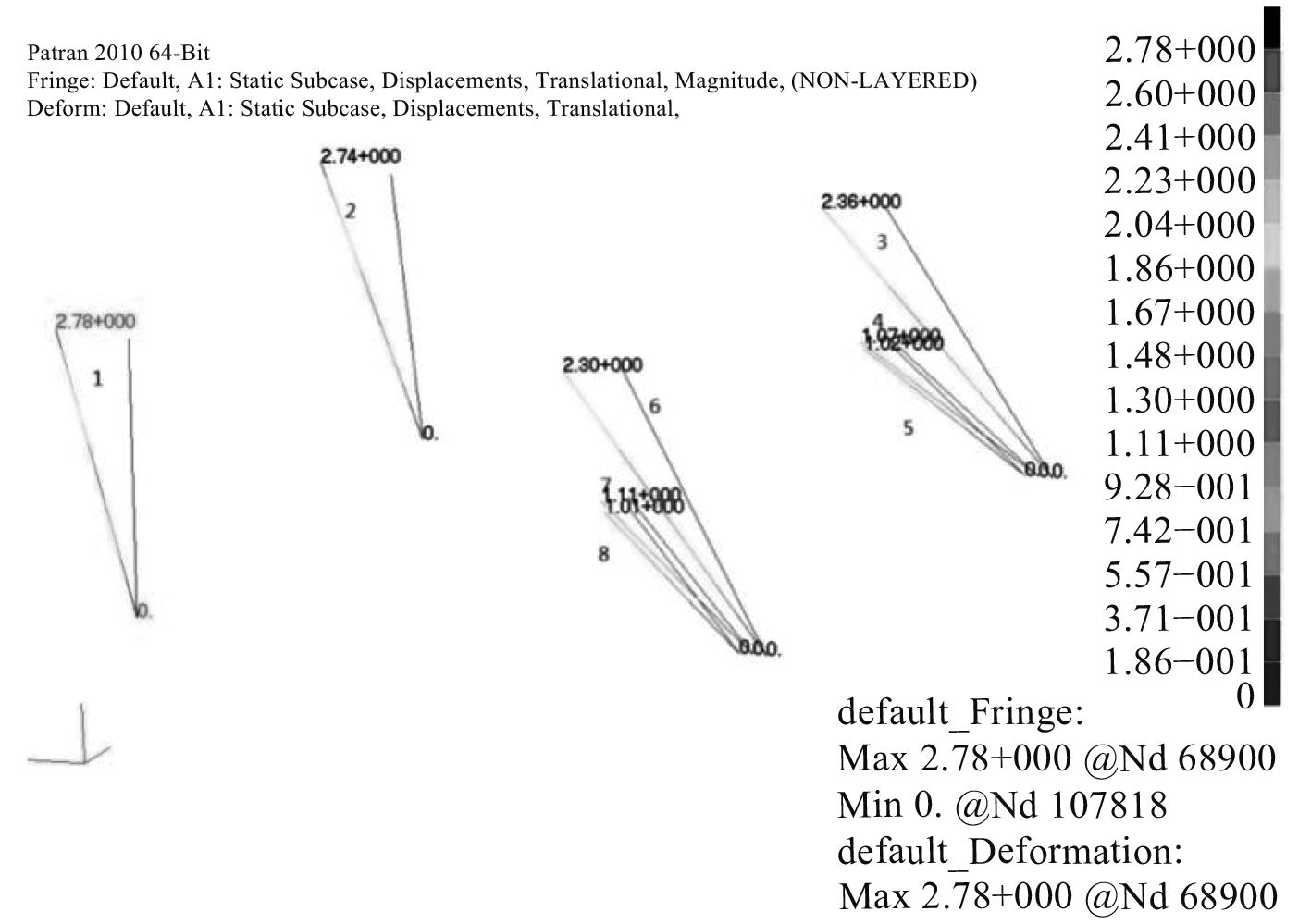
拉杆的变形如图14所示,位移值如表3所示。最大变形量为2.78 mm。
|
|
表 3 拉杆与集装箱连接点位移值 |
|
图 14 拉杆与集装箱连接点位移云图 Fig. 14 Displace nephogram of the connecting point of container and tie rod |
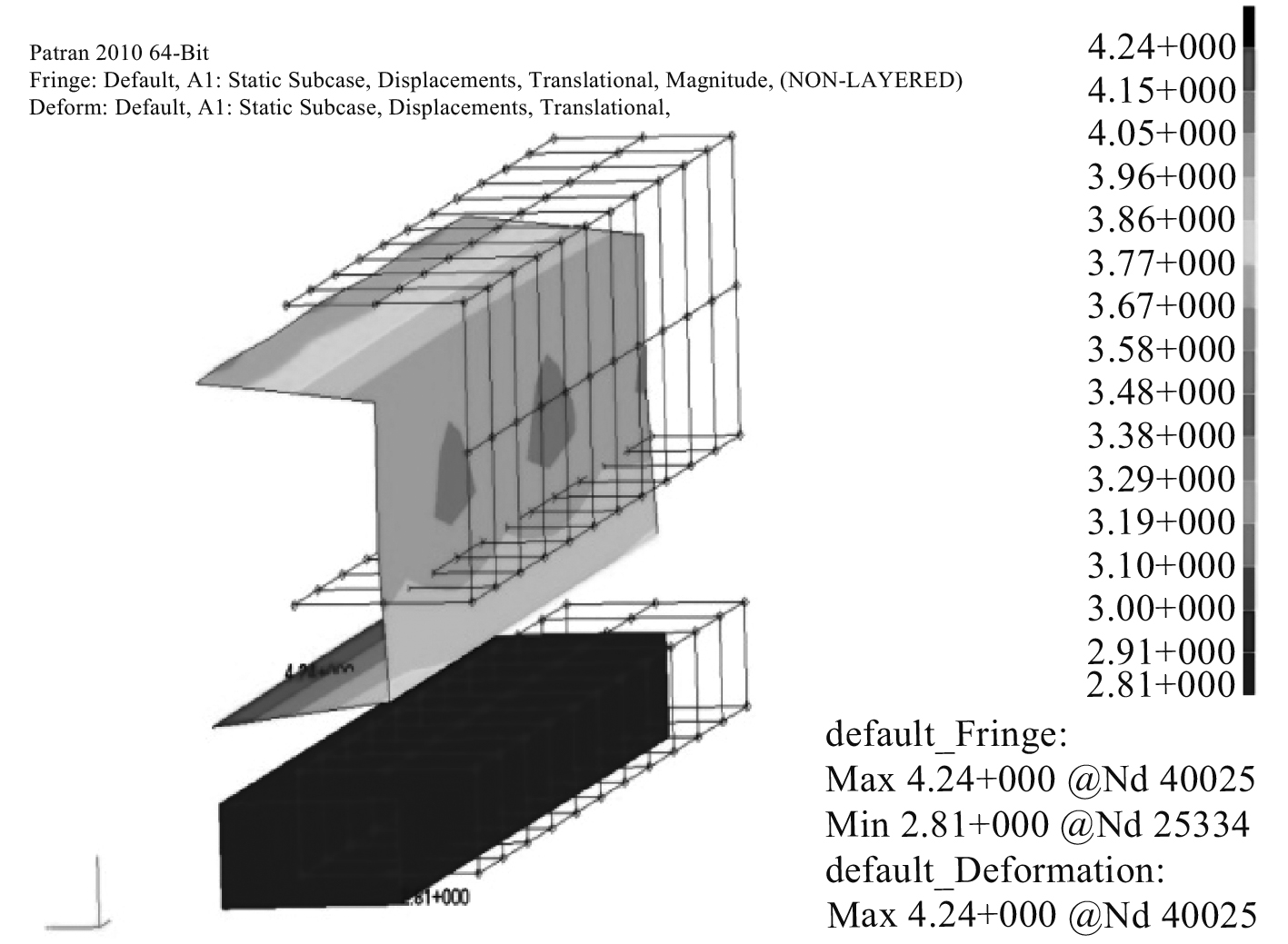
机库为满足风雨密要求,上、下层集装箱之间加装密封材料,取上2层集装箱密封处进行位移分析,该位置的位移云图如图15所示。密封垫处上、下层集装箱最大位移分别为4.24 mm,2.81 mm,相对位移为1.4 mm,在密封结构允许位移范围内,不影响集装箱之间风雨密性。
|
图 15 上下层集装箱连接处位移云图 Fig. 15 Displace nephogram of the connecting point of upper and lower containers |
本文首先对机库进行受力分析,再建立机库有限元模型并计算,得到机库结构应力值,以及变形和位移量,最终依据相关规范及所用材料强度评估机库的强度与变形是否满足要求,所述的强度分析计算方法,对船舶上加装的拼装式结构的强度计算具有参考作用。根据上述分析计算过程得到的结果,可以得知拼装结构是否满足海上工况下的强度和变形量要求,若计算的结果不满足要求,可采取相应的措施改进设计。例如,极端受力情况下机库侧壁结构强度不足时,应采用强度更高材料制造的集装箱垒成侧壁;极端受力情况下机库顶板上出现的最大变形量过大时,需要对顶板进行结构加强。
| [1] |
KOTNIK J. Container architecture[M]. Barcelona, Links International, 2009.
|
| [2] |
朱世光. 散货船舱口盖风雨密检查与纠正措施[J]. 中国水运, 2018, 18(3): 97-98. |
| [3] |
GJB/Z119-99, 水面舰艇结构设计计算方法[S]. GJB/Z119-99.
|
| [4] |
BORVIK T, HANSSEN A G, DET S, et al. On the ballistic and blast load response of a 20 ft ISO container protected with aluminum panels filled with a local mass –phase I, design of protective system[J]. Engineering Structures, 2008(30): 605-1620. |
| [5] |
BORVIK T, HANSSEN A G, DET S, et al. On the ballistic and blast load response of a 20 ft ISO container protected with aluminum panels filled with a local mass –phase Ⅱ, validation of protective system[J]. Engineering Structures, 2008(30): 1621-1631. |
| [6] |
GIRIUNAS K, SEZEN H, DUPAIX R B. Evaluation, modeling, and analysis of shipping container building structures[J]. Engineering Structures, 2012(43): 48-57. |
| [7] |
李浩. 船舶横摇运动特性研究[D]. 青岛, 中国海洋大学, 2012, 1−60. http://cdmd.cnki.com.cn/Article/CDMD-10423-1012506014.htm
|
| [8] |
陈怡然, 周岱, 归洛圣. 草帽型大跨空间结构的风压数值模拟与关键参数影响分析[J]. 振动与冲击, 2013, 32(15): 37-40. DOI:10.3969/j.issn.1000-3835.2013.15.007 |
| [9] |
李成玉, 戚玉林, 许成祥, 孙嘉冬. 方钢管混凝土柱-钢梁T形件节点受力性能研究[J]. 建筑结构学报, 2017, 38(1): 409-416. |
| [10] |
兰夏燕, 万舟, 李进, 唐高峰. ANSYS Workbench 软件中两种螺栓连接仿真方法的研究[J]. 机械制造, 2017, 55(6): 59-61. DOI:10.3969/j.issn.1000-4998.2017.06.017 |
| [11] |
李邦国, 路华鹏. Patran2006与Nastran2007有限元分析实例指导教程[M]. 北京, 机械工业出版社, 2011.
|
| [12] |
张津宁. 加筋板及船体梁极限强度的非线性有限元方法研究[D]. 杭州, 浙江工业大学, 2015, 1−98. http://cdmd.cnki.com.cn/Article/CDMD-10337-1015435102.htm
|
| [13] |
张海华, 沈继华, 吴赞, 郦羽. 5万吨级前置预旋导轮结构设计及强度直接计算方法研究[J]. 中国造船, 2013, 54(4): 120-125. DOI:10.3969/j.issn.1000-4882.2013.04.014 |
| [14] |
张超, 纪肖, 凌伟. 起重机基座支撑结构强度分析[J]. 船海工程, 2014, 43(6): 54-59. DOI:10.3963/j.issn.1671-7953.2014.06.015 |
| [15] |
王琨博. 20英尺低温液体罐式集装箱的结构强度计算[J]. 中国化工装备, 2015(5): 15-18. |
 2020, Vol. 42
2020, Vol. 42
