0 引　言

由于受到本舰机动与海流的影响，拖线阵会出现弯曲。拖线阵弯曲导致水听器相对位置发生变化，使得水听器信号之间的时延差或相位差不再满足预成波束形成所设定的线性关系，从而导致空间处理的性能下降，并且使得方位估计误差增大。因此，在拖线阵出现弯曲后，需要进行阵形估计，对空间处理的加权向量进行修正。

拖线阵阵形估计已经得到较深入的研究，目前主要采用声学方法、流体力学方法和拟合法。声学方法^{[1 – 4]}通过不同水听器接收信号的延迟来获取水听器间的相对位置信息，这种方法需要辅助声源，在实际声呐设备中的应用受到限制，流体力学方法^{[5 – 6]}通过对数学模型的解算，得到水听器的相对位置，但其对本舰的机动形式有要求，适用条件较苛刻。拟合法^{[7 – 9]}将畸变的线阵看成一条光滑可导的曲线，在线阵内安装多个辅助传感器，采取高阶多项式或者高阶傅里叶级数对其进行拟合，此种方法属于直接测量，对环境适应性较强。

文献[7]在拖线阵内安装航向传感器，采用高阶多项式对水平面畸变的阵形进行估计。文献[8]在垂直布放的线阵内安装多个倾角传感器，采用傅里叶级数对垂直平面内畸变的阵形进行估计，取得比较好的效果。与垂直阵估计不同，拖线阵在水平面的畸变一般较大，畸变较大时，航向传感器的位置偏离原位置更远，因此不能认为不变，利用高阶多项式拟合法难点在于：1）阵形畸变较大时，辅助传感器的位置需要进行估计，使得算法复杂且不容易收敛；2）对辅助传感器的精度要求高。

本文利用拖线阵内的多个航向传感器数据，采用二阶多项式对阵形进行拟合，对算法进行仿真验证，结果表明该方法能够较好实现对阵形的估计，对传感器的精度要求低。

1 平面内阵形畸变估计方法

当本舰机动时，根据文献[10]中的Water Pulley模型，阵形的畸变形式会从阵首向阵尾无衰减地传播，传播的速度等于拖曳速度，当机动的半径远大线阵的长度时，阵的形状一般接近于勾形或者可以近似为圆弧形。

据此，采用以下方法对满足Water Pulley模型下的阵形进行估计：

如图1所示，在拖线阵内均匀布放多个航向传感器，编号 $i = 1,2,3.....N$ ,阵总长 $L$ ，只考虑拖线阵的水平畸变，弧线OPD为畸变的阵形，为以第1个阵元为坐标原点，正北方为 $X$ 轴，正东方为 $Y$ 轴，建立坐标系 $XOY$ ，直线OD连接畸变后的阵首与阵尾并与其过原点的垂线组成坐标系 ${X'}O{Y'}$ ,线阵上的航向传感器输出角 $\theta $ 表示航向传感器所在位置的切线与X轴的夹角。

为了使算法简单可靠，设畸变后的阵形在 $XOY$ 下为二阶多项式，表示为：

$y = f(x) = {a_2}{x^2} + {a_1}x{\text{。}}$

(1)

其中： $x$ 为阵元横坐标； $y$ 为阵元纵坐标； ${a_2}$ 为二阶系数； ${a_1}$ 为一阶系数。设第 $i$ 个和第 $j$ 个航向传感器的横坐标为 ${x_i}$ 和 ${x_j}$ ，则2个航向传感器间的曲线长度 ${l_{ij}}$ ：

${l_{ij}} = \int_{{x_i}}^{{x_j}} {\sqrt {1 + {{\left[ {\frac{{dy}}{{dx}}} \right]}^2}}{\rm d}x}{\text{，}}$

(2)

又因为航向传感器输出角满足如下关系：

$\begin{aligned} & {k_i} = \tan ({\theta _i}) = 2{a_2}{x_i} + {a_1} {\text{，}}\\ & {k_j} = \tan ({\theta _j}) = 2{a_2}{x_j} + {a_1}{\text{，}} \end{aligned} $

(3)

代入式（2）有：

${l_{ij}} = \frac{1}{{4{a_2}}}\left( {{k_j}\sqrt {1 + k_j^2} - {k_i}\sqrt {1 + k_i^2} + \ln \left(\frac{{{k_j} + \sqrt {1 + k_j^2} }}{{{k_i} + \sqrt {1 + k_i^2} }}\right)} \right){\text{。}}$

(4)

式中： ${l_{ij}}$ 已知（安装距离），从而估计出二阶系数 ${a_2}$ ，再根据坐标原点处的航向角 ${\theta _0}$ 即可估计出一阶系数 ${a_1} = \tan ({\theta _0})$ ，但由于实际中航向传感器输出存在误差，需增强上述估计算法的精度。

针对二阶系数 ${a_2}$ ，采用平均方法减小估计误差：

$ \begin{align} &{a_2} = \frac{1}{{C_M^2}}\sum\limits_{i = 1,j \ne i}^M \frac{1}{{4{l_{ij}}}}\\ &\left( {{k_j}\sqrt {1 + k_j^2} - {k_i}\sqrt {1 + k_i^2} + \ln \left(\frac{{{k_j} + \sqrt {1 + k_j^2} }}{{{k_i} + \sqrt {1 + k_i^2} }}\right)} \right) {\text{。}} \end{align} $

(5)

式中： $M$ 为航向传感器的个数； $C_M^2$ 为 $M$ 中任取2个的组合个数。

针对一阶系数 ${a_1}$ ，在二阶系数 ${a_2}$ 估计基础上，采用迭代算法进行估计，迭代流程图如图2所示。

2 仿真结果与分析 2.1 仿真1

设本舰向正北直航，在t=0时刻开始向左方机动，机动半径R=200 m，航速20 m/s，机动5 s后保持直航。以本舰初始航向即正北向为X轴，以正东向为Y轴，设机动过程满足water pulley模型。

线阵128阵元，阵元间距0.5 m，阵上5个航向传感器编号1～5号，从第1个阵元位置开始布放，间距12.7 m，不考虑航向传感器与阵元的位置重叠，只考虑声振段，不考虑拖缆与隔振段。

根据离散化求解Water Pulley模型^[10]的方法，得到图3阵形。

图3中横轴表示正北向，纵轴表示正东向，坐标原点为开始机动前阵首所处的位置，图中反映了10 s内阵形的连续变化，可以看到在water pulley模型下，后面的阵形运动轨迹，都是阵首轨迹的重复，其直观形状与抛物线或者指数函数近似。

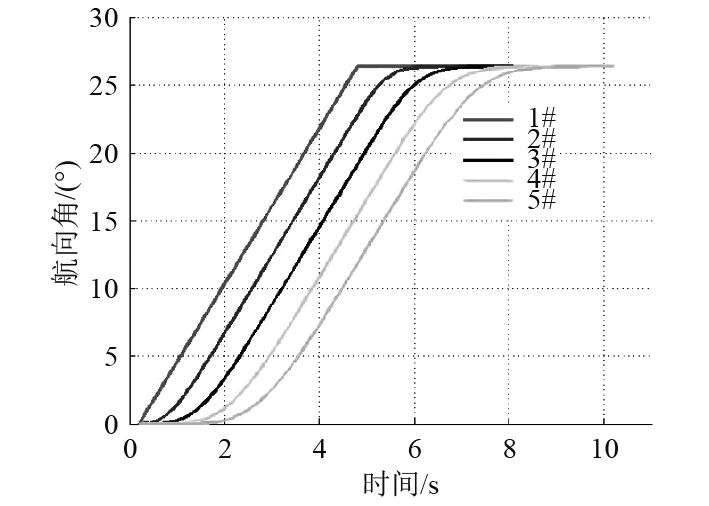
图4中为10 s内线阵上5个航向传感器所在位置的航向角度随时间的变化，5个位置分别以不同颜色的线条表示，其反映了后4个航向角度跟随第1个航向角度变化。

将上述过程中第3 s的阵形作为真实阵形，将第3 s时，5个位置的航向角作为真实航向传感器的输出，忽略航向传感器误差，采用上述算法进行估计，得到阵形估计结果如图5所示。

图5中横轴X表示北向，Y轴由X轴与竖直向下的方向，通过右手系决定，坐标原点为第1个阵元。“○”表示真实的阵形，“△”表示航向传感器的安装位置，“*”表示算法拟合得到的阵形，结果该算法能较好地拟合出阵形，表明算法有效。

2.2 仿真2

为了对阵形估计结果的精准度进行描述，定义阵元平均误差为：

$e = \frac{1}{M}\sum\limits_{i = 1}^M {\sqrt {{{\left( {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} }_i} - {x_i}} \right)}^2} + {{\left( {{{\hat y}_i} - {y_i}} \right)}^2}} }{\text{。}}$

其中： $M$ 为阵元的个数； ${x_i}$ 为第 $i$ 个阵元横坐标的实际值； ${y_i}$ 为第 $i$ 个阵元纵坐标的实际值； ${\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} _i}$ 为第 $i$ 个阵元横坐标的估计值； ${\hat y_i}$ 为第 $i$ 个阵元纵坐标的估计值，所以 $e$ 刻画了对整个阵形估计的误差。

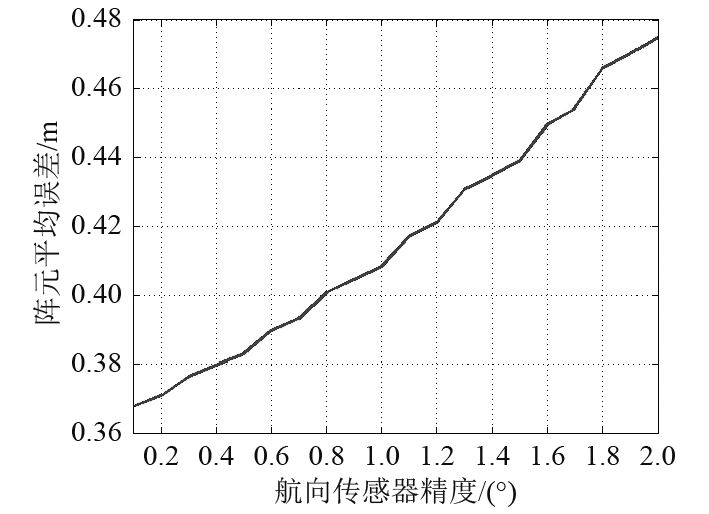
在仿真1的条件下，对航向传感器输出角引入随机误差，增大随机误差，研究传感器精度对估计结果的影响，得到结果如图6所示。

图6中，通过改变航向传感器的精度，根据蒙特卡罗方法，将50次仿真结果取平均，得到阵形估计的阵元平均位置误差，可以看到，当航向传感器精度在±1°以内时，阵元的平均位置误差小于0.42 m，当航向传感器的精度在±2°时，阵元的平均位置误差小于0.48 m，均小于阵元的间距。表明该算法对航向精度具有较好的宽容性。

3 结　语

本文采用二阶多项式对本舰机动时畸变的拖线阵阵形进行估计，相对于高阶多项式的估计方法，不需要对辅助传感器的位置进行迭代估计，增强了算法的稳定性，由于待估计的参数少，通过多次估计各参数，再取平均的方法降低传感器带来的误差，从而降低对传感器精度的要求，本文提出的方法易于工程实现，具有一定的实用价值。