UUV作为一种新型海上军事装备与海上科研装备,凭借其出色的隐蔽性、环境适应性,能够在水下载人平台难以抵达的区域执行的多种任务,在军民领域均获得了广泛关注。在军事应用中,UUV的突出特点是具有极强的隐蔽性与及安全性,且造价低廉。它的体积远小于潜艇等有人平台,使得敌方的反潜兵力难以发现及破坏,无人驾驶的特征使其可以前往危险海域执行任务,低廉的造价使UUV可以大量部署,在水下战场中以数量上的优势取得主动权,形成非对称优势。
从隐蔽性角度考虑,理想过程是UUV能够始终潜在水下,然而由于导航原理与技术限制,电磁信号无法透入水下,当前成熟的基于电磁信号的组合导航技术在水下无法使用。常见的几种水下辅助导航系统也存在一定的缺陷与弊端。多普勒导航系统在深海区域受水深限制无法使用,在军事行动中在浅海区域使用也容易因声波而暴露位置;水声定位导航系统需要其他兵力或设备进行保障,在民用领域中这些保障设备对资金的需求较大,在军用领域中这些水上或水下的保障设备目标较大且机动性不高,基于声波的方式也仍未解决隐蔽性问题,限制条件较多。
考虑到UUV与控制平台的必要交互(如自身状态或无法处理的问题等),UUV需要定期上浮通信。通常采用的方式是在上浮通信过程中以SINS/GPS组合导航的方式校准系统误差。然而卫星导航系统的输出频率通常不高,且受海面环境影响卫星信号的持续稳定跟踪存在一定难度,校准过程消耗时间较长,部分情况下甚至可达数十分钟,长时间的水面状态将对隐蔽性造成极大破坏[1]。若仅采用GPS提供的位置和速度进行重置,由于无法确定姿态失准角及陀螺漂移量,在后续航行中导航误差将继续发散。
基于星敏感器的天文导航系统(CNS)输出的是高精度姿态信息,在位置和时间已知情况下,任意恒星相对当前位置的赤经和赤纬均可确定[2]。在UUV的校准过程中,可由星敏感器确定载体姿态,同时由GPS确定载体位置和速度,并通过合适的观测方式确定出陀螺的漂移,降低校准时间且提高估计精度。
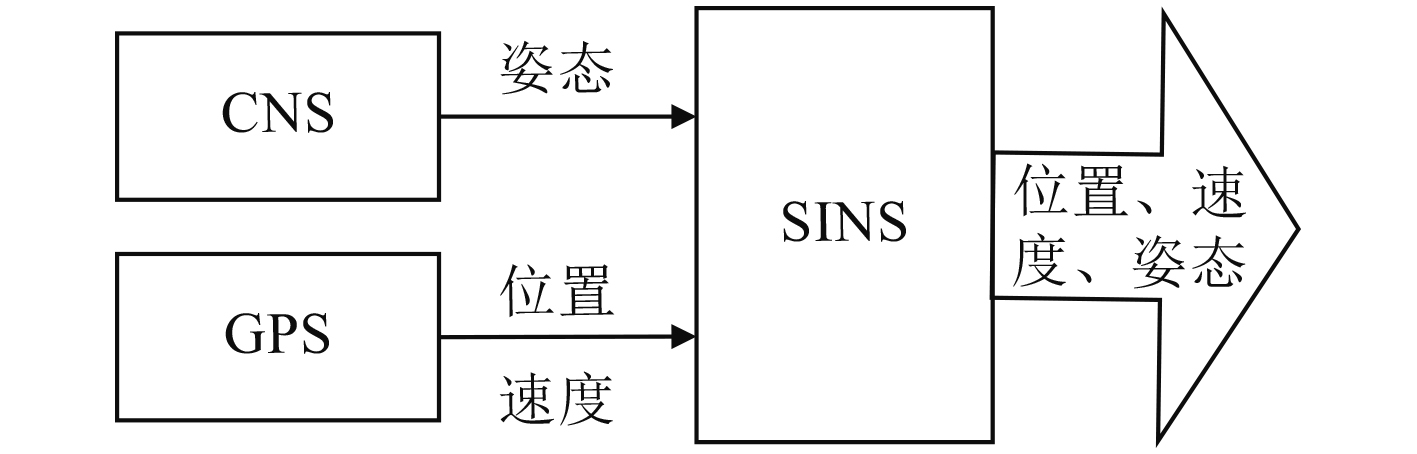
|
图 1 CNS/GPS/SINS组合系统框图 Fig. 1 Integratedsystemof CNS/GPS/SINS |
陀螺仪的系统性误差主要包括4部分:常值项、随温度变化项、逐次启动项和工作期间变化项。常值项为每次开机均会存在的常数型误差,可由内场标定结果进行补偿;温变项也可根据内场标定结果,结合传感器当前工作温度进行相应补偿;逐次启动项在每次开机过程中均发生变化,但在当次工作阶段内保持不变,主要通过对准或组合导航过程对其进行标校;工作期间变化项是在每次开机后都会随时间发生缓慢变化的误差项,理论上可以通过构建复杂的模型进行修正,但实际上实现难度极大[3]。
考虑到真正决定惯性导航系统精度和组合模型设计的是经过修正常值项后的误差,因此文章假定常值误差项及温变项已获得补偿,只考虑逐次启动项和工作期间变化项。这2项误差可等效为随机常数误差和随机误差,随机常数误差主要体现为常值漂移和标度因子误差,当考虑标度因子误差与其他轴向不相关时,可以等效为常值漂移的附加项,因此陀螺的误差模型可表示为[4]:
| $\left\{ {\begin{array}{*{20}{l}} {\varepsilon = \xi + {n_r}}\text{,} \\ {\dot \xi = 0} \text{。} \end{array}} \right.$ | (1) |
式中:
姿态的表示方式通常有欧拉角法、余弦矩阵法和四元数法,三者理论上是等价的,但根据模型的不同,在3种方法在计算复杂度及精度上存在差异。姿态余弦矩阵法易于理解,但由于呈非线性,且在部分180°附近容易出现奇点,在高阶展开过程中也容易丢失精度,而四元数方法能够有效避免这些问题,因此文章中主要采用四元数进行计算,此时载体姿态可以表示为[5 – 7]:
| $\psi = {\rm{arc}}\tan \left( {\frac{{2\left( {{q_1}{q_2} - {q_0}{q_3}} \right)}}{{q_0^2 - q_1^2 + q_2^2 - q_3^2}}} \right)\text{,}$ | (2) |
| $\theta = {\rm{arc}}\sin \left( {2\left( {{q_2}{q_3} + {q_0}{q_1}} \right)} \right)\text{,}$ | (3) |
| $\gamma = {\rm{arc}}\tan \left( { - \frac{{2\left( {{q_1}{q_3} - {q_0}{q_2}} \right)}}{{q_0^2 - q_1^2 - q_2^2 + q_3^2}}} \right)\text{。}$ | (4) |
式中:
CNS是以星敏感器为核心的导航定位系统。星光信号经光敏元件光电转换后,可结合导航星库确定载体姿态,具有精度高、质量小、功耗低、无漂移和工作方式多样等特点,同样具有无源自主导航能力,是一种性能优良、发展前途广阔的姿态测量部件[2]。
在惯性空间内,可认为由地心指向恒星的矢量是稳定的。此时,载体测得的星矢量仅与载体坐标(b系)相对惯性坐标系(i系)的姿态有关,考虑到导航坐标系(n系)通常选取为地理坐标系(t系),因此也可认为星矢量与地球坐标系(e系)、n系和i系的相对关系有关。假设星敏感器的测量坐标系(s系)与b系一致,由星敏感器测得的星矢量可表示为
| $ \tilde {{C}}_b^i = {{{U}}_i}{{U}}_b^{\rm T}{\left( {{{{U}}_b}{{U}}_b^T} \right)^{ - 1}}\text{,} $ | (5) |
根据GNSS或计算机给定的时间可以确定
| $\tilde {{C}}_b^n = {{C}}_e^n{{C}}_i^e\tilde {{C}}_b^i\text{。}$ | (6) |
其中:
令CNS的真实姿态四元数为
| $\delta Q = \hat Q_b^n \otimes {\left( {Q_b^n} \right)^{ - 1}} = {\left[ {\begin{array}{*{20}{c}} {\delta e}&{\delta q} \end{array}} \right]^{\rm T}}\text{,}$ | (7) |
其中:
假设四元数已正规化,则逆与共轭相等:
| ${\left( {Q_b^n} \right)^{ - 1}} = {\left( {Q_b^n} \right)^*}\text{,}$ | (8) |
将式(8)代入式(7)后求导可得:
| $\delta \dot Q = \dot {\hat Q}_b^n \otimes {\left( {Q_b^n} \right)^*} + {\hat Q}_b^n \otimes {\left( {{\dot Q}_b^n} \right)^*}\text{,}$ | (9) |
约定三维矢量与四元数乘时,将三维矢量扩展为四元数的矢量部分,标量部分为0,根据四元数微分方程有[10]:
| $\dot Q_b^n = \frac{1}{2}\omega _{nb}^n \otimes Q_b^n\text{,}$ | (10) |
将式(10)代入式(9)可得:
| $\begin{split} \delta \dot Q =& \frac{1}{2}\hat \omega _{nb}^n \otimes \hat Q_b^n \otimes {\left( {Q_b^n} \right)^*} + \hat Q_b^n \otimes \frac{1}{2}{\left( {\omega _{nb}^n} \right)^*} \otimes {\left( {Q_b^n} \right)^*}= \\ & \frac{1}{2}\hat \omega _{nb}^n \otimes \delta Q + \hat Q_b^n \otimes \frac{1}{2}{\left( {\omega _{nb}^n} \right)^*} \otimes {\left( {Q_b^n} \right)^*} \text{。} \end{split} $ | (11) |
根据四元数乘法规则,令
| $\hat Q_b^n = {\left[ {\delta \hat e,\delta \hat q} \right]^{\rm T}}\text{,}$ |
则有:
| $\hat Q_b^n \otimes {\left( {\omega _{nb}^n} \right)^*} = \left[ {\begin{array}{*{20}{c}} 0&{\omega {{_{nb}^n}^{\rm T}}} \\ { - \omega _{nb}^n}&{\omega _{nb}^n \times } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\delta \hat e} \\ {\delta \hat q} \end{array}} \right]\text{,}$ | (12) |
将式(12)代入式(11)右边第2部分可得:
| $\begin{split} & \hat Q_b^n \otimes \frac{1}{2}{\left( {\omega _{nb}^n} \right)^*} \otimes {\left( {Q_b^n} \right)^*}= \\ & \qquad \frac{1}{2}\left[ {\begin{array}{*{20}{c}} 0&{\omega {{_{nb}^n}^T}} \\ { - \omega _{nb}^n}&{\omega _{nb}^n \times } \end{array}} \right] \otimes \hat Q_b^n \otimes {\left( {Q_b^n} \right)^*} = \\ & \qquad \frac{1}{2}\left[ {\begin{array}{*{20}{c}} 0&{\omega {{_{nb}^n}^T}} \\ { - \omega _{nb}^n}&{\omega _{nb}^n \times } \end{array}} \right] \otimes \delta Q \text{。} \end{split} $ | (13) |
将式(13)代入式(11)可表示为:
| $\delta \dot Q = \frac{1}{2}\left\{ {\left[ {\begin{array}{*{20}{c}} 0&{ - \hat \omega {{_{nb}^n}^{\rm T}}} \\ {\hat \omega _{nb}^n}&{\hat \omega _{nb}^n \times } \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} 0&{\omega {{_{nb}^n}^{\rm T}}} \\ { - \omega _{nb}^n}&{\omega _{nb}^n \times } \end{array}} \right]} \right\} \otimes \delta Q\text{。}$ | (14) |
将
| $\delta \dot Q = \frac{1}{2}\left[ {\begin{array}{*{20}{c}} 0&{ - {\varepsilon ^T}} \\ \varepsilon &{2\hat \omega _{nb}^n \times - \varepsilon \times } \end{array}} \right] \otimes \delta Q\text{,}$ | (15) |
考虑
| $\delta \dot q = \hat \omega _{nb}^n \times \delta q + \frac{1}{2}\varepsilon \text{,}$ | (16) |
根据式(1),取状态向量为:
| ${{{X}}^{\rm T}} = \left[ {\begin{array}{*{20}{l}} {\delta {q_1}}&{\delta {q_2}}&{\delta {q_3}}&{{\xi _{x1}}}&{{\xi _{x2}}}&{{\xi _{x3}}} \end{array}} \right]\text{,}$ |
则状态方程为:
| $\dot {{X}} = {{AX}} + {{W}}\text{。}$ |
其中:
| $ {{A}} = \left[ {\begin{array}{*{20}{c}} {\hat \omega _{nb}^n \times }&{\frac{1}{2}{I_{3 \times 3}}} \\ {{0_{3 \times 3}}}&{{0_{3 \times 3}}} \end{array}} \right], {{W}} = {\left[ {\begin{array}{*{20}{c}} {{n_{1 \times 3}}}&{{O_{1 \times 3}}} \end{array}} \right]^{\rm T}}\text{。} $ |
由于CNS测得的是载体的高精度姿态输出,令其转换为四元数后表示为
| ${{Z}} = {{HX}} + v = {{{I}}_{3 \times 3}}{{X}} + v\text{,}$ |
式中
连续时间系统不符合计算机采样计算过程,需要进行状态方程的离散化。离散化后系统可表示为:
| $\left\{ {\begin{array}{*{20}{l}} {{{{X}}_{k|k - 1}} = {{{\varPhi}} _{k|k - 1}}{{{X}}_{k - 1|k - 1}} + {{{W}}_k}}\text{,} \\ {{{{Z}}_k} = {{{H}}_k}{{{X}}_{k|k}} + {{{V}}_k}} \text{,} \end{array}} \right.$ | (17) |
时序上的滤波过程为:
| ${{{X}}_{k|k - 1}} = {{{\varPhi}} _{k|k - 1}}{{{X}}_{k - 1|k - 1}}\text{,}$ | (18) |
| ${{{P}}_{k|k - 1}} = {{{\varPhi}} _{k|k - 1}}{P_{k - 1|k - 1}}{{\varPhi}} _{k|k - 1}^{\rm T} + {{{Q}}_k}\text{,}$ | (19) |
| ${{{K}}_k} = {{{P}}_{k|k - 1}}{{H}}_k^{\rm T} {{R}}_k^{ - 1}\text{,}$ | (20) |
| ${{{X}}_{k|k}} = {{{X}}_{k - 1|k - 1}} + {{{K}}_k}\left( {{{{Z}}_k} - {{{H}}_k}{{{X}}_{k|k - 1}}} \right)\text{,}$ | (21) |
| ${{{P}}_{k|k}} = \left( {{{I}} - {{{K}}_k}{{{H}}_k}} \right){{{P}}_{k|k - 1}} \text{。}$ | (22) |
为验证算法有效性,采用Matlab进行仿真分析,模拟UUV海上上浮校准过程中,采用CNS进行脱落常值标定。
3.1 仿真参数设置假设UUV的上浮点坐标为135.00°E,25.00°N,测星时刻为2018.12.01日05时30分00秒,惯性坐标系取2018.12.01日00时00分00秒的地球坐标系,GPS的定位误差为20 m,UUV陀螺仪的常值漂移分别为0.05°/h,0.1°/h和0.2°/h,CNS测量精度为5'',SINS采样间隔0.02 s,CNS输出频率为2 Hz。3颗选定的单位星矢量在惯性坐标系内的坐标表示为:
| $\left\{ {\begin{array}{*{20}{c}} {{{[ - 0.146\;13,0.475\;36,0.443\;98]}^{\rm T}}}\text{,} \\ {{{[ - 0.219\;20,0.713\;04,0.665\;98]}^{\rm T}}}\text{,} \\ {{{[ - 0.423\;45,0.275\;01,0.703\;60]}^{\rm T}}} \text{。} \end{array}} \right.$ |
根据上述仿真设定,利用Matlab进行仿真验证,对陀螺仪常数漂移的仿真结果如图2~图4所示。
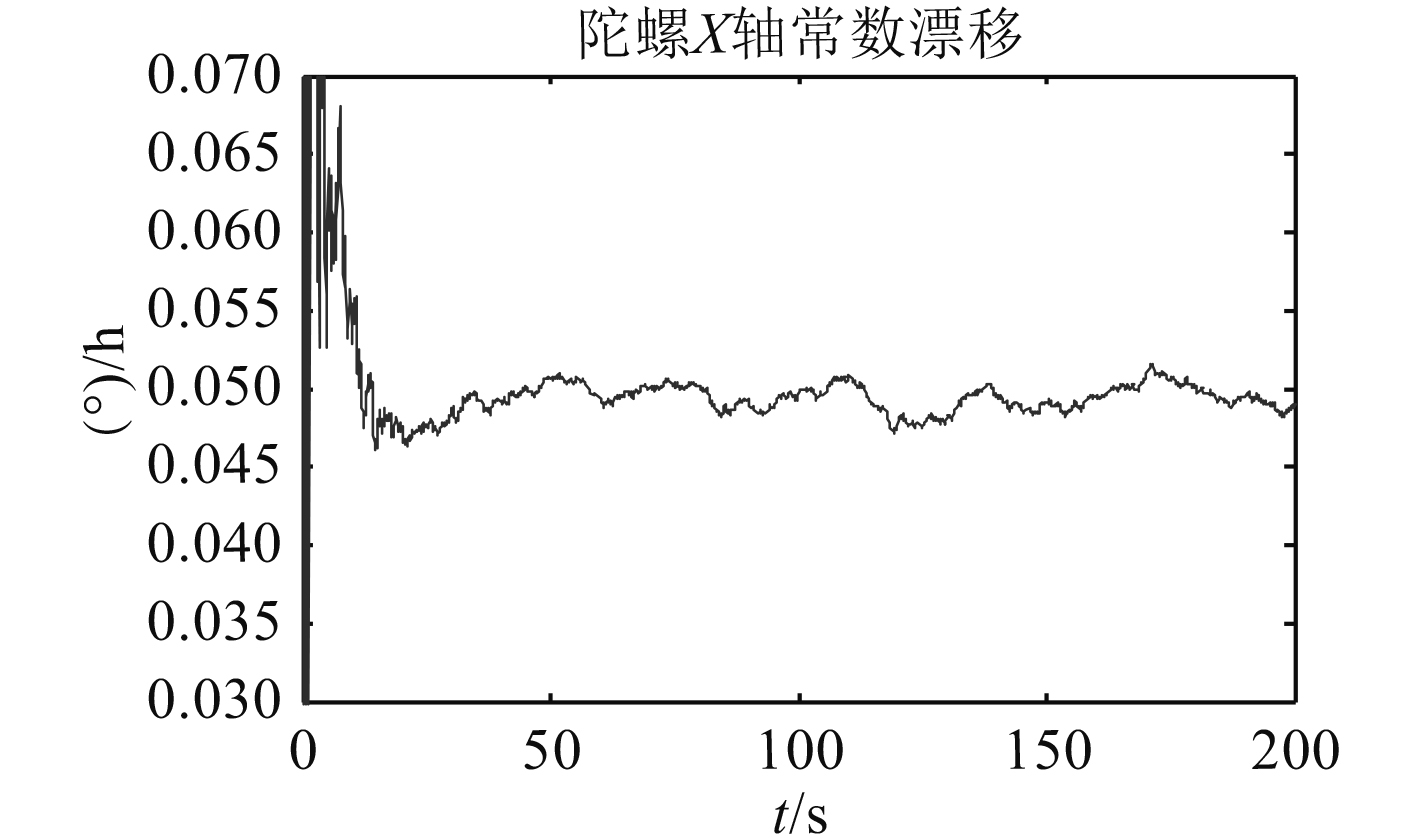
|
图 2 X轴方向陀螺常值漂移估计 Fig. 2 Random constant drift in axis X |
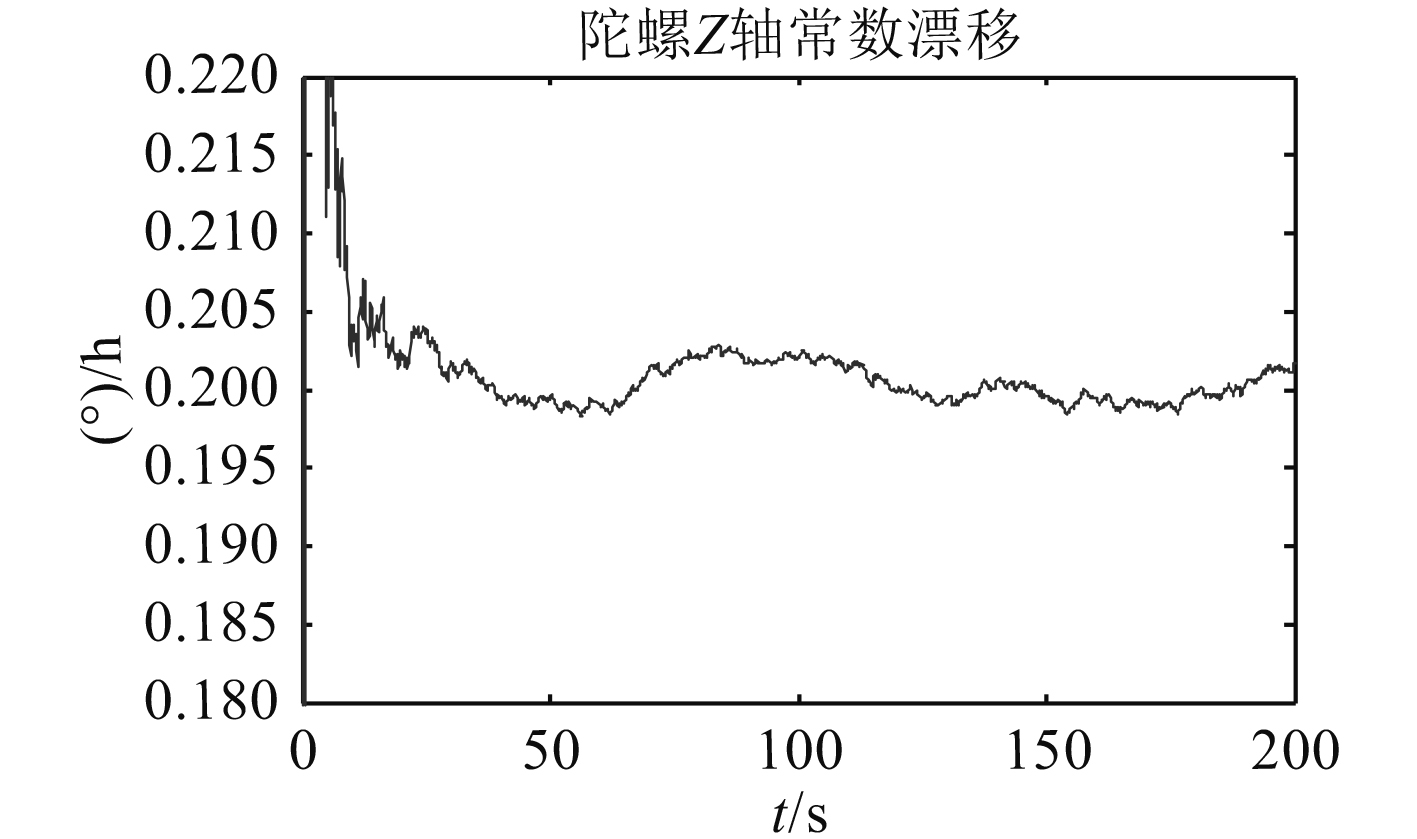
|
图 4 Z轴方向陀螺常值漂移估计 Fig. 4 Random constant drift in axis Z |
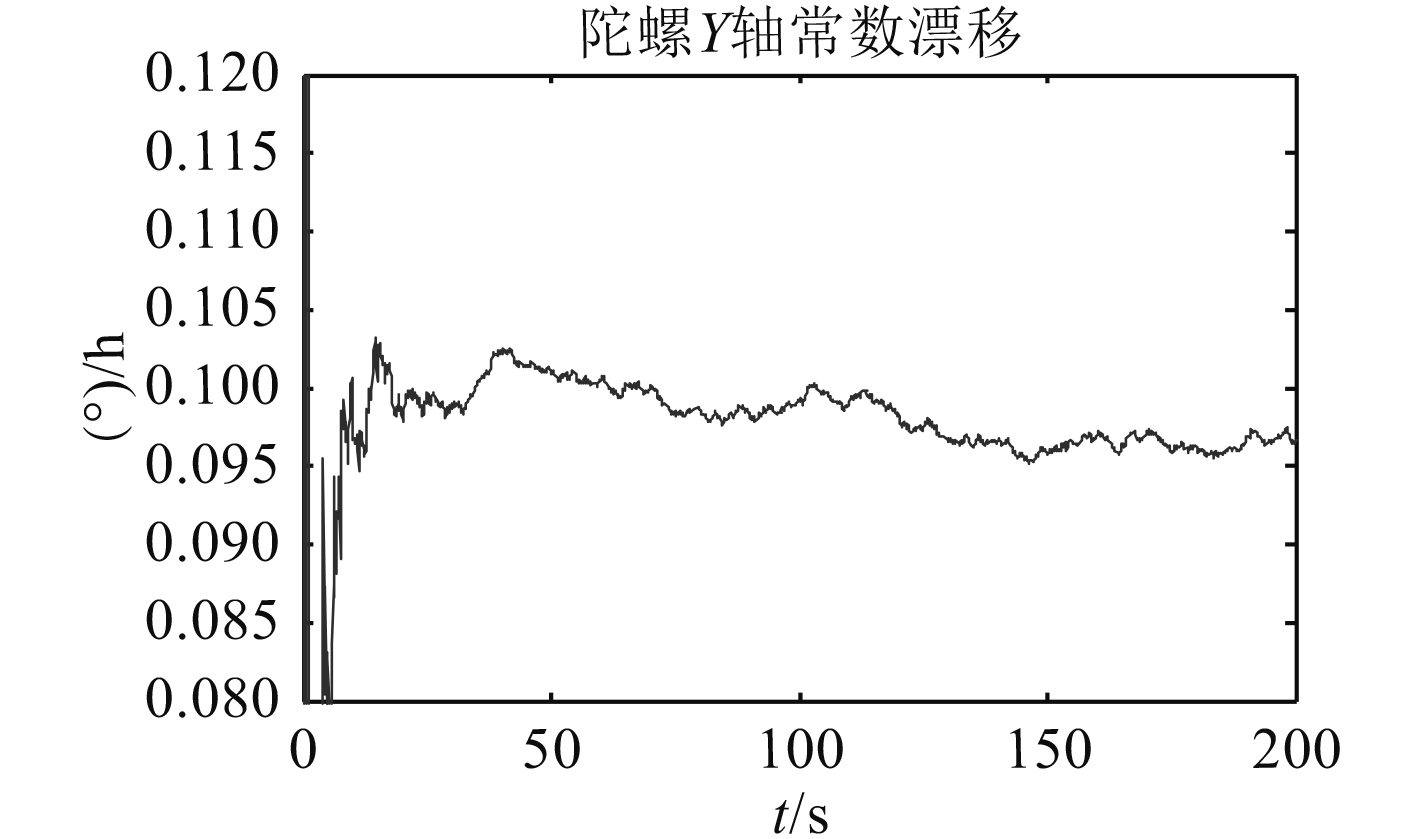
|
图 3 Y轴方向陀螺常值漂移估计 Fig. 3 Random constant drift in axis Y |
仿真结果表明,该模型可以在20 s左右进入稳定状态,在50 s左右即可获得较为准确的陀螺常值漂移估计值,精度可达95%以上。
4 结 语CNS能够提供不随时间发散的稳定的高精度姿态信息,而GPS能够提供不随时间发散的稳定的位置和速度信息,二者组合在一起时具有极强的互补性。GPS/SINS系统进行失准角和陀螺漂移校准时,需要较大机动以增强可观性,而这与UUV上浮后需要停车,避免螺旋桨击打海面造成损坏这一工程实现的实际情况不相吻合,引入CNS后能够有效解决这种问题。利用Matlab对标定系统进行仿真,验证了其在标定陀螺常值漂移方面的可行性。以这种方法进行标定后,可结合CNS给出的精确姿态,降低GPS/SINS组合导航中状态变量的维数,缩短上浮校准时间,为增强UUV的隐蔽性与安全性提供一种解决问题的思路。
| [1] |
王新龙. 捷联式惯导系统动、静基座初始对准[M]. 西安: 西北工业大学出版社, 2013.
|
| [2] |
刘朝山, 刘光斌, 王新国, 等. 弹载星敏感器原理及系统应用[M]. 北京: 国防工业出版社, 2010.
|
| [3] |
PAUL D. Groves. Principles of GNSS, Inertial, andMultisensor Integrated Navigation Systems[M]. London: Artech HOUSE, 2013.
|
| [4] |
付梦印, 郑辛, 邓志红, 等.传递对准理论与应用[M]. 北京: 科学出版社,2012.
|
| [5] |
牟宏伟. 水下航行器组合导航系统与信息融合技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2013. http://www.cnki.com.cn/Article/CJFDTotal-ZGXJ200903020.htm
|
| [6] |
齐昭. 船用捷联惯导/天文/计程仪组合导航关键技术研究[D]. 哈尔滨: 哈尔滨工程大学. 2015 http://cdmd.cnki.com.cn/Article/CDMD-10217-1017242644.htm
|
| [7] |
张鹏. 船用星敏感器/惯性导航系统在线标定及组合导航技术研究[D]. 哈尔滨: 哈尔滨工程大学. 2016.
|
| [8] |
肇慧, 沈继红, 陈涛. SINS/CNS组合导航系统在线标定技术[J]. 计算机工程与应用, 2013, 49(19): 1-5. DOI:10.3778/j.issn.1002-8331.1304-0227 |
| [9] |
邓红, 刘光斌, 陈昊明, 等. 发射惯性坐标系下误差角与数学平台失准角的推导与仿真[J]. 宇航学报, 2011, 32(4): 781-786. DOI:10.3873/j.issn.1000-1328.2011.04.012 |
| [10] |
王国臣, 齐昭, 张卓. 水下组合导航系统[M]. 北京: 国防工业出版社, 2016.
|
 2020, Vol. 42
2020, Vol. 42
