2. 中国科学院机器人与智能制造创新研究院,辽宁 沈阳 110016;
3. 中国科学院大学,北京 100049
2. Institutes for Robotics and Intelligent Manufacturing, Chinese Academey of Sciences, Shenyang 110016, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
随着人类对海洋的开发日益增多,水下机器人越来越多被用来执行水下任务,如海洋矿产勘探,海洋数据收集等。精确可靠的导航系统是水下机器人成功完成任务不可或缺的部分[1]。
由于捷联惯导(SINS)具有高可靠性和完全独立等优点,SINS被广泛应用在水下机器人导航中。SINS通过惯导计算机采集的惯性测量单元(IMU)的输出信息,进行数值积分求解水下机器人的姿态、速度和位置等导航参数。随着时间推移,IMU中的陀螺和加速度计的误差会逐渐增加,这将导致SINS的导航误差会逐渐增大。为了提高导航性能,有必要引入辅助传感器来限制误差增长。目前水下机器人导航系统多采用由多个导航传感器组成的综合导航系统[2]。多普勒计程仪(DVL)是一种高精度的速度测量仪器。由SINS和DVL结合的组合导航系统,于20世纪初在丹麦的MARIDAN AUV上成功应用后,在水下机器人领域的应用越来越广泛[3]。
DVL是根据多普勒效应,测量出水下机器人相对于海底或者海流的速度。通过卡尔曼滤波器(KF)采用集中滤波的方式将DVL提供的高精度的速度数据和SINS的数据进行融合能够有效抑制导航系统的累计误差。由于DVL数据的更新频率相对于SINS较低,会影响AUV的组合导航精度[4]。对于DVL处在对底工作模型的情况,由于DVL对海底环境的依赖会使DVL在使用过程中出现以下问题[4]:
1)由于海底地形变化导致DVL返回数据频率不固定。
2)由于海底存在强烈的吸波物质,导致DVL发出的声波无法被返回。
3)当海底存在海沟超出了DVL的量测范围,导致DVL信号丢失。
当上述情况发生时,滤波器无法得到频率稳定、精度可靠的DVL数据,情况严重时会导致AUV测速数据无效,这不仅会影响滤波器的稳定,同时会带来较大的导航误差。解决上述问题主要有2种方法:1种为隔离法,即直接隔离数据失效的DVL;第2种方法为替换法,即替换掉DVL的测速数据[4]。采用第1种方法,组合导航系统将变为惯性导航,导航精度会大大降低。第2种方法是目前大部分学者采用的。考虑到硬件成本,一般不采用通过增加传感器的方式解决上述问题。目前大多数情况下,通过设计一个估计器的方式来处理频率不稳以及数据失效等问题。Semeniuk和Noureldin等[5]提出了一种基于人工智能的分段预测器来克服GPS卫星信号失效的问题。Hasan等[6]介绍了一种神经网络模糊系统,用于预测GPS信号失效时INS的误差。这些方法均可以解决传感器信号不稳的问题,而不用了解传感器的特性。基于上述智能方法在GPS/INS组合导航方面的广泛使用,Zhu等[7]通过采用线性的偏最小二乘回归估计器(PLSR)和支持向量(SVR)估计器相结合的方法,建立了惯导速度与多普勒速度输出的映射关系,在DVL数据失效后实时估计水下机器人对底的速度。该方法通过仿真得到了较好的效果。该方法中PLSR算法随着时间推移,当新信息加入时新信息对于拟合的影响较小。对于SVR算法,在线性过程中和PLSR算法共同使用时增加了计算机负荷造成了资源的不必要浪费。当水下机器人运动过程发生非线性过程时,如由匀速到加速的转换过程,由于先前的训练的数据处于线性过程,在线性到非线性的转换过程起始时SVR表现并不十分好。
针对DVL相对于SINS数据刷新频率不稳影响组合导航精度和由于一段时间内DVL数据失效导致组合导航精度降低等问题,本文提出一种SVR辅助SINS/DVL组合导航方法,并针对组合导航过程中由于运动变化引起的非线性问题,提出了一种动态改变SVR训练数据集尺度和样本的方法解决该问题。
1 SINS/DVL组合导航系统水下机器人组合导航系统是由SINS和一些辅助传感器构成,辅助传感器是提高SINS精度必不可少的条件。水下机器人组合导航系统中常用的辅助传感器包括DVL、深度计、全球定位系统(GPS)。由于GPS在水下无法使用,所以水下机器人在水下航行时无法通过GPS进行校准,长航程水机器人会定期浮上水面通过GPS对整个导航系统进行校准。深度计一般用来提供深度信息。多传感器辅助的组合导航系统一般采用联邦滤波算法[8]。本文主要讨论SINS/DVL组合导航部分。
1.1 系统模型组合导航一般有直接滤波算法和间接滤波算法。直接滤波具有简单明了容易实现的特点,但该方法的系统方程一般为非线性,需要广义滤波进行处理,而且采用的状态变量是导航的输出参数,有时差值会比较大(如姿态角),给计算带来一定困难,影响估计的准确性,不适合有较高精度要求的场合。间接滤波算法以各子系统的误差量作为系统状态变量,即以导航输出参数的误差作为滤波估计对象。在间接法滤波中,卡尔滤波器接收导航子系统对同一导航输出参数的差值,并经滤波计算得到误差量的最优估计[9]。本文采用间接滤波算法,算法示意图如图1所示。
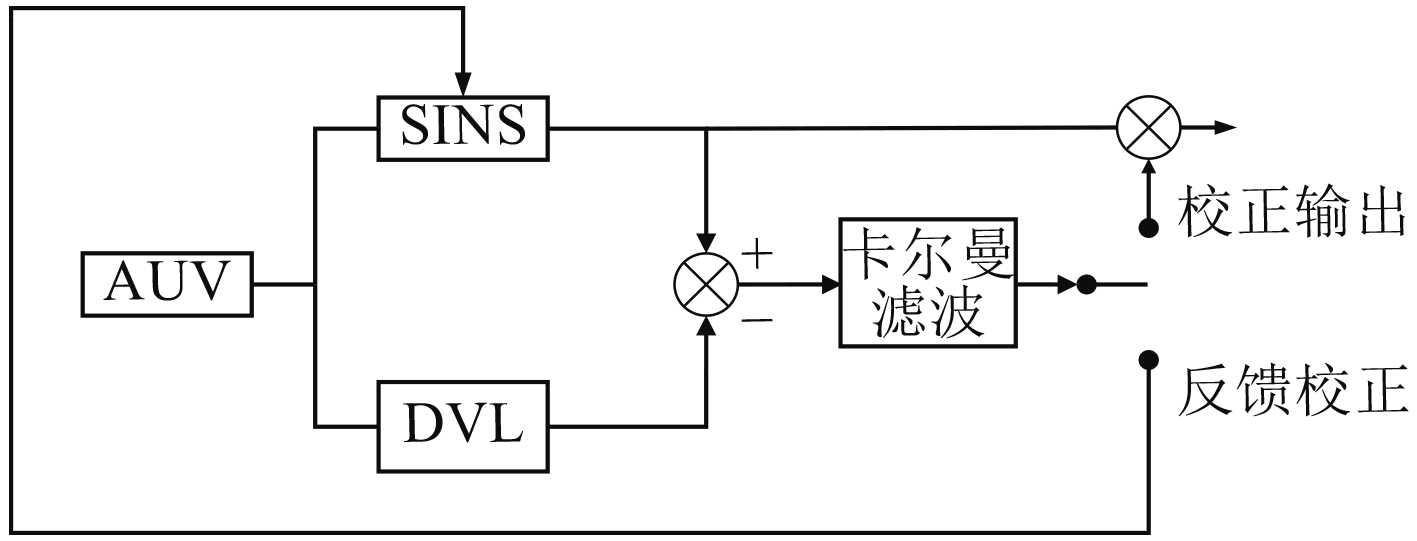
|
图 1 间接滤波算法 Fig. 1 Indirect filtering algorithm |
考虑建立惯性导航系统模型,采用状态参数为17维,包括8个导航解误差(经纬度、速度、姿态误差)、3个陀螺漂移误差、3个加速度误差、DVL对地速度、偏流角、刻度系数误差。
系统变量:
| $ \begin{split} {X_{SINS}} =\,& [ {{\phi _e}}\quad {{\phi _n}}\quad {{\phi _u}}\quad {\delta {V_e}}\quad {\delta {V_n}}\quad {\delta {V_u}}\quad {\delta L} \\ & \delta \lambda\quad {{\varepsilon _e}}\quad {{\varepsilon _n}}\quad {{\varepsilon _u}}\quad {\Delta {A_e}}\quad {\Delta {A_n}}\quad {\Delta {A_u}} ] \text{,} \end{split} $ | (1) |
| $ {X_{DVL}} = [\begin{array}{*{20}{c}} {\delta {V_d}}&{\delta \Delta }&{\delta C} \end{array}]'\text{。} $ | (2) |
式中的变量是基于导航坐标系n系下建立的。
状态方程:
| $\left[ \begin{array}{l} {X_{SINS}} \\ {X_{DVL}} \\ \end{array} \right] = \left[ {\begin{array}{*{20}{c}} {{F_{SINS}}}&0 \\ 0&{{F_{DVL}}} \end{array}} \right]\left[ \begin{array}{l} {X_{SINS}} \\ {X_{DVL}} \\ \end{array} \right] + \left[ \begin{array}{l} {W_{SINS}} \\ {W_{DVL}} \\ \end{array} \right]\text{。}$ | (3) |
式中F为系统状态转移矩阵W为系统噪声矩阵。本文取SINS和DVL的东向和北向速度的差值:
| $Z = \left( {\begin{array}{*{20}{c}} {{V_{SINS{\rm{e}}}} - {V_{DVL{\rm{e}}}}} \\ {{V_{SINSn}} - {V_{DVLn}}} \end{array}} \right)\text{。}$ | (4) |
量测方程:
| $Z = \left[ {\begin{array}{*{20}{c}} {{H_{SINS}}}&0 \\ 0&{{H_{DVL}}} \end{array}} \right]\left[ \begin{array}{l} {X_{SINS}} \\ {X_{DVL}} \\ \end{array} \right] + \left[ {\begin{array}{*{20}{c}} {{V_{SINS}}} \\ {{V_{DVL}}} \end{array}} \right]\text{。}$ | (5) |
式中:H为系统量测方程,V为观测噪声并满足高斯白噪声特性。本文的滤波方法采用卡尔曼滤波。
从式(1)可以看出,滤波器的状态量均为微小量,滤波过程中传感器数据刷新频率发生变化或传感器数据在一段时间内无效均会造成滤波器不稳定,发生误差过大,滤波不收敛等现象,造成一段时间内导航误差过大。
2 变训练数据集的SVR预测方法 2.1 支持向量回归(SVR)原理SVR是在Vapnik提出的支持向量机的概念的基础上拓展而来的[10]。给出样本训练集为:
| $f\left( x \right) = \omega \times \varphi \left( x \right) + b\text{。}$ | (6) |
式中:ω为权值矢量;b为偏差;
| ${\rm{min}}\frac{1}{2}|\left| \omega \right|{|^2} + C\mathop \sum \nolimits_i^n \left( {\delta + {\delta ^*}} \right)\text{,}$ | (7) |
| ${\rm{s.t.}}\left\{ {\begin{aligned} & {{y_i} - {\omega ^{\rm{T}}}\varphi \left( x \right) - b \leqslant \varepsilon + {\delta _i}}\text{,}\\ & {{\omega ^{\rm{T}}}\varphi \left( x \right) + b - {y_i} \leqslant \varepsilon + \delta _i^*}\text{,}\\ & {{\delta _i} \geqslant 0,\delta _i^* \geqslant 0,i = 1,2,3, \ldots ,n}\text{。} \end{aligned}} \right.$ | (8) |
综合目标函数和约束条件,建立拉格朗日方程,引入核函数和二次规划求解拉格朗日方程的SVR回归模型为:
| $ \begin{aligned} & {\rm{max}}L\left( {\alpha ,{\alpha ^*}} \right) = \\ & - \frac{1}{2}\sum\nolimits_{i,j = 1}^n {\left( {{\alpha _i} + \alpha _i^*} \right)} \left( {{\alpha _j} + \alpha _j^*} \right)k\left( {{x_i},{x_j}} \right) - \\ & \varepsilon \sum\nolimits_{i = 1}^n {\left( {{\alpha _i} + \alpha _i^*} \right)} + \sum\nolimits_{i = 1}^n {{y_i}} \left( {{\alpha _i} + \alpha _i^*} \right)\text{,}\\ & {\rm{s.t.}}\sum\nolimits_{i = 1}^n {\left( {{\alpha _i} - \alpha _i^*} \right)} = 0\text{,}\left( {0 \leqslant {\alpha _i},\alpha _i^* \leqslant Ci = 1, \ldots ,n} \right)\text{。}\!\!\!\!\!\! \end{aligned} $ | (9) |
通过上式求解最终可以得到SVR的方程为:
| $f\left( x \right) = \mathop \sum \nolimits_{i = 1}^n \left( {{\alpha _i} - \alpha _i^*} \right)k\left( {x,{x_i}} \right) + b\text{,}$ | (10) |
其中核函数
根据DVL在数据有效时的速度数据和惯导相同时刻的速度数据建立训练样本
对于通过SVR回归曲线而言,如果拟合曲线的时间序列过长,会导致在在当前时刻拟合精度较低并影响滤波器稳定。所以在SVR回归过程中采用随时间移动的窗口,随着时间的移动,窗口的右边不断有新数据加入,窗口的左边不断有数据剔除。
由于在AUV运动过程中,AUV变速时会存在一个非线性过程。当AUV发生变速时由于当前时刻SVR训练集中的数据大部分属于AUV平稳运动的过程,并且集中的数据存在一定的噪声,所以SVR回归无法快速跟踪AUV变速这一过程。由于物理原因和传感器的极限不能提高DVL数据的刷新频率,不能使这一段时间内训练集的数据迅速变化为变速过程中的数据。根据上述原因,提出一种改变训练集大小的方法来解决这一问题。该方法在检测到水下机器人存在突然变速的行为时,迅速减小训练集的大小,快速剔除平稳运动过程中的训练数据,使变速后的数据样本快速充满训练集,更快速回归变速后的曲线。
设数据集的大小为N,引入训练集尺度因子βt,βt表示当前时刻计算得到的尺度因子。经过仿真分析,给出βt的表达式:
| ${\beta _t} = f\left( {{\Delta _t},\Delta v,\Delta a} \right)\text{。}$ | (11) |
式中:
设稳定时间单位时间长度为t0,
| ${\Delta _t} = 1 - {e^{ - \mu {t_\Delta }/{t_0}}}\text{,}$ | (12) |
式中μ>1为比例系数。
| $\Delta v = \frac{{{v_{i + 1}} - {v_i}}}{{{t_{i + 1}} - {t_i}}}\text{,}$ | (13) |
| $\Delta a = \frac{{{a_{i + 1}} - {a_i}}}{{{t_{i + 1}} - {t_i}}}\text{。}$ | (14) |
此时尺度因子为:
| $\left\{ {\begin{array}{*{20}{l}} {{\beta _t} = {\Delta _t} - \theta \left( {1 - {e^{ - \rho \Delta v}}} \right)}\text{,}&{\Delta a \leqslant \Delta {a_0}}\text{,}\\ {{\beta _t} = {e^{ - \rho \eta \Delta a}}}\text{,}&{\Delta a > \Delta {a_0}}\text{。} \end{array}} \right.$ | (15) |
式中:ρ和η均为比例系数ρ<1,η>1,η可以根据水下机器人的机动能力选取,如果机器人机动能力强η相应的增大,反之η取小。θ为比例系数,0.5<θ<1。
此时训练集的大小:
| ${n_t} = {\beta _t}N\text{。}$ | (16) |
本文提到的DVL数据失效是指DVL数据较短时间内DVL无数据上传和DVL数据存在野值的情况。若DVL长时间无数据或DVL数据长时间错误则视为DVL故障,为避免造成不必要的损失,水下机器人应立即进行相关应急处理,如抛载上浮等。
DVL数据野值检验:
| $v_{def}^2 < {({v_{svr}} - {v_{dvl}})^2}\text{。}$ | (17) |
式中:vdef为给定的速度误差值,设置值的大小可以根据DVL的精度进行选取,vsvr为SVR算法估计的速度值,vdvl为多普勒量测的速度值。式(17)成立时则认为该值为野值,若不成立则为正常值。
2.4 SVR辅助的SINS/DVL组合导航流程DVL正常运行时,由于多普勒数据刷新频率低,通过SVR回归预测DVL的速度值,将预测值的频率相对DVL数据频率提高,协调SINS和预测数据频率后,将预测值作为量测值给入滤波器进行滤波处理。处理流程如图2所示。
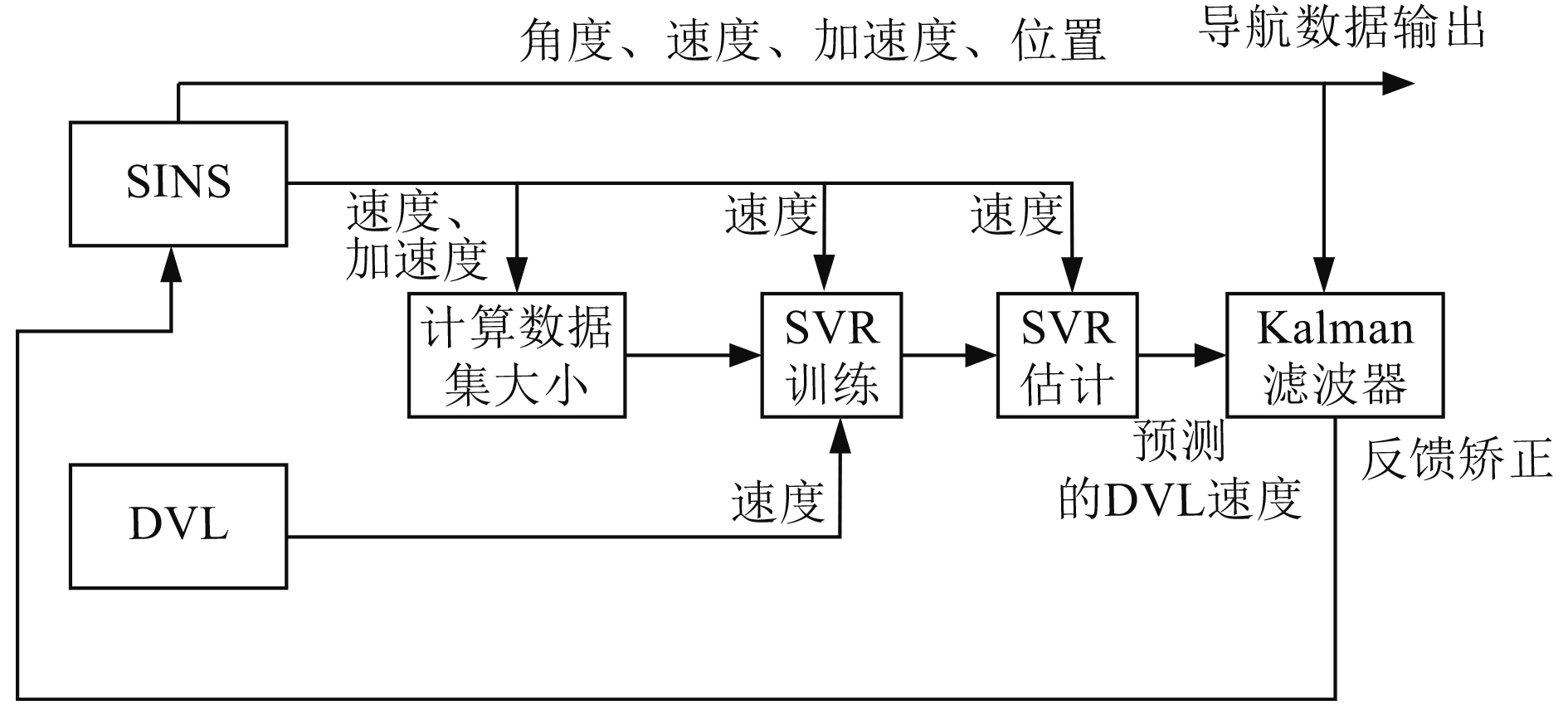
|
图 2 DVL正常工作情况下程序流程图 Fig. 2 The program flow chart of DVL under normal working condition |
由于DVL数据无效时间较为短暂,DVL数据无效时,认为水下机器人不进行较大幅度的加速减速等机动行为。通过前一段时间训练的SINS速度和DVL速度的对应关系预测当前时刻的速度关系,此时不在计算训练数据集大小,训练数据集的大小不再进行变化,处理流程如图3所示。
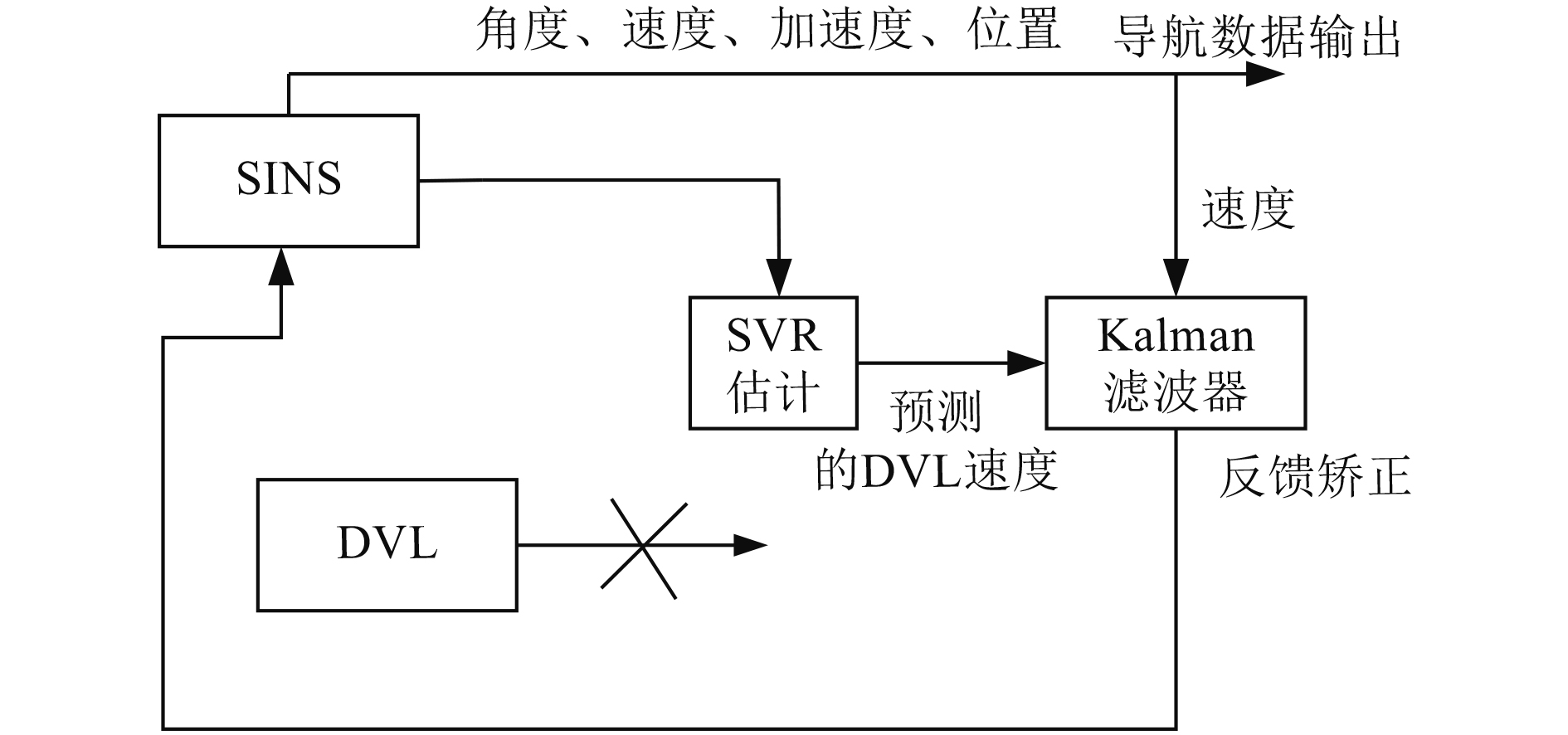
|
图 3 DVL不正常工作情况下程序流程图 Fig. 3 The program flow chart of DVL under abnormal working condition |
为了验证上述算法的有效性,进行仿真试验,将变训练集大小的SVR算法,用于SNS/DVL组合导航系统。表1给出了各传感器的规格,仿真时间为960 s,图4显示了水下机器人运行的轨迹包括经纬度、深度。
|
|
表 1 传感器精度 Tab.1 Sensor accuracy |
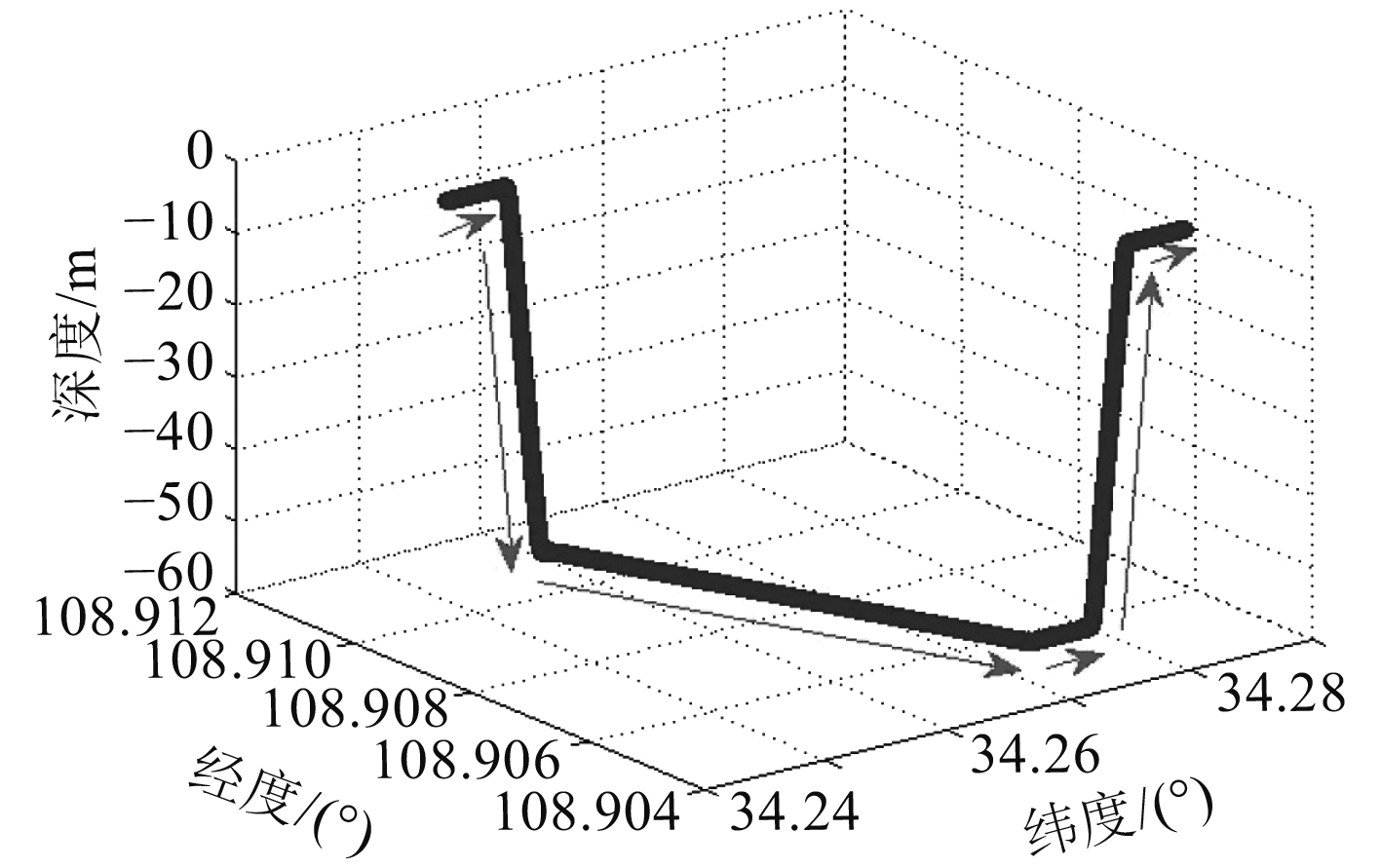
|
图 4 水下机器人运动路径 Fig. 4 The sailing trajectory of the underwater vehicle. |
仿真中水下机器人按照图4中箭头的指向运动。为了验证充分,水下机器人设定的运动过程:100 s的静止,10 s的匀加速,100 s的匀速,70 s的下潜,20 s左转弯,300 s匀速,20 s右转弯,100 s的匀速,70 s的上浮,100 s的匀速,10 s减速,60 s静止,仿真结束。仿真中设置SINS数据的刷新周期为0.1 s,DVL工作周期为2 s,仿真过程中对于DVL数据的刷新周期,设置在1.2~0.8 s之间随机变化。
3.1 DVL正常工作时SVR辅助的SINS/DVL组合导航DVL正常工作时海底地形不平坦,导致DVL返回数据频率不稳定,通过SVR回归得到的曲线预测DVL速度值,使DVL数据稳定,并协调SINS和DVL的数据频率,小幅度的提升DVL数据频率。
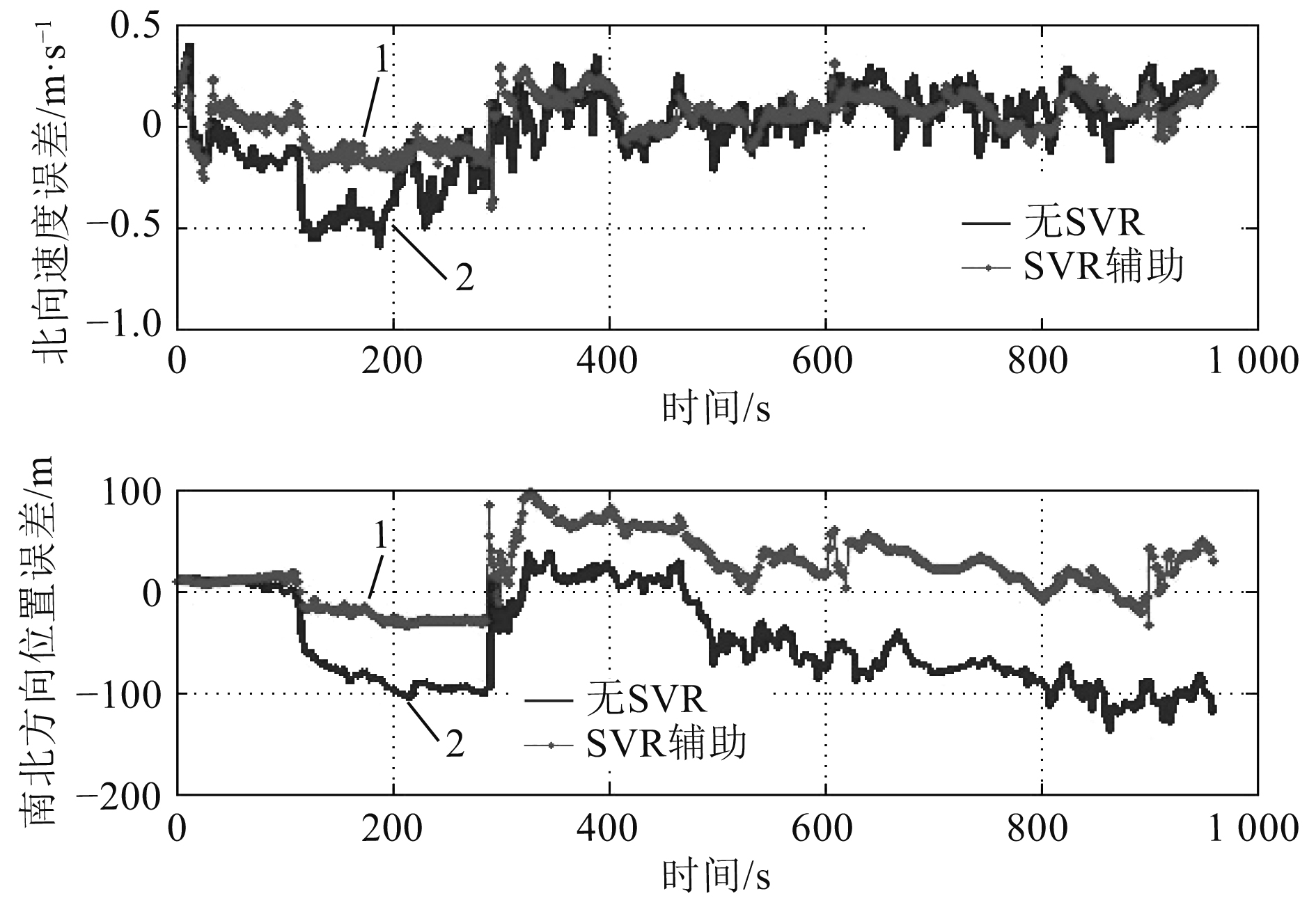
图5和图6中的曲线1为SVR辅助情况下的SINS/DVL组合导航曲线,曲线2为不加SVR辅助情况下的SINS/DVL组合导航曲线。可以看出SVR辅助情况下,东向、北向速度及经纬度误差下降较为明显。

|
图 5 东向速度误差和经度误差 Fig. 5 Eastward velocity error and longitude error |
|
图 6 北向速度误差和纬度误差 Fig. 6 North velocity error and latitude error |
|
|
表 2 速度及距离误差数据 Tab.2 Speed and distance error data |
从上述图形和数据中可以看出在SVR辅助的情况下,速度误差和误差波动幅度明显降低,由于路径规划过程中航行的方向在不断变化,位置误差属于速度的累积误差,经度误差出现了变大的情况也较为合理,经纬度误差的波动情况也明显下降,所以稳定DVL数据频率,通过SVR预测的方法小幅度提升数据频率对提升导航精度是有效的。在仿真中发现水下机器人的机动行为越少,在SVR辅助的情况下提升精度越高。航行情况如文中所示的情况时东向速度误差减少65.48%,误差均方差减少96.65%。北向速度误差减少29.51%,误差均方差减少98.10%。SVR回归对速度有明显的平滑性,使误差收敛幅度较大。经纬度误差是速度误差的累计,从图像中看经纬度误差具有明显的收敛性,经度误差收敛性提高37.59%,纬度误差收敛性提升52.9%。从上述数据可以看出,变训练集的SVR算法对导航经度提升幅度明显。同时发现预测数据的频率提升较少时精度会有所提高,但随着频率提升的越高误差将会急剧增大,所以提升频率的幅度大小与精度的关系还需要进一步研究。
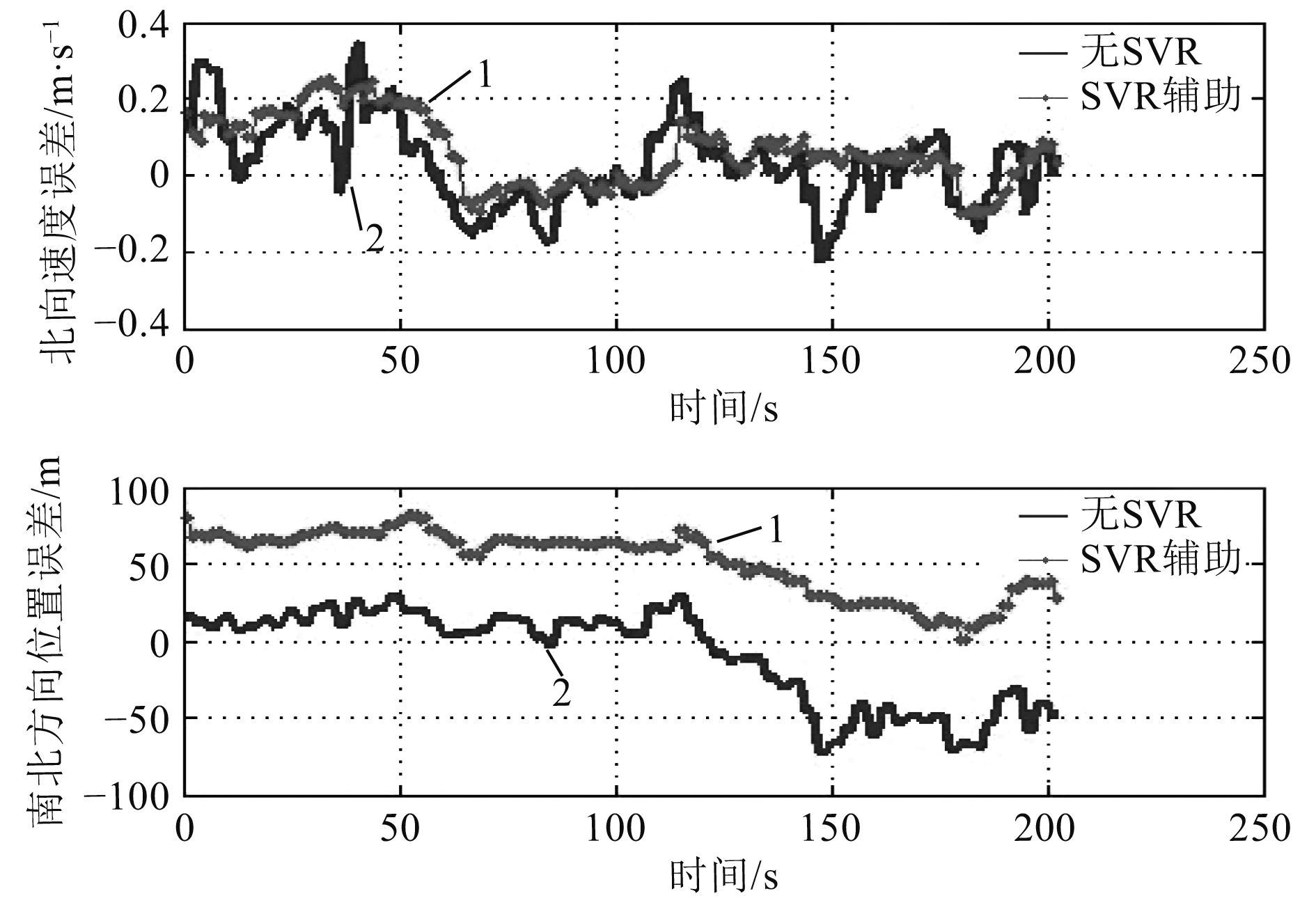
3.2 DVL数据无效时SVR辅助的SINS/DVL组合导航在上述仿真运动规划中,水下机器人在350~550 s为匀速运动,在该时间段内DVL数据无效。DVL数据无效即人为的去掉该时间段内的DVL数据。仿真情况如图8所示。
|
图 8 DVL速度无效时的北向速度和纬度误差曲线 Fig. 8 The northern velocity and latitude error curves of DVL when the speed is invalid |
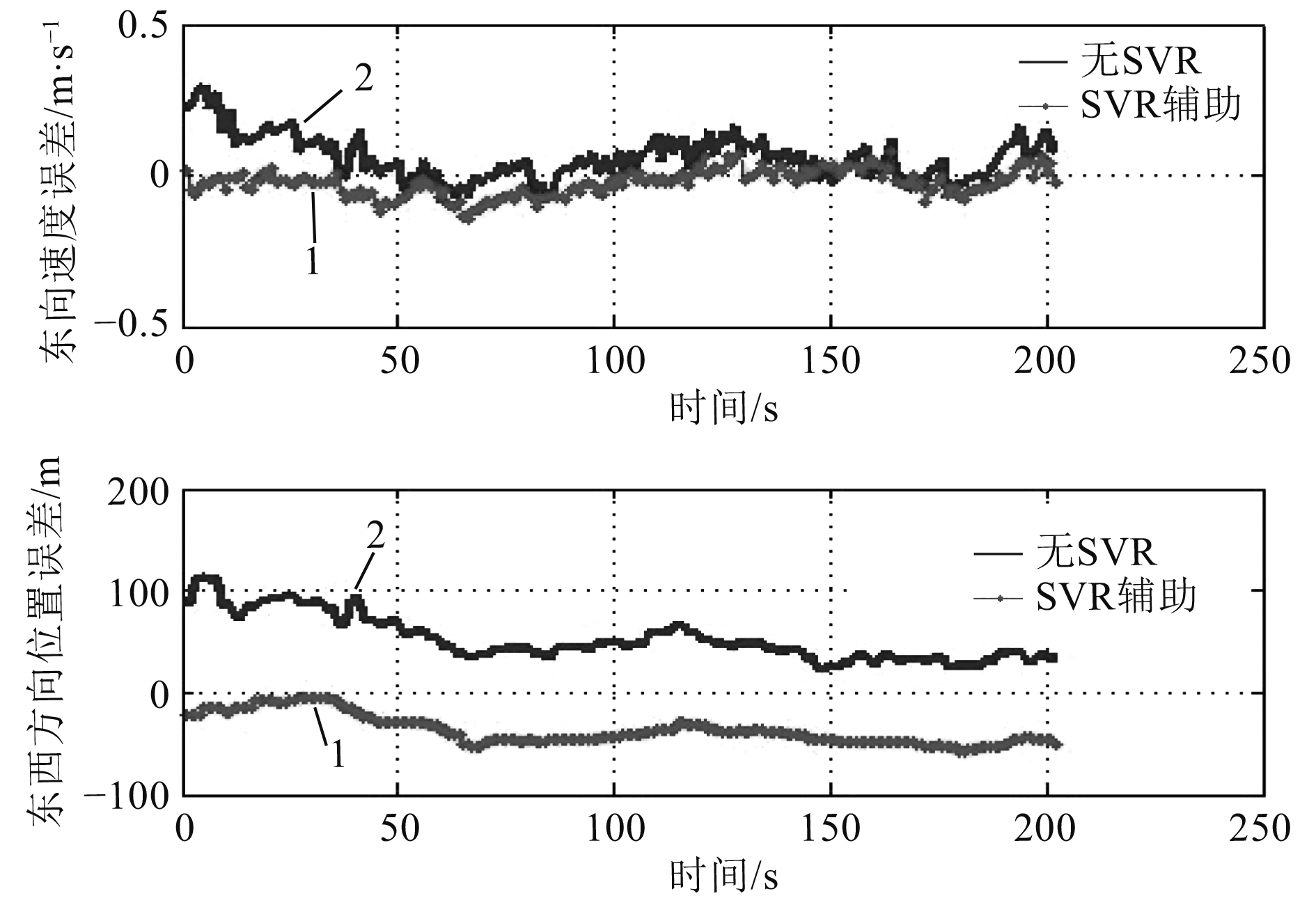
图7和图8中的曲线1为SVR辅助情况下的SINS/DVL组合导航曲线,曲线2为不加SVR辅助情况下的SINS/DVL组合导航曲线。当DVL数据无效时,单纯比较误差大小是看不出效果的,应该在基础误差(即DVL数据无效前一刻的误差),观察误差的波动情况(即观察误差在这一段时间内的方差),可以看出相对的误差增长幅度。图中曲线1的波动幅度明显小于曲线2。
|
图 7 DVL速度无效时的东向速度和经度误差曲线 Fig. 7 The eastward velocity and longitude error curves of DVL when the speed is invalid |
从表3中可以看出,当DVL数据失效时,东向速度误差收敛性提升64.81%,北向速度收敛性提升37.4%,经度误差收敛性提升57.88%,纬度误差收敛性提升54.29%。SVR辅助的SINS/DVL组合导航系统,在DVL数据失效时对于导航误差具有明显的抑制。
|
|
表 3 速度及距离误差均方差 Tab.3 Mean square error of velocity and distance |
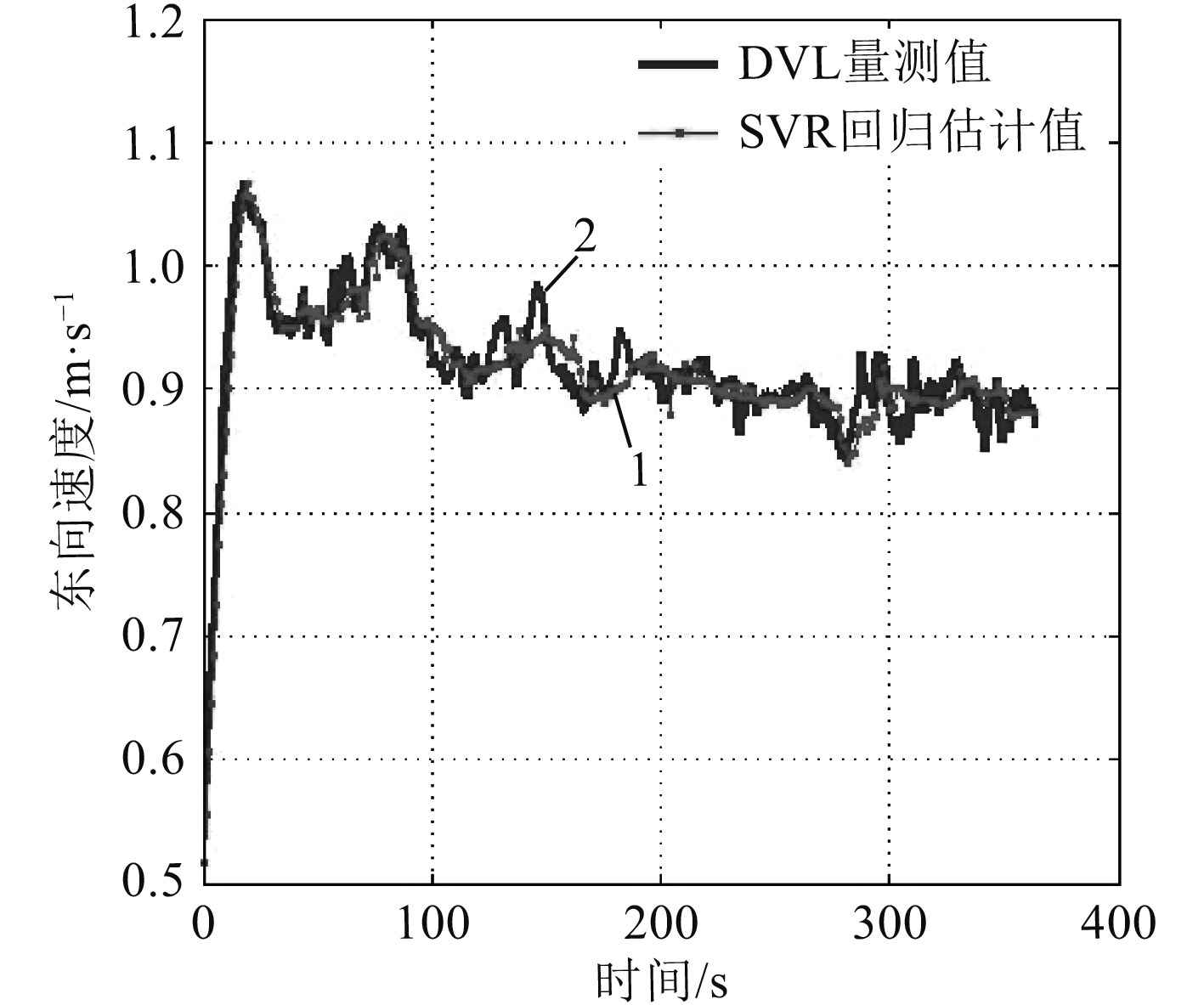
为了更加充分地验证本文提出算法的有效性,采用2017年12月AUV湖上航行试验的部分导航数据。该AUV长9.5 m,直径534 mm,空气中净重1.5 t,最大下潜深度为200 m。选取数据为前向速度不变AUV先转弯再匀速的一段数据(航向角由240°~69°并且在转弯过程中深度值和pitch角有小范围的波动)。
|
图 9 DVL数据正常时的东向速度 Fig. 9 Eastward speed when DVL data is normal |
|
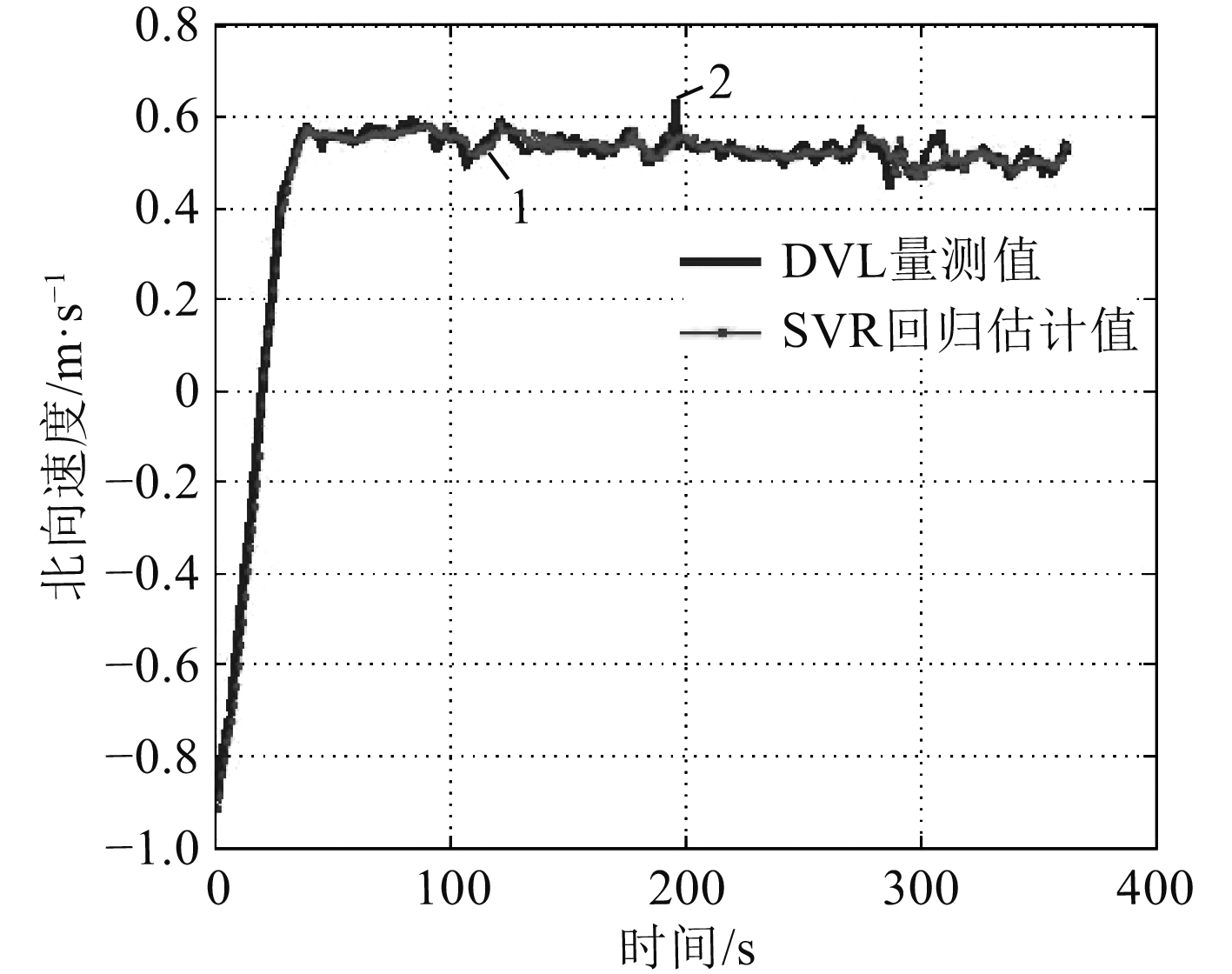
图 10 DVL数据正常时东向速度 Fig. 10 Northward speed when DVL data is normal |
图9和图10为SVR回归的情况,可以看出跟踪效果较好,在东向速度和北向速度完成变速后东向速度收敛性提升33.47%,北向速度收敛性提升27.99%。在平稳运行的过程中,SVR回归对曲线具有一定的平滑性,这同时也验证了仿真过程中经过SVR回归并适当提高数据频率会在一定程度上提高导航精度。
在AUV平稳运行过程中,一般DVL数据无效时间较短仅为数秒,并且未在AUV数据中找到连续多次上传数据均为野值的情况,所以在转弯阶段(15~20 s)和(100~110 s)分别去掉一段DVL速度数据,通过去掉部分数据当作DVL数据无效的情况。在去掉DVL速度数据时,通过比较SVR估计数据和真实量测数据来分析算法的有效性。
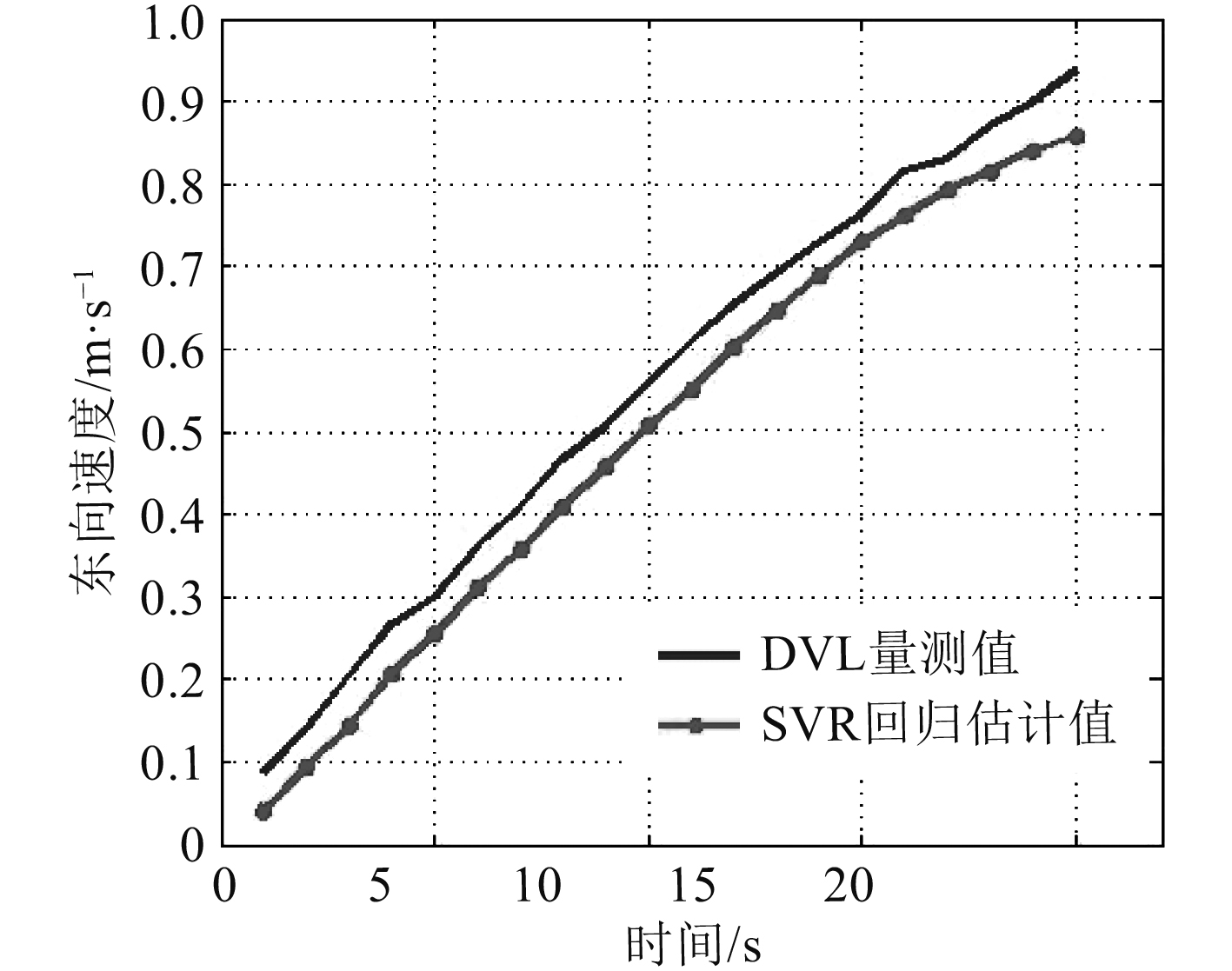
图11中在DVL数据无效阶段相对于量测值的误差均值为0.053 m,为量测值的6.17%。图12中数据误差值为0.031 m,为量测值的6.10%。可以看出在DVL数据无效时,SVR回归能够较好预测出DVL的数据值,且预测值相对于DVL真实量测误差较小,并且预测值误差的数量级已经达到了量测噪声的量级。
|
图 11 15~20 s数据无效时的东向速度 Fig. 11 15~20 s Eastward speed when data is invalid |

|
图 12 100~110 s数据无效时的北向速度 Fig. 12 100~110 s Northward speed when data is invalid |
由于SINS数据记录的不够充分,并且图9~图12中SVR=预测的DVL数据已经能够说明算法的有效性,所以不再进行经纬度数据的验证和分析。
5 结 语本文通过研究水下机器人航行过程中由于海底地形等外部环境的变化带来的DVL数据频率变化及失效等问题,提出了一种变训练集的SVR辅助SINS/DVL组合导航的方法。通过变换训练集大小提高在水下机器人机动时速度曲线的跟踪速度,解决了水下机器人运动时带来的非线性变化,并通过仿真和实际航行数据验证了该方法能够解决数据频率变化和数据无效等问题,增强了导航系统的稳定性,为后续的水下机器人试验打下基础。对于变换数据集的方法,确定尺度因子参数的数值是有难度的,仿真中确定了参数的大致范围,后续将会尝试一些优化方法确定优化参数具体值,将继续考虑在DVL数据失效的同时水下机器人机动的情况下,改进该算法并达到抑制导航误差的目的。
| [1] |
尹伟伟, 郭士荦. 非卫星水下导航定位技术综述[J]. 舰船电子工程, 2017, 37(3): 8-11. DOI:10.3969/j.issn.1672-9730.2017.03.003 |
| [2] |
SHABANI, M; GHOLAMI, A. Improved underwater integrated navigation system using unscented filtering approach[J]. Navig., 2016, 69: 561-581. DOI:10.1017/S0373463315000752 |
| [3] |
LARSEN M B. High performance doppler-inertial navigation-experimental result[C]//Ocean 2000 MITS/IEEE Conference and Exhibition. RI, USA: IEEE, 2000.
|
| [4] |
赵俊波, 葛锡云. 水下SINS/DVL组合导航技术综述[J]. 水下无人系统学报, 2018, 26(1): 2-9. |
| [5] |
SEMENIUK, L; NOURELDIN, A. Bridging GPS outages using neural network estimates of INS position and velocity errors[J]. Meas. Sci. Technol., 2006, 17: 2783-2798. DOI:10.1088/0957-0233/17/10/033 |
| [6] |
HASAN, A. M.; SAMSUDIN, K.; RAMLI, A. R.; AZMIR, R.S. Automatic estimation of inertial navigation system errors for global positioning system outage recovery[J]. Aerosp. Eng., 2011, 255: 86-96. |
| [7] |
ZHU Yixian, CHENG Xianghong, HU Jie, et al. A novel hybrid approach to deal with dvl malfunctions for underwater integrated navigation systems[J]. Applied Sciences., 2017, 7: 759. DOI:10.3390/app7080759 |
| [8] |
ZHAO L Y, LIU X J, WANG L, et al. A pretreatment method for the velocity of DVL based on the motion constraint for the integrated SINS/DVL[J]. Appl. Sci., 2016, 6: 79. DOI:10.3390/app6030079 |
| [9] |
潘峰, 徐德民. 远程AUV组合导航滤波算法[D]. 西安: 西北工业大学. 2006 http://cdmd.cnki.com.cn/Article/CDMD-10699-2006127067.htm
|
| [10] |
周志华. 机器学习[M]. 北京: 清华大学出版社. 2016.
|
 2020, Vol. 42
2020, Vol. 42
