0 引　言

近年来，在舰船噪声测试领域，体积阵以其宽频带、高增益的优势备受青睐。相对于圆柱形体积阵，螺旋双锥体积阵能够更有效的抑制干扰，更有利于实现宽频带处理。螺旋双锥体积阵也是美国近年来开展噪声测试系统研究的重点对象。

螺旋双锥体积阵波束形成是舰船辐射噪声测量领域的基础和关键。恒定束宽波束形成器能满足信号通过基阵无线性畸变的要求。现有的设计方法主要针对均匀分布线阵，如随频率变化改变阵元数或基阵等效孔径，随频率变化改变阵元振幅的权值等，但这些方法都不能有效的应用到螺旋双锥体积阵中。

本文提供了一种螺旋双锥体积阵宽带恒定束宽波束形成方法，能有效解决螺旋双锥体积阵接收信号模型及对应的恒定束宽波束形成方法问题。

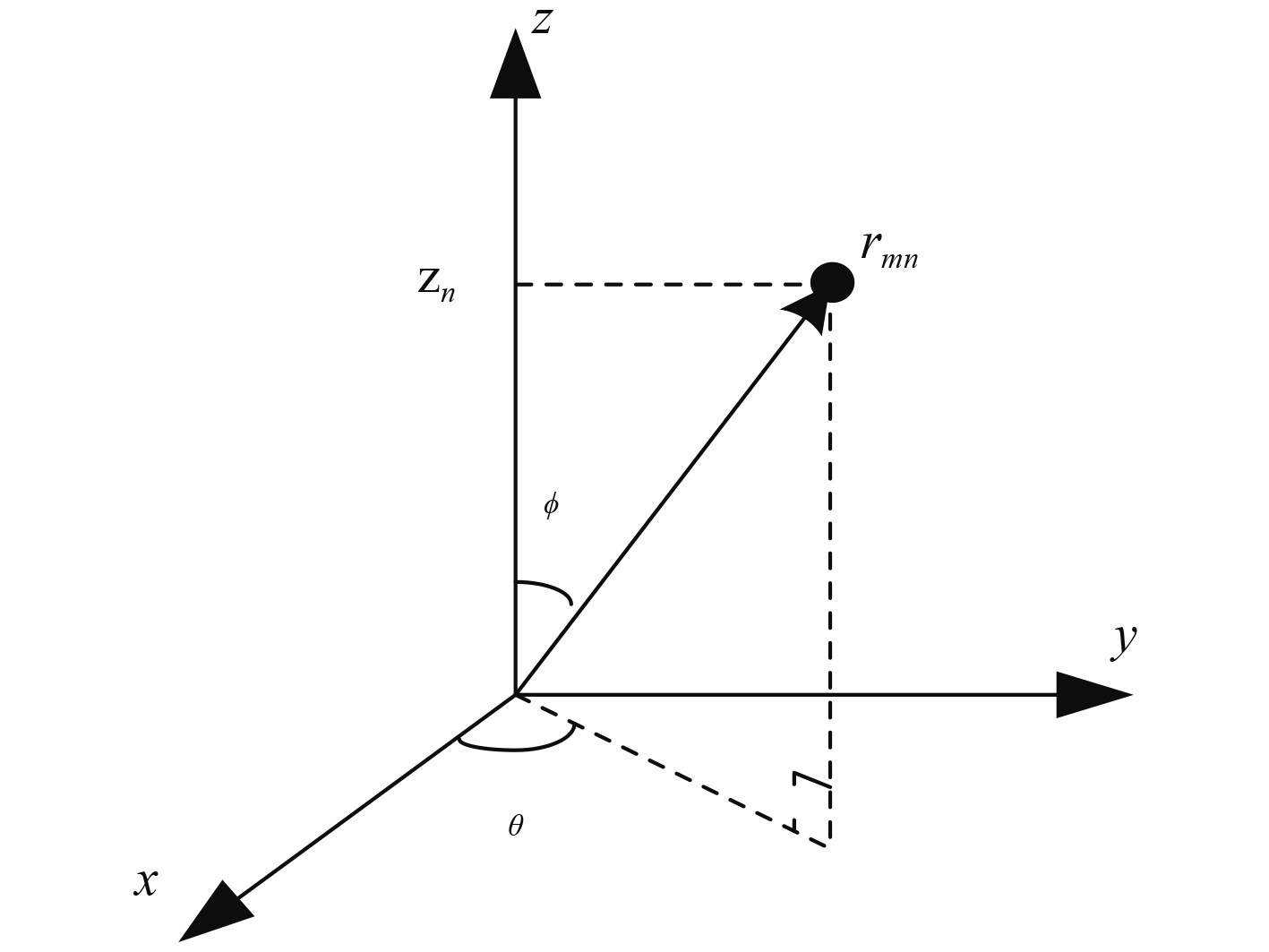
1 螺旋双锥体积阵接收信号模型 1.1 螺旋双锥体积阵阵列模型

螺旋双锥体积阵阵元坐标图如图1所示。各圆周半径为 ${r_n}$ ，阵元均匀分布，对于第n个圆周第m个阵元，位置向量可写为：

${{{r}}_m} = ({r_{xm}},{r_{ym}},{r_{zm}}) = ({r_n}\cos {\theta _m},{r_n}\sin {\theta _m},{z_n})\text{，}$

(1)

平面波从 ${{r}}$ 方向入射到基阵：

${{r}} = (\sin \phi \cos \theta ,\sin \phi \sin \theta ,\cos \phi )\text{，}$

(2)

得时延为：

${\tau _m} = {{r}} \cdot {{{r}}_m}/c = [{r_m}\sin \phi \cos ({\theta _m} - \theta ) + {z_n}\cos \phi ]/c\text{，}$

(3)

其中，c为声速。

以原点为参考点，得到阵列响应向量：

$ \begin{aligned} & {{A}}(f,\theta ) = [{e^{j(2{\text{π}} f{r_1}\sin \phi \cos ({\theta _1} - \theta ) + {z_1}\cos \phi )/c}} \\ & \cdots {e^{j(2\pi f{r_m}\sin \phi \cos ({\theta _m} - \theta ) + {z_n}\cos \phi )/c}}{]^{\rm T}} \text{。}\\ \end{aligned} $

(4)

1.2 设计参考频率下的波束图

假设宽带信号的频率范围为 $f \in [{f_L},{f_U}]$ ，令参考频率 ${f_0} = {f_U}$ ，若要形成指向 ${\theta _s}$ 的波束，则加权向量：

${{{w}}_{{f_0}}} = diag({\bf{w}}){{{A}}^H}({f_0},{\theta _s})\text{，}$

(5)

其中， ${{w}} = [{w^1} \cdots {w^M}]$ 是加权向量。则参考波束图为：

${{B}}({f_0},\theta ) = \left| {{{{w}}_{{f_0}}}{{A}}({f_0},\theta )} \right|\text{。}$

(6)

1.3 宽带恒定束宽波束的形成

宽带恒定束宽波束形成的实质是：确定波束形成的加权向量，使得 ${{B}}(f,\theta ) = \left| {{{{w}}_f}{{A}}(f,\theta )} \right| \cong {{B}}({f_0},\theta )$ 。

具体实现如下：

由平面波分解公式 ${e^{jz\cos \Psi }} = \sum\limits_{ - \infty }^\infty {{J_n}(z){{(j)}^n}{e^{ - jn\Psi }}} $ ，把阵列响应向量的各分量表示成以下Bessel函数和的形式：

$\begin{array}{l} a({r_m},{\phi _m},\theta ;f) = {e^{j2\pi f{r_m}\cos ({\phi _m} - \theta )/c}} = \\ \sum\limits_{ - \infty }^\infty {{{(j)}^n}{J_n}(2\pi f{r_m}/c){e^{jn{\phi _m}}}{e^{ - jn\theta }}}\text{，} \\ \end{array} $

(7)

令

${[{\tilde{ T}}(f)]_{mn}} = {(j)^n}{J_n}(2\pi f{r_m}/c){e^{jn{\phi _m}}}\text{，}$

(8)

${[{\tilde{ w}}(\theta )]_n} = {e^{ - jn\theta }} \; m = 1, \cdots ,M;n = 0, \pm 1, \pm 2, \cdots\text{，} $

(9)

${{A}}(\theta ,f) = {\tilde{ T}}(f){\tilde{ w}}(\theta )\text{，}$

(10)

取 $\left| n \right| = {n_\varepsilon }$ 可对 ${\tilde{ T}}(f)$ 和 ${\tilde{ w}}(\theta )$ 进行截断处理，其中， $\varepsilon $ 是符合精度要求的小量， ${n_\varepsilon }$ 是Bessel函数的阶次。截断处理后，得

$ {{A}}(\theta ,f) \cong {{T}}(f){{w}}(\theta )\text{。} $

(11)

其中： ${{T}}(f)$ 的大小为 $M \times (2{n_\varepsilon } + 1)$ ， ${{w}}(\theta )$ 的大小为 $(2{n_\varepsilon } + 1) \times 1$ 。

波束形成向量设计为：

${{{w}}_f} = {{{w}}_0}{{T}}\text{，}$

(12)

其中：

${{T}} = {{T}}({f_0}){{{T}}^ + }(f) = {{T}}({f_0}){[{{T}}{(f)^H}{{T}}(f)]^{ - 1}}{{{T}}^H}(f)\text{，}$

(13)

则波束图为：

$\begin{array}{l} {{B}}(f,\theta ) = \left| {{{{w}}_f}{{A}}(f,\theta )} \right| \cong \left| \begin{array}{l} {{{w}}_{{f_0}}}{{T}}({f_0}){[{{T}}{(f)^H}{{T}}(f)]^{ - 1}} \\ {{{T}}^H}(f){{T}}(f){{w}}(\theta ) \\ \end{array} \right| = \\ \left| {{{{w}}_{{f_0}}}{{T}}({f_0}){{w}}(\theta )} \right| \cong \left| {{{{w}}_{{f_0}}}{{A}}({f_0},\theta )} \right|\text{。} \\[-10pt] \end{array} $

(14)

即可得到恒定束宽波束图。

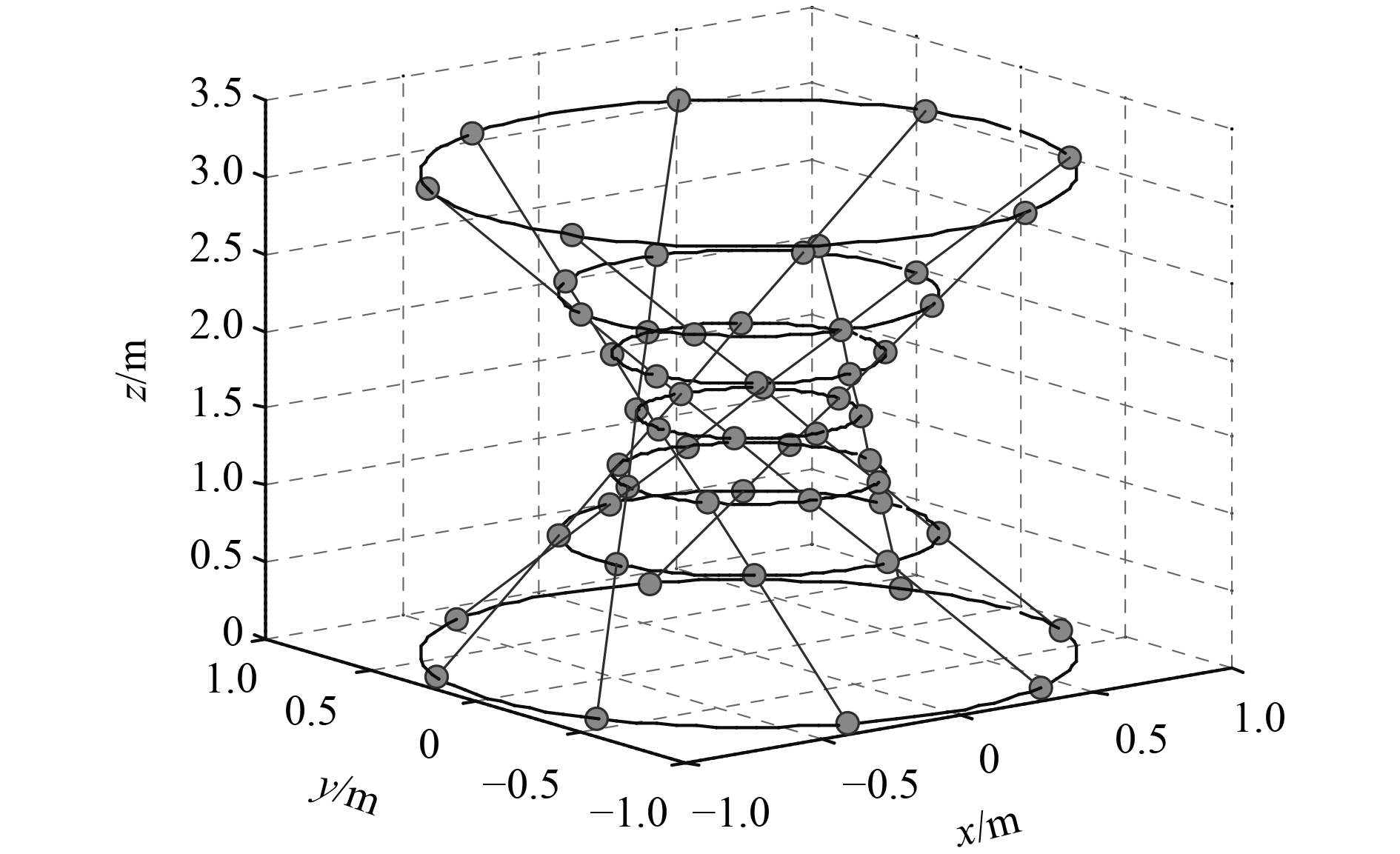
2 实　例

考虑如图2所示的螺旋双锥体积阵列，阵元数为 $M = {N_{cir}} \times {N_L} = 8 \times 7 = 56$ ，各阵元的坐标已知，声源位于阵列的远场。假设波束形成处理的频率范围为500～1 000 Hz，参考频率 ${f_0} = 1\;{\rm{kHz}}$ ，选取 ${n_\varepsilon } = 3$ 。把处理频带均匀划分为r=20个子带，并利用以上叙述的恒定束宽波束形成方法处理在每个子带内产生一个指向 $({\theta _s},{\varphi _s}) = ({0^ \circ },{90^ \circ })$ 方向的理想波束。

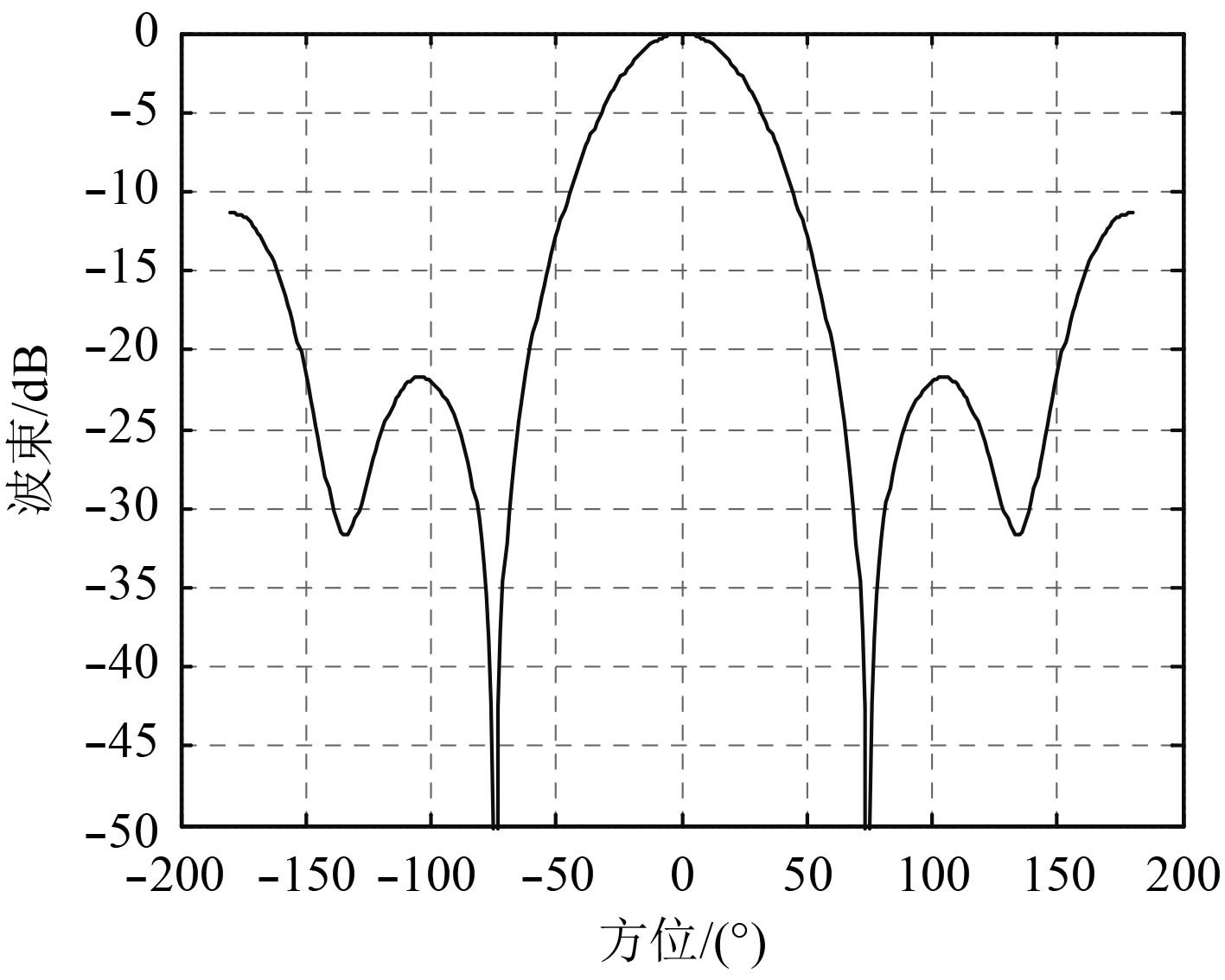
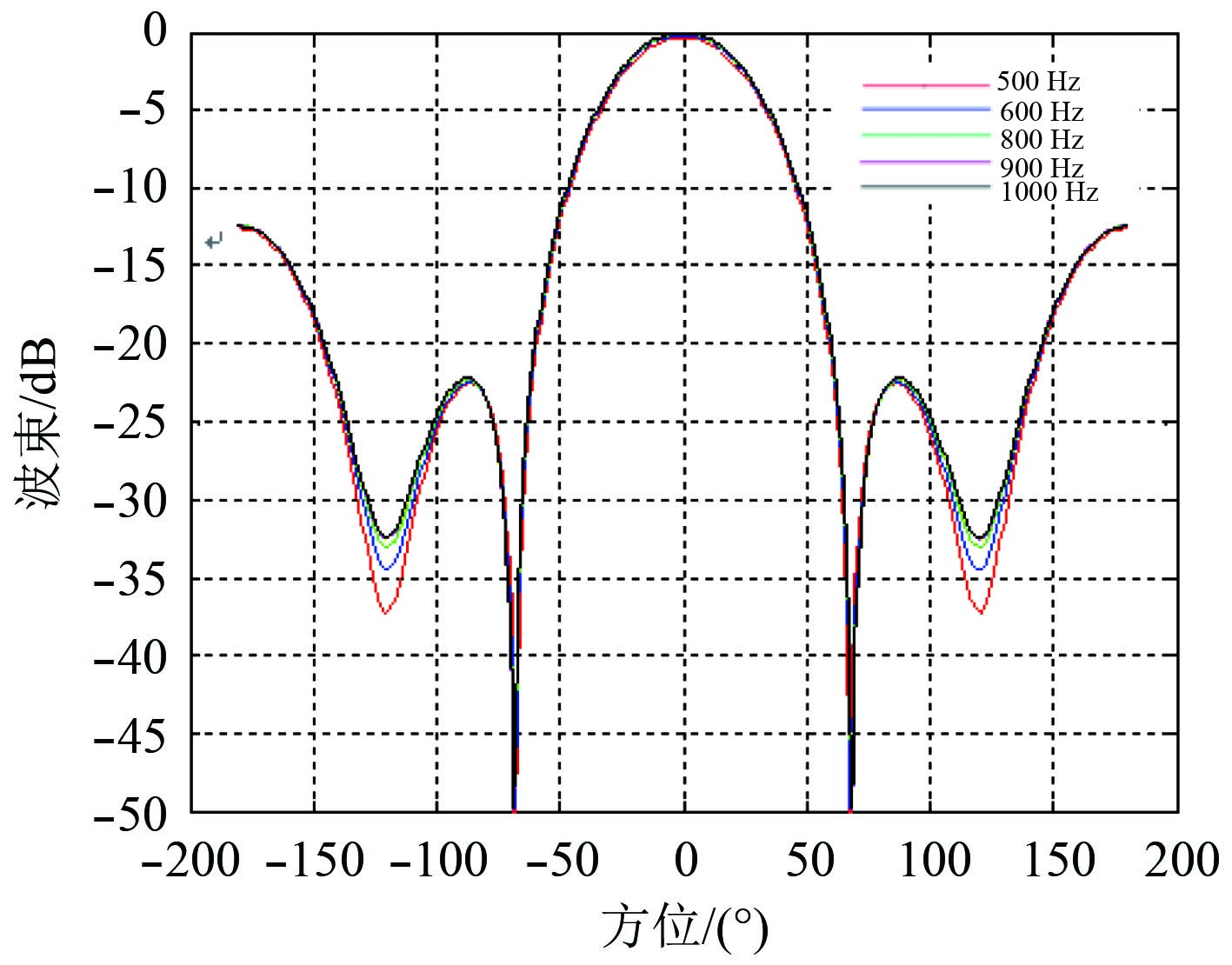
得到的参考波束图如图3所示。图4为螺旋双锥体积阵列不同频点上的恒定束宽波束叠加的波束图，图中所取频点分别为500 Hz，600 Hz，800 Hz，900 Hz和1 000 Hz。可见，其与图3的参考波束图一致，主波束在整个范围内表现出良好的恒定束宽特性和较低旁瓣级。从图4可以看出，波束的主瓣宽度为Θ–3 dB≈30°，表明该波束形成器具有很好的空间指向特性和抗噪声干扰能力。

3 结　语

本文建立了螺旋双锥体积阵接收信号模型，将阵列响应向量表示成以Bessel函数为核函数的形式。确定参考频率，将宽带划分成多个子带，使得子带内各频率分量上的波束图与参考频率上的波束图一致。通过计算机仿真，得到螺旋双锥体积阵宽带恒定束宽波束图。仿真结果表明，本文提出的宽带恒定束宽波束形成方法能有效地运用到螺旋双锥体积阵宽带信号处理中，简易且高效。

本文采用螺旋双锥体积阵接收处理宽带信号，解决了垂直线阵、矢量水听器和平面阵的各种局限，且比圆柱阵更有效的抑制干扰，更有利于实现宽频带处理。本文的方法可以用到任意的情况中，即基阵是三维的，信号从任意方向入射的情况。