舰船设备的抗冲击能力直接关系到舰船的生命力和战斗力,因此必须保证和提高舰船设备的抗冲击性能。大型的舰船设备都需要进行实船爆炸冲击实验或冲击仿真模拟分析。虽然实验获得的抗冲击结果更可靠,但是实验成本高、周期长。因此,舰船动力设备抗冲击性能数值仿真计算成为重要的分析方法之一。
美国在大量舰船爆炸实验的基础上,提出了美国军用规范MIL-S901模拟舰船设备的冲击环境,规定舰船设备冲击实验要求,以考核舰船设备的抗冲击性能。德国在BV043/73冲击标准的基础,提出了BV043-85标准[1~2],规定了舰船设备冲击时域信号的波形、幅值和作用时间,并且考虑到舰船类型、安装部位等因素的影响。我国对舰船设备抗冲击理论的研究较晚,我国国军标GJB-1060.1-91中的动力学分析方法主要参考美国军标中的一维DDAM[3~5],只能通过设备的应力来评估其抗冲击性能,不能满足特定场合通过加速度响应评估设备抗冲击性能的需求。
本文基于国军标GJB-1060.1-91[6]中动力学分析方法设计了船舶风机双层隔振装置的冲击谱,用Abaqus软件对其进行抗冲击性能仿真计算,得到中间筏体垂向的抗冲击特性。在DDAM设计的冲击谱基础上,基于遗传算法[7~8]得到冲击谱的时域冲击信号。基于时域冲击信号对风机双层隔振装置进行冲击仿真计算,得到了隔振器的最大冲击加速度
1 动力学设计分析方法动力学设计分析方法是将线弹性系统简化为承受给定冲击输入的质量弹簧系统,通过建立和求解系统中的力和变形,再运用这些力和变形计算危险区域的应力和变形,最后将所求的应力和变形与许用应力值相比较。
1.1 舰船设备抗冲击性能动力学设计分析方法 1.1.1 无阻尼系统的运动微分方程| $ \left[ {{m}} \right]\left\{ {\ddot x} \right\}{\rm{ + }}\left[ k \right]\left\{ x \right\}{\rm{ = }}0\text{,} $ | (1) |
式中,m为质量,k为刚度。假定
| $ {{{P}}_a}{\rm{ = }}\frac{{{{\left\{ {{{\bar x}_i}} \right\}}^{\rm{T}}}\left[ m \right]}}{{{{\left\{ {{{\bar x}_i}} \right\}}^{\rm{T}}}\left[ m \right]\left\{ {{{\bar x}_i}} \right\}}}\text{,} $ | (2) |
| $ {M_{na}} = {P_a}\sum\limits_i {{m_i}{{\bar x}_i} = \frac{{{{\sum\limits_i {\left[ {{m_i}{{\bar x}_i}} \right]} }^2}}}{{\sum\limits_i {{m_i}{{\bar x}_i}^2} }}}\text{。} $ | (3) |
在基础激励z作用下的无阻尼振动系统的运动方程为:
| $ \left[ {{m}} \right]\left\{ {\ddot x} \right\}{\rm{ + }}\left[ k \right]\left\{ x \right\}{\rm{ = - }}\left[ {{m}} \right]\left\{ 1 \right\}\ddot z\left( t \right)\text{。} $ | (4) |
由于固有振型的正交性特性,位移响应是所有模态的线性组合,即
| $ {\ddot q_i} + {\omega _i}^2{q_i} = - \frac{{{{\left\{ {{{\bar x}_i}} \right\}}^{\rm T}}\left[ m \right]\left\{ 1 \right\}}}{{{{\left\{ {{{\bar x}_i}} \right\}}^{\rm T}}\left[ m \right]\left\{ {{{\bar x}_i}} \right\}}}\ddot z\left( t \right)\text{,} $ | (5) |
将式(5)代入式(4)可得:
| $ {\ddot q_i} + {\omega _i}^2{q_i}{\rm{ = }} - {p_a}\ddot z\left( t \right)\text{,} $ | (6) |
根据Duhamel积分,在零初始条件下的模态位移解为:
| $ {q_i} = - \frac{{{p_i}}}{{{\omega _i}^2}}\int_0^t {z\left( \tau \right)} \sin {\omega _i}\left( {t - \tau } \right){\rm d}\tau \text{。} $ | (7) |
由式(7)得到系统的最大模态位移为:
| $ {q_{im}} = - \frac{{{p_i}{v_i}}}{{{\omega _i}}}\text{,} $ | (8) |
式中,Vi为速度由冲击谱确定。
第i阶模态中最大的位移为:
| $ \left\{ {{x_i}} \right\} = \left\{ {{{\bar x}_i}} \right\}{q_{im}}\text{,} $ | (9) |
第i阶模态中的动态力为:
| $ \left\{ {{F_i}} \right\} = \left[ k \right]\left\{ {{{\bar x}_i}} \right\}{q_{im}}\text{,} $ | (10) |
作用在各质点上的动态力为:
| $ {F_{ia}} = {m_i}{\bar x_{ia}}{P_a}{A_i}\text{。} $ | (11) |
Abaqus软件谱分析中主要提供3种模态合成的方法:平方和的均方根(SRSS),绝对值求和(ABS)和美国海军研究室求和(NRL)。GJB-1060.1-91中要求使用NRL方法合成隔振装置的位移和应力。其中NRL的计算公式为:
| $ {x_i} = {x_{ib}} + \sqrt {\sum\limits_a {{x_{ia}}^2 - x_{ib}^2} }\text{。} $ | (12) |
式中,
用Hypermesh软件建立舰船风机双层隔振系统的有限元模型。在有限元建模中,筏体和风机采用四面体单元,基座采用六面体单元。风机双层隔振装置有限元模型如图1所示。其中,坐标轴XYZ分别为横向,纵向和垂向。筏体通过6JX-45型隔振器和6JX-25型隔振器分别与风机和基座相连接。隔振器简化为三向弹簧,分别定义3个方向的动刚度。在保证风机质量和重心不变的前提下,将它简化成圆环体。

|
图 1 风机双层隔振装置有限元模型 Fig. 1 Finite element model of the double-layer vibration isolation device of the fan |
风机双层隔振装置安装位置在船体,按照国军标GJB-1060.1-91中的要求,应采用弹性设计。根据模态分析获得的频率和模态质量设计冲击谱,优先考虑低频率的模态,应该保证参与的模态质量大于分析系统的80%,DDAM设计冲击谱见表1。表2是风机双层隔振装置在船体安装时,3个方向的加速度和速度设计值。由表2可知,风机双层隔振装置受垂向冲击影响较大,只要垂向合成的应力能够满足材料许用应力,横向纵向的应力就能满足要求。表3是风机双层隔振装置按照GJB-1060.1-91中选取的模态频率、模态质量及冲击谱设计加速度值。
|
|
表 1 设计冲击谱 Tab.1 Design shock spectrum |
|
|
表 2 船体安装时的A0,V0 Tab.2 A0 and V0 during hull installation |
|
|
表 3 垂向冲击设计加速度 Tab.3 Design acceleration of vertical impact |
式中:ma为模态质量,t,A0为标称加速度谱,m/s2;Va为标称速度谱,m/s2。
2.3 筏体的应力合成通过Abaqus中的谱分析,选择NRL模态合成方法进行应力合成,得到筏体的应力云图如图2所示。可以看出,筏体应力集中的区域在布置隔振器的位置附近,其中最大应力出现在筏体与基座相连接的隔振器处,其最大值为66.5 MPa,远远小于材料的许用应力235 MPa,因此,风机双层隔振装置受冲击时不会失效。

|
图 2 垂向冲击时筏体的应力云图 Fig. 2 Stress cloud diagram of raft during vertical impact |
以上依据GJB-1060.1-91指定的方法对风机双层隔振装置进行抗冲击性能分析,以冲击谱为输入激励,计算筏体应力是否超过材料的许用值。但是很多场合需要通过机械设备的加速度响应评价其是否符合抗冲击性能要求,而机械设备的加速度响应需要通过输入冲击时域信号进行计算。很多工程应用中是根据德国军标BV043-85中的经验公式将冲击谱转换为三角波或半正弦波的时域曲线,这种方法转换的时域曲线与实际爆炸冲击信号的特性相差较大。为此,本文基于遗传算法对DDAM方法设计的冲击谱进行时域合成,得到更符合实际的时域冲击信号。
3.1 冲击谱的时域信号形式实际爆炸冲击信号具有高频振荡然后快速衰减的特性。所以,如何选取合适的基波函数的组合形式来表示待合成的冲击谱时域信号至关重要。以衰减的正弦基波函数的组合形式来表示冲击谱的时域信号方法[9]已经被使用多年,衰减正弦基波的组合形式被证明可以匹配冲击谱,所以冲击谱的时域信号形式可以表示为:
| $ x = \sum\limits_{i = 1}^n {{A_i}} {e^{ - \xi {\omega _i}t}}\sin \left( {{\omega _i}t + {\varphi _i}} \right)\text{。} $ | (13) |
式中:
遗传算法工具箱要求构造合适的适应度函数,所以需要将冲击谱的时域信号进行换算。1981年Smallwood提出的改进的递归数字滤波法,改进的递归数字滤波法[10~11]具有计算速度快、效率高的优点。本文采用改进的递归数字滤波法进行冲击谱换算,递归公式为:
| $ {y_i} = {b_0}{x_i} + {b_1}{x_{i - 1}} + {b_2}{x_{i - 2}} + {q_1}{y_{i - 1}} + {q_2}{y_{i - 2}}\text{。} $ | (14) |
式中:ωn为系统无阻尼固有频率;ω0为系统有阻尼固有频率;i表示第i个频率点;y1和y2分别为第1个和第2个冲击响应谱,均为0。阻尼比
| $ \left\{ \begin{gathered} {b_0} = 1 - \exp \left( { - D} \right){{\sin \left( E \right)} / E}\text{,} \\ {b_1} = 2\exp \left( { - D} \right)\left[ {{{\sin \left( E \right)} / E} - \cos \left( E \right)} \right] \text{,} \\ {b_2} = 2\exp \left( { - D} \right)\left[ {{{\left[ {\exp ( - D)} \right]} / E} - {{\sin E} / E}} \right] \text{,} \\ {q_1} = 2\exp ( - D)\cos (E) \text{,} \\ {q_2} = - \exp ( - 2D)\text{,} \\ D = \xi {\omega _n}\vartriangle t \text{,} \\ {\omega _n} = 2\pi {f_n}\text{,} \\ {\omega _0} = {\omega _n}\sqrt {1 - {\xi ^2}} \text{,} \\ E = {\omega _0}\vartriangle t \text{,} \\ {y_1} = 0 \text{,} \\ {y_2} = 0 \text{。} \\ \end{gathered} \right.$ |
遗传算法中的适应度是描述个体性能的重要指标,适应度函数更直接影响到遗传算法的收敛速度和是否能找到最优解。不同的适应度函数会获得不同的优化结果,所以构造合适的适应度函数至关重要,适应度函数为:
| $ F = \sum\limits_{i = 1}^n {\frac{{{{\left( {y({f_i}) - {y_0}({f_i})} \right)}^2}}}{n}}\text{。} $ | (15) |
式中:y(f)是通过改进的递归数字滤波法对冲击谱的时域信号进行换算得到的冲击谱;y0(f)是由DDAM方法计算得到的冲击谱。
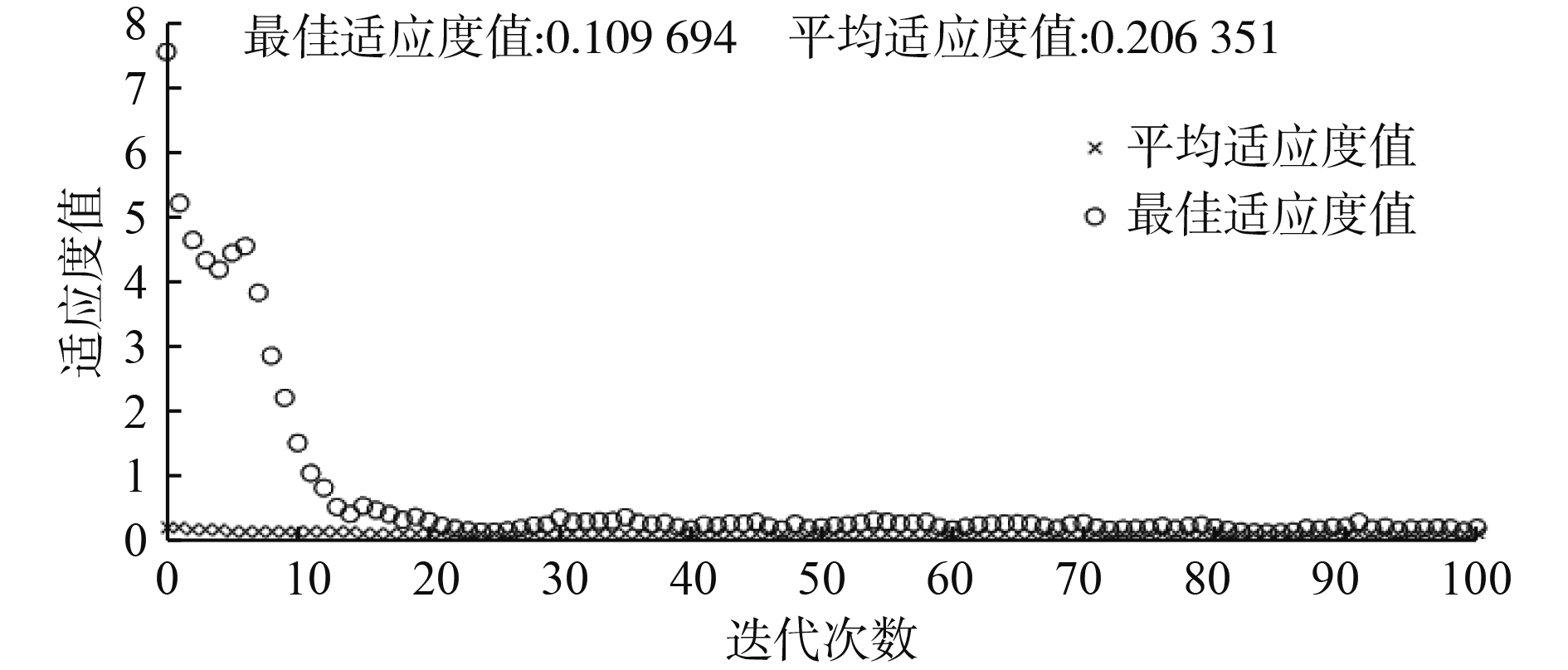
根据DDAM方法设计的冲击谱,在25~800 Hz频率范围内,按照1/6倍频程划分有30个中心频率点。遗传算法中遗传种群数目为50,变异概率为0.05,交叉概率为0.8。幅值Ai的取值范围为[−2.5,2.5],相位为[−π,π],通过遗传算法计算得到的最终适应度值为0.109 694。
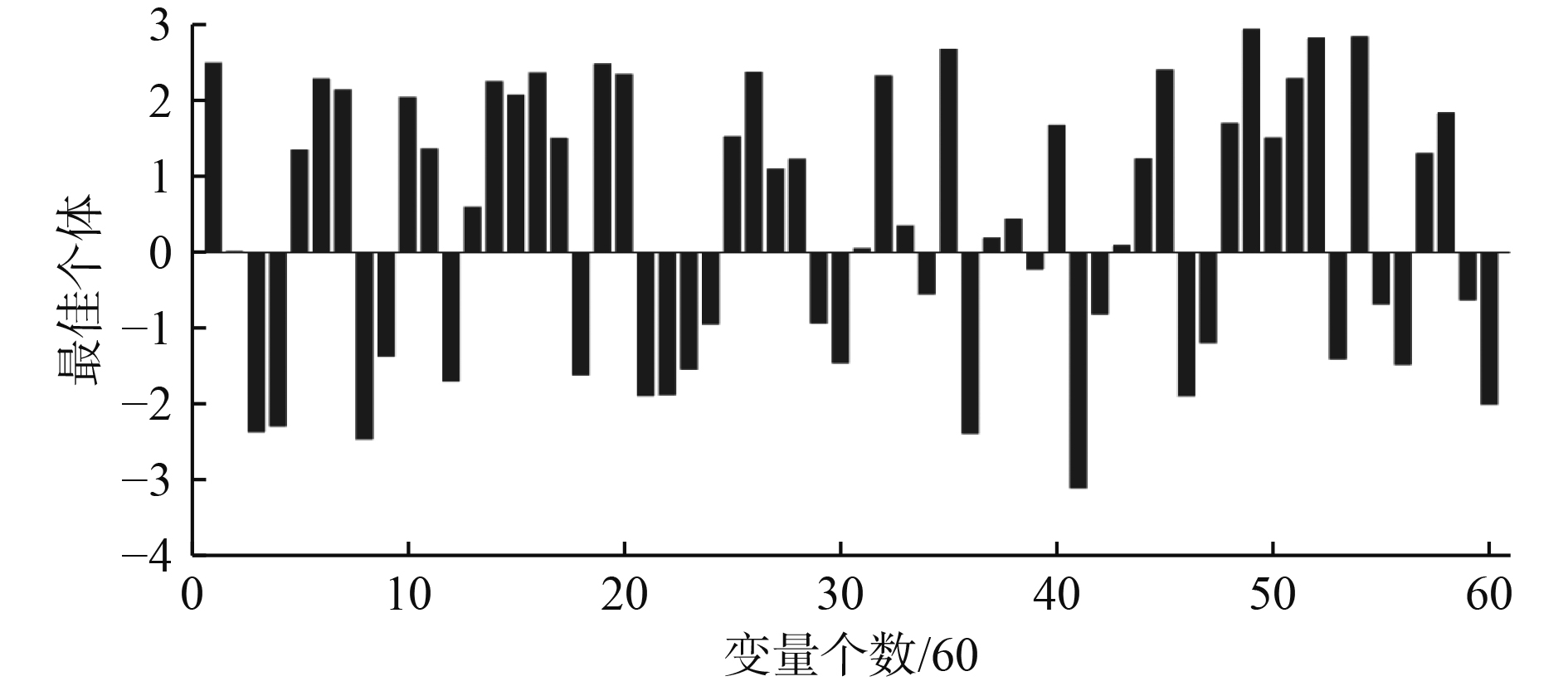
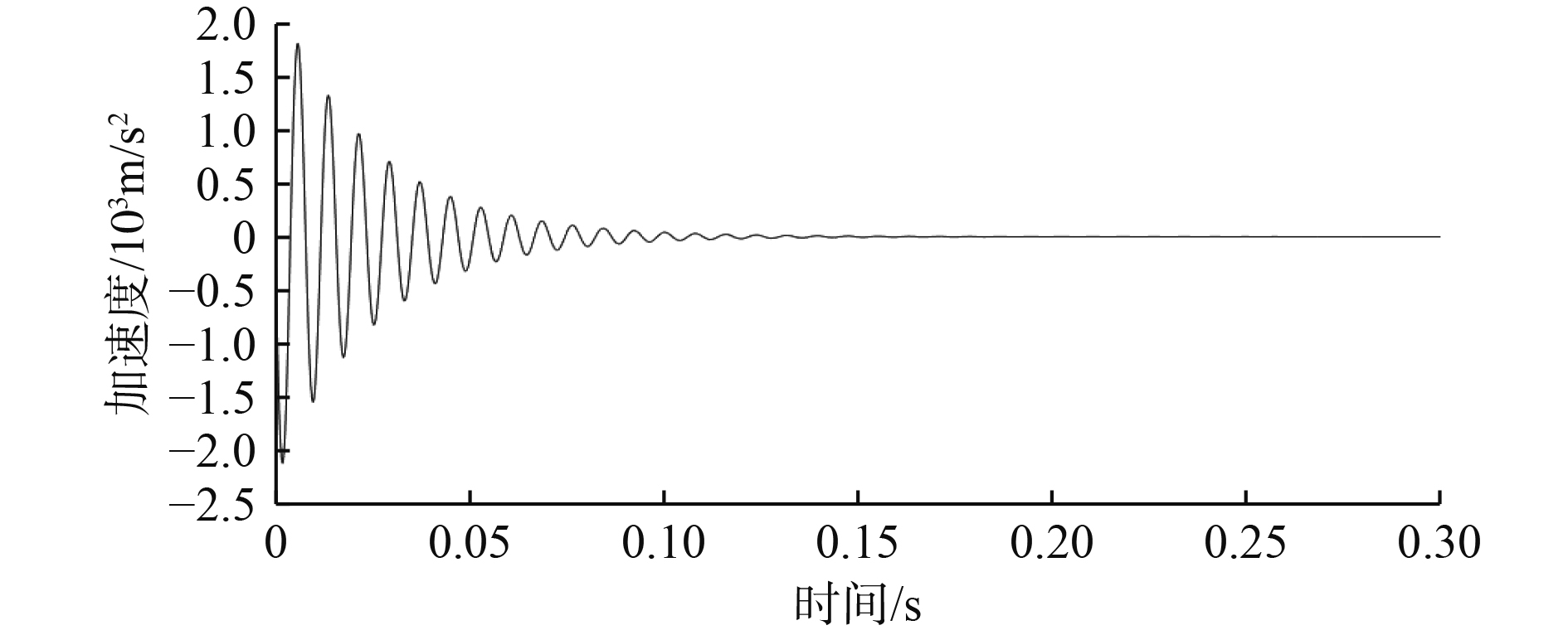
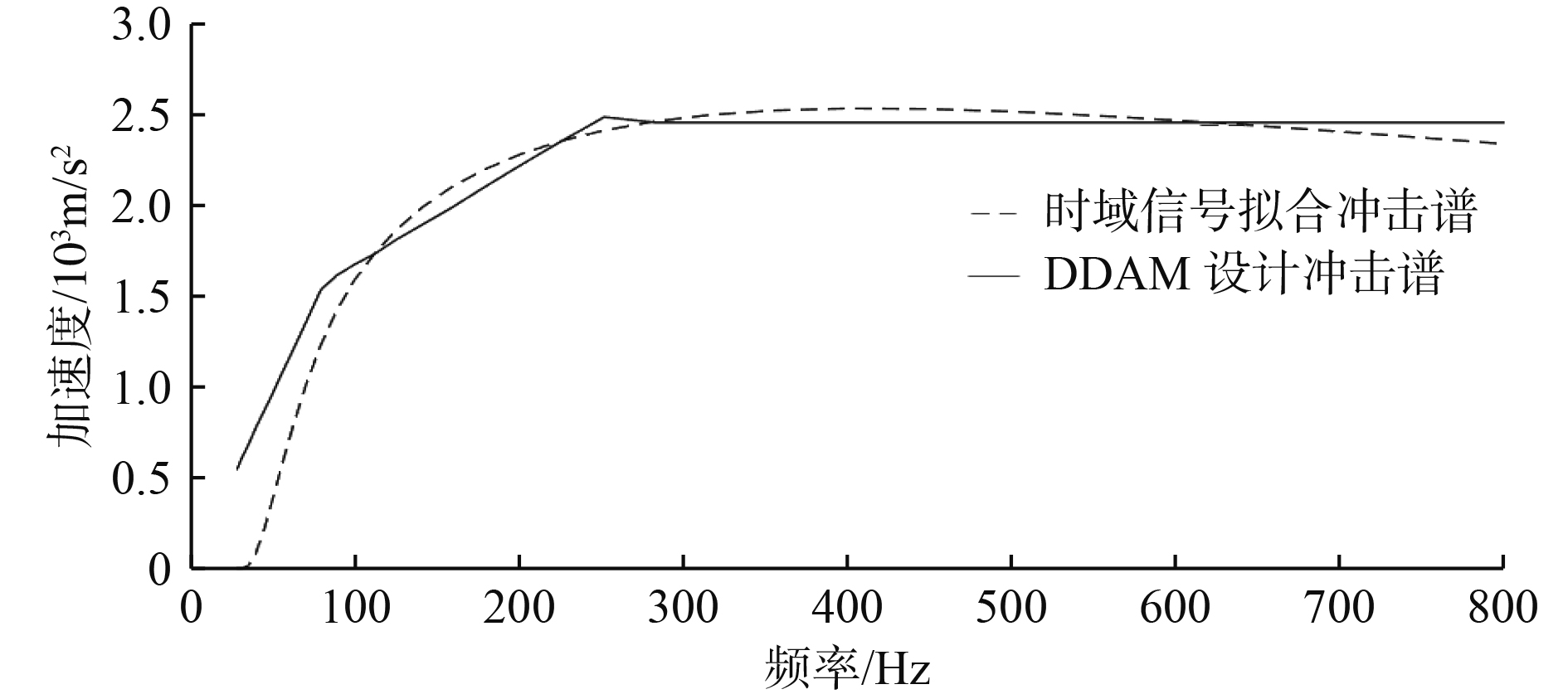
图3为最佳适应度和平均适应度。可以看出,迭代到100代时,最佳适应度值向0.1收敛。图4为遗传算法优化中,最佳个体对应的幅值和相位,相应的幅值和相位构成了冲击谱时域信号。图5为最佳个体对应的各个频率下的幅值和相位得到的冲击时域信号。冲击谱转换得到的冲击时域信号中的高频成分振荡后快速衰减,与实际爆炸冲击信号的特点相似。冲击时域信号通过改进的递归数字滤波法得到的冲击谱和通过DDAM设计的冲击谱关系,如图6所示。可以看出,冲击时域信号转换后的冲击谱和DDAM设计的冲击谱具有很好的一致性,表明通过遗传算法得到的冲击谱时域信号能满足计算要求。
|
图 3 适应度值变化图 Fig. 3 Variation of fitness values |
|
图 4 最佳个体幅值和相位 Fig. 4 Optimal individual amplitude and phase |
|
图 5 冲击信号时间历程 Fig. 5 Time history of impact signal |
|
图 6 冲击谱曲线 Fig. 6 Shock spectrum curve |
采用Abaqus对风机双层隔振装置进行抗冲击分析,计算其加速的响应。首先按照GJB-1060.1-91设计出冲击谱,然后采用遗传算法和改进的递归算法转换得到其冲击时域信号。将冲击谱时域信号施加在基座的底座上,输出上层隔振器上、下两端的垂向加速度响应和筏体的最大应力云图,如图7~图9所示。
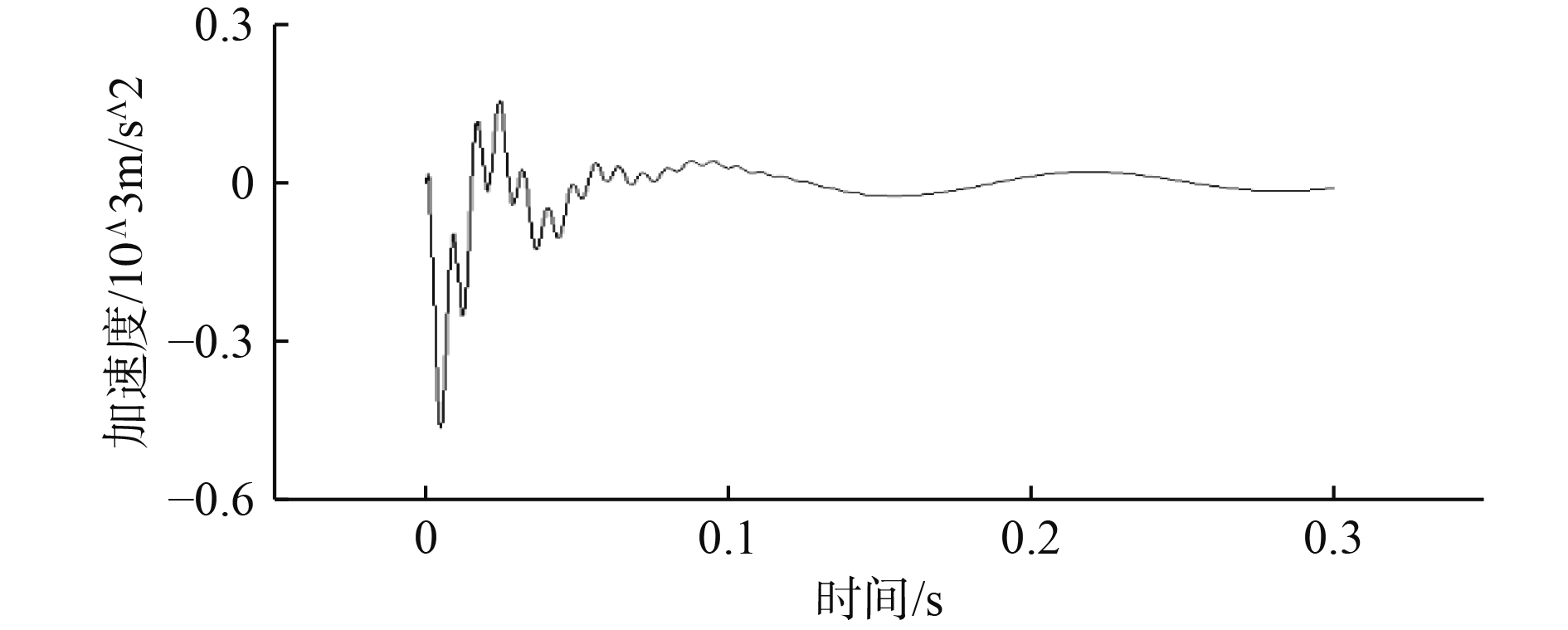
|
图 7 上层隔振器下端的加速度响应 Fig. 7 Acceleration response at lower end of upper vibration isolator |

|
图 9 筏体垂向冲击的应力云图 Fig. 9 Stress cloud diagram of vertical impact of raft |
由图7和图8可以看出,上层隔振器上、下端的加速度响应峰值分别46 g和14 g,与图5中输入冲击信号的峰值212 g相比,分别降低了166 g和198 g。表明风机双层隔振装置的隔冲效果明显。图9可以看出,在冲击时域信号下筏体的最大应力和DDAM冲击谱激励下的最大应力误差为9.1%,表明合成的冲击时域信号与DDAM方法设计的冲击谱有很好的一致性。因此,基于遗传算法改进的DDAM方法能拓展GJB-1060.1-91中舰船设备抗冲击性能分析方法的应用范围。
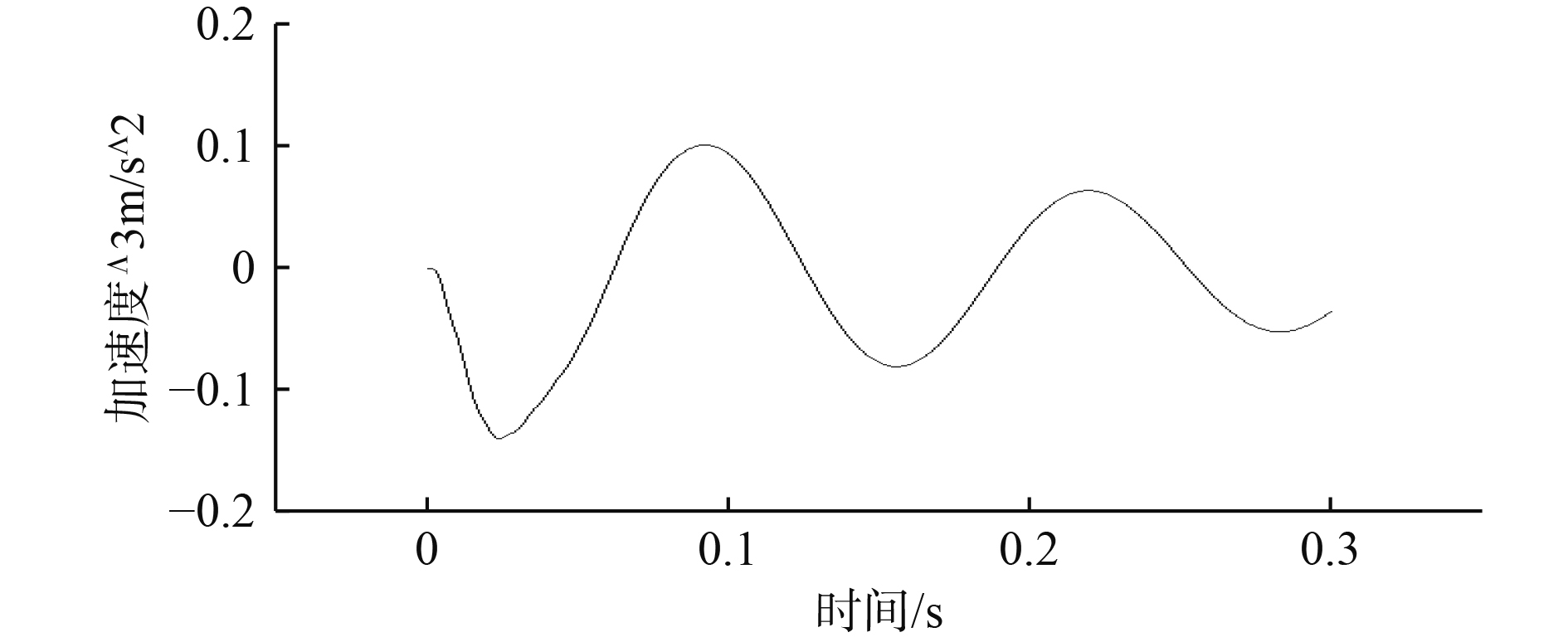
|
图 8 上层隔振器上端的加速度响应 Fig. 8 Acceleration response at upper end of upper vibration isolator |
1)本文基于GJB-1060.1-91中的动力学设计分析方法设计了风机双层隔振装置的冲击谱,并对风机双层隔振装置进行抗冲击计算,得到的筏体的应力云图表明,应力主要集中在隔振器安装的部位,且最大应力远远小于材料的许用值,可以保证筏体在冲击环境中的安全性。
2)利用衰减正弦基波的组合形式表示待合成的冲击时域信号,通过遗传算法和改进的递归数字滤波法获得冲击谱的时域信号。冲击谱时域信号转换后的频域信号与DDAM设计的冲击谱具有很好的一致性。通过遗传算法对冲击信号时域合成,可以解决GJB-1060.1-91中DDAM方法只能在频域上计算的缺点,而且相比较于德国军标BV043-85中通过经验公式设计的三角波或半正弦波,更符合爆炸冲击时域信号的特点,有助于拓展GJB-1060.1-91中舰船设备抗冲击性能分析方法的工程应用范围。
3)对风机双层隔振装置进行抗冲击计算,上层隔振器上端的冲击加速度响应峰值为14g,与输入冲击加速度峰值212g相比降低了198g,表明风机双层隔振装置的隔冲效果明显。
| [1] |
童水光, 魏超, 费钟秀, 等. 船用齿轮箱系统抗冲击特性数值仿真[J]. 振动与冲击, 2012, 31(12): 79-85. |
| [2] |
陈海龙, 姚熊亮, 张阿漫, 等. 船用典型动力设备抗冲击性能评估研究[J]. 振动与冲击, 2009, 28(2): 45-50. DOI:10.3969/j.issn.1000-3835.2009.02.012 |
| [3] |
赵应龙, 何琳, 吕志强. 应用DDAM进行船舶浮筏隔振装置抗冲击计算[J]. 工程力学, 2007, 24(4): 159-167. DOI:10.3969/j.issn.1000-4750.2007.04.028 |
| [4] |
计晨, 汪玉, 赵建华, 等. 舰用柴油机抗冲击性能频域分析[J]. 振动与冲击, 2010, 29(11): 171-176. DOI:10.3969/j.issn.1000-3835.2010.11.037 |
| [5] |
浦军, 石邦凯. 基于DDAM的某舰用升降装置抗冲击分析[J]. 舰船科学技术, 2017, 39(15): 128-132. |
| [6] |
GJB-1060.1-91, 中华人民共和国国家军用标准-舰船环境条件要求机械环境[S].北京: 国防科学技术工业委员会, 1991.
|
| [7] |
曹源, 汪凤泉, 桂益俊. 基于遗传算法的冲击信号拟合[J]. 东南大学学报(自然科学版), 2007, 37(2): 320-323. DOI:10.3321/j.issn:1001-0505.2007.02.027 |
| [8] |
曹源, 汪凤泉, 童丽萍. 冲击响应谱匹配的改进多目标遗传算法研究[J]. 应用科学学报, 2007, 25(3): 311-316. DOI:10.3969/j.issn.0255-8297.2007.03.018 |
| [9] |
马道远, 庄方方, 徐振亮. 基于遗传算法的冲击响应谱时域合成方法[J]. 强度与环境, 2015, 42(5): 49-53. |
| [10] |
华师韩, 田恒春. 冲击响应谱计算相关参数选择的研究[J]. 遥测遥控, 2005, 26(6): 50-55. DOI:10.3969/j.issn.2095-1000.2005.06.011 |
| [11] |
任昌, 潘宏侠. 基于冲击信号的冲击响应谱研究[J]. 火炮发射与控制学报, 2010(3): 21-24. DOI:10.3969/j.issn.1673-6524.2010.03.006 |
 2020, Vol. 42
2020, Vol. 42
