2. 海军工程大学 动力工程学院,湖北 武汉 430033
2. College of Power Engineering, Naval University of Engineering, Wuhan 430033, China
轴系是船舶推进系统的重要组成,其校中质量对推进系统乃至整个船舶的长期安全可靠运行具有重要意义。为改善轴系轴承的负荷分配、轴段应力分布等,使轴系处于更为优良的工作状态,目前国内外船厂普遍采用合理校中技术。在轴系合理校中优化理论研究方面,周瑞平[1]、周瑞[2]运用最优化方法得到轴承的最优变位值,使轴系尾后轴承负荷最小;Reeves[3]和魏颖春等[4]基于有限元法建立了校中模型,通过优化程序对船舶轴系的各轴承进行了合理变位;陆金铭等[5]提出了一种基于反影响数矩阵的校中优化方法,并用该方法对实船轴系进行了双向校中。在轴系校中与轴系振动间相互作用规律的研究方面,杨俊等[6]通过数学建模得出了不对中轴系激励力幅值与振动的相互关系;方国强[7]用有限元法对轴系校中参数与轴系振动特性的相关性开展了仿真研究;刘学伟等[8]用传递矩阵法分别建立了轴系校中与弯曲振动数学模型,并发现在不同校中实例中,高频段的轴承响应具有明显差别。
现有轴系校中技术在实施过程中都是从静力学角度出发,将轴系敷设成轴承负荷、轴段应力等处于规定范围内的某一曲线状态,以确保轴系强度满足安全运行要求,并未考虑校中对轴系振动的影响。本文在合理校中的基础上,利用奇异函数法和传递矩阵法分别构建了轴系校中计算和轴系振动模型,并用雷诺方程实现模型间的参数转化,最后利用多目标优化技术对轴系双向校中模型进行求解。这样,在校中时就将轴系振动特性计入了优化过程中,且能满足原有轴系校中的各项要求。研究结果表明,该方法能有效改善轴系的受力状态和振动特性,提高校中质量。
1 理论依据 1.1 奇异函数法与校中状态参数计算轴系校中的实质是轴承位置的改变,不同轴系校中方案下,轴系状态参数如轴系轴承负荷、轴段应力、截面转角等也不同。根据《CB/Z 338-2005船舶推进轴系校中》标准中的规定,校中完成后轴系各状态参数应在合理范围内,因而轴系校中的前提是求解这些状态参数。奇异函数法是一种计算轴系校中状态参数较为精确简洁的方法,其基本表达式如下:
| $F(x) = < x - a{ > ^n}\text{。}$ | (1) |
将轴系承受的载荷用奇异函数表示后,当已知特定校中方案下各轴承变位,结合静力平衡条件即可计算出轴系各状态参数[9]。
1.2 传递矩阵法与轴系弯曲振动求解以螺旋桨末端为坐标原点,沿船艏方向为x轴,过原点垂直于x轴向上为y轴建立直角坐标系xoy,根据该坐标系对船舶推进轴系进行简化如图1所示。图中F(t)为施加在螺旋桨处的单位横向简谐力,k1,k2,k3,k4,k5为各轴承支承刚度。本文采用修正后的Timoshenko梁自由弯曲振动方程求解轴系振动的场传递矩阵,其表达式如下:
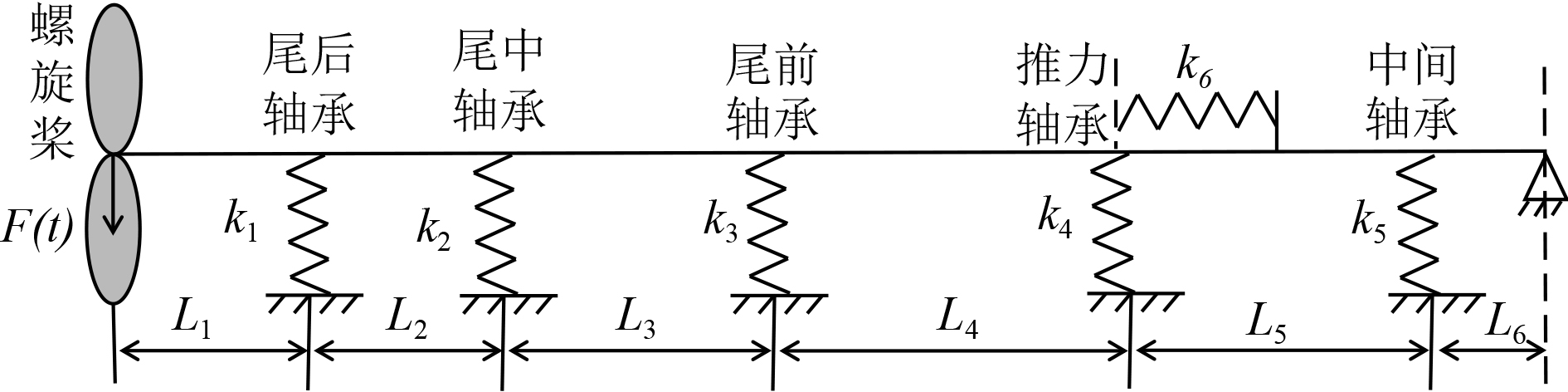
|
图 1 船舶推进轴系简化图 Fig. 1 Simplified diagram of ship propulsion shafting |
| $EI\frac{{{\partial ^{\rm{4}}}y}}{{\partial {x^4}}} + m\frac{{{\partial ^2}y}}{{\partial {t^2}}} - m{r^2}\frac{{\partial {y^4}}}{{\partial {x^2}\partial {t^2}}} - \frac{{EI}}{{K'AG}}m\frac{{\partial {y^4}}}{{\partial {x^2}\partial {t^2}}} = 0\text{。}$ | (2) |
式中:E,G分别为梁的弹性,剪切模量;A为梁横截面;I为梁截面惯性矩;m为梁单位长度质量;r为梁半径;K'为梁有效剪切系数;y(x,t)为梁位移变形量。
求解式(2)可得出梁振型函数,并进一步求得轴系各状态参数[8]。设图1中轴系最左端状态矢量为[y0a0M0Q0],最右端状态矢量为[y a M Q],[Ti]为各轴段场传递矩阵,[Pi]为各集中质量及轴承支承点处的传递矩阵,则有:
| ${[y{\rm{ }}a{\rm{ }}M{\rm{ }}Q]^{\rm{T}}} = [T]{[{y_0}{\rm{ }}{a_0}{\rm{ }}{M_0}{\rm{ }}{Q_0}]^{\rm{T}}}\text{。}$ | (3) |
式中,[T]=P0T1P1T2P2T3P3T4P4T5P5T5P6。
结合轴系边界条件可对式(3)进行求解,并得出各支承轴承处状态参数,其中位移响应y(x,t)与轴承刚度的乘积即经轴承传递到基座上的作用力。
用一个周期内传递到基座的能量平均值,即用稳态传递功率流来衡量推进轴系各支承轴承处弯曲振动情况如下式:
| $ \begin{split} {{\rm{Q}}_i} =& \frac{w}{{2{\text{π}} }}\int_0^{2{\text{π}}/\omega } {\rm Re}({F_i}){\rm Re}({v_i})dt =\\ & \frac{1}{2}{\rm Re}\left\{ {{F_i}(\omega )} \cdot {\left[ {j\omega {y_i}^{\rm{*}}(\omega )} \right]} \right\}\text{。} \end{split} $ | (4) |
式中:Re()表示取实部;“*”表示取共轭;vi,Fi分别为第i个轴承的速度响应与传递到基座上的作用力;vi可由位移响应yi微分后求得。
1.3 雷诺方程与轴系校中参数的转化轴承刚度主要取决于油膜刚度。为求解不同校中方案下的轴系振动响应,须将轴系校中时的轴承负荷变化量转化为轴承刚度变化量。这要用到求解轴承润滑特性的雷诺方程:
| $ \frac{\partial }{{\partial x}}\left(\frac{{{h^3}}}{\mu }\frac{{\partial p}}{{\partial x}}\right) + \frac{\partial }{{\partial z}}\left(\frac{{{h^3}}}{\mu }\frac{{\partial p}}{{\partial z}}\right) = 6U\frac{{\partial h}}{{\partial x}}\text{。} $ | (5) |
式中:x为圆周切向;z表示轴向;h为油膜厚度;μ为润滑油动力粘度;p为油膜压力;U为轴径圆周切向速度。
用有限差分法迭代求解无量纲化后的式(5),可得出轴承静平衡时的位置与油膜压力分布;根据轴承静平衡位置,并用扰动法求解各轴承油膜刚度如下式:
| ${K_y} = \frac{{\left| {{F_{y1}} - {F_{y2}}} \right|}}{{2\Delta x}}\text{。}$ | (6) |
式中:Fy1,Fy2为轴心由静平衡位置经垂向分别向上、下扰动距离
综上各式,可将轴系校中过程中各轴承负荷实时换算成轴承油膜刚度,并用于1.2中轴承弯曲振动响应求解。
2 优化模型的构建轴系校中时主要有两类优化算法:轴承轴向位置优化和合理校中优化,分别指各轴承位置沿轴系纵向与垂向进行优化。本节将整合这2种算法,并在校中时考虑减轻轴系弯曲振动,对轴系进行双向校中优化。
2.1 设计变量的选取轴系双向校中优化通常只调节中间轴承轴向位置及舷内各轴承垂向位置。因此,以各中间轴承的轴向变位值xn与舷内各轴承的垂向变位值ym为设计变量:
| $X = ({x_1},{x_2},{x_3} \cdots {x_n}),Y = ({y_1},{y_2},{y_3} \cdots {y_m})\text{。}$ | (7) |
式中:n,m分别为中间轴承和舷内轴承个数。
2.2 优化目标的定义 2.2.1 中间轴承轴向位置优化目标的选定校中轴系须先确定各轴承轴向位置[5]。中间轴承轴向位置的改变,不但会影响各轴承本身承载,还会改变整个轴系的轴承负荷均匀度,影响轴系的运转性能。因而将轴承负荷均匀度作为第一优化目标:
| $ {S_1} = \min{\left(\frac{1}{n}\sum\limits_{i = 1}^n {({R_i} - \overline R } )^2\right)}{^{\frac{1}{2}}}\text{。} $ | (8) |
式中:Ri为第i个支承轴承负荷;
以中间轴承所处轴向位置对各轴承负荷的影响程度,即综合负荷影响数作为第二优化目标:
| $ {S_2} = \min\left(\sqrt {\sum\limits_{{n_1}}^{{n_2}} {{{({R_{im}})}^2}} } \right)\text{。} $ | (9) |
式中:m为中间轴承序号;n1,n2分别为起始、终止轴承序号;Rim为中间轴承对第i个轴承的负荷影响数。
一些文献还将尾轴承负荷最小作为中间轴承轴向位置的优化目标,因中间轴承离尾轴承较远,其位置变化对尾轴承负荷影响数较小,在此未考虑。
2.2.2 轴承垂向位置优化目标的选定轴承最优轴向位置应使艉轴承负荷达到最小,以减轻“边缘负荷”现象;还应有合适的轴承负荷均匀度,防止轴系不均匀磨损和其他损伤事故发生,故设定第一优化目标为艉后轴承负荷:
| ${f_1} = \min({R_1})\text{,}$ | (10) |
式中:R1表示尾后轴承负荷。
以轴承负荷均匀度作为第二优化目标,计算过程同式(10)。
在0~120 Hz单位横向简谐激励力作用下,选取尾后轴承、尾前轴承及推力轴承三处传递功率流之和最小作为第三优化目标函数:
| ${f_3} = \min \left(\sum {{Q_1} + } \sum {{Q_2} + } \sum {{Q_3}}\right) \text{。}$ | (11) |
式中:Q1,Q2,Q3分别为尾后、尾前、推力轴承处的传递功率流。
2.3 约束条件的确定 2.3.1 中间轴承轴向位置优化约束条件受轴系结构强度与安装误差限制,轴承轴向位置L应遵循下式:
| ${L_{{\rm{min}}}} \leqslant L \leqslant {L_{{\rm{max}}}}\text{。}$ | (12) |
式中:
另外,为不影响轴系法兰的安装与对中,轴承中心到两端法兰中心间距应为0.2倍轴承间距左右。
2.3.2 轴承垂向位置优化约束条件根据轴系校中标准的要求,轴承垂向位置优化应遵循下列条件[10]:
1)轴承负荷约束。轴系运转时各轴承负荷应处于一定范围内,既不超过生产厂家的最大负荷限制,也不出现脱空现象:
| $ \left[ {{R_{i{\rm{min}}}}} \right] \leqslant {R_i} \leqslant \left[ {{R_{i\max }}} \right]{\text{。}} $ | (13) |
式中:[Rimin]和[Rimax]分别为轴系第i个轴承最小、最大允许负荷,可由下式导出:
| $\left[ {{R_{i{\rm{max}}}}} \right] = \left[ P \right] \cdot L \cdot d,\left[ {{R_{i{\rm{\min}} }}} \right] = \left({W_{\text{左}}} + {W_{\text{右}}} + \sum {P}\right) \cdot 20\% \text{。}$ | (14) |
式中:[P]为轴承材料许用压强;L为轴衬工作长度;W左,W右分别为轴承左,右侧轴段质量;ΣP为轴承两跨轴上的总载荷。
2)轴段弯曲应力约束。不同轴段的最大许用弯曲应力不同:[σ尾轴]≤20 MPa、[σ中间轴]≤20 MPa、[σ推力轴]≤15 MPa。
3)螺旋桨下沉角约束。不同的尾后轴承材料,对螺旋桨下沉角要求不同:
| $\left\{ \begin{array}{l} {\text{对铁梨木尾后轴承}}:\;\;\left[ {{\theta _{\rm{max}}}} \right] = 3 * {10^{{\rm{ - }}4}}\;\;{\rm rad};\\ {\text{对白合金尾后轴承}}:\;\;\left[ {{\theta _{\rm{max}}}} \right] = 2.5 * {10^{{\rm{ - }}4}}\;\;{\rm rad} \end{array} \right.$ | (15) |
4)主机输出端法兰处剪力与弯矩约束。对主机与推进轴系直接相连的轴系,在校中时须使主机输出端法兰处剪力、弯矩处于制造厂家规定的范围内。
2.4 优化模型的求解轴系双向校中是一个多目标优化问题,其一般式为:
| $\left\{ \begin{array}{l} {\rm{min}}{\rm{ }}F(x) = {\rm{min}}({f_1}(X),{f_2}(X) \cdots {f_n}(X))\text{,}\\ {\rm{ }}X = ({x_1}、{x_2} \cdots {x_n})\text{,}\\ {\rm s.t}.{\rm{ }}g{}_i(x) \le 0,{\rm{ }}i = {\rm{1,2}} \cdots m{\rm{ , }}h{}_i(x) = 0{\rm{ , }}i = {\rm{1,2}} \cdots n\text{。} \end{array} \right.{\rm{ }}$ | (16) |
式中:F(x)为目标函数;X为优化变量;gi(x),hi(x)分别为等式,不等式约束。
本文采用线性加权和法构造评价函数求解该多目标优化模型,即构造函数:
| ${\rm{min}}{\rm{ }}F(x) = {\rm{min}}(\sum\limits_{i = {\rm{1}}}^n {{w_i}} {f_i}(X)\text{。}$ | (17) |
式中,wi≥0且
用层次分析法来确定上式中各优化目标加权系数。在运用层次分析法之前,须对各子目标进行统一量纲处理:
| $\min f(x) = \min \left(\sum\limits_{i = 1}^n {\frac{{{f_i}(x)}}{{\min({f_i}(x))}}} \right)\text{。}$ | (18) |
用层次分析法确定各子目标加权系数基本步骤如下[11]:
1)根据各子目标重要程度和相关性建立判断矩阵;
2)计算判断矩阵各行乘向量,确定各元素权重,即各子目标加权系数;
3)检验判断矩阵一致性。
当判断矩阵一致性检验通过后,将计算得出的各权重系数用于对各子目标加权处理,将其转化为单目标优化函数再进行求解。
3 优化算法及计算流程基于上述构建的轴系双向校中优化模型,在Isight优化软件中,将Pointer优化器与Matlab组件相结合,编制优化计算程序,其基本流程如图2所示。
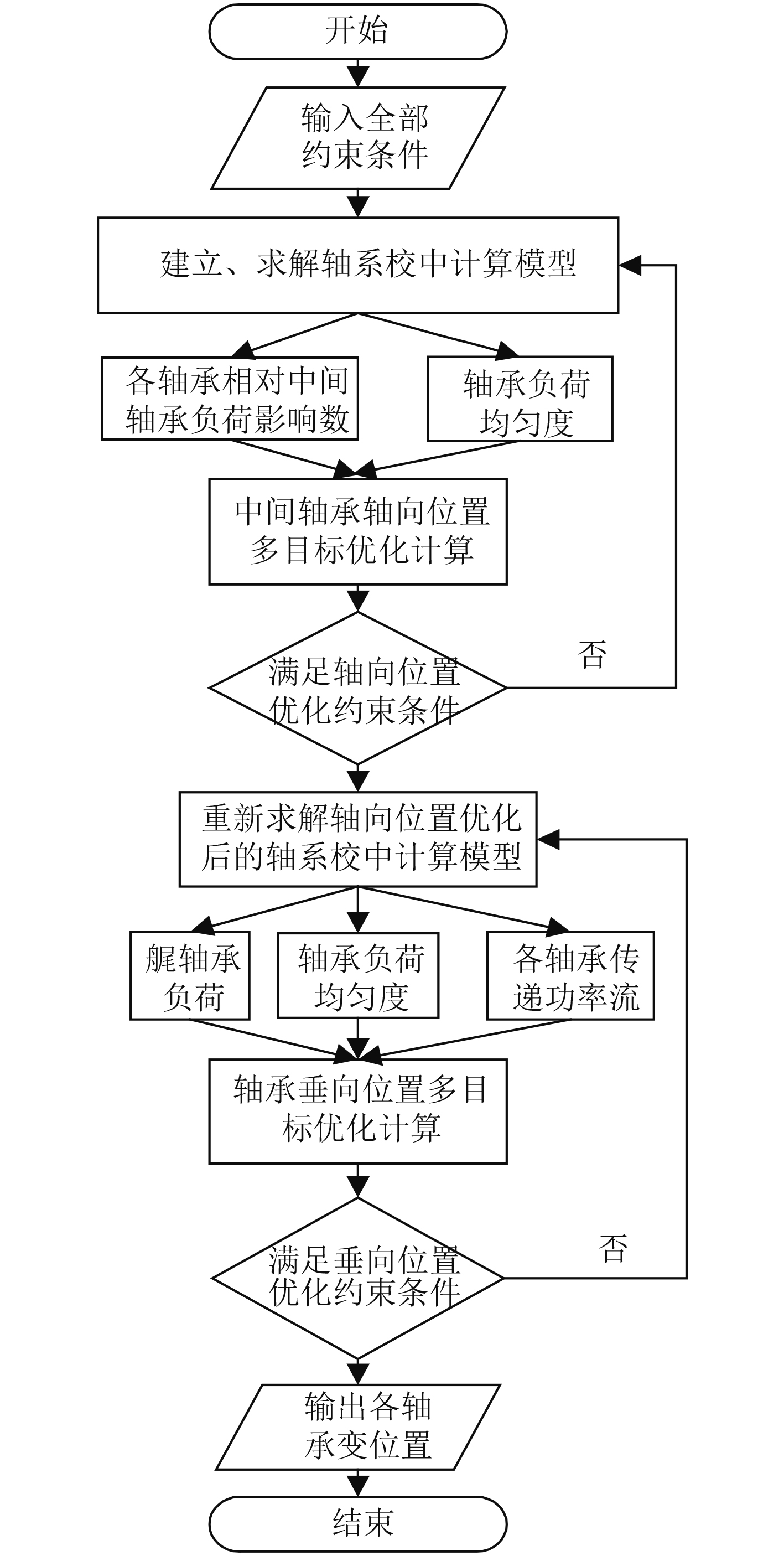
|
图 2 优化计算流程图 Fig. 2 Flow diagram of optimum calculation |
程序中优化计算模块包含了优化变量、约束条件、输出变量、目标函数的定义与设置,它能根据选定的计算方法对模型进行求解,并输出各轴承优化后的变位值。另外,文中采用的Pointer优化算法是Isight优化软件提供的一种智能优化专家,其整合了线性单纯形法、序列二次规划法、最速下降法与遗传算法,而且能够自动地形成一种最优的优化策略,从而充分发挥优化设计的优越性。
4 工程应用某船舶推进轴系结构如图3所示。该轴系总长20.27 m,由首至尾依次为主推进装置、轮胎离合器、中间轴承、弹性联轴器、推力轴承、尾前轴承、尾承、尾后轴承、螺旋桨。合理简化该轴系各结构得到其计算模型如图4所示。
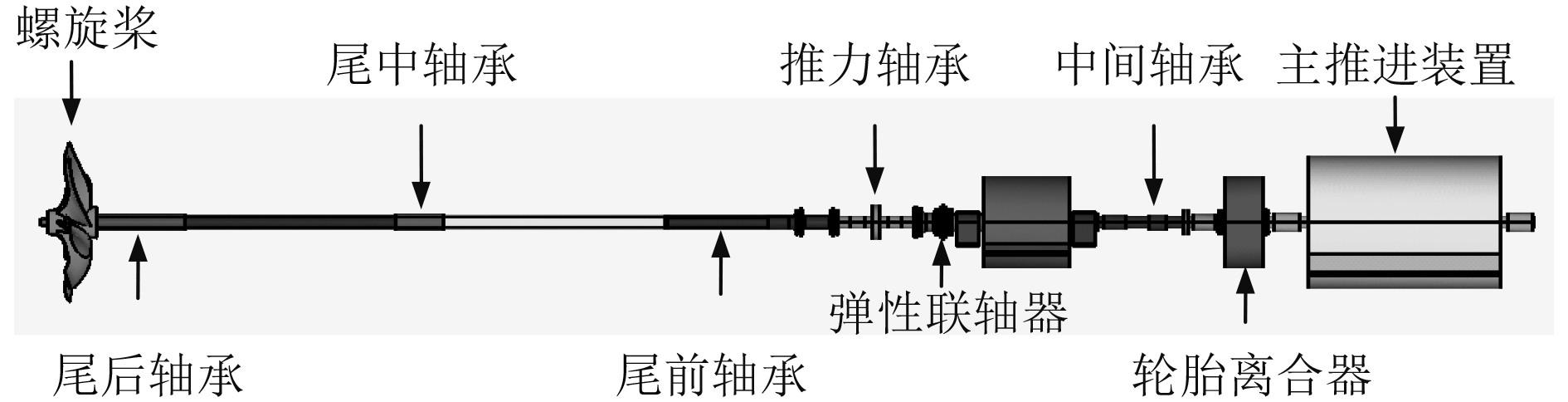
|
图 3 某船舶推进轴系结构示意图 Fig. 3 The schematic diagram of ship propulsion |
|
图 4 某船舶推进轴系校中计算模型 Fig. 4 The module diagram for ship propulsion shafting alignment calculation |
对中间轴承位置进行轴向优化,得出中间轴承布置在20.105 m时,加权形成的单目标函数有最优值。优化前后各轴承负荷如表1所示。可以看出,经中间轴承轴向位置优化后,各轴承负荷变得更为均匀,轴承负荷均匀度下降了5.7%,轴系受力状态更为合理。
|
|
表 1 中间轴承轴向位置优化后轴承负荷表 Tab.1 Load of bearings after optimization of intermediate bearing's axial position |
表2为优化前后各轴承相对于中间轴承的负荷影响数取值。由表2可知,优化后各轴承相对于中间轴承的负荷影响数均有所下降,其中尾中轴承相对于中间轴承的负荷影响数下降最为明显,减少了约31%。
|
|
表 2 各轴承相对于中间轴承负荷影响数表 Tab.2 The load influence value of each bearing relative to the intermediate bearing |
将中间轴承轴向位置优化结果作为输入条件之一代入轴承垂向位置优化流程,导入各约束条件与优化目标,计算得出各轴承垂向变位值如表3所示。由表3可知优化后轴系变为曲线状态,其中尾中、推力轴承垂向位置都处于理论中心线以下。
|
|
表 3 轴承垂向优化变位表(mm) Tab.3 Vertical displacement value of bearings (mm) |
表4为轴承垂向位置优化后各轴承负荷值。由表4可知,优化后艉后轴承负荷降为67 514 N,艉中轴承负荷由3 191 N变为9 100 N,达到轴承许用负荷范围要求。各轴承负荷均匀度有所增大,这是由于垂向位置校中优化约束条件比中间轴承位置校中时更为严格。
|
|
表 4 轴承垂向优化后轴承负荷表 Tab.4 Load of bearings after optimization of bearings' vertical position |
图5为4种不同校中状态下,在螺旋桨处施加单位横向简谐力,尾后轴承、尾前轴承、推力轴承3处的传递函数曲线。由图5可知,经中间轴承轴向位置优化后,各轴承振动传递函数频谱图与初始状态时基本一致;轴承垂向位置校中优化后,各轴承传递功率流级在6 Hz附近低频段的数值有所增大,其他频率范围内均有下降。与轴承位置垂向优化相比,考虑减轻轴系弯曲振动的轴承垂向位置优化后,尾后、尾前、推力轴承处的振动传递曲线均有下降,轴系振动特性改善明显。
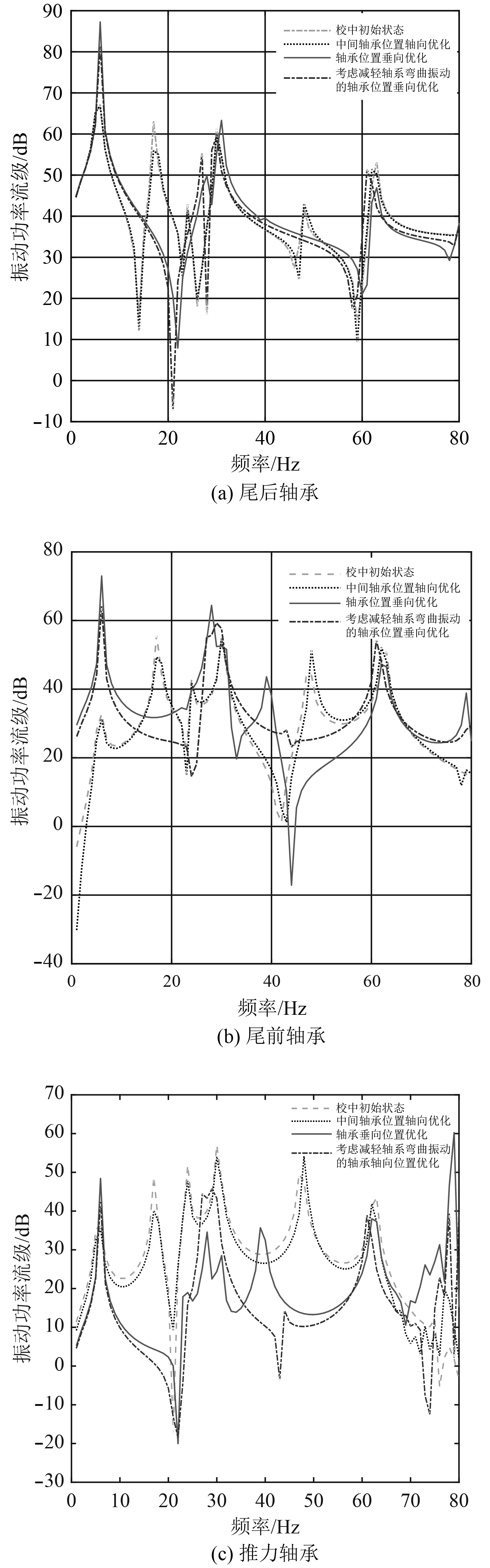
|
图 5 尾后、尾前、推力轴承处传递函数曲线 Fig. 5 Transfer function curve of rear bearing, front bearing and thrust bearing |
提出一种以奇异函数、传递矩阵法及雷诺方程为理论基础的,考虑减轻轴系振动的轴系轴承位置双向校中优化方法,该方法以中间轴承轴向变位值、各轴承垂向变位值作为优化变量,分别以中间轴承对各轴承综合负荷影响数、轴承负荷均匀度和尾后轴承负荷、轴承负荷均匀度及尾后、尾前、推力轴承处的传递功率流之和最小作为优化目标。以某船舶推进轴系为例,基于Isight优化软件与Matlab组件,对其进行了校中优化。优化结果表明,各目标函数在校中前后均得到了不同程度地优化,且各约束变量均达到了标准规定的范围内,这也验证了本文在常规轴系校中的基础上,将考虑减轻轴系振动作为优化目标之一,以进一步提高轴系校中质量、改善轴系振动特性的优化计算方法的合理、有效性。
| [1] |
周瑞平. 超大型船舶推进轴系校中理论研究[D]. 武汉: 武汉理工大学, 2005. ZHOU Rui-ping. The theoretic studies on the proplusion shafting alignment of ultra-large vessels[D]. Wuhan: Wuhan University of Technology, 2005. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y776874 |
| [2] |
周瑞. 舰船推进轴系校中的多目标优化计算方法[J]. 中国舰船研究, 2013, 8(3): 73-77. ZHOU Rui. A multi-object optimization method for the shafting alignment in ship propulsion systems[J]. Chinesen Journal of Ship Research, 2013, 8(3): 73-77. |
| [3] |
REEVES J D, VLAHOPOULOS N. Optimized alignment of a USCG polar class icebreaker wing shaft using a distributed bearing finite-element model[J]. Marine Technology, 1999, 36(4): 238-247. |
| [4] |
魏颖春, 杨川. 基于有限元法的船舶艉轴承负荷优化[J]. 船海工程, 2011, 40(5): 62-64. WEI Ying-chun, YANG Chuang. Load optimization of marine stern bearing on the finite element method[J]. Ship and Ocean Engineering, 2011, 40(5): 62-64. DOI:10.3963/j.issn.1671-7953.2011.05.018 |
| [5] |
陆金铭, 周海港, 顾卫俊, 等. 船舶轴系优化校中[J]. 船海工程, 2010, 39(3): 51-54. LU Jin-ming, ZHOU Hai-gang, GUI Wei-jun. Optimization of the location of bearings in shaft line alignment[J]. Ship and Ocean Engineering, 2010, 39(3): 51-54. DOI:10.3963/j.issn.1671-7953.2010.03.013 |
| [6] |
杨俊, 王隽, 王刚伟. 船舶推进轴系校中对轴系振动影响分析[J]. 动力学与控制学报, 2016, 14(2): 157-164. YANG Jun, WANG Juan, WANG Gang-wei. Analysison the effect of marine propulsion shafting alignment on its vibration[J]. Journal of Dynamics and Control, 2016, 14(2): 157-164. DOI:10.6052/1672-6553-2015-041 |
| [7] |
方国强. 轴系校中参数与轴系振动特性相关性仿真研究[J]. 舰船科学技术, 2016, 38(1): 67-71. FANG Guo-qiang. The correlation rules of typical hull shafting vibration characteristics with alignment parameters[J]. Ship Science and Technology, 2016, 38(1): 67-71. DOI:10.3404/j.issn.1672-7649.2016.1.014 |
| [8] |
刘学伟, 何其伟, 蒋竞超, 等. 考虑船舶轴系校中与弯曲振动的轴承优化布置[J]. 舰船科学技术, 2016, 38(7): 44-48+53. LIU Xue-wei, HE Qi-wei, JIANG Jing-chao. Optimization of ship shaft bearings location considering shaft alignment and lateral vibration[J]. Ship Science and Technology, 2016, 38(7): 44-48+53. DOI:10.3404/j.issn.1672-7619.2016.07.010 |
| [9] |
冷坳坳. 舰船推进轴系校中技术研究[D]. 武汉: 武汉理工大学, 2015.
|
| [10] |
CB/Z 338-2005, 船舶推进轴系校中[S].
|
| [11] |
李宁, 王李管, 贾明涛. 基于层次分析法的矿井六大系统模糊综合评价[J]. 中南大学学报(自然科学版), 2015, 46(2): 631-637. DOI:10.11817/j.issn.1672-7207.2015.02.035 |
 2020, Vol. 42
2020, Vol. 42
