船舶电力系统在实际运行中,由于战斗破损、违规操作和设备本身问题可能会发生故障或非正常运行。船舶中压直流电力推进系统作为一项新兴技术,具有极高的自动化和电气化程度,为船舶供配电系统的可靠性带来了空前的挑战。因此,开展船舶MVDC配电网络重构研究,具有非常重要的现实意义。
船舶电力系统配电网络重构技术主要涉及2个方面,为船舶电力系统稳态分析和配电网络重构算法设计。船舶电力系统稳态分析以潮流计算方法为主,常用的有前推回代法、牛顿-拉夫逊法、节点电势法等[1];配电网络重构算法,国外多以Agent智能算法方法和预测性重构技术为主,国内则常使用改进智能优化算法,如改进遗传算法、粒子群算法等[2]。
与传统船舶电力系统相比,船舶MVDC电力系统中存在许多电力电子设备,是典型的交直流混合系统。文献[3]采用牛顿拉夫逊法对MVDC配电网络进行潮流计算研究,得到了较为准确的结果。然而当应用于网络故障重构时,雅克比矩阵的反复迭代过程中容易出现奇异矩阵,而且不易对故障位置进行编码,因此重构技术中不宜使用其进行潮流计算。文献[4]介绍了一种改进的节点电势法对交流系统进行稳态分析,在计算过程中引用高斯迭代法,有效的避免了节点导纳阵奇异导致的计算错误,可将其进行改进,使之适用于MVDC配电网络的潮流计算。文献[5]在节点电势法的基础上采用遗传算法对配电网络的重构进行优化计算,但遗传算法涉及的计算量过大,运算速度慢,而且容易“早熟”,对内部参数的选择要求较高。文献[6]采用专家系统方法对船舶电力系统网络重构进行求解,但实际应用中很难获取全部的知识。本文提出了一种改进的节点电势法对MVDC配电网络进行潮流计算,可得出配电网络各线路电流、功率等参数;在基本粒子群算法构架基础上引入了自适应权重法和杂交池算法,并设计“定向变异法”加以改进,用于配电网络故障重构优化计算。算例测试结果表明,该方法能够较快速、准确的提供有效的重构方案。
1 拓扑建模 1.1 网络故障的提取船舶MVDC主配电网络是由多个连接发电机及AC-DC变换电路的主配电板(直流母线)连接而成,主配电板下通过DC-DC变换电路及DC-AC变换电路与负载相接,或直接接连负载,各配电板由馈线连接。
由于MVDC主电板下为辐射状配电网络,因此可将主配电网看作根节点,将各级母线设为节点,并从主配电网开始按宽度优先搜索顺序给各路节点和支路进行编号,并按编号顺序建立节点–支路关联矩阵,便于后续的潮流计算。
下面阐述如何建立节点-支路关联矩阵,并利用该模型追踪提取配电网络故障。N个节点L条支路的配电网络可按节点支路编号建立N×L的矩阵M,当电流从编号i节点流入,经支路j,从编号p节点流出,则Mij=−1,Mip=+1;若节点i与支路j没有直接相连,则Mij=0[7]。
按支路编码顺序建立L×1向量X,若编号i支路正常工作,则Xi=1,若该支路断开,则Xi=0。然后将该向量扩展为对角矩阵。节点导纳矩阵如下式:
| $\begin{split} &{{{M}}_1} = {{M}} \cdot {\rm{diag}}(X) \text{,} \\ & \left[ {{{\dot Y}_y}} \right] = \left[ {{{{M}}_1}} \right]\left[ {\dot Y} \right]{\left[ {{{{M}}_1}} \right]^{\rm T}}\text{。} \\ \end{split} $ | (1) |
节点导纳阵Yy中,连接2个节点间故障支路的元素将被清零,网络的故障便被提取并体现在了节点导纳阵中。
1.2 配电网络中各设备的数学模型与普通的交流船舶电力系统相比,MVDC综合电力推进系统中存在着一定数量的电流变换器,如逆变器、DC-DC变换器等。在进行潮流计算之前,应首先建立这些换流设备等效电路,并以此求出其等效的支路导纳或得出相应的数学模型[8]。
本文采用文献给出的逆变器及DC-DC变换器的等效电路,经测试,能够适用于MVDC配电网络的潮流计算。
在舰船 MVDC 系统中,换流器由发电机端的 AC/DC 换流器及负载端的DC/AC换流器构成。考虑到换流器需采用不同控制方式,以及电压源型换流器结构简单、储能效率高、损耗低、动态响应快等优点,本文选用使用全控器件的电压源型换流器,在忽略换流器功率损耗的情况下,等效电路如图1所示。

|
图 1 换流器等效电路图 Fig. 1 Converter equivalent circuit diagram |
数学模型为:
| $\begin{split} &{P_{\rm{d}}} = {U_d}{I_d} \text{,} \\ & {P_1} = A + B{I_{\rm{c}}} + C{I_c}^2 \text{,} \\ & A = \frac{{6.62{S_N}}}{{600{S_B}}} \text{,} \\ &B = \frac{{1.8V_N^{\rm{d}}}}{{{\rm{600V}}_{\rm{B}}^{\rm{d}}}}\text{,} \\ & C = \frac{{3.0{{(V_N^d)}^2}{S_B}}}{{600{{(V_B^d)}^2}{S_N}}}\text{,} \\ &{P_C} = {P_{\rm{d}}} + {P_1} \text{,} \\ & {U_S} = \frac{{\cos {\sigma _c}M}}{{\sqrt 2 }}{U_{\rm{d}}}\text{,} \\ & {I_{\rm{s}}} = \frac{{\sqrt 2 {I_d}}}{{M\cos {\sigma _{\rm{c}}}}} \text{。} \end{split} $ | (2) |
其中:Pd为交流侧功率;P1为换流器件损耗功率;Pc为交流侧功率;SN,VNd为换流器额定容量,直流侧额定电压;SB,VBd为系统基准容量,直流基准电压。
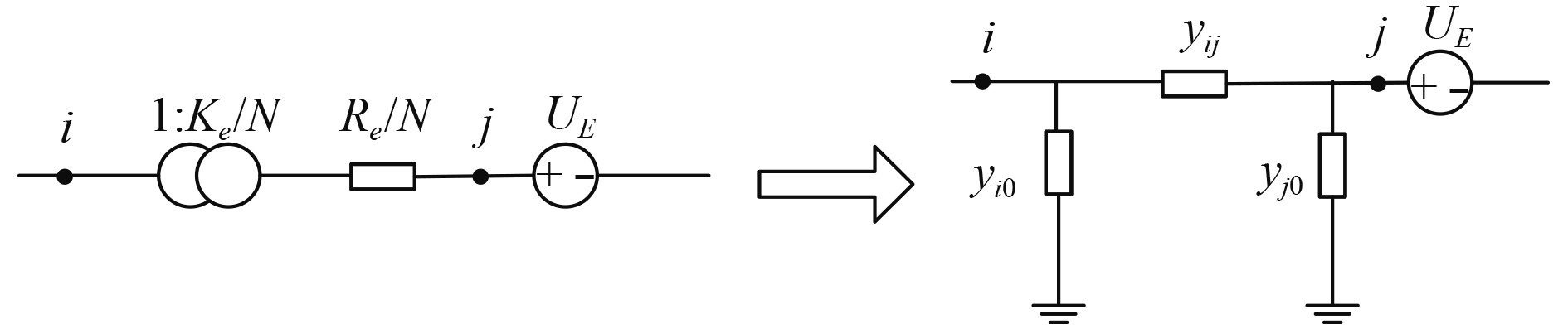
在舰船 MVDC系统中,直流变换器是连接主配电板和分配电板的重要设备。利用一个周期内电感和电容吸收的能量与释放的能量相等的原理[9],建立如图2所示的DC/DC变换器等效电路图。
|
图 2 DC/DC变换器等效电路图 Fig. 2 DC/DC converter equivalent circuit diagram |
图中各节点电流及导纳可用下式分别计算:
| $\begin{split} &{I_{\rm{i}}} = \frac{{{U_i}{K_e}^2}}{{N{R_E}}} - \frac{{{U_j}{K_e}}}{{{R_E}}} = ({y_{ij}} + {y_{i0}}){U_i} - {y_{ij}}{U_j}\text{,} \\ & {I_{\rm{i}}} = \frac{{{U_i}{K_e}^2}}{{N{R_E}}} - \frac{{{U_j}{K_e}}}{{{R_E}}} = ({y_{ij}} + {y_{i0}}){U_i} - {y_{ij}}{U_j}\text{,} \\ &{y_{ij}} = \frac{{{K_e}}}{{{R_e}}}\text{,} \\ & {y_{i0}} = \frac{{K_e^2 - {K_e}N}}{{N{R_E}}}\text{,} \\ &{y_{j0}} = \frac{{N - {K_e}}}{{{R_E}}}\text{。} \end{split} $ | (3) |
另外,在船舶电力系统中,存在大量的电动机型的负载,电动机属于典型的非线性负载,因此亦需对其建立等效电路,得出其等效数学模型,便于潮流计算。本文采用了如图3所示的T型电动机等效电路,并通过式(4)建立其数学模型。

|
图 3 T型电动机等效电路图 Fig. 3 T-motor equivalent circuit diagram |
| $\begin{split} &\frac{{{{\left| {{u_1}} \right|}^2}}}{{{{\left| {{r_1} + \frac{{{r_2}}}{s} + j({x_1} + {x_2})} \right|}^2}}} \cdot \frac{{1 - s}}{s}{r_2} = {p_2}\text{,} \\ & {z_{eq}} = \frac{{({r_m} + j \cdot {x_m})}}{{\left[ {{r_1} + \frac{{{r_2}}}{s} + j \cdot ({x_1} + {x_2})} \right]}} \text{。} \\ \end{split} $ | (4) |
式中:S为式中较小的解;zeq为电动机等效电抗。
2 MVDC配电网络潮流计算节点电势法是一种适用于船上电力系统的潮流计算方法,它的主要思想是假设以电力系统某一发电机电势不变的情况下,给各节点电势赋以初值,通过建立系统的节点导纳矩阵,反复迭代,求出系统各参数,直到达到精度要求。
根据MVDC配电网络的特点,可假设某一根节点的直流母线电势不变,由有载调压设备实现。将发电机连同整流变换器看作电流源,各级负载看作电流源,各电流变换器按其数学模型求出支路等效导纳,与负载直接相连的逆变器可与负载并作电流源处理。
先建立网络拓补模型,生成节点导纳矩阵。按编号给各节点电势赋初值生成节点电势向量U,确定各支路的压降—列向量[Ub]l×1和电流—列向量[Ib]l×1,即
| $\begin{array}{l} \left[ {{{\dot U}_b}} \right] = {\left[ {M_1} \right]^{\rm T}}\left[ {\dot U} \right]\text{,} \\ \left[ {{I_b}} \right] = \left[ {\dot Y} \right]\left[ {{{\dot U}_b}} \right]\text{。} \\ \end{array} $ | (5) |
由此得到求取节点电势的迭代公式:
| ${\left[ {\dot U} \right]^{(k + 1)}} = \left[ {{{\dot Y}_y}} \right] - 1\left[ {{{\dot s}_i}/\dot u_i^{(k)}} \right]\text{。}$ | (6) |
其中:[Yy]-1为[Yy]的逆矩阵;[U](k+1)为第k+1步迭代过程中的节点电势列向量;ui(k)为第k步迭代过程中节点i的电势向量共轭值。
根据KCL设置迭代精度条件,当某一节点合成电流小于预设值时,结束迭代。再根据已有数据求出各负载电流,功率等参数。
在实际运算中,可能会出现节点导纳阵奇异或求逆困难的情况,可采用高斯迭代法计算节点电势U:
| $\dot u_i^{(k + 1)} = \frac{1}{{{y_{ij}}}} \cdot \left[ {\dot i_i^{(k)} - \sum\limits_{j = 0}^{i - 1} {{y_{ij}}} \cdot \dot u_j^{(k + 1)} - \sum\limits_{j = i + 1}^{n - 1} {{y_{ij}}} \cdot \dot u_j^{(k)}} \right]\text{。}$ | (7) |
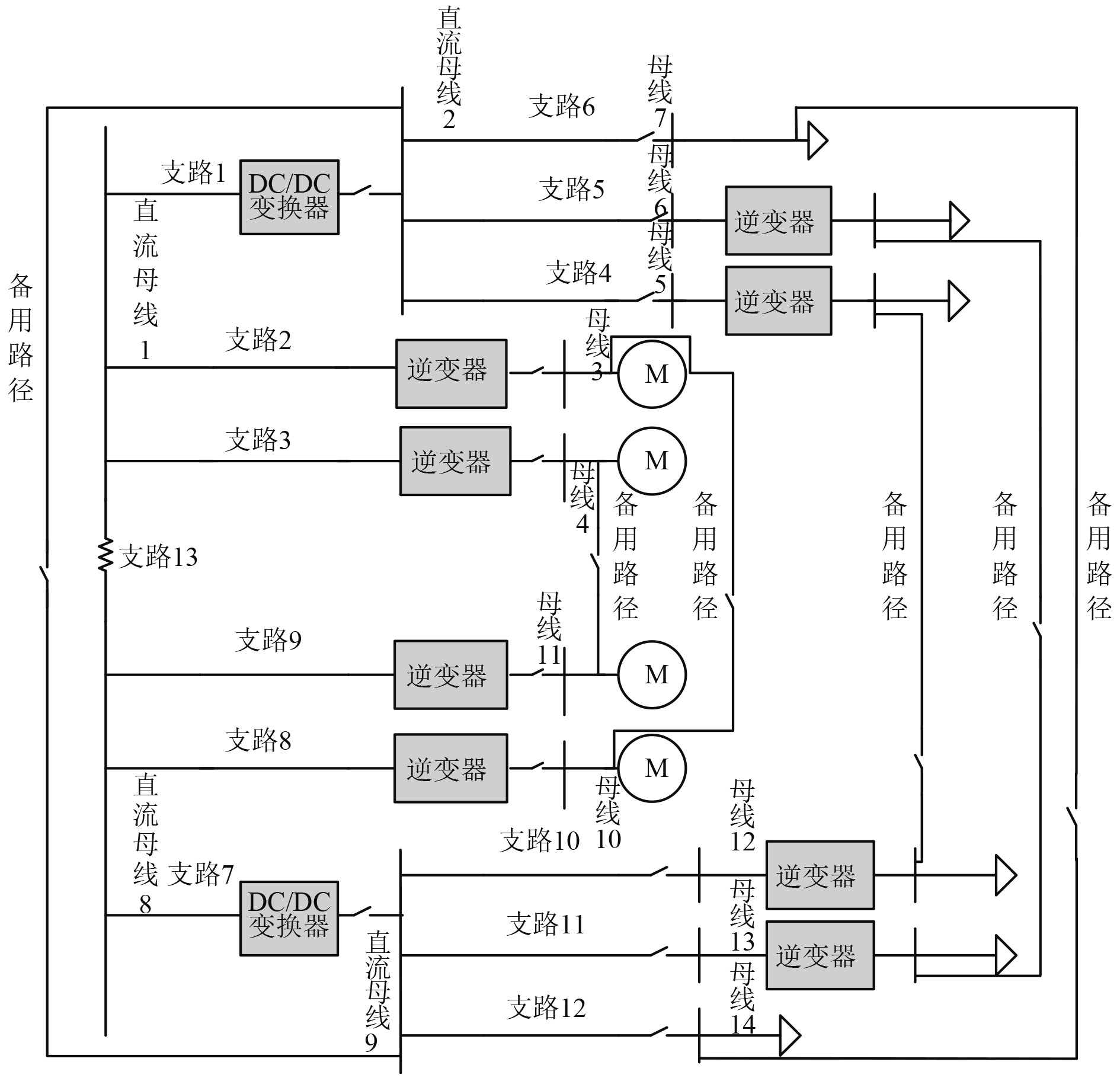
图4为船舶中压直流综合电力推进系统的电路简图。以此图为例,采用节点电势法对其进行配电网络的潮流计算。
|
图 4 船舶中压直流综合电力推进系统配电网络简图 Fig. 4 Schematic diagram of the distribution network of a ship's medium-voltage DC integrated electric propulsion system |
采用节点电势法对如图4所示电路中所有负载全部连接于正常路径工作情况下进行潮流计算,所得各母线电压与电流如表1所示,单位均为标幺值。
|
|
表 1 配电网络潮流计算数据 Tab.1 Distribution network load flow calculation data |
可见,在配电网络重构过程中,可采用该方法对配电网络进行潮流计算,按所得结果判断电流和功率是否超出线路容量和发电机最大功率限制。
3 配电网络的稳定性分析对于配电网络重构技术来说,重构后网络的稳定性往往是容易忽略的一个问题,而MVDC船舶电力系统配电网络运行环境多变,如果重构算法一味追求负荷量指标,而忽视系统稳定性,在实际运用中则有可能造成配电网络重新故障,电压崩溃,故障重构工作功亏一篑。
在MVDC配电网络中,直流支路经逆变器进行电力变换供给交流或直流负载,在此过程中主要起输电作用,因此研究其稳定性意义不大。本文主要对MVDC配电网络中交流支路进行稳定性分析。对于位于节点k与节点m之间的交流支路k–m来说,其稳定性指标可由该支路的潮流二次方程判别式得出:
| $\begin{aligned} {L_{pm}} = x{v_k}^2 - 4{z^2}Q_m' \text{,} \\ {L_{qm}} = rv_k^2 - 4{z^2}{P_m}' \text{。} \end{aligned} $ | (8) |
式中:vk为节点k的电压;z为支路k–m的等值阻抗;Pm′和Qm′分别为流出支路k–m注入的有功功率和无功功率;Lpm为无功潮流方程判别式表示的静态电压稳定性指标;Lkm为有功潮流方程判别式表示的静态电压稳定性指标[10]。
此外,还需对配电网络中的动态负载电机支路进行稳定性分析,对式(4)的第1个方程变形可得出如下形式的二次方程:
| ${\rm{a}}{s^2} + bs + c = 0\text{。}$ | (9) |
式中:
| $\begin{aligned} &a = {p_1}{{\rm{r}}_{\rm{1}}}^2 + {\left| {{{\rm{u}}_1}} \right|^2}{r_2}\text{,}\\ &{{b}} = {p_2}({x_1}^2 + 2{x_1}{x_2} + {x_2}^2 + 2{r_1}{r_2}) - {\left| {{u_1}} \right|^2}{r_2}\text{,}\\ &{{c}} = {p_2}{r_2}^2\text{。} \end{aligned}$ | (10) |
该二次方程的判别式可作为动态负载支路的稳定性指标。
4 配电网络重构数学模型在MVDC船舶电力系统网络中,重要负载通过转换开关,在正常供电路径受损或事故时,可采用备用路径供电。各电源均有一定的供电区域,通过主配电板直流母线之间的跨接线,可在正常或系统故障时进行全局网络的供电。网络的上述特点,使得在网络重构时,网络结构可以调整。在船舶电力系统网络重构时,要考虑重要负载尽可能恢复供电,次要负载可以卸载,而像陆地电力网络重构时所要考虑的网损最小等经济因素可先不预考虑。在任何情况下,都要保证一级负载的供电。
网络重构的主要任务是在系统出现故障时,确定哪些ABT或MBT需要打开或闭合,是重要负载恢复供电且最大限度恢复供电。
考虑一级负载的恢复,目标函数为:
| $\max {L_{j1}} = \sum\limits_{i = 1}^k {{x_i}} {L_{j1i}}\text{;}$ | (11) |
考虑一、二级负载的恢复,目标函数为:
| ${\rm{max}}({L_{j1}} + {L_{j2}}) = \sum\limits_{i = 1}^k {{x_i}} {L_{j1i}} + \sum\limits_{p = 1}^m {{x_p}} {L_{j2p}}\text{。}$ | (12) |
式中:i=1,2,···,k;p=1,2,···,m;Lj1为一级负载;Lj2为二级负载;Xi、Xp=1或0,表示负载的供电与不供电。
若考虑非重要负载的恢复,目标函数为:
| ${\rm{max}}({L_{j1}} + {L_{j2}} + {L_{j3}}) = \sum\limits_{i = 1}^k {{x_i}} {L_{j1i}} + \sum\limits_{p = 1}^m {{x_p}} {L_{j2p}} + \sum\limits_{h = 1}^n {{x_h}} {L_{j3h}}\text{。}$ | (13) |
式中:Lj3为三级负载;Xh=1或0表示三级负载的供电与不供电。
由于开关操作需要投入一定的时间和人力,因此开关操作越少越好,而且开关的转换尽量采用自动转换开关,其目标函数为:
| ${\rm {Min}}({f_2}) = \Delta X\text{,}$ | (14) |
式中ΔX为开关动作次数。
考虑重构后稳定性因素,应对重构方案进行稳定性指标分析,选取所有支路中稳定性最低支路的稳定性指标作为最终指标,应优先选取稳定性指标最高的方案。
| ${\rm{Max}}({f_3}) = {\rm {Min}}(S)\text{,}$ | (15) |
式中S为网络支路稳定性指标向量。
一般情况下,网络重构时在保证重要负载能够全部恢复及稳定性较高的情况下,优先考虑以较小的开关操作次数恢复所有重要负载的供电。其最终目标函数为:
| ${{f}} = {w_1}\max ({l_{j1}} + {l_{j2}} + {l_{j3}}) + {{{w}}_{\rm{2}}}{\rm {Min}}({f_2}) + {w_3}{\rm {Max}}({f_3})\text{。}$ | (16) |
式中:w1,w2,w3为分配的权重数。
根据发电机和各线路容量限制设置约束条件:
| $\begin{array}{l} \alpha \sum {P \leqslant {P_{\max }}} \text{,} \\ {I_b} \leqslant {I_b}_{\max }\text{。} \\ \end{array} $ | (17) |
式中:α为发电机出功占比;P为网络各部分消耗功率;Pmax为发电机最大限制功率;Ibmax为支路上的线路电流最大容量限制。
5 改进粒子群算法粒子群算法(Particles Swarm Optimization,PSO)是美国社会心理学家James Kennedy和电气工程师Russell Eberhart在1995年提出的一种智能搜索算法[11]。1997年,Kennedy和Eberhart第1次提出了一种离散二进制PSO算法,从此PSO不但可以求解连续变量的优化问题,而且还可以求解离散变量的优化问题。由于PSO容易实现和寻优能力强,因此得到国内外许多领域学者们的青睐。PSO虽然收敛速度快,但是收敛精度低,易于陷入局部最优解。另一方面,船舶重构优化问题规模大,重构实时性要求高。因此在配电网络重构过程中,一般采用改进的粒子群算法。
船舶配电网络重构运算对象是一系列开关序列X,其元素可取0(表示正常路径断开,且不走备用路径)、1(表示走正常路径)、2(表示走备用路径),因此其优化变量为离散变量,应采取离散二进制粒子群算法[12]。
本文粒子的取值为3种,即0,1,2,采用一种新的方法规定X的更新法则。
首先按照基本粒子群算法采用常数学习因子c1和c2及常惯性权重w,粒子根据如下公式来更新自己的速度和位置[13]。
| $\begin{array}{l} \!{v_{i,j}}(t + 1) \!= \!w{v_{i,j}}(t)\! +\! {c_1}{r_1}\left[ {{p_{i,j}}\! -\! {x_{i,j}}(t)} \right] + {c_2}{r_2}\left[ {{p_{g,j}} - {x_{i,j}}(t)} \right]\text{,}\\ \!{x_{i,j}}(t + 1) = {x_{i,j}}(t) + {v_{i,j}}(t + 1),j = 1,2, \cdots ,d \text{。} \end{array}$ | (18) |
其中:w为惯性权重;c1和c2为正的学习因子;r1和r2为0~1均匀分布的随机数;pi为粒子本身的最优解,即个体极值;pg为整个种群目前找到的最优解,即全局最优。
根据此时xi,j(t+1)的取值范围确定其最终取值[14]:
| $\left( { - \infty ,0.5} \right) \to 0,[0.5,1.5) \to 1,[1.5, + \infty ) \to 2\text{。}$ |
由于MVDC配电网络重构运算量较大,网络拓补结构复杂,基本粒子群算法的性能并不足以快速准确地得出重构最优解,因此本文在基本粒子群算法的基础上加以改进,以期达到优化要求。
1)为平衡PSO算法的全局搜索能力,采用非线性的动态惯性权重系数公式,其表达式如下:
| $w = \left\{ \begin{array}{l} {w_{\min }} - \frac{{({w_{\max }} - {w_{\min }}) * (f - {f_{\min }})}}{{({f_{avg}} - {f_{\min }})}},f \leqslant {f_{avg}}\text{;} \\ {w_{\max }},f > {f_{avg}}\text{。} \\ \end{array} \right.$ | (19) |
式中:wmin,wmax分别为w的最大值和最小值;f为粒子当前的函数值;favg和fmin分别为当前所有微粒的平均目标值和最小目标值。
当各微粒目标值趋于一致或趋于局部最优时,将使惯性权重增加;当各微粒的目标值比较分散时,将使惯性权重减少,使得微粒靠拢于较好的搜索区域。
2)在每次迭代过程中,当所有粒子的个体最优解都已确定后,将这些个体记录下来,并令其每一位按照一定概率重新生成新的坐标,然后计算其适应度,并按照结果更新粒子个体极值和全局最优值。这样可使得寻优过程中,增加“优等粒子”的多样性,避免粒子的“早熟”现象。
3)借鉴遗传算法中的杂交概念,在每次迭代中,根据杂交概率选取指定数量的粒子放入杂交池内,池中的随机粒子可两两杂交,产生同样数目的子代粒子,后用子代粒子代替父代粒子。子代粒子位置由父代粒子位置进行算数交叉得到[15]:
| ${\rm{child}}(x) = p \cdot paren{t_1}(x) + (1 - p) \cdot paren{t_2}(x)\text{,}$ | (20) |
其中,p为0~1之间的随机数。
子代速度由下式计算:
| ${\rm{child}}(v) = \frac{{paren{t_1}(v) + paren{t_2}(v)}}{{\left| {paren{t_1}(v) + {\rm{paren}}{t_2}(v)} \right|}}\left| {paren{t_1}(v)} \right|\text{,}$ | (21) |
改进后的粒子群算法步骤如下:
1)初始化种群中各微粒的位置和速度;
2)计算出每个微粒的适应度,将当前各微粒的位置和适应度函数值存储在各微粒的pbest中,将所有pbest中适应值最优的个体和适应值存储在gbest中;
3)更新粒子的速度和位移;
4)采用非线性的动态惯性权重系数公式更新权重w;
5)对每个微粒,将其当前适应值与pbest进行比较,如更优,则将该值更新pbest,然后更新gbest;
6)使pbest中的微粒每一位按一定概率重新生成新的坐标,计算新微粒的适应度值,然后更新pbest和gbest;
7)根据杂交概率选取一定数量的粒子放入杂交池内,池内粒子随机两两杂交,产生同样数目的子代粒子;
8)若满足迭代停止条件,则输出最终结果;若不满足,则返回步骤3继续运行算法。
6 算例分析以图4为例,依照广度搜索法给各支路开关编号,设负载1,2,6,7为一级负载,负载3,4,8,9为二级负载,负载5,10为三级负载,并以2种不同位置的支路故障为例,采取本文所设计的配电网络故障重构算法编写程序,得到结果如表2所示。
|
|
表 2 配电网络重构计算数据表 Tab.2 Distribution network reconstruction calculation data table |
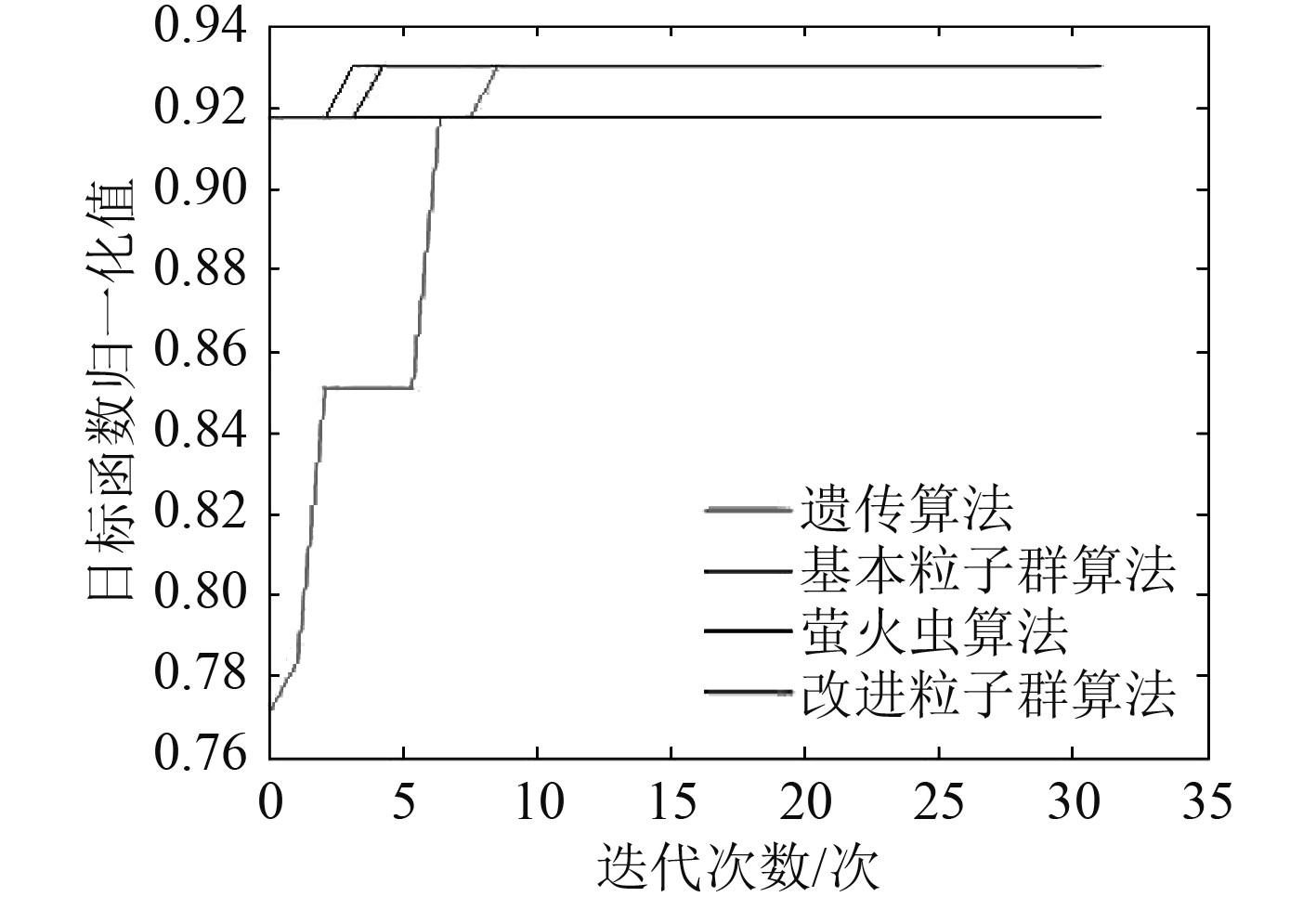
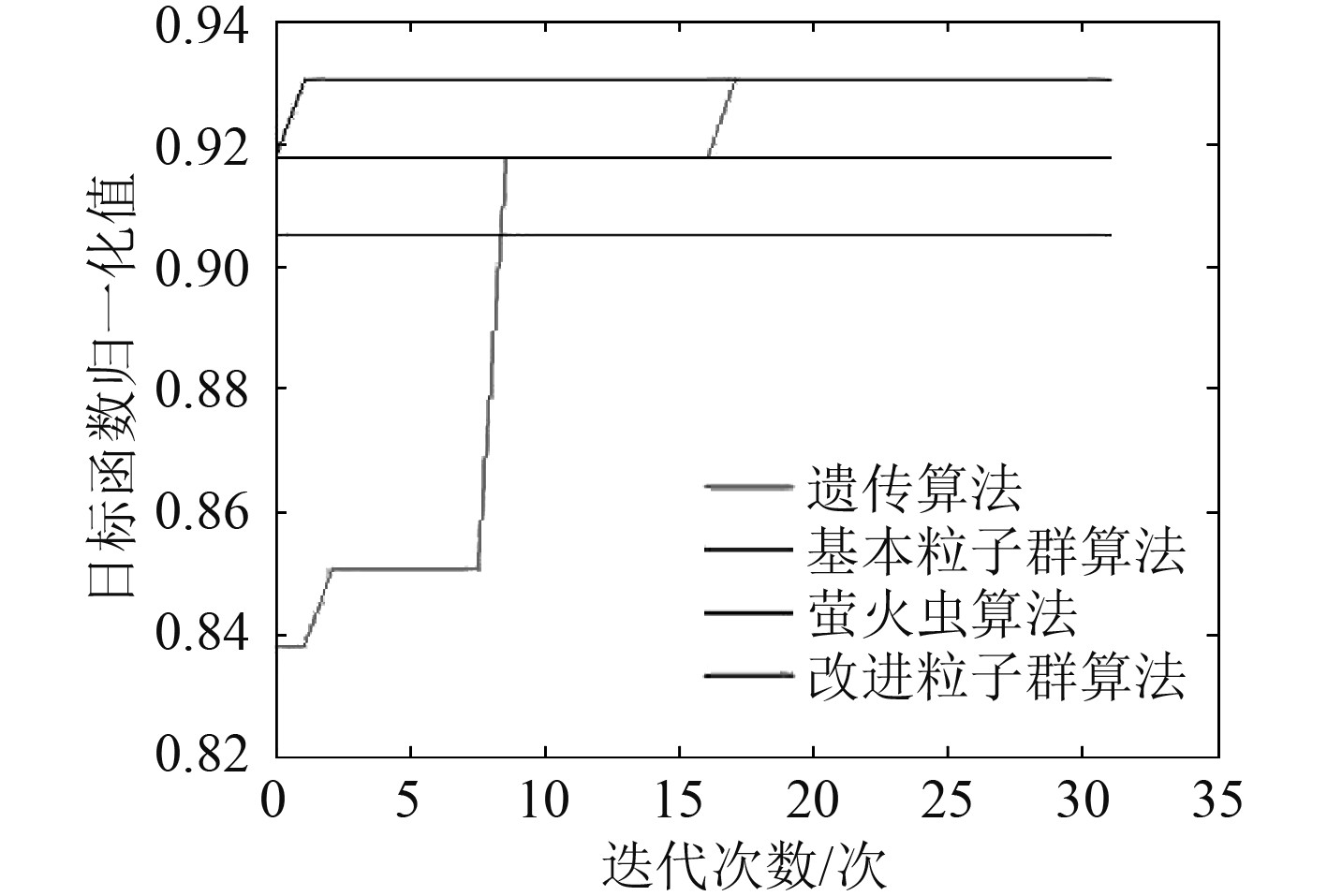
为体现改进粒子群算法的特点,以表中故障2为例,分别采用遗传算法、基本粒子群算法、萤火虫算法、本文所设计的改进粒子群算法,进行重构优化仿真,设置30次迭代数,分别运行5次程序,得到仿真结果如图5~图9所示。
|
图 5 仿真结果1 Fig. 5 Simulation results 1 |

|
图 9 仿真结果5 Fig. 9 Simulation results 5 |
|
图 6 仿真结果2 Fig. 6 Simulation results 2 |

|
图 7 仿真结果3 Fig. 7 Simulation results 3 |

|
图 8 仿真结果4 Fig. 8 Simulation results 4 |
可见,本文的改进粒子群算法相对于其他算法,具有较快的收敛速度,基本在5次迭代以内就可以达到最优解;具有优良的稳定性,5次运行程序的结果都得到了最大优化解,即最佳重构方案1121102211101所对应的最优解;克服了基本粒子群算法“早熟”的缺陷,基本粒子群算法虽然收敛速度较快,但大多没有收敛于最优解,而本文改进的粒子群算法每次都能收敛于最优解。由此可见,该算法具有优异的寻优性能,可以较好地适用于船舶中压直流综合电力推进系统配电网络的故障重构。
7 结 语采用节点–支路关联矩阵构建的船舶中压直流综合电力推进系统配电网络的拓补数学模型可以将网络的故障位置反映于节点导纳阵中,将该模型运用于节点电势法的求解过程,可以求解出配电网络的不同支路故障情况下的潮流分布,这一特性可以很好地适用于配电网络的故障重构模型的求解。
本文建立的船舶中压直流综合电力推进系统配电网络故障重构模型,综合考虑了负荷恢复量和开关动作量,并根据潮流计算结果检验系统容量约束。将自适应权重法和杂交池算法相结合,并采用“定向变异法”改进的粒子群算法,自适应权重法平衡粒子的全域搜索能力,杂交池算法提高了粒子的多样性,“定向变异法”可提高优等粒子的搜索能力,有效避免算法“早熟”。将该算法运用于重构模型的求解,算例测试结果表明,该算法可以较快速、较准确地提供完备的重构方案。
本文所建立配电网络重构模型并没有考虑重构后电力系统的稳定性问题,这一点可采取相应方法进一步研究。
| [1] |
孔祥楠. 船舶交流电力系统潮流计算研究[D]. 大连: 大连海事大学, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10151-1011118976.htm
|
| [2] |
楚玉华. 基于改进粒子群算法的船舶电力系统网络重构[D]. 镇江: 江苏科技大学, 2016. http://www.cnki.com.cn/Article/CJFDTotal-DLZS201103007.htm
|
| [3] |
兰海, 鲍鹏, 王婉婷. 舰船中压直流综合电力推进系统设计及稳态分析研究[J]. 中国造船, 2017, 58(2): 222-229. |
| [4] |
冀欣, 张晓峰. 基于节点电势法的舰船电力系统潮流计算方法[J]. 船海工程, 2007, 36(5): 132-135. DOI:10.3963/j.issn.1671-7953.2007.05.041 |
| [5] |
傅荟璇. 大型船舶电力系统网络拓补重构技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2006. http://cdmd.cnki.com.cn/Article/CDMD-10217-2007116675.htm
|
| [6] |
DING Z, SRIVASTAVA S, CARTES D. Expert system based dynamic load shedding scheme for shipboard power systems[C]// IEEE Industry Applications Conference-Forty-First IAS Annual Meeting. Tampa, USA: IEEE, 2007: 1338-1344.
|
| [7] |
庄劲武. 舰艇电力系统稳态参数计算方法的研究[J]. 海军工程大学学报, 2000, 20(5): 20-24. DOI:10.3969/j.issn.1009-3486.2000.05.005 |
| [8] |
THUAN Thanh Nguyena, b, THANG Trung Nguyenc, ANH Viet Truonga, et al. Multi-objective electric distribution network reconfiguration solution using runner-root algorithm[J]. Applied Soft Computing, 2017, 52(10): 93-108. |
| [9] |
张卫平, 关晓菡, 刘元超, 等. DC/DC变换器稳态建模的教学方法[J]. 电气电子教学学报, 2008, 30(5): 101-104. DOI:10.3969/j.issn.1008-0686.2008.05.039 |
| [10] |
傅旭, 王宏, 杨欣, 等. 考虑N_1静态电压稳定约束的电力系统负荷裕度新算法[J]. 陕西电力, 2016, 44(3): 33-38. |
| [11] |
EBERHART R C, KENNEDY J. Particles swarm optimization[C]//IEEE International Conference on Neural Network. Perth, Australia, IEEE, 1995: 1942-1948.
|
| [12] |
张威, 施伟峰, 胡红钱. 船舶区域配电系统全智能体重构及其优化研究[J]. 电力系统保护与控制, 2016, 44(4): 9-15. DOI:10.7667/PSPC20160402 |
| [13] |
韩敏, 何冰, 郑丹晨. 基于参考点的高维多目标粒子群算法[J]. 控制与决策, 2017, 32(4): 607-612. |
| [14] |
朱志宇, 郑晨阳. 基于混沌自适应差分进化算法的舰船电力系统网络重构[J]. 江苏科技大学学报(自然科学版), 2013, 27(2): 154-158. |
| [15] |
龚纯, 王正林. 精通MATLAB最优化计算[M]. 北京: 电子工业出版社, 2002.
|
 2020, Vol. 42
2020, Vol. 42
