2. 福建省船舶与海洋工程重点实验室,福建 厦门 361021
2. Fujian Provincial Key Laboratory for Naval Architecture and Ocean Engineering, Xiamen 361021, China
钻柱升沉补偿系统是保障海洋浮式钻井平台安全高效作业的必要装置。常用的升沉补偿系统有天车型、游车型和绞车型补偿系统,其中天车型升沉补偿系统应用比较广泛[1-3]。钢丝绳摇摆装置是天车型升沉补偿系统重要组成部分,对补偿系统的功用有着至关重要的影响,其设计质量是确保钻井安全和提高钻井效率的基础[1-2]。在天车型钻柱升沉补偿系统的设计阶段,设计人员就面临着一个亟需解决的课题,即如何从多种可行的钢丝绳摇摆装置设计方案中正确选择出一种最佳的设计方案。
目前,国内外学者针对海上钻井钻柱升沉补偿系统的研究几乎都聚焦于钻井钻柱升沉补偿系统的设计和仿真分析上[3],而对钻柱升沉补偿系统设计方案综合评价问题的研究几乎处于空白状态,尚未见到公开的研究成果。国内外学者针对其他设计方案的综合评价问题,已开展了大量的研究工作,提出了包括层次分析法、模糊综合评估法、灰色关联分析法、TOPSIS法、相对熵排序法等在内的一系列综合评价方法,取得了一系列重要研究成果[4-11]。
基于此,本文根据浮式钻井钻柱天车型升沉补偿系统摇摆装置的特点,在广泛参考相关研究文献的基础上,综合运用层次分析法、变异系数法、灰关联分析和TOPSIS法,构建一种简单实用的浮式钻井钻柱天车型升沉补偿系统摇摆装置设计方案优选方法。
1 优选思路针对浮式钻井船钻柱天车型升沉补偿系统摇摆装置设计方案的特点,在参考相关研究文献的基础上,分别运用变异系数法和层次分析法确定评价指标的主客观权重,然后运用相对熵原理计算出指标的综合权重,以提高权重的准确性[4-11]。综合运用灰关联分析和TOPSIS法,建立一种基于相对熵加权-灰色TOPSIS的浮式钻井天车型升沉补偿系统摇摆装置设计方案优选方法。优选思路如图1所示。
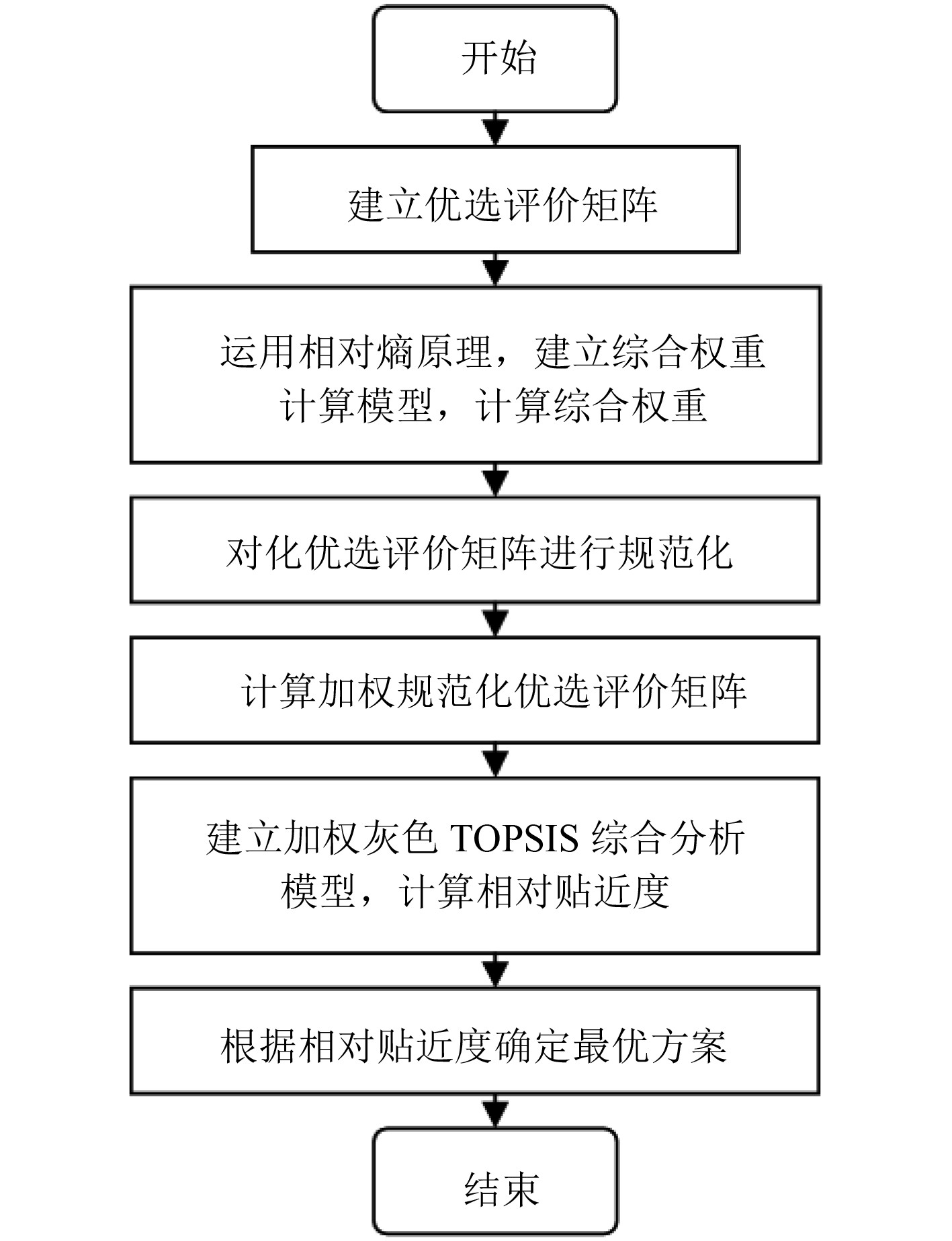
|
图 1 浮式钻井钻柱升沉补偿系统设计方案优选思路 Fig. 1 Optimal process of the design scheme of heave compensation system for floating drilling string |
设有
| ${ A} = {[{a_{ij}}]_{m \times n}}\text{。}$ | (1) |
式中:
在评价浮式钻井钻柱天车型升沉补偿系统摇摆装置设计方案时,必须合理确定评价指标的权重。目前确定指标权重的方法可分为主观赋权法和客观赋权法两大类。由于主观赋权法和客观赋权法各有其优缺点,只有将通过主观赋权法和客观赋权法确定的权重有机结合起来,才能使所确定的权重更加合理[4-11]。本文采用相对熵原理将主观赋权法所得权重与客观赋权法所得权重进行综合,得到评价指标的综合权重,具体步骤如下:
1)层次分析法(AHP)是主观赋权法中的一种代表性方法,故本文运用层次分析法[4]来确定指标的主观权重
2)变异系数法是确定客观赋权法中的一种常用方法,故本文应用变异系数法[5-6]来确定指标的客观权重
| ${\beta _j} = \frac{{{\sigma _j}/{\delta _j}}}{{\displaystyle\sum\limits_{j = 1}^n {{\sigma _j}/{\delta _j}} }}\text{,}$ | (2) |
式中:
3)若主客观权重的综合权重向量为
| $ \left\{ \begin{array}{l} \min D =\displaystyle \sum\limits_{j = 1}^n {\left({\omega _j}\ln \dfrac{{{\omega _j}}}{{{\alpha _j}}}\right) + \displaystyle\sum\limits_{j = 1}^n {\left({\omega _j}\ln \dfrac{{{\omega _j}}}{{{\beta _j}}}\right)} }\text{,} \\ \displaystyle\sum\limits_{j = 1}^n {{\omega _j} = 1;{\omega _j} > 0} \text{。} \end{array} \right. $ | (3) |
采用拉格朗日乘子法求解优化模型,可最得优解
| ${\omega _j} = \frac{{\sqrt {{\alpha _j}{\beta _j}} }}{{\displaystyle\sum\limits_{j = 1}^n {\sqrt {{\alpha _j}{\beta _j}} } }}\text{。}$ | (4) |
为消除不同指标间量纲的差异,需要对指标值进行量纲进行规范化处理。规范化后的优选矩阵为:
| ${ B} = {[{b_{ij}}]_{m \times n}}\text{。}$ | (5) |
式中:
对规范化矩阵
| $ C = {[{c_{ij}}]_{m \times n}}\text{。}$ | (6) |
式中:
1)确定正理想解和负理想解
正理想解就是设想最好的方案,由所有评价对象指标值中的最优值组成;负理想解就是假定最坏的方案,由所有评价对象指标值中的最劣值组成[9-11]。即
| ${D^ + } = \left(\mathop {\max }\limits_{1 \leqslant i \leqslant m,j \in {C^ + }} {c_{ij}},\mathop {\min }\limits_{1 \leqslant i \leqslant m,j \in {C^ - }} {c_{ij}}\right) = (d_j^ + )\text{,}$ | (7) |
| ${D^ - } = \left(\mathop {\min }\limits_{1 \leqslant i \leqslant m,j \in {C^ + }} {c_{ij}},\mathop {\max }\limits_{1 \leqslant i \leqslant m,j \in {C^ - }} {c_{ij}}\right) = (d_j^ - )\text{,}$ | (8) |
式中:
2)计算正关联度和负关联度
第
| $f_i^ + = \frac{1}{n}\sum\limits_{j = 1}^n {e_{ij}^ + }\text{,} $ | (9) |
| $ f_i^ - = \frac{1}{n}\sum\limits_{j = 1}^n {e_{ij}^ - }\text{。} $ | (10) |
式中:
3)计算正距离和负距离
第
| $g_i^ + = \sqrt {\sum\limits_{j = 1}^n {{{[{c_{ij}} - d_j^ + ]}^2}} }\text{,} $ | (11) |
| $g_i^ - = \sqrt {\sum\limits_{j = 1}^n {{{[{c_{ij}} - d_j^ - ]}^2}} }\text{。} $ | (12) |
4)计算相对贴近度
分别对正关联度
| ${z_i} = \frac{{[\lambda x_i^ + + (1 - \lambda )y_i^ - ]}}{{[\lambda x_i^ + + (1 - \lambda )y_i^ - ] + [\lambda x_i^ - + (1 - \lambda )y_i^ + ]}}\text{。}$ | (13) |
式中:
各方案的相对贴近度反映了各方案与正负理想方案之间曲线的位置关系。按照各方案的相对贴近度的大小进行排序,相对贴近度越大则表示该方案越好,反之则越差。
3 案例分析 3.1 建立优选矩阵根据参考文献[1],选取浮式钻井钻柱天车型升沉补偿系统摇摆装置的下摇臂最大力比系数、下摇臂平均力比系数、上摇臂最大力比系数、下摇臂平均力比系数、钢丝绳窜动长度和钢丝绳直弯交变长度等6个指标(分别以
| $ A = {[{a_{ij}}]_{4 \times 6}} = \left[\!\! {\begin{array}{*{20}{c}} {4.95}&{1.32}&{5.15}&{1.94}&{1.04}&{4.50} \\ {2.50}&{1.08}&{2.90}&{1.82}&{1.19}&{3.39} \\ {2.80}&{1.12}&{3.18}&{1.78}&{1.16}&{4.52} \\ {3.25}&{1.28}&{2.77}&{1.98}&{1.17}&{3.28} \end{array}}\!\! \right]\text{。}$ |
根据AHP计算原理和步骤[4]以及式(2)~式(4),经计算可得评价指标的主观权重、客观权重和综合权重分别为:
| $ \begin{split} & \alpha = (0.094\;2,0.526,0.094\;2,0.052\;6,0.555\;9,0.150\;5)\text{,}\\ & \beta = (0.316\;7,0.095\;8,0.310\;6,0.049\;5,0.058\;1,0.169\;3)\text{,}\\ & \omega = (0.214\;5,0.088\;2,0.212\;5,0.063\;4,0.223\;2,0.198\;3)\text{。} \end{split} $ |
根据式(5)和式(6)可得加权规范化矩阵:
| $ \begin{split} & B = \!{[{b_{ij}}]_{4 \times 6}} \\ & =\! \left[ \!\!\! \!\! {\begin{array}{*{20}{c}} {0.2145} \!\!&\!\! {0.088\;2}\!\!&\!\!{0.212\;5}\!\!&\!\!{0.050\;7}\!\!&\!\!{0.000\;0}\!\!&\!\!{0.195\;1} \\ {0.000\;0}\!\!&\!\!{0.000\;0}\!\!&\!\!{0.011\;6}\!\!&\!\!{0.012\;7}\!\!&\!\!{0.223\;2}\!\!&\!\!{0.017\;6} \\ {0.026\;3}\!\!&\!\!{0.014\;7}\!\!&\!\!{0.036\;6}\!\!&\!\!{0.000\;0}\!\!&\!\!{0.178\;6}\!\!&\!\!{0.198\;3} \\ {0.065\;7}\!\!&\!\!{0.075\;3}\!\!&\!\!{0.000\;0}\!\!&\!\!{0.063\;4}\!\!&\!\!{0.193\;5}\!\!&\!\!{0.000\;0} \end{array}} \!\! \!\! \right]{\text{。}} \end{split} $ |
1)由于6个评价指标均为成本性指标,因此,根据式(7)和式(8),正负理想解分别为
2)按式(9)~式(13)可求得正负关联度、正负距离及相对贴近度,计算结果如表1所示。
|
|
表 1 正负关联度、正负距离及相对贴近度计算结果 Tab.1 Calculation results of positive and negative correlation degree, positive and negative distance and relative closeness degree |
3)根据表1的数据,4个浮式钻井钻柱天车型升沉补偿系统摇摆装置设计方案的优劣排序为:方案2>方案4>方案2>方案1,即方案2为最优方案。
4 结 语摇摆装置设计方案的选择是浮式钻井钻柱天车型升沉补偿系统设计开发过程中的一个重要环节,对浮式钻井钻柱天车型升沉补偿系统的补偿效果有着至关重要的影响。本文所建立的浮式钻井钻柱天车型升沉补偿系统摇摆装置设计方案优选方法,在统筹考虑主观赋权法和客观赋权法各自优缺点的基础上,运用相对熵原理建立了一种将层次分析法和差异系数法所确定的主客观权重综合起来的权重计算模型,使确定的综合权重更加准确;构建了一种将灰关联分析法与TOPSIS法有机结合起来的加权-灰色TOPSIS综合优选模型,克服了灰关联度法和TOPSIS各自本身的局限性,使相对贴近度的计算过程和结果更为全面、准确,较好地解决了摇摆装置设计方案的选择问题。另外,本文所建立的优选方法,原理简单,使用方便,对其他设计方案的优选决策也具有较好的参考价值。
| [1] |
刘振东, 张彦廷, 黄鲁蒙, 等. 海洋钻井天车升沉补偿系统不同摇摆装置性能分析[J]. 中国石油大学学报(自然科学版), 2018, 42(6): 145-152. DOI:10.3969/j.issn.1673-5005.2018.06.017 |
| [2] |
徐涛. 深海钻井升沉补偿装置机理研宄与设计[D]. 成都: 西南石油大学, 2016.
|
| [3] |
熊云峰, 陈章兰. 钻井钻柱升沉补偿系统国内研究现状及发展重点[J]. 舰船科学技术, 2018, 40(12): 78-83. DOI:10.3404/j.issn.1672-7649.2018.12.016 |
| [4] |
史俊伟, 孟祥瑞, 董羽, 等. 基于地表沉陷控制的膏体充填材料的性能优化研究[J]. 中国安全生产科学技术, 2017, 13(10): 143-149. |
| [5] |
祝志川. 基于变异系数-G1法的混合交叉赋权方法[J]. 统计与决策, 2017(12): 79-81. |
| [6] |
李乃文, 张丽, 牛莉霞. 煤矿井下安全系统脆弱性的系统动力学仿真研究[J]. 中国安全生产科学技术, 2017, 13(10): 86-92. |
| [7] |
水庆象, 范波峰. 基于FAHP-Retropy的耦合定权法的高速公路路线方案优选模型[J]. 数学的实践与认识, 2018, 48(4): 121-128. |
| [8] |
张目, 黄春燕, 李岩. 基于相对熵和可变模糊集理论的战略性新兴产业企业信用评价[J]. 数学的实践与认识, 2014, 44(13): 18-26. |
| [9] |
刘凌刚, 耿俊豹, 魏曙寰, 等. 基于灰色关联TOPSIS法的舰船装备维修方案决策[J]. 火力与指挥控制, 2018, 43(5): 54-57. DOI:10.3969/j.issn.1002-0640.2018.05.011 |
| [10] |
沈丹杰, 刘兴旺, 何洪明. 灰色关联改进TOPSIS法进行桥梁评价的应用[J]. 河北农业大学学报, 2018, 41(1): 116-121. |
| [11] |
赵丽娜, 王立晓. 基于灰关联TOPSIS法的交通方式选择模型[J]. 交通科技与经济, 2017, 19(3): 10-13. |
 2020, Vol. 42
2020, Vol. 42
