2. 高新船舶与深海开发装备协同创新中心,上海 200240;
3. 上海交通大学 船舶海洋与建筑工程学院,上海 200240;
4. 中电科海洋信息技术研究院有限公司,北京 100041
2. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai 200240, China;
3. School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, China;
4. CETC Ocean Information Co., Ltd., Beijing 100041, China
在下潜、作业和回收过程中,由于海洋环境本身的复杂性和时变性,水下潜器要受到海流、脐带缆等因素的作用,这些因素都会使水下潜器的原本运动轨迹由于扰动而产生偏差,因此,研究复杂海洋环境下的带缆水下潜器航迹跟踪控制就变得尤为重要。
带缆水下潜器的脐带缆与潜器本体的耦合作用不可忽视,目前,对于脐带缆运动的研究方法主要包括有限差分法、集中质量法、直接积分法等[1-3]。其中,有限差分法能够在较小计算量的情况下对大时间尺度的运动进行模拟,因此实际应用最为广泛。
目前国内外在水下潜器的轨迹跟踪控制研究中,常采用的方法有PID控制、滑模控制、反步控制等。PID控制[4-5]在工业生产中广泛应用,它是一种简单的、易于实现的线性控制。但水下潜器工作环境的复杂性以及水动力参数的非线性使得该方法很多情况下无法满足航迹跟踪的要求。滑模控制[6-8]广泛应用于国内外水下机器人的控制研究中,具有良好的鲁棒性,但是该方法会不可避免地导致系统出现抖振现象。反步控制法是目前处理非线性系统最常用的控制方法之一,由于不需要对系统的非线性模型进行处理,可以有效保留系统的非线性项。该方法在移动机器人的路径跟踪中取得了较好的效果[9-10]。但当跟踪轨迹出现拐点或跟踪误差过大时,会造成控制器输出速度大幅跳变的问题。
本文根据水下潜器的运动学方程和动力学方程分别设计了运动学反步控制器和动力学滑模控制器。传统滑模变结构控制系统中的抖振现象,可以在设计滑模动力学控制器时通过将切换项替换为自适应项得到解决。同时,在设计反步运动学控制器时,通过引入生物启发神经动力学模型平滑传统反步控制器由于跟踪误差较大而出现的速度跳变。在航迹跟踪仿真阶段,对水下潜器的折线路径进行了仿真,并对有缆和无缆时的仿真结果进行了比较分析。
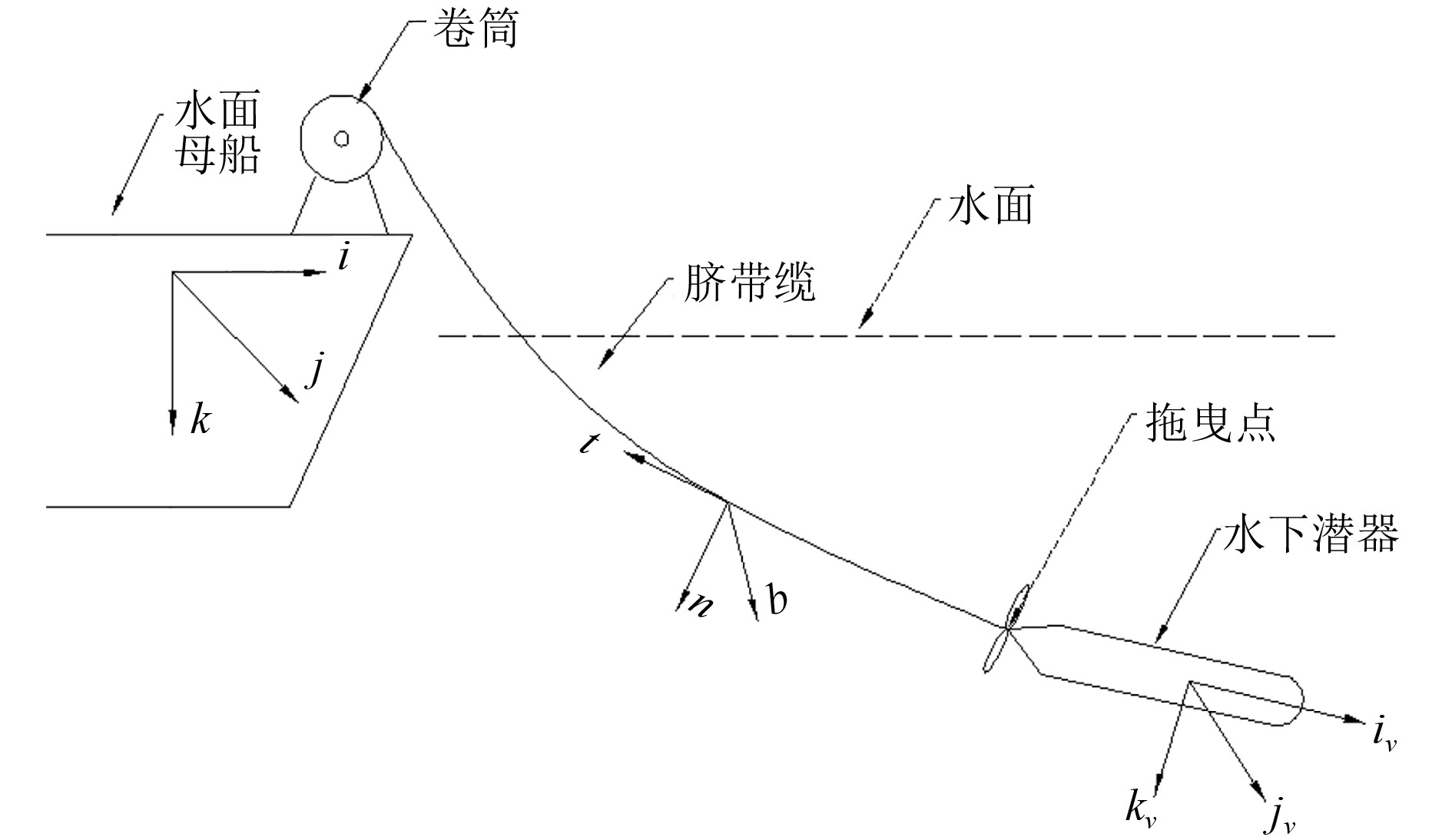
1 脐带缆-潜器多体系统运动模型结合脐带缆应用的工程背景[11-12],建立如图1所示的脐带缆-潜器多体系统,整个潜器系统由水面母船、水下潜器以及脐带缆3部分构成。针对该系统建立3个坐标系:船体固定的大地坐标系i-j-k、脐带缆局部坐标系t-n-b和水下潜器局部坐标系iv-jv-kv。脐带缆和水下潜器的质量相较于水面母船可以忽略不计,因此整个系统中水面母船静止,脐带缆和水下潜器的运动不会对母船的位置产生影响。
|
图 1 多体系统与坐标系示意图 Fig. 1 Multi-body system and coordinate system |
将脐带缆简化为细长柔性圆柱体。对水中的脐带缆作受力分析,它将受到重力、浮力、阻力、惯性力以及水面母船和水下潜器的拉力作用,进一步对单位微元脐带缆进行分析,可以得到脐带缆的动力平衡方程式:
| $\frac{{\partial {{T}}}}{{\partial S}} + {{W}} + {{{D}}_{{N}}}{{ + }}{{{D}}_{{T}}}{+{ I}} = 0\text{。}$ | (1) |
式中:S为脐带缆拉伸状态时的弧长;T为脐带缆的张力;W为重力与浮力之差;DN为法向流体阻尼力;DT为切向流体阻尼力;I为惯性力。
为求解上述偏微分方程,需要添加边界条件。在整个系统中,脐带缆连接着水面母船和水下潜器,因此脐带缆运动学和动力学边界条件由脐带缆首端边界条件和尾端边界条件2部分组成。
1.2 水下潜器的运动和动力学模型根据刚体动力学进行受力分析,作用于水下潜器的力包括重力、浮力、流体阻力、惯性力、脐带缆作用力和推进器推力。为了便于求解,采用将脐带缆作用力作为外力并单独求解的弱耦合形式建立水下运载器的力平衡方程,在对平衡方程化简后得到如下矩阵形式的动力学方程[13]:
| ${{M}}{\dot{ v}}{\rm{ + }}{{C}}\left( {{v}} \right){{v}}{\rm{ + }}{{D}}\left( {{v}} \right){{v}} + {{g}} = {{{F}}_{{T}}} + {{{F}}_{{C}}}\text{。}$ | (2) |
式中:M为惯性力系数,包括刚体惯性力系数MR和附加质量惯性力系数MA;C(ν)为柯氏力与向心力系数,包括刚体柯氏力与向心力系数CR和附加质量柯氏力和向心力系数CA;g为潜器受到的浮力和重力之和;FT为推进器推力;FC为脐带缆作用力。
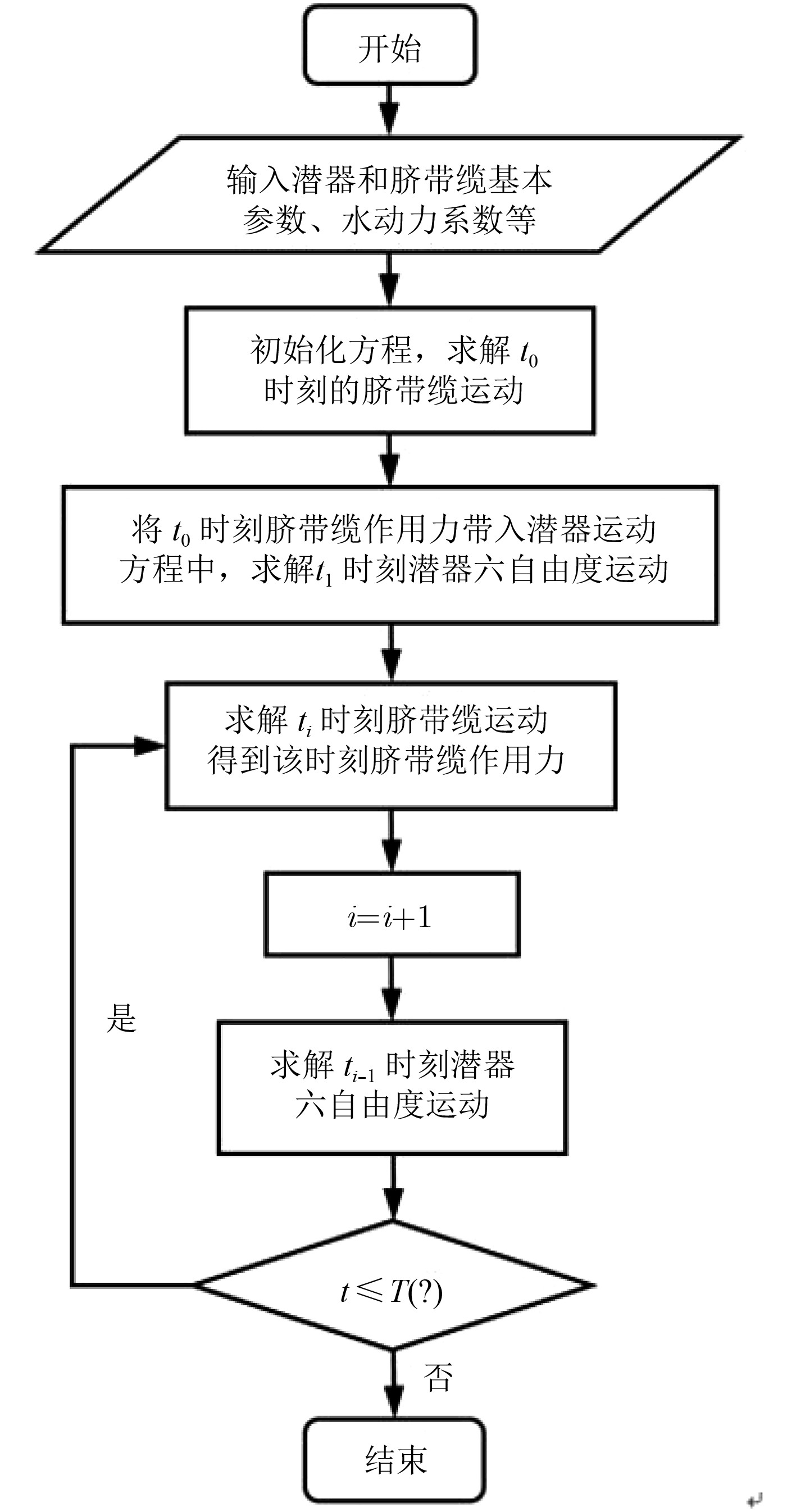
对于式(2)的常微分方程组,可以采用4阶龙格库塔方法进行求解。首先将加速度水动力系数、速度水动力系数和水下潜器基本参数代入计算合并项中的
|
图 2 多体系统运动数值仿真流程图 Fig. 2 Flow chart of numerical simulation of multi-body system motion |
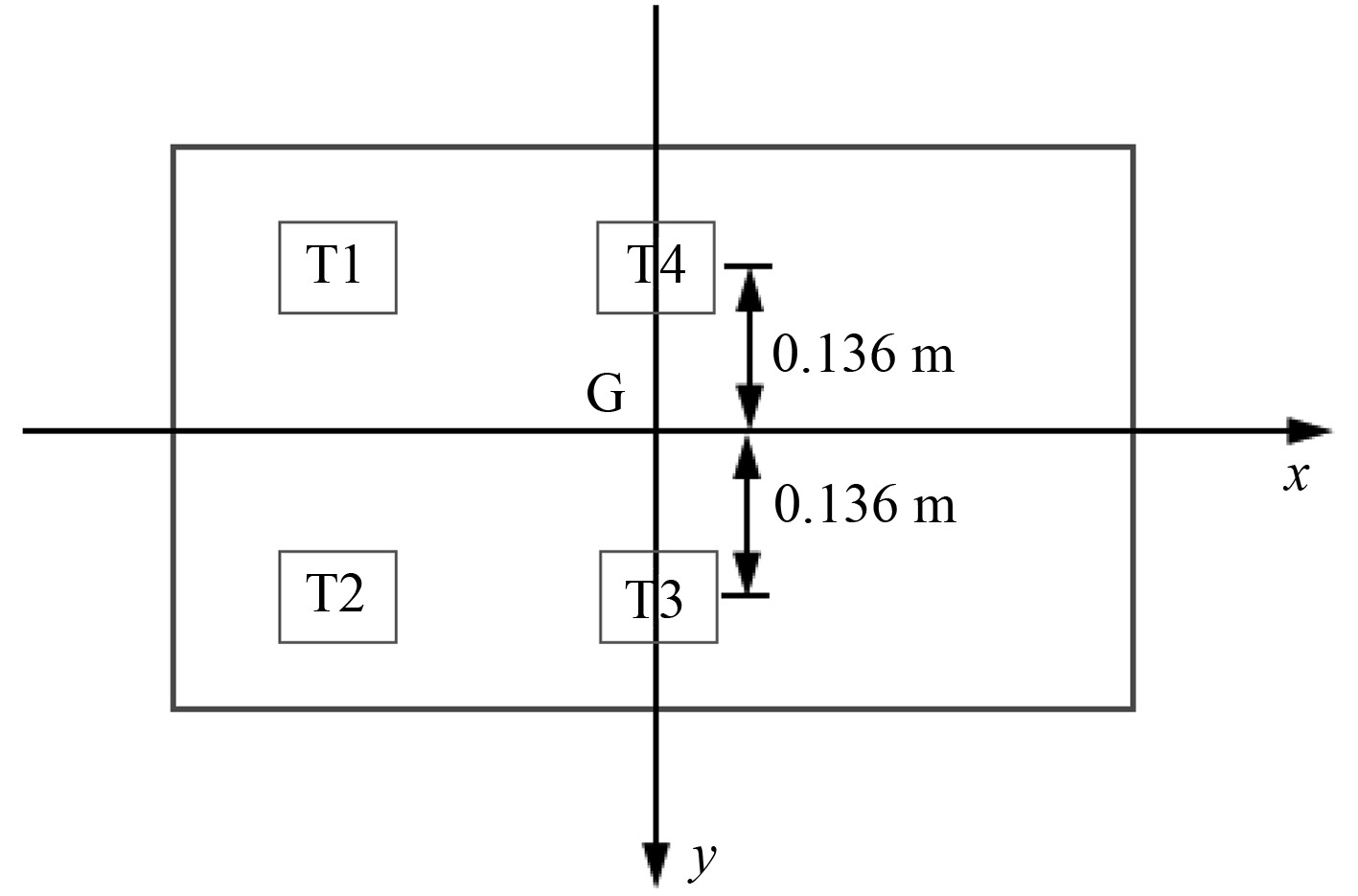
本文选取的水下潜器模型为Deep Ocean Engineering公司生产的Triggerfish系列,该款ROV为开架式结构,采用2个水平推进器T1,T2和2个斜向45°的推进器T3,T4为动力装置。图3给出了该潜器的外观图。图4给出了该潜器的简略俯视图。水平推进器T1和T2通过协同作用可使水下潜器产生纵向运动和转向运动,斜向推进器T3和T4通过协同作用可以使潜器产生垂向运动和侧向运动。

|
图 3 Triggerfish ROV结构图 Fig. 3 Structure of Triggerfish ROV |
|
图 4 TRiggerfish ROV俯视图 Fig. 4 Vertical view of Triggerfish ROV |
根据上述水下潜器模型的驱动力实际情况,潜器只能作纵向、横向、垂向和首摇运动。因此,这里设定横摇角和横摇角速度为Φ=0,p=0;纵摇角和纵摇角速度为θ=0,q=0。惯性坐标系下,水下潜器期望的位置和姿态角为
| $ \begin{split} {{{e}}_{\bf{\mu }}} =\,& \mu - {\mu _d} = {\left[ {{e_x},{e_y},{e_z},{e_\psi }} \right]^{\rm T}} =\\ &{\left[ {x - {x_d},y - {y_d},z - {z_d},\psi - {\psi _d}} \right]^{\rm T}}\text{。} \end{split} $ | (3) |
带缆水下潜器航迹跟踪的目标就是要在一定的时间内,使潜器的实际运动轨迹与期望的轨迹相吻合。换言之,就是通过控制器输出适当的控制量,使得误差
对纵向、横向、垂向和首摇4个自由度运动,基于Lyapunov稳定性理论和反步设计策略,设计运动学控制律[14],得到如下的中间虚拟速度
| $\left\{ \begin{array}{l} {u_i} = - {e_x}\cos \psi - {e_y}\sin \psi + {{\dot x}_d}\cos \psi + {{\dot y}_d}\sin \psi \text{,} \\ {v_i} = {e_x}\sin \psi - {e_y}\cos \psi + {{\dot y}_d}\cos \psi - {{\dot x}_d}\sin \psi \text{,} \\ {w_i} = - {e_z} + {{\dot z}_d} \text{,} \\ {r_i} = {{\dot \psi }_d} - \sin {e_\psi }\text{。} \end{array} \right.$ | (4) |
可以看出,在跟踪路径的拐点处,跟踪误差
生物启发神经动力学模型是在Hodgkin和Huxley[15]利用电路原理提出的生物膜模型基础上,由Grossberg[16]首次提出的该模型的生物启发形式。生物膜电压可用下面的状态方程表示:
| $ \begin{split} {C_m}\frac{{d{V_m}}}{{dt}} =\,& - \left( {{E_p} + {V_m}} \right){g_p} + \left( {{E_{Na}} - {V_m}} \right){g_{Na}} -\\ &\left( {{E_k} + {V_m}} \right){g_k}\text{。} \end{split} $ | (5) |
式中:Cm为膜电容;Vm为膜电压;Ep,ENa,EK分别为生物膜中无源漏极电流,钠离子和钾离子的能斯特电势;gp,gNa和gk分别为无源漏极,钠离子和钾离子的电导率。
令Cm=1,V=Ep+Em,A=gp,VU=ENa+Ep,VL=EK+Ep,S+=gNa,S-=gk,式(5)可变为如下形式:
| $\dot V = - AV + \left( {{V_U} - V} \right){S^ + }\left( t \right) - \left( {{V_L} + V} \right){S^ - }\left( t \right)\text{,}$ | (6) |
式中:V为神经元活动(膜电位),在水下潜器航迹跟踪控制中表示虚拟中间速度,参数A、VU和VL分别表示为神经活动的负衰减率、上限和下限。变量S+(t)和S–(t)分别表示兴奋性和抑制性输入,反应外界环境对神经元的刺激作用,在水下潜器航迹跟踪控制中,它代表了跟踪误差
当存在兴奋性输入S+(t)(S+>0)时,神经元活动V增大并自动获得控制项
式(6)的输出特性并结合运动学控制器的设计,将其改造如下:
| $\begin{array}{l} {{\dot V}_{si}} = - A{V_{si}} + \left( {{V_U} - {V_{si}}} \right)f\left( {{e_i}} \right) - \left( {{V_L} + {V_{si}}} \right)g\left( {{e_i}} \right)\text{,}\\ i = x,y,z,\psi \text{。} \end{array}$ | (7) |
式中:
| $\left\{ \begin{array}{l} {u_c} = - {V_{sx}}\cos \psi - {V_{sy}}\sin \psi + {{\dot x}_d}\cos \psi + {{\dot y}_d}\sin \psi \text{,} \\ {v_c} = {V_{sx}}\sin \psi - {V_{sy}}\cos \psi + {{\dot y}_d}\cos \psi - {{\dot x}_d}\sin \psi \text{,} \\ {w_c} = - {V_{sz}} + {{\dot z}_d}\text{,} \\ {q_c} = {{\dot \psi }_d} - \sin {V_{s\psi }} \text{。} \end{array} \right.$ | (8) |
对于一个实际的航迹跟踪控制过程来说,动力学控制器的目标就是在考虑动力学模型式(2),计算出推进器推力和力矩使潜器的实际速度v→vc。在脐带缆等干扰因素存在的情况下,为了实现对潜器速度的稳定跟踪控制,本文设计一个具有较强鲁棒性的滑模变结构控制器对速度进行跟踪控制,推进器推力由速度误差产生并作用于潜器本体上,实现潜器的纵向、横向、垂向和首摇运动。
定义虚拟速度跟踪误差为:
| $ {{{e}}_c} = {{{v}}_c} - {{v}}\text{,} $ | (9) |
滑模变结构控制[9-16]的2个基本问题:1)切换面或者滑模面的设计;2)控制函数的求解或控制律的设计。这里将滑模面设计如下:
| $ {{s}} = {{\dot{ e}}_c} + 2\Lambda {{{e}}_c} + {\Lambda ^2}\int {{{{e}}_c}} \text{,} $ | (10) |
将式(10)对时间求导得:
| $ {\dot{ s}} = {{\ddot{ e}}_c} + 2\Lambda {{\dot{ e}}_c} + {\Lambda ^2}{{{e}}_c} = {{\ddot{ e}}_c} + 2\Lambda \left( {{{{\dot{ v}}}_c} - {\dot{ v}}} \right) + {\Lambda ^2}{{{e}}_c}\text{,} $ | (11) |
当系统在切换面(滑模面)上运行的时候,有
| $ {\dot{ s}} = {{\ddot{ e}}_c} + 2\Lambda {{\dot{ e}}_c} + {\Lambda ^2}{{{e}}_c} = {{\ddot{ e}}_c} + 2\Lambda \left( {{{{\dot{ v}}}_c} - {\dot{ v}}} \right) + {\Lambda ^2}{{{e}}_c} = 0 \text{,} $ | (12) |
将式(2)代入式(12),得
| $ {{\ddot{ e}}_c} + 2\Lambda \left( {{{{\dot{ v}}}_c} - {{{M}}^{ - 1}}\left( {{{{F}}_{{T}}} + {{{F}}_{{C}}} - {{Cv}} - {{Dv}} - {{g}}} \right)} \right) + {\Lambda ^2}{{{e}}_c} = 0\text{,} $ | (13) |
考虑到水下潜器系统的动力学不是完全已知的,将推进器所提供的推力
| ${{{F}}_{{T}}} = {{\hat{ F}}_{{T}}} + {{\tilde{ F}}_{{T}}}\text{,}$ | (14) |
式中:
| ${{{F}}_{{\bf{Teq}}}} = {\hat{ M}}\left( {{{{\dot{ v}}}_c} + \frac{{{{{\ddot{ e}}}_c}}}{{2\Lambda }} + \frac{\Lambda }{2}{{{e}}_c}} \right) + {\hat{ Cv}} + {\hat{ Dv}}{\rm{ + }}{\hat{ g}}{\rm{ - }}{{{F}}_{{C}}}\text{,}$ | (15) |
由于式(15)中的
| $ {{\ddot{ e}}_c} = - {k_c}{{\dot{ e}}_c}\text{,} $ | (16) |
传统的滑模变结构控制可设计为:
| $ {{{F}}_{{T}}} = {{{F}}_{{\bf{Teq}}}} + k\operatorname{sgn} {{s}} \text{,} $ | (17) |
为了消除式(17)中不连续切换项ksgn s产生的抖振问题,将传统控制中的切换项替换掉,由自适应项代替来改善控制律:
| ${{{F}}_{{\bf{Tad}}}} = {{\tilde{ F}}_{{\bf{Test}}}} + \left( {K + \frac{{{\hat{ C}}}}{{2\Lambda }}} \right){{s}\text{,}}$ | (18) |
其中:
| ${{\dot{ {\bf \tilde F}}_{{\bf{Test}}}}} = \Omega {{s}}\text{,}$ | (19) |
完整控制律下的推进器推力为:
| $ {{{F}}_{{T}}} = {{{F}}_{{\bf{Teq}}}} + {{{F}}_{{\bf{Tad}}}} = {{{F}}_{{\bf{Teq}}}} + {{\tilde{ F}}_{{\bf{Test}}}} + \left( {K + \frac{{{\hat{ C}}}}{{2\Lambda }}} \right){{s}}\text{。} $ | (20) |
本文选取的脐带缆与水下潜器连接点处的位置坐标为rc=[–0.6,0,0],假设脐带缆在水中受到的浮力与其重力相平衡;脐带缆与母船相连接的卷筒半径为0.01 m,其转动惯性矩为0.01 m2,脐带缆与卷筒之间的摩擦力很小,因此可以忽略卷筒处的阻尼力矩Гf。
3.1 折线路径仿真结果与分析为实现水下潜器纵向、横向、垂向和首摇运动的仿真模拟,在惯性坐标系下,设计如下仿真期望路径和期望速度:0–15 s时间段内,期望路径为
|
|
表 1 基于生物启发神经动力学的反步运动学控制器参数 Tab.1 Parameters of backstepping sliding mode controller based on bio-inspired neurdynamics |
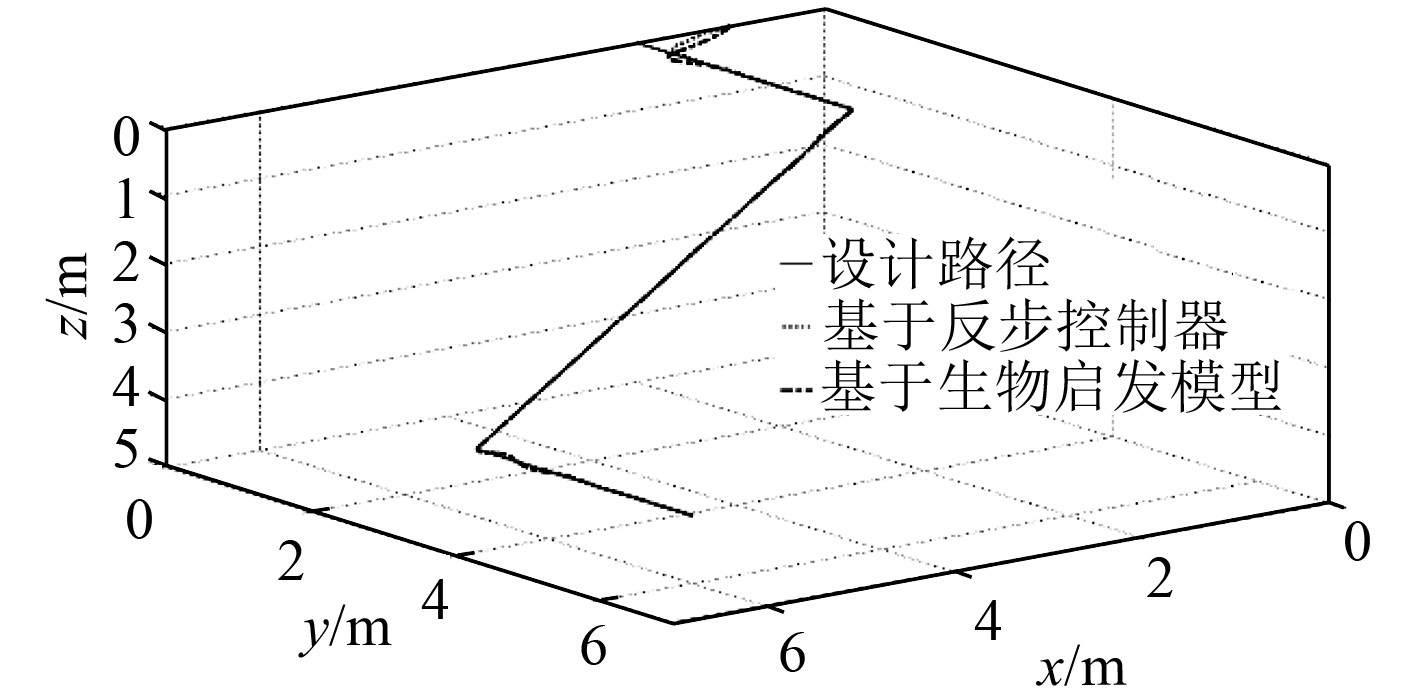
对无缆状态下的水下潜器进行简单折线路径跟踪,通过对简单反步控制器以及基于神经动力学模型反步控制器仿真结果的对比,验证所设计控制器的有效性。2种方法的路径跟踪结果见图5,路径跟踪速度曲线见图6。
|
图 5 折线路径航迹跟踪 Fig. 5 Trajectory tracking of fold line |
|
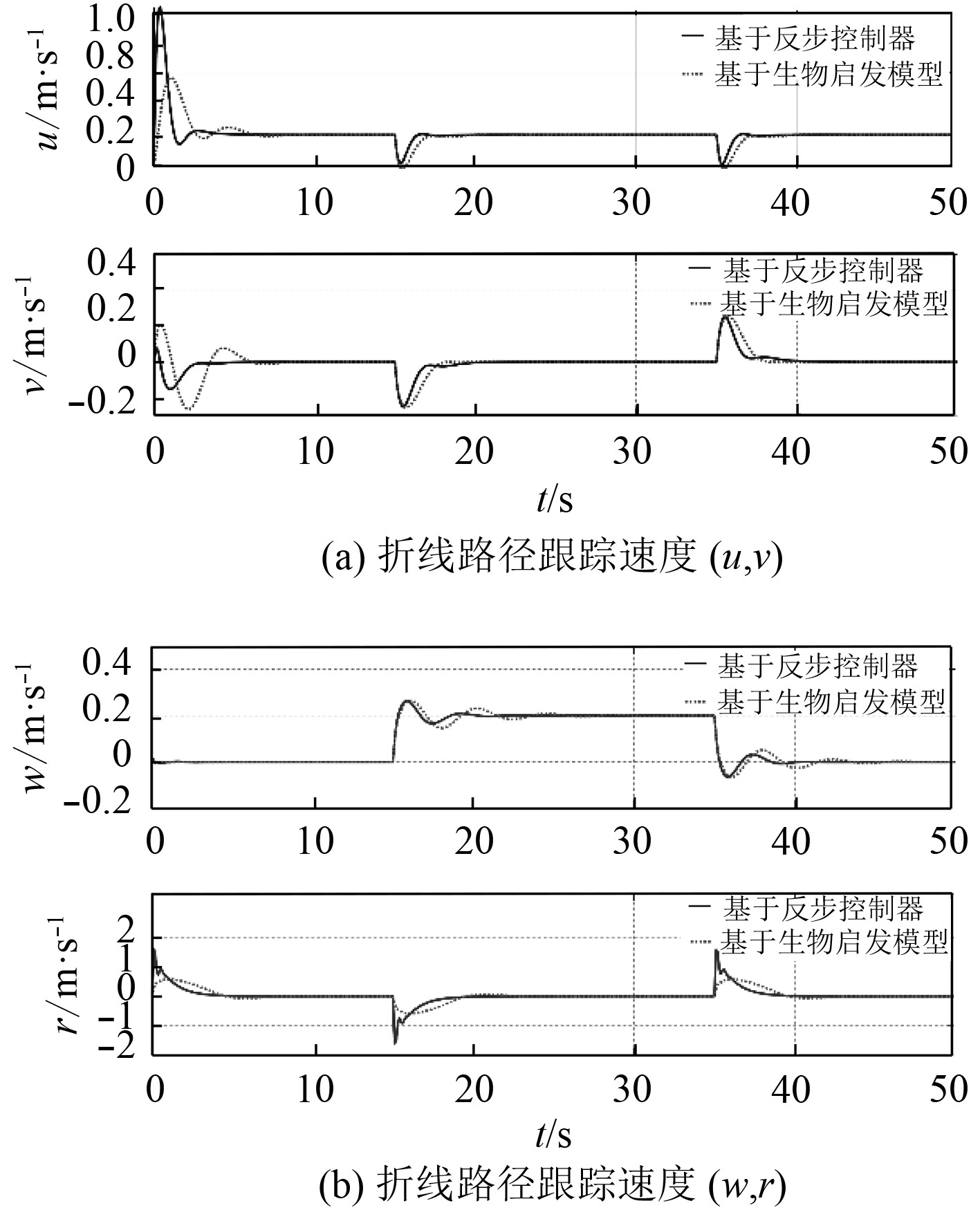
图 6 折线路径跟踪速度(u,v)和折线路径跟踪速度(w,r) Fig. 6 Tracking velocity (u, v) of fold line and Tracking velocity (w, r) of fold line |
从图5可以看出,对于空间折线路径,普通反步控制器与基于神经动力学模型的反步滑膜控制器在跟踪性能上,两者均能实现较好的跟踪效果,两者的跟踪路径均能紧紧贴合设计路径。但是从图6的跟踪速度来看,普通反步控制器在初始位置和路径拐点处均出现了速度跳变的情况,而引入神经动力学模型的反步控制器的输出速度更加平滑与稳定。以图6(b)速度r为例,当t=0 s,t=15 s和t=35 s时,通过对比两者的跟踪速度可以发现,普通反步控制器输出速度最大跳变值的绝对值均超过1 rad/s,而引入了神经动力学模型后控制输出速度小于0.5 rad/s。这是因为在t=0 s时潜器的首向角从0°转为90°,t=15 s从90°转为0°,t=35 s时从0°转为90°,首向角的突变引起了首向角跟踪误差突变,而普通反步控制器是直接以位置误差构造设计的,因此会产生很大的速度跳变。这种速度跳变在实际潜器的路径跟踪意味着潜器需要提供很大的加速度,这要求推进器提供巨大的推力,有时候甚至超出了推进器的推力范围。这种现象既影响了路径跟踪效果,同时也会影响推进器的使用寿命,而在引入神经动力学模型之后,控制器能够较好地平滑由于位置或者状态突变引起的速度跳变现象。
3.2 脐带缆折线路径跟踪效果的影响水下潜器在无流情况下,有无脐带缆的水下潜器在0–50 s内的空间折线路径跟踪结果如图7所示。有无脐带缆的水下潜器跟踪速度曲线如图8所示,无缆水下潜器跟踪误差与带缆水下潜器跟踪误差如图9所示。
|
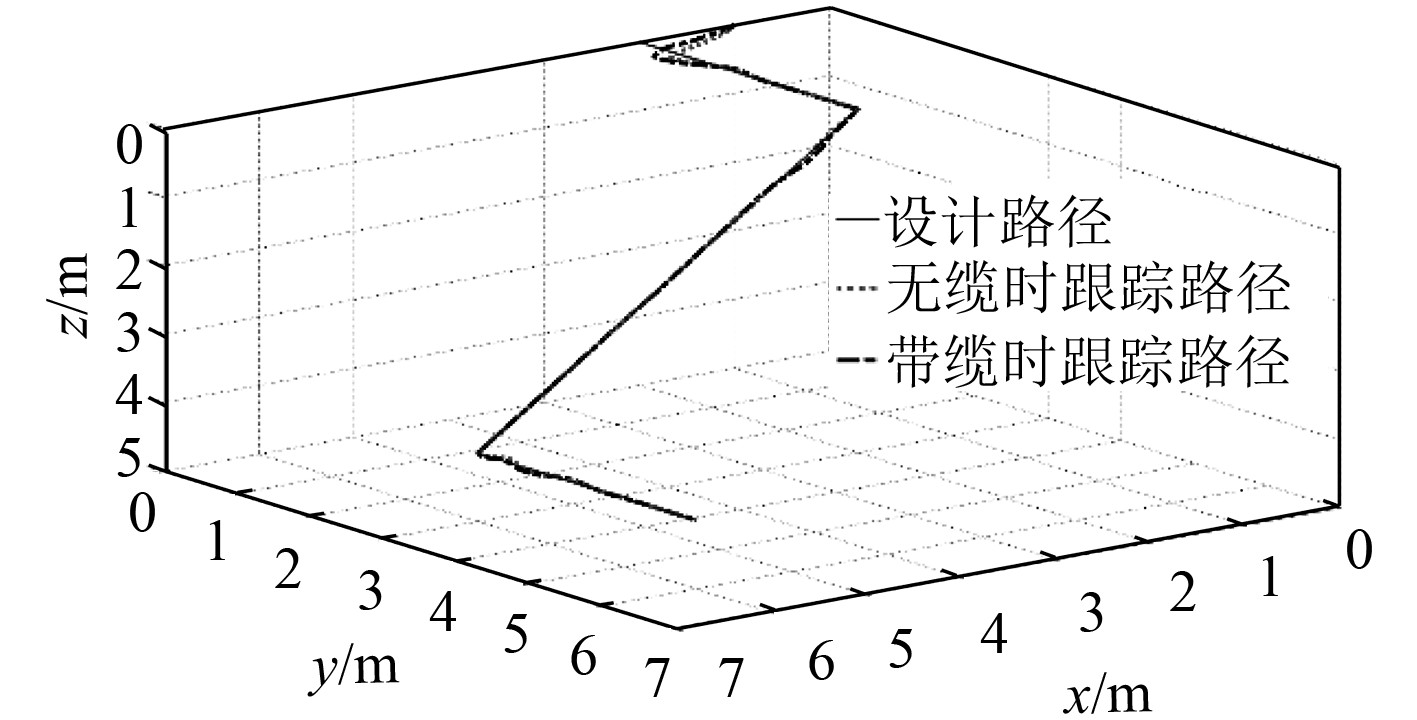
图 7 折线路径航迹跟踪 Fig. 7 Trajectory tracking of fold line |
|
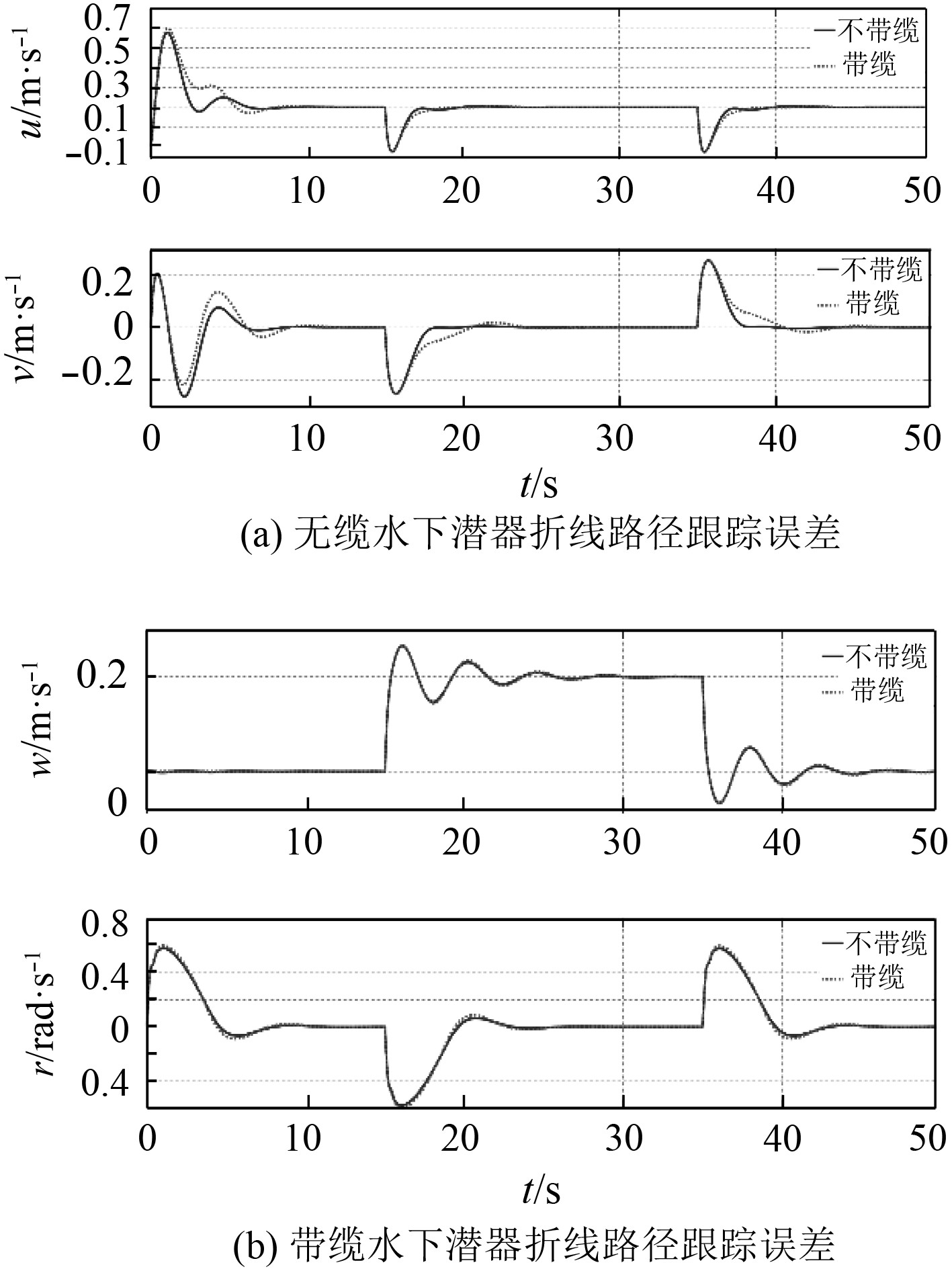
图 8 折线路径跟踪速度(u,v)和折线路径跟踪速度(w,r) Fig. 8 Tracking velocity (u,v) of fold line and Tracking velocity (w,r) of fold line |
|
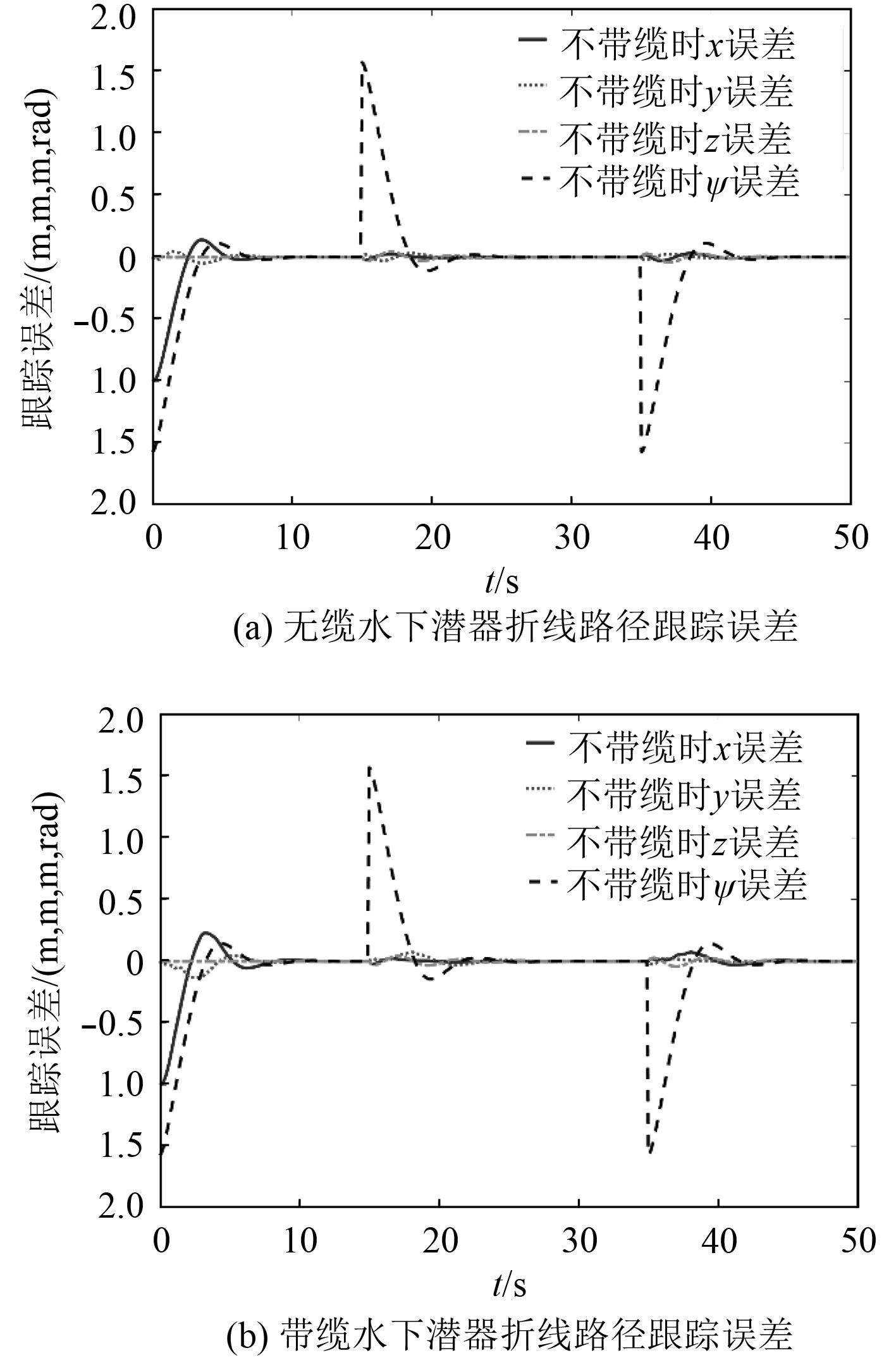
图 9 无缆水下潜器折线路径跟踪误差和带缆水下潜器折线路径跟踪误差 Fig. 9 Underwater vehicle’s tracking error of broken line and tethered underwater vehicle′s tracking error of broken line |
由图7可以看出,对于有缆和无缆的水下潜器,所设计的控制器均能够对折线运动路径实现较好的跟踪。由图8比较有缆和无缆时的跟踪速度,可以看出2种情况下基本无差别,但无缆情况下的速度u,v能够更快的稳定下来。从图9比较有缆和无缆时的跟踪误差可以看出,在无缆的情况下,控制器在仿真初始阶段和离散路径拐点处的X,Y方向的跟踪误差更小,同时能够更快地稳定下来,实现更好地航迹跟踪,这可以从图7中无缆潜器跟踪路径较有缆潜器跟踪路径更快地贴合设计路径反映出来。由此,可以看出脐带缆会使带缆水下潜器的航迹跟踪效果变差,在实际工程应用中需要重点考虑。
4 结 语本文主要对带脐带缆水下潜器的航迹跟踪控制进行研究。在控制器设计阶段,通过引入生物启发神经动力学模型平滑反步运动学控制器输出速度出现跳变的问题,同时以自适应项代替切换项设计滑模动力学控制器,解决传统滑模变结构控制中的抖振问题。在航迹跟踪仿真阶段,先根据试算结果,确定控制器参数,然后对水下潜器的折线路径进行了仿真,并对有缆和无缆时的仿真结果进行了比较分析。
1)引入神经动力学模型的反步滑模控制器能够较好地实现带缆水下潜器的航迹跟踪,平滑反步控制器产生的速度跳变;
2)相比计入了变缆长脐带缆非线性实时作用力的影响的带缆水下潜器,无缆水下潜器的跟踪速度能更快达到稳定。脐带缆的作用使得水下潜器航迹跟踪的初始阶段和跟踪路径拐点处出现较大的跟踪误差。
| [1] |
ABLOW C M, SCHECHTER S. Numerical simulation of undersea cable dynamics[J]. Ocean Engineering, 1983, 10(6): 443-457. DOI:10.1016/0029-8018(83)90046-X |
| [2] |
CHAI Y. T., VARYANI K. S., BARLTROP N. D. P.. Three-dimensional Lump-Mass formulation of a catenary riser with bending, torsion and irregular seabed interaction effect[J]. Ocean Engineering, 2002, 29(12): 1503-1525. DOI:10.1016/S0029-8018(01)00087-7 |
| [3] |
SUN Y., LEONARD J. W., CHIOU R. B.. Simulation of unsteady oceanic cable deployment by direct integration with suppression[J]. Ocean Engineering, 1994, 21(3): 243-256. DOI:10.1016/0029-8018(94)90001-9 |
| [4] |
Antonelli Gianluca. Adaptive/integral actions for 6-DOF control of AUVs[C]. Proceedings 2006 IEEE International Conference on Robotics and Automation, 2006: 3214-3219.
|
| [5] |
TANG Zhijie, HE Qingbo, WANG Shua, et al. An improved generalized predictive control for AUV yaw[C]. 2ndInternational Conference on Mechatronics and Intelligent Materials, 2012: 1709-1713.
|
| [6] |
刘金琨. 滑模变结构控制MATLAB仿真[M]. 北京: 清华大学出版社, 2005: 2-3, 236-276.
|
| [7] |
吴宝举, 李硕, 王晓辉. 自治水下机器人自适应滑膜控制[J]. 机械设计与制造, 2010, 7: 142-144. DOI:10.3969/j.issn.1001-3997.2010.01.059 |
| [8] |
KHAN I, BHATTI A I, KHAN Q, et al. Sliding mode control of lateral dynamics of an AUV[C]// Proceedings of 2012 9th International Bhurban Conference on Applied Sciences and Technology, 2012: 27-31.
|
| [9] |
HASSAN K K. Nonlinear systems [M]. Publishing House of Electronics Industry, 2012: 589-603.
|
| [10] |
贾鹤鸣. 基于反步法的欠驱动UUV空间目标跟踪非线性控制方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2012. JIA Heming. Study of nonlinear control method of underactuated UUV Target tracking based on backstepping method [D]. Harbin: Harbin Engineering University, 2012. |
| [11] |
WU Jiaming. Simulation of a two-part underwater towed system [D]. Pokfulam, Hong Kong: The University of Hong Kong. 1998.
|
| [12] |
李霄霄, 马宁, 刘晗, 等. 脐带缆在潜器下放过程中的运动建模与仿真[J]. 海洋工程, 2016, 34(2): 47-55. |
| [13] |
FOSSEN T I. Marine control systems: guidance, navigation and control of ships, rigs and underwater vehicles [M]. Marine Cybernetics, 2002: 15-109.
|
| [14] |
SUN B, ZHU D, DING F, et al. A novel tracking control approach for unmanned underwater vehicles based on bio-inspired neurodynamics[J]. Journal of Marine Science and Technology, 2013, 18(1): 63-74. DOI:10.1007/s00773-012-0188-8 |
| [15] |
HODGKIN A L, HUXLEY A F. A quantitative description of membrane current and its application to conduction and excitation in nerve[J]. The Journal of Physiology, 1952, 117(4): 500-544. DOI:10.1113/jphysiol.1952.sp004764 |
| [16] |
GROSSBERG S. Nonlinear neural networks: Principles, mechanisms, and architectures[J]. Neural Networks, 1988, 1(1): 17-61. DOI:10.1016/0893-6080(88)90021-4 |
| [17] |
FANG M C, HOU C S, LUO J H. On the motions of the underwater remotely operated vehicle with the umbilical cable effect[J]. OCEAN ENGINEERING-OXFORD-, 2007, 34: 1275-1289. DOI:10.1016/j.oceaneng.2006.04.014 |
 2020, Vol. 42
2020, Vol. 42
