随着国家提出并制定建设“海洋强国”的战略发展方针,人们逐步将目光聚焦在海洋,越发重视对海洋科学领域的发展,尤其是对深海领域的探索与开发。在强大的需求牵引下,一大批先进的海洋技术装备应运而生[1]。其中最为典型的就是以“蛟龙”号为代表的深海载人潜水器。深海载人潜水器是一种可以携带人员下潜到一定深度完成观察及作业的水下平台,其下潜深度通常可以达到水下上千米,水下作业时间也在不断延长。由于潜水器运行环境及作业工况的特殊性,需要人员长时间持续在密闭狭小空间内保持高效率作业,因而创造一个良好的人员工作环境是必不可少前提,而潜器内部的热舒适性设计则是面临的首要问题。
载人潜水器内的热舒适性最直观反应在舱内温湿度,该指标与众多因素相关,主要包括外界环境温度、隔热层材料与厚度、空调温度与风量、总热源大小、蓄热体热容大小等。为确保舱内温湿度适宜,前期设计时就要统一考虑这些因素。而目前关于这方面的研究资料较少,尤其对于水下载人潜器这类新型平台,相关性最高就属李杰[3]基于“蛟龙”号提出了一种带隔热层的潜器传热模型,但未给出具体计算方法。其他可借鉴资料包括马君[4]基于热传导理论评估了鱼雷装药室隔热涂层方案的安全性、罗志伟[5]提出一种导弹隔热层传热计算的理论模型及近似方法都只是重点分析了隔热层单一因素对隔热效果的影响,并未考虑其他因素。
本文重点是为了提出一种高效快速的近似计算方法用于解决载人潜水器从水面巡航、下潜至定深作业时的热交换问题,为潜水器内部与人员热舒适性相关的参数如隔热层选材及厚度、空调风量等的设计和优化提供了理论支撑。
1 潜器传热的数学描述 1.1 应用背景潜水器为了受压均匀,通常采用金属制成的圆柱状或球状耐压结构。潜水器的航行状态包括:水面巡航、匀速下潜、水下巡航3种。通常在完成水面停留后便开始下潜运动,此时外界海水温度随着下潜深度逐渐降低,达到规定潜深后,潜水器可保持在该深度定深巡航作业。在与海水接触的过程中,潜水器壳体、隔热层不断通过对流、传导方式与外界海水、舱内空气进行热交换。由于深海环境温度低,为了避免舱内热量损失造成的低温对人与设备影响,通常在内壁张贴隔热层作为阻热措施。另外,当潜水器水面巡航时,外界环境温度可能较高(夏季,南海海面温度高达35 ℃),此时舱内由于敷设隔热层,再加上舱内设备、人员的散热,热量堆积使舱内气温迅速攀升,此时必须采用空调等手段快速降温。
1.2 基本假设在考虑建立传热模型时,为了便于计算,需要对问题模型在合理的范围内简化。因此,提出以下几项假设条件:
1)本文的计算仅考虑厚度方向的热传递,忽略长度和宽度的影响,也即一维热传递问题;
2)由于舱壁厚度、隔热层厚度与潜水器的直径、长度相比是一个小量,因而采用平壁传热模型,而非圆柱或球形传热,整个计算在笛卡尔坐标系中完成;
3) 所有物体材料均匀且它们的热物理属性与温度无关;
4)在隔热层与舱壁接触处,隔热层表面温度与舱内壁温度相等;
5)舱内空气仅通过对流方式与隔热层进行换热;
6)与外界海水直接接触的金属耐压舱壁外表面,其温度与海水温度时刻保持一致。
1.3 建立数学模型建立舱内一维导热的传热模型如图1所示。令与舱内大气接触的隔热层边界面为原点。用x表示厚度方向坐标,隔热层厚度为Li,舱壁厚度为Lh,潜水器直径为D,假设2中已说明,当(Li+Lh)/D<<1时,可以认为是平壁传热。
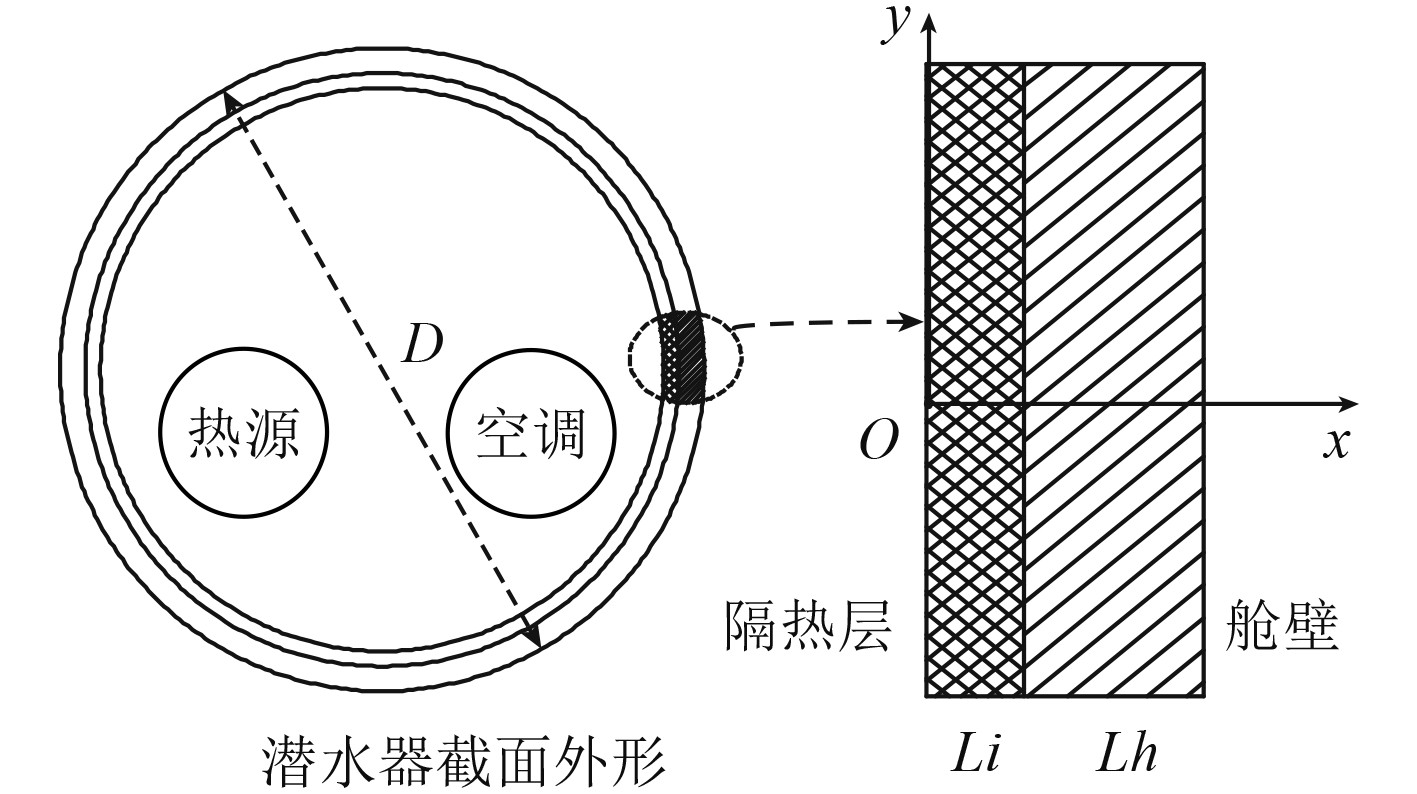
|
图 1 隔热层的传热模型 Fig. 1 Heat transfer model of insulation layer |
本文计算的是从潜水器开始下潜到定深巡航作业这段时间内的热量的传递以及舱壁温度、隔热层温度、舱内气体温度随时间的变化关系。
1)控制方程
一维瞬态热传导方程[5]可表示为:
| $\frac{\partial }{{\partial x}}\left( {{k_i}\frac{{\partial T}}{{\partial x}}} \right) = {\rho _i}{c_i}\frac{{\partial T}}{{\partial t}}\begin{array}{*{20}{c}} {} \end{array}\left( {0 < x < {L_i}} \right)\text{,}$ |
| $\frac{\partial }{{\partial x}}\left( {{k_h}\frac{{\partial T}}{{\partial x}}} \right) = {\rho _h}{c_h}\frac{{\partial T}}{{\partial t}}\begin{array}{*{20}{c}} {} \end{array}\left( {{L_i} < x < ({L_i} + {L_h})} \right)\text{。}$ |
式中:下角标
对于舱内的气体温度,其控制方程通过能量守恒关系得到:
| ${C_g}{V_g}{\rho _g} \cdot \frac{{{T_g}\left( {{t_0} + \Delta t} \right) - {T_g}\left( {{t_0}} \right)}}{{\Delta t}} = {Q_1} - {Q_2} - {Q_3}\text{。}$ |
式中:
| ${Q_2}\left( t \right) = {C_g}{V_{ac}}{\rho _g}\left( {{T_g}\left( t \right) - {T_{ac}}} \right)\text{,}$ |
| ${Q_3}\left( t \right) = {h_i}\left( {{T_g}\left( t \right) - T\left( {0,t} \right)} \right)\text{。}$ |
式中:
2)初始条件
当
| $T\left( {x,0} \right) = {T_{sea}}\text{,}$ |
潜水器舱内初始气体温度定为27 ℃:
| ${T_g}\left( 0 \right) = 27\text{。}$ |
3)边界条件
边界包括3个面,分别对应的x坐标为0,
| ${\left. { - {k_i}\frac{{\partial T}}{{\partial x}}} \right|_{x = 0}} = {h_i}\left( {{T_g} - T\left( {0,t} \right)} \right)\text{。}$ |
当x=
| $T\left( {{L_i} + {L_h},t} \right) = {T_{sea}}\text{。}$ |
式中:
在工程应用上,要获取解析解十分困难,尤其是对于复杂初始或边界条件问题。合适的方法是在工程应用的允许误差范围内采用数值计算的方法获取其近似解。本文拟采用有限差分的方法对上述问题进行求解。其中,首要步骤就是对计算域离散和写出节点处控制方程的差分格式表达式。
按图2所示,将隔热层与舱壁沿着厚度方向划分为若干节点控制体,各控制体内仅包含一个节点,为方便计算,计算中对控制体的传热计算都简化至对节点的计算。
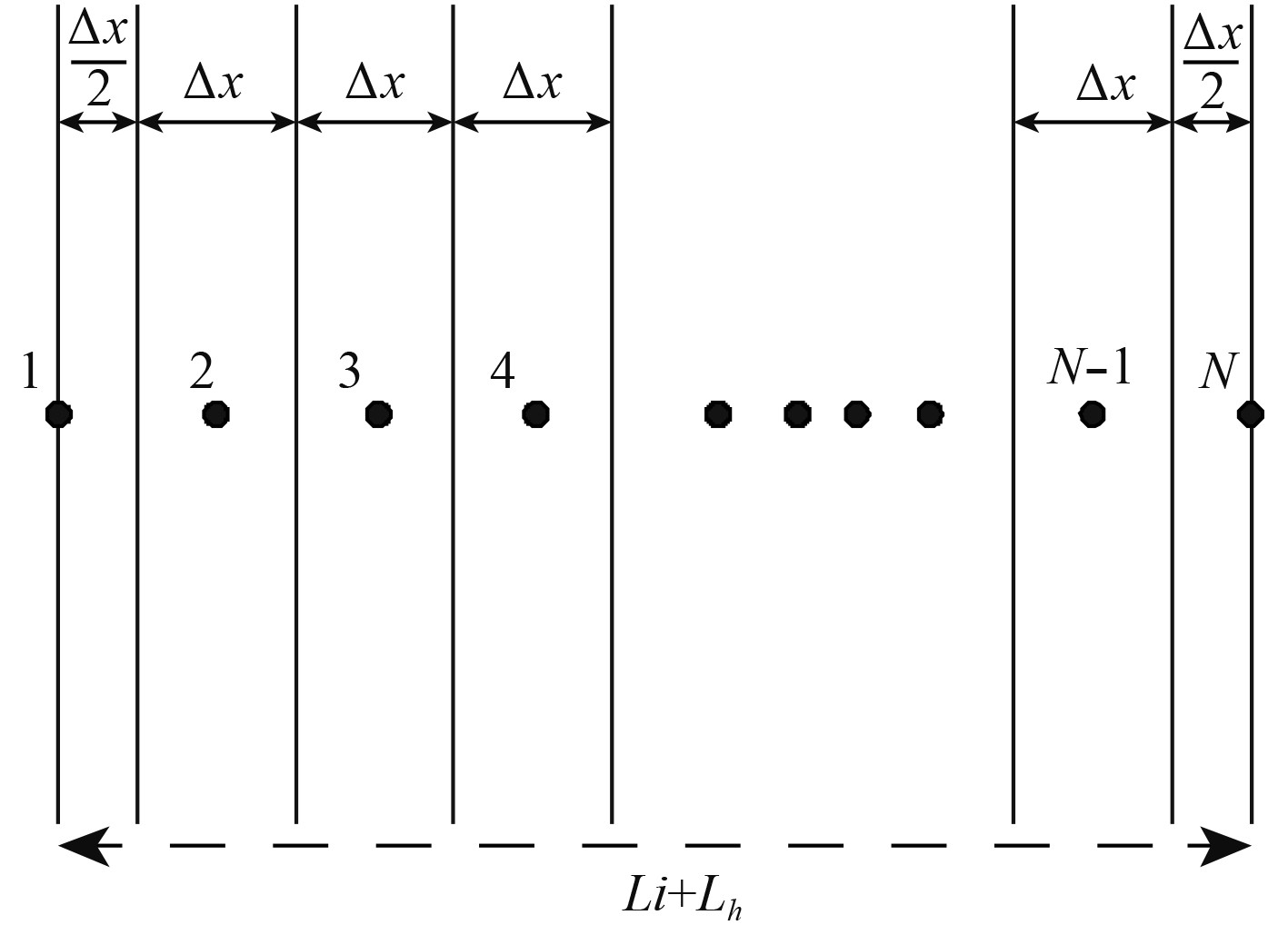
|
图 2 计算域节点划分图 Fig. 2 Computational domain node sketch |
其次对导热的时间-空间区域进行离散(见图3),横坐标即空间节点坐标,纵坐标为时间节点坐标,为保持计算连续性,对横纵坐标均进行等分,横坐标间距为
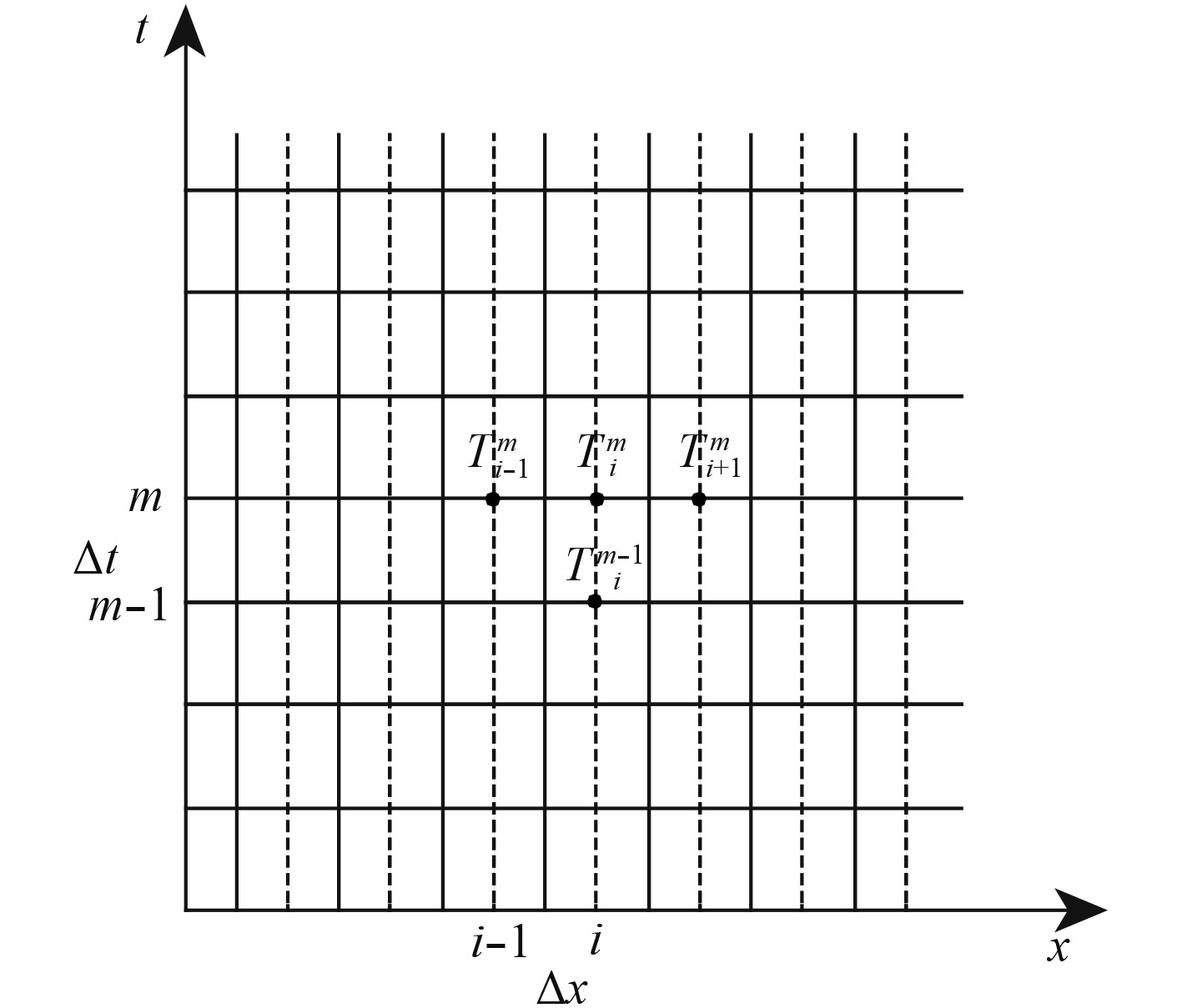
|
图 3 时间空间区域离散图 Fig. 3 Time-space region scatter graph |
| $\frac{{T_i^m - T_i^{m - 1}}}{{\Delta t}} = \alpha \frac{{T_{i - 1}^m - 2 \cdot T_i^m + T_{i + 1}^m}}{{\Delta {x^2}}}\text{。}$ |
式中
| $\frac{1}{{\Delta t}}T_i^{m - 1} = - \frac{\alpha }{{\Delta {x^2}}}T_{i - 1}^m + \left( {\frac{{2\alpha }}{{\Delta {x^2}}} + \frac{1}{{\Delta t}}} \right)T_i^m - \frac{\alpha }{{\Delta {x^2}}}T_{i + 1}^m\text{,}$ |
可以发现m-1时刻的温度要通过后一时刻m的温度得到,而m时刻温度属未知,因此需要同时求解,可将上述差分格式写成矩阵求解形式。
| $ { A} \cdot{ B} ={ C}\text{,} $ |
| ${{ A} = {\left[\!\! {\begin{array}{*{20}{c}} {{b_1}}\!\!\!&\!\!\!{{c_1}}\!\!\!&\!\!\!0\!\!\!&\!\!\!0\!\!\!&\!\!\!0\!\!\!&\!\!\!0 \\ { - \dfrac{\alpha }{{\Delta {x^2}}}}\!\!\!&\!\!\!{\dfrac{1}{{\Delta t}} + \dfrac{{2\alpha }}{{\Delta {x^2}}}}\!\!\!&\!\!\!{ - \dfrac{\alpha }{{\Delta {x^2}}}}\!\!\!&\!\!\!0\!\!\!&\!\!\!0\!\!\!&\!\!\!0 \\ 0\!\!\!&\!\!\!{ - \dfrac{\alpha }{{\Delta {x^2}}}}\!\!\!&\!\!\!{\dfrac{{2\alpha }}{{\Delta {x^2}}} + \dfrac{1}{{\Delta t}}}\!\!\!&\!\!\!{ - \dfrac{\alpha }{{\Delta {x^2}}}}\!\!\!&\!\!\!0\!\!\!&\!\!\!0 \\ 0\!\!\!&\!\!\!0\!\!\!&\!\!\! \ddots \!\!\!&\!\!\! \ddots \!\!\!&\!\!\! \ddots \!\!\!&\!\!\!0 \\ 0\!\!\!&\!\!\!0\!\!\!&\!\!\!0\!\!\!&\!\!\!{ - \dfrac{\alpha }{{\Delta {x^2}}}}\!\!\!&\!\!\!{\dfrac{{2\alpha }}{{\Delta {x^2}}} + \dfrac{1}{{\Delta t}}}\!\!\!&\!\!\!{ - \dfrac{\alpha }{{\Delta {x^2}}}} \\ 0\!\!\!&\!\!\!0\!\!\!&\!\!\!0\!\!\!&\!\!\!0\!\!\!&\!\!\!0\!\!\!&\!\!\!1 \end{array}}\!\! \right]_{N \times N}}}\text{,}$ |
| ${ B}= {\left[ {T_1^m,T_2^m,T_3^m \ldots T_{N - 1}^m,T_N^m} \right]^{\rm{T}}}\text{,}$ |
| ${ C} = {\left[ {{d_1},\frac{1}{{\Delta t}}T_2^{m - 1},\frac{1}{{\Delta t}}T_3^{m - 1} \ldots \frac{1}{{\Delta t}}T_{N - 1}^{m - 1},{d_N}} \right]^{\rm{T}}}\text{。}$ |
式中:N为x轴划分的总节点个数,其值为
| $h\left( {T_g^{m + 1} - T_1^{m + 1}} \right) + k\frac{{T_2^{m + 1} - T_1^{m + 1}}}{{\Delta x}} = \rho \frac{{\Delta x}}{2}c\frac{{T_1^{m + 1} - T_1^m}}{{\Delta t}}\text{。}$ |
将上式变换得到:
| $\begin{gathered} \left( {\frac{1}{{\Delta t}} + 2\frac{\alpha }{{\Delta {x^2}}} + 2\frac{h}{{\rho c\Delta x}}} \right)T_1^m - 2\frac{\alpha }{{\Delta {x^2}}}T_2^m= \\ 2\frac{h}{{\rho c\Delta x}} \cdot T_g^m + \frac{1}{{\Delta t}}T_1^{m - 1} \text{,} \end{gathered} $ |
由此可知:
但值得注意的是在隔热层与舱壁交界面处的计算,由于两者热物性材料不同,因此上述A矩阵需要进行调整。本文在假设4中说明了设定交界面处隔热层的节点与壳体的节点温度相同,假定交界面处的节点编号为j,同样根据能量守恒,即流入与流出该节点的热量差等于该节点处的内能增加值,依次写出计算方程并化简得到:
| $\begin{gathered} \frac{1}{{\Delta t}}T_j^m = \left( {\frac{1}{{\Delta t}} + \frac{{2{k_i} + 2{k_h}}}{{\Delta {x^2}\left( {{c_i}{\rho _i} + {c_h}{\rho _h}} \right)}}} \right)T_j^{m + 1} - \\ \frac{{2{k_i}}}{{\Delta {x^2}\left( {{c_i}{\rho _i} + {c_h}{\rho _h}} \right)}}T_{j - 1}^{m + 1} - \frac{{2{k_h}}}{{\Delta {x^2}\left( {{c_i}{\rho _i} + {c_h}{\rho _h}} \right)}}T_{j + 1}^{m + 1} \text{。} \end{gathered} $ |
因此,最后考虑隔热层情况下的传热矩阵A如下式所示。
式中:字母的下角标i,h分别表示隔热层和耐压壳体。该矩阵形式上属于三对角矩阵,可以先通过LU分解后采用牛顿追赶法进行求解。
| $ { A}=\scriptsize{\left[\!\!\!\!\begin{array}{*{20}{c}} {\dfrac{1}{{\Delta t}} + 2\dfrac{{{k_i}}}{{{\rho _i}{c_i}\Delta {x^2}}} + 2\dfrac{{{h_i}}}{{{\rho _i}{c_i}\Delta x}}} \!\!\!\!\!\!\!\!\!&\!\!\!\!\!\!\!\!\! { - 2\dfrac{{{k_i}}}{{{\rho _i}{c_i}\Delta {x^2}}}} \!\!\!\!\!\!\!\!\!&\!\!\!\!\!\!\!\!\! 0 \!\!\!\!\!\!\!\!\!&\!\!\!\!\!\!\!\!\! 0 \\ { - \dfrac{{{k_i}}}{{{\rho _i}{c_i}\Delta {x^2}}}} \!\!\!\!\!\!\!\!\!&\!\!\!\!\!\!\!\!\! {\dfrac{1}{{\Delta t}} + 2\dfrac{{{k_i}}}{{{\rho _i}{c_i}\Delta {x^2}}}} \!\!\!\!\!\!\!\!\!&\!\!\!\!\!\!\!\!\! { - \dfrac{{{k_i}}}{{{\rho _i}{c_i}\Delta {x^2}}}} \!\!\!\!\!\!\!\!\!&\!\!\!\!\!\!\!\!\! 0 \\ 0 \!\!\!\!\!\!\!\!\!&\!\!\!\!\!\!\!\!\! { - \dfrac{{{k_i}}}{{{\rho _i}{c_i}\Delta {x^2}}}} \!\!\!\!\!\!\!\!\!&\!\!\!\!\!\!\!\!\! {\dfrac{1}{{\Delta t}} + 2\dfrac{{{k_i}}}{{{\rho _i}{c_i}\Delta {x^2}}}} \!\!\!\!\!\!\!\!\!&\!\!\!\!\!\!\!\!\! { - \dfrac{{{k_i}}}{{{\rho _i}{c_i}\Delta {x^2}}}} \\ 0 \!\!\!\!\!\!\!\!\!&\!\!\!\!\!\!\!\!\! 0 \!\!\!\!\!\!\!\!\!&\!\!\!\!\!\!\!\!\! \ddots \!\!\!\!\!\!\!\!\!&\!\!\!\!\!\!\!\!\! \ddots \\ 0 \!\!\!\!\!\!\!\!\!&\!\!\!\!\!\!\!\!\! 0 \!\!\!\!\!\!\!\!\!&\!\!\!\!\!\!\!\!\! 0 \!\!\!\!\!\!\!\!\!&\!\!\!\!\!\!\!\!\! { - \dfrac{{2{k_i}}}{{\Delta {x^2}\left( {{c_i}{\rho _i} + {c_h}{\rho _h}} \right)}}} \\ 0 \!\!\!\!\!\!\!\!\!&\!\!\!\!\!\!\!\!\! 0 \!\!\!\!\!\!\!\!\!&\!\!\!\!\!\!\!\!\! 0 \!\!\!\!\!\!\!\!\!&\!\!\!\!\!\!\!\!\! 0 \\ 0 \!\!\!\!\!\!\!\!\!&\!\!\!\!\!\!\!\!\! 0 \!\!\!\!\!\!\!\!\!&\!\!\!\!\!\!\!\!\! 0 \!\!\!\!\!\!\!\!\!&\!\!\!\!\!\!\!\!\! 0 \\ 0 \!\!\!\!\!\!\!\!\!&\!\!\!\!\!\!\!\!\! 0 \!\!\!\!\!\!\!\!\!&\!\!\!\!\!\!\!\!\! 0 \!\!\!\!\!\!\!\!\!&\!\!\!\!\!\!\!\!\! 0 \\ 0 \!\!\!\!\!\!\!\!\!&\!\!\!\!\!\!\!\!\! 0 \!\!\!\!\!\!\!\!\!&\!\!\!\!\!\!\!\!\! 0 \!\!\!\!\!\!\!\!\!&\!\!\!\!\!\!\!\!\! 0\\ 0 \!\!\!\!\!\!\!\!\!&\!\!\!\!\!\!\!\!\! 0 \!\!\!\!\!\!\!\!\!&\!\!\!\!\!\!\!\!\! 0 \!\!\!\!\!\!\!\!\!&\!\!\!\!\!\!\!\!\! 0 \\ 0 \!\!\!\!\!\!\!\!\!&\!\!\!\!\!\!\!\!\! 0 \!\!\!\!\!\!\!\!\!&\!\!\!\!\!\!\!\!\! 0 \!\!\!\!\!\!\!\!\!&\!\!\!\!\!\!\!\!\! 0\\ \ddots \!\!\!\!\!\!\!\!\!&\!\!\!\!\!\!\!\!\! 0 \!\!\!\!\!\!\!\!\!&\!\!\!\!\!\!\!\!\! 0 \!\!\!\!\!\!\!\!\!&\!\!\!\!\!\!\!\!\! 0 \\ {\dfrac{1}{{\Delta t}} + \dfrac{{2{k_i} + 2{k_h}}}{{\Delta {x^2}\left( {{c_i}{\rho _i} + {c_h}{\rho _h}} \right)}}} \!\!\!\!\!\!\!\!\!&\!\!\!\!\!\!\!\!\! { - \dfrac{{2{k_h}}}{{\Delta {x^2}\left( {{c_i}{\rho _i} + {c_h}{\rho _h}} \right)}}} \!\!\!\!\!\!\!\!\!&\!\!\!\!\!\!\!\!\! 0 \!\!\!\!\!\!\!\!\!&\!\!\!\!\!\!\!\!\! 0 \\ \ddots \!\!\!\!\!\!\!\!\!&\!\!\!\!\!\!\!\!\! \ddots \!\!\!\!\!\!\!\!\!&\!\!\!\!\!\!\!\!\! 0\\ 0 \!\!\!\!\!\!\!\!\!&\!\!\!\!\!\!\!\!\! { - \dfrac{{{k_h}}}{{{\rho _h}{c_h}\Delta {x^2}}}} \!\!\!\!\!\!\!\!\!&\!\!\!\!\!\!\!\!\! {\dfrac{1}{{\Delta t}} + 2\dfrac{{{k_h}}}{{{\rho _h}{c_h}\Delta {x^2}}}} \!\!\!\!\!\!\!\!\!&\!\!\!\!\!\!\!\!\! { - \dfrac{{{k_h}}}{{{\rho _h}{c_h}\Delta {x^2}}}}\\ 0 \!\!\!\!\!\!\!\!\!&\!\!\!\!\!\!\!\!\! 0 \!\!\!\!\!\!\!\!\!&\!\!\!\!\!\!\!\!\! 0 \!\!\!\!\!\!\!\!\!&\!\!\!\!\!\!\!\!\! 1 \end{array}\!\! \right]}\text{。} $ |
通过与主流的传热计算软件AMESim进行计算结果对比的方式来验证上述计算方法的正确性,并评估计算误差。
计算问题可描述为:某型水下载人潜水器,潜水器内部空间净容积为54 m3,换热内表面积为113 m2,载人潜水器壳体由金属耐压层与非金属隔热层两部分组成,金属耐压层的厚度为30 mm,非金属隔热层的厚度为16 mm,潜水器内部艇员加设备的总散热量为5.6 kW,潜水器内部配置有空调,空调的设定温度为17 ℃,送风量为0.5 m3/s。现希望通过上述2种方法对该载人潜水器从水面巡航到水下1 000 m定深作业过程中舱内的气温变化情况进行计算。
舱内的空气密度1.175 kg/m3,定容比热容为717.7J/(kg×K);耐压层材料的导热系数、比热容和密度[7]为9.5 W/(m×K),611J/(kg×K)和4500 kg/m3;隔热层材料的导热系数、比热容和密度[6]为0.04 W/(m×K),660J/(kg×K)和2400 kg/m3。舱内气体流速0.2 m/s,隔热层内壁面与空气的对流换热系数根据雷诺数、普朗特数等计算努塞尔数求解得到。计算过程中由于壳体外侧的边界条件为海水温度,因此需要知道不同深度的海水温度情况,根据文献[8]提供的数据,并利用指数函数拟合得到海水温度随深度x变化如下式。海水水面温度约30.4 ℃,在0~300 m处温度下降剧烈,随后变化较缓慢,在1 000 m处达到4.7 ℃,潜水器下潜速度为0.025 m/s,到达1 000 m需11.1 h,随后开始定深巡航,因此,外界海水温度稳定在4.7 ℃。
| ${T_{sea}} = 16.16{e^{ - 0.007478x}} + 14.21{e^{ - 0.001098x}}\text{,}\begin{array}{*{20}{c}} {}&{0 \leqslant x \leqslant 1000} \text{。} \end{array}$ |
外界海水温度随时间的变化关系如图4所示。

|
图 4 海水温度随时间变化关系 Fig. 4 Temperature of seawater varies with time |
当不考虑敷设16 mm隔热层计算舱内气体温度随时间的变化情况如图5所示。
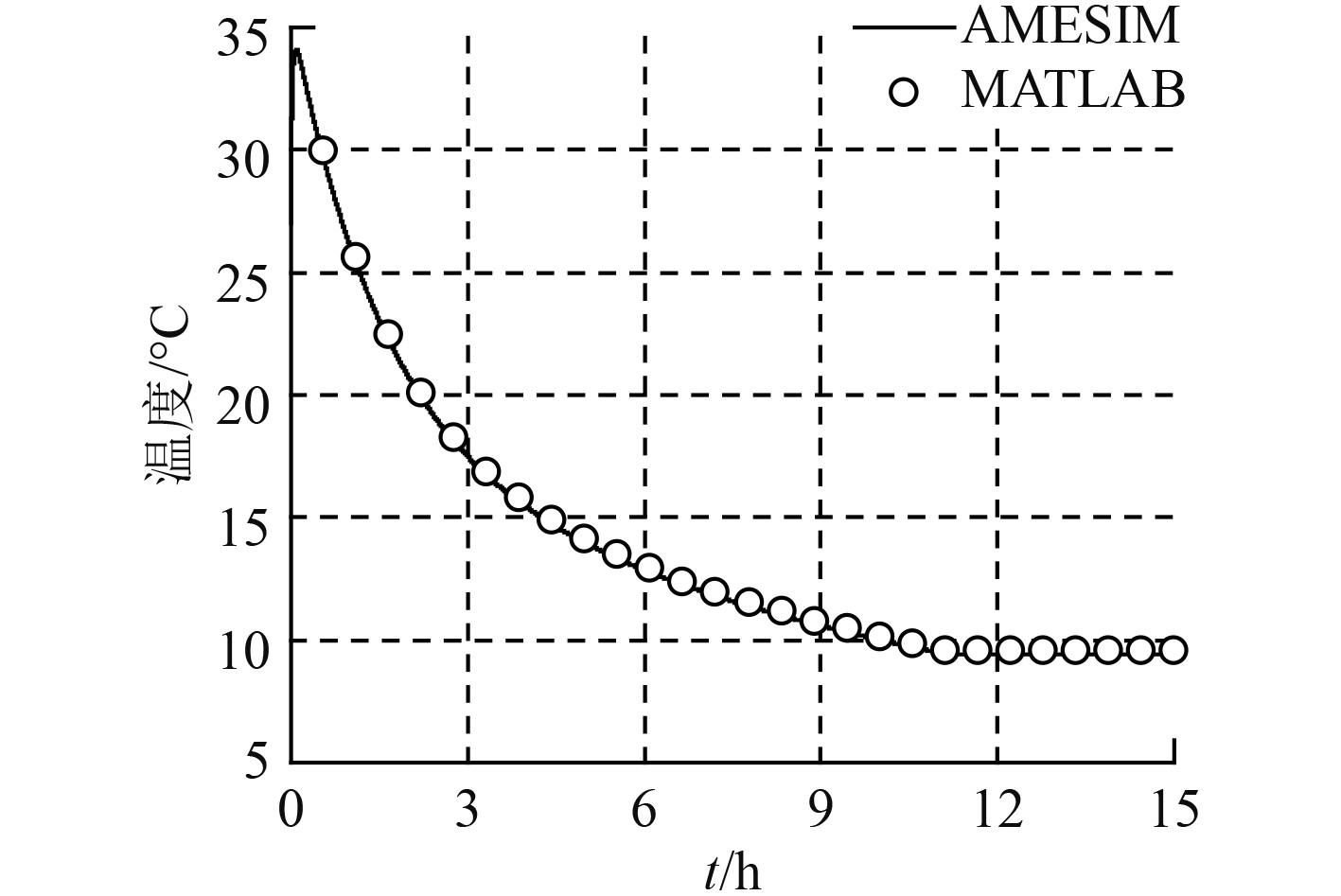
|
图 5 无隔热层下潜舱内气温变化 Fig. 5 Temperature varies with time without thermal insulation |
可以看出2种方式的计算结果数值与趋势上十分吻合,在不考虑隔热层情况下,舱内的气温从初始27 ℃骤升至34 ℃,原因是此时海水温度较高,舱内的散热量不能通过壳体热传递方式被带走,导致气温快升。当随着下潜深度的加大,外界海水温度降低,热传递热量增大,此时舱内温度开始下降,下降的趋势与海水温度变化趋势基本一致。当海水温度长时间稳定在4.7 ℃后,舱内热传递也达到平衡,舱内的气温稳定在9.5 ℃。
上述计算结果表明,载人潜水器稳定后舱内气温长时间维持在9.5 ℃,而该温度过低不利于人员及部分设备的长时间工作,因此,需要考虑敷设隔热层进行保温。
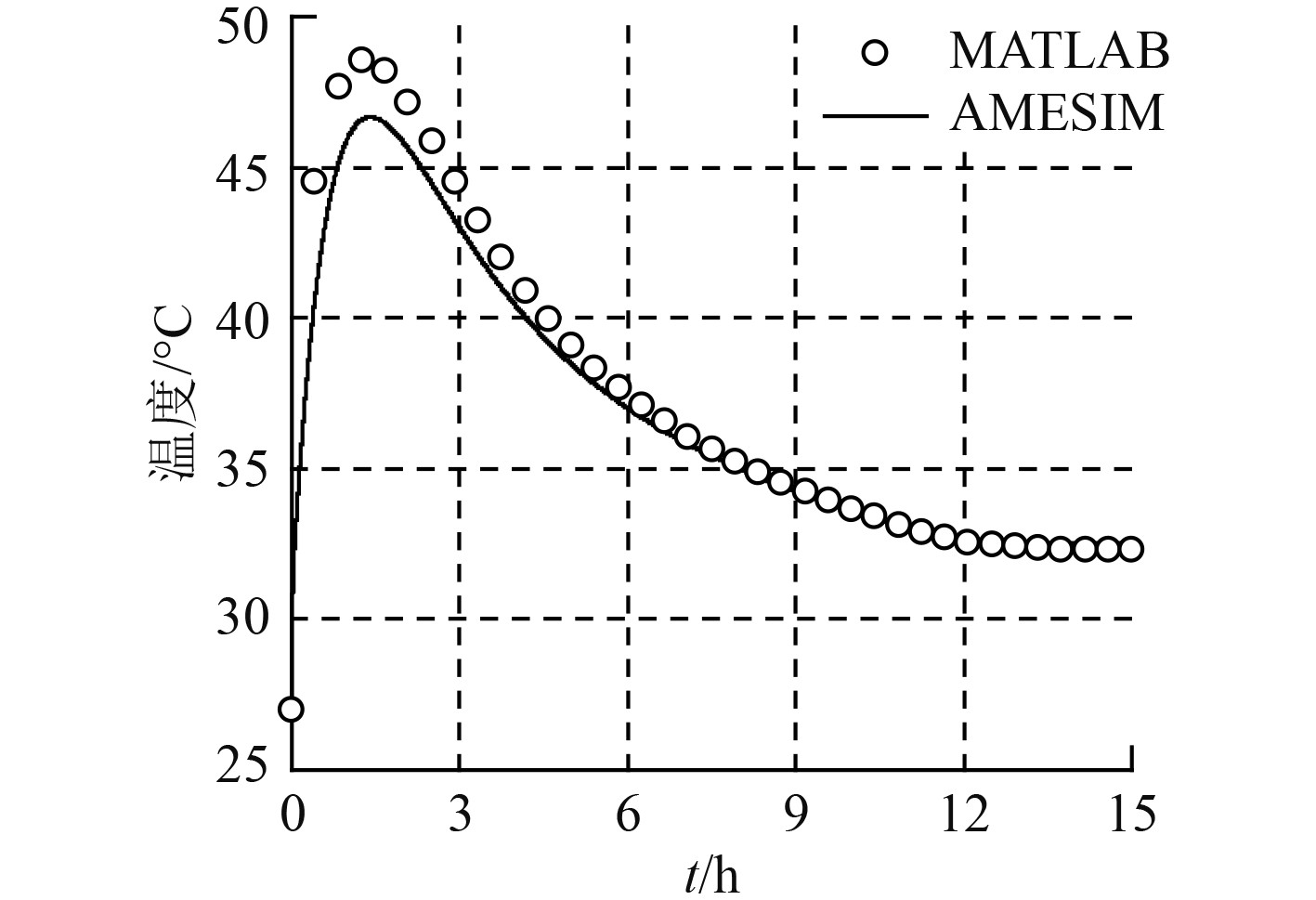
3.2 有隔热层不开启空调当敷设16 mm的隔热层后计算舱内气体温度的变化情况如图6所示。
|
图 6 敷设隔热层下潜舱内气温变化 Fig. 6 Temperature varies with time with thermal insulation |
2种软件的计算结果吻合也较好,仅在最高气温值上存在较小差异,Matlab计算最高温度为48 ℃,AMESim计算最高温度为47 ℃,相差仅为1 ℃。从计算结果可以看出,敷设隔热层后,由于隔热层的保温效应,舱内气温显著上升,且气温的变化速率相对无隔热层时更加平缓。舱内的最高温度在1.5 h到达最大47 ℃,最后的平衡温度约为32 ℃。
载人潜水器稳定后舱内气温长时间维持在32 ℃,而该温度又过高不利于人员及设备运行,可采用2种方式降温:一种是减小隔热层厚度,另一种是在舱内加设空调。由于本文主要目的是提出一种传热计算模型及方法,因此,此处考虑通过加设空调方式来再次进行计算对比校验,验证计算模型及方法的正确性。
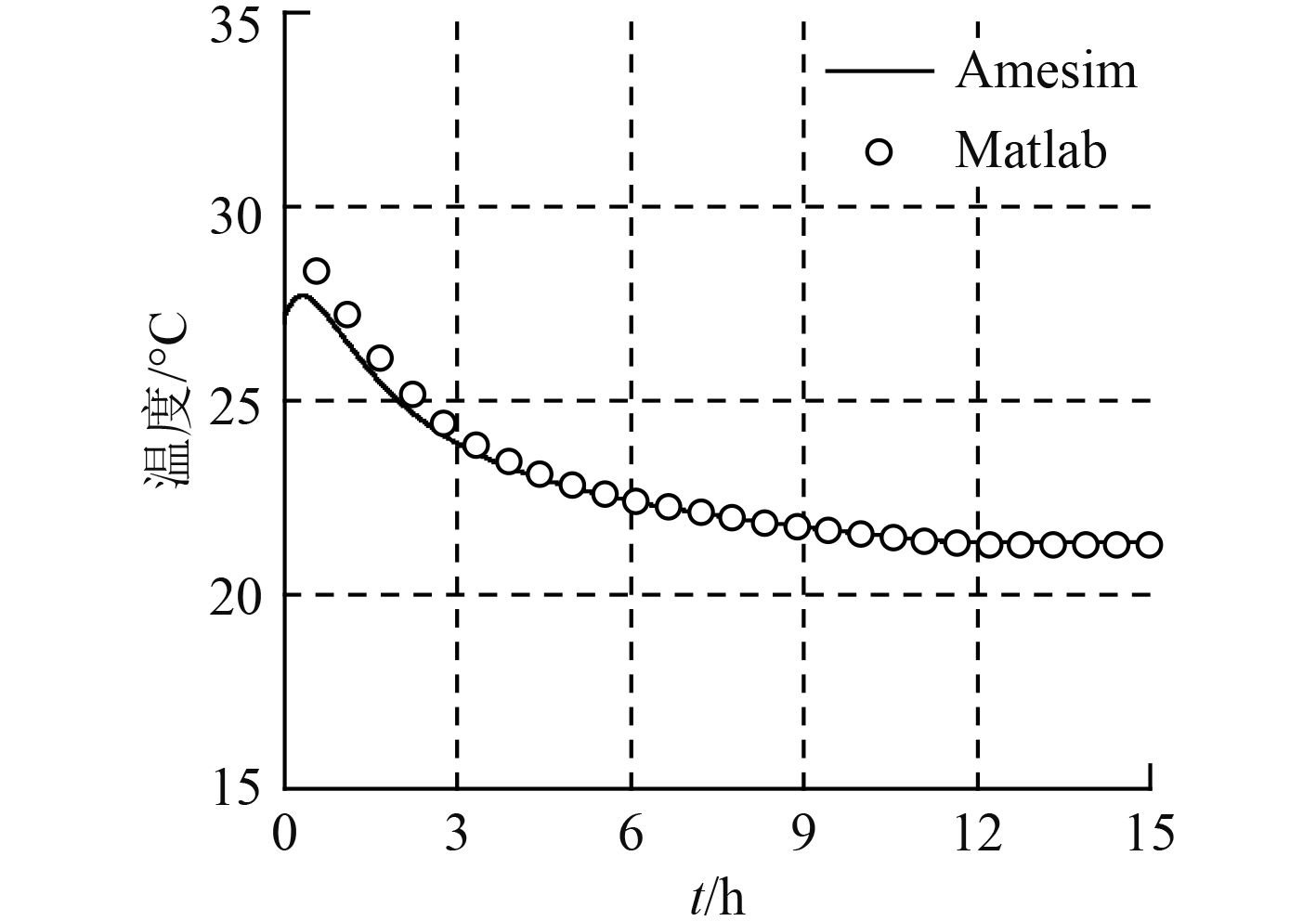
3.3 有隔热层开启空调在敷设隔热层并开启空调后,2种方式计算的结果也十分吻合,仅在最高温度上相差约1 ℃,如图7所示。开启空调后,舱室内的气温始终保持在一个适宜的水平,最高温度约28 ℃,最后平衡温度为22 ℃,且整个气温变化速率相对平缓。
|
图 7 敷设隔热层开空调下潜舱内气温变化 Fig. 7 Temperature varies with time with thermal insulation and air conditioning |
本文提出了一种用于具有热源、隔热层、空调等多因素综合影响下的水下载人潜水器热交换计算模型,并利用有限差分方法给出了该模型的数值计算过程。尽管给定了部分假设,但通过与主流传热计算软件的计算结果对比发现该计算模型及方法仍具有较高准确性。后期,通过利用该计算方法可为水下载人潜器在舱室热舒适性上的工程研究及优化,重点包括隔热层材料及厚度的选取、空调参数选配、舱室环境温度预估等问题提供更便捷计算方法。
| [1] |
刘涛, 王璇, 王帅. 深海载人潜水器发展现状及技术进展[J]. 中国造船, 2012(3): 233-243. LIU Tao, WANG Xuan, WANG Shuai. The current status and technical development of deep sea manned submersible[J]. Shipbuilding of China, 2012(3): 233-243. |
| [2] |
刘峰, 崔维成, 李向阳. 中国首台深海载人潜水器——蛟龙号[J]. 中国科学: 地球科学, 2010, 53(12): 1407-1410. LIU Feng, CUI Weicheng, LI Xiangyang. China's first deep manned submersible[J]. China Earth Sci, 2010, 53(12): 1407-1410. |
| [3] |
李杰, 宋保银. 舱壁保温层对深潜器舱内温度的影响[J]. 造船技术, 2017(3): 24-29. LI Jie, SONG Baoyin. Effect of insulation layer on cabin temperature of deep diving submersible[J]. Marine Technology, 2017(3): 24-29. DOI:10.3969/j.issn.1000-3878.2017.03.006 |
| [4] |
马君, 赵保瑚. 鱼雷战斗部装药室隔热设计分析[J]. 鱼雷技术, 1999(4): 18-20. MA Jun, ZHAO Baohu. Research on insulation design for torpedo warhead[J]. Torpedo Technology, 1999(4): 18-20. |
| [5] |
罗志伟, 孟范源, 郑钢铁. 一种导弹隔热层内传热计算的近似方法[J]. 战术导弹技术, 2004(1): 29-34. LUO Zhiwei, MENG Fanyuan, ZHENG Gangtie. An approximate method of computing heat conduction inside insulation package of missile[J]. Tactical Missile Technology, 2004(1): 29-34. DOI:10.3969/j.issn.1009-1300.2004.01.008 |
| [6] |
杨世铭, 陶文铨. 传热学(第四版)[M]. 北京: 高等教育出版社, 2006.
|
| [7] |
弗兰克P英克鲁佩勒. 传热和传质基本原理[M]. 北京: 化学工业出版社, 2016.
|
| [8] |
任强, 于非, 俞建成. 国产水下滑翔机2014年南海海试实验数据分析[J]. 海洋技术学报, 2017(1): 52-57. REN Qiang, YU Fei, YU Jiancheng. Analysis on the experimental data acquired from the sea tests for domestic underwater glider in the south china sea in 2014[J]. Ocean Technology, 2017(1): 52-57. |
 2020, Vol. 42
2020, Vol. 42
