2. 高新船舶与深海开发装备协同创新中心,上海 200240
2. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai 200240, China
船舶在营运过程中可能产生有害振动并影响正常运营,此时需要对船体结构采取有效的减振措施,在结构上敷设阻尼是常用、高效的减振方法之一[1]。
要达到良好的减振效果,需要选取合适的阻尼材料和合理的敷设方式。粘弹性阻尼材料由于其性能参数受频率和温度影响较大,给敷设阻尼材料结构的动力学性能预测带来了较大的困难。随着对粘弹性阻尼研究的深入,各种粘弹性阻尼模型被提出,如复模量模型、分数导数模型、GHM模型等[2-6],一些具有严格解析解的模型仅仅能够处理几何结构和边界条件较为简单的复合结构,难以运用到工程结构上。Johnson等[7]提出了模态应变能法,通过忽略结构刚度矩阵的虚部得到的实模态振型来代替结构的复模态振型,求出结构的应变能进而求得结构的模态损耗因子。常规的模态应变能法在求取损耗因子时忽略了阻尼的温频依赖特性,因此所得的损耗因子可能会有较大的偏差。由于温频等效原理可以将阻尼材料的温度影响转化为等效频率的影响[8],在计算中只需研究粘弹性材料的频变效应。邓年春等[9]提出了一种新的建立约束阻尼板的结构动力学计算模型的方法,描述了粘弹性材料随频率变化的特性。孙社营[10]利用模态应变能法并结合2次迭代的方式考虑了粘弹性材料的频变特性对模态阻尼比的影响。这些方法虽考虑了材料温频特性影响,但是计算过程较复杂,工程适用性不强。
本文在模态应变能法的基础上,结合有限元分析,推导出考虑粘弹性阻尼材料损耗因子和弹性模量频变特性的模态损耗因子修正计算公式,并通过算例[10]进行验证。在此基础上,结合阻尼加筋板结构的模型试验,利用模态叠加法计算获得传递函数和随机响应计算结果,并与试验结果进行对比分析,验证了该方法的工程适用性。
1 理论分析及修正公式推导 1.1 模态应变能法基本原理粘弹性自由阻尼结构的自由振动方程如下:
| $M\ddot x + Kx = 0{\text{,}}$ | (1) |
由于结构中有粘弹性材料,因此其刚度矩阵K为复常数,即
| $K = {K_R} + i{K_I}{\text{,}}$ | (2) |
| ${K_R}{\rm{ = }}{K_e} + {K_{vR}}{\text{,}}$ | (3) |
| ${K_I} = {\eta _v} \cdot {K_{vR}}{\text{。}}$ | (4) |
式中:
假设式(1)的解形式为:
| $X = {\phi ^{*(r)}}{e^{i\omega _r^*t}}{\text{,}}$ | (5) |
可以得到如下形式的复特征向量和复特征值[11]:
| ${\phi ^{*(r)}}{\rm{ = }}\phi _{^R}^{*(r)} + i\phi _I^{*(r)}{\text{,}}$ | (6) |
| $\omega _r^* = {\omega _r}\sqrt {1 + i{\xi ^{(r)}}} {\text{。}}$ | (7) |
式中:
结合式(1)、式(2)及式(5)、式(6)可以得到
| $\omega _r^2{\rm{(}}1 + i{\xi ^{(r)}}{\rm{) = }}\frac{{{\phi ^{*(r)T}}{K_R}{\phi ^{*(r)}}}}{{{\phi ^{*(r)T}}M{\phi ^{*(r)}}}} + i\frac{{{\phi ^{*(r)T}}{K_I}{\phi ^{*(r)}}}}{{{\phi ^{*(r)T}}M{\phi ^{*(r)}}}}{\text{。}}$ | (8) |
由于粘弹性阻尼刚度较弹性层非常小,用
| $ \begin{split} & {\xi ^{(r)}} = \frac{{{\phi ^{(r)T}}{K_I}{\phi ^{(r)}}}}{{{\phi ^{(r)T}}{K_R}{\phi ^{(r)}}}}{\rm{ = }}{\eta _v}\frac{{{\phi ^{(r)T}}{K_{vR}}{\phi ^{(r)}}}}{{{\phi ^{(r)T}}{K_R}{\phi ^{(r)}}}}{\rm{ = }}\\ & \quad \quad{\eta _v}\frac{{V_v^{(r)}}}{{{V^{(r)}}}}{\rm{ = }}{\eta _v}\frac{{V_v^{(r)}}}{{V_e^{(r)} + V_v^{(r)}}}{\rm{ = }}{\eta _v}{R^{(r)}}{\text{。}} \end{split} $ | (9) |
式中:
在粘弹性阻尼结构中,由于粘弹性材料的弹性模量
若已求得在粘弹性阻尼弹性模量为
| $R_{_{ref}}^{(r)} = \frac{{V_{vref}^{(r)}}}{{V_{eref}^{(r)} + V_{vref}^{(r)}}}{\text{,}}$ | (10) |
则以该结果为基准并结合式(10),在弹性模量为E时,其r阶模态弹性应变能比为:
| ${R^{(r)}} = \frac{{V_v^{(r)}}}{{V_e^{(r)} + V_v^{(r)}}} = \frac{{\frac{E}{{{E_{ref}}}}V_{vref}^{(r)}}}{{V_{eref}^{(r)} + \frac{E}{{{E_{ref}}}}V_{vref}^{(r)}}} = \frac{{E'}}{{\frac{1}{{R_{ref}^{(r)}}} - 1 + E'}}{\text{。}}$ | (11) |
式中:
在结构模态应变能计算过程中,阻尼的损耗因子对模态应变能计算结果无影响,即粘弹性阻尼的频变效应对式(9)中的弹性应变能比
| ${\xi ^{(r)}}{\rm{ = }}{\eta _v}{R^{(r)}}{\rm{ = }}{\eta _v}({\omega _r}) \cdot {R^{(r)}}{\text{。}}$ | (12) |
结合式(11)、式(12),可以得到同时考虑粘弹性阻尼损耗因子和弹性模量频变效应的模态损耗因子的修正计算公式为:
| $\xi _{{\omega _r}}^{^{(r)}} = {\eta _v}({\omega _r}) \cdot \frac{{E'({\omega _r})}}{{\frac{1}{{R_{_{ref}}^{(r)}}} - 1 + E'({\omega _r})}}{\text{。}}$ | (13) |
式中:
利用修正计算公式(13)计算阻尼结构的模态损耗因子时,取关注频率范围内阻尼弹性模量均值作为参考弹性模量

|
图 1 采用修正公式计算模态损耗因子流程 Fig. 1 Calculating modal loss factor by correction formula |
为了对修正公式(13)进行验证,选取了文献[10]中的压筋板模型进行计算分析。该压筋板尺寸为1 000×920×2.5 mm,压筋截面为弧形,宽为50 mm,高度为20 mm,材料为Q235-A钢,边界条件为自由支撑。其中对于Q235-A材料,弹性模量为212 GPa,泊松比为0.288,密度为7860 kg/m3。对于粘弹性阻尼材料,其厚度为6 mm,在25 ℃时弹性模量E和损耗因子与频率f的关系如下:
| ${\rm {Log}}E = 7.51 + \frac{{2.27{f^{0.79}}}}{{67.6 + {f^{0.79}}}}{\text{,}}$ | (14) |
| ${\rm {Log}}\eta = 0.23 - 0.1{\rm {Log}}f - 0.02\sqrt {1 + 25{{({\rm {Log}}f - 2.04)}^2}}{\text{。}} $ | (15) |
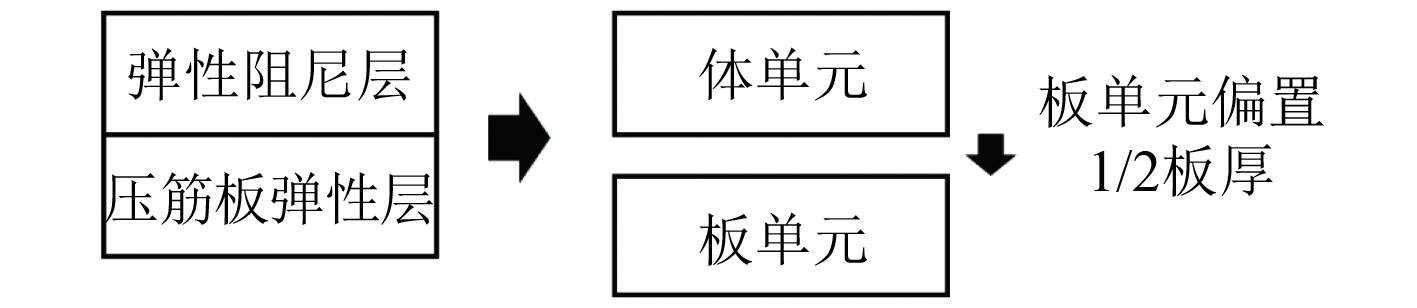
模型的弹性层用板单元进行模拟,阻尼层用体单元进行模拟,为了正确模拟弹性层和阻尼层的接触情况,板单元节点位置向下偏置一半板厚,压筋部分不进行阻尼处理。
|
图 2 压筋板有限元模拟方式 Fig. 2 Finite element simulation of ribbed plate |

|
图 3 压筋板有限元模型 Fig. 3 Finite element model of ribbed plate |
采用修正计算公式(13),取阻尼基准弹性模量E=75 MPa进行模态损耗因子的计算,结果如表1所示。计算结果表明,修正后计算结果的计算精度有明显改善,与文献[10]试验结果误差很小,验证了该修正公式的正确性。
|
|
表 1 压筋板模态损耗因子的计算与试验对比 Tab.1 Comparison of calculation and experimental modal loss factor |
完整的随机响应由输入随机激励、振动系统和输出随机响应组成。其中随机激励、随机响应以功率谱密度的形式表示(PSD)。随机系统的响应分析可分为2步:一是求取系统的传递函数;二是根据输入激励PSD谱,通过传递函数求取系统的随机响应PSD谱。

|
图 4 随机响应示意图 Fig. 4 Random response diagram |
在工程中一般会关注每个1/3倍频程的加速度有效值以及整个频率范围内的加速度有效值,2个加速度的定义分别如下:
| ${a_{1/3}} = \sqrt {\int_{{f_l}}^{{f_u}} {PSD{\rm d}f} } {\text{。}}$ | (16) |
| ${a_{mean}} = \sqrt {\sum {a_{1/3}^2} } {\text{。}}$ | (17) |
式中:PSD为随机响应输出加速度谱;fl和fu分别为1/3倍频程加速度上限和下限;
|
|
表 2 1/3倍频程范围 Tab.2 Range of 1/3 octave |
试验模型为某船双层底内底加筋板结构,板厚为10 mm,设计尺寸为1000×1270 mm,沿短边方向间隔390 mm设置了2根10号球扁钢。因工装设计要求,模型沿纵向、横向向四周分别延伸200 mm,板的总尺寸相应变为1400 mm×1570 mm,骨材也相应延伸,如图5所示。为了模拟船舶板架的简支边界条件,在四周边界上焊接外围T型材,以方便施加边界条件。设计和加工了上下2层支撑基座,模型间以圆钢接触以模拟边界条件。

|
图 5 船舶加筋板试验模型 Fig. 5 Model of ribbed plate in experiment |

|
图 6 试验支撑基座 Fig. 6 Support base in experiment |
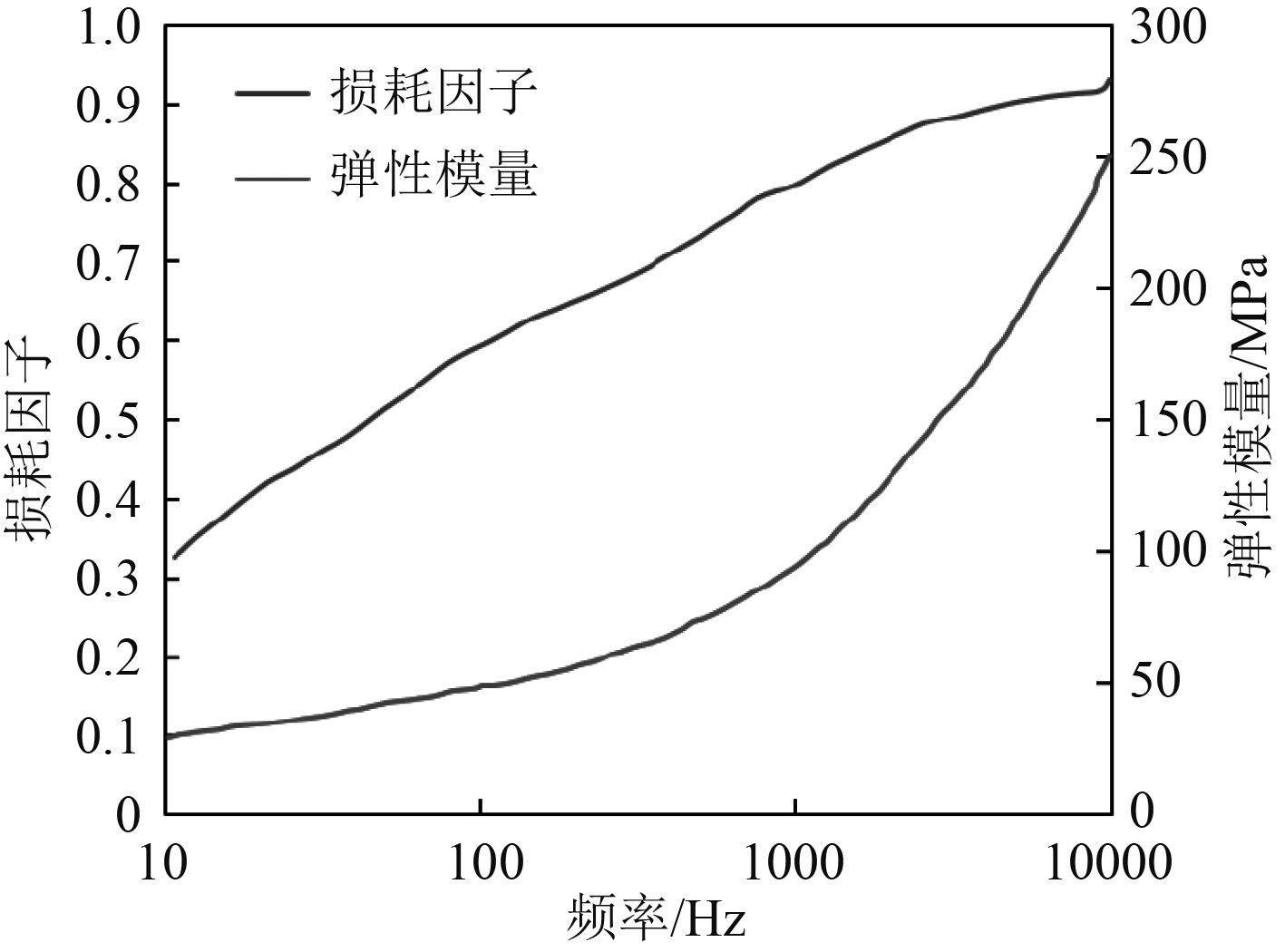
加筋板模型钢材为Q235钢,敷设阻尼材料为丁基橡胶,厚度为20 mm,密度为1 700 kg/m3,泊松比为0.49,丁基橡胶的损耗因子和弹性模量的频变特性如图7所示[12]。
|
图 7 丁基橡胶频变特性图 Fig. 7 Frequency change characteristic of butyl rubber |
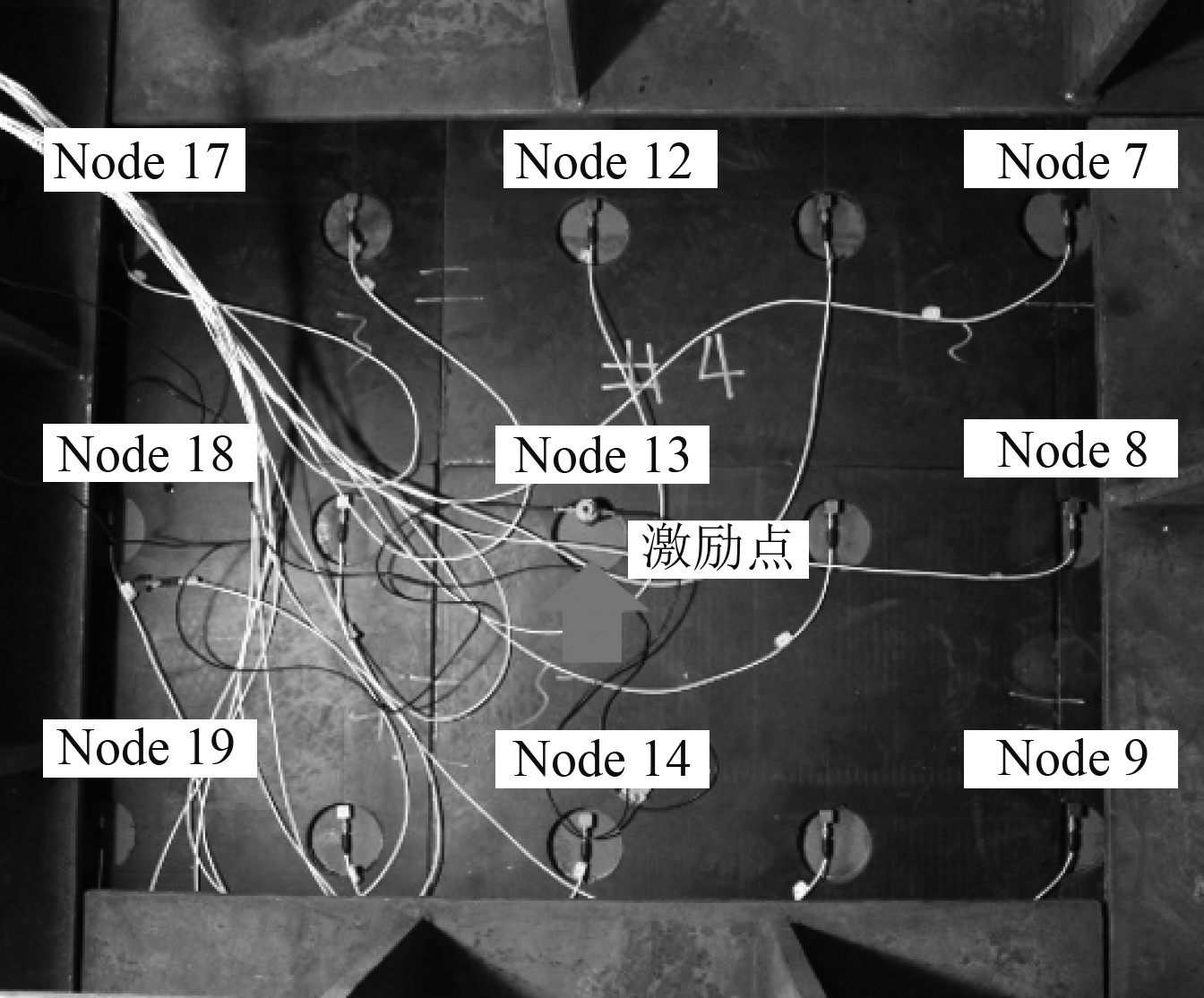
试验中采用单点激励多点输出的方式,并使用传递函数法进行数据分析。激振器的激振力通过安装在激振杆和试件之间的力传感器测得,激振信号为图8所示的随机信号。结构的随机响应结果由测点上的加速度传感器测得,测点分布如图9所示,获得每个测点的传递函数和1/3倍频程加速度响应谱后,通过式(16)、式(17)对响应谱数据进行处理,得到各测点1/3倍频程加速度有效值

|
图 8 随机激励PSD谱 Fig. 8 Random incentive PSD spectrum |
|
图 9 试验测点分布 Fig. 9 Test nodes distribution |
计算模型随机响应时,首先采用模态应变能法并结合修正公式(13)计算得到模态损耗因子,然后利用模态叠加法求得结构的传递函数,最后根据激励PSD谱

|
图 10 随机响应计算流程 Fig. 10 Random response calculation process |
| ${S_{yy}}(\omega ) = {\left| {H(\omega )} \right|^2}{S_{xx}}(\omega ){\text{。}}$ | (18) |
修正前后的各阶模态频率和模态损耗因子的计算结果如表3所示。
|
|
表 3 阻尼加筋板模型的模态损耗因子计算值 Tab.3 Calculation modal loss factor of the model |
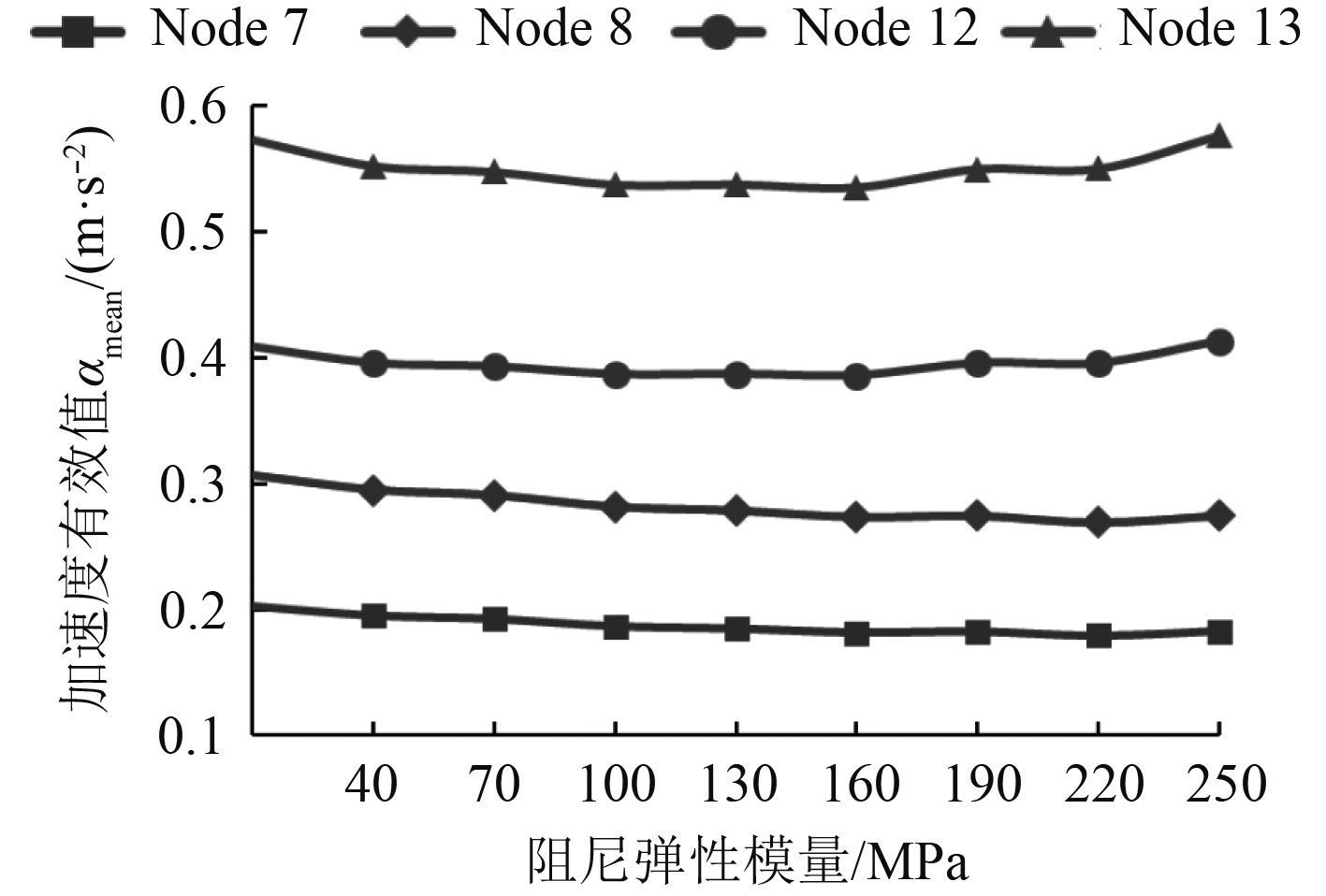
计算得到模态损耗因子后,利用模态叠加法求解MCK方程以获得结构的传递函数。根据式(2)~式(4)可知,刚度矩阵中含有阻尼刚度项,其阻尼弹性模量的频变特性不仅对模态损耗因子有较大影响,而且对MCK方程的刚度项也会产生直接的影响,进而影响传递函数的求解,因此,需要研究弹性模量的变化对随机响应计算结果的影响。常用粘弹性阻尼的弹性模量范围一般为10~250 MPa,仅考虑阻尼弹性模量对刚度矩阵的影响,获得一系列不同弹性模量取值下模型随机响应计算结果,如图11所示。考虑到模型对称性,仅关注node7,node8,node12,node13测点的计算结果。
|
图 11 加筋板加速度有效值随阻尼弹性模量变化图 Fig. 11 Acceleration RMS of stiffened plate with different damping elastic modulus |
可以看出,粘弹性阻尼材料的弹性模量在常用范围内变化时,在不考虑弹性模量对模态阻尼比影响时,弹性模量的变化对随机响应计算结果影响较小。因此,在计算粘弹性阻尼结构随机响应时,仅考虑阻尼弹性模量频变效应对模态损耗因子的影响,忽略其与MCK方程刚度矩阵的耦合作用,即取阻尼材料的弹性模量为定值。
求得阻尼加筋板的传递函数后,根据输入激励PSD谱数据,进一步计算得到考虑粘弹性阻尼频变效应的随机响应结果,并与试验结果进行对比如表4所示。
|
|
表 4 阻尼加筋板模型的随机响应计算值和试验值对比 Tab.4 Comparison of calculation and experiment results of damped stiffened plate model |
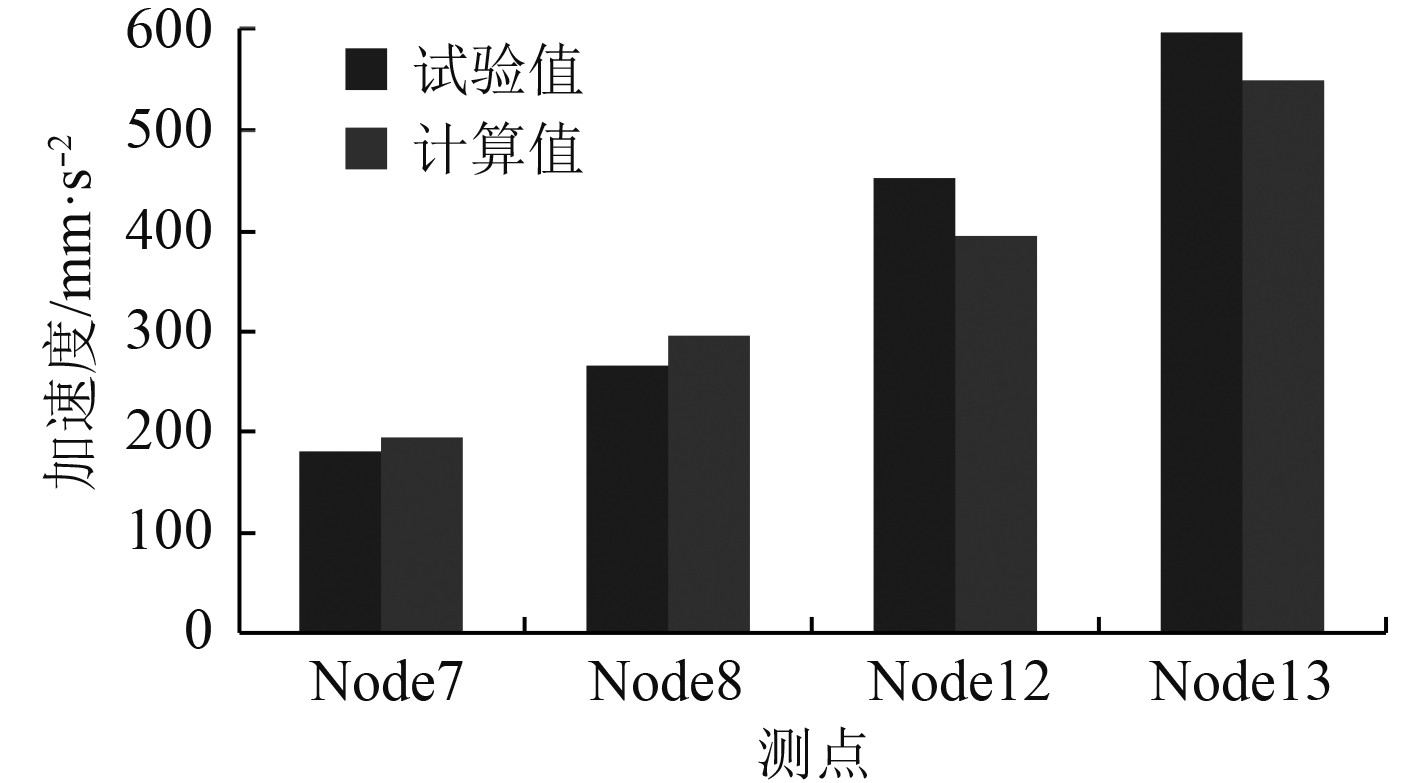
|
图 12 各测点频率段加速度有效值amean Fig. 12 Acceleration RMS amean of each node |
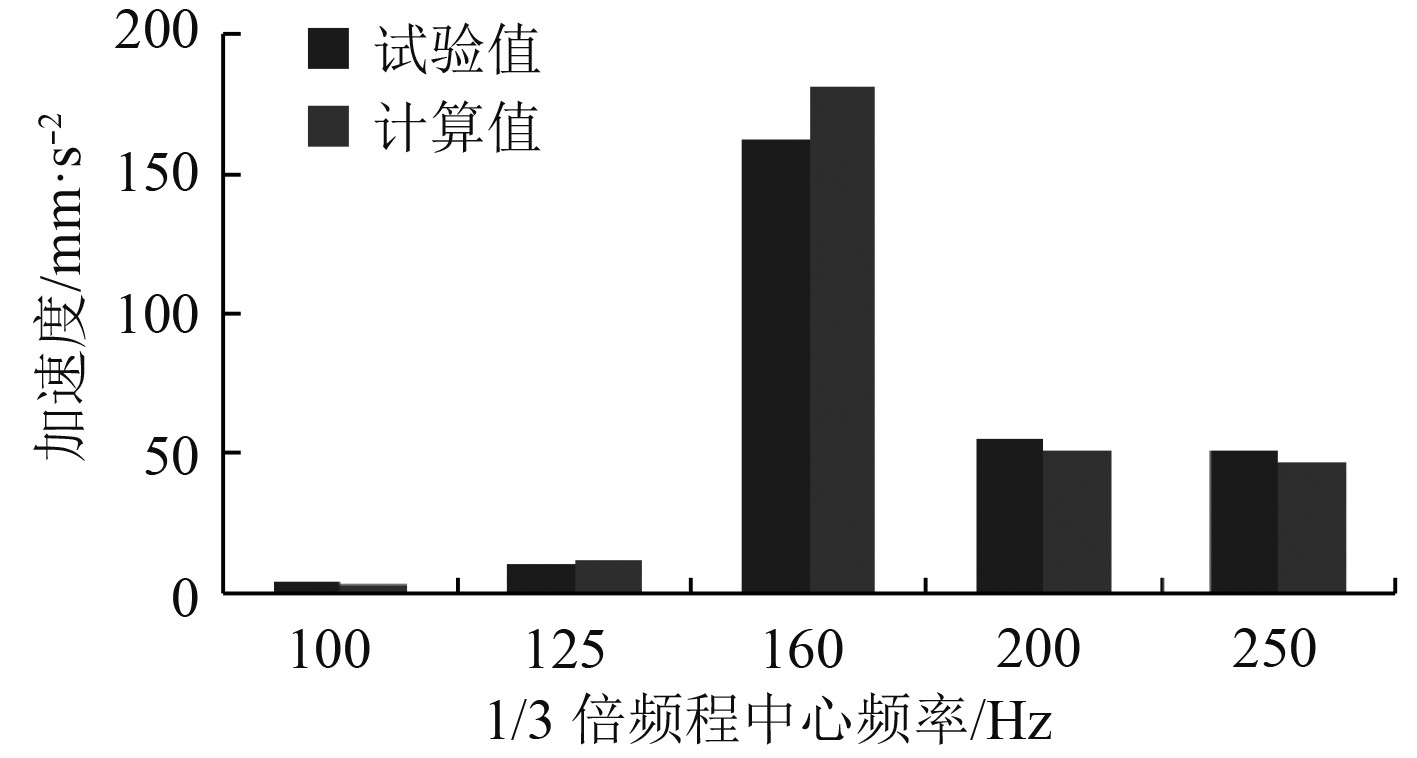
|
图 13 node7 1/3倍频程加速度有效值a1/3 Fig. 13 Acceleration RMS a1/3 of node7 |

|
图 14 node8 1/3倍频程加速度有效值a1/3 Fig. 14 Acceleration RMS a1/3 of node8 |
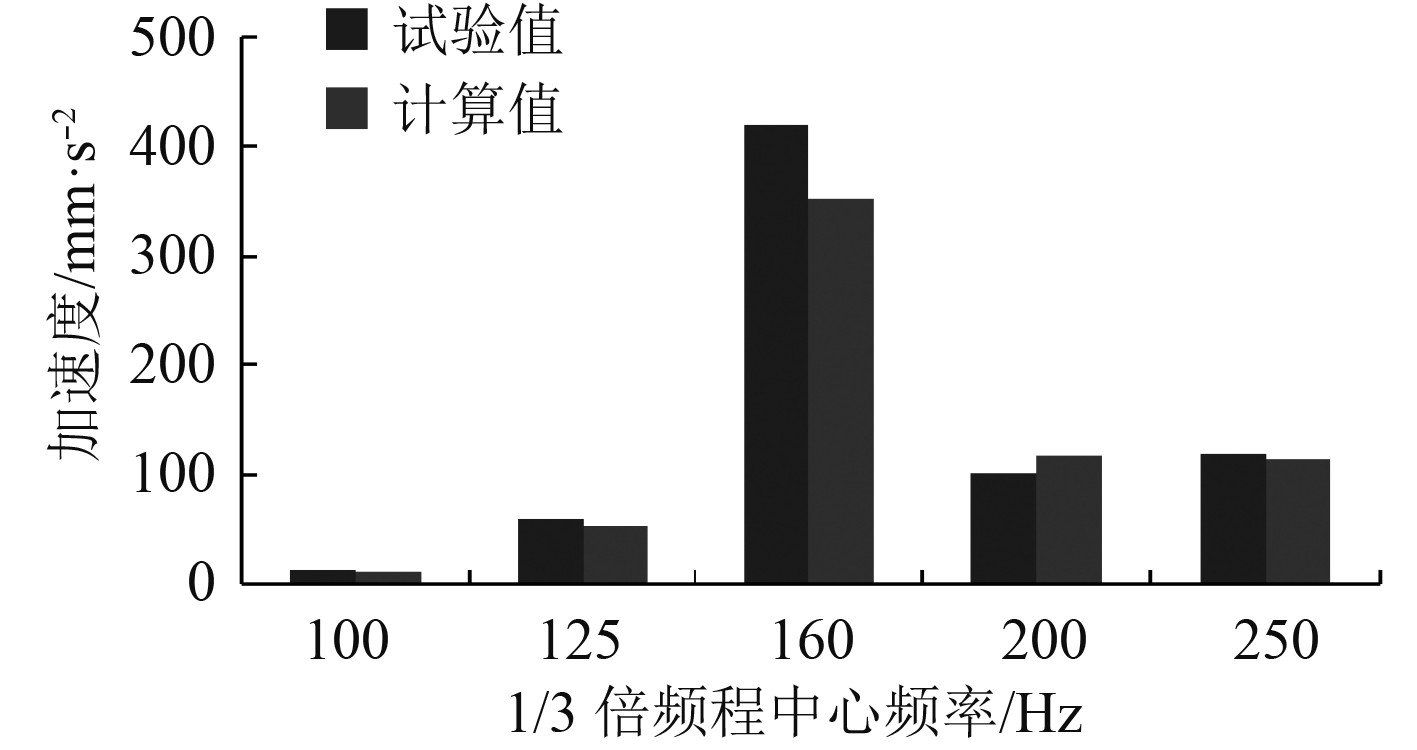
|
图 15 node12 1/3倍频程加速度有效值a1/3 Fig. 15 Acceleration RMS a1/3 of node12 |
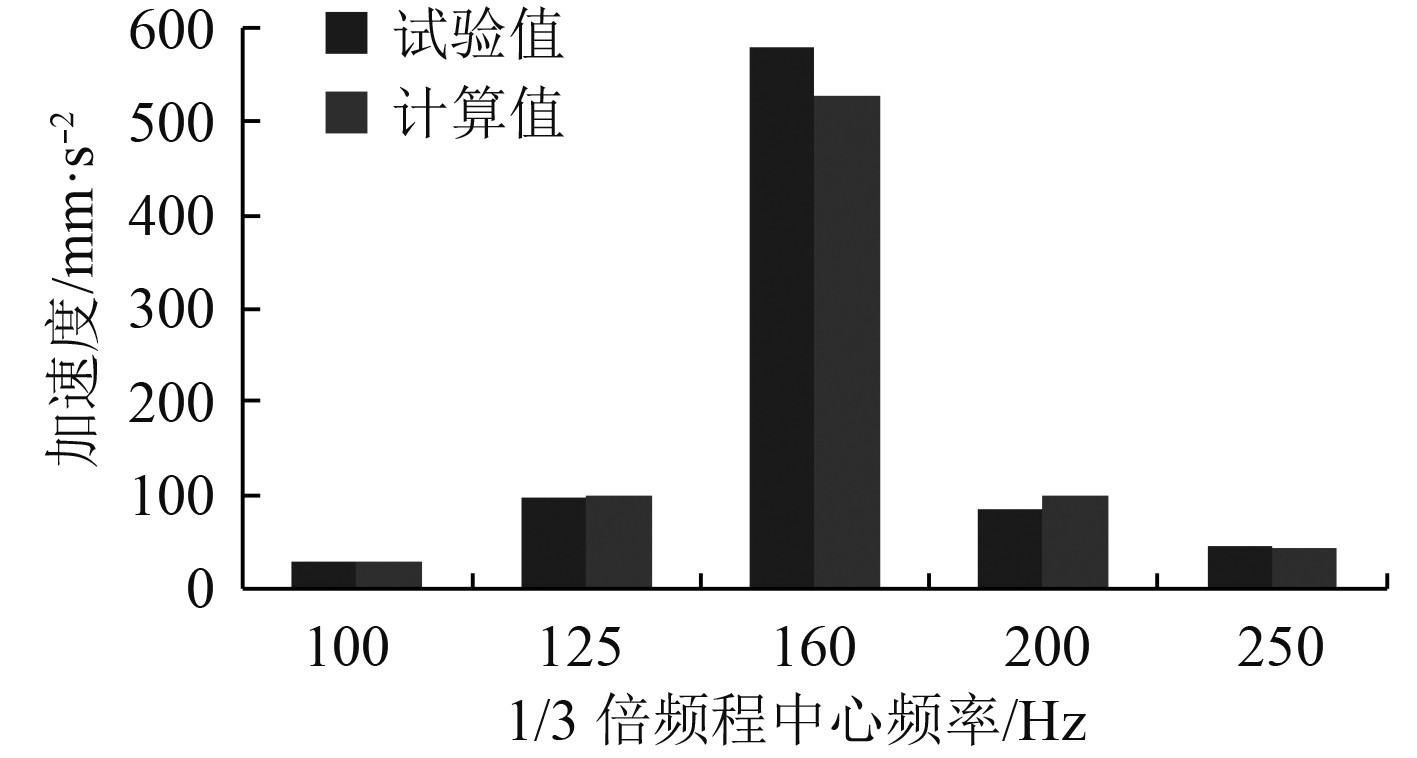
|
图 16 node13 1/3倍频程加速度有效值a1/3 Fig. 16 Acceleration RMS a1/3 of node13 |
由表4可知,各测点在计算频率段的加速度有效值
本文推导出同时考虑粘弹性阻尼损耗因子和弹性模量频变特性的模态损耗因子修正公式,并给出适用于粘弹性阻尼加筋板结构的随机响应计算流程。通过对阻尼压筋板模态损耗因子的算例验证,以及船舶阻尼加筋板随机响应的试验和计算研究,得出以下结论:
1)利用修正公式计算所得阻尼压筋板模态损耗因子与文献[10]中的试验结果误差很小,验证了该修正公式的正确性。
2)在随机响应计算中可忽略阻尼弹性模量频变与MCK方程刚度矩阵的耦合作用,仅考虑其对模态损耗因子的影响。
3)采用基于修正模态阻尼损耗因子的随机响应计算流程,可以获得较好的数值计算结果,相关修正公式和计算方法可以为阻尼减振的工程应用提供参考。
| [1] |
周云. 粘弹性阻尼减震结构设计[M]. 武汉: 武汉理工大学, 2006: 116–128.
|
| [2] |
LU Y P, EVERSTINE G C. More on finite element modeling of damped composite systems[J]. Journal of Sound & Vibration, 1980, 69(2): 199-205. |
| [3] |
HU Y C, HUANG S C. The frequency response and damping effect of three-layer thin shell with viscoelastic core[J]. Computers & Structures, 2000, 76(5): 577-591. |
| [4] |
IU V P, CHEUNG Y K, LAU S L. Non-linear vibration analysis of multilayer beams by incremental finite elements, Part II: Damping and forced vibrations[J]. Journal of Sound & Vibration, 1985, 100(3): 373-382. |
| [5] |
BAGLEY R L, TORVIK P J. On the fractional calculus model of viscoelastic behavior[J]. Journal of Rheology (1978-present), 1986, 30(1): 133-155. DOI:10.1122/1.549887 |
| [6] |
MCTAVISH D J, HUGHES P C. Modeling of linear viscoelastic space structures[J]. Asme Transactions Journal of Vibration Acoustics, 1993, 115(1): 103-110. DOI:10.1115/1.2930302 |
| [7] |
JOHNSON C D, KIENHOLZ D A. Finite element prediction of damping in structures with constrained viscoelastic layers[J]. Aiaa Journal, 2012, 20(20): 1284-1290. |
| [8] |
CAO X, MLEJNEK H P. Computational prediction and redesign for viscoelastically damped structures[J]. Computer Methods in Applied Mechanics & Engineering, 1995, 125(1-4): 1-16. |
| [9] |
邓年春, 邹振祝, 杜华军, 等. 约束阻尼板的有限元动力分析[J]. 振动工程学报, 2003, 16(4): 489-492. DENG Nian-chun, ZOU Zhen-zhu, DU Hua-jun, et al. A finite element dynamic analysis of constrained plates[J]. Journal of Vibration Engineering, 2003, 16(4): 489-492. DOI:10.3969/j.issn.1004-4523.2003.04.021 |
| [10] |
孙社营. 阻尼压筋板的动态力学性能研究[J]. 噪声与振动控制, 2000(02): 19-23. SUN She-ying. Dynamic investigation of a damped stiffened plate[J]. Noise and Vibration Control, 2000(02): 19-23. DOI:10.3969/j.issn.1006-1355.2000.02.003 |
| [11] |
RAO D K. Frequency and loss factors of sandwich beams under various boundary conditions[J]. ARCHIVE Journal of Mechanical Engineering Science 1959-1982(vols 1-23), 1978, 20(5): 271-282. |
| [12] |
祝驰誉, 温华兵. 丁基橡胶阻尼材料对基座减振的实验研究[J]. 造船技术, 2015(2): 50-53. ZHU Chi-yu, WEN Hua-bin. An experimental study on butyl rubber damping material applied to base structure[J]. Marine Technology, 2015(2): 50-53. DOI:10.3969/j.issn.1000-3878.2015.02.011 |
 2020, Vol. 42
2020, Vol. 42
