隔振是应用广泛且行之有效的振动控制措施,隔振系统的演化过程显示了工程需求的不断变化和对隔振机理认识的不断深入[1-2]。单层隔振是最早开始研究并应用的隔振方法,但在用于低转速大型设备的隔振时,支承刚度须设计得很小和系统的稳定性要求相矛盾[3]。为改进其不足,在被隔离体和基础之间插入2层隔振器,并在它们之间安装一刚性质量块构成双层隔振系统,该系统的支承刚度优于单层隔振系统,而且在激励频率大于二次谐振频率后传递率的衰减量是单层隔振系统衰减量的平方,同时兼顾了系统的稳定性和衰减性[4-5]。若要获取更优的隔振效果则需提供必要的中间质量,但过多的附加质量受到舰船空间和重量的约束。为此,将多台动力设备集中布置在同一中间结构(筏体)上构成浮筏隔振系统,该隔振系统考虑了工程限制的同时也能收到较好的隔振效果[6-7]。但相比于双层隔振系统,高频扰动下,浮筏隔振系统的中间筏体柔性结构与基础等柔性子结构由于波动效应会发生动力耦合,被激发结构与周围介质耦合而辐射高频噪声[8-9]。为了控制高频噪声,文献[10]提出了分散中间质量隔振系统,即将整体式中间结构分散为若干个中间质量块(刚性),每个分散中间质量块安装在上下级隔振器之间,可以避免整体中间结构弹性模态被激发而带来新的结构声问题。
文献[11]阐述了分散中间质量隔振系统在舰船成功应用的实例。但关于该系统振动特性的分析存在:1)结论基于简单的集总参数系统,将隔振器及安装基础视为无质量弹簧元件和刚性结构,未考虑高频激励下子系统的波动效应[12-13];2)对分散中间质量避免中间结构的波动效应,降低子系统间发生动力耦合几率来改善系统高频隔振效果的机理探讨较少且设置中间结构质量参数一致的浮筏隔振系统作为对照是必要的;3)探究分散中间质量削弱隔振器驻波效应进而提升高频隔振效果的本质对理解该隔振系统的隔振机理是必要的。
针对舰船分散中间质量隔振系统研究中的不足,利用导纳矩阵分析法,导出系统的能流传递函数,建立该系统的分布参数解析模型。研究复杂激励下分散中间质量隔振系统的能量波动特性;探讨分散中间质量对隔振器驻波的削弱作用、中间结构的波动效应及机器与分散中间质量的质量比对系统隔振性能的影响。
1 动力学建模与分析 1.1 隔振系统耦合振动传递矩阵建模从工程中舰船隔振设计的角度出发,大中型动力机械或发电机组的隔振装置一般相对坐标平面对称布置。因此,建立图1所示的柔性基础上分散中间质量多支承隔振系统的动力学模型。按耦合界面将系统分为机器子结构A,上下层隔振器B,D和分散中间质量块C及柔性基础子结构E,m个分散中间质量与上下层隔振器如图1所示安装。按照振动传递方向定义各子系统的输入输出端及其广义绕动力和速度矢量,建立总体系统的耦合振动传递模型,如图2所示。
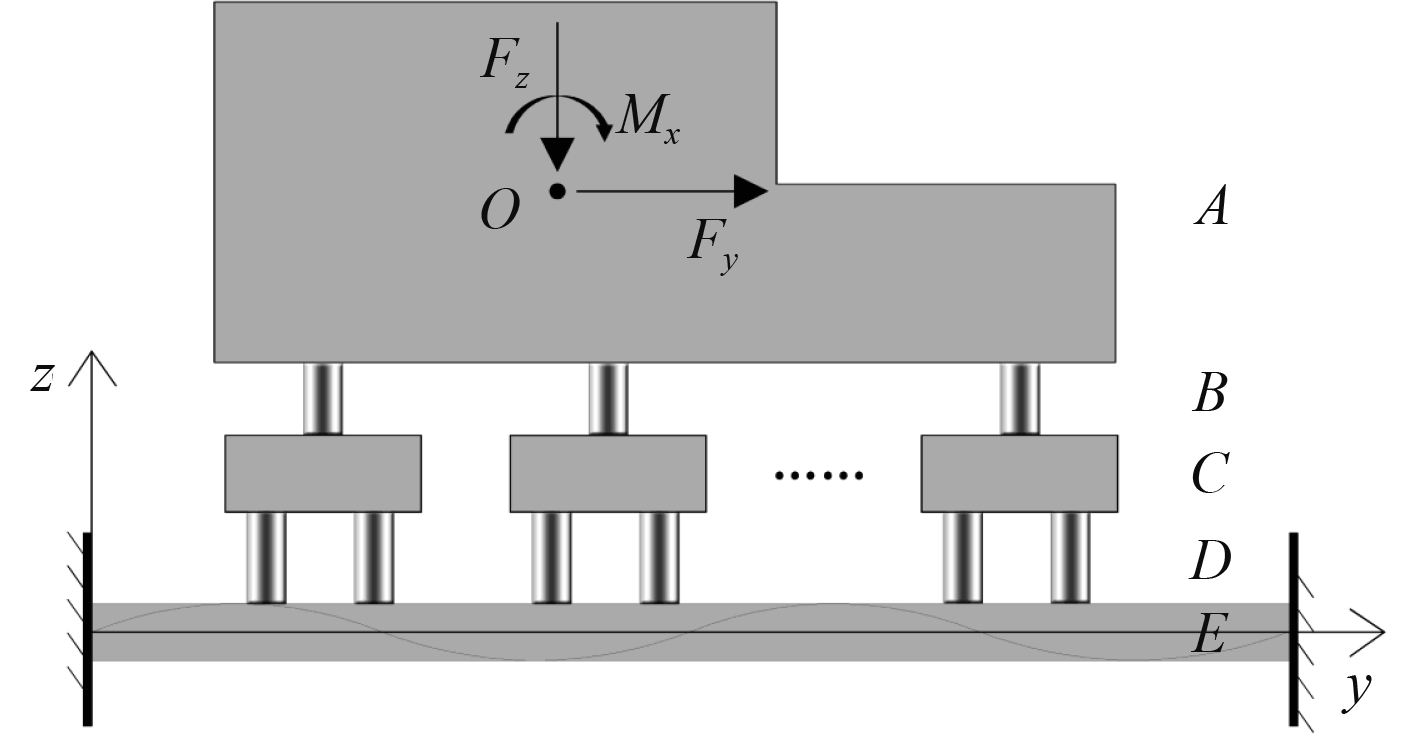
|
图 1 分散中间质量多支承隔振系统模型 Fig. 1 Multi mounts isolation system with intermediate dispersed mass. |

|
图 2 隔振系统耦合振动传递模型 Fig. 2 Coupled vibration transfer model of vibration isolation system |
动力设备通常刚度很大,工程激励的强度通常很难激发其弹性模态,故一般视为刚性结构。充分考虑舰船动力设备激励的多维特性,机器子结构受到由沿y,z的力扰动和绕x轴的力矩扰动组成的复杂激励,分别用
| ${{{F}}_A} = {\left[ {F_{ay}^1,F_{az}^1,M_{ax}^1,F_{ay}^2,F_{az}^2{\rm{,}}M_{ax}^2{\rm{, }}\cdots{\rm{ ,}}F_{ay}^m{\rm{,}}F_{az}^m{\rm{,}}M_{ax}^m} \right]^{\rm{T}}}{\text{,}}$ |
| ${{{V}}_A} = {\left[ {v_{ay}^1,v_{az}^1,\dot \theta _{ax}^1,v_{ay}^2,v_{az}^2{\rm{,}}\dot \theta _{ax}^2{\rm{, }}\cdots{\rm{ ,}}v_{ay}^m,v_{az}^m{\rm{,}}\dot \theta _{ax}^m} \right]^{\rm{T}}}{\text{。}}$ |
利用牛顿第二定律和对应矢量的几何关系建立振源刚性子结构的动力学方程,用导纳矩阵表示为:
| $\left[ {\begin{array}{*{20}{c}} {{{{V}}_O}} \\ {{{{V}}_A}} \end{array}} \right]{{ = }}\left[ {\begin{array}{*{20}{c}} {{{{A}}_{11}}}&{{{{A}}_{12}}} \\ {{{{A}}_{21}}}&{{{{A}}_{22}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{{F}}_O}} \\ {{{{F}}_A}} \end{array}} \right]{\text{,}}$ | (1) |
式中,
| $\begin{split} &{{{T}}_0} = \left[ {{t_1}{\rm{ }}{t_2}{\rm{,}} \cdots {t_k} \cdots {\rm{, }}{t_m}} \right],{{R}} = {{{T}}_0}^{\rm{T}}{\text{,}}\\ &{{{t}}_k} = \left[ {\begin{array}{*{20}{c}} 1&0&0&1&0&0 \\ 0&1&0&0&1&0 \\ b&{ - {a_{2k - 1}}}&1&b&{ - {a_{2k}}}&1 \end{array}} \right]{\text{。}} \end{split}$ |
式中:Ma和Ia分别表示机器质量与转动惯量;
基于Snowdon的Long rod理论,考虑粘弹性橡胶隔振器的分布参数特性,将其模化为损耗因子为η,密度为ρ,弹性模量为E的圆筒形杆。为便于分析,尚不涉及橡胶隔振器的温变、频变及大变形特征。
隔振器子系统输入、输出广义力与速度响应为:
| $\begin{split} &{{{F}}_{Bt}} = {\left[ {F_{bty}^1,F_{btz}^1,M_{btx}^1,F_{bty}^2,F_{btz}^2,M_{btx}^2, \cdots ,F_{bty}^m,F_{btz}^m,M_{btx}^m} \right]^{\rm{T}}} {\text{,}} \\ & {{{V}}_{Bt}} = {\left[ {v_{bty}^1,v_{btz}^1,\dot \theta _{btx}^1{\rm{,}}v_{bty}^2,v_{btz}^2{\rm{,}}\dot \theta _{btx}^2{\rm{,}} \cdots {\rm{,}}v_{bty}^m,v_{btz}^m{\rm{,}}\dot \theta _{btx}^m} \right]^{\rm{T}}}{\text{,}} \\ & {{ F}_{Bb}} = \left[ {F_{bby}^1,F_{bbz}^1,M_{bbx}^1,F_{bby}^2,F_{bbz}^2,M_{bbx}^2, \cdots ,} \right. \hfill \\ &\;\;\;\qquad \left. {F_{bby}^m,F_{bbz}^m,M_{bbx}^m} \right]_{\rm T}{\text{,}} \\ & {{{V}}_{Bb}} = {\left[ {v_{bby}^1,v_{bbz}^1,\dot \theta _{bbx}^1{\rm{,}}v_{bby}^2,v_{bbz}^2{\rm{,}}\dot \theta _{bbx}^2{\rm{,}} \cdots {\rm{,}}v_{bby}^m,v_{bbz}^m{\rm{,}}\dot \theta _{bbx}^m} \right]^{\rm{T}}}{\text{,}} \\ & {{{F}}_{Dt}} \!= \!{\left[ {F_{dty}^1,F_{dtz}^1,M_{dtx}^1,F_{dty}^2,F_{dtz}^2,M_{dtx}^2, \! \cdots \! ,F_{dty}^{{\rm{2}}m},F_{dtz}^{{\rm{2}}m},M_{dtx}^{{\rm{2}}m}} \right]^{\rm{T}}} {\text{,}}\\ &{{{V}}_{Dt}} = {\left[ {v_{dty}^1,v_{dtz}^1,\dot \theta _{dtx}^1{\rm{,}}v_{dty}^2,v_{dtz}^2{\rm{,}}\dot \theta _{dtx}^2{\rm{,}} \cdots {\rm{,}}v_{dty}^{{\rm{2}}m},v_{dtz}^{{\rm{2}}m}{\rm{,}}\dot \theta _{dtx}^{{\rm{2}}m}} \right]^{\rm{T}}} {\text{,}} \\ & {{ F}_{Db}} = \left[ {F_{dby}^1,F_{dbz}^1,M_{dbx}^1,F_{dby}^2,F_{dbz}^2,M_{dbx}^2, \cdots ,} \right. \\ &\;\;\;\qquad\left. {F_{db{\text{y}}}^{{\text{2}}m},F_{db{\text{z}}}^{{\text{2}}m},M_{dbx}^{{\text{2}}m}} \right]^{\rm T}{\text{,}} \\ & {{{V}}_{Db}} = {\left[ {v_{dby}^1,v_{dbz}^1,\dot \theta _{dbx}^1{\rm{,}}v_{dby}^2,v_{dbz}^2{\rm{,}}\dot \theta _{dbx}^2{\rm{,}} \cdots {\rm{,}}v_{dby}^{{\rm{2}}m},v_{dbz}^{{\rm{2}}m}{\rm{,}}\dot \theta _{dbx}^{{\rm{2}}m}} \right]^{\rm{T}}} {\text{。}} \\ \end{split} $ |
上、下层隔振器动态特性用导纳矩阵描述为:
| $\left[ {\begin{array}{*{20}{c}} {{{{V}}_{Bt}}} \\ {{{{V}}_{Bb}}} \end{array}} \right]{{ = }}\left[ {\begin{array}{*{20}{c}} {{{{B}}_{11}}}&{{{{B}}_{12}}} \\ {{{{B}}_{21}}}&{{{{B}}_{22}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{{F}}_{Bt}}} \\ {{{{F}}_{Bb}}} \end{array}} \right]{\text{,}}$ | (2) |
| $\left[ {\begin{array}{*{20}{c}} {{{{V}}_{Dt}}} \\ {{{{V}}_{Db}}} \end{array}} \right]{{ = }}\left[ {\begin{array}{*{20}{c}} {{{{D}}_{11}}}&{{{{D}}_{12}}} \\ {{{{D}}_{21}}}&{{{{D}}_{22}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{{F}}_{Dt}}} \\ {{{{F}}_{Db}}} \end{array}} \right]{\text{。}}$ | (3) |
式中:Bij、Dij(i,j=1,2)分别为上下层各隔振器的传递矩阵元素,可由模态分析法建立的隔振器速度导纳推导得到,其具体形式见参考文献[14]。
1.4 分散中间质量块与中间筏体结构中间质量块具有沿着y,z轴平移和绕x轴转动3个自由度。将中间筏体模化为两端自由的欧拉梁,计及柔性,其动态特性分解为刚体模态及弹性模态两部分。输入、输出质量块和筏体的广义力及速度响应均为:
| $ \begin{split} &{{{F}}_{Ct}} = {\left[ {F_{cty}^1,F_{ctz}^1,M_{ctx}^1,F_{cty}^2,F_{ctz}^2,M_{ctx}^2, \cdots ,F_{cty}^m,F_{ctz}^m,M_{ctx}^m} \right]^{\rm{T}}} {\text{,}} \\ &{{{V}}_{Ct}} = {\left[ {v_{cty}^1,v_{ctz}^1,\dot \theta _{ctx}^1,v_{cty}^2,v_{ctz}^2,\dot \theta _{ctx}^2, \cdots ,v_{cty}^m,v_{ctz}^m,\dot \theta _{ctx}^m} \right]^{\rm{T}}} {\text{,}} \\ &{{{F}}_{Cb}}\!\! =\!\! {\left[ {F_{cby}^1,F_{cbz}^1,M_{cbx}^1,F_{cby}^2,F_{cbz}^2,M_{cbx}^2, \cdots ,F_{cby}^{{\rm{2}}m},F_{cbz}^{2m},M_{cbx}^{2m}} \right]^{\rm{T}}} {\text{,}} \\ & {{{V}}_{Cb}} = {\left[ {v_{cby}^1,v_{cbz}^1,\dot \theta _{cbx}^1,v_{cby}^2,v_{cbz}^2,\dot \theta _{cbx}^2, \cdots ,v_{cby}^{{\rm{2}}m},v_{cbz}^{2m},\dot \theta _{cbx}^{2m}} \right]^{\rm{T}}} {\text{。}}\\ \end{split} $ |
分散中间质量和柔性筏体的动力学特性用导纳矩阵表达如下:
| $\left[ {\begin{array}{*{20}{c}} {{{{V}}_{Ct}}} \\ {{{{V}}_{Cb}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{{C}}_{11}}}&{{{{C}}_{12}}} \\ {{{{C}}_{21}}}&{{{{C}}_{22}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{{F}}_{Ct}}} \\ {{{{F}}_{Cb}}} \end{array}} \right]{\text{,}}$ | (4) |
| $\left[ {\begin{array}{*{20}{c}} {{{{V}}_{Ct}}} \\ {{{{V}}_{Cb}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{{C}}^{11}}}&{{{{C}}^{12}}} \\ {{{{C}}^{21}}}&{{{{C}}^{22}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{{F}}_{Ct}}} \\ {{{{F}}_{Cb}}} \end{array}} \right]{\text{。}}$ | (5) |
式中:
导纳矩阵的具体元素见文献[15]。Mck及Ick分别表示第k个中间质量块的质量及绕x轴的转动惯量;bc=l/2,l表示中间质量块的厚度;ac2k与ac2k-1分别表示在以分散中间质量块重心为原点的局部坐标系中下层隔振器上端面的坐标。
1.5 柔性基础子系统对于基础结构,将其模化为两端固定的欧拉梁,输入基础子系统的广义力和速度响应分别为:
| ${{{F}}_{\rm{E}}} = {\left[ {F_{ey}^1,F_{ez}^1,M_{ex}^1,F_{ey}^2,F_{ez}^2,M_{ex}^2, \cdots ,F_{ey}^{{\rm{2}}m},F_{ez}^{2m},M_{ex}^{2m}} \right]^{\rm{T}}}{\text{,}}$ |
| ${{{V}}_{\rm{E}}} = {\left[ {v_{ey}^1,v_{ez}^1,\dot \theta _{ex}^1,v_{ey}^2,v_{ez}^2,\dot \theta _{ex}^2, \cdots ,v_{ey}^{{\rm{2}}m},v_{ez}^{2m},\dot \theta _{ex}^{2m}} \right]^{\rm{T}}}{\text{,}}$ |
其动态特性可描述为:
| ${{{V}}_{{E}}}{{ = M}}{{{F}}_{{E}}}{\text{。}}$ | (6) |
式中,M为两端固定梁的速度导纳矩阵。导纳矩阵的具体元素见文献[15]。
1.6 耦合系统振动特性传递矩阵根据耦合界面力与速度的关系,综合式(1)~式(6),可得机器的速度响应和输入基础的力、速度响应为:
| ${{{V}}_O}{{ = }}\left( {{{{A}}_{11}} - {{{A}}_{12}}{{{R}}_1}} \right){{{F}}_O}{\text{,}}$ |
| ${{{F}}_E}{\rm{ = }}{{{P}}_2}{{{R}}_2}{{{P}}_1}{{{R}}_1}{{{F}}_O}{\text{,}}$ |
| ${{{V}}_E}{{ = E}}{{{P}}_2}{{{R}}_2}{{{P}}_1}{{{R}}_1}{{{F}}_O}{\text{。}}$ |
因此,输入系统和基础的功率流分别为:
| $ {\rm{ }}{P_o} = 0.5{R_e}\left\{ {{{{F}}_O}^H{{{V}}_O}} \right\}{\rm{ }}, \;\;{P_e} = 0.5{R_e}\left\{ {{{{F}}_E}^H{{{V}}_E}} \right\}{\text{。}} $ |
式中:
其中:
算例中取分散中间质量个数m=4,r=Mc/Ma为中间质量与机器质量比,其中Mc表示各个分散中间质量块的质量之和,除特别说明外,各中间质量块质量相等。
2.1 中间结构对系统能流传递的影响设置浮筏隔振系统作为对照组,中间筏体因其大尺度结构而被视为非刚体,算例中筏体长2 m,宽0.5 m,厚0.1 m。已知分散中间质量被视为刚体,为说明中间结构的柔性对隔振系统振动能量传递的影响,保持2种隔振系统中间子结构质量参数一致,其余材料参数不变。隔振系统主要结构特征参数如表1所示,基础子结构和筏体的固有频率分别如表2和表3所示。
|
|
表 1 隔振系统主要结构特征参数 Tab.1 Parameters used in the proposed isolation system |
|
|
表 2 安装基础固有频率 Tab.2 Nature frequency of installation foundation |
|
|
表 3 中间筏体固有频率 Tab.3 Nature frequency of intermediate raft |
图3表示分散中间质量隔振系统在复杂激励下的振动能流波动频谱图。机器和分散中间质量的前3阶刚体模态为低频段能流传递的主导模态。在中高频段,基础的弹性模态及隔振器驻波效应成为能流传递波峰集中出现的主要原因。图4为对照组在复杂激励下的振动能流波动频谱图。中间筏体的2阶弯曲模态(367.6 Hz)在F=366.9 Hz被激发,此时筏体柔性模态频率与隔振器第1阶驻波(F=401.4 Hz)频率密集间隔出现,隔振器驻波和柔性筏体的弹性波发生耦合使得能流传递波峰变高,导致较窄频带范围内能流传递剧烈增加超20 dB,系统高频结构噪声辐射值骤升。
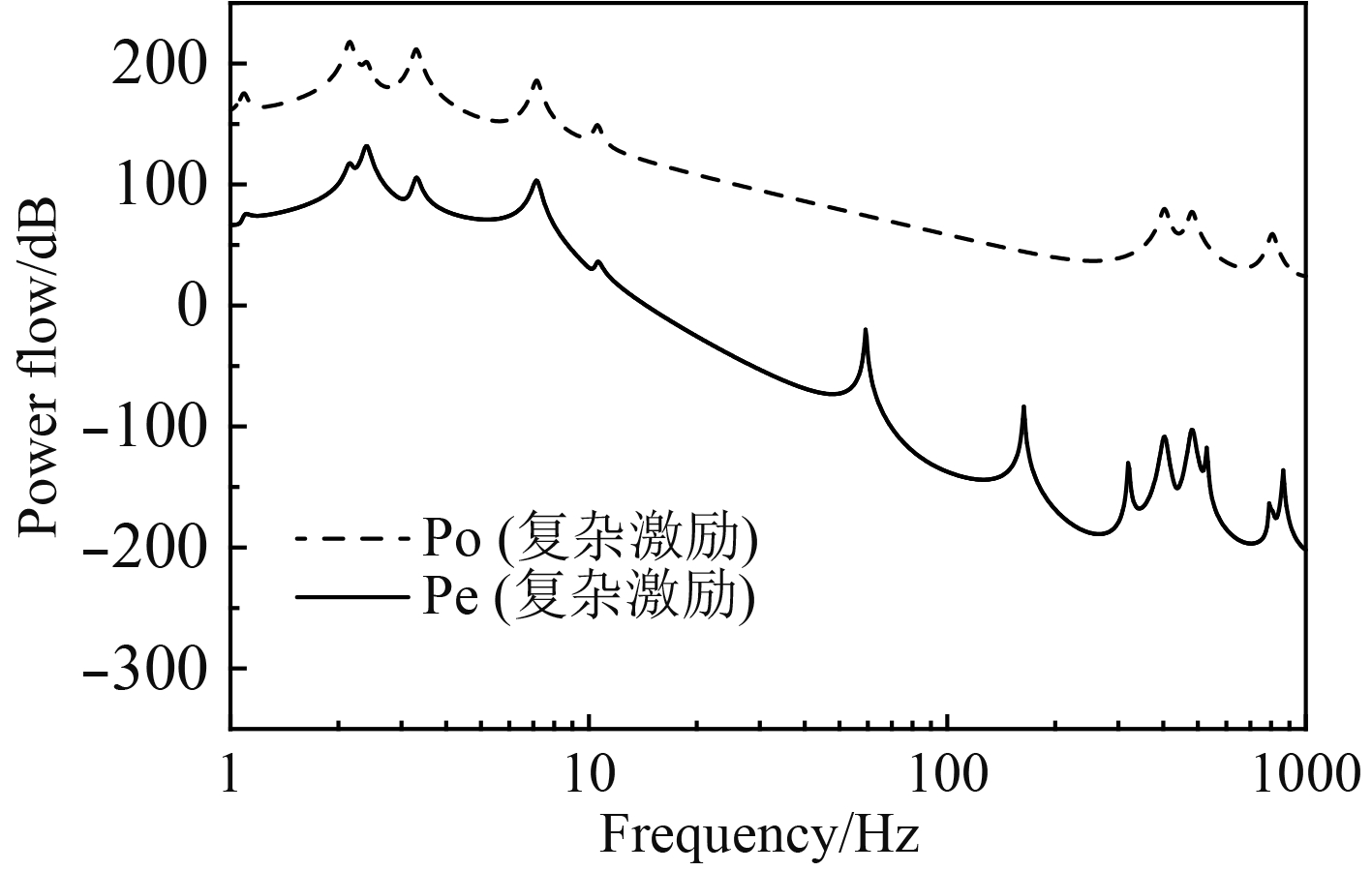
|
图 3 复杂激励下分散中间质量隔振系统能流谱 Fig. 3 Energy flow of the dispersed intermediate mass vibration isolation system under complex excitations |
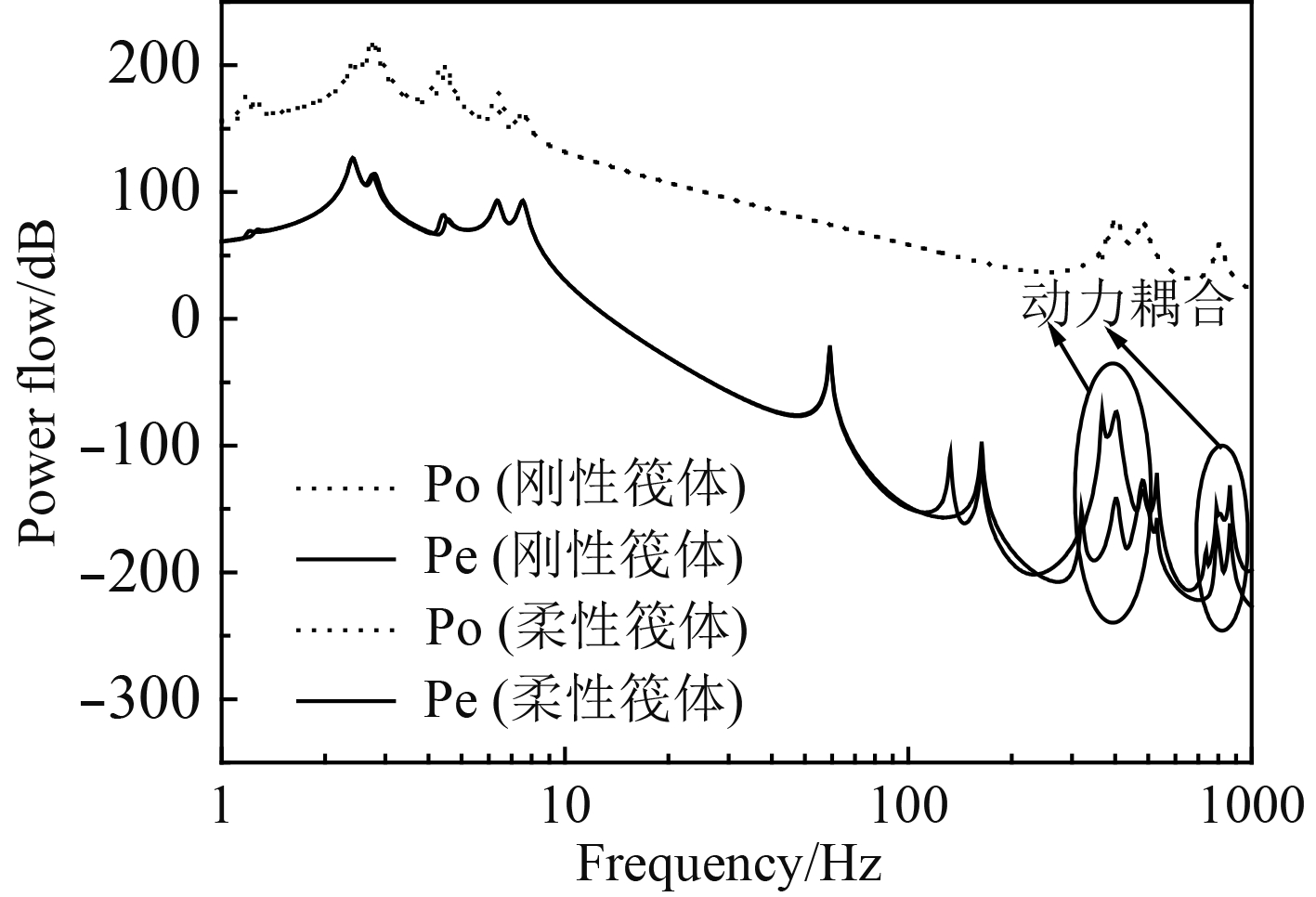
|
图 4 筏体添加柔性前后浮筏隔振系统能流谱 Fig. 4 Energy flow of floating raft isolation system before and after adding flexibility to raft |
为突出分析主要矛盾,清晰阐述分散中间隔振系统的振动机理,本文后续分析外扰激励均仅施加垂向力。
图5为垂向激励下分散中间质量隔振系统和浮筏隔振系统的能流波动情况。可以看出,在高频段,筏体奇次弯曲模态被激发使得能流曲线出现了2个波峰,同时,柔性基础的第1阶(58.8 Hz)、3阶(320.2 Hz)、5阶(790.5 Hz)弯曲模态被激发。其中基础的第5阶模态频率(790.5 Hz)和隔振器的第2阶纵向驻波(F=801.4 Hz)相差很小,筏体和基础的弹性波在F=804.8 Hz附近发生耦合,传递到基础的能量被放大,导致系统高频隔振效果变差。相比之下,通过分散中间质量传递到基础的能流曲线仅出现了基础模态和隔振器纵向驻波导致的波峰,这是由于传递路径中的中间质量被视为刚体,振动传递的大部分能量被质量块以刚体运动的形式耗散,从而避免了目标频段内各柔性子结构相互耦合时弹性波对能量传递的加剧作用。
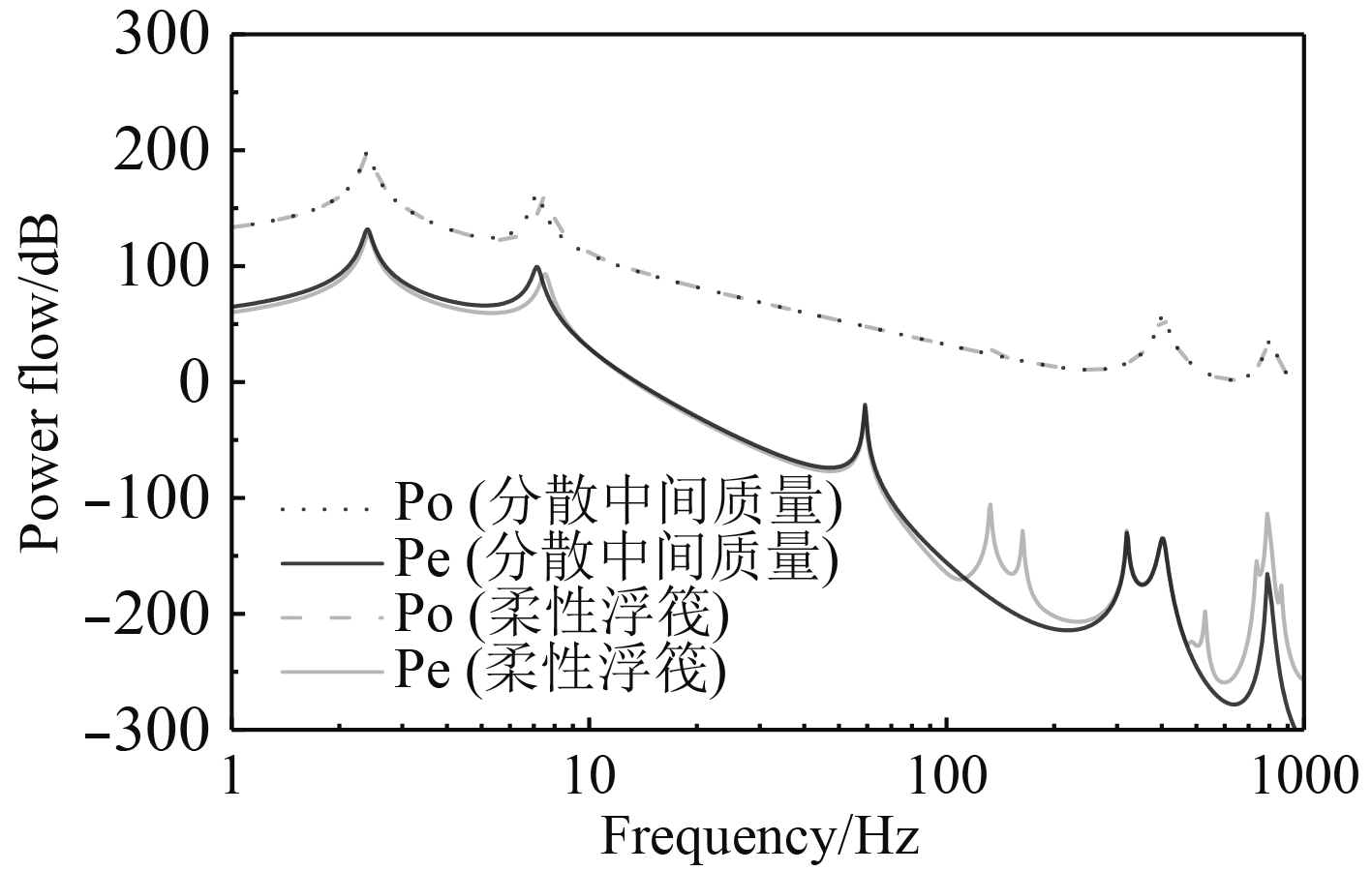
|
图 5 分散中间质量隔振系统与浮筏隔振系统能流谱 Fig. 5 Energy flow of dispersed intermediate mass isolation system and floating raft isolation system |
通过上文分析,中间结构及基础的波动效应对高频激励下系统的能量波动影响较大。同时,隔振器的驻波效应也是引起系统高频段能流剧烈传递的主要因素。
为进一步分析隔振器驻波对系统振动能量传递的影响,图6模拟了分散中间质量安装前后隔振系统在整个频段的振动能流波动频谱图。安装前,能流曲线出现了前4阶隔振器驻波(F=200.7 Hz,401.4 Hz,602.1 Hz,804.8 Hz),此时隔振器的纵向几何尺寸和其弹性波的半波长存在一定倍数关系。安装后,驻波频率提高,在1 000 Hz内之只出现了2阶(F=401.4 Hz,804.8 Hz),原因是隔振器纵向尺寸与其弹性波半波长的几何关系发生了变化,使得隔振器内部行波和反射波叠加产生驻波的频率提高。同时,中高频段能流曲线下降速率明显变快,传递到基础的能量显著降低。
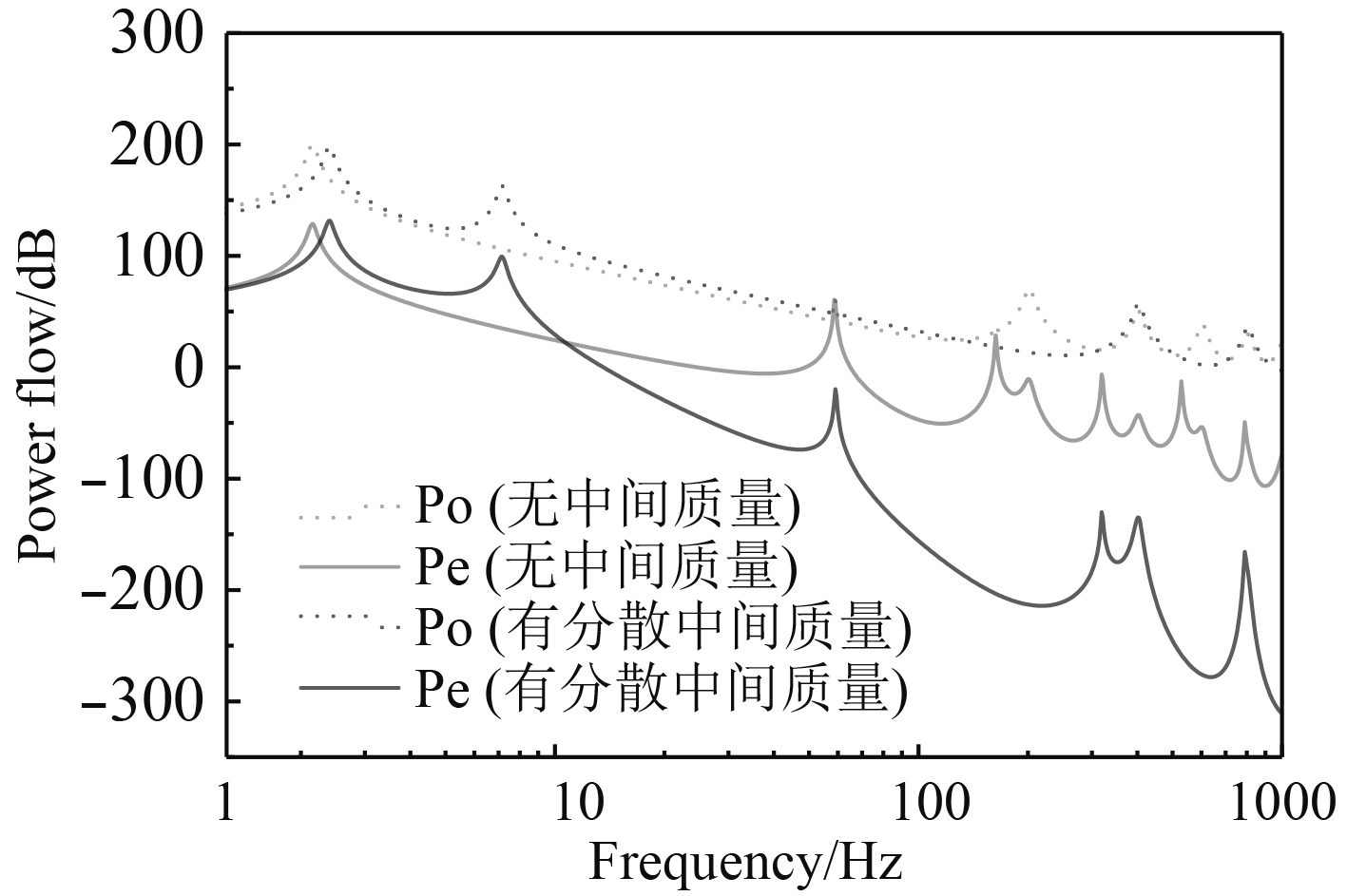
|
图 6 安装分散中间质量前后系统能流谱 Fig. 6 System energy flow spectrum before and after installing dispersed intermediate mass |
图7为上下层隔振器总纵向几何尺度参数变化时,隔振系统的振动能流波动频谱图。可见,低频共振频率随着隔振器高度的增加而左移,系统的支承刚度变低的同时获得了较宽的有效隔振范围。此外,隔振器纵向尺寸的增大使得高频段隔振器驻波导致的能流曲线波峰数量增加,系统高频振动能量传递加剧。因此,为控制隔振系统低频共振和中高频时剧烈的能量传递,在理论设计和工程应用中均需要准确考察不同动力设备的激励频谱,合理选择隔振器的几何尺寸,使其为系统提供足够支承刚度的同时也可以获得优异的隔振效果。
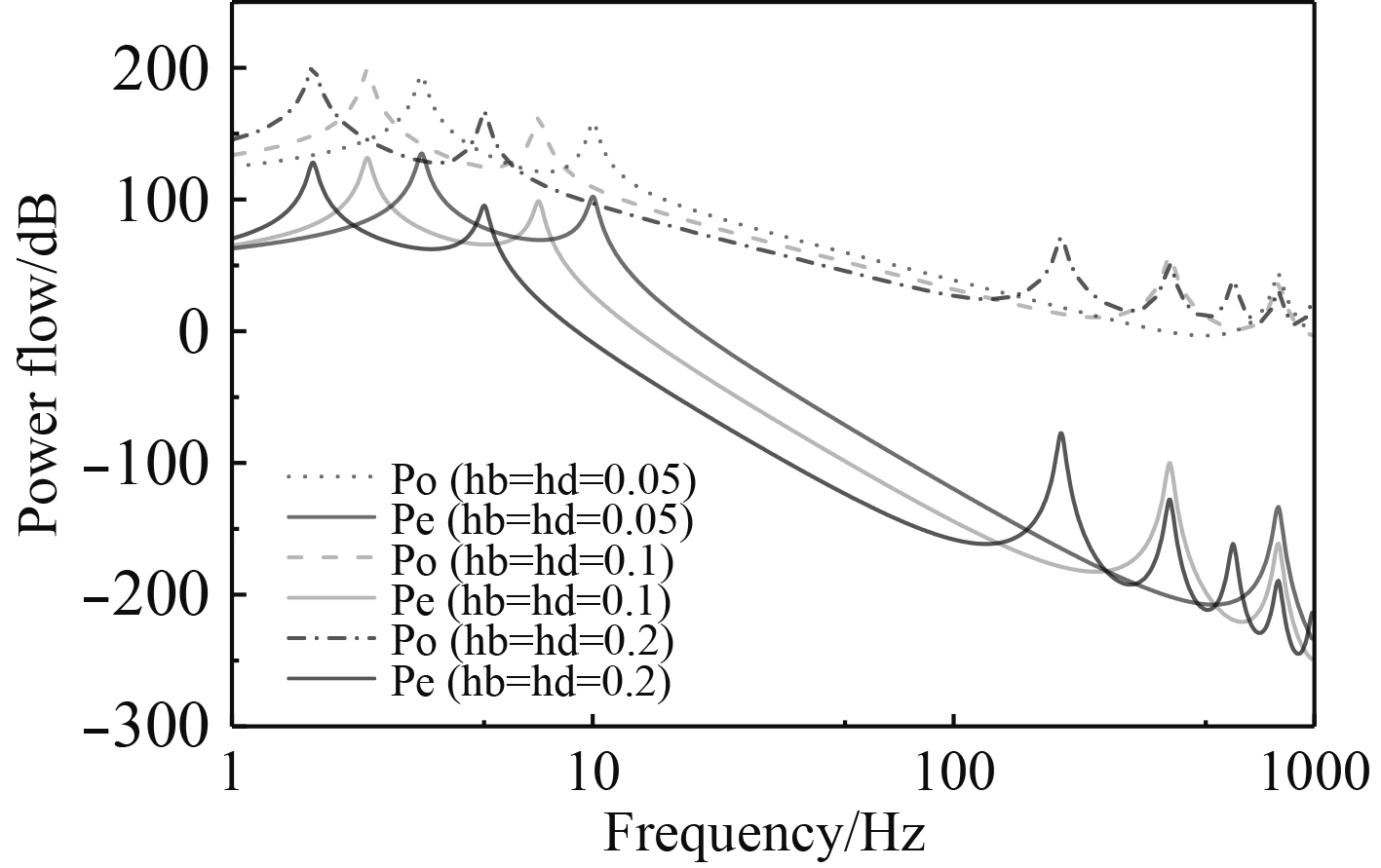
|
图 7 隔振器不同纵向尺度下系统能流谱 Fig. 7 Energy flow of isolators with different longitudinal scales |
相较于其他隔振系统,分散中间质量具有易拆卸的优点,这也为改善系统隔振效果增大了实际操作空间。研究分散质量块与机器的质量比可以为优化该隔振系统的性能提供一定的理论指导。
图8为不同质量比(r=Mc/Ma)时,分散中间质量隔振系统的振动能流波动频谱图。随着r值增大,中间质量带来的共振频率左移,系统在更宽的频率范围内得到较好的隔振效果,同时,高频共振区域的能量传递曲线有所降低。因此,在工程实际中,可以通过适当增大中间质量来提升隔振装置在整个频段的隔振效果,但是同时要兼顾舰船对隔振装置的重量和空间要求。
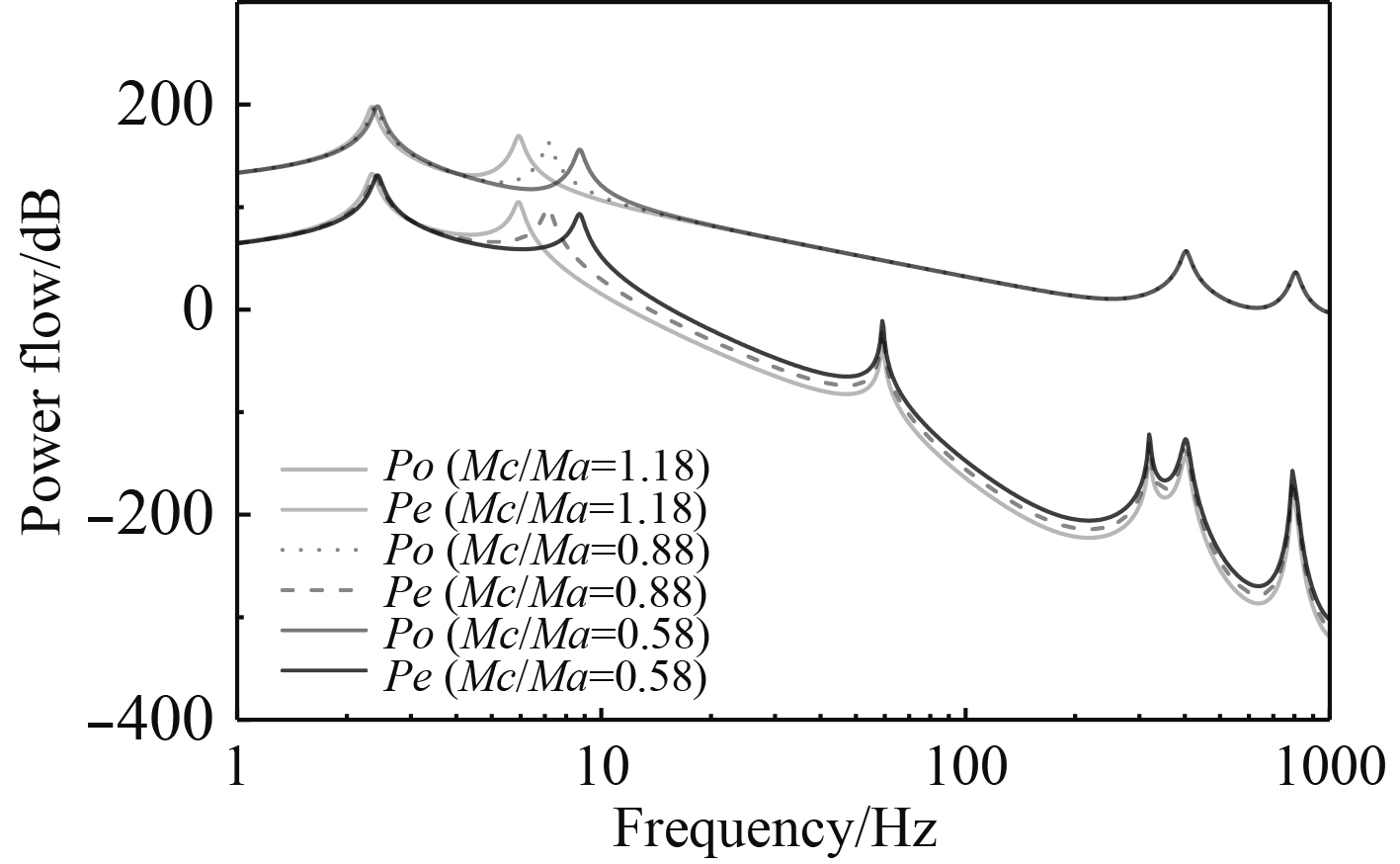
|
图 8 不同质量比(r=Mc/Ma)时系统功率流谱 Fig. 8 Energy flow at different mass ratio (r = Mc /Ma) |
针对舰船分散中间质量隔振系统,考虑其分布参数特性,对其进行理论建模并进行数值模拟,同时设置等中间质量的浮筏隔振系统作为参照,详细阐述了该隔振系统的振动能量波动特性,得到如下结论:
1)分散中间质量隔振系统相较于目前常见的浮筏隔振系统,分散中间质量削减了传递路径中的柔性信息,避免了中间结构的波动效应,减弱了子系统间的高频动力耦合交互作用,有效抑制了系统高频噪声的产生;
2)分散中间质量的插入改变了原有隔振器中行波和反射波的叠加条件,降低了目标频段内驻波出现的几率,明显削弱了分布参数隔振器的驻波效应,对于抑制高频段能流传递起到了至关重要的作用;
3)增大中间质量,中间质量带来的刚体模态频率左移,且对驻波的削弱作用增强,故可以适当调节中间质量的大小来拓宽有效隔振区间并改善高频隔振效果;
4)本文所采用的研究思路及建模方法不受所选取研究对象的限制,可以拓展到更高维度,更加复杂的动力耦合系统建模研究。
| [1] |
宋孔杰, 张蔚波, 牛军川. 功率流理论在柔性振动控制技术中的应用与发展[J]. 机械工程学报, 2003, 39(9): 23-28. DOI:10.3321/j.issn:0577-6686.2003.09.004 |
| [2] |
尚国清, 李巍. 关于舰船浮筏系统的特征演化[J]. 舰船科学技术, 1999(1): 21-23. |
| [3] |
SNOWDON J. C.. Vibration isolation: use and characterization[J]. The Journal of the Acoustical Society of America, 1979, 66(5): 1245-1274. DOI:10.1121/1.383546 |
| [4] |
魏强, 朱英富, 张国良. 舰船基座上双层隔振系统能量流数值分析[J]. 舰船科学技术, 2004, 26(6): 5-9, 20. |
| [5] |
何琳, 徐伟. 舰船隔振装置技术及其进展[J]. 声学学报, 2013, 38(2): 128-136. |
| [6] |
周刘彬, 杨铁军, 张攀, 等. 基于弹性舱段结构的浮筏主动隔振系统实验研究[J]. 振动与冲击, 2013, 32(17): 161-165. DOI:10.3969/j.issn.1000-3835.2013.17.031 |
| [7] |
张树桢, 陈前. 浮筏隔振系统的非共振响应分析[J]. 振动工程学报, 2014, 27(3): 326-332. DOI:10.3969/j.issn.1004-4523.2014.03.003 |
| [8] |
王真, 赵志高, 刘芳. 全柔性浮筏隔振系统建模与隔振性能分析[J]. 振动.测试与诊断, 2017, 37(1): 70-75. |
| [9] |
李建彰. 高速型船舶振动响应计算分析[J]. 舰船科学技术, 2018, 40(1): 23-26. DOI:10.3404/j.issn.1672-7649.2018.01.004 |
| [10] |
UNGAR E E, DIETRICH C W. High-frequency vibration isolation[J]. Journal of Sound and Vibration, 1966, 4(2): 224-241. DOI:10.1016/0022-460X(66)90123-4 |
| [11] |
WINBERG M, HANSEN C, CLAESSON I, et al. Active control of engine vibrations in a Collins class submarine[M]. 2003.
|
| [12] |
杜冬, 禇德英, 孙中涛, 等. 多个小中间质量隔振最优设计及其性能研究[J]. 振动与冲击, 2008, 27(7): 36-41. DOI:10.3969/j.issn.1000-3835.2008.07.009 |
| [13] |
王孚懋, 宋孔杰. 小中间质量对复杂系统隔振效果的影响及最优设计[J]. 振动工程学报, 1991(3): 10-17. |
| [14] |
SUN L, LEUNG A Y T, LEE Y Y, et al. Vibrational power-flow analysis of a MIMO system using the transmission matrix approach[J]. Mechanical systems and signal processing, 2007, 21(1): 365-388. DOI:10.1016/j.ymssp.2005.07.001 |
| [15] |
Advanced applications in acoustics, noise and vibration[M]. CRC Press, 2004.
|
 2020, Vol. 42
2020, Vol. 42
