航行体水下航行时,排气系统产生的高温废气直接在水下排放,会在附近海面区域形成与周围环境差异明显的热特征。红外热成像系统可以通过海水表面的这种热特征确定水下航行体的位置[1-2]。显然,水下排气是航行体水下航行时的主要热源之一,是产生红外辐射的重要因素,直接影响航行体水下航行时的隐蔽性。航行体水下连续排气,产生的气泡在浮力作用下诱导周围海水上浮,形成典型的气泡羽流。气泡羽流涉及气泡动力学、气-液两相流、传热及传质学等理论,现象和机理非常复杂。现有研究对于气泡动力特征方面研究比较成熟[3-4],但是对于单个气泡与液体存在温度差的热特征研究不足。在气泡羽流方面,基本上不考虑液体的来流速度[5-6],且对于气泡与液体之间存在温度差异的研究鲜见。对于航行体水下排气方面的研究,绝大多数也没有考虑排气在水中的温度变化[7-8]。本文基于流动与传热仿真计算软件Fluent平台,围绕航行体高温废气水下排放的热特性及其影响因素开展研究,研究结果对提高航行体水下隐蔽性具有参考价值。
1 数学模型航行体水下排气是典型的两相流动问题。建立数学模型时,将海水视为连续相,废气排放形成的气泡视为离散相。海水控制方程包括连续性方程、动量方程、能量方程和组分方程,在Euler坐标系内的通用表达式为[9]:
| $\frac{{\partial \left( {\rho {u_i}\phi } \right)}}{{\partial {x_j}}} = \frac{\partial }{{\partial {x_j}}}\left( {{\varGamma _\phi }\frac{{\partial \phi }}{{\partial {x_j}}}} \right) + {S_\phi } + {S_{p\phi }}{\text{。}}$ | (1) |
方程左边为对流项,右边第一项为扩散项,最后两项为源项。式中:φ为通用变量;Γφ为输运系数;Sφ为海水本身的源项;Spφ为海水与气泡相互作用产生的源项;i,j分别代表x,y,z坐标空间,取值为1,2,3,其中各项的具体表达式可参见文献[9]。
海水中废气排放形成的气泡作为离散相,在Lagrange坐标系下描述,选用颗粒轨道模型封闭方程组[9]。颗粒轨道模型计算过程相对复杂,但随着CFD技术的迅速发展,该模型已经用于商业软件中(如Fluent),使该模型在工程模拟中应用更加广泛。把气泡视为球形颗粒,则Magnus力为0,忽略气泡与海水之间的辐射换热,则气泡离散相的控制方程如下:
| $ \left\{ \begin{aligned} & {N_k} = \mathop \smallint \nolimits {n_k}{v_{kn}}{\rm d}A = {\rm{const}}{\text{,}}\\ & \frac{{{\rm d}{v_{ki}}}}{{{\rm d}t}} = \frac{{\left( {{v_i} - {v_{ki}}} \right)}}{{{\tau _{rk}}}} + {g_i} + \left( {{v_i} - {v_{ki}}} \right)\frac{{{{\dot m}_k}}}{{{m_k}}}{\text{,}}\\ & \frac{{{\rm d}{T_k}}}{{{\rm d}t}} = \frac{{\left[ {{{\dot m}_k}\left( {{c_p}T - {c_k}{T_k}} \right) - {Q_k}} \right]}}{{\left( {{m_k}{c_k}} \right)}}{\text{。}} \end{aligned} \right. $ | (2) |
式中:Nk为气泡数总通量;nk为气泡数密度;mk为单个气泡的质量,kg;vkn和vki为气泡速度分量,m/s;vi为海水速度分量,m/s;A为面积,m2;τrk为扩散弛豫时间,s(值越小,表示气泡追随海水越容易);gi为重力分量,m/s2;Tk和T分别为气泡和海水的温度,K;cp和ck为比热,J/(kg·K);Qk为气泡与海水间的对流换热,J。
2 数值模拟 2.1 计算模型本文以试验数据齐全的Suboff航行体模型[11]为基础建立计算模型。航行体指挥台围壳采用了流线型结构,航行阻力较小。研究表明,航行体水下航行时其外表面对指挥台围壳后部的流场影响可以忽略[12]。建立计算模型时,可以仅考虑指挥台围壳及计算流体区域,而不必考虑航行器本体的影响。这样既可以大大降低计算规模,又可以保证计算精度在允许的范围之内。用Solidworks软件按照1∶1比例建立的航行体指挥台围壳三维模型如图1所示。

|
图 1 航行体指挥台围壳三维模型 Fig. 1 3D model of superstructure hull |
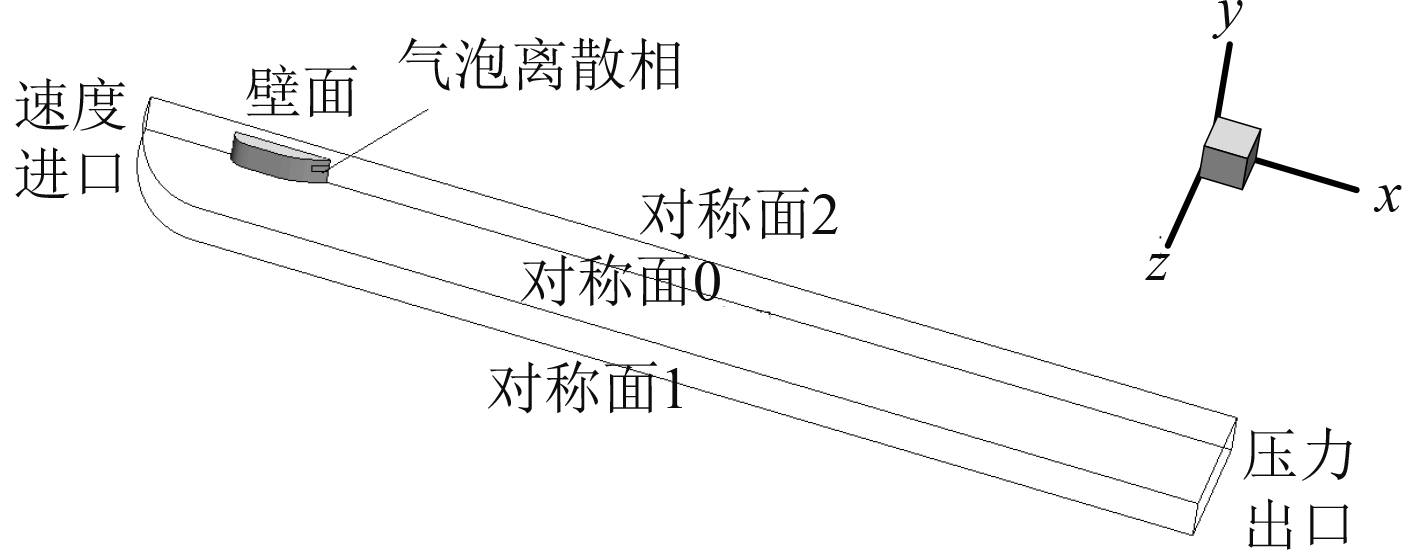
为了降低模拟计算工作量,建模过程中忽略海水横向流动速度,利用航行体水下排气过程中物理模型和流场的对称性,只取计算模型和计算区域的一半作为模拟对象。经过多次试算,确定数值模拟计算区域如图2所示。计算区域由半圆柱体和长方体构成,该区域长108 m,宽8 m。航行体指挥台围壳前缘距离计算区域圆柱形入口8 m,指挥台围壳后缘距离计算区域出口10倍围壳长,长方体宽度为1/2指挥台围壳宽度的8倍。航行体沿x轴负方向运动,y轴负方向为重力方向,z轴为横向轴,坐标原点位于指挥台围壳底部前缘。
|
图 2 计算区域 Fig. 2 Calculation region |
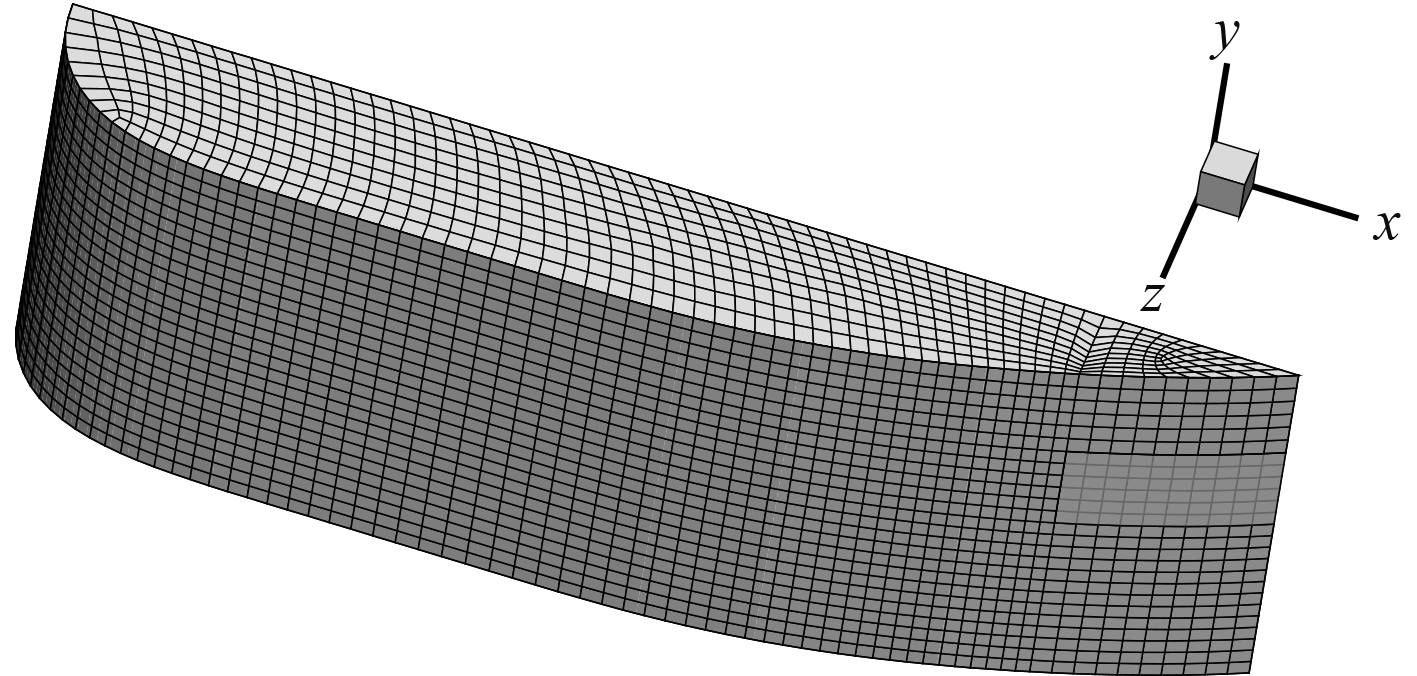
模型设置过程中,根据航行体航速、湍流强度和水力直径确定速度入口边界条件。通过湍流强度和水力直径确定压力出口边界条件,并将计算区域的右侧面和底面设置为对称边界条件。假定海水自由液面不随时间变化,将海水自由液面的边界条件设为对称边界条件。图3为计算模型网格划分情况,将排气口设置为面射流源,并设置为离散型初始条件。假定形成的气泡尺寸分布满足Rosin-Ranmmler分布,最小气泡直径1.5 mm,最大气泡直径4 mm,气泡平均直径2.8 mm,分布指数n为2.60。数值模拟时,根据航行体排气工况设置气泡初始温度、初始速度,给定气泡总质量流量,气泡初始运动方向沿排气口所在平面的法向。
|
图 3 围壳表面网格及离散相边界条件 Fig. 3 Shell surface mesh and boundary conditions |
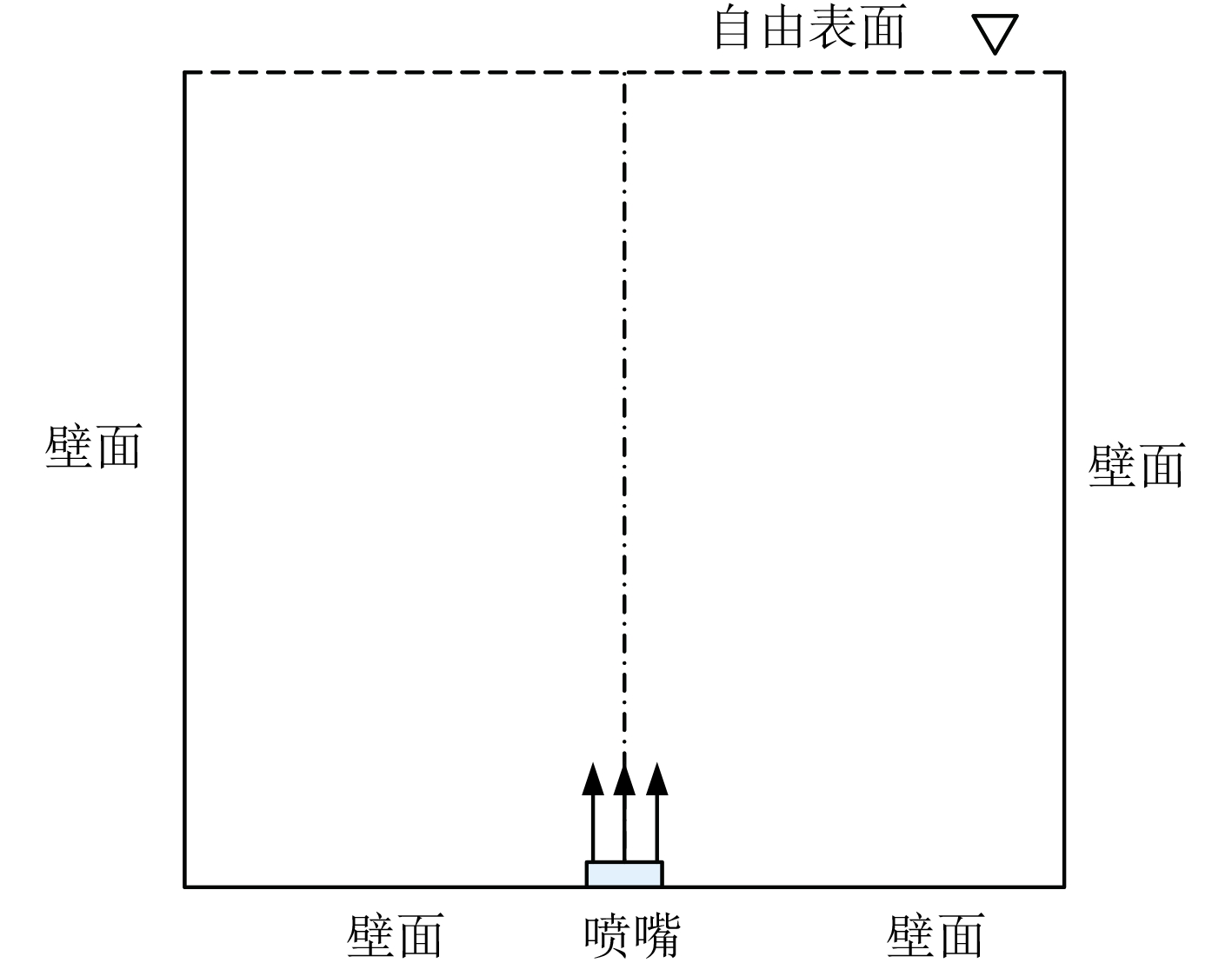
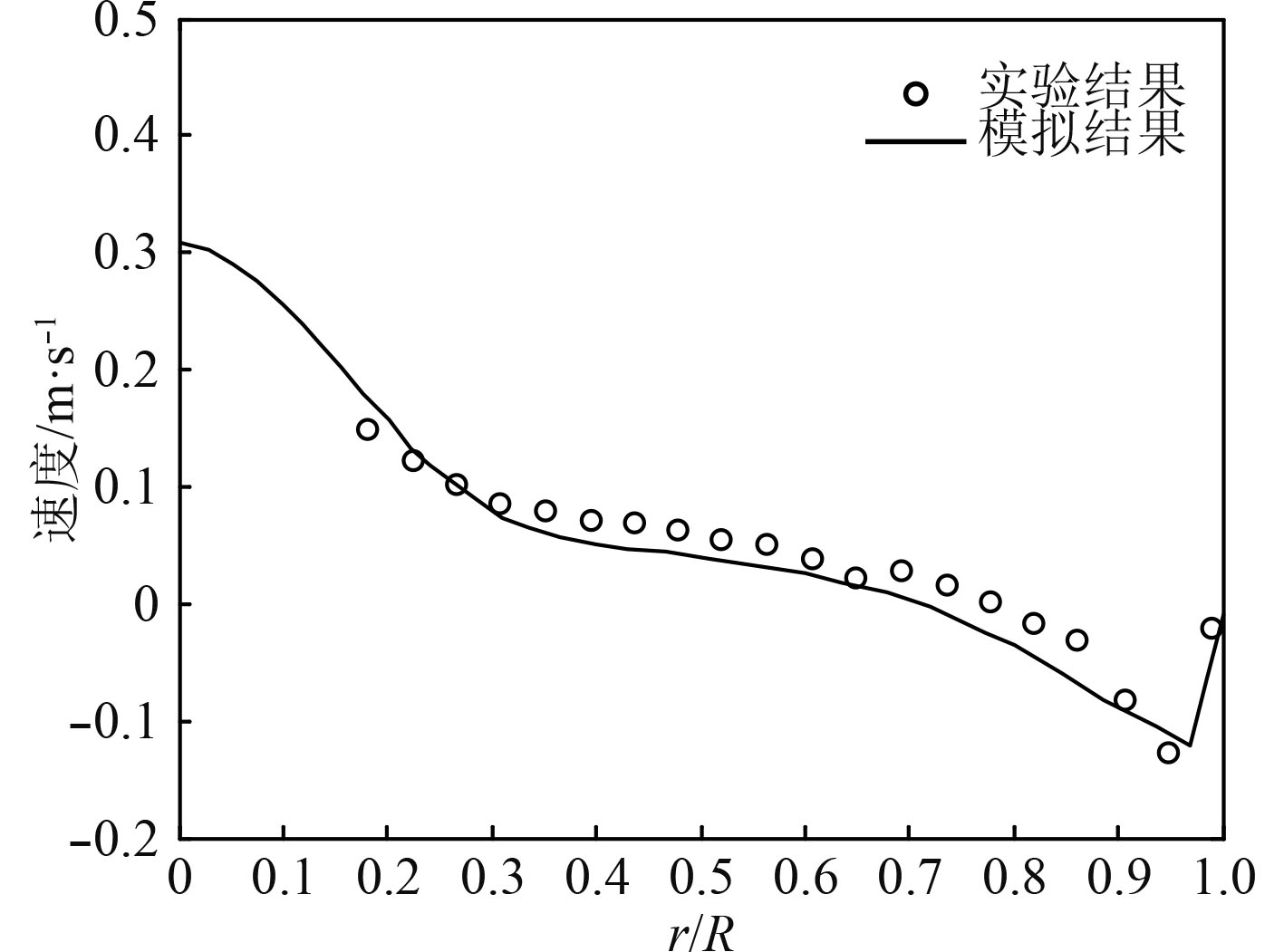
为了对建立的数理模型与采用的计算方法进行验证,对文献[13]描述的问题进行数值模拟,计算区域及边界条件如图4所示。其中,容器尺寸为500×500 mm2,进气喷嘴大小为24 mm。初始条件为:液体静止,气流进入速度为3 m/s,含气率0.02。整个计算区域划分为250×125个长方形结构网格。通过数值模拟计算,距离容器底部300 mm处的液相速度模拟结果与文献[13]实验结果的比较如图5所示。可见,本文建立的数理模型与采用的计算方法能够满足水下气体排放的数值模拟要求。
|
图 4 计算区域及边界示意图 Fig. 4 Calculation region and boundaries |
|
图 5 液相速度模拟结果与实验结果的比较 Fig. 5 Simulated and experimental values of liquid phase velocity |
航行体水下航行时,根据工作任务及工作要求的不同,动力系统排气温度、排气流量、航行体航速、所处海域海水温度等均可能发生变化,从而导致在海面形成不同的热特征。本文建立了航行体水下排气模型,采用控制变量法研究航行体水下排气时,排气温度、排气流量、海水温度和航行体航速等因素对排气浮升规律与海面热特征的影响。
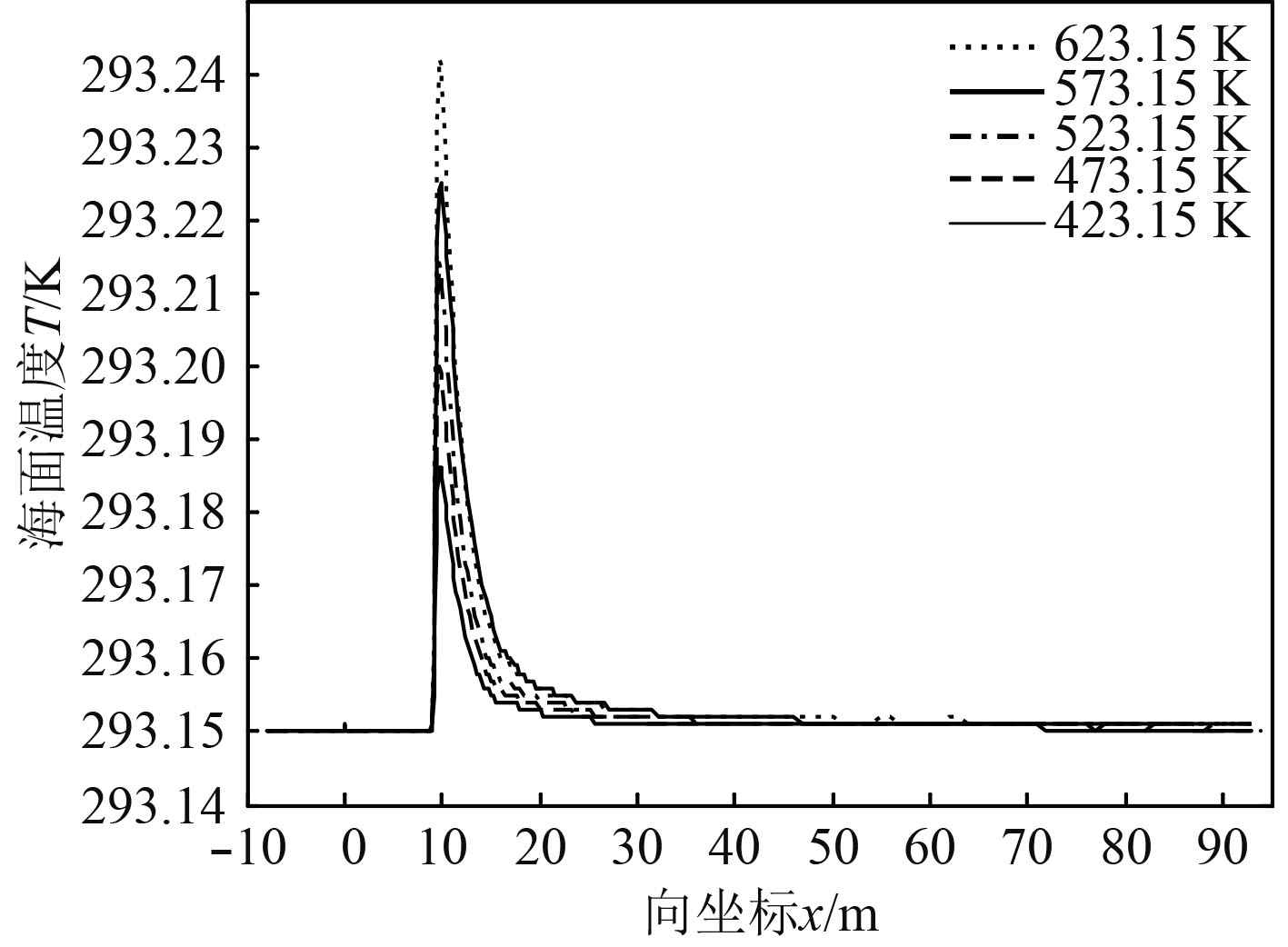
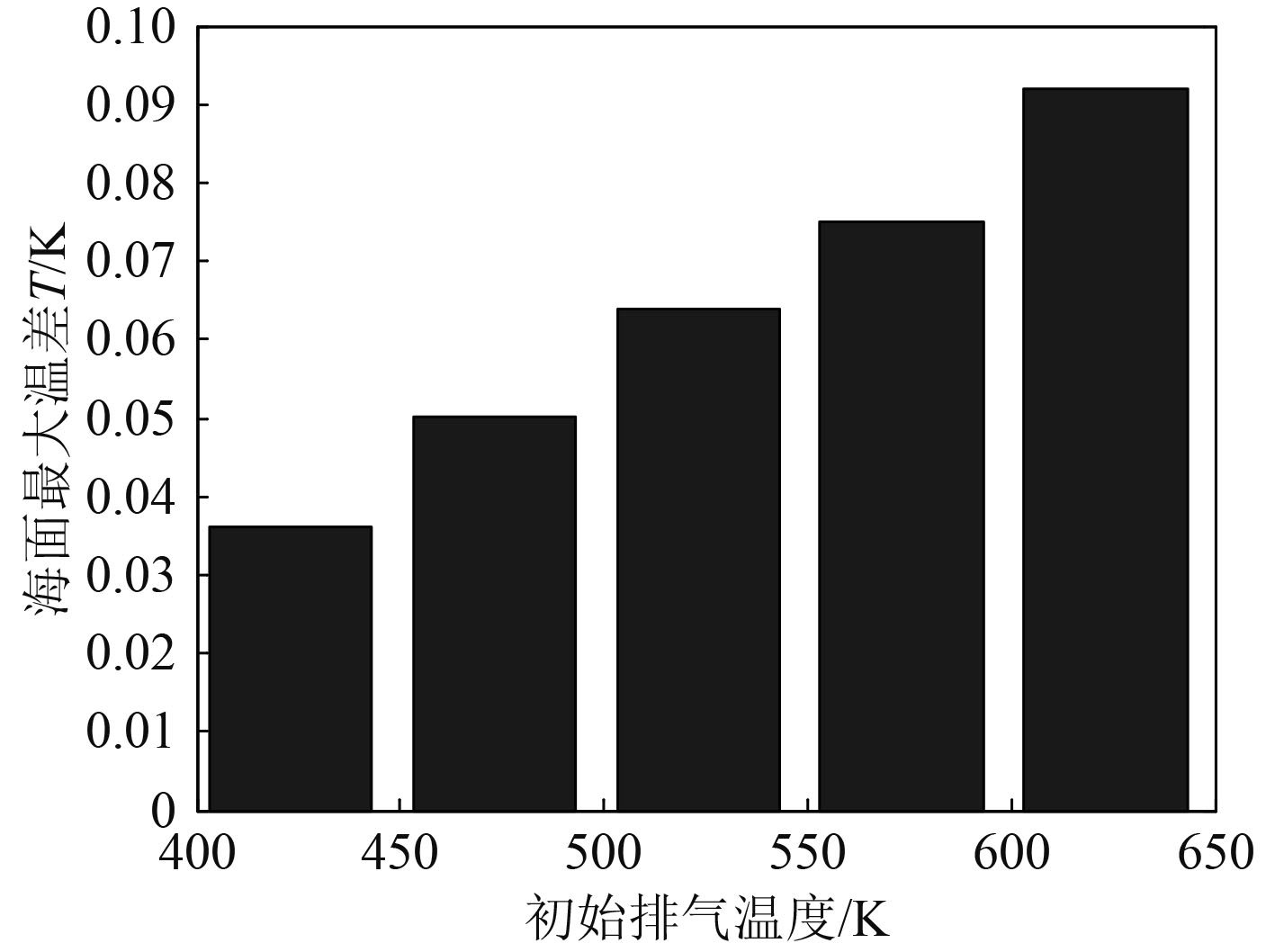
3.1 排气温度的影响控制航行体航速5 kn、发动机3台、环境海水温度293.15 K保持不变,对排气温度分别为423.15 K,473.15 K,523.15 K,573.15 K,623.15 K时在海面形成的热特征进行数值模拟与结果分析。如图6所示,排气温度不同时,在海面形成的温度峰值分别为293.186 K,293.200 K,293.214 K,293.225 K,293.242 K。且由于排气量和排气初始速度相同,排气沿x轴运动9.88 m后浮升至海面形成最高温度。此外,不同初始排气温度条件下,海面温度沿x轴向衰减速度均很快。如图7所示,航行体初始排气温度不同时,与周围环境海水形成的最大温差分别为0.036 K,0.050 K,0.064 K,0.075 K,0.092 K。研究表明,降低航行体初始排气温度有利于水下航行的隐蔽性。
|
图 6 不同排气温度时海面温度分布 Fig. 6 Effect of exhaust temperature on sea surface temperature |
|
图 7 不同排气温度下的海面最大温差 Fig. 7 Sea surface MAX temperature difference vs. exhaust temperature |
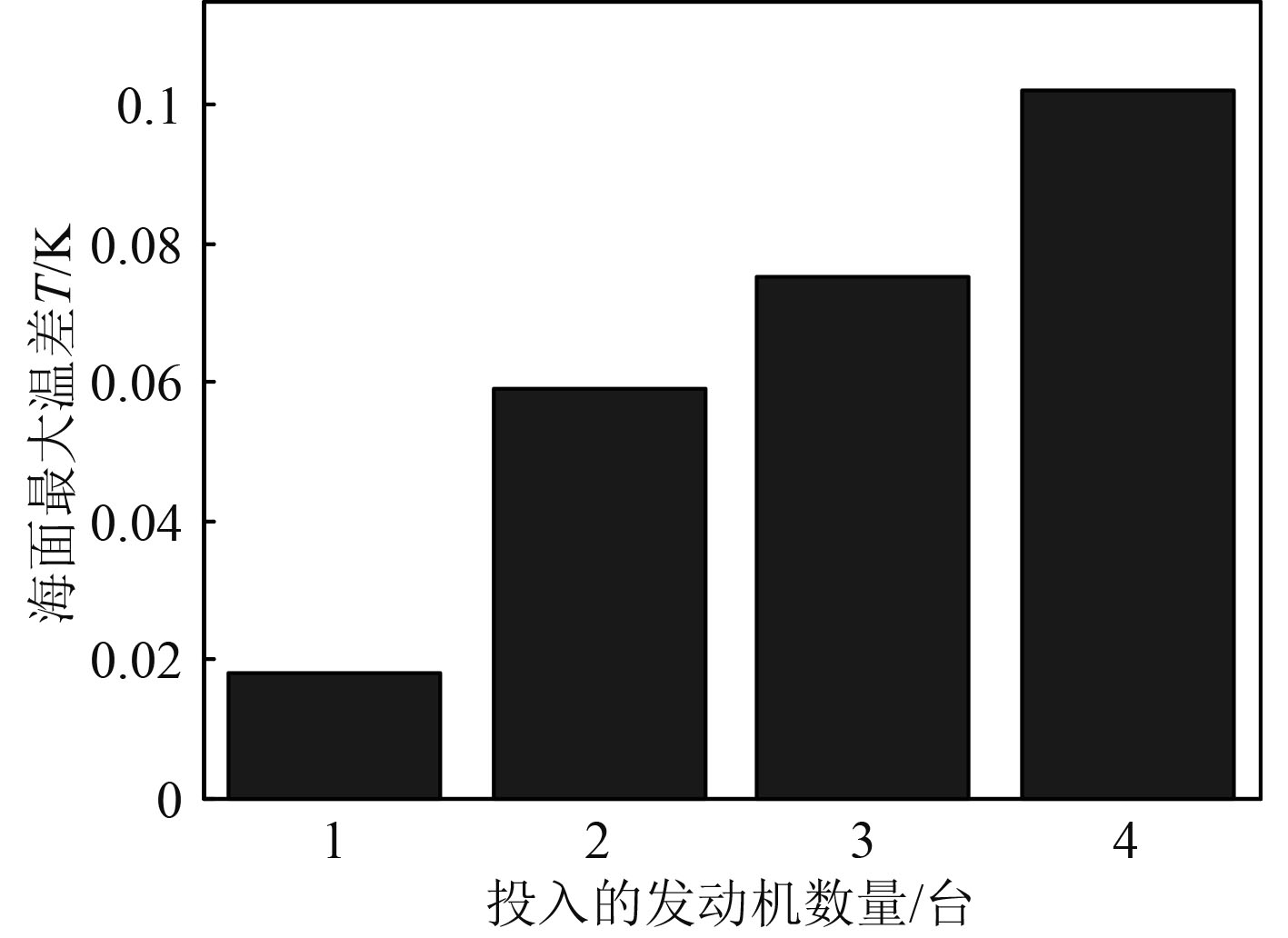
控制航行体航速5 kn、环境海水温度293.15 K、排气温度573.15 K保持不变,对航行体投入不同数量发动机时在海面形成的热特征进行数值模拟与结果分析。如图8所示,分别投入1台、2台、3台、4台发动机时,在海面形成的最高温度值分别为293.168 K,293.209 K,293.225 K,293.252 K。且不同的初始排气量会导致排气的初始速度不同,废气浮升至海面的轴向运动距离也不一样,沿x轴向分别运动3.27 m、1.04 m,1.04 m,0.7 m后浮升至海面,形成明显的热特征。此外,不同初始排气量条件下,海面温度沿x轴向衰减速度均很快。如图9所示,航行体不同的初始排气量,与周围环境海水形成的最大温差分别为0.018 K,0.059 K,0.075 K,0.102 K。从数值模拟结果分析看,当航行体排气流量较大时,周围海水吸收热量较多,当地海水温度升幅较大,在海面形成的温度场分布较广,且梯度较大,不利于航行体的隐蔽性。可见,为了提高航行体水下航行的隐蔽性,应尽量降低航行体排气流量。

|
图 8 不同排气量时海面温度分布 Fig. 8 Effect of exhaust displacement on sea surface temperature |
|
图 9 不同排气量下的海面最大温差 Fig. 9 Sea surface MAX temperature difference vs. exhaust displacement |
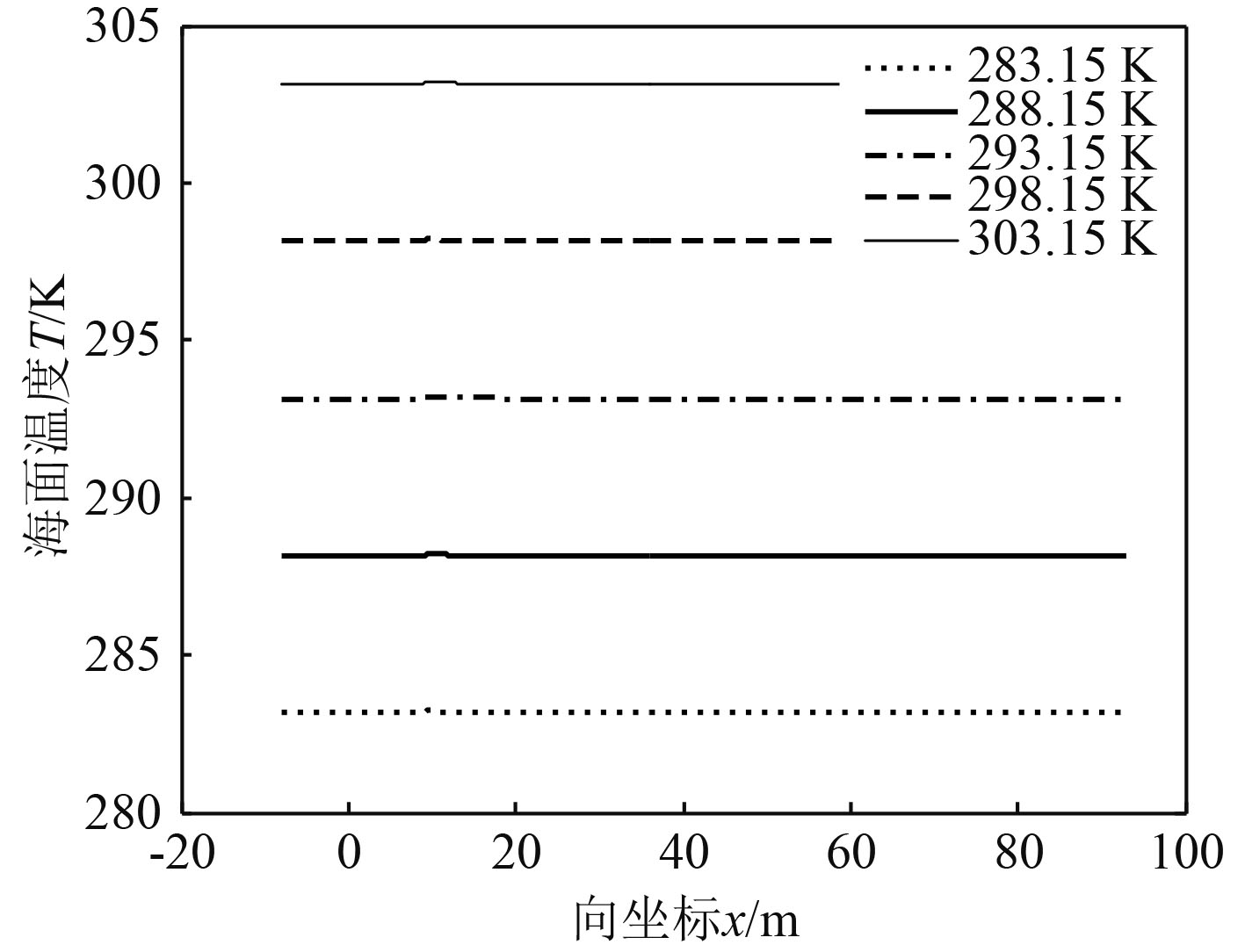
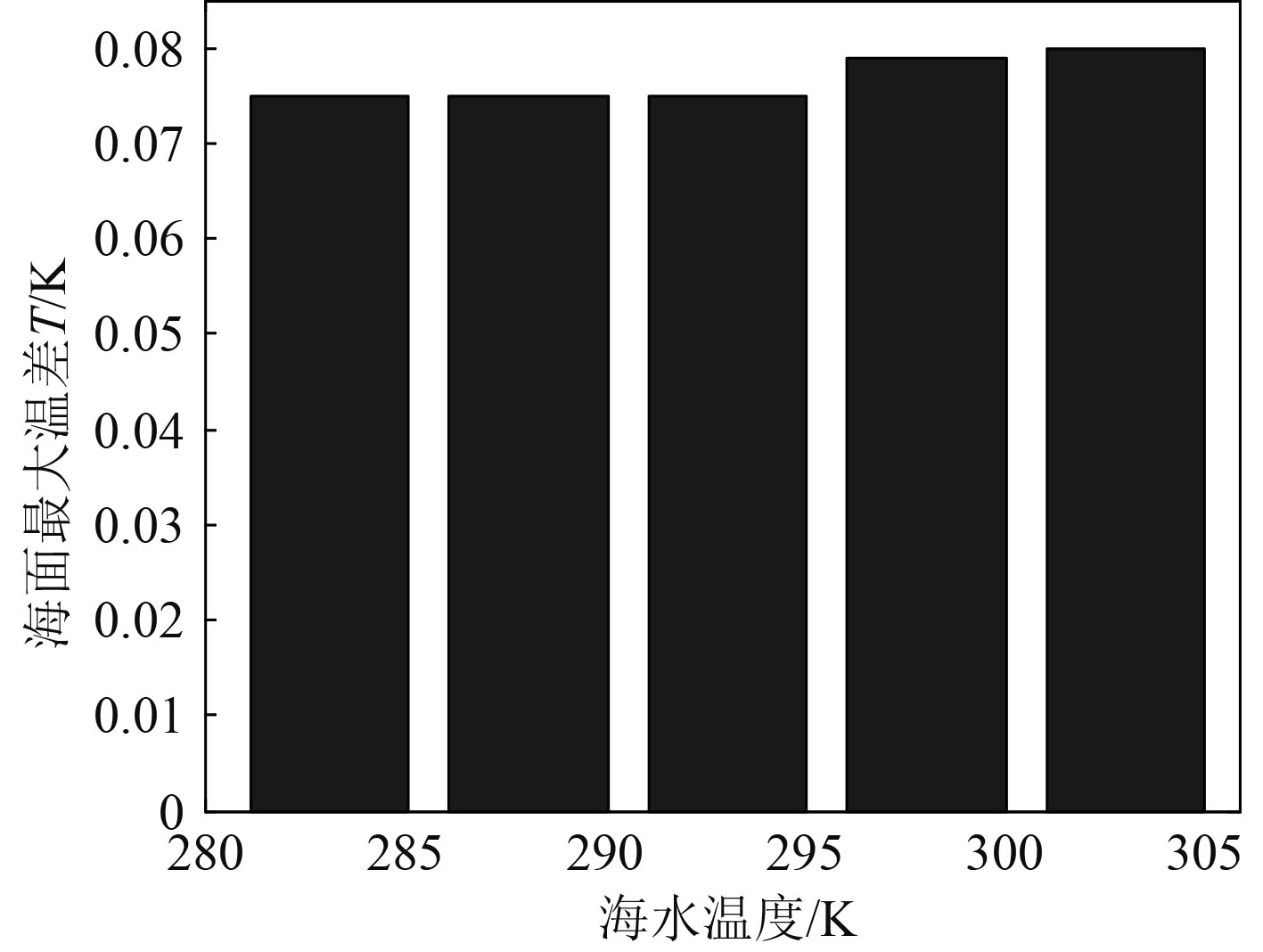
控制航行体航速5 kn、发动机3台、排气温度573.15 K保持不变,对环境海水温度分别为283.15 K,288.15 K,293.15 K,298.15 K,303.15 K时在海面形成的热特征进行数值模拟与结果分析。如图10所示,不同海水温度条件下,在海面形成的最高温度值分别为303.225 K,298.225 K,293.225 K,288.229 K,283.230 K,温度峰值在海面出现的位置均为x=9.88 m处,且不同初始排气温度条件下,海面温度沿x轴向衰减速度均很快。如图11所示,不同的海水温度条件,与周围环境海水形成的最大温差分别为0.075 K,0.075 K,0.075 K,0.079 K,0.080 K。研究表明,当航行体向不同温度海水排气时,环境海水温度越高,排气口上方附近海水温度也越高,但在海面形成的温度分布相似,与周围环境海水的温差差异不大。显然,其他条件相同时,海域或季节的不同对航行体水下排气在海面形成的热特征影响不大。
|
图 10 不同海水温度下海面的温度分布 Fig. 10 Effect of sea temperature on sea surface temperature |
|
图 11 不同海水温度下海面最大温差 Fig. 11 Sea surface MAX temperature difference vs. sea temperature |
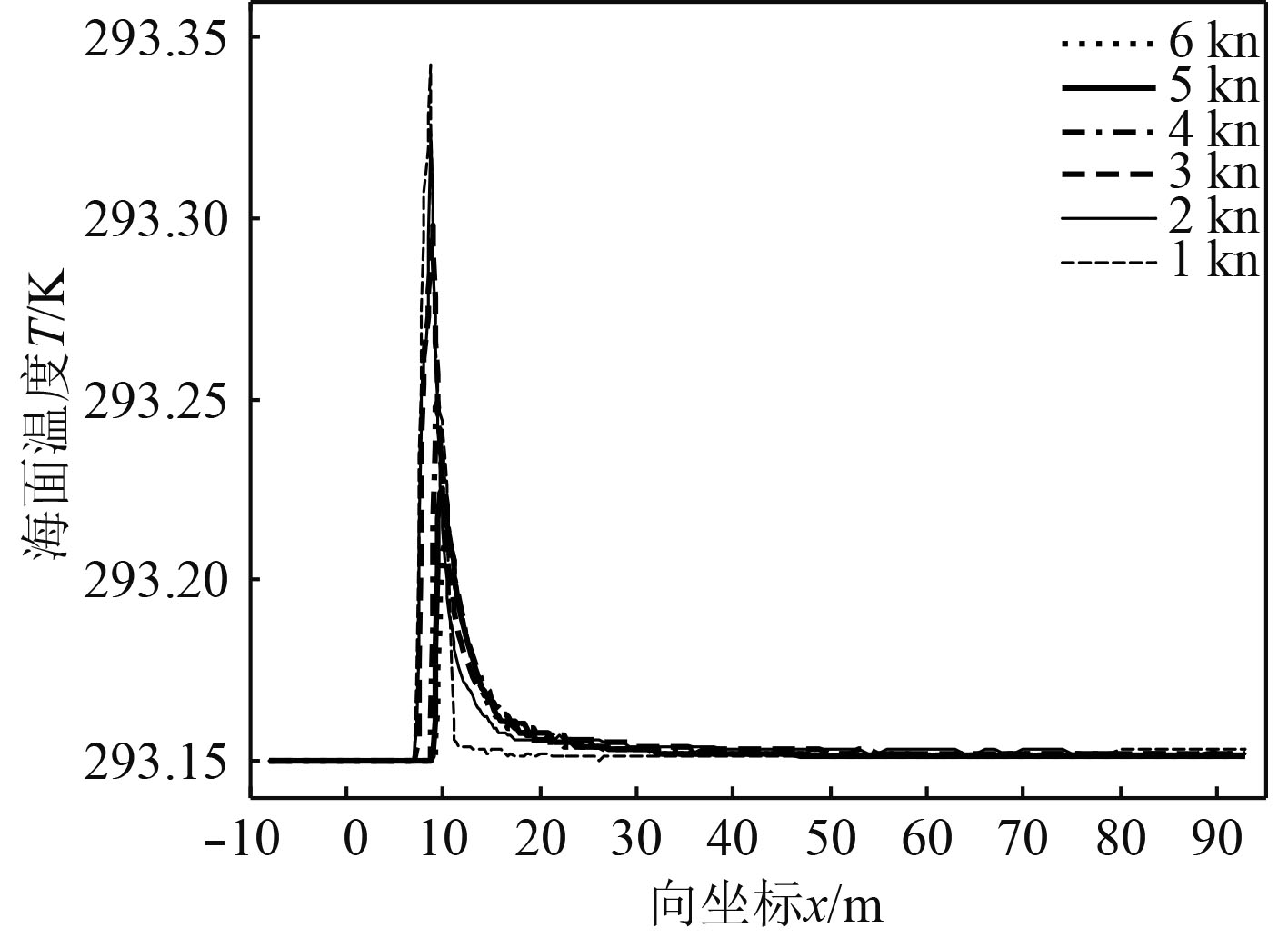
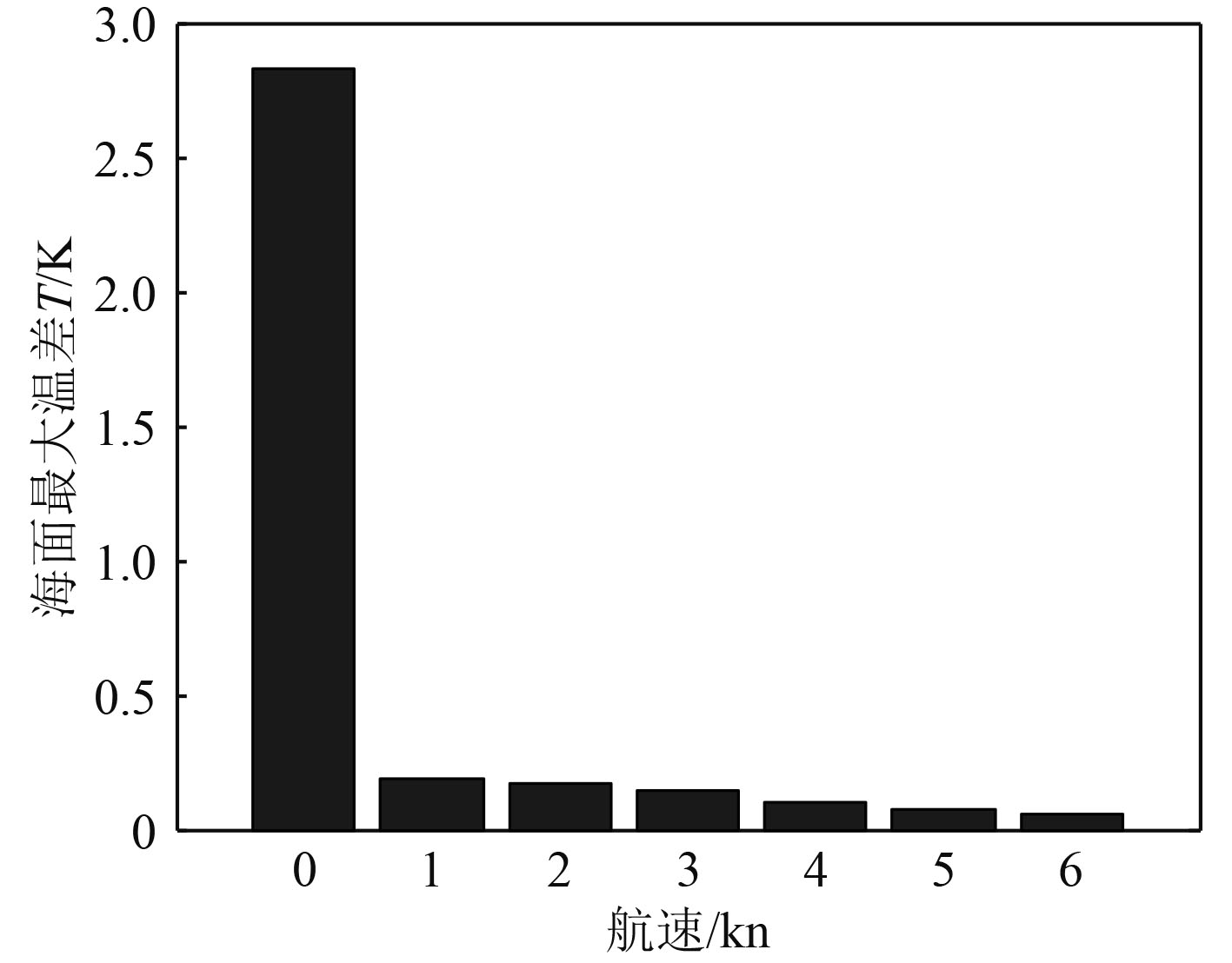
控制航行体发动机3台、环境海水温度293.15 K、排气温度573.15 K保持不变,对航行体分别为0 kn,1 kn,2 kn,3 kn,4 kn,5 kn,6 kn时在海面形成的热特征进行数值模拟与结果分析。如图12和图13所示,不同航速条件下,在海面形成的最高温度不同,且温度沿x轴向衰减速度都很快,在海面形成的温度峰值分别为295.975 K,293.342 K,293.323 K,293.298 K,293.249 K,293.225 K,293.210 K,温度峰值在海面出现的位置分别为x=8.70 m,x=8.70 m,x=8.84 m,x=8.96 m,x=9.42 m,x=9.88 m,x=10.17 m处,与周围环境海水形成的最大温差分别为2.825 K,0.192 K,0.173 K,0.148 K,0.099 K,0.075 K,0.060 K。从数值模拟结果分析看,航行体水下悬停排气时,水下排放的高温废气与周围静止海水换热效果差,附近海水温度快速上升,在海面形成的温度场分布区域小,梯度大,对于航行体水下航行隐蔽性非常不利。显然,为了提高航行体水下航行的隐蔽性,应尽量提高航行体水下航速。
|
图 12 不同航速下的温度分布 Fig. 12 Effect of submersible speed on sea surface temperature |
|
图 13 不同航速下的海面最大温差 Fig. 13 Sea surface MAX temperature difference vs. submersible speed |
本文针对航行体水下排气两相流问题,用Euler-Lagrange方法建立数理计算模型,采用计算流体力学与计算传热学方法,进行数值模拟分析,研究了航行体水下排气时,排气温度、航行速度、排气流量和海水温度等因素对海面热特征的影响。研究结果表明,排气初始温度、航行体水下航速、航行体排气流量对航行体水面热特征影响较大。为了提高航行体水下隐蔽性能,应降低排气初始温度,提高航行体水下航速,减少航行体排气流量,而环境海水温度的变化对航行体水下排气热特征的影响不太明显。
| [1] |
鲁新平, 沈振康. 红外热成像系统应用于反潜探测的分析[J]. 红外与激光工程, 2002, 31(3): 217-219, 236. DOI:10.3969/j.issn.1007-2276.2002.03.007 |
| [2] |
张建奇, 方小平. 红外物理 [M]. 西安: 西安电子科技大学出版社, 2004.
|
| [3] |
张建生, 孙传东, 卢迪. 水中气泡的特性研究[J]. 西安工业学院学报, 2000, 20(1): 1-8. DOI:10.3969/j.issn.1673-9965.2000.01.001 |
| [4] |
李帅, 孙龙泉, 张阿漫. 水中上浮气泡动态特性研究[J]. 物理学报, 2014, 63(18): 287-299. |
| [5] |
吴凤林, G Tsang. 关于气泡羽流的研究[J]. 水动力学研究与进展, 1989, 4(1): 104-112. |
| [6] |
马霞, 李国栋, 高扬, 等. 不同曝气量和纵横比下针孔喷射气泡羽流摆动特性的数值模拟研究[J]. 水动力学研究与进展A辑, 2016, 31(4): 433-440. |
| [7] |
王治云, 李永胜, 杨茉. 水下排气两相流动及气泡粒径分布的数值模拟[J]. 能源工程, 2017(6): 49-52. |
| [8] |
鲍文春, 权晓波, 魏海鹏. 航行体排气水下发射流体动力数值仿真研究[J]. 导弹与航天运载技术, 2014(5): 14-18. |
| [9] |
周力行. 多相湍流反应流体力学 [M]. 北京: 国防工业出版社, 2002.
|
| [10] |
Fluent Inc. Fluent 6.3 user’s guide [Z]. Lebanon, USA: Fluent Inc, 2006.
|
| [11] |
GROVES N C, HUANG T T, CHANG M S. Geometric Characteristics of DARPA SUBOFF Models[R]. Bethesda, MD: David Taylor Research Center, 1989.
|
| [12] |
卢云涛. 全附体潜艇的流场和流噪声的数值研究 [D]. 上海: 上海交通大学, 2008. http://cdmd.cnki.com.cn/article/cdmd-10248-2008052695.htm
|
| [13] |
DOMGIN J F, GARDIN P. Experimental and numeriacl investigation of gas stirred ladles [C]//M Brunet. Second International Conference on CFD in the Minerals and Process Industries. Melbourne, Austrilia: CSIRO, 1999.
|
 2020, Vol. 42
2020, Vol. 42
