在船舶舱室中,结构振动引起的噪声有着低频、宽带的特点。常规的低频噪声隔声控制受到质量定律[1]的约束,总是需要更为质密宽厚的材料。而可以在某些低频频段下实现完全隔声的轻质声学超材料为船舶舱室减振降噪设计提供了新的思路。
声学超材料是一种单胞在几何尺寸上远小于声波波长的材料,其概念最早被刘正猷等[2]提出,而后的研究都集中在了板片等厚度远小于长宽尺寸的结构。2006年,Wang等[3]将端部镶有质量块的金属薄片周期性地插到弹性直杆上,发现了低频带隙。2010年,梅军等[4]提出一种薄膜型声学超材料,采用中心放置微小质量块并四边固支的薄膜,可以在低频有效的抑制声波的传播。Christina J Naify等[5]也提出了一种基于局域共振机理的膜类声学超材料,并提出可以通过改变质量块重量来改变隔声量峰值。Zhang Y[6]讨论了薄膜张力、薄膜厚度、薄膜密度及质量块重量对薄膜阻尼区隔声量特性的影响。张炜权等[7]在此基础上从影响机理、数值计算等方面研究讨论了全频段薄膜隔声特性。
大量的理论和实验研究都说明薄膜声学超材料具有非常丰富的声学特性,其 “负等效质量密度”特性有着潜在而广泛的应用前景。以往研究多讨论了等厚度的薄膜,对表面形状也呈周期性变化的变厚度薄膜研究甚少。本文在梅军等研究的基础上,利用商用有限元软件Ansys和Virtual. Lab Acoustic数值计算变厚度薄膜型声学超材料单胞(membrane acoustic metamaterial cell with variable thickness,MAMVT)的工作频率,并模拟单胞的驻波管实验。研究了变厚度薄膜型声学超材料单胞隔声性能随结构参数(包括质量块质量、薄膜厚度以及薄膜张力)的变化规律,为薄膜型声学超材料在船舶降噪方面的设计与应用提供参考依据。
1 MAMVT工作频率及隔声量计算方法 1.1 MAMVT工作频率所谓薄膜单胞的工作频率是指薄膜在光学振动模式下的固有频率,而光学振动模式在这里是指薄膜和加在薄膜中间的质量块反向振动,在这样的振型下可以对频率成分比较复杂的声波进行选择性吸收;对应的,薄膜与质量块同向振动称为声学振动模式,此时声波几乎全部透过[8]。图1展示了光学振动模式的振型图,正是由于这样的特性,对于多胞元的薄膜声学超材料,可以用单胞的工作频率来大致描述带隙的分布频段,对声学超材料的带隙研究提供参考。
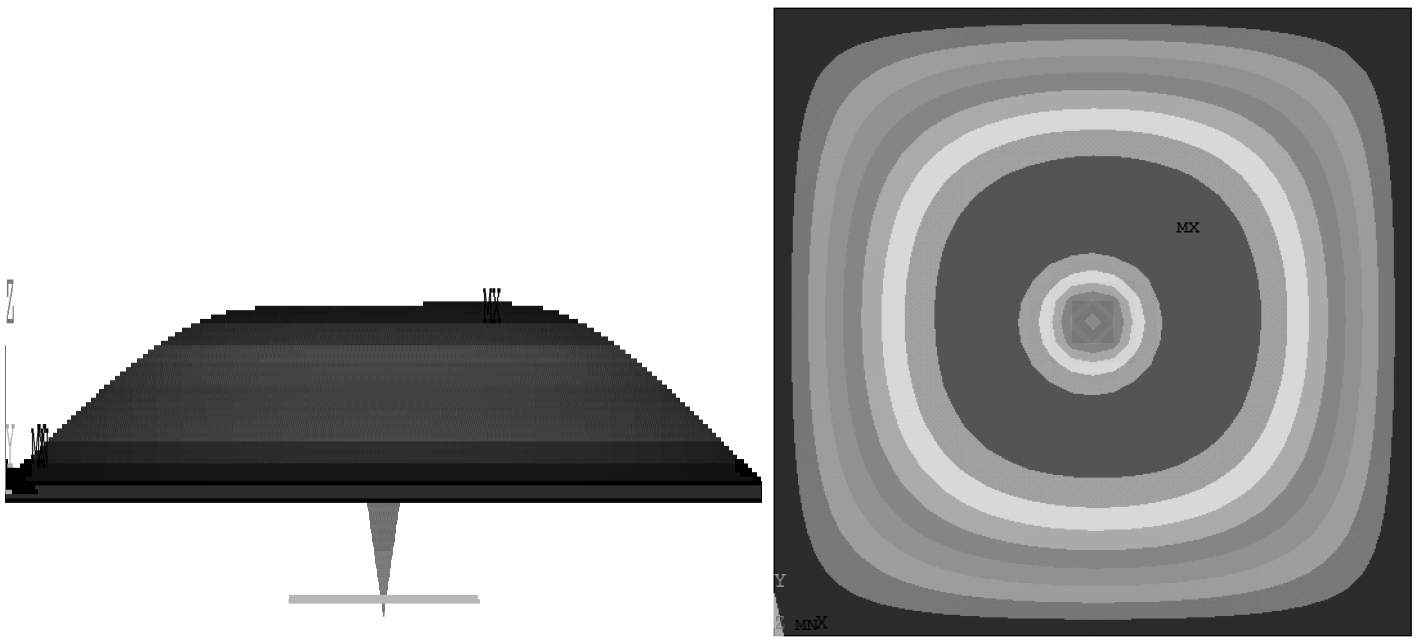
|
图 1 薄膜光学振动模式振型图 Fig. 1 Membrane vibration diagram of optical mode |
本文通过在Ansys和Virtual. Lab Acoustic中建立MAMVT驻波管测量模型来数值计算单胞在0~1 500 Hz频率内的隔声性能随结构参数(包括质量块质量、薄膜厚度以及薄膜张力)的变化规律。
1.2.1 驻波管隔声量测量原理在驻波管中测量试件隔声量常采用四传感器法。四传感器法较于三传感器法,是考虑了在驻波管接收腔末端的吸声尖劈在低于截止频率时吸声系数急剧下降,不能保证透射部分行波场的条件,在透射部分也采用了双传感器。这样可以把正向透射波与末端的反射波分开,使得吸声尖劈的吸声性能对隔声量测试的影响减为最小,其原理如图2所示。
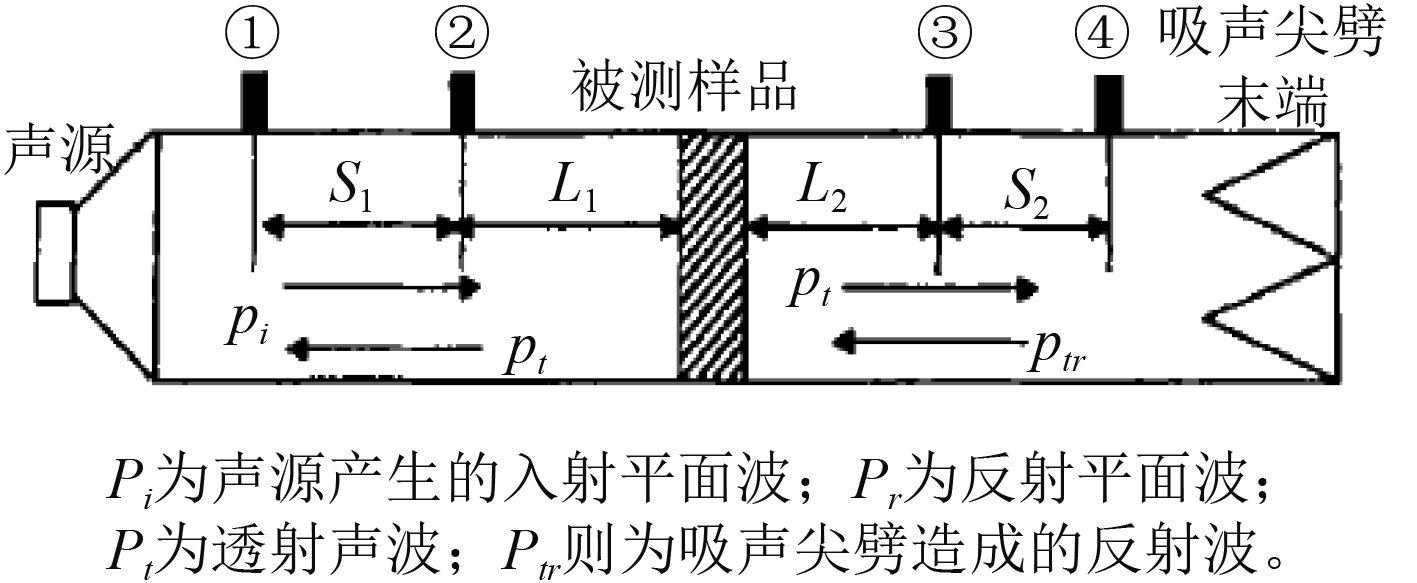
|
图 2 四传感器法原理示意图 Fig. 2 Schematic diagram of four-microphone method |
四传感器法的隔声量的计算公式为:
| $TL = - 20log\left| {\frac{{\sin\left( {k{S_1}} \right)}}{{\sin\left( {k{S_2}} \right)}} \circ \frac{{{p_3}{e^{jk{S_2}}} - {p_4}}}{{{p_1} - {p_2}{e^{ - jk{S_1}}}}}{e^{jk\left( {{L_1} + {L_2}} \right)}}} \right|{\text{。}}$ | (1) |
其中:S1为传感器①和传感器②的距离;S2为传感器③和传感器④的距离;L1为传感器②与被测样品正表面的距离;L2为传感器③与被测样品背面的距离;P1,P2,P3,P4分别为传感器①②③④测得的复声压。并且,L1和L2一般应大于管的直径。传感器间距S1和S2测试时尽量保证两者相等。
由于在仿真建模中可以直接设置完全的吸收边界,无需考虑透射腔中的反射波,所以这里采用三传感器法计算,即选取入射端2个测量点和透射端1个测量点来计算隔声量,其原理如图3所示。

|
图 3 三传感器原理示意图 Fig. 3 Schematic diagram of three-microphone method |
被测样品置于驻波管的中央,其厚度为d。样品的前方为声波的入射部分,后方为透射部分。由于样品表面的反射,入射部分形成驻波场,必须采用驻波分离方法,即用2个传感器把入射波与反射波分开,并且在透射部分,理论上要求只存在透射波。这样,计算隔声量的公式简化为:
| $ TL = - 20\log\left| {\frac{{2\sin\left( {k{S_1}} \right) \circ {p_3}}}{{{p_2}{e^{ - jk{S_1}}} - {p_1}}}{e^{jk\left( {{L_1} + {L_2}} \right)}}} \right|{\text{。}} $ | (2) |
式中:S1为传感器①和传感器②的距离;L1为传感器②与被测样品正表面的距离;L2为传感器③与被测样品背面的距离;P1,P2,P3分别为传感器① ② ③测得的复声压。
1.2.2 驻波管隔声量有限元模型在Ansys中建立长为1 200 mm的驻波通道,截面为边长60 mm的正方形(与薄膜同等大小),将其作为要导入到Virtual.Lab Acoustic中的声学网格;将Ansys中的薄膜网格及薄膜结构模态作为要导入到Virtual.Lab Acoustic中的结构网格和结构模态。在通道两边设置吸收边界,并选择平面声源进行计算,声源实部为1 Pa,虚部为0 Pa,频率为5~1 500 Hz。为了保证计算精度,需要在一个波长内划分至少6个单元,即单元尺寸为5 mm。流体参数使用空气参数。选择的测量点A,B,C,D的坐标分别为A(−300,30, 30),B(−150, 30, 30),C(300, 30, 30)。建立的有限元模型如图4所示。
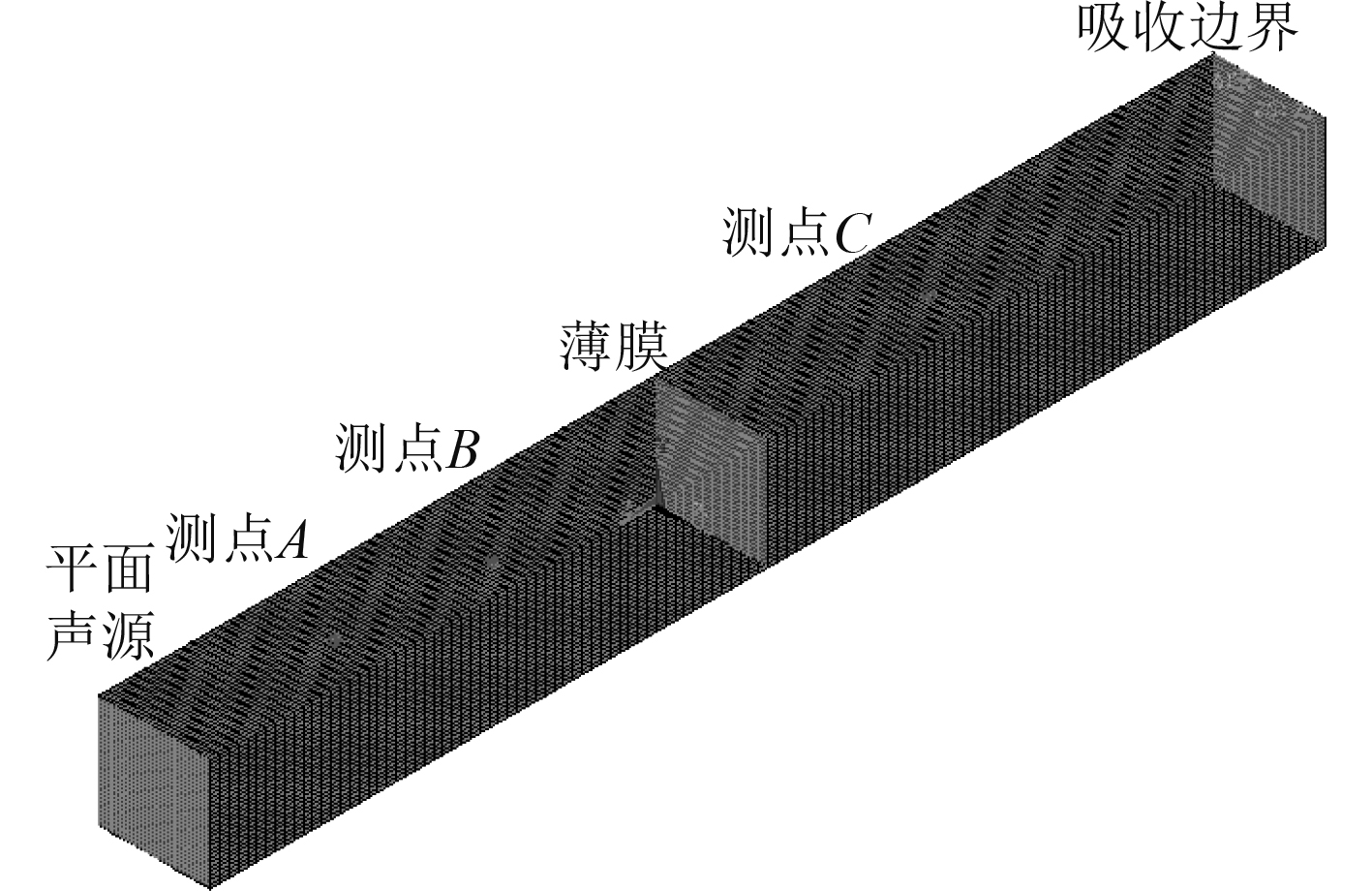
|
图 4 驻波管实验有限元模型 Fig. 4 The finite element model of the standing wave tube test of MAMCT |
采用长宽都为60 mm的薄膜,其密度为980 kg/m3,弹性模量为2×105 Pa,泊松比为0.49;薄膜等效厚度hm为0.5 mm,质量块为0.3 g。分别采用了4种不同的变厚度薄膜形状,如图5所示。为了排除形状改变对质量的影响,4种薄膜的总体积保持不变。

|
图 5 变厚度薄膜形状图 Fig. 5 The schematic diagram of the thickness variation of the membrane |
由于薄膜在无应力作用时不存在刚度,更谈不上固有频率,于是预先在薄膜边界上施加了0.1 N的拉力使其产生一定的刚度,薄膜的边界条件如图6所示。
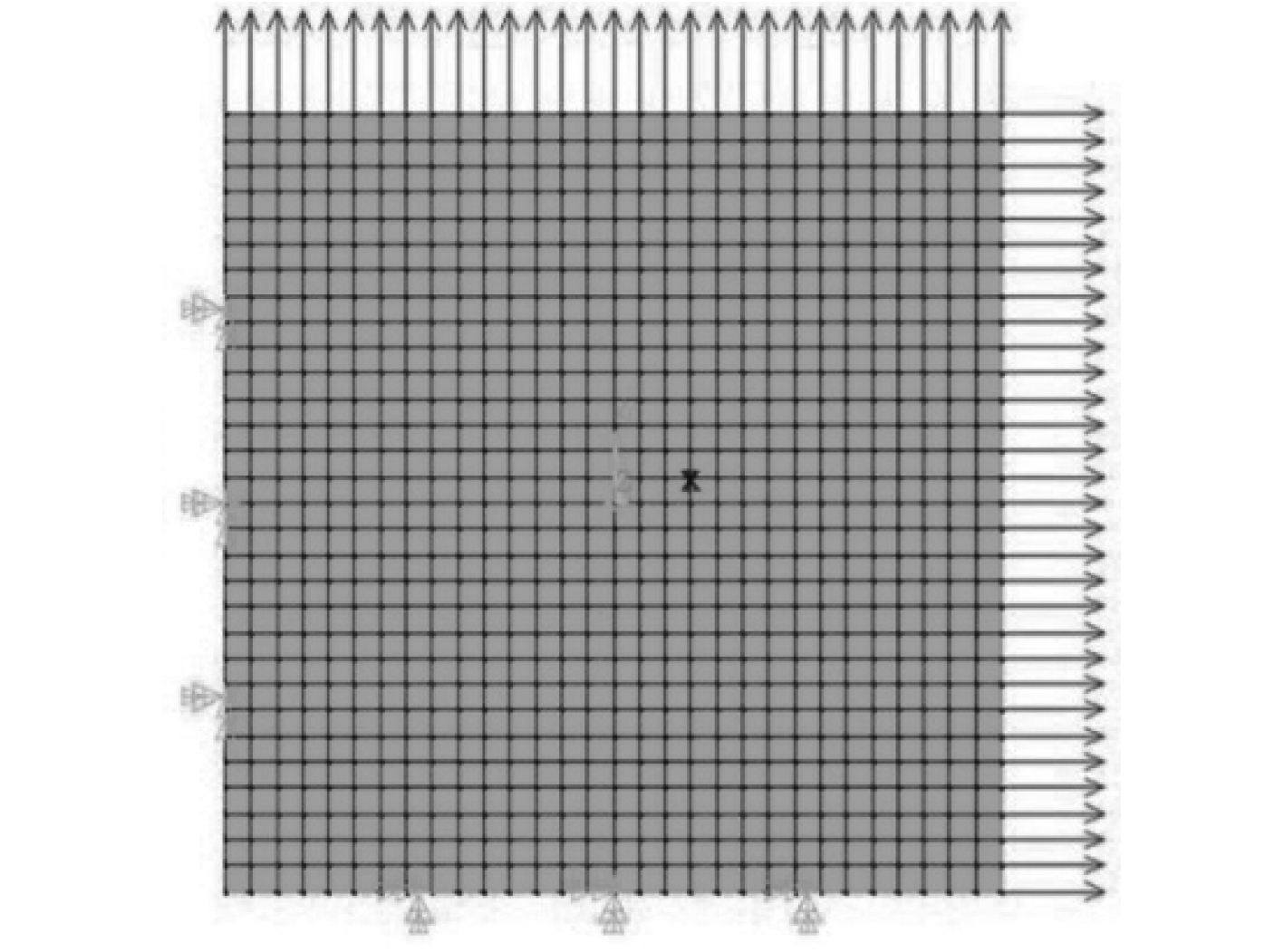
|
图 6 薄膜边界条件 Fig. 6 Schematic diagram of boundary conditions of the membrane |
经计算后发现,4种形状的变厚度薄膜工作频率分别为136.4 Hz,140.47 Hz,154.9 Hz,149.48 Hz其中形状1的工作频率更低,由其组成的多胞元结构能在更低频段获得带隙。所以本文在后面的研究都是围绕形状1展开的。
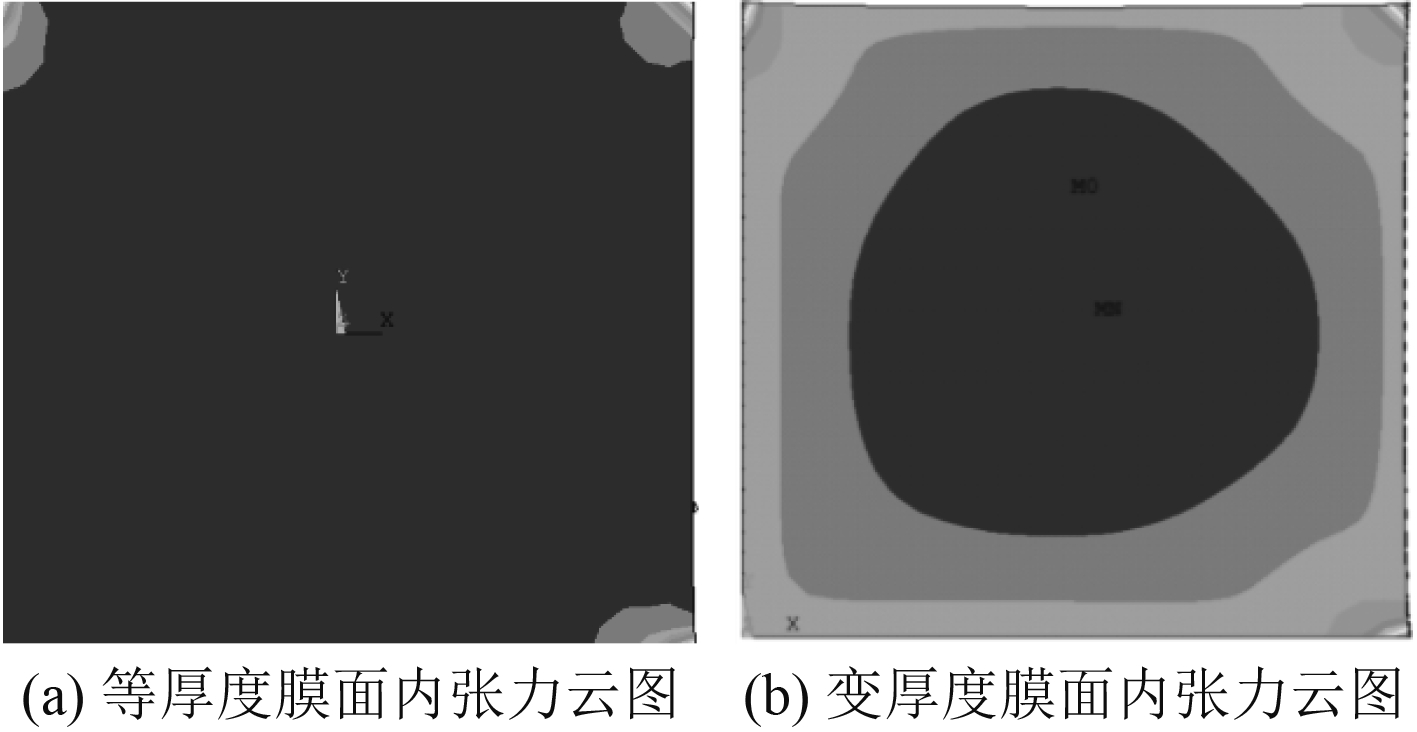
2.2 MVMAT张力薄膜内部所受张力的改变实质上受薄膜所受拉力的控制。对于二维的等厚度薄膜,其面内所受张力均匀,如图7(a)所示,其固有频率和张力有明确的数学表达。而对于变厚度的薄膜,由于其质量块和厚度变化的关系,其面内所受张力并不均匀,如图7(b)所示,其固有频率和张力的关系可以利用模态分析,数值计算得到。
|
图 7 薄膜面内张力云图 Fig. 7 In plane tension nephogram of film |
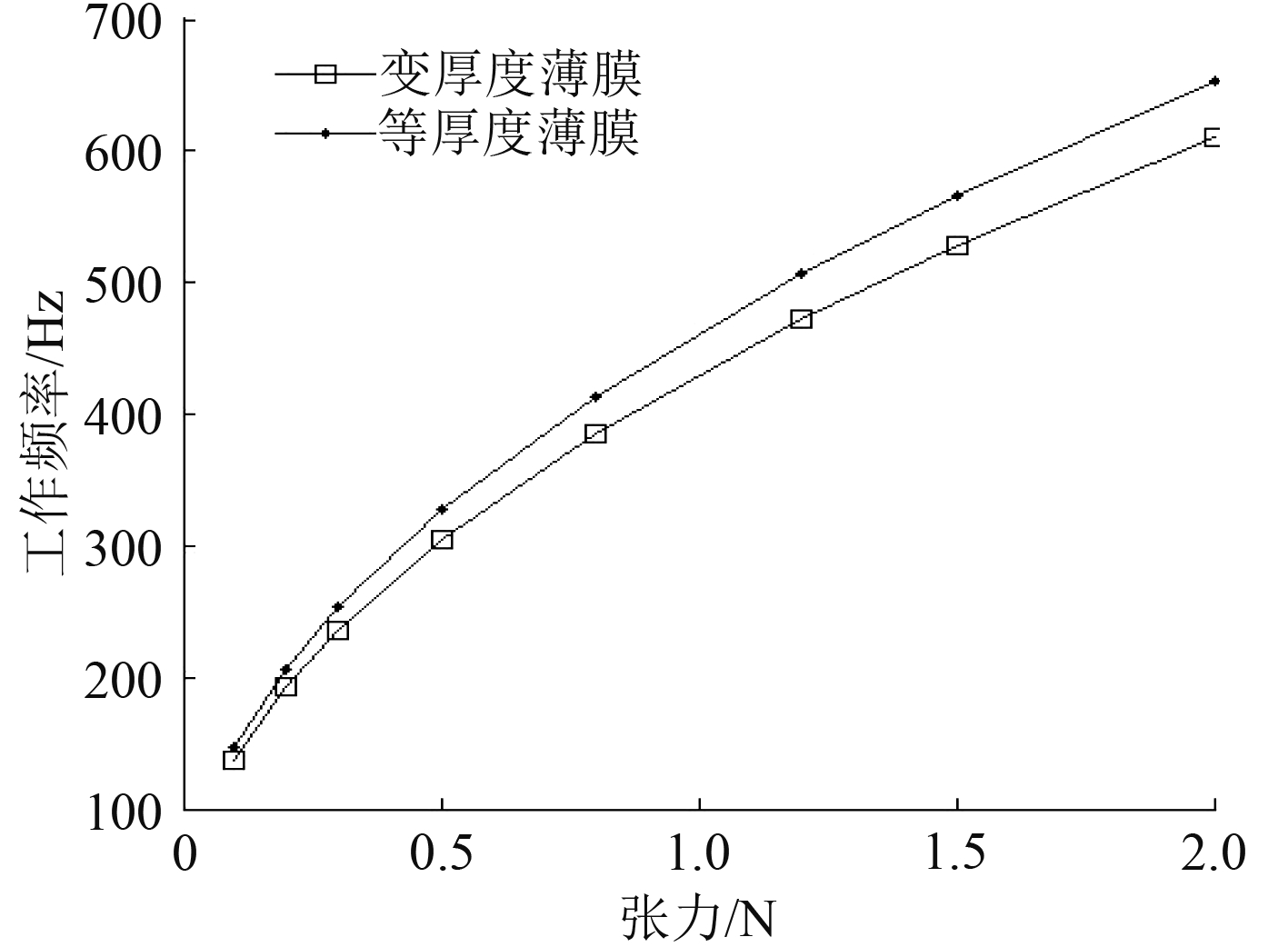
图8为数值计算得到的薄膜型声学超材料单胞工作频率随张力的变化关系。发现随着张力的增加,工作频率增加,但变厚度薄膜工作频率整体都要比等厚度薄膜的低,这意味着变厚度薄膜可以在相对更低的频率下实现有效的隔声。
|
图 8 薄膜工作频率随张力变化图 Fig. 8 The relation between tension of the membrane and the working frequency |
在保证薄膜形状和所受拉力不变的情况下,改变薄膜的等效厚度hm,其工作频率的变化规律如图9所示。

|
图 9 薄膜工作频率随厚度变化图 Fig. 9 The relation between average thickness of the membrane and the working frequency |
可以看出,随着薄膜厚度的增加,其工作频率在厚度变化范围为[0.5 mm,1.5 mm]的区间内快速降低,后趋于平缓,但总体上变厚度薄膜的工作频率在同样条件下要比等厚度的低。
3 MAMVT隔声特性影响因素分析变厚度薄膜型声学超材料单胞工作频率表征了其有效的隔声频段,并不能完整地说明其隔声特性,似要探讨其隔声量随结构参数的变化规律。
本节通过商业有限元软件Ansys建立模型并导入到声学计算软件Virtual.Lab Acoustics中来模拟薄膜单胞在驻波管中隔声量的测量,讨论其隔声特性随结构参数的变化规律。
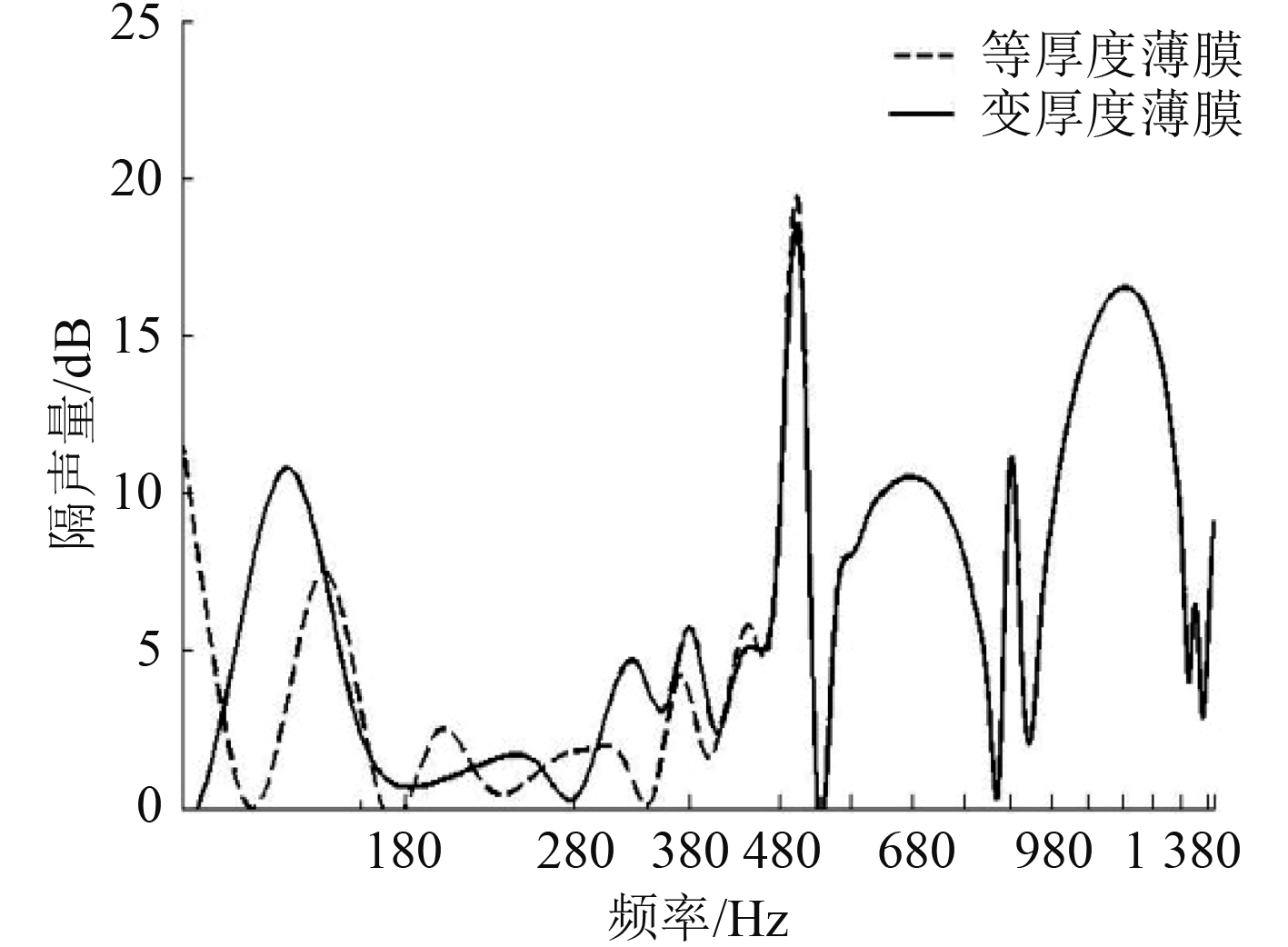
3.1 变厚度薄膜与等厚度薄膜的比较采用的薄膜等效厚度都为0.5 mm,质量块质量为0.3 g,所受张力为0.1 N。图10比较了等厚度薄膜和变厚度薄膜在0~1 500 Hz频率段内的隔声量。
|
图 10 薄膜隔声量图 Fig. 10 Sound insulation of MAMVT and MAMCT |
可以看出,变厚度薄膜第1次峰值出现的频率(即工作频率)要比同样条件下的等厚度薄膜要低,验证了图8中的计算结果,且在峰值频率下,变厚度薄膜的隔声量要比等厚度膜大2.5 dB,但二者的变化趋势在频段内相似,尤其是在频率480 Hz以上,变厚度薄膜隔声量与等厚度的薄膜隔声量几乎相同。
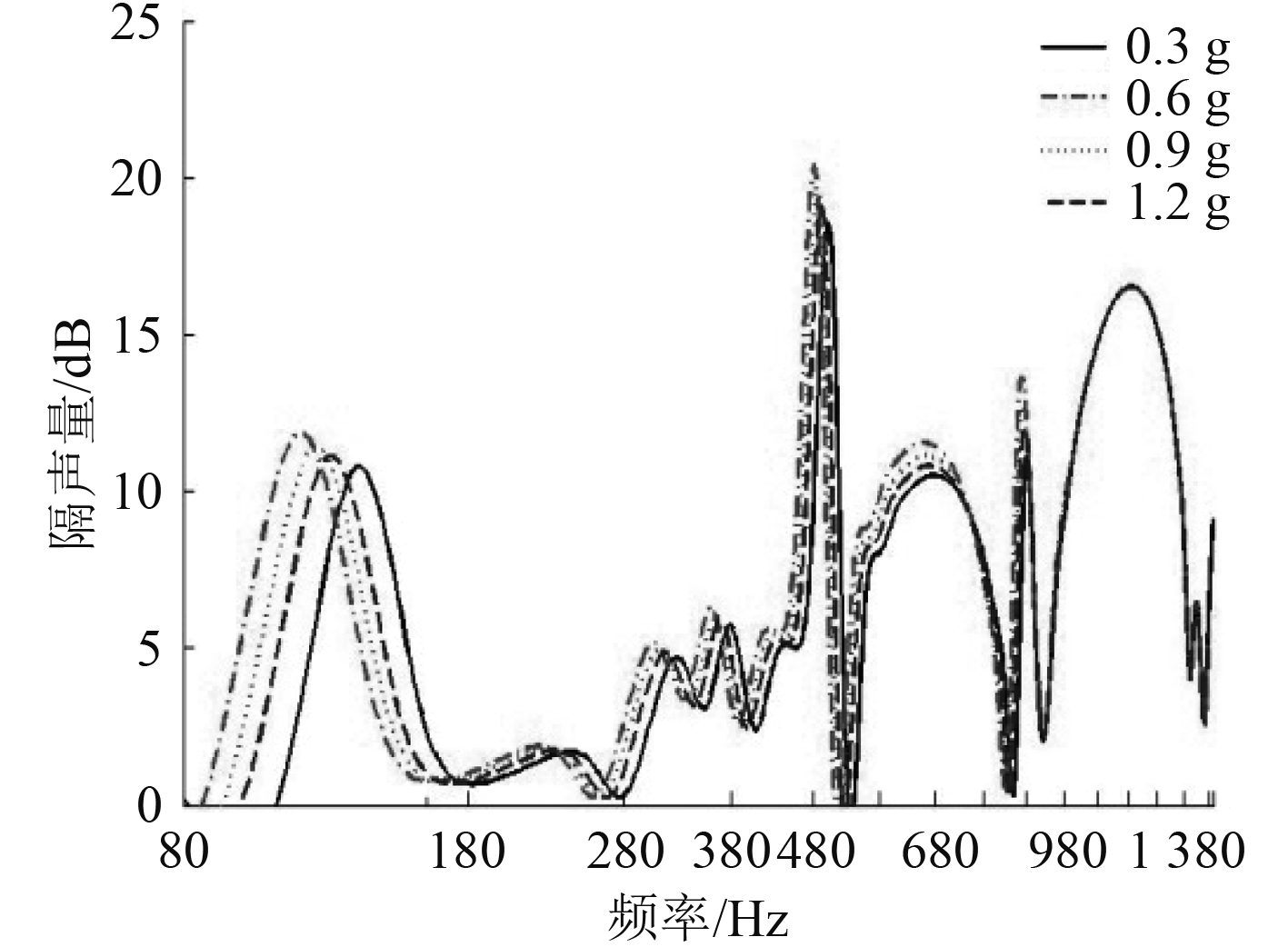
3.2 MAMVT质量块分别取质量块为0.3 g,0.6 g,0.9 g和1.2 g的变厚度薄膜进行比较,如图11所示。
|
图 11 质量块对薄膜隔声量的影响 Fig. 11 Variation of sound insulation curve with increasing mass of mass block |
可以看出,随着附加质量块质量的增大,隔声量曲线的第1次峰值逐渐增大,峰值出现的频率也在减小但不显著。但同样附加质量块的质量线性增大,隔声量曲线峰值的变化量却逐渐减小,这说明当质量块的质量增大到一定程度时,质量块质量对隔声量的影响也会减弱。尤其频率在1 000 Hz以上时,质量块质量对隔声量几乎没有影响。
3.3 MAMVT厚度如图12所示,选取等效厚度分别为0.5 mm,0.7 mm和0.9 mm的薄膜计算其在频段内的隔声量。可以看出,在高频段(大于340 Hz)时,厚度的改变不影响隔声量的变化特性,只是在峰值上有差异,尤其在450 Hz以上,薄膜厚度的变化对隔声量几乎没有影响。在频率范围为30~340 Hz之间,随着厚度的增加,第1次出现隔声峰值的频率降低,但降低趋势变缓,第1次出现谷值的频率降低,且谷值增加。
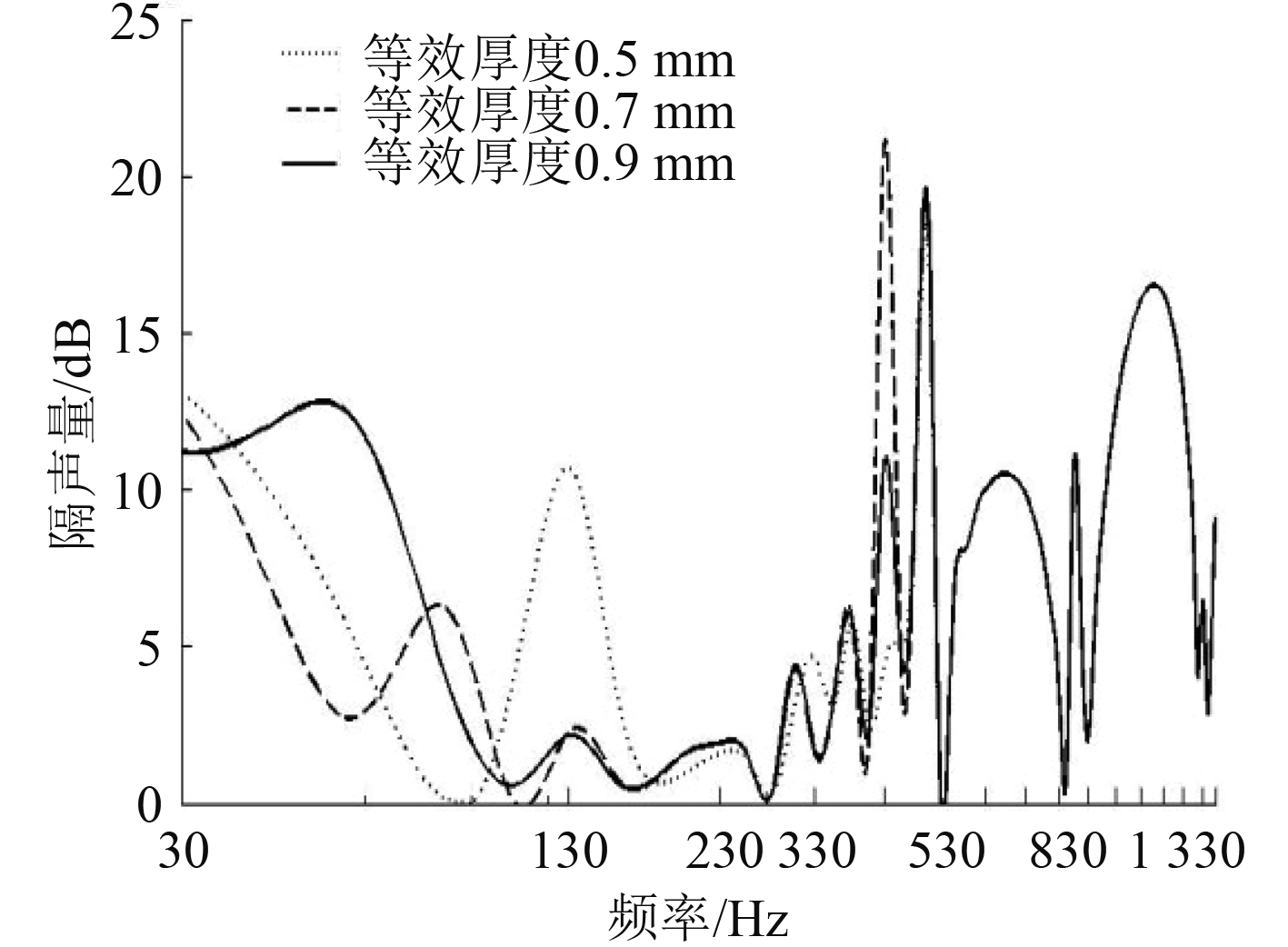
|
图 12 薄膜厚度对隔声量的影响 Fig. 12 Variation of sound insulation curve with increasing thickness of MAMVT |
薄膜张力的作用是提供薄膜刚度,随着薄膜张力的增加,薄膜的整体刚度增加,如图13(a)所示。随着张力的增加,在30~400 Hz的频段内隔声量曲线抬升,工作频率处的峰值显著增加,但工作频率也相应提高,且随着张力的增加,隔声量曲线抬升的幅度变缓。在高频段内,隔声曲线峰值随着张力的增加变得尖锐,不同张力下隔声量随频率增加变化速度变快。
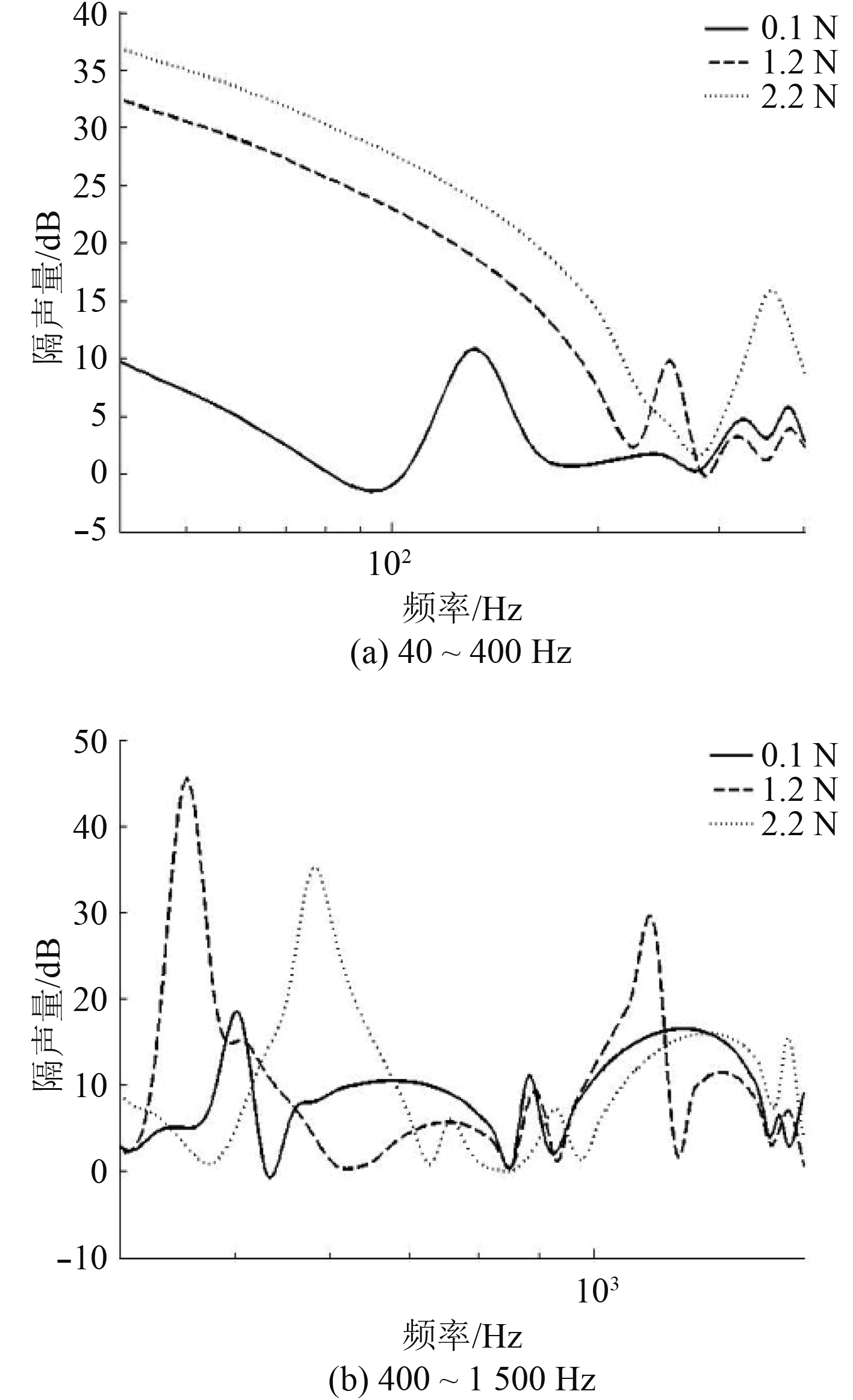
|
图 13 薄膜张力对隔声量的影响 Fig. 13 Variation of sound insulation curve with increasing tension of MAMVT |
本文研究变厚度薄膜型声学超材料单胞隔声性能随结构参数(包括质量块质量、薄膜厚度以及薄膜张力)的变化规律,并同等厚度薄膜做比较,讨论了二者在全频段隔声量特性的异同,通过计算发现:
1)变厚度薄膜型声学材料在同等条件下可以获得更低的工作频率,且在工作频率上有更好的隔声表现;
2)随着厚度的增加,变厚度薄膜第1次出现隔声峰值的频率降低,但降低趋势变缓,第1次出现谷值的频率降低,且谷值增加;
3)随着附加质量块质量的增大,变厚度薄膜隔声量曲线的第1次峰值逐渐增大,峰值出现的频率也在减小但不显著,当质量块的质量增大到一定程度时,质量块质量对隔声量的影响减弱;
4)随着薄膜张力的增加,薄膜的整体刚度增加,隔声量曲线抬升,工作频率处的峰值显著增加,但工作频率也相应提高,且随着张力的增加,隔声量曲线抬升的幅度变缓;
5)在高频段内,厚度和质量块的变化对于隔声量的影响不大,但隔声量曲线随着张力的增加会变得尖锐。
以上结论可以为薄膜型声学超材料在船舶降噪方面的设计与应用提供一定参考依据。
| [1] |
BOLTON J S, SHIAU N M, KANG Y J. Sound transmission through multi-panel structures lined with elastic porous materials[J]. Journal of Sound and Vibration, 1996, 191(3): 317-347. DOI:10.1006/jsvi.1996.0125 |
| [2] |
LIU Z, ZHANG X, MAO Y, et al. Locally resonant sonic materials[J]. Science, 2000, 289(5485): 1734-1736. DOI:10.1126/science.289.5485.1734 |
| [3] |
Gang W, YAO-Zong L, JI-Hong W, et al. Formation mechanism of the low-frequency locally resonant band gap in the two-dimensional ternary phononic crystals[J]. Chinese Physics, 2006, 15(2): 407. DOI:10.1088/1009-1963/15/2/029 |
| [4] |
梅军, 杨旻, 杨志宇, 等. 薄膜型负质量密度声学超常介质[J]. 物理, 2010, 39(04): 243-247. |
| [5] |
NAIFY C J, CHANG C M, MCKNIGHT G. Transmission loss and dynamic response of membrane-type locally resonant acoustic metamaterials[J]. Journal of Applied Physics, 2010, 108(11): 114905. DOI:10.1063/1.3514082 |
| [6] |
YANG Z, DAI H.M., CHAN N.H., et al. Acoustic metamaterial panels for sound attenuation in the 50-1000 Hz regime[J]. Applied Physics Letters, 2010, 96: 041906. DOI:10.1063/1.3299007 |
| [7] |
张炜权, 吴九汇, 马富银, 等. 薄膜低频隔声性能的张力依赖性[J]. 振动工程学报, 2016(04): 616-622. |
| [8] |
张晶. 薄膜声学超材料板的力学特性研究[D]. 哈尔滨: 哈尔滨工业大学, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10213-1014082972.htm
|
| [9] |
曹瑞. 薄膜型声学超材料隔声性能的研究[D]. 哈尔滨: 哈尔滨工业大学, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10213-1015981292.htm
|
| [10] |
张俊生. 薄膜二维振动数理方程的推导与求解[J]. 榆林学院学报, 2006(06): 29-31. DOI:10.3969/j.issn.1008-3871.2006.06.013 |
| [11] |
曲波, 朱蓓丽. 驻波管中隔声量的四传感器测量法[J]. 噪声与振动控制, 2002, 22(6): 44-46. DOI:10.3969/j.issn.1006-1355.2002.06.014 |
 2020, Vol. 42
2020, Vol. 42
