随着全球气温逐渐升高,冰区航行的船舶数量呈上升的趋势。相比于其他区域航行的船舶,在冰区航行的船舶螺旋桨会与冰块相互作用[1-2]。螺旋桨和冰块的作用形式有多种,冲击作用即冰桨碰撞是一种常见的作用形式。冰桨碰撞会对螺旋桨带来明显影响,严重时会导致螺旋桨损坏[3-4]。因此研究冰桨碰撞对于船舶在冰区航行的可靠性与安全性有着重要意义。
国外对于冰桨接触的研究较早。国外的学者通过一系列的模拟试验,选用不同的冰型研究了冰阻力对螺旋桨水动力的影响,并且通过改进数值方法分析了冰桨相互作用,得到的数值结果与试验结果较好吻合[5 – 6]。此外还对冰桨相互作用时螺旋桨上的振动、扭矩和周期冰载荷进行了估计[7 – 8]。国内对于冰桨接触的研究起步较晚。国内的学者计算分析了冰块在切削作用下对螺旋桨的影响,以及冰载荷作用下船舶螺旋桨的附连水效应,在此基础上分析了冰载荷下附连水效应对于轴系各种振动固有频率的影响[9 – 10]。
显式动力学是将显式算法运用到动力学方程,显式算法最大的优点是具有较好的稳定性。显式动力学方程采用中心差分法,不用像隐式方法求解大规模的刚度矩阵,而是将非线性问题包括在方程的内力矢量中,一般不需要进行平衡迭代,时间步长只要取的足够小,一般不存在收敛性问题,相比于隐式算法,显式算法的计算成本要小于隐式算法。
显式动力学方法具有很多优势,为此考虑基于显式动力学理论,利用非线性有限元分析软件Ansys模拟仿真冰块和螺旋桨在多种条件下的碰撞情况。根据结果得出不同条件下冰块与桨的碰撞规律,为船舶在冰区环境下的安全性和可靠性提供参考。
1 显式动力学方程显式动力学基于动力学方程,主要用于计算求解三维非弹性结构的碰撞,以及冲击作用下的变形动力响应,在工程领域有着广泛的运用[11]。冲击即抛射体以一定速度向靶体进行撞击,同时在较短时间内能量发生迅速转化的过程。冲击作用可以在极短时间内向靶体施加高强度载荷,进而引起靶体结构的运动甚至材料的破坏。冲击问题的研究有着重要的理论学术价值。显式动力学是求解冲击碰撞问题常用的方法,其求解方法采用中心差分法进行求解计算。在时间t时的加速度为:
| $ {a_t} = {M^{ - 1}}\left( {F_t^{ext} - F_t^{int}} \right){\text{。}} $ | (1) |
式中:
| $ F_t^{int } = \sum {\left( {\int {{B^{\rm T}}{\sigma _n}{\rm d}\varOmega + {F^{hg}}} } \right) + {F^{contact}}} {\text{。}} $ | (2) |
式中:
节点的速度与位移由下面公式得到:
| $ {V_{t + \Delta t/2}} = {V_{t - \Delta t/2}} + {a_t}\Delta {t_t}{\text{,}} $ | (3) |
| $ {u_{t + \Delta t}} = {V_t} + {V_{t + \Delta t/2}}\Delta {t_{t + \Delta t/2}}{\text{,}} $ | (4) |
其中:
| $ \Delta {t_{t + \Delta t/2}} = 0.5\left( {\Delta {t_t} + \Delta {t_{t + \Delta t}}} \right){\text{。}} $ | (5) |
新的几何构型由初始位置与位移增量叠加得到:
| $ {x_{t + \Delta t}} = {x_0} + {u_{t + \Delta t}}{\text{。}} $ | (6) |
为了保证整个计算的收敛,在设置时间步长时通常采用较小的时间步长,其步长的设置如下式:
| $ \Delta {\rm{t}} \leqslant \Delta {t_{ct}} = \frac{2}{{{\omega _{\rm{max} }}}}{\text{。}} $ | (7) |
式中:
| $ \left| {{K^e} - {\omega ^2}{M^e}} \right| = 0{\text{。}} $ | (8) |
在实际冰桨碰撞的过程中,与桨叶碰撞的冰块多为小块碎冰[8]。海冰通过与桨叶的接触对桨叶造成一定的作用力。为了确保后面的计算结果,本文设定冰块为小正方体。冰块的模型如图1所示,海冰的参数如表1所示。

|
图 1 冰块模型 Fig. 1 Ice model |
|
|
表 1 海冰性质参数表 Tab.1 The property parameter table of ice |
本文的研究对象为某多功能船舶的螺旋桨。螺旋桨的具体参数如表2所示。桨叶的模型建立和网格划分由Ansys前处理模块处理。网格的划分方式采用自动划分,网格的单元尺寸为15 mm,由于冰块与桨叶发生碰撞会产生很大的应力,因此在划分网格时细化了桨叶的网格,桨叶的网格单元尺寸为10 mm,螺旋桨划分完成的网格数为112478,螺旋桨模型和网格划分模型如图2和图3所示。
|
|
表 2 螺旋桨基本参数 Tab.2 Propeller basic parameters |

|
图 2 螺旋桨模型 Fig. 2 Propeller model |

|
图 3 螺旋桨网格划分模型 Fig. 3 Propeller meshing model |
冰块和螺旋桨模型建立完成后,可以得到冰桨碰撞模型。本文主要分析冰块对桨叶的碰撞,因此冰块碰撞位置为上方桨叶。为确保在较短时间内完成碰撞过程,冰块与桨叶的碰撞距离很接近。冰和桨的碰撞模型如图4所示。

|
图 4 冰和桨碰撞模型 Fig. 4 Ice and propeller collision model |
冰—桨实际碰撞过程非常复杂,除了和螺旋桨自身形状、材料相关外,还与冰块的运动速度、冰块大小、碰撞位置,以及海水流体环境有关。本文忽略海水的流动情况,假设冰块为正方体,桨叶静止不动,采用Ansys有限元软件模拟仿真冰块和螺旋桨的碰撞情况,主要考虑碰撞速度、碰撞位置和冰块大小对冰浆碰撞的影响。
3.1 碰撞速度的影响分析船舶的航行速度为10~17 kn,洋流的速度一般为5 kn,当船舶在冰区海域航行时,冰块对于船舶的相对速度为5~22 kn,即2.5~8.75 m/s。因此选定冰块冲击速度为2 m/s,4 m/s,6 m/s,8 m/s,速度方向沿y轴负向。研究对象为B3级冰区航行的多用途船舶螺旋桨,根据中国船级社《钢制海船入级规范》规定,冰块厚度如表3所示。根据参考文献[9],假定冰块为边长为0.15 m的正方形,冰块的撞击位置为桨叶叶面的0.6 R区域,运动时间为0.05 s。
|
|
表 3 冰块设计厚度 Tab.3 Design Ice thickness |
使用Ansys有限元软件分析碰撞过程桨叶受到的应力以及桨叶的整体变形。有限元计算得到的应力和变形分布如图5和图6所示。

|
图 5 不同速度部分时刻桨叶应力云图 Fig. 5 Blade stress contours at different speed |
|
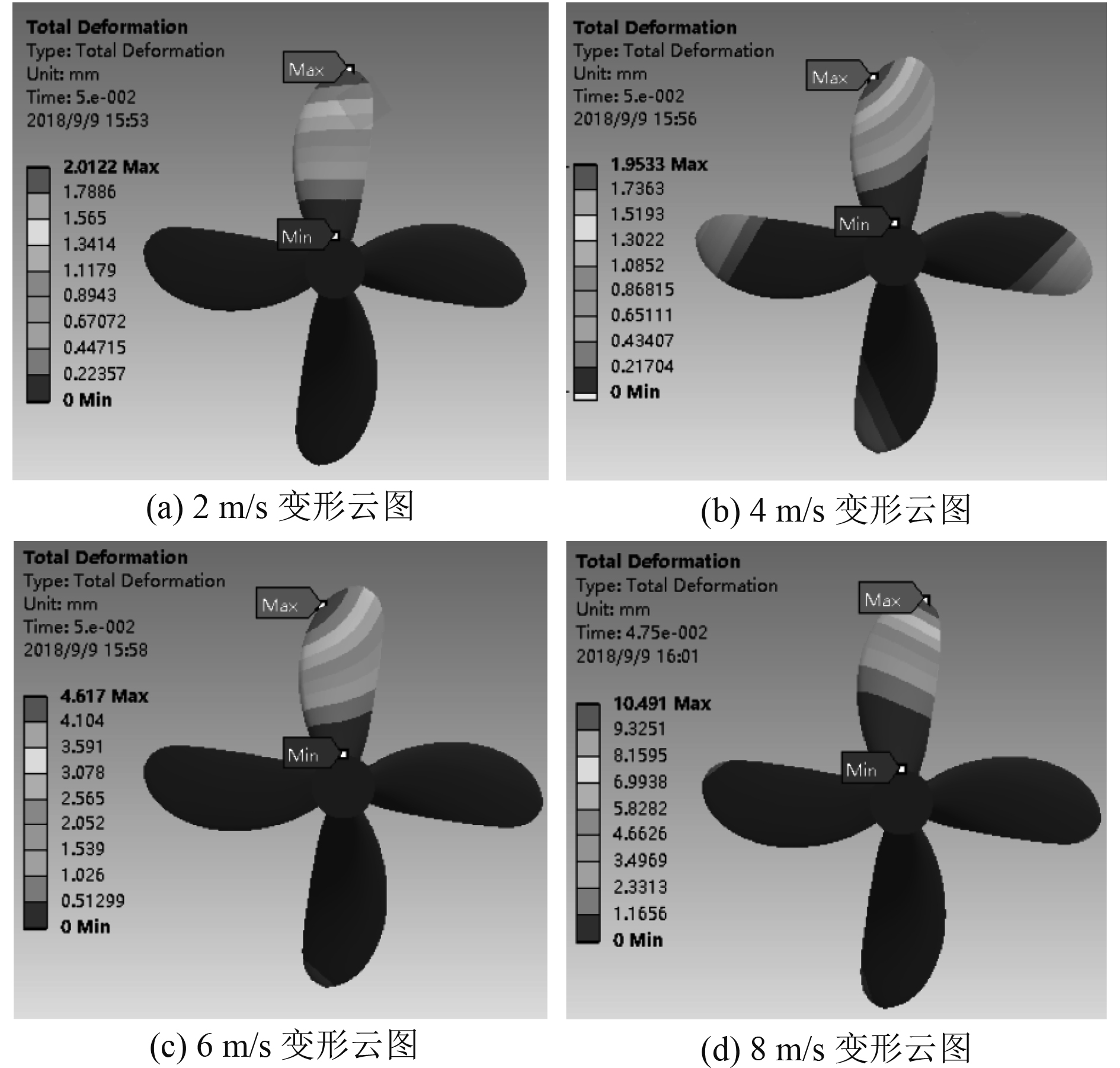
图 6 不同速度部分时刻桨叶的变形云图 Fig. 6 Blade stress deformation at different speed |
图5和图6为冰桨碰撞过程中,桨叶受到的应力云图和变形云图。由图5可知当冰块与螺旋桨发生碰撞时桨叶会产生较大的应力,且随着冰桨相对速度的增大桨叶受到的最大应力在逐渐增大。冰块的速度越大,运动过程中产生的冲量也越大,碰撞时对桨叶产生的作用力也越大,因此桨叶受到的应力也越大。桨叶受到的最大应力位于桨叶与桨轴的连接位置,可见碰撞过程中冲击力是由碰撞位置传递到桨轴处。
由图6可知,在冰块与桨叶开始碰撞时,桨叶的最大变形主要集中在碰撞区域附近。随着碰撞过程的继续桨叶的变形位置逐渐发生变化,最终桨叶的最大变形位于桨叶的边缘,且变形沿着径向逐渐减小。这是因为桨叶的边缘相对较薄,当桨叶受到外界作用力时,越薄的位置越容易受到变形影响。因此在工程应用中可以适当加大桨叶厚度,从而提高结构的承载能力。
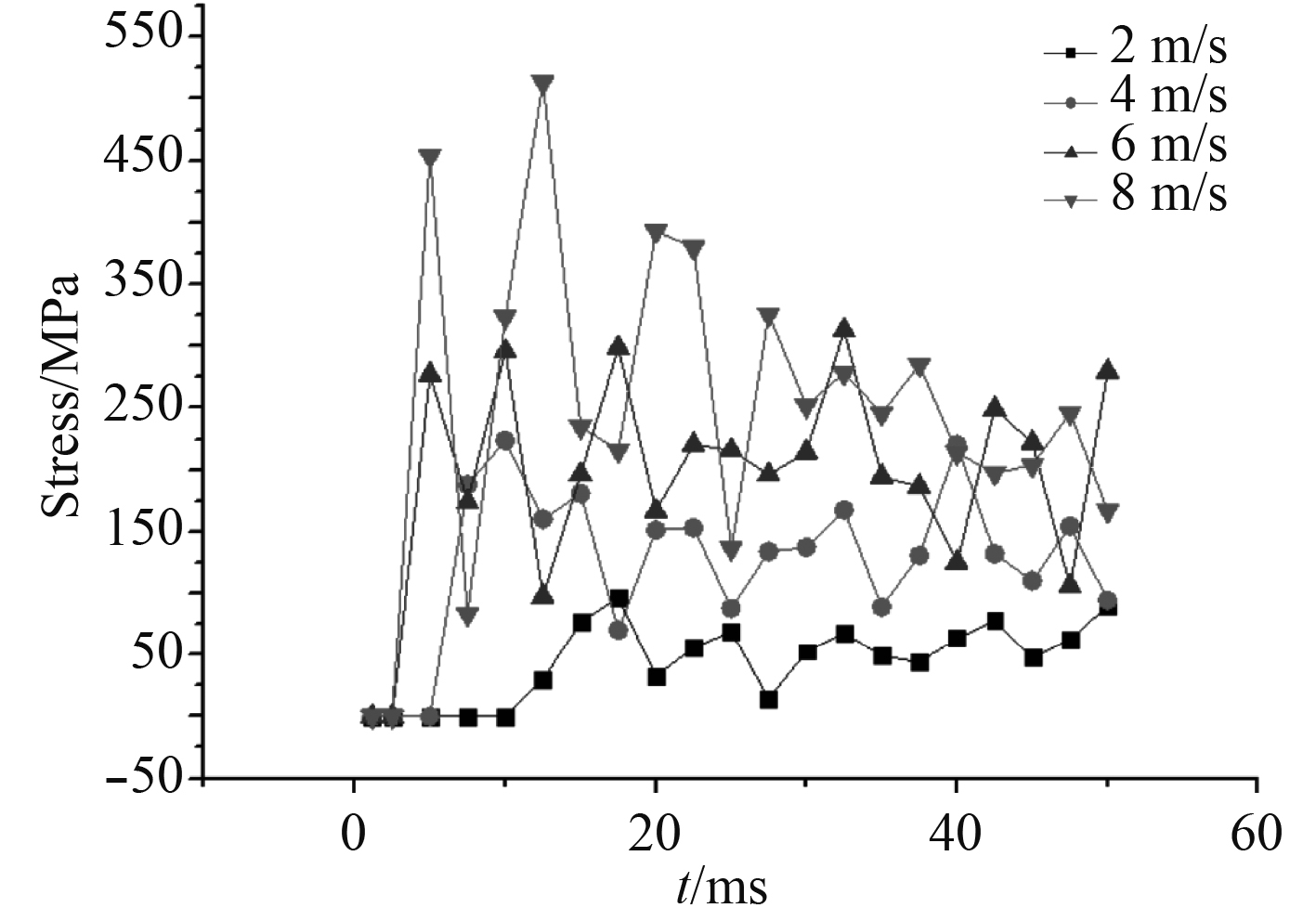
图7给出了最大碰撞力随时间变化的曲线。由图7可以看出,不同速度下变化趋势基本相同,随着速度的增大,碰撞过程越剧烈,碰撞后进入峰值的时间也越短,碰撞产生的冲击力也越大,桨叶受到的应力也越大。当冰块速度为8 m/s时桨叶受到的最大应力为513.36 MPa,要明显大于其他速度碰撞产生的应力。因此冰块速度越大,碰撞后桨叶受到的应力也越大,桨叶受到的损害也越大。
|
图 7 最大应力时历曲线 Fig. 7 Maximum stress-time curve |
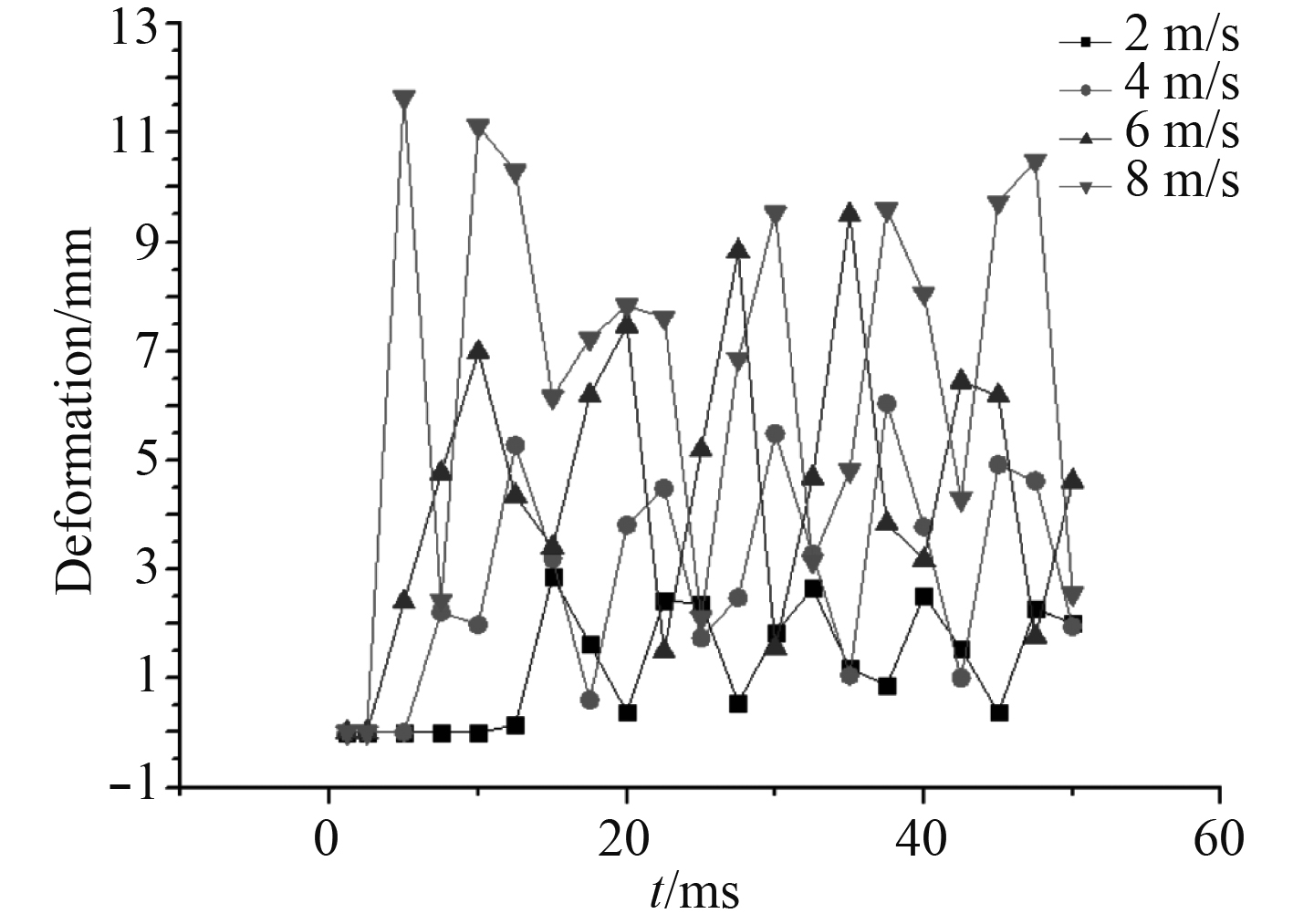
图8给出了桨的最大变形随时间变化的曲线。由图8可知,桨叶受到冰块冲击后桨叶的变形在不断变化,很明显可以看出随着速度的增大,桨叶的变形也会明显增大,当冰块速度为8 m/s时桨叶的最大变形为11.65 mm,冰块速度为2 m/s时的最大变形为2.86 mm。可见冰块速度为8 m/s时桨叶的变形要远大于2 m/s时的变形。由此可以得出结论,桨叶受到的变形随着冰块速度的增加而增大。
|
图 8 最大变形时历曲线 Fig. 8 Maximum deformation-time curve |
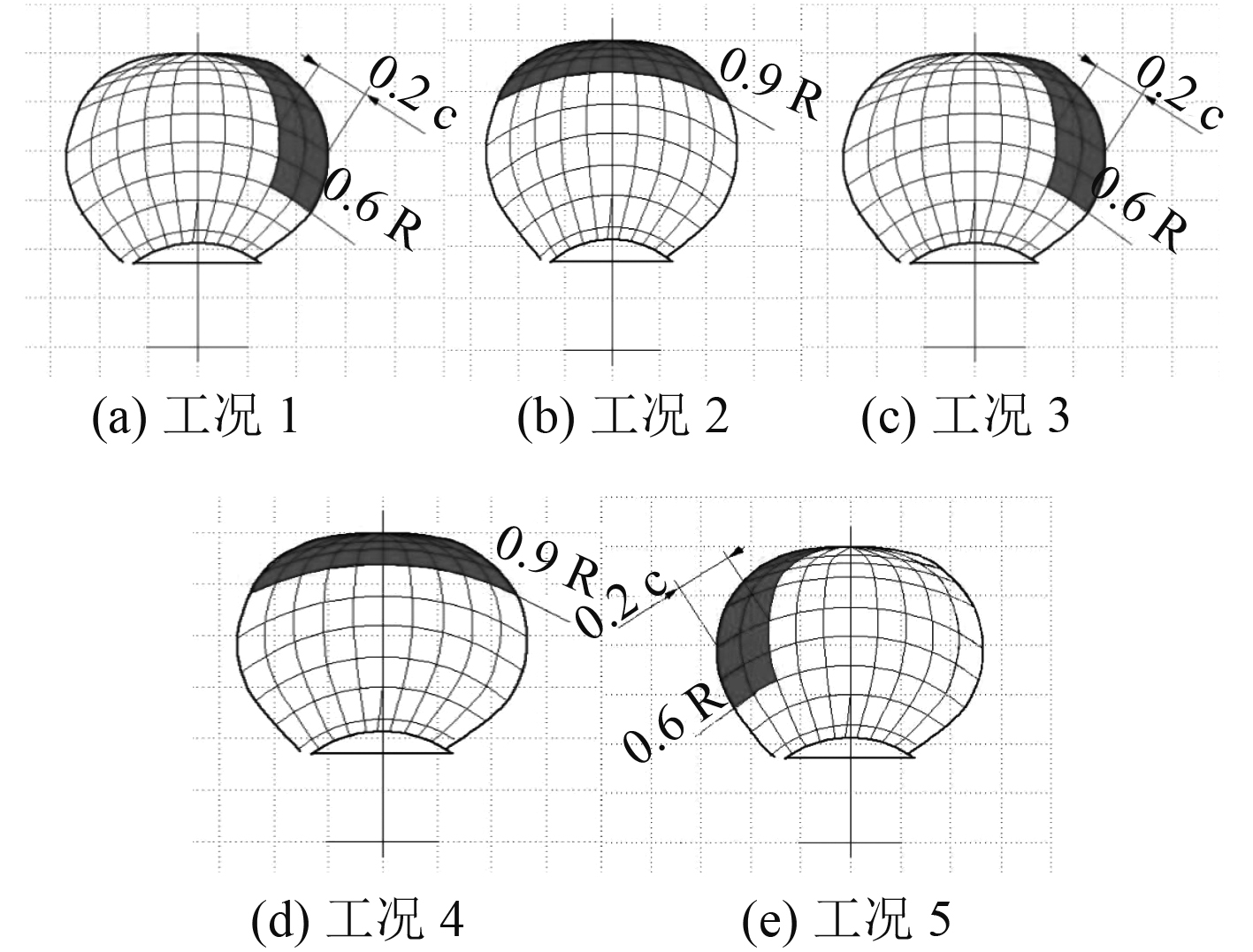
由于螺旋桨的形状不规则,且各处厚度不同,冰和桨在不同位置发生碰撞时,桨叶受到的损伤也不相同。由IACS的规范,将螺旋桨和冰块的碰撞分为五种计算工况和受力区域[12],如图9和表4所示。
|
图 9 各工况受力区域示意图 Fig. 9 Schematic diagram of the force area of each working condition |
|
|
表 4 计算工况 Tab.4 Calculation condition |
由于考虑的是叶片压力面的碰撞,因此设置碰撞位置为工况3、工况4、工况5,冰块的速度为6 m/s,海冰边长为0.15 m,运动方向沿y轴负向,运动时间为0.05 s。3种工况下冰桨模型如图10所示。
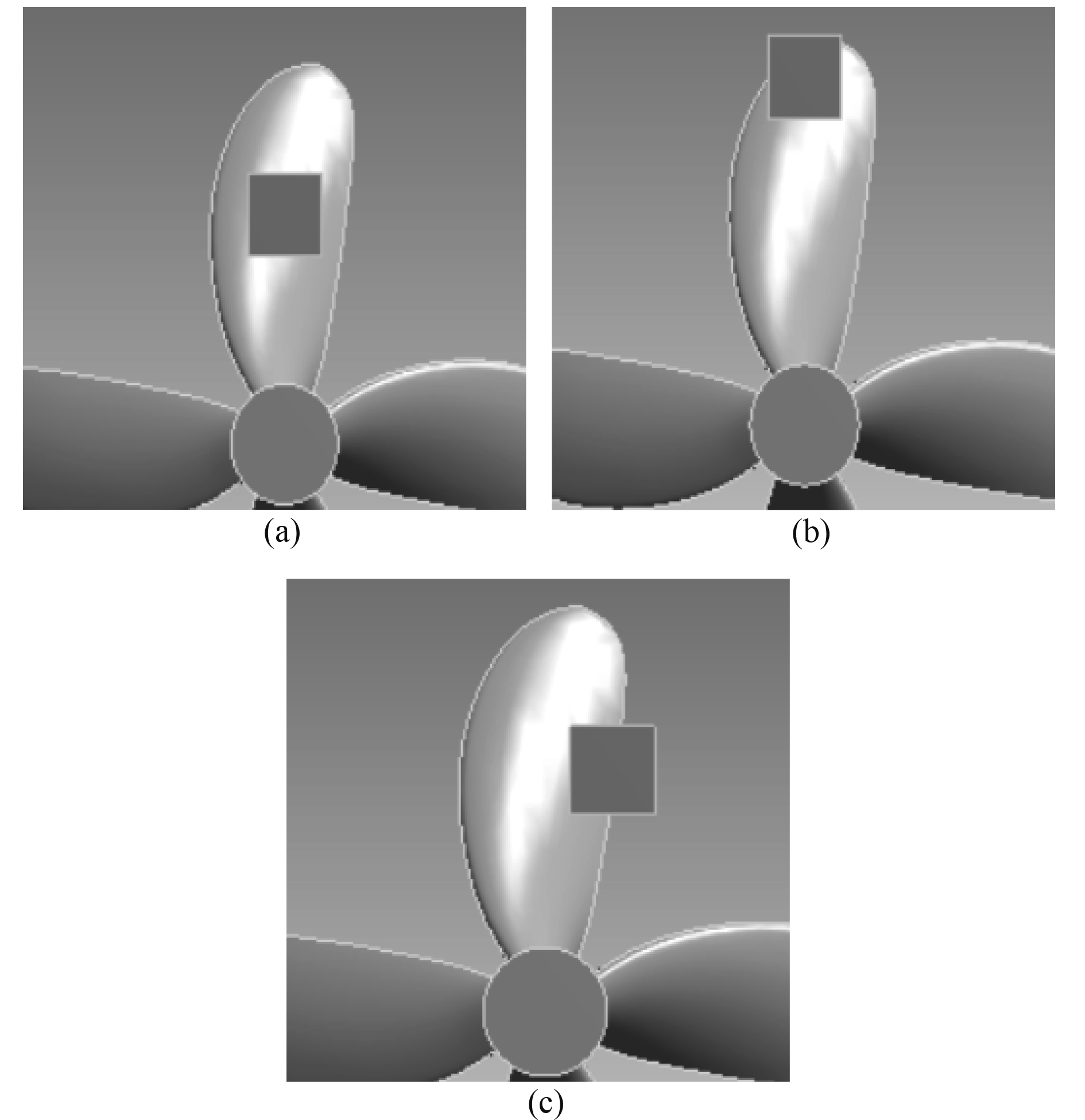
|
图 10 海冰初始时刻与冰块的相对位置 Fig. 10 The relative position of the sea ice at the initial moment to the ice |
冰桨碰撞的应力时历曲线如图11所示。通过观察可知,在冰块和螺旋桨碰撞的短时间内,桨叶的应力达到最大值,之后桨叶的应力逐渐减小。桨叶的应力在刚开始达到最大是因为碰撞的瞬间二者的接触面积很小,随着时间的推移二者的接触面积逐渐增大,桨叶的应力开始有所减少。与此同时海冰会逐渐脱离桨盘面,之后桨叶的应力保持在一定的大小范围。由图11可知,3条曲线整体变化趋势相同,在开始的时候应力会有很大的变化,之后应力会逐渐趋于平稳,工况3的整体数值要大于另外2个工况。对于螺旋桨来说桨叶整体较薄,桨叶厚度对碰撞影响不大。由于工况3的径向位置更靠近桨的轴心,冰块与桨叶接触的时间更长,脱离桨叶盘面用的时间也更长。冰桨接触力的大小与冰块强度和接触面积有关,3种工况冰块的情况完全一样,因此接触面积的不同导致了冰桨接触作用力的差别,由于工况3冰块与桨叶的接触时间更长,这样进一步增加了冰桨接触面积,所以工况3的应力值相对较大。工况5的数值相对较小,这是因为工况5的冰块位于桨叶的边缘,与桨叶的接触面积较小,接触时间较短,因此桨叶受到的应力较小。
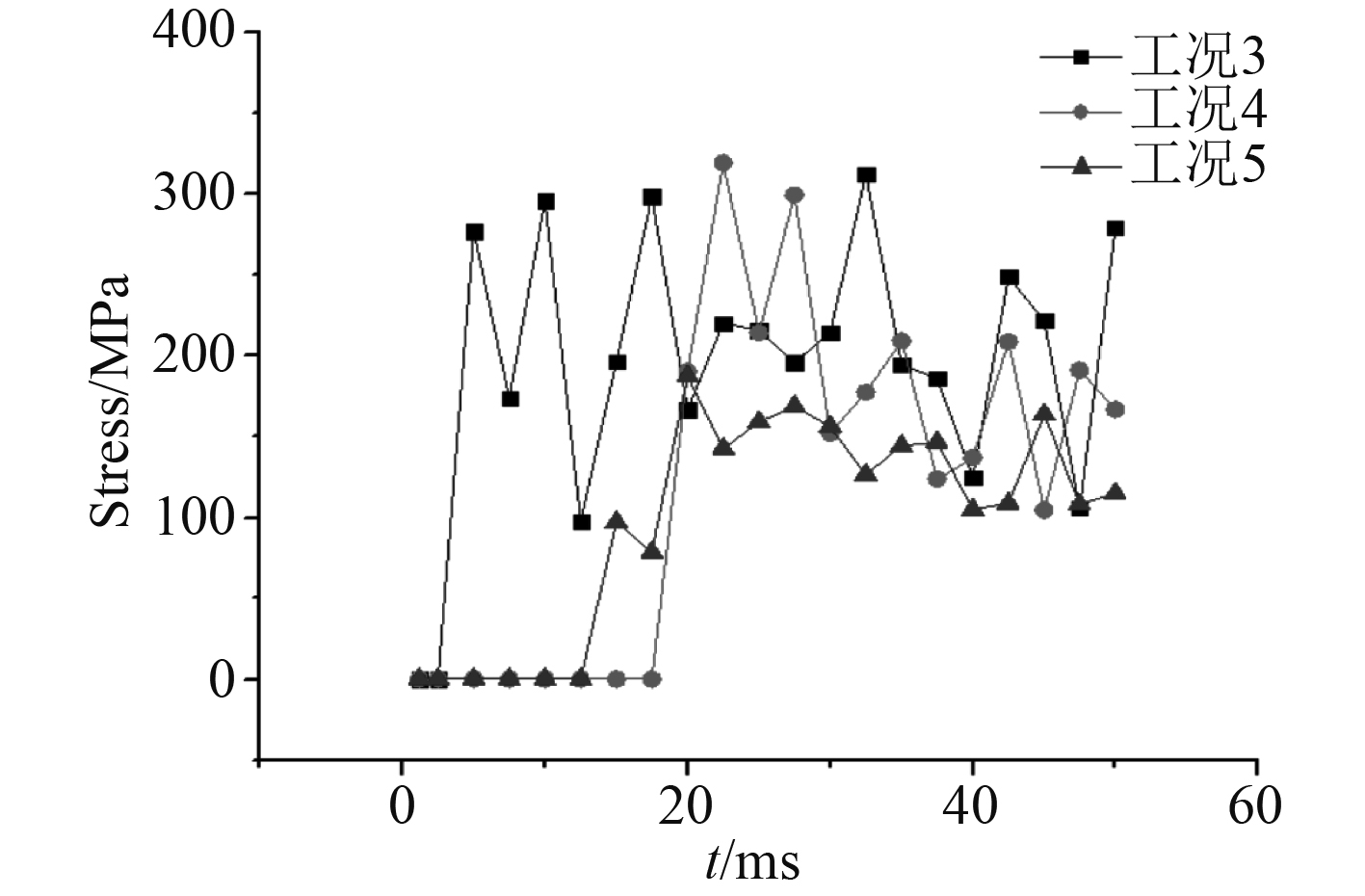
|
图 11 最大应力时历曲线 Fig. 11 Maximum stress-time curve |
本文所分析的螺旋桨,叶梢区域外轮廓收拢的较快,所以对冰块接触角度影响较大。因此螺旋桨在设计时,为确保桨叶形状合理,应减小冰桨碰撞时两者的碰撞角度,从而降低碰撞时桨叶受到的应力,提高螺旋桨结构的可靠性。
3.3 冰块大小影响分析由于与螺旋桨碰撞的冰块多为小碎冰块,根据表3的设计厚度,这里假设冰块为正方体,边长分别为0.1 m,0.15 m,0.2 m,撞击位置为桨叶叶面0.6 R区域,速度大小为6 m/s,方向沿y轴负向。
图12为桨叶受到的最大应力时历曲线。由图12可知冰块与桨叶发生碰撞的瞬间,应力会在瞬间达到很大,之后的过程应力在不断波动。冰块的尺寸对应力的影响很明显,边长0.2 m的海冰碰撞产生的最大应力为460.15 MPa,明显要大于边长0.1 m的海冰产生的最大应力166.86 MPa。因此随着海冰尺寸的增大,海冰与桨叶碰撞产生的应力也有所变大,对螺旋桨的损害也越大。

|
图 12 最大应力时历曲线 Fig. 12 Maximum stress-time curve |
图13为桨叶的变形时历曲线。由图13可知整个碰撞过程桨叶的变形在一定范围内波动,冰块的尺寸对桨叶的变形影响较大。当冰块尺寸为0.2 m时,碰撞后桨叶的变形为11.77 mm,要明显大于冰块为0.1 m的变形3.44 mm。
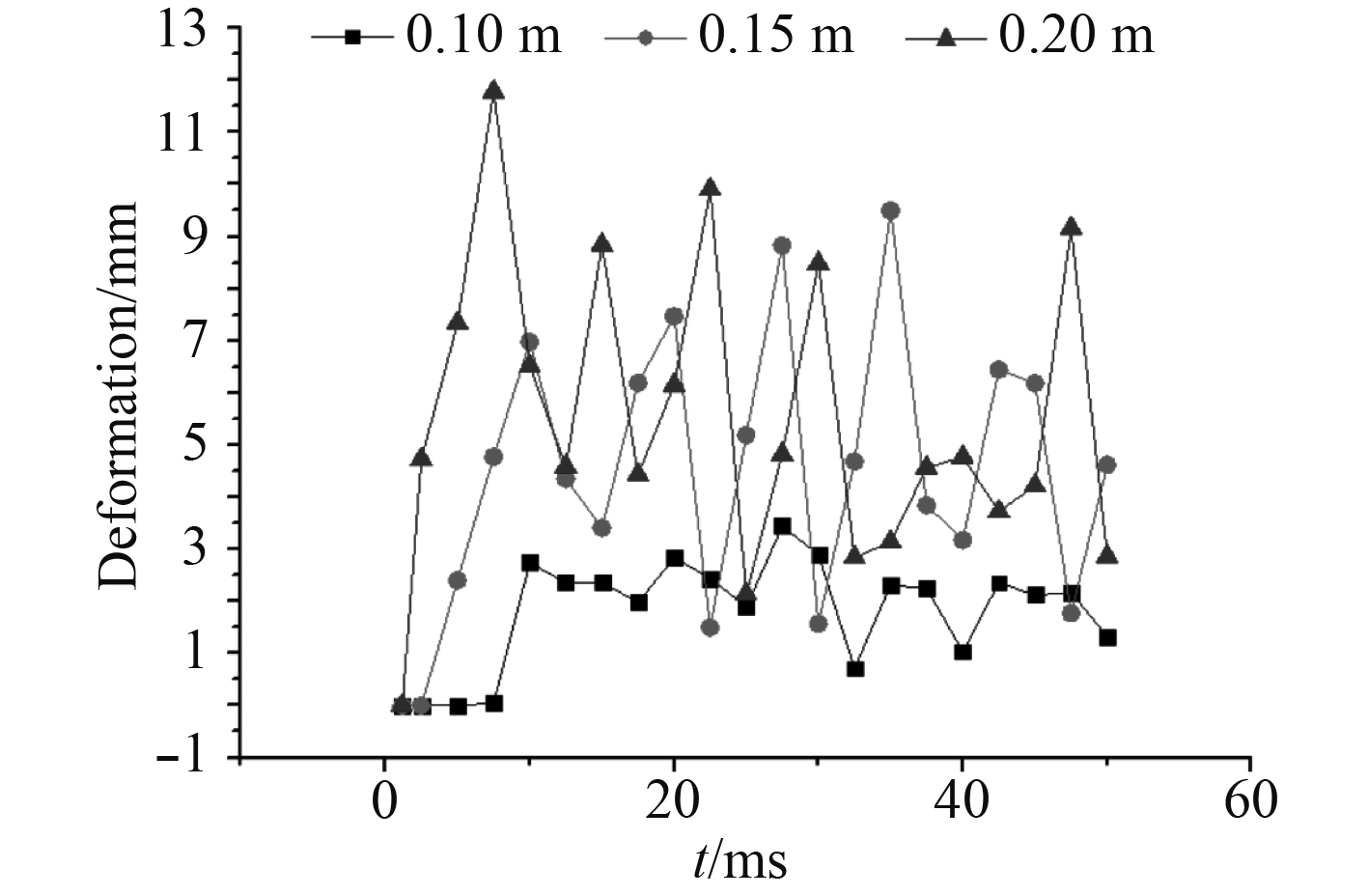
|
图 13 最大变形时历曲线 Fig. 13 Maximum deformation-time curve |
海冰的尺寸不同,对桨叶的应力和变形影响很大。由牛顿运动定律可知,要确保海冰的加速度相同,冰块的尺寸越大,所需要的外力也越大,冰桨之间的接触力也越大,这就造成了碰撞后桨叶产生的应力和变形也越大。由图13也可看出,冰桨的接触力在不断变化,这是因为碰撞产生的是动冰力,而动冰力在不断的变化,所以碰撞后桨叶的应力和变形也在变化。当冰块的尺寸增大后,冰桨之间的接触面积有所增大,所以冰桨接触力也相应增大,这也是桨叶的应力和变形增大的影响因素。
4 结 语本文对冰桨碰撞进行了分析研究,利用Ansys有限元软件模拟仿真冰块和螺旋桨的碰撞情况,主要考虑碰撞速度、碰撞位置和冰块大小,可以得出以下结论:
1)桨叶受到的应力和冰块的速度大小有关。随着冰块运动速度的增加,桨叶受到的撞击力越大,发生的变形也越大,螺旋桨越容易发生损坏。桨叶受到的最大应力位于桨叶与桨轴的连接位置,可见碰撞过程中冲击力由碰撞位置传递到桨轴处,桨叶的最大变形开始主要集中在碰撞区域附近,之后最大变形位于桨叶边缘。
2)冰桨接触力主要取决于接触面积。由于桨叶整体较薄,桨叶厚度对碰撞影响不大。冰桨接触力的大小与冰块强度和接触面积有关,由于工况3、工况4、工况5冰块的情况完全一样,因此接触面积的不同导致了冰桨接触作用力的差别。
3)冰块的尺寸对碰撞有很大影响。冰块边长为0.2 m时桨叶受到的最大应力为460.15 MPa,变形为11.77 mm要明显大于0.1 m时的最大应力166.86 MPa和3.44 mm。因此冰块尺寸越大,碰撞后对桨叶的损害也越大。
4)螺旋桨受损最明显的地方是桨叶边缘,因此螺旋桨在设计时可以适当增大桨叶的厚度,从而提高结构刚度和承载能力。
| [1] |
耿厚才, 于瑶, 周鑫元, 等. 冰区加强船冰载荷计算与轴系设计[J]. 船舶工程, 2015(11): 31-33. GENG Hou-cai, YU yao, ZHOU Xing-yuan, et al. Ice impact calculations and relevant shafting design for vessel with ice class[J]. Ship Engineering, 2015(11): 31-33. |
| [2] |
胡志宽, 桂洪斌. 基于SPH法的冰与船舶螺旋桨碰撞数值模拟[C]// 船舶与海洋结构学术会议暨中国钢结构协会海洋钢结构分会理事会第三次会议. 2014. HU Zhi-kuan, GUI Hong-bin. SPH—Based numerical simulation of ship propeller under ice impact[C]// Conference on Ships and Marine Structures and the Third Meeting of the Council of the China Steel Structure Association Marine Steel Structure Branch. 2014. |
| [3] |
ABS.Guidance Notes on Ice Class[Sl, 2005.
|
| [4] |
齐奎利. 冰载下极地船舶结构强度评估研究[D]. 上海: 上海交通大学, 2013. QI Kui-li. Study on assessment of structural strength for polar ships under ice loads[D]. Shanghai: Shanghai Jiaotong University, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10248-1013021166.htm |
| [5] |
WANG J, AKINTURK A, JONES S J, et al. Ice loads on a model podded propeller blade in milling conditions[C]// ASME 2005 24th International Conference on Offshore Mechanics and Arctic Engineering. American Society of Mechanical Engineers, 2005: 931-936.
|
| [6] |
WANG J, AKINTURK A, JONES S J, et al. Ice loads acting on a model podded propeller blade (OMAE2005-67416)[J]. Journal of Offshore Mechanics & Arctic Engineering, 2007, 129(3): 236-244. |
| [7] |
KARULINA M M, KARULIN E B, BELYASHOV V A, et al. Assessment of periodical ice loads acting on screw propeller during its interaction with ice[C]// Icetech. 2008. http://cdmd.cnki.com.cn/Article/CDMD-10248-1013021166.htm
|
| [8] |
WANG J, AKINTURK A, BOSE N. Numerical prediction of propeller performance during propeller-ice interaction[J]. Marine Technology & Sname News, 2009, 46(3): 123-139. |
| [9] |
孙文林. 冰区航行船舶螺旋桨强度研究[D]. 哈尔滨: 哈尔滨工程大学, 2016. SUN Wen-lin. Research on the propeller strength of ice-going ships[D]. Harbin: Harbin Engineering University, 2016. |
| [10] |
吴帅. 冰载荷下螺旋桨附连水效应及轴系振动研究[D]. 大连: 大连理工大学, 2016. WU Shuai. Research on the entrained water effect of propeller and the vibration performance of propulsion shafting under ice impact[D]. Dalian: Dalian University of Technology, 2016. |
| [11] |
胡志宽, 桂洪斌, 夏鹏鹏, 等. 冰载荷下船舶螺旋桨强度的有限元分析[J]. 船舶工程, 2013(5). HU Zhi-kuan, GUI Hong-bin, XIA Peng-peng, et al. Finite element analysis of ship propeller strength under ice loads[J]. Ship Engineering, 2013(5). |
| [12] |
International association of classification societies, requirements concerning polar class[S], 2015.
|
 2020, Vol. 42
2020, Vol. 42
