潜航器在海底探测、海洋开发以及军事上都有着广泛应用,而深度控制效果对潜航器的性能有着重要的影响,快速跟踪并维持在目标深度附近是潜航器的常见控制目标[1]。潜航器的执行机构有水平舵、螺旋桨、压载水舱以及波动鳍等[2-5]。利用水平舵对潜航器进行深度控制的方法具有执行机构响应快,控制量输入精准的特点。水平舵作为执行机构被广泛应用于潜航器,其产生的升力与航速密切相关。当潜航器航速较高时,水平舵能够产生的升力较高,具有较强的控制力,而当潜航器在低航速状态下航行时,控制力大幅降低,使潜航器深度控制的难度大幅增加[6]。另一方面,潜航器在航行过程中会受到波浪的扰动。相较于深水,潜航器在近水面航行时收到的波浪扰动力大幅增加,波吸力将使潜航器难以维持在目标深度附近[7]。
PID控制方法凭借着不依赖模型参数、适应范围广、简单易用的优势在众多领域得到了广泛的应用。其控制思想是根据控制目标与实际行为之间的误差来确定消除此误差的控制量。然而,PID方法也存在着诸多缺点。首先,该方法是根据已经存在的偏差来计算纠正偏差的控制量,因而产生滞后。其次,PID中微分项的获取在工程中并不容易,处理不当会产生噪声放大的不良效果。同时,为保证消除稳态误差而存在的积分项可能会导致积分饱和等现象。最后,PID三项线性加权的方式未必能组合出最佳的控制量[8]。面对PID方法存在的缺点,国内外已经有多种控制方法被提出,包括模糊PID与滑模等控制方法[9 – 10]。
20世纪80年代末期,韩京清提出自抗扰(ADRC)控制方法,在保留了PID方法不依赖模型参数优点的基础上,通过微分跟踪器、扩张状态观测器以及非线性加权3个部分弥补了PID的不足。自抗扰控制方法已经被应用在诸多领域并取得了很好的效果[11]。本文为解决潜航器在近水面、低航速下受波浪扰动大,控制力降低,目标深度难以维持的问题,设计自抗扰深度控制器,通过扩张状态观测器观测扰动并及时进行补偿[12]。仿真与实验结果证明,相比于传统PID控制方法,本文所设计的深度控制器使得潜航器具有更好的深度控制性能。
1 问题的提出潜航器在近水面、低航速状态下航行时,深度控制难度较大[13]。本文潜航器具有首尾水平舵各一对,尾垂直舵一对。由于潜航器纵稳性较强,且在低航速下纵倾对深度变化影响较小,故重点考虑垂荡运动,水平舵亦均用于进行深度控制,在总力矩输出为0的情况下产生升沉控制力。潜航器升沉运动方程可以表示为:
| $ \left\{ {\begin{aligned} & {\dot z = - u \cdot \sin \theta + w \cdot {\rm{cos}}\theta }{\text{,}}\\ & {\left( {m - {Z_{\dot w}}} \right)\dot w - {Z_w}w - {Z_{\left| w \right|w}}\left| w \right|w - {Z_{\dot q}}\dot q - }\\ & \quad \quad{{Z_q}q = {\delta _s}{Z_{{\delta _s}}} + {\delta _b}{Z_{{\delta _b}}} + {Z_0}}{\text{。}} \end{aligned}} \right. $ | (1) |
式中:u为航速;w为垂荡速度;z为深度;δb和δs分别为首尾水平舵舵角;Z0与M0分别为扰动力与力矩[14]。
潜航器深度控制力来源于水平舵的升力,升力公式为
由于本文潜航器的工况为近水面,波浪的扰动力相比于在深水中要更加剧烈,所以深度控制的难度显著增加,需要提高控制力。而航速较低的情况下潜航器水平舵升力降低,需要设计更高效的控制器,因此本文采用自抗扰技术设的深度控制器。
自抗扰控制器主要包含3个部分,即跟踪微分器、扩张状态观测器与非线性加权[8]。
1)跟踪微分器可以提取微分信号,并且相对于传统差分的方法具有噪声放大效果不明显的优势,同时还可以安排过渡过程以避免由于初始偏差过大引起的超调问题。
| $ \left\{ {\begin{split} &{{v_1}\left( {k \!+\! 1} \right) \!=\! {v_1}\left( k \right) \!+\! h\cdot{v_2}\left( k \right)}{\text{,}}\\ &{{v_2}\left( {k \!+\! 1} \right) \!=\! {v_2}\left( k \right) \!+\! h\cdot {\rm{fhan}}\left( {{v_1}\left( k \right) \!-\! v\left( k \right),{v_2}\left( k \right),r,h} \right)}{\text{。}} \end{split}} \right. $ | (2) |
式中:
2)扩张状态观测器能够观测控制目标的值及其微分信号,并且将除控制输入量以外的合力作为总扰动(包括模型误差与环境扰动力)观测出以便给予补偿。
| $ \left\{ {\begin{aligned} & {e = {z_1} - y}{\text{,}}\\ & {\mathop {{z_1}}\limits^ \cdot = {z_2} - {\beta _{01}}e}{\text{,}}\\ & {\mathop {{z_2}}\limits^ \cdot = {z_3} - {\beta _{02}}{f_1} + bu\left( t \right)}{\text{,}}\\ & {{z_3} = - {\beta _{03}}fal\left( {e,\alpha ,\delta } \right)}{\text{。}} \end{aligned}} \right. $ | (3) |
式中:
3)非线性加权能够将控制目标的偏差及其微分信号进行高效的组合以产生合适的控制输入量。
| $ \left\{ {\begin{array}{*{20}{l}} {{e_1} = {v_1}\left( k \right) - {z_1}\left( k \right)}{\text{,}}\\ {{e_2} = {v_2}\left( k \right) - {z_2}\left( k \right)}{\text{,}}\\ {{u_0}\left( k \right) = {\beta _{01}}fal\left( {{e_1},{\alpha _1},\delta } \right) + {\beta _{02}}fal\left( {{e_1},{\alpha _2},\delta } \right)}{\text{,}}\\ {u\left( k \right) = {u_0} - \dfrac{{{z_3}\left( k \right)}}{b}}{\text{。}} \end{array}} \right. $ | (4) |
式中:
由于在实际实验过程中传感器存在噪声干扰,且扩张状态观测器观测其微分信号时噪音的干扰作用将被放更大,进而容易导致执行机构出现高频振动,一方面影响控制效果,另一方面可能导致机械损坏。本文将自抗扰控制技术中的跟踪微分器(TD)用于滤波,相比传统的一阶差分,TD滤波器能够在相同的相位滞后情况下产生更好的滤波效果[16]。
| $ \left\{ {\begin{array}{*{20}{l}} {{v_1}\left( {k + 1} \right) = {v_1}\left( k \right) + h\cdot{v_2}\left( k \right)}{\text{,}}\\ {{v_2}\left( {k + 1} \right) = {v_2}\left( k \right)} +\\ \qquad\qquad\;\;\;{ h\cdot fhan\left( {{v_1}\left( k \right) - v\left( k \right),{v_2}\left( k \right),r,{h_0}} \right)}{\text{。}} \end{array}} \right. $ | (5) |
式中:
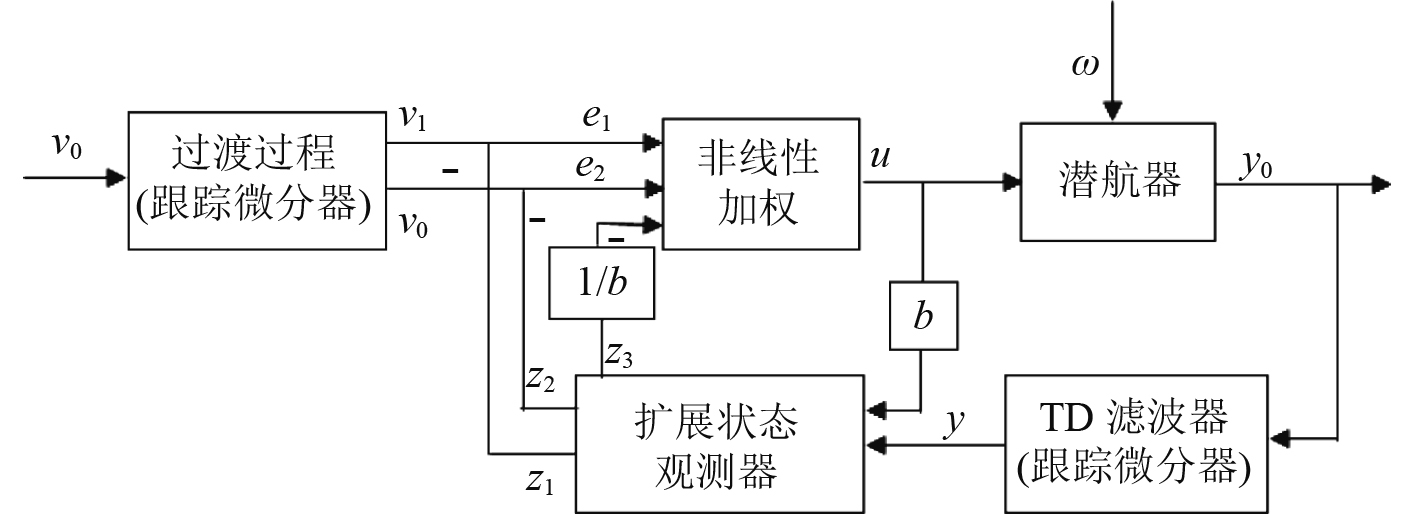
|
图 1 自抗扰控制器结构图 Fig. 1 Structure of ADRC |
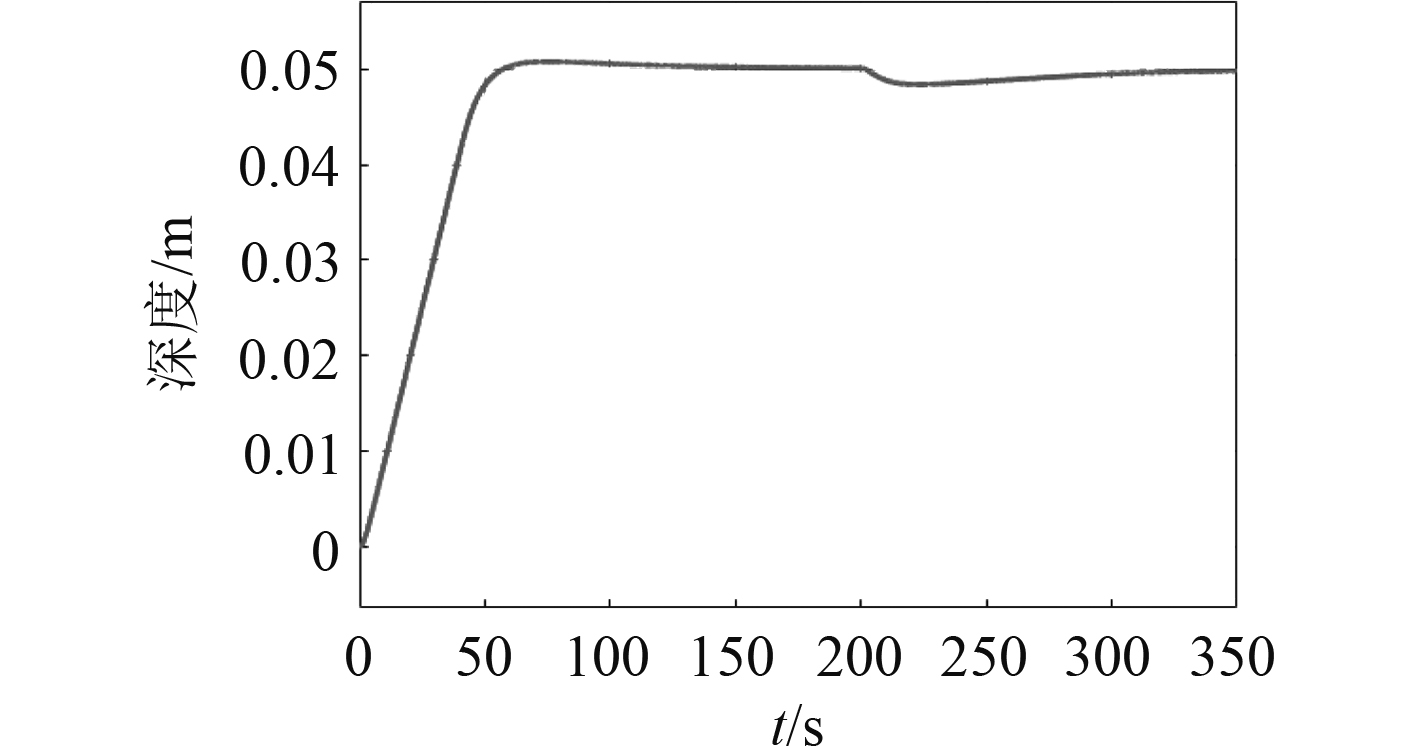
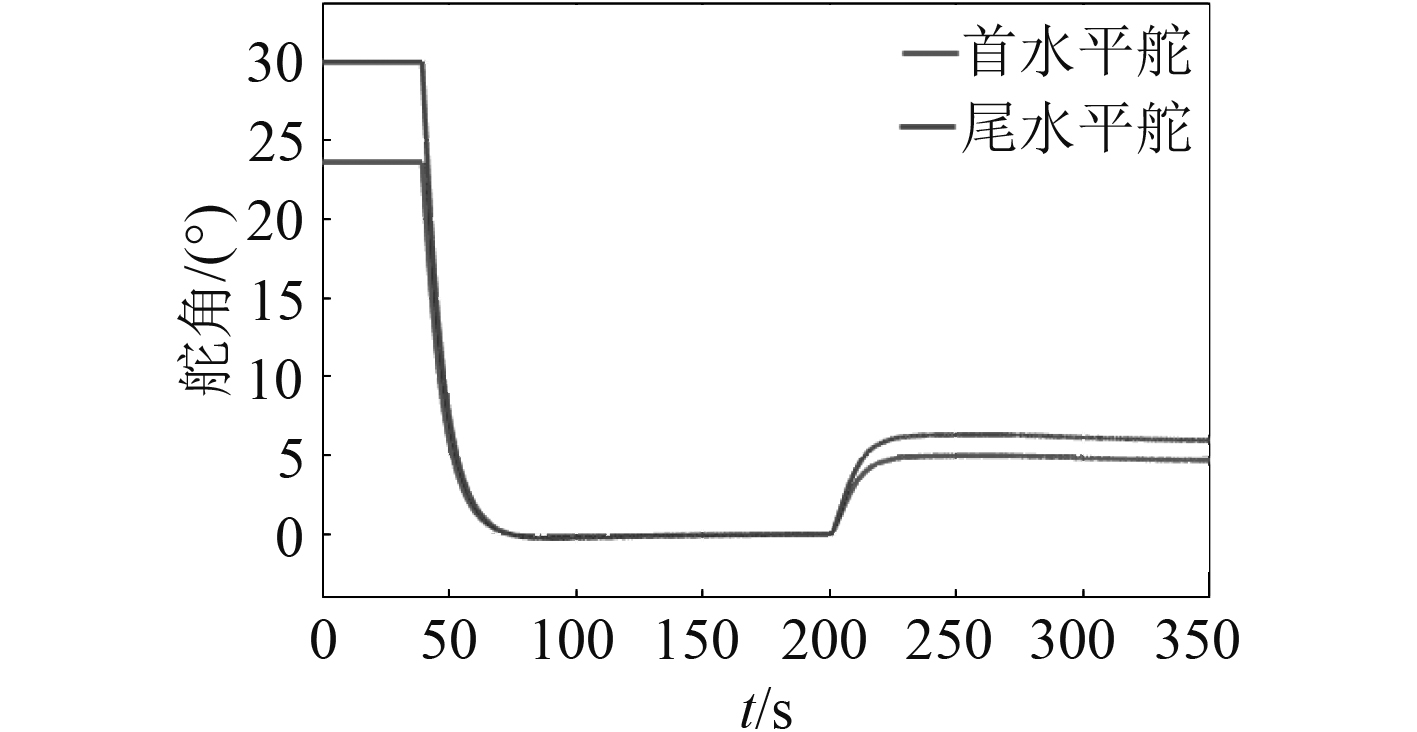
本文对作为研究对象的潜航器进行建模,根据实际参数建立了Simulink仿真模型,并采取不同的控制器对潜航器深度控制进行仿真。PID控制器的控制效果如图2所示,执行机构舵角如图3所示。其中控制器参数为Kp=3000,Ki=50,Kd=0。
|
图 2 PID控制器深度控制效果 Fig. 2 Depth (PID) |
|
图 3 PID控制器水平舵舵角变化 Fig. 3 Angle of planes (PID) |
在无干扰的情况下,调节时间为48.1 s。在仿真过程的第200 s处,施加常值扰动以模拟波吸力。受波吸力的影响,潜航器深度减至4.84 cm,之后由控制器缓慢调节至5 cm。
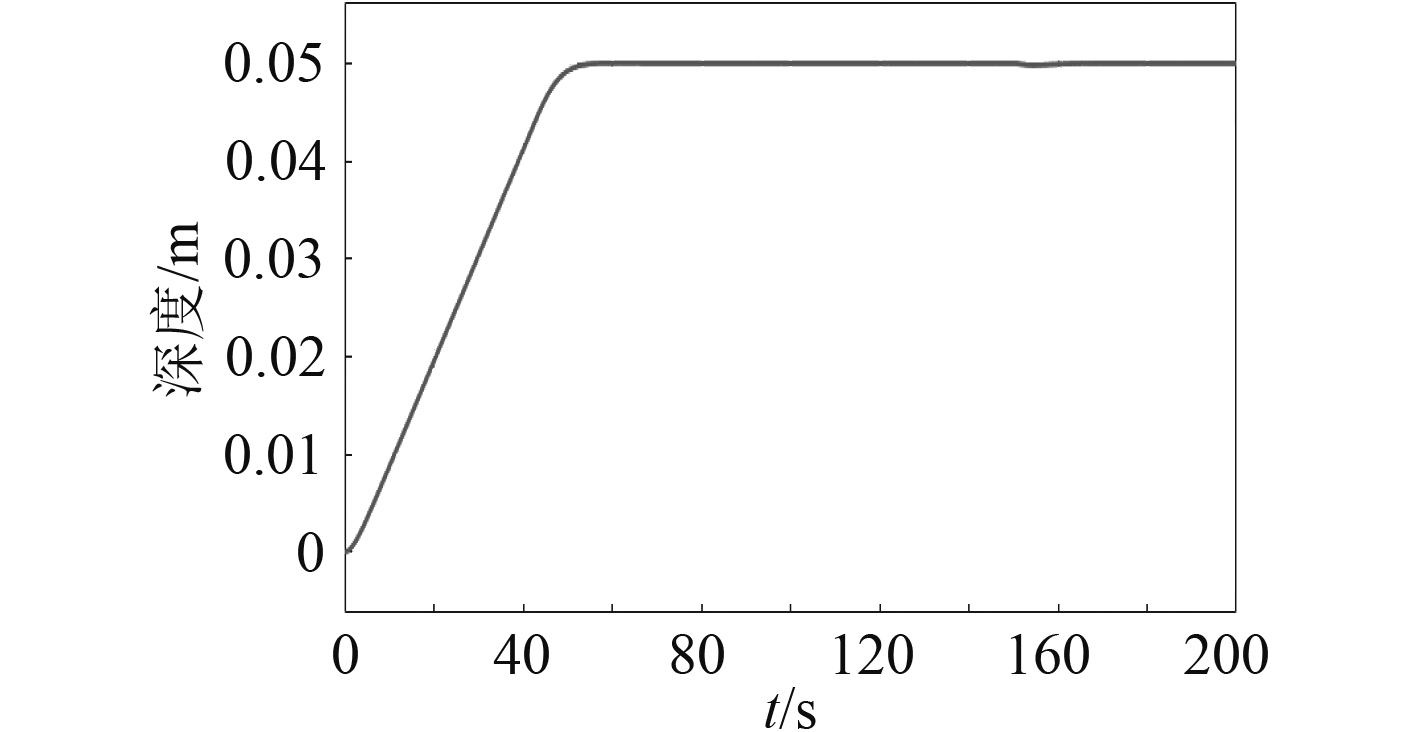
自抗扰控制仿真结果如图4所示,执行机构舵角如图5所示。其中控制器参数如下:
|
图 4 深度控制效果 Fig. 4 Deprh (ADRC) |

|
图 5 ADRC控制器水平舵舵角变化 Fig. 5 Angle of planes (ADRC) |
过渡过程参数r=0.01,h=0.05;
扩张状态观测器参数β1=20,β2=60,β3=90,δ=0.01;
非线性加权参数β1=80,β2=400,δ=0.01。
调节时间为46.4 s。受波吸力的影响,最小深度达到了4.96 cm,之后由控制器调节至5 cm。
由仿真结果可以看出,当收到波吸力的影响时,潜航器具有深度减小的趋势。PID控制器若无积分项则会存在稳态误差,维持在偏离目标的某一深度。存在积分项的PID控制器依靠积分项消除稳态误差使潜航器回到目标深度附近,但由于偏差的积分需要时间,所以具有明显的控制滞后现象。与PID控制方法不同的是,面对扰动ADRC控制方法通过扩张状态观测器观测扰动并快速调整舵角及时给予补偿,使得潜航器在收到扰动力后能够快速抵消波吸力对潜航器深度的影响,保持在目标深度附近。相较于PID控制器,ADRC控制器能够更有效抵抗波浪扰动,具有更好的深度控制效果。
4 实 验为验证仿真结果,本文对潜航器深度控制进行了水池实验验证。由于水池长度有限,为保证足够长稳态运动段,潜航器水池实验采取分段控制的方法。第1阶段,潜航器首先由压载水舱控制下潜,在下潜深度达到0.65 m且升沉速度不大于0.05 m/s时进入第2阶段。此时关闭水泵,同时启动螺旋桨,由水平舵进行深度控制。由于压载水舱控制精度有限,将导致第2阶段潜航器具有非零浮力状态,需要基于水平舵的深度控制器予以克服。实验工况设定为速度0.17 m/s,目标深度0.7 m。
在实验过程中,由于传感器存在测量噪声,使用TD滤波器对传感器数据进行滤波以避免微分项中噪声较大影响控制效果。实验验证了波浪扰动下ADRC深度控制器的深度控制效果,深度变化如图6所示。
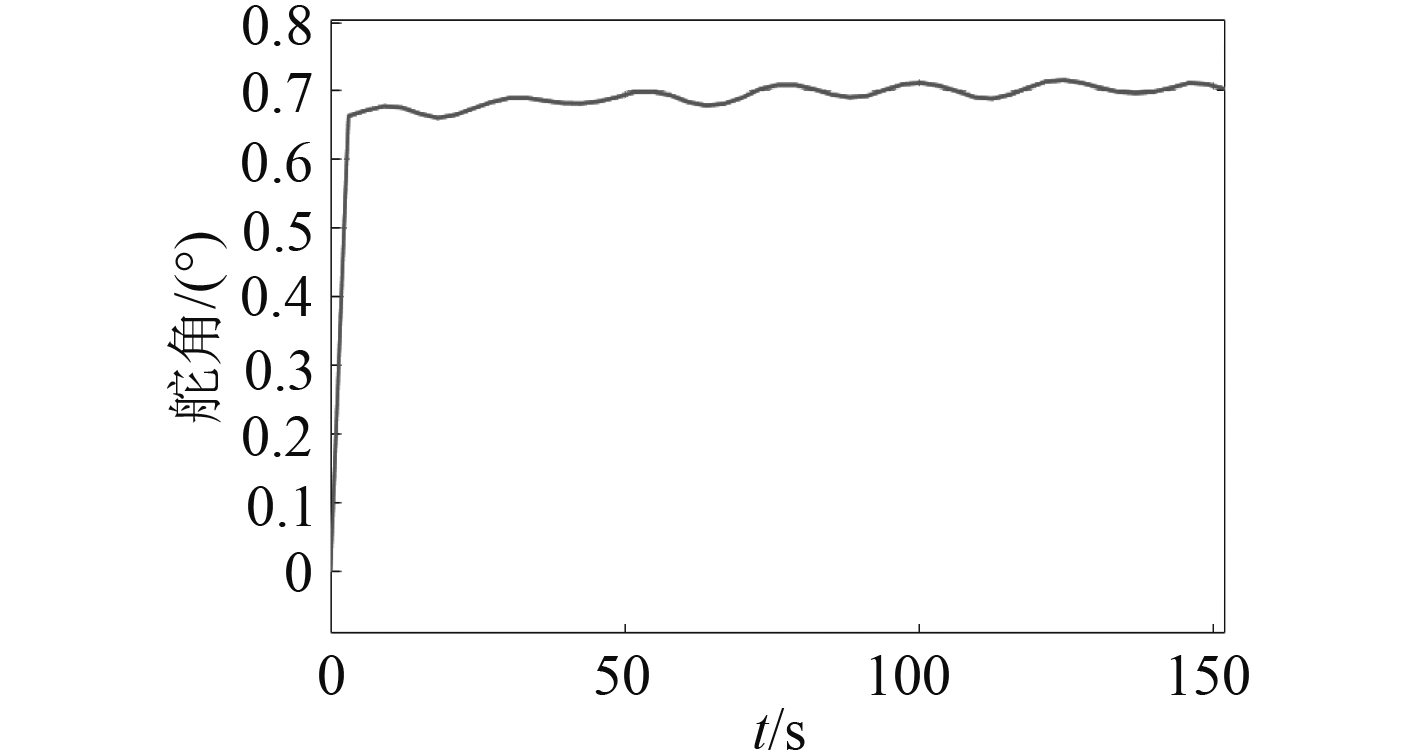
|
图 6 深度控制实验效果 Fig. 6 Depth |
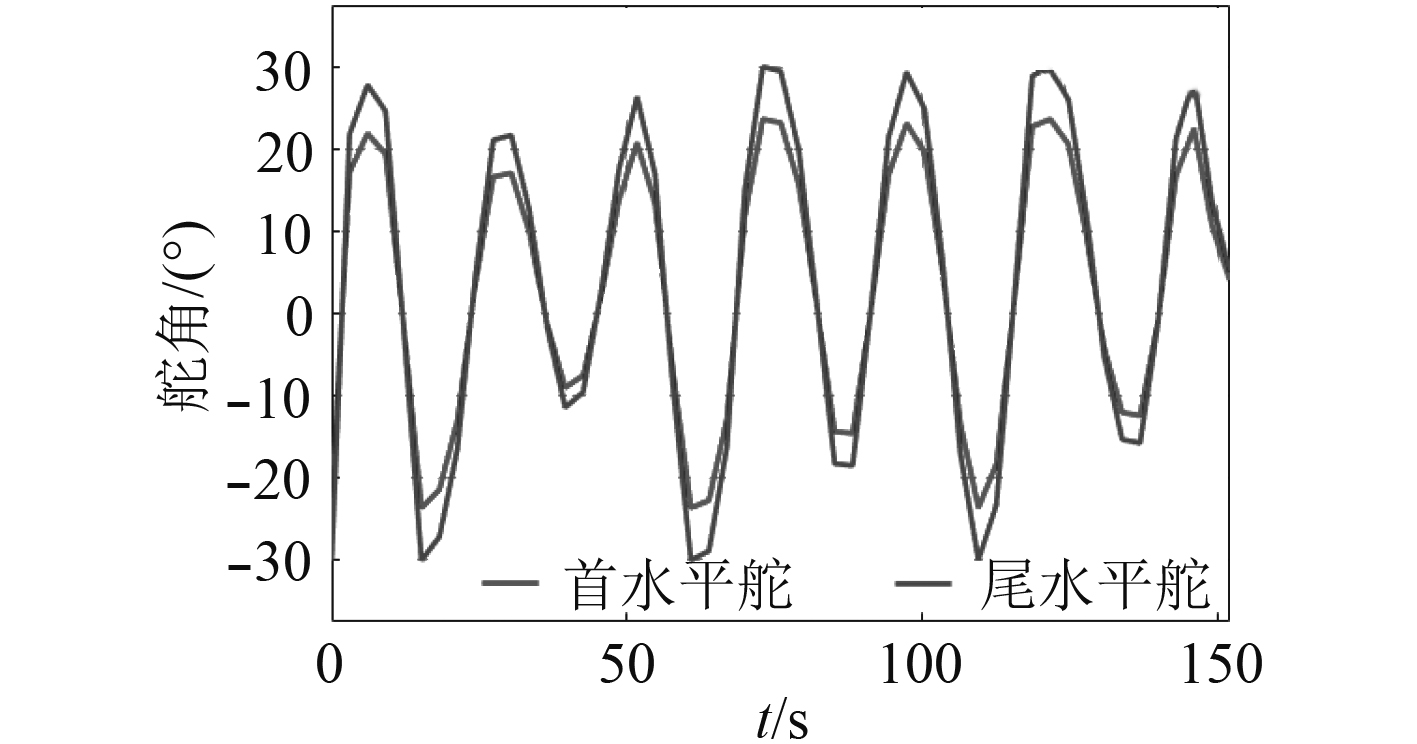
|
图 7 水平舵舵角变化实验结果 Fig. 7 Angle of planes |
在深度首次到达0.7 m后,潜航器在控制器作用下平均深度为0.700 48 m。面对波浪的扰动,潜航器在航速下有效抵抗了波吸力的影响,没有在波吸力的作用下体现出被吸至水面的趋势,维持在了0.7 m处的目标深度附近,验证了ADRC控制器具有良好的控制效果。
5 结 语潜航器时常需要根据要求保持在某一目标深度附近,其控制性能决定对潜航器完成任务的质量。水平舵在潜航器上被广泛采用,但由于水平舵提供的控制力与航速的平方成正比,所以在低航速状态下,水平舵控制力大幅降低,此时传统的PID控制方法无法发挥执行机构最大控制力,难以保证深度控制效果。同时潜航器在近水面受波浪力的扰动更大,二阶波浪力将使潜航器具有被吸至水面的趋势,使得潜航器更加难以保持深度。
为此,本文基于自抗扰控制技术(ADRC)设计深度控制器。通过仿真对比了在受到扰动后不同控制器的控制效果。PID控制器中的比例项依靠偏差可以抵消扰动但无法消除稳态误差。控制器中的积分项可以消除稳态误差误差,但是偏差的积分需要时间所以在受到扰动后深度回到目标值的时间较长。利用自抗扰技术中扩张状态观测器能够及时观测扰动并进行补偿的特点,ADRC控制器能够在受到扰动后及时做出反应,使潜航器的深度在扰动下保持在目标深度。最后,进行了水池实验,实验中潜航器始终保持在目标深度0.7 m处附近,验证了潜航器ADRC深度控制器在波浪扰动下的良好表现。压载水深度控制调节能力强但控制量不精确,而基于自抗扰控制技术的水平舵控制具有控制量精确且能观测总扰动的特点。未来的研究方向是将压载水控制与水平舵控制结合起来,面对高强度的扰动使用压载水进行大幅度调节,而扰动与压载水合作用力作为总扰动再由水平舵进行精确控制。
| [1] |
ZHANG J, LIAN L, TONG G. Robust control and simulation of near-surface submarine[J]. Ocean Engineering, 2006, 24(4): 32-31. |
| [2] |
LICÉAGA-CASTRO E, UGALDE-LOO C E, NAVARRO-LÓPEZ E M. Efficient multivariable submarine depth-control system design[J]. Ocean Engineering, 2008, 35(17): 1747-1758. |
| [3] |
GAO Fu-dong, PAN Cun-yun, HAN Yan-yan, et al. Nonlinear trajectory tracking control of a new autonomous underwater vehicle in complex sea conditions[J]. Journal of Central South University, 2012, 19(7): 1859-1868. DOI:10.1007/s11771-012-1220-1 |
| [4] |
FONT R, GARCÍA-PELÁEZ J. On a submarine hovering system based on blowing and venting of ballast tanks[J]. Ocean Engineering, 2013, 72(7): 441-447. |
| [5] |
林龙信, 沈林成, 张代兵. 仿生波动鳍的试验研究[J]. 哈尔滨工程大学学报, 2008, 29(5): 489-492. DOI:10.3969/j.issn.1006-7043.2008.05.011 |
| [6] |
JIN H, PAN L, WANG L. Adaptive variable structure control with neuron for low speed stabilizing of submarine near surface[J]. Control & Decision, 2010, 25(4): 562-566+571. |
| [7] |
LICEAGA-CASTRO E, VAN d M G M. Submarine H ∞, depth control under wave disturbances[J]. Control Systems Technology IEEE Transactions on, 1995, 3(3): 338-346. DOI:10.1109/87.406981 |
| [8] |
HAN J. From PID to Active Disturbance Rejection Control[J]. IEEE Transactions on Industrial Electronics, 2009, 56(3): 900-906. DOI:10.1109/TIE.2008.2011621 |
| [9] |
LIN X, HU D, DUAN Z. The Research on Fuzzy-PID Control of the Submarine Course[C]// International Symposium on Computational Intelligence & Design. IEEE, 2013: 281-284.
|
| [10] |
ASHRAFIUON H, MUSKE K R, MCNINCH L C, et al. Sliding-Mode Tracking Control of Surface Vessels[J]. IEEE Transactions on Industrial Electronics, 2008, 55(11): 4004-4012. DOI:10.1109/TIE.2008.2005933 |
| [11] |
XUE W, BAI W, YANG S, et al. ADRC with adaptive extended state observer and its application to air-fuel ratio control in gasoline engines[J]. IEEE Transactions on Industrial Electronics, 2015, 62(9): 5847-5857. DOI:10.1109/TIE.2015.2435004 |
| [12] |
CUI R, CHEN L, YANG C, et al. Extended state observer-based integral sliding mode control for an underwater robot with unknown disturbances and uncertain nonlinearities[J]. IEEE Transactions on Industrial Electronics, 2017, 64(8): 6785-6795. DOI:10.1109/TIE.2017.2694410 |
| [13] |
DUAN W, WANG L, CHEN J. Calculation of vertical second-order drift loads on a submarine floating near the free water surface based on Taylor expansion boundary element method[J]. Journal of Harbin Engineering University, 2017, 38(1): 8-12. |
| [14] |
T I. FROSSEN, Guidance and control of ocean vehicles. 1994.
|
| [15] |
L. ZHANG, Y B. LI. Fluid Mechanics, 220-221, 2006
|
| [16] |
L. WU, J. HAN. TD Filter and its applications[J]. Computing Technology and Automation, 2003, 22(s1): 61-63. |
 2020, Vol. 42
2020, Vol. 42
