0 引　言

反舰导弹是打击舰船的主要装备，多采用半穿甲战斗部，战斗部会穿透舰船外壳在舱室内部进行爆炸，爆炸所产生的爆炸产物和爆炸冲击波不仅会对舰船的船体结构造成破坏，还会对舱室内部的仪器设备和船员造成威胁。因此，舰船舱室在内部爆炸载荷作用下的毁伤情况一直受到多方面的持续关注，对后续舰船的防护研究起着至关重要的作用。

反舰导弹的战斗部侵彻入到舱室，在舱室内部进行爆炸，主要的毁伤因素是爆炸产物和爆炸所产生的冲击波。由于爆炸是一种复杂的非线性动态响应过程，再由于舱室的封闭性，爆炸冲击波会在舱室内部多次反射，爆炸所产生的毁伤远比自由大气中爆炸的情况复杂的多，毁伤效果也更严重。因此开展舱室内部爆炸研究，了解密闭空间爆载载荷特性和结构毁伤机理，对提高舰船的生命力和毁伤评估都具有重要的工程应用价值。

当舰船受到反舰武器攻击，舱室内部发生爆炸时所产生的载荷不同于在空气中爆炸时所产生的载荷。当炸药在空气中爆炸时，对结构物的作用只有冲击波载荷。而当炸药在舰船内部舱室发生爆炸时，不仅形成对结构的冲击波载荷，而且由于密闭空间的限制，爆炸所产生的高温、高压产物无法及时向外扩散，导致舱室内部温度升高，形成准静态气体压力。此时，舰船舱室所承受的是冲击波载荷和准静态气体压力的双重载荷作用。

1 舱室内部爆炸过程数值模拟 1.1 材料模型

数值模拟中所选取的材料模型类型和参数对其仿真计算的结果有较大影响。为了准确地对舱室内部爆炸舰船结构毁伤的动态响应进行数值模拟研究，考虑到舰船的特殊性，有限元计算模型材料选为907A、921A钢，采用Cowper-Symonds应变率强化模型。有限元模型材料参数如表1所示。TNT炸药采用高能密度空气模拟，精度为1 600 kg/m³，比内能为4.19 GJ/m³。根据朱锡等^[1]《船舶结构毁伤力学》一书中对921A钢各种力学性能的试验研究，907A钢取应变率敏感性常数为：D=6180，P=1.56。907A钢取应变率敏感性常数为：D=42306，P=2.116。

1.2 有限元仿真模型

在舱室内部爆炸结构动态响应的有限元数值模拟研究中，所选取的中部三舱段模型长为31 m，宽为17.4 m，高为11.6 m，中间舱室为炸药所在舱室。有限元模型中，在每层甲板和舷侧结构上都设计有加强筋。整体有限元模型及炸药的布置情况如图1所示。选取炸药当量为150 kg的球形TNT炸药，炸药位置在左舷侧外1.2 m，2甲板以上1.4 m。

2 舱室内部爆炸载荷特性研究 2.1 舱室内部爆炸冲击波参数计算

由图2所示的空气冲击波 $\Delta p(t)$ 曲线可以明显看出爆炸所产生的冲击波能量主要集中在正压区。因此就破坏作用而言，正压区的影响远大于负压区，负压区的影响可不予考虑。一般来说，通常用以下3个参数来衡量冲击波对目标的破坏作用：1）冲击波的峰值压力 $\Delta {p_m}$ ；2）冲击波正压持续时间 ${\tau _ + }$ ；3）比冲量 ${I_ + }$ ， ${I_ + } = \int {\begin{array}{*{20}{c}} {{\tau _ + }} \\ 0 \end{array}} p(t){\rm d}t$ 。以上3个参数作为冲击波的主要特征量表征了冲击波破坏作用的大小^[2]。

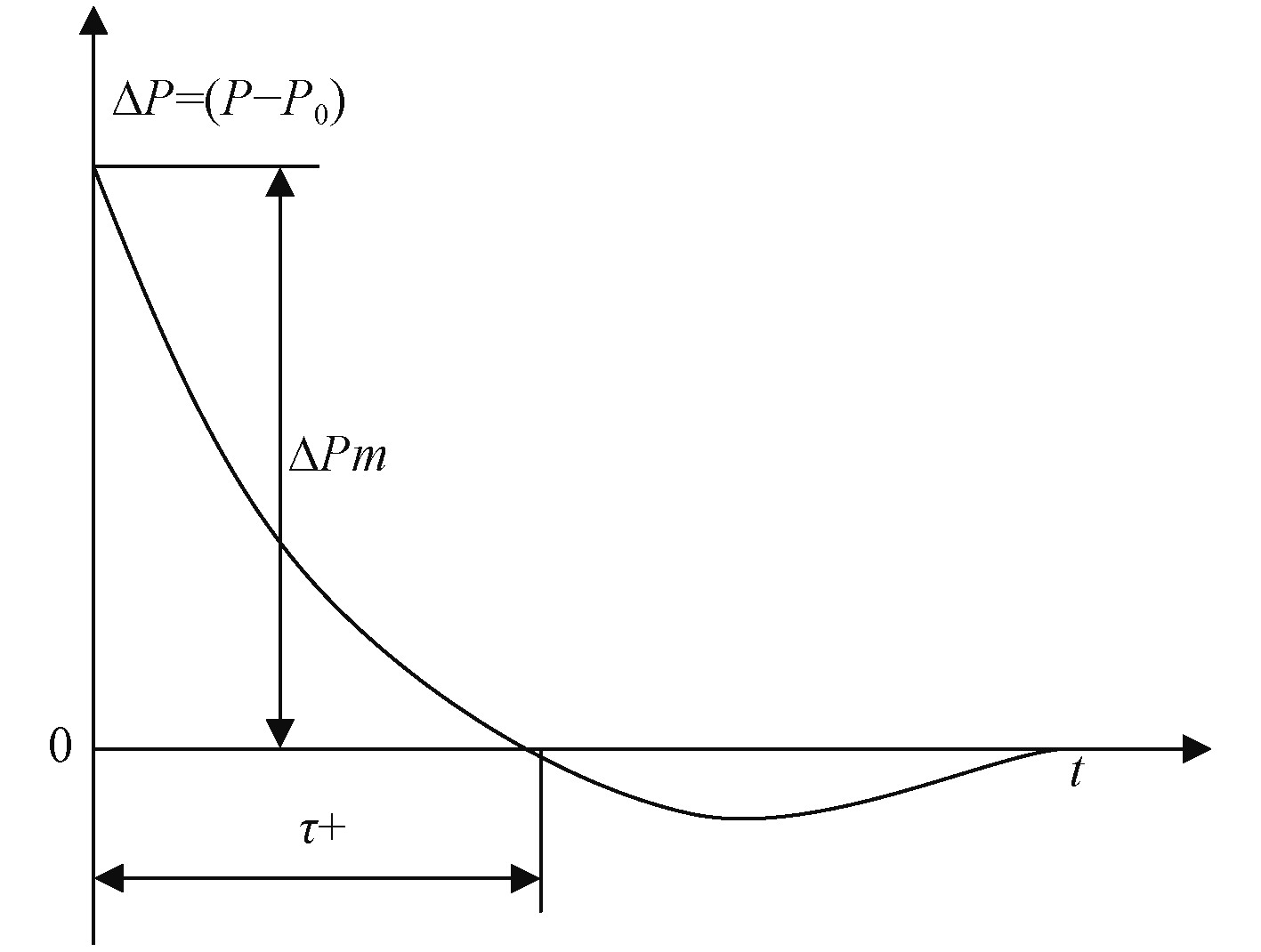
大量实验研究结果表明，炸药在空气中爆炸存在相似律，根据相似理论基础、通过量纲分析和实验标定参数的方法可得到上述爆炸冲击波3个主要特征量的经验计算公式。

2.1.1 爆炸空气冲击波峰值超压 $\Delta {p_m}$ 的计算公式

对于裸露的TNT球形装药在无限空气中爆炸，爆炸空气冲击波峰值超压 $\Delta p$ 存在下列算公式^[3]：

CaдOBCKий得到

$\Delta p = \frac{{0.076}}{{\bar r}} + \frac{{0.025}}{{{{\bar r}^2}}} + \frac{{0.65}}{{{{\bar r}^3}}}{\text{，}}$

(1)

Henrych得到

$\Delta p = \frac{{1.379}}{{\bar r}} + \frac{{0.543}}{{{{\bar r}^2}}} - \frac{{0.035}}{{{{\bar r}^3}}} + \frac{{0.0006}}{{{{\bar r}^4}}}(0.05 \leqslant \bar r \leqslant 0.3){\text{，}}$

(2)

$\Delta p = \frac{{0.6076}}{{\bar r}} - \frac{{0.032}}{{{{\bar r}^2}}} + \frac{{0.209}}{{{{\bar r}^3}}}(0.3 \leqslant \bar r \leqslant 1){\text{，}}$

(3)

$\Delta p = \frac{{0.0649}}{{\bar r}} + \frac{{0.3973}}{{{{\bar r}^2}}} + \frac{{0.3226}}{{{{\bar r}^3}}}(1 \leqslant \bar r \leqslant 10){\text{。}}$

(4)

我国国防工程设计规范中规定的计算公式

$\Delta p = \frac{{0.082}}{{\bar r}} + \frac{{0.265}}{{{{\bar r}^2}}} + \frac{{0.686}}{{{{\bar r}^3}}}(1 \leqslant \bar r \leqslant 15){\text{。}}$

(5)

式中： $\Delta p$ 为空气冲击波峰值超压，kgf/cm²； $\bar r = $ ${r / {\sqrt[3]{{\tilde w}}}}$ 称为对比距离， $r$ 为爆炸空气冲击波的传播距离，m， $\tilde w$ 为装药量，kg。

2.1.2 空气冲击波正压区作用时间 ${\tau _ + }$ 的计算

空气冲击波正压时间 ${\tau _ + }$ 是衡量爆炸对目标破坏程度的重要参数之一。J.Henrych^[4]通过大量的TNT炸药爆炸试验数据导出超压作用时间的经验公式：

$ \begin{aligned} {\tau _ + } = & {10^{ - 3}}\left( {0.107 + 0.444\bar R + 0.264{{\bar R}^2} - } \right.\\ & \left. {0.129{{\bar R}^3} + 0.0335{{\bar R}^4}} \right)\sqrt[3]{W}{\text{。}} \end{aligned} $

(6)

式中： $ 0.05 \leqslant \bar R = \dfrac{R}{{\sqrt[3]{W}}} \leqslant 3{\text{，}} \left( {{\rm m}/{\rm k}{{\rm g}^{1/3}}} \right){\text{。}}$

化学爆炸的正压作用时间一般为毫秒量级，瞬间即可对结构物产生巨大的破坏。

2.1.3 空气冲击波比冲量 ${I_ + }$ 的计算

炸药在空中爆炸时，爆炸空气冲击波对各种结构或建筑物的破坏作用与作用于结构上的冲量直接相关^[5]。为此，必须先知道爆炸空气冲击波的比冲量的大小。与前面分析的超压、正压区作用时间一样，爆炸空气冲击波的比冲量仍然服从相似律。由量纲分析可得正压区比冲量：

${I_ + } = \frac{C}{{\overline r }}\sqrt[3]{{\tilde w}}{\text{。}}$

(7)

与前面超压的处理方法相同，当使用其他种类的炸药时，把 $\tilde w$ 当作该种炸药的TNT当量即可。

2.2 舱室内部爆炸载荷简化计算研究 2.2.1 舱室内部爆炸载荷特性研究

当炸药在舱室内部进行爆炸时，都将产生内部爆炸载荷。炸药在空气中爆炸时，炸药能量向四周扩散，对结构物的作用只有冲击波载荷，当炸药在舱室内部爆炸时，一方面形成对结构的冲击波载荷，另一方面，由于结构物的限制作用，爆炸产生的高温、高压产物无法及时向外扩散，导致结构内温度升高，形成准静态的气体压力。此时，结构物要承受冲击波和准静态气体压力的双重荷载作用，可简化为图3所示的双直线形式^[6]。

图中，等效载荷分为2个阶段：第1阶段内的初始峰值为P₀，0～t₁时刻迅速下降到P₁；第2阶段从t₁～t₂，超压降至0。对于完全封闭的空间，在药量较大时等效载荷第2阶段可认为压力恒定，即t₂无穷大。

2.2.2 舱室内部爆炸等效加载方法研究

本文中，初始破口较小，可以忽略不计，近似看成是完全封闭的空间。根据之前有限元计算的结果，能够拟合出压力值与爆距、时间的函数曲线，再将其在Dytran里面通过场函数和施加Pressure，等效成静载，模拟炸药在舱室内部爆炸的情况，从而实现对内爆载荷的简化计算。具体的施加函数如下：

$ \begin{split} P = & 19086206 - 356151.8 \times \\ & \sqrt[2]{{\left( {{{(x - 68.5)}^2} + {{(y + 7.18277)}^2} + {{(z - 7.806)}^2}} \right.}}-\\ & \frac{{38481449.53}}{{\ln (\sqrt[2]{{({{(x - 68.5)}^2} + {{(y + 7.18277)}^2} + {{(z - 7.806)}^2}}})}}+\\ & \frac{{195637319.1}}{{{{(x - 68.5)}^2} + {{(y + 7.18277)}^2} + {{(z - 7.806)}^2}}}{\text{，}}\\[-17pt] \end{split} $

(8)

$ P = 3778.062 \times {e^{( - 15497.5 \times t + 689.2734 \times \sqrt t )}} + 48874227 \times t{\text{。}} $

(9)

式（8）为压力与爆距（x，y，z）的函数，式（9）为压力与时间（t）的函数。

舱内爆炸载荷与敞开环境下的爆炸载荷有较大区别，由于舰船结构的影响，舱内爆炸下，舱室板架结构承受的冲击载荷除壁面反射冲击波外，在舱室角隅部位还有强度远大于壁面反射冲击波和汇聚波，以及这些冲击波的多次反复作用。舱内爆炸下舱室板架中部结构所承受的初始冲击载荷强度与敞开环境爆炸下壁面反射冲击载荷强度相当，而舱内爆炸下舱内爆炸荷的强度远大于敞开环境爆炸下壁面反射冲击载荷。舱内爆炸下舱室板架结构的主要失效模式是沿角隅部位发生撕裂失效并发生大挠度外翻变形。为了更好地模拟炸药在内部舱室发生爆炸后破坏的形貌，在靠近爆点爆炸舱室边界和角隅施加8倍放大系数的Pressure，爆炸舱室其他边界角隅处施加4倍放大系数的Pressure，在爆炸舱室其他地方施加1倍的Pressure具体加载情况如图4～图7所示。

3 计算结果分析比较

由于爆炸所产生的冲击波是迅速作用在舱室结构上的一个动态的载荷，而简化计算方法的等效加载则是长时间静态的一个载荷持续作用在舱室结构上的，所以取爆炸后稳定时间点0.015 s，对2种方法下相同当量和舱段的动态响应进行对比。

3.1 爆炸舱室结构的动态响应对比分析

通过对计算结果进行分析可以看出，炸药爆炸产生冲击波后，冲击波在舱室内部传播开来，先作用于与爆心距离最近的舷侧板架结构，然后结构应力通过舷侧向四周传播开来，冲击波在空气域又传播了一段时间到达甲板结构，对甲板结构产生冲击作用，最后舱壁应力和甲板应力在甲板与舱壁接触处产生耦合作用，产生应力集中。同时，在舷侧角隅处也存在应力集中，这主要是舱壁、甲板、舷侧的应力以及空气中冲击波多重耦合的缘故。存在应力集中的角隅区域，舱壁结构容易破坏，从应力云图中看出与爆心距离很近的甲板结构受到的冲击作用很大，容易撕裂并伴随着大面积的塑性变形，而且由于一甲板和二甲板的作用，塑性变形区域大致呈椭圆形，压力通过开口耗散使得开口处发生了外翻。

3.2 炸舱室结构的应力对比分析

本文重点研究在密闭空间冲击波作用下的爆炸舱室结构的动态响应，并在此基础上进行内爆载荷的简化计算，因此在研究简化计算方法可行性时对应力进行对比分析是至关重要的。通过图8对比分析，可以清楚看到爆炸舱室的应力对比，不管是爆炸毁伤的破损位置，还是应力扩展的趋势都是极其相似的，误差为2.58%。具体计算结果如表2所示。

3.3 炸舱室结构的应变对比分析

由图9可以看出，靠近爆点一侧的舷侧、舷侧与上下甲板的交接处、舷侧与左右横舱壁的交界处及近爆点一侧的舱室角隅处，结构都发生了失效。简化计算方法与多欧拉耦合计算方法大体相似，在发生失效的位置、形状、趋势大致相同，不同的是简化计算方法在大开口的结构处和远爆点一侧的舱室角隅处并没有发生失效，而且在横舱壁与甲板的交界处损毁的并没有那么严重。具体计算结果如表3所示。

3.4 炸舱室结构的位移对比分析

由图10可以看出，靠近爆点一侧的舷侧、舷侧与上下甲板的交接处、舷侧与左右横舱壁的交界处及近爆点一侧的舱室角隅处，结构都发生了较大的位移，并随着位移的进一步扩大，结构发生了破损、撕裂。简化计算方法与多欧拉耦合计算方法计算结果大体相似，在发生位移的位置、形状、变化趋势大致相同，不同的是简化计算方法的最大位移处发生在近爆点一侧的舷侧与上甲板交界处，而多欧拉耦合算法的最大位移处在近爆点一侧的舷侧与横舱壁的交接角隅处。这可能是由于爆炸所产生的是瞬间冲击波，而简化计算方法是将冲击波载荷等效成了静载，持续施加在爆炸舱室的板架结构上，所以简化计算方法发生的位移更大，但由于爆炸产生的冲击波在舱室角隅处会发生汇聚并反射，所以多欧拉耦合算法下产生位移的结构区域更大。误差最大为9.19%。具体计算结果如表4所示。

3.5 炸舱室结构的破口对比分析

由之前的位移图可以看出，靠近爆点一侧的舷侧、舷侧与上下甲板的交接处、舷侧与左右横舱壁的交界处及近爆点一侧的舱室角隅处，结构都发生了较大的位移，并随着位移的进一步扩大，结构发生了破损、撕裂。简化计算方法与多欧拉耦合计算方法计算结果大体相似，在发生位移、破口的位置、形状、变化趋势大致相同，不同的是简化计算方法所计算产生的破口比多欧拉耦合算法计算所产生的破口大，塑性变形区域比多欧拉耦合算法的计算结果稍小一些，迎爆点的最大位移量也大得多。这可能是由于爆炸所产生的是瞬间冲击波，而简化计算方法是将冲击波载荷等效成了静载，持续施加在爆炸舱室的板架结构上，所以简化计算方法产生的破口更大，但由于爆炸产生的冲击波在舱室角隅处会发生汇聚并反射，所以多欧拉耦合算法下产生位移的结构区域更大。具体计算结果如表5所示。

4 结　语

本文通过建立选取舰船的典型三舱段有限元模型，并选取了合适的材料参数，对舰船在舱室内部爆炸载荷作用下的结构动态响应进行数值模拟分析。提出一种关于内部爆炸载荷计算的简化计算方法，对多欧拉耦合计算方法和简化计算方法数值模拟的结果进行比较分析，得出以下结论：

1）舱室内部爆炸时，首先冲击波会作用到最近的板架结构，并随着进一步的传播在板架连接处和角隅处汇聚、反射，对舰船结构造成进一步的毁伤；

2）由数值仿真和各种计算结果的比较分析可以发现，无论是从应力、应变、位移及破口方面考虑，内爆载荷简化计算方法的误差最大不超过10%，始终控制在误差允许的范围之内，并能够节省大量的计算时间和计算成本，具有一定的可行性，为后续计算提供了简化计算方法。