穿甲弹有着体积小、动能大、穿透力强、精度高等特点,被广泛应用于世界各国先进的近程反导舰炮武器中,如“密集阵”、“守门员”、“海上卫士”均采用穿甲弹[1]。这些近程反导舰炮武器的拦截近界一般能到500 m左右,承担着水面舰艇末端反导的重要使命,必须对反舰导弹达到“一中即毁”的效果。穿甲弹在与反舰导弹相互作用时,以直接碰撞的形式与反舰导弹相遇,而且,近程反导舰炮武器以对本舰近距离来袭导弹拦截为目的,穿甲弹与反舰导弹相遇时往往是命中反舰导弹弹体头部及侧面前部的部分区域。因此,对穿甲弹开展命中反舰导弹弹体头部及侧面前部区域时的毁伤效应研究是非常有意义的。文献[2 − 3]研究了脱壳穿甲弹对超音速反舰导弹战斗部壳体的侵彻问题和对JDAM弹壳体的侵彻情况,而没有涉及弹丸引爆带壳装药战斗部的毁伤分析。本文从近程反导舰炮用于舰艇反导时弹丸和目标的相遇过程出发,建立了弹丸与目标相遇模型,针对舰炮反导时重点作用的反舰导弹前端部位建立了易损性模型,针对K级和C级2种毁伤情况给出包括引爆带壳装药战斗部和穿透战斗部前端壳体的毁伤效应计算模型。以某典型反舰导弹为例,对穿甲弹对其的毁伤效果进行研究,给出了造成K级毁伤时弹丸与目标相遇时比动能与相遇角的关系和C级毁伤的比动能量值范围,为近程反导舰炮使用穿甲弹对反舰导弹的毁伤威力研究提供一定基础支撑。
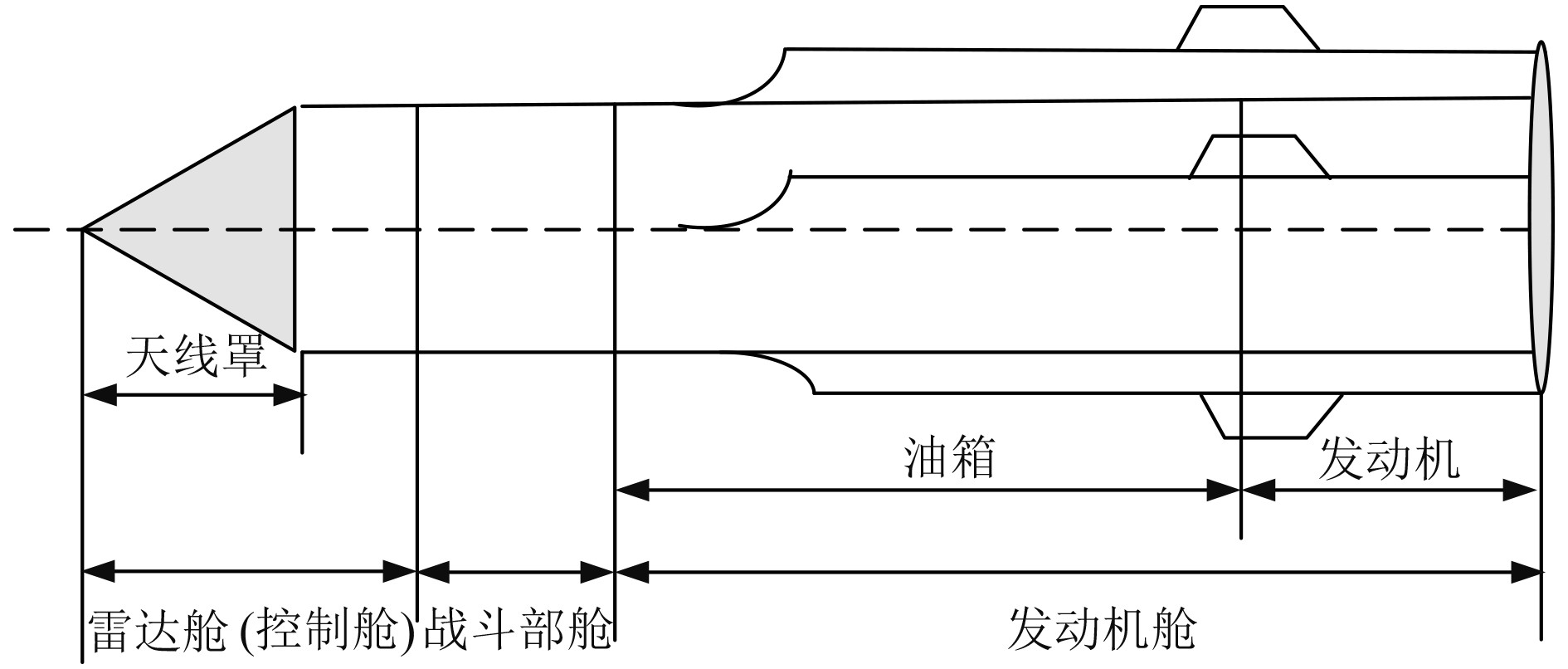
1 穿甲弹与反舰导弹相遇模型典型反舰导弹的结构如图1所示。大多数反舰导弹头部是雷达舱(控制舱),然后是战斗部舱,后面是发动机舱。
|
图 1 典型反舰导弹结构图 Fig. 1 Structure diagram of typical anti-ship missile |
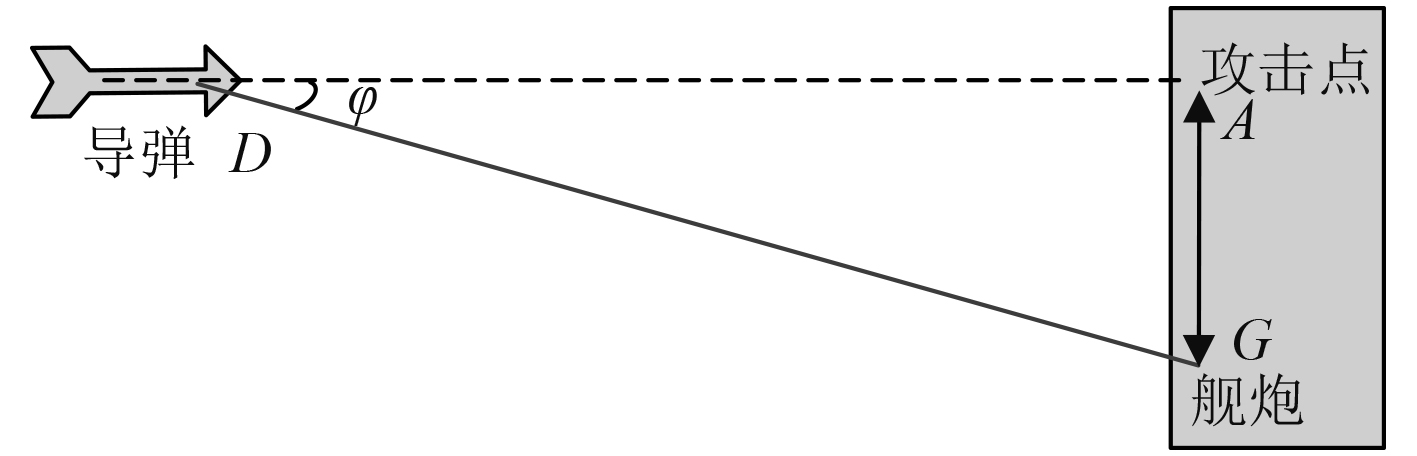
当反舰导弹攻击舰艇时,舰艇上安装的近程反导舰炮发射穿甲弹对其拦截,穿甲弹与反舰导弹的相遇过程示意图如图2所示。
|
图 2 反舰导弹与穿甲弹相遇过程示意图 Fig. 2 Schematic diagram of encounter process of anti-ship missile and AMDS |
设G为舰炮武器中心、D为反舰导弹中心,A为反舰导弹在舰船上的攻击点,GD为穿甲弹的飞行轨迹,穿甲弹与导弹相遇的夹角为φ,由图2可知:
| $ {\rm{\varphi }} = {\rm{arcsin}}\left( {{{AG}}/{{DG}}} \right)\text{。} $ | (1) |
一般近程反导舰炮武器的拦截范围为2 000~500 m,而舰艇的长度一般为150~300 m,AG长度的范围就为0~300 m,代入式(1)可以得到φ的范围一般在0°~37°之间。
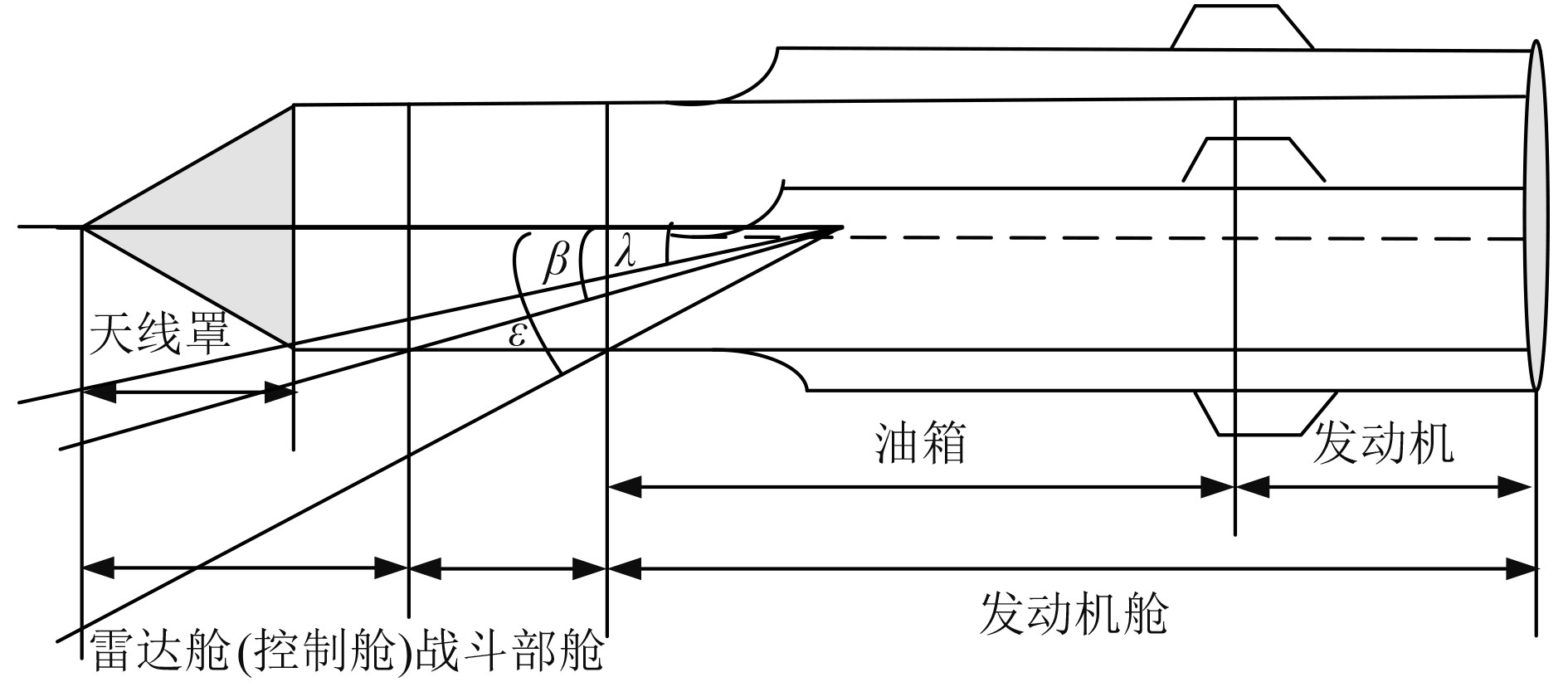
将穿甲弹与反舰导弹的相遇夹角插入图1中得到穿甲弹与反舰导弹的相遇模型如图3所示。
|
图 3 穿甲弹与反舰导弹相遇模型 Fig. 3 The encounter model of AMDS and anti-ship missile |
由图3可以看出,当穿甲弹与反舰导弹相遇夹角φ满足0°<φ<λ时,穿甲弹穿透反舰导弹天线罩、前端控制舱,命中导弹战斗部;当穿甲弹与反舰导弹相遇夹角φ满足λ<φ<β时,穿甲弹从侧面穿透反舰导弹控制舱,命中导弹战斗部;当穿甲弹与反舰导弹相遇夹角φ满足β<φ<ε时,穿甲弹从侧面穿透导弹蒙皮从侧面命中战斗部;当穿甲弹与反舰导弹相遇夹角φ满足ε<φ时,穿甲弹穿透蒙皮命中导弹后部发动机舱。由于φ的范围一般在0°~37°之间,而根据典型反舰导弹各部分的结构尺寸,ε一般大于37°,因此本文重点对φ<ε的情况进行研究。
2 典型反舰导弹前端易损性模型按照功能的丧失程度,将典型反舰导弹划分为2个毁伤等级[4 − 5]:
1)K级毁伤。反舰导弹被摧毁,功能完全丧失。
2)C级毁伤。反舰导弹部分功能丧失,不能准确命中目标。
分析造成K级毁伤的原因,主要有:1)战斗部燃烧、爆炸,油箱或发动机爆炸;2)反舰导弹结构解体;3)反舰导弹失控坠海,反舰导弹控制仪系统彻底损坏或反舰导弹气动外形大面积损坏。
分析造成C级毁伤的原因,主要有:1)反舰导弹控制部件失效,导弹失去制导控制;2)反舰导弹气动外形局部被破坏,飞行轨迹偏移。
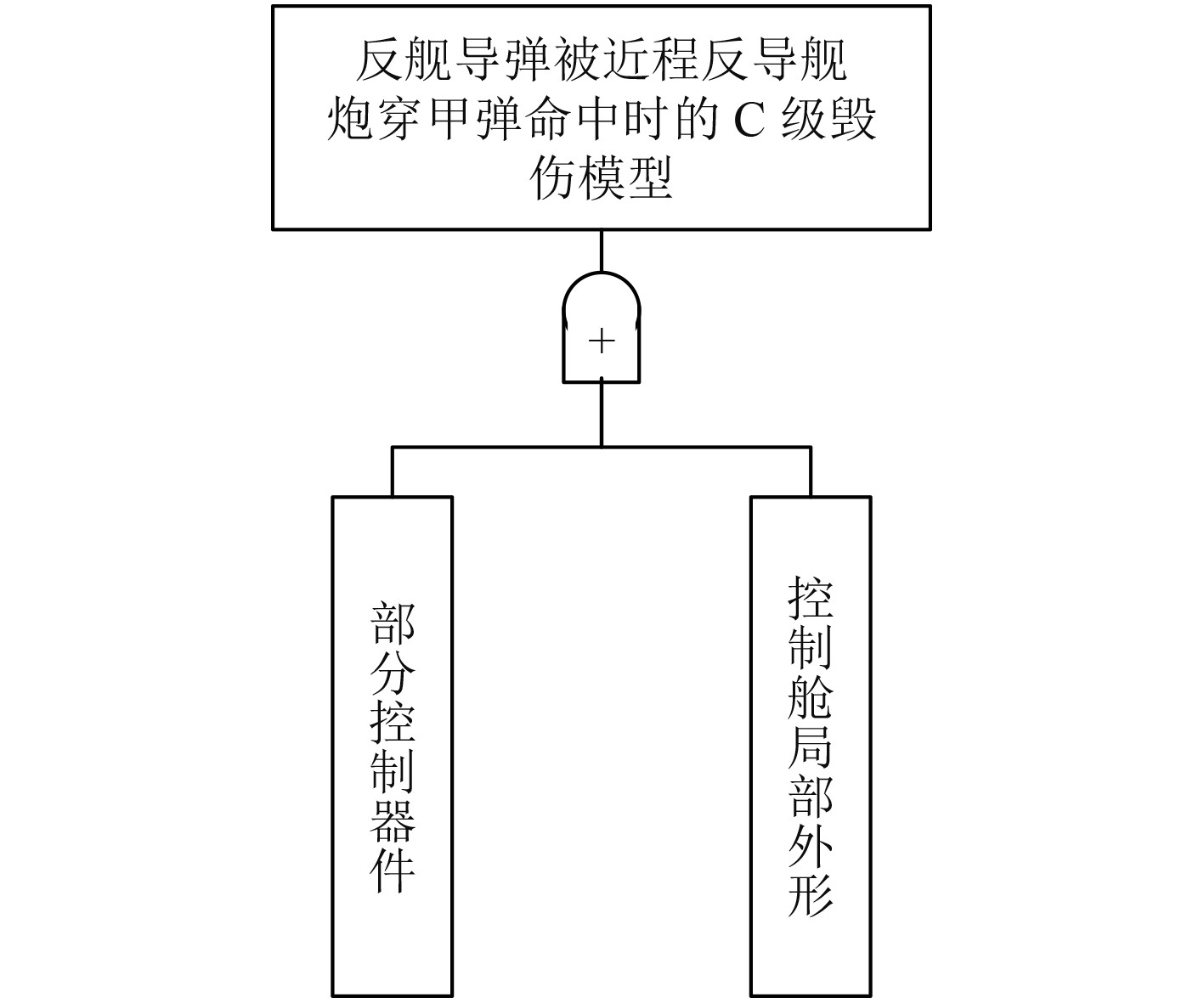
造成K级毁伤的部件为战斗部、弹体、油箱、发动机、控制仪;造成C级毁伤的部件为部分控制器件、部分弹体结构。根据前文的分析,φ<ε时,穿甲弹基本是穿透反舰导弹的控制舱命中战斗部或是直接命中战斗部,而且近程反导舰炮使用的穿甲弹弹丸较小,全航路命中导弹的数量也较少,想对导弹弹体造成大面积损坏比较困难。因此,在近程反导舰炮使用穿甲弹毁伤反舰导弹的过程中,造成反舰导弹K级毁伤的部件主要考虑战斗部;造成反舰导弹C级毁伤的部件主要为部分控制器件、控制舱的局部外形。建立近程反导舰炮使用穿甲弹毁伤反舰导弹的K级毁伤树如图4所示,C级毁伤树如图5所示。

|
图 4 近程反导舰炮使用穿甲弹毁伤反舰导弹的K级毁伤树 Fig. 4 Level K damage tree of anti-ship missile damaged by AMDS in close-in weapon system |
|
图 5 近程反导舰炮使用穿甲弹毁伤反舰导弹的C级毁伤树 Fig. 5 Level C damage tree of anti-ship missile damaged by AMDS in close-in weapon system |
根据第2节建立的K级毁伤树,穿甲弹对反舰导弹K级毁伤主要是引爆反舰导弹战斗部。在穿甲弹与反舰导弹相遇时,首先由于相遇位置和角度不同,穿甲弹从与反舰导弹相遇到与战斗部相遇的过程中需穿透的遮挡物不同;其次,不同相遇角下引爆带壳装药的速度也不同。因此,在建立战斗部引爆模型时分为2个步骤,第1步只计算不同相遇角下引爆战斗部带壳装药所需的速度;第2步以第1步计算的速度作为剩余速度,结合不同的遮挡物厚度,计算不同相遇角下要想引爆战斗部穿甲弹与反舰导弹相遇所需的最小速度,进而得到穿甲弹与反舰导弹的比动能。
3.1.1 引爆带壳装药战斗部的速度计算反舰导弹战斗部的装药多为钝感炸药,在炸药晶粒中添加了钝感剂,使得战斗部中装药的成分和微观结构复杂。当战斗部中装药受到猛烈撞击时,由于摩擦、变形等因素,使得装药在局部急剧升温,当温度高于炸药的分解温度时,炸药发生分解,产生热量,并向周围的炸药扩展,引起更多的炸药温度升高、分解,此时炸药发生爆燃,进而转变为爆轰。研究这种爆轰以及炸药与惰性材料相互作用的现象时通常采用点火增长模型。
点火增长模型中,未反应炸药JWL状态方程和爆轰产物JWL状态方程可以表示为[6]:
| $\begin{split} &{{{p}}_{{{AB}}}}\left( {{V}} \right) = {{A}}\left( {1 - \frac{{{\omega }}}{{{{{R}}_1}{{V}}}}} \right){{{e}}^{ - {{{R}}_1}{{V}}}} +\\ & {{B}}\left( {1 - \frac{{{\omega }}}{{{{{R}}_2}{{V}}}}} \right){{{e}}^{ - {{{R}}_2}{{V}}}}{ + \frac{{{{\omega e}}}}{{{V}}}}, \end{split} $ | (2) |
| $ \frac{{{\rm d}{p}_{s}}}{{\rm d}V} = - {{A}}{{{R}}_1}{{{e}}^{ - {{{R}}_1}{{V}}}} - {{B}}{{{R}}_2}{{{e}}^{ - {{{R}}_2}{{V}}}} - \frac{{\left( {{{\omega }} + 1} \right){{C}}}}{{{{{V}}^{{{\omega }} + 2}}}}, $ | (3) |
式中:pAB,ps为反应物压力;V为反应物体积;A,B,R1,R2、ω为常量,与炸药的爆炸威力相关。
反应速率方程为[7]:
| $ \begin{split} & \frac{{\partial {{F}}}}{{\partial {{\tau }}}} = {{I}} \cdot {\left( {1 - {{F}}} \right)^{{b}}} \cdot {\left( {{\rm{\rho }}/{{\rm{\rho }}_0} - 1 - {{a}}} \right)^{{x}}} + {{{G}}_1}(1-{{F}}{)^{{c}}}\times\\ & {{{F}}^{{d}}} \cdot {{{p}}^{{y}}} + {{{G}}_2}{\left( {1 - {{F}}} \right)^{{e}}} \cdot {{{F}}^{{g}}} \cdot {{{p}}^{{z}}}, \end{split} $ | (4) |
式中:F为炸药反应度;ρ为密度;ρ0为初始密度; p为气体压力;I,b,a,x,G1,c,d,y,G2,e,g,z为常数。
为研究穿甲弹和战斗部壳体高速碰撞和炸药爆轰引起的强烈冲击载荷问题,采用Johnson-Cook模型[8]。
此模型定义屈服应力为:
| ${\sigma _Y} = \left( {A + B{\varepsilon ^{\rm{n}}}} \right)\left( {1 + C{\rm{ln}}{{\overline \varepsilon }^{\rm{*}}}} \right)\left( {1 - {T^{*{\rm{m}}}}} \right),$ | (5) |
其中:
| ${T^*} = \frac{{T - {T_{\rm{r}}}}}{{{T_{\rm{m}}}{\rm{ - }}{{\rm{T}}_{\rm{r}}}}}\text{。}$ | (6) |
式中:
穿甲弹与反舰导弹相遇时,依靠大比动能穿透反舰导弹的带壳装药前部遮挡物,应用THOR方程得到在穿甲弹和导弹接触时的最小穿透不同遮挡物厚度和材料时的极限速度以及穿透后的弹丸剩余速度。THOR方程的一般形式为:
| $ {{{V}}_{{r}}} = {{{V}}_{{c}}} - {10^{{{{C}}_1}}} \cdot {\left( {{{{t}}_0}{{S}}} \right)^{{{\rm{\alpha }}_1}}}{{m}}_{{f}}^{{{\textit{β}}_1}}{\left( {\sec {\rm{\theta }}} \right)^{{{\rm{\gamma }}_1}}} \cdot {\rm{V}}_{\rm{C}}^{{{\rm{\lambda }}_1}}, $ | (7) |
| $ {{{V}}_{{{bl}}}} = {\left[ {{{10}^{{{{c}}_1}}} \cdot {{\left( {{{{t}}_0}{{S}}} \right)}^{{{\rm{\alpha }}_1}}}{{m}}_{{f}}^{{{{\beta }}_1}}{{\left( {\sec {{\theta }}} \right)}^{{{{\gamma }}_1}}}} \right]^{1/\left( {1 - {{{\lambda }}_1}} \right)}}\text{。} $ | (8) |
式中:t0为目标厚度,cm;mf为破片质量,g;VC为破片速度,m/s;上标c,α,β,γ和λ为目标材料特性参数;S为破片撞击目标时的接触面积,cm2。
3.2 穿甲弹对导弹目标C级毁伤效应研究方法穿甲弹对反舰导弹C级毁伤主要是命中控制舱后对部分控制器件和控制舱局部外形造成破坏。在进行C级毁伤效应研究时,把C级毁伤部件采用等效厚度分别等效成不同厚度的钢板。采用THOR公式分别计算在不同交会角下对每个毁伤部件的毁伤速度,计算比动能,应用数据对公式进行拟合,从而得到穿甲弹对不同导弹目标在不同交会角下造成C级毁伤的比动能。
4 穿甲弹对反舰导弹的毁伤效应仿真 4.1 穿甲弹对典型反舰导弹K级毁伤效应仿真计算穿甲弹对典型反舰导弹K级毁伤效应时,通过建模软件建立穿甲弹与带壳装药模型,将建立好的模型导入到Autodyn数值仿真软件中,计算穿甲弹在不同角度引爆带壳装药的速度,根据遮挡物厚度,进而计算得到弹目交会时速度以及造成K级毁伤的比动能。
4.1.1 建立数值仿真模型仿真时,穿甲弹以美国“密集阵”使用的脱壳穿甲弹为原型,弹芯材料为钨合金,弹丸质量为70 g,弹丸直径为12 mm。反舰导弹战斗部壳体材料为钢,战斗部壳体前端厚度为40 mm,两侧厚度均为17.5 mm。应用TG建模软件,分别建立穿甲弹、壳体、装药模型。将建立的模型导入到Autodyn数值仿真软件,并给模型添加材料,穿甲弹与带壳装药0°交会角时数值模型如图6所示。

|
图 6 数值仿真模型图 Fig. 6 Numerical simulation model diagram |
在Autodyn软件中赋予穿甲弹不同的速度,由于反舰导弹目标自身具速度,因此设置穿甲弹速度时需要考虑弹目相对速度,采用夹逼的方法不断缩小设置速度的范围,在炸药中设置观测点,在某速度下仿真计算结束后,通过查看炸药的压力—时间曲线、反应度—时间曲线和反应过程图判断炸药是否爆轰及穿甲弹在该速度下是否引爆带壳装药,如果压力—时间曲线中压力有跃升之后压力逐渐下降、反应度—时间曲线中反应度达到1和反应过程图中有稳定的波向前传播即认为已经引爆带壳装药,经过多次仿真计算得到在不同交会角下的起爆速度。
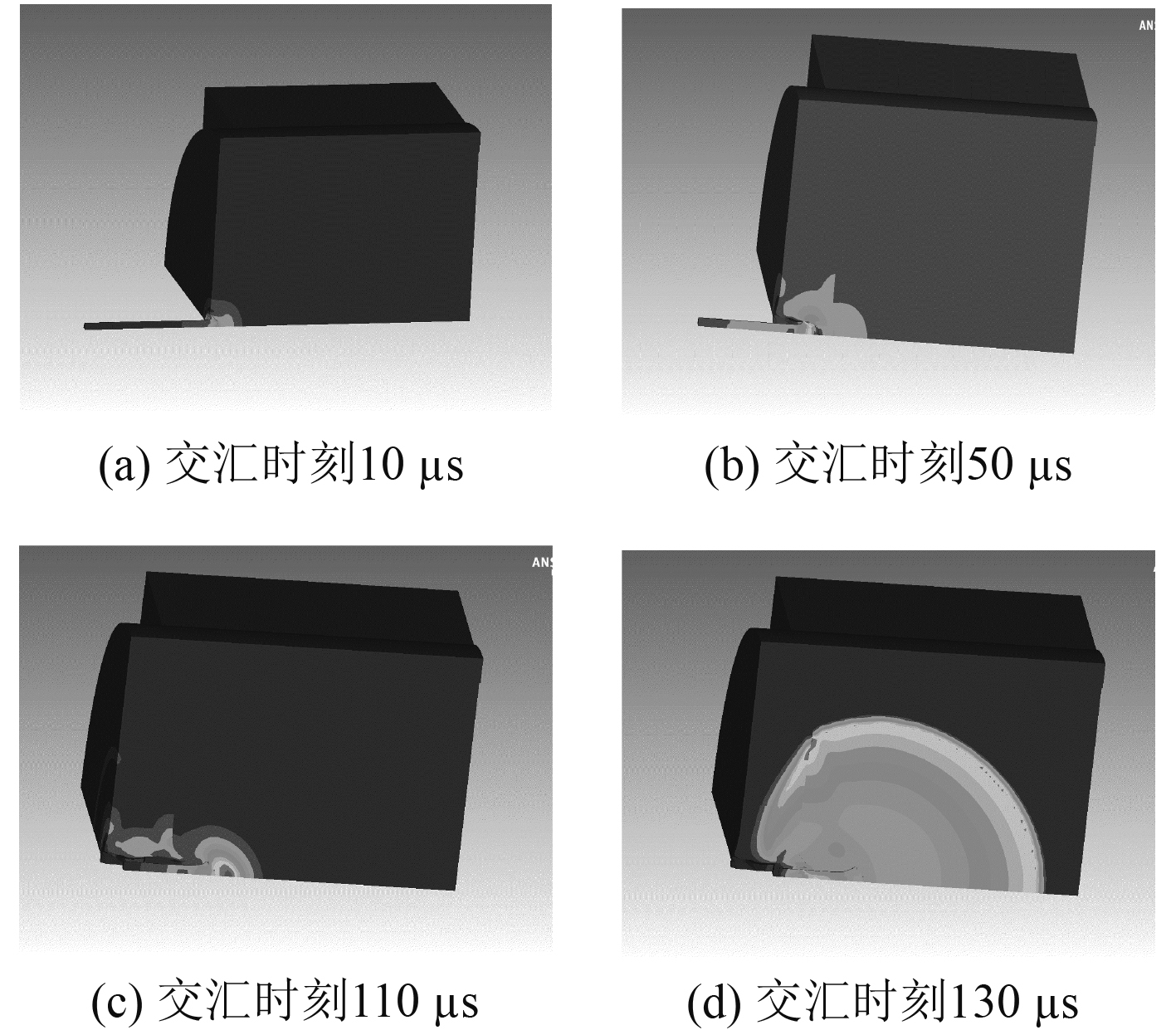
|
图 7 穿甲弹对导弹战斗部冲击起爆过程图 Fig. 7 Process chart of impact initiation of AMDS on missile warhead |
|
图 8 反应度—时间曲线 Fig. 8 Response-time curve |
仿真计算所用的不同穿甲弹与反舰导弹相遇角度时战斗部遮挡物厚度见表1。
|
|
表 1 不同相遇角时战斗部遮挡物厚度 Tab.1 Cover thickness of warhead at different meeting angles |
通过THOR公式计算在不同角度下穿透遮挡物厚度的速度,从而得到穿甲弹对某典型反舰导弹K级毁伤时角度与比动能关系曲线如图9所示。

|
图 9 穿甲弹对某典型导弹K级毁伤时角度与比动能关系曲线 Fig. 9 Relationship between the angle and specific kinetic energy of a typical missle damaged by AMDS at K level |
仿真计算所用的某型反舰导弹C级毁伤部件的厚度见表2。
|
|
表 2 某典型反舰导弹C级毁伤部件的等效厚度 Tab.2 Equivalent thickness of level C damaged parts of a typical anti-ship missile |
通过THOR公式计算穿透不同毁伤部件的速度,进而得到穿甲弹对某典型反舰导弹C级毁伤的比动能。经对典型反舰导弹舱段计算,在穿甲弹与导弹相遇角度范围内对反舰导弹C级毁伤所需的比动能为5~1 300 J/cm2。
5 结 语本文对近程反导舰炮使用穿甲弹对反舰导弹的毁伤效应进行研究,给出毁伤效应的研究方法,建立了弹目交互模型、K级和C级易损性模型、毁伤效应计算模型,并以某典型反舰导弹为例,得到2种毁伤等级下穿甲弹对典型反舰导弹毁伤所需比动能的初步计算结果,为近程反导舰炮武器系统毁伤威力研究提供一定基础支撑。
| [1] |
王宝成, 冯宇晨. 近程反导舰炮武器系统的发展趋势[J]. 火炮发射与控制学报, 2018(3): 94-96. WANG Bao-cheng, FENG Yu-chen. Development trend about the weapon system of the short range antimissile naval gun[J]. Journal of gun launch & control, 2018(3): 94-96. |
| [2] |
王诚成, 谢晓方, 孙涛, 等. 舰炮弹丸对典型反舰导弹的毁伤分析[J]. 哈尔滨工程大学学报, 2015, 36(3): 358-361. WANG Cheng-cheng, XIE Xiao-fang, SUN Tao, et al. Damage analysis of naval gun projectiles to a typical anti-ship missile[J]. Journal of Harbin Engineering University, 2015, 36(3): 358-361. |
| [3] |
邢军好, 陈有伟, 季信源. 脱壳穿甲弹毁伤JDAM分析及计算模型[J]. 指挥控制与仿真, 2011, 33(1): 47-50. XING Jun-hao, CHEN You-wei, JI Xin-yuan. Analysis and calculation model on JDAM damaged by APDS[J]. Command Control & Simulation, 2011, 33(1): 47-50. DOI:10.3969/j.issn.1673-3819.2011.01.012 |
| [4] |
李向东, 杜忠华. 目标易损性[M]. 北京: 北京理工大学出版社, 2013: 158-169.
|
| [5] |
王树山. 终点效应学[M]. 北京: 科学出版社, 2019. : 52-54
|
| [6] |
郝鹏程, 冯其京, 洪滔, 等. 钝感炸药点火增长模型的欧拉数值模拟[J]. 爆炸与冲击, 2012, 32(3): 243-249. HAO Peng-cheng, FENG Qi-jing, HONG Tao, et al. Euler numerical simulation of ignition growth model of insensityve explosive[J]. Explosion and shock waves, 2012, 32(3): 243-249. DOI:10.3969/j.issn.1001-1455.2012.03.004 |
| [7] |
陈清畴, 蒋小华, 李敏, 等. HNS-ⅠⅤ炸药的点火增长模型[J], 爆炸与冲击, 2012, 32(3): 328-332. CHEN Qing Chou, JIANG Xiao Hua, LI Min, et al. Ignition growth model of HNS-ⅠⅤ explosive[J]. Explosion and shock waves, 1980, 23(12): 328-332. |
| [8] |
李建光, 施琪, 曹结东. Johnson-Cook本构方程的参数标定[J]. 兰州理工大学学报, 2012, 38(2): 164-167. LI Jian-guang, SHI Qi, CAO Jie-dong. Parameters calibration for Johnson-Cook constitutive equation[J]. Journal of Lanzhou University of Technology, 2012, 38(2): 164-167. DOI:10.3969/j.issn.1673-5196.2012.02.038 |
 2019, Vol. 41
2019, Vol. 41
