2. 江苏自动化研究所,江苏 连云港 222006
2. Jiangsu Automation Research Institute, Lianyungang 222006, China
舰炮随动系统控制策略通常采用PID控制器,其输入信号是变化规律未知时间函数,要求被控对象按即定规律变化并与输入信号的误差保持在规定范围内。控制器参数调节的好坏直接影响控制系统的反应时间和稳定性[1 − 2],PID控制器参数优化设计往往在单机检验时进行设定,在舰炮武器系统全系统联动时会根据系统控制精度再次进行PID控制器参数调整,这依赖于经验公式或数据统计结果[3]。虽然舰炮随动反馈装置可以较好地满足系统的跟踪精度和快速性的要求,但是舰炮武器系统要适应不同作战需求,带炮样式中存在的非线性运动等不确定因素的存在,导致上述参数的设定并不能很好保证受控系统的快速性、准确性和平稳性。为了保证系统跟踪性能,除了提高分系统及设备自身的精度外,重要的是还需采用先进的控制策略,如为了适应非线性、慢时变、纯滞后、参数与结构的不确定性,解决传统PID控制很难再得到理想的效果,采用参数自调整自适应PID算法、模糊控制自适应PID算法[4]、基于广义Hermite-Biehler定理[5]等方法计算舰炮随动控制系统PID控制器参数稳定域。上述伺服随动控制方法多基于经典控制理论,结合自适应处理、参数辨识的研究成果,侧重于舰炮本体进行控制,较少考虑对受控对象输入数据的约束限制。
舰炮伺服控制系统通常采用的三环回路控制结构[6],即位置环、速度环、电流环。计算机作为位置环控制器核心,对整个伺服控制系统以及舰炮整体采取集中控制、离散处理。速度环和电流环分别集成在伺服驱动器内部,速度环和电流环采用PI控制器。舰炮伺服系统的控制精度从选用更高精度的伺服驱动器以及执行机构和改进位置环控制器算法2个方面进行提高,主要用于解决高速度和平稳度问题[7]。国内外学者考虑利用系统的动态特性和运动学信息,通过状态估计的方法,间接估计系统的速度。大部分文献则采用位置、速度控制环节,一是存在相应的相角滞后,影响系统的稳定裕度,甚至造成系统的不稳定;二是会降低系统带宽,造成系统响应速度变慢,跟踪能力下降。
舰炮随动系统为非线性控制系统,受舰艇摇摆影响,系统参数时变性强,具有大惯量、变负载、动平台的特征。某舰炮为了保证有快速的响应能力,在3个环路又增加了加速度环。本文从舰炮伺服随动系统被告控制对象仿真模型出发,建立火控设备外部输入数据控制关系,分析产生随动不平稳的因素,给出了可行性改进措施,并根据作战样式进行了实船验证,对于研究舰炮PID控制算法具有重要意义。
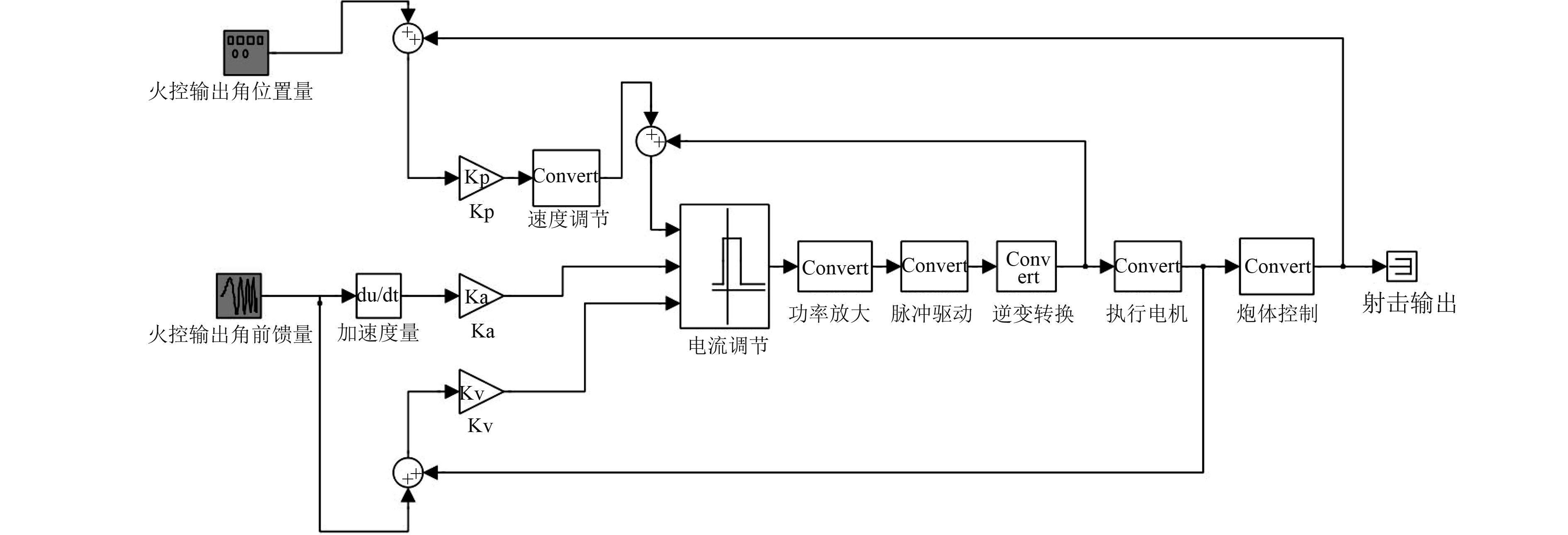
1 舰炮随动控制系统建模某舰炮质量重、惯性高,为了保证系统响应快的需求,在伺服系统中增加了加速度环路的建模控制,如图1所示。
|
图 1 某舰炮伺服随动系统控制模型 Fig. 1 Control models of a naval gun servo system |
火控根据火炮架位反馈与当前火控预测量进行对比,当角误差较大时则采用大角度调转过程,否则使用火控设备的输出数据进行伺服控制。实际应用中尽管能保证快速调转,但对输入的速度量较敏感,出现了大角度调转过程中舰炮不稳定,低速跟踪过程中电机有异响等现象。
产生上述现象的主要原因是舰炮随动系统对火控输出的角前馈量过于敏感,在角前馈的基础上又进行了一次微分控制,得到加速度量,同时增加利用加速度量对电流电机进行控制,当速度、加速度与实际运动不匹配或者火控解算角速度前馈含有噪声时,如舰炮阶跃或者跟踪速度不平稳。影响火控角速度解算精度的因素主要有:目标跟踪扰动误差、火控滤波预测误差、进行摇摆变换的舰船姿态数据误差、测量精度及数据传输误差、火控输出角前馈模型误差等,上述因素产生的误差在角位置上不明显,但是角前馈是根据角位置求导而来的,尽管火控在前馈输出时采用了平滑滤波处理,但在舰炮伺服控制又利用火控输出的角前馈量再次求导得到角加速度量,并在舰炮电流控制中增加这一控制量,同时根据角加速度量的大小进行电机控制以保证能够响应快速跟踪性能。
2 伺服随动控制火控角前馈平稳处理 2.1 跟踪过程处理方法信号处理中采用频域分析方法,通过研究信号的频谱特征对信号处理,较常用的是离散傅里叶变换,但该方法不能表达时域信息,因此在某些方面应用还存在一定的局限性,后续发展为短时傅里叶变换可以表达时域信息,但在相空间中的分辨率是固定的,不能反应信号的瞬时特性,后来又发展了小波分析算法,充分发挥频域分析和时域分析的优点,提供了灵活的信号处理分析方法,并广泛应用于信号处理、图像处理、语音识别、雷达成像、医疗分析等领域。
设
| $ {C_\psi } = \int_0^\infty {\frac{{{{\left| {\hat \psi (\omega )} \right|}^2}}}{\omega }{\rm d}\omega } < \infty \text{,} $ | (1) |
则
| $ \begin{array}{l} Wf(a,b) = \left\langle {f,{\psi _{a,b}}} \right\rangle = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \int_{ - \infty }^\infty {f(t)\dfrac{1}{{\sqrt a }}} {\psi ^*}\left(\dfrac{{t - b}}{a}\right){\rm d}t\text{,} \end{array} $ | (2) |
式中:
式(2)称为
| $ \begin{split} {\psi _{j,k}}(t) =& \frac{1}{{\sqrt {a_0^j} }}\psi \left(\frac{{t - ka_0^j{b_0}}}{{a_0^j}}\right) =\\ & a_0^{ - j/2}\psi (a_0^{ - j} - k{b_0}) \text{。} \end{split} $ | (3) |
其中:
推导出相应的离散小波变换
| $ \begin{split} Wf(j,k) =& \left\langle {f,{\psi _{j,k}}(t)} \right\rangle = \\ &\int_{ - \infty }^\infty {f(t)} \psi _{j,k}^*(t){\rm d}t =\\ & a_0^{ - j/2}\int_{ - \infty }^\infty {f(t)} {\psi ^*}(a_0^{ - j}t - k{b_0}){\rm d}t \text{。} \end{split} $ | (4) |
若
| $ {\psi _{j,k}}(t) = {2^{ - j/2}}\psi ({2^{ - j}} - k) \text{,} $ | (5) |
相应的二进制离散小波变换为
| $ Wf(j,k) = {2^{ - j/2}}\int_{ - \infty }^\infty {f(t)} {\psi ^*}({2^{ - j}}t - k){\rm d}t \text{。} $ | (6) |
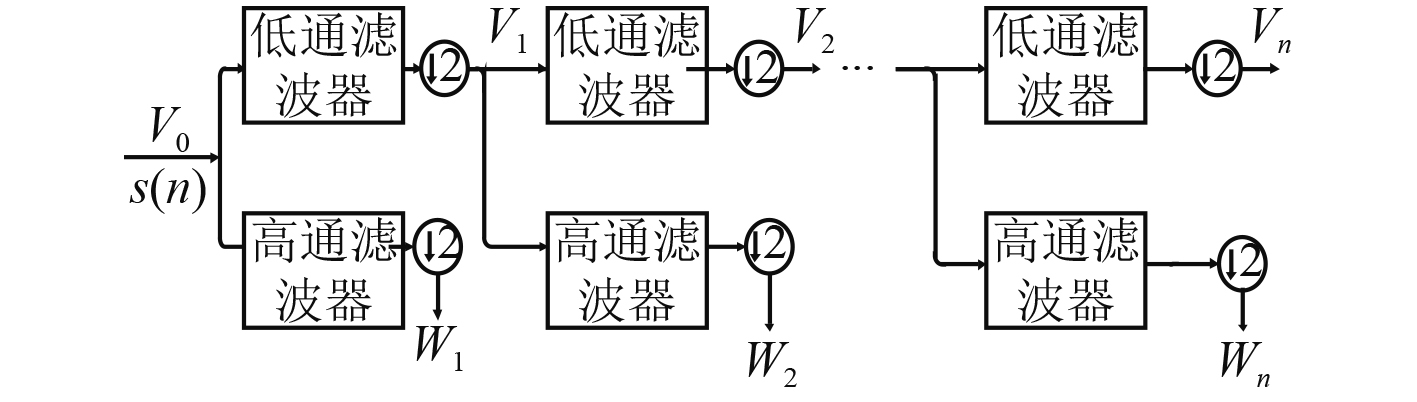
对于二进制离散小波变换,可以从频率空间的部分导出。如果将原始信号
|
图 2 二进制离散小波变换二抽取空间分解图 Fig. 2 Wavelet packet decomposition tree |
火控设备输出的诸元反馈是非平稳的、非线性、非高斯信号,适用于上述信号处理的方法就是小波变换,可实现信噪分离,小波多分辨率分解能够将信号在不同的尺度上拓展,把信号分解为高频部分和低频部分,就可以使信号中有效成分和干扰噪声分离开。小波信号降噪的准则满足光滑性和相似性,光滑性是指大部分情况下,降噪后的信号至少和原信号具有同等的光滑性,相似性是指降噪后的信号和原信号的方差估计应满足极大极小均方误差最小准则。小波信号降噪的基本原理是选定一种小波,对信号进行N层小波分解,对分解得到的各层系数特别是高频部分选取阈值处理,降噪处理后的数据通过小波重建恢复信号。
阈值选取有硬阈值和软阈值2种处理方法[8]。软阈值处理是将信号的绝对值与阈值进行比较,不大于阈值的点变为零,大于阈值的点变为该点值减去阈值后向零考近。硬阈值则是将大于阈值的点保持不变,不大于阈值的点变为零。硬阈值较好保留信号边缘等局部特征,软阈值则是在硬阈值的基础上将边界外的不连续点收敛到零,可避免间断,重建信号比较光滑,工程上多采用软阈值方法。
软阈值函数
| $ {W_s}(x,\lambda ) = \left\{ {\begin{array}{*{20}{l}} {{\mathop{\rm sgn}} (x)(\left| x \right| - \lambda )}\text{,}&{\left| x \right| > \lambda }\text{,}\\ 0\text{,}&{\left| x \right| \leqslant \lambda }\text{。} \end{array}} \right. $ | (7) |
硬阈值函数
| $ {W_h}(x,\lambda ) = \left\{ {\begin{array}{*{20}{c}} x\text{,}&{\left| x \right| > \lambda }\text{,}\\ 0\text{,}&{\left| x \right| \leqslant \lambda }\text{。} \end{array}} \right. $ | (8) |
阈值的选取可以采用固定模型和Birge-Massart策略确定阈值[9]。前者设定阈值
为了克服硬阈值和软阈值缺陷,也提出了半软阈值方法[10]:
| $\begin{split} {W_s}(x,{\lambda _1},{\lambda _2}) =& \operatorname{sgn} (x)\frac{{{\lambda _2}(\left| x \right| - {\lambda _1})}}{{{\lambda _2} - {\lambda _1}}}({\lambda _1} < \left| x \right| < {\lambda _2}) +\\ & x(\left| x \right| > {\lambda _2})\text{,} \end{split} $ | (9) |
其中,
改进的软阈值方法:
| $ {W_s}(x,\lambda ) = \left\{ {\begin{array}{*{20}{c}} {x + \lambda - \dfrac{\lambda }{{2k + 1}}}\text{,}&{x < - \lambda }\text{,}\\ {\dfrac{1}{{(2k + 1){\lambda ^{2k}}}}{x^{2k + 1}}}\text{,}&{\left| {\rm{x}} \right| \leqslant \lambda }\text{,}\\ {x - \lambda + \dfrac{\lambda }{{2k + 1}}}\text{,}&{x > \lambda }\text{。} \end{array}} \right. $ | (10) |
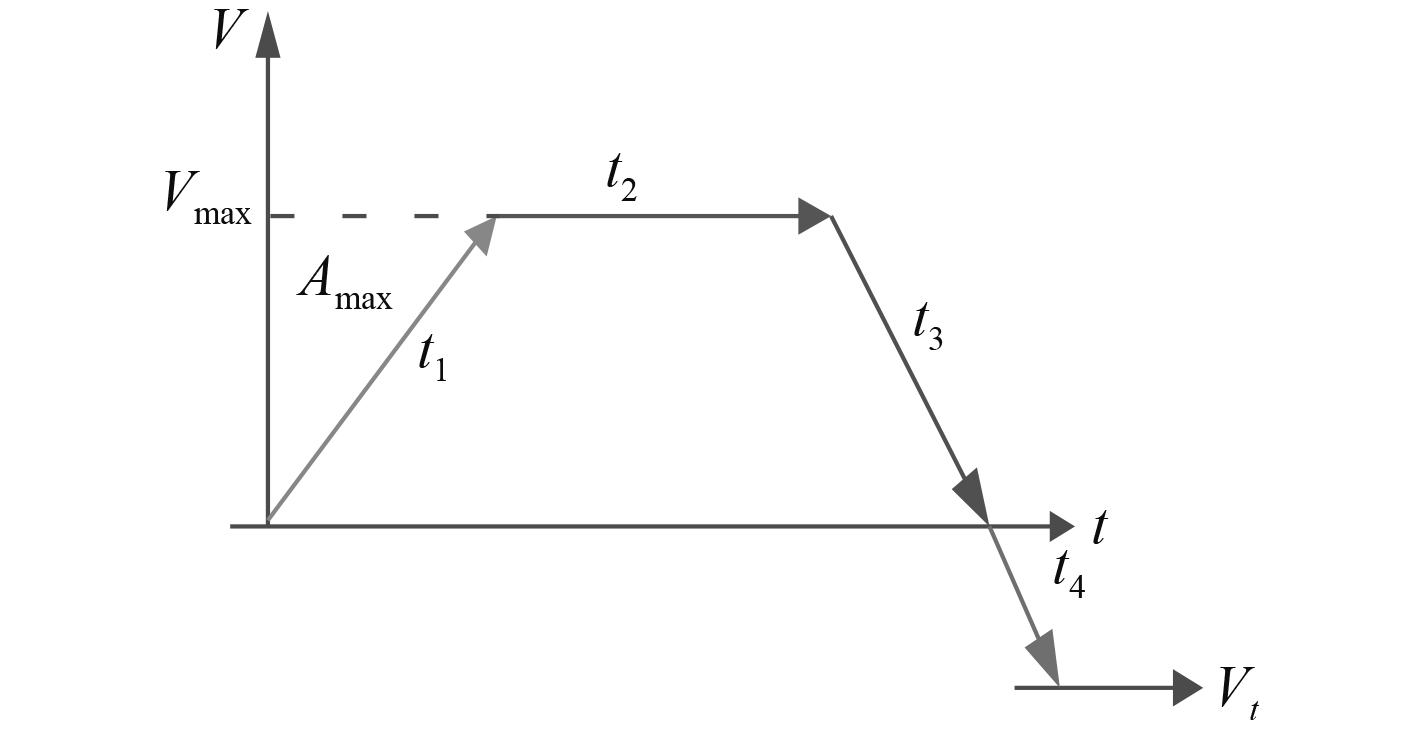
舰炮在正常跟踪过程之外,还存在调转、阶跃等大角度运动情况,这些往往考核舰炮的最大调转速度和反应时间,与跟踪时的信号不同,因此调转过程要从火炮的运动学方面进行建模。从当前舰炮架位加速向目标运动,可分为相遇问题和追赶问题。相遇时从当前架位加速向目标运动,并与目标反向行运动,共有加速段
|
图 3 舰炮调转相遇示意图 Fig. 3 Pre drive gun intercept process |
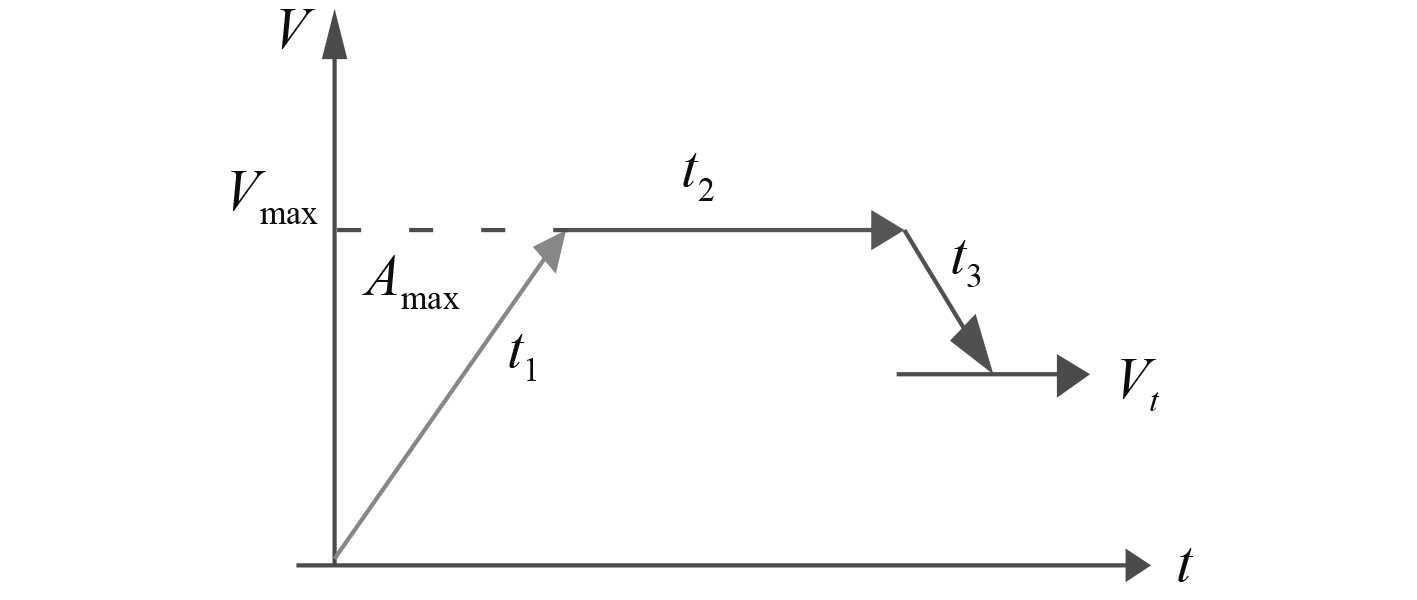
追赶时则需解决与目标同向运动时平稳过渡,共有加速段
|
图 4 舰炮调转追赶示意图 Fig. 4 Pre drive gun pursuit process |
设定火炮最大速度
则满足如下原则:火炮架位
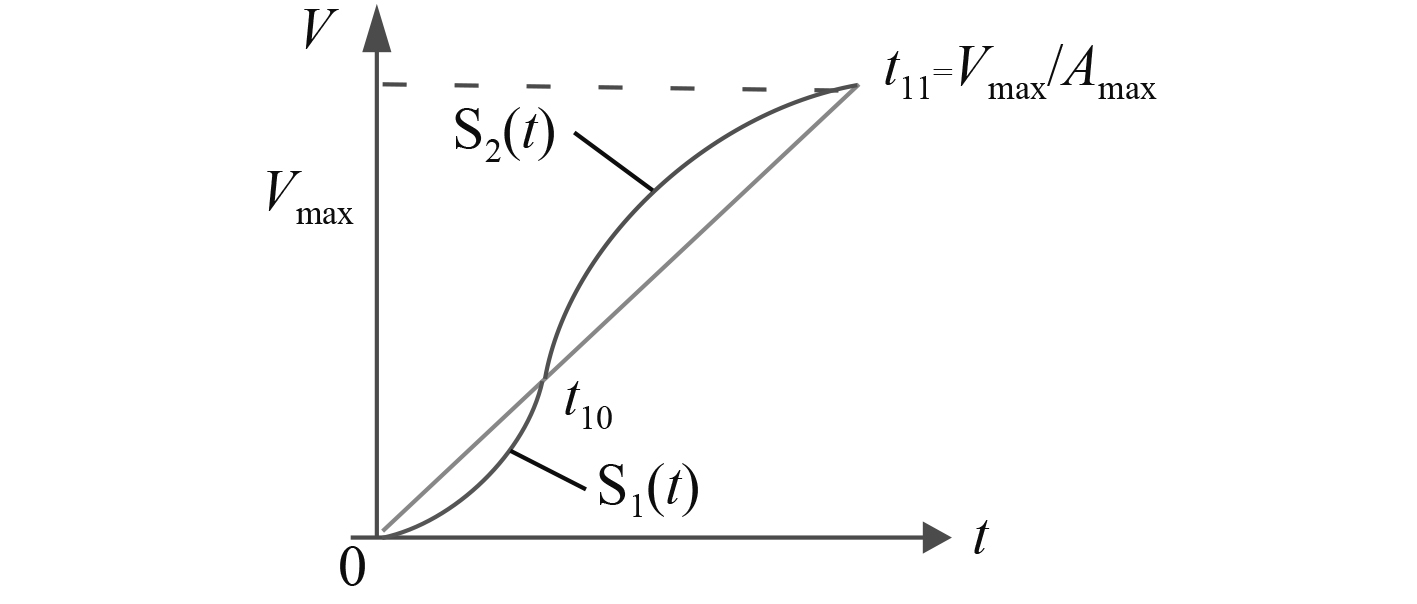
以加速段为例说明,如图5所示。
|
图 5 舰炮调转加速过程示意图 Fig. 5 Pre drive gun acceleration process |
按如下原理进行处理时,需满足2个条件,初始速度为0,加速度结束达到最大速度
| $ \begin{array}{c} {S_1}(0) = 0\text{,}\\ {S_1}({t_{10}}) = {S_2}({t_{10}})\text{,}\\ {S_2}({t_{11}}) = {V_{\max }}\text{,}\\ {t_{11}} = \dfrac{{{V_{\max }}}}{{{A_{\max }}}}\text{,}\\ \dfrac{1}{2}{A_{\max }}{t_{11}}^2 = \int_0^{{t_{10}}} {{S_1}(t)dt} + \int_{{t_{10}}}^{{t_{11}}} {{S_2}(t){\rm d}t} \text{。} \end{array} $ | (11) |
设原始信号为
| $ \begin{array}{l} {L_1}(x) = \sum\limits_{i = 0}^N {\left| {{x_i}} \right|}\text{,} \\ {L_2}(x) = \sqrt {\dfrac{1}{N}\sum\limits_{i = 0}^N {\left| {{x_i}} \right|} }\text{,} \\ {L_{\infty} }(x) = \mathop {\max }\limits_{0 \leqslant i \leqslant N} \left| {{x_i}} \right| \text{。} \end{array} $ | (12) |
信噪比定义
| $SNR = 10\log \frac{{L_2^2(x)}}{{L_2^2(x - \hat x)}}(\rm dB)\text{,}$ | (13) |
定义相应的能量比
| $E{R_p} = \frac{{{L_p}(\hat x)}}{{{L_p}(x)}}\text{。}$ | (14) |
其中:p表示1,2,
信噪比和能量比能够反映噪声前后的改善因子,因此仿真计算中可作为衡量小波变换质量的评估要素。
|
|
表 1 不同小波降噪重构后信号能量比及信噪比 Tab.1 Energy ratio and SNR of different wavelet denoising reconstruction |
|
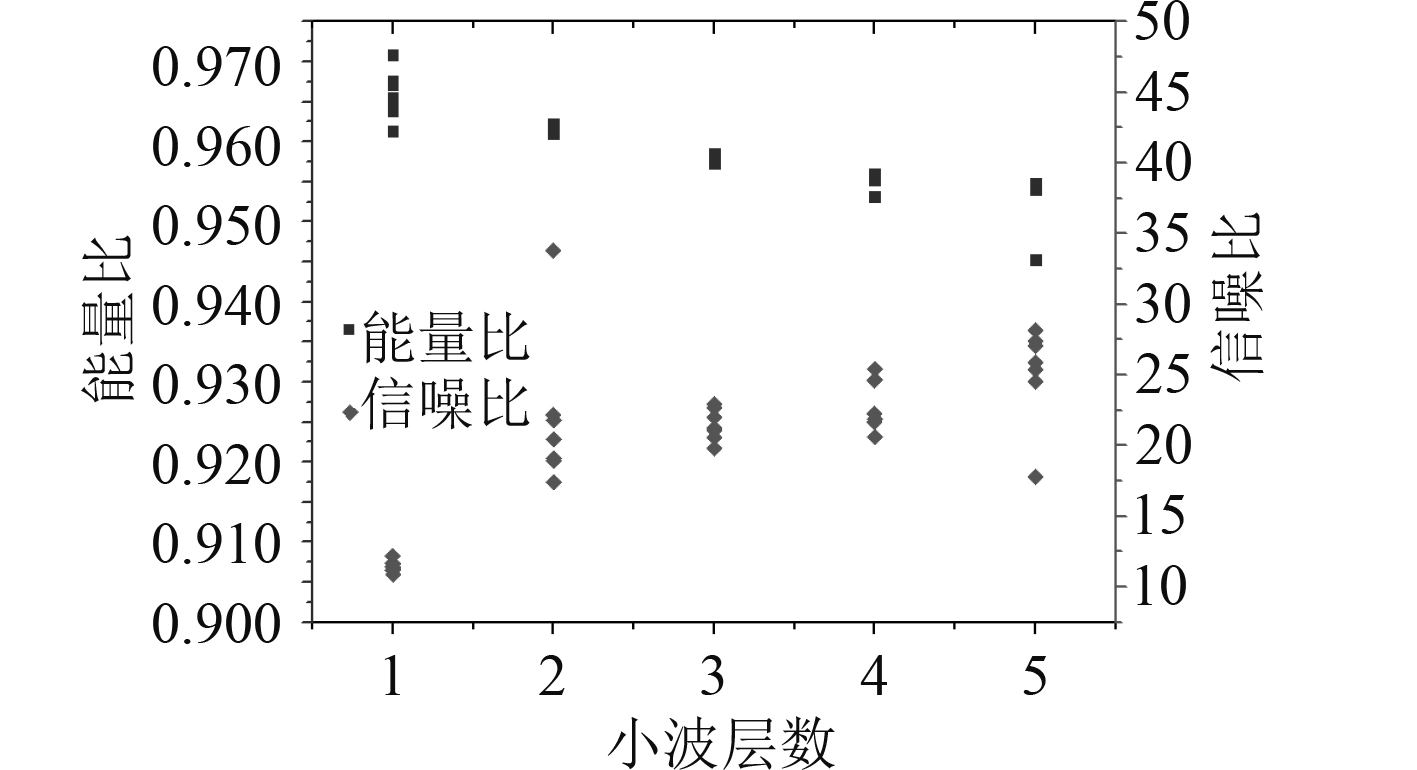
图 6 不同小波变换层数能量比及信噪比图 Fig. 6 Energy ratio and SNR of different wavelet levels |
从图6和表1可以看出,经过2层小波降噪重构后信号信噪比SNR可达20 dB,
|
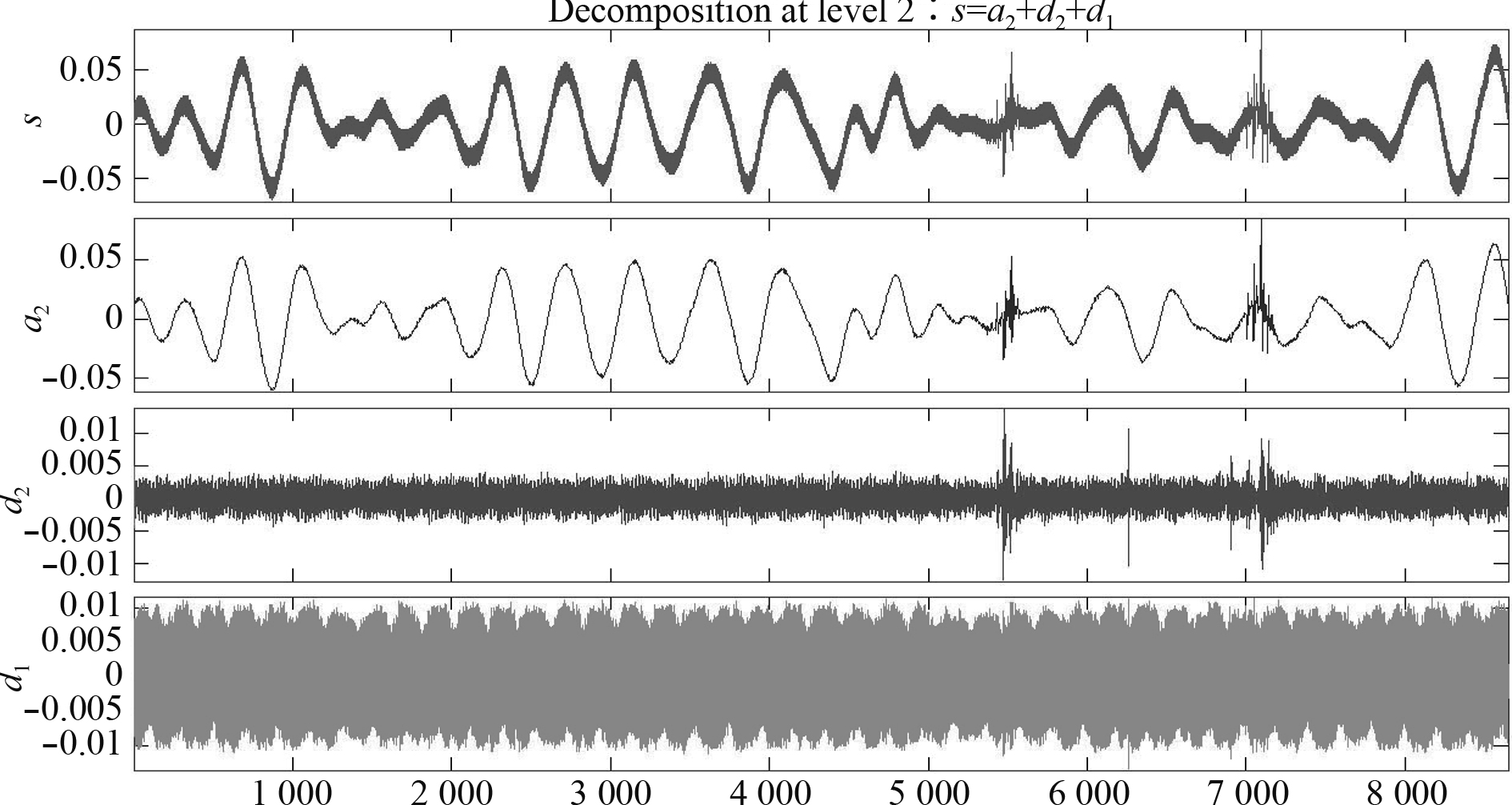
图 7 跟踪速度前馈的小波2层降噪过程 Fig. 7 Gun tracking velocity wavelet decomposition at level 2 |
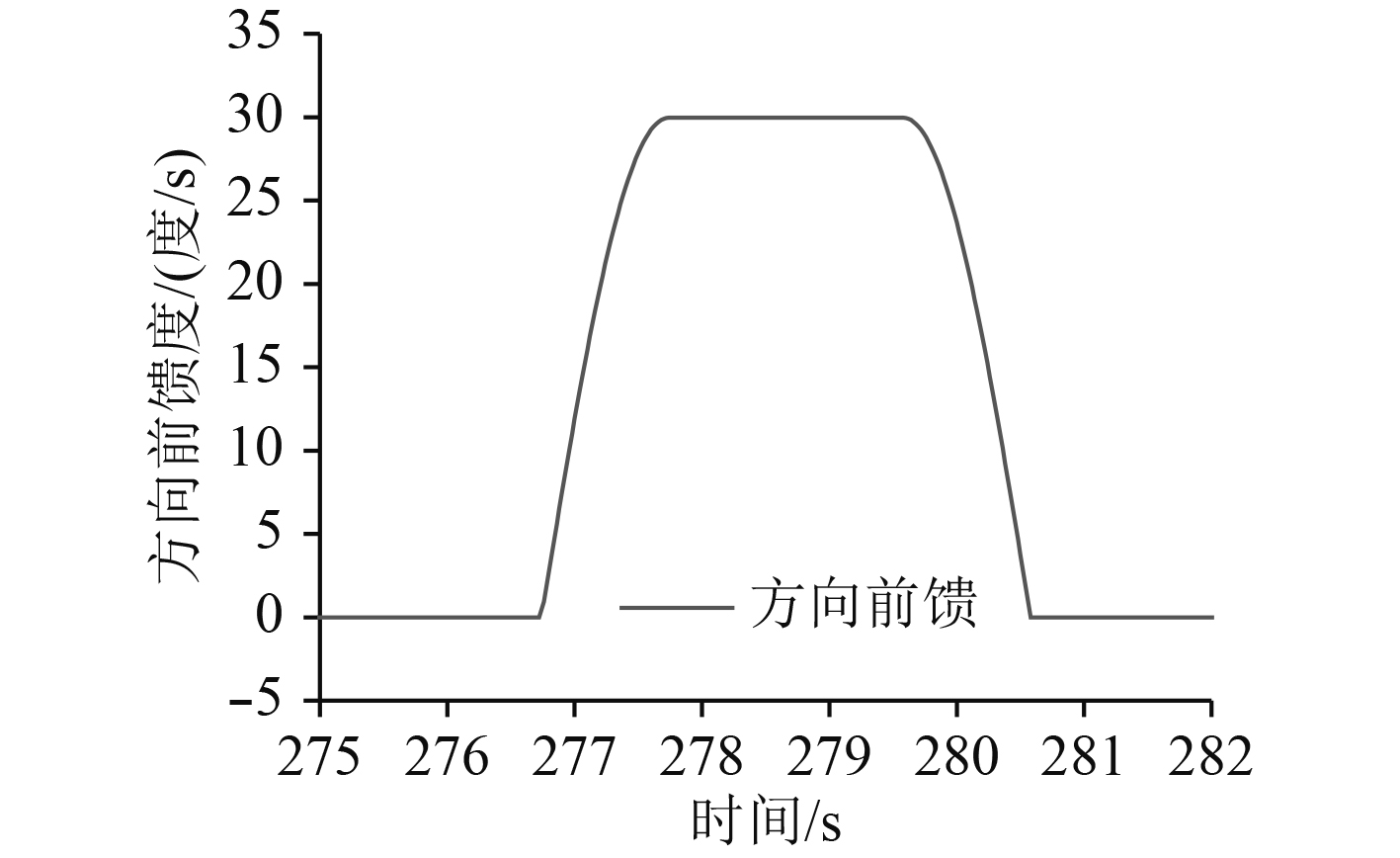
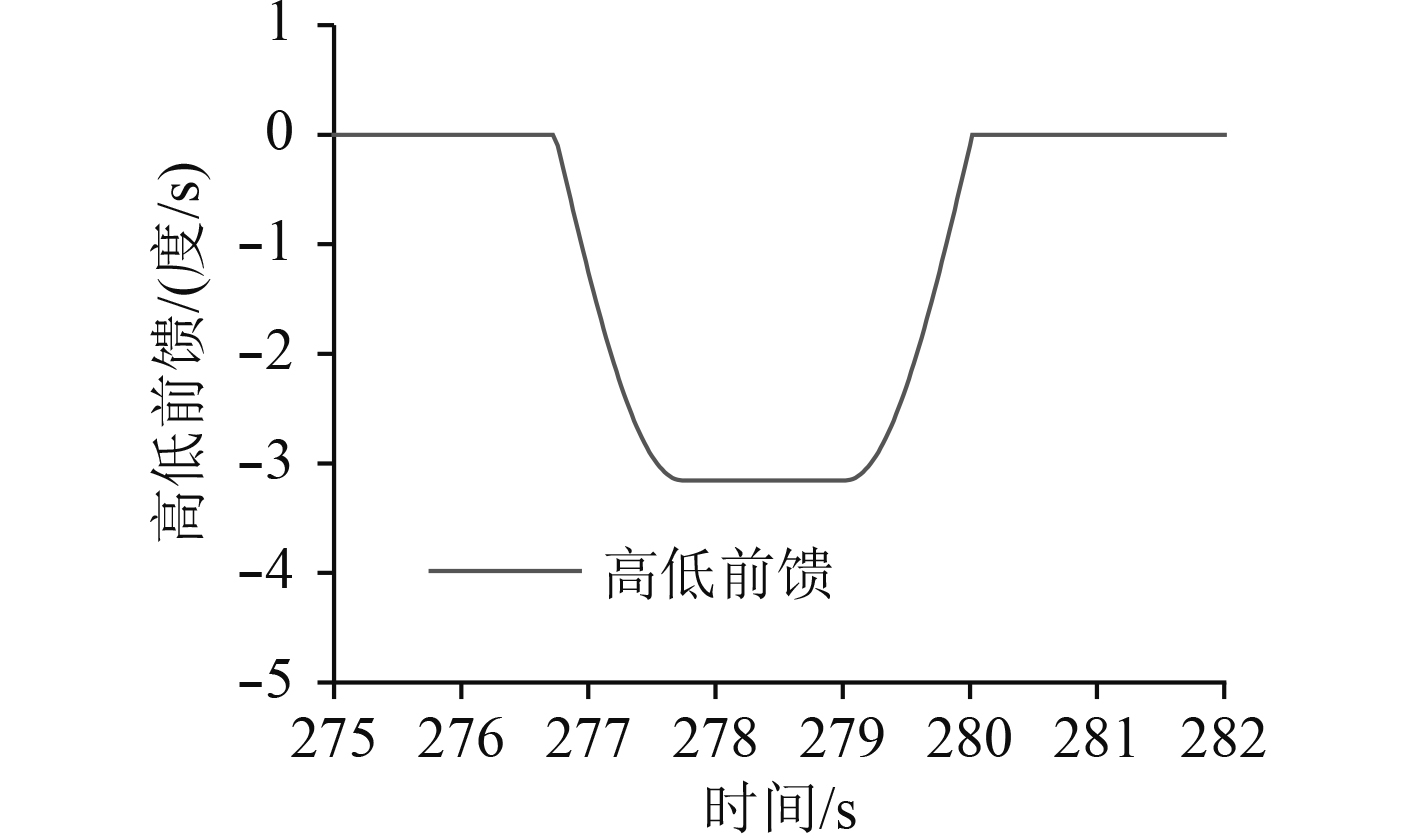
采用带炮优化的前馈处理过程见图8和图9,火炮协调过程前馈平稳。
|
图 8 预先带炮方向前馈图 Fig. 8 Pre drive gun bearing velocity |
|
图 9 预先带炮高低前馈图 Fig. 9 Pre drive gun elevation velocity |
舰炮伺服随动系统采用PID控制机理,引入加速度量控制虽能满足舰炮武器系统快速响应的需求,但也带来了火控输出前馈敏感性现象。本文从小波变换信号降噪重构和调转过程运动建模,对火控输出前馈进行平滑处理,解决了高灵敏度舰炮伺服运动过程中的快速响应和平稳性问题。该方法在装备中得到了应用,在满足系统跟踪精度技术指标的前提下,实现了对大惯量、变负载、动平台舰炮本体的平稳性控制,可为工程应用提供参考。
| [1] |
王茂林, 张志华, 武翰文. 基于遗传算法的舰炮随动系统PID参数整定[J]. 四川兵工学报, 2013, 34(7): 30-32. |
| [2] |
邵中年, 张志瑞. 基于根轨迹法的随动系统PID控制[J]. 四川兵工学报, 2012, 33(2): 93-95, 110. |
| [3] |
任挺, 焦自平, 徐文科. 舰炮随动系统满意PID控制器设计[J]. 火炮发射与控制学报, 2009(4): 55-57, 65. DOI:10.3969/j.issn.1673-6524.2009.04.015 |
| [4] |
吴军波. 某型舰炮瞄准随动系统自适应模糊PID控制方法研究[D]. 沈阳: 东北大学, 2014.
|
| [5] |
夏全国, 张志华. 舰炮随动控制系统PID控制器参数稳定域计算研究[J]. 舰船电子工程, 2014, 34(5): 50-53. |
| [6] |
王丹峰, 申中华. 某舰炮伺服系统建模仿真[J]. 机电产品开发与创新, 2018, 31(1): 54-57. DOI:10.3969/j.issn.1002-6673.2018.01.019 |
| [7] |
宋彦. 伺服系统提高速度平稳度的关键技术研究与实现[D]. 长春: 中科院长春光机所, 2010.
|
| [8] |
于凤芹. 实用小波分析十讲[M]. 西安: 西安电子科技大学出版社, 2013.
|
| [9] |
李媛. 小波变换及其工程应用[M]. 北京: 北京邮电大学出版社, 2010.
|
| [10] |
周伟主编. MATLAB小波分析高级技术[M]. 西安: 西安电子科技大学出版社, 2006.
|
 2019, Vol. 41
2019, Vol. 41
