舰船辐射噪声是评价舰船隐蔽性的重要指标之一,如何对潜艇机械噪声源进行精确地定位,对其传递途径进行判断,准确查找潜艇机械噪声的来源,是潜艇机械噪声控制和减震降噪工作的重要环节 [ 1]。
通过大量理论研究与实验测试发现,影响声源定位精度的因素诸多,其中阵列几何结构是影响阵列声源定位精度的一个重要因素 [ 2]。阵列结构问题已在阵列细化技术研究领域中被提出,其研究多侧重在结构优化方面,近几年国内出现很多关于阵列结构形式的声源定位性能研究报道,包括线性阵 [ 3]、平面阵列 [ 4]和立体阵列 [ 5- 6]。分析可知任何一种阵列结构均由阵元按照不同方式构成,不同的阵列结构在声源的定位性能上各有差异,因此阵列结构对噪声源定位技术的基础性作用不容忽视。
本文着眼于研究不同阵列结构对声源定位性能的影响,首先建立 n元基阵的数学模型,给出线阵,线圆组合阵模型中各阵元几何关系方程组,在此基础上,分别推导了线阵、线圆组合阵的定位算法。最后进行仿真实验,分析不同阵列结构和算法在不同条件下的最优组合。
1 阵列的数学模型首先,假设存在 M个窄带信号,阵列由 N个阵元组成,阵列中每个阵元的最终输出都可以表示为 M个再带信号与加性噪声的和。因此,将 N个阵元在特定时刻接受的信号排列成一个列矢量,可得窄带远场信号的DOA数学模型:
| $\begin{split} { G} =& { AF} + { V}{\text{,}} \\ \left[ \begin{array}{l} {g_1}\\ {g_2}\\ \vdots \\ {g_N} \end{array} \right] =& \left[ {\begin{array}{*{20}{c}} {{a_1}({\theta _1})}&{{a_1}({\theta _2})}& \cdots &{{a_1}({\theta _M})}\\ {{a_2}({\theta _1})}&{{a_2}({\theta _1})}& \cdots &{{a_2}({\theta _M})}\\ \cdots & \cdots & \cdots & \cdots \\ \cdots & \cdots & \cdots &{{a_N}({\theta _M})} \end{array}} \right] \times \\&\left[ {\begin{array}{*{20}{c}} {{F_1}}\\ {{F_2}}\\ \vdots \\ {{F_M}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{V_1}}\\ {{V_2}}\\ \vdots \\ {{V_N}} \end{array}} \right]{\text{。}} \end{split}$ | (1) |
式中: G 为阵列的快拍数据矢量; V 为噪声数据矢量; F 为空间信号矢量; A 为空间阵列的流型矩阵。
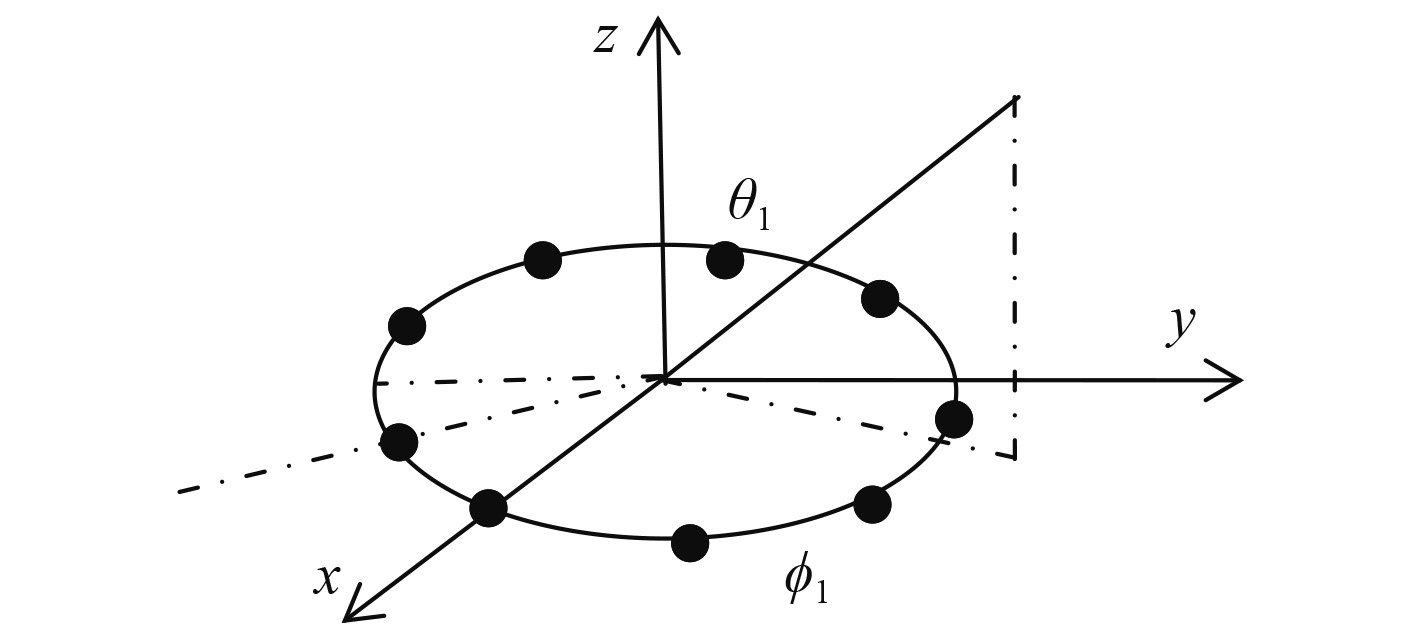
1.1 圆阵的数学模型利用平面阵列可以获取目标声源的方位角和俯仰角,典型的平面阵列包括圆阵和矩形阵列。圆阵的阵元结构如 图1所示,圆阵的半径为
|
图 1 圆阵 Fig. 1 Circular array |
假设平面波的振幅为
| $ g(q,t) = {A_1}\exp \left(j\left(2{\text{π}}{f_1}\left(t - \frac{{{\tau _{q1}}}}{c}\right)\right)\right)\text{,} $ | (2) |
其中,
| $ {\tau _{q1}} = - {R_0}\sin {\theta _1}\cos {\varphi _{q1}}{\text{,}} $ | (3) |
在这种情况下,因为阵元的方位角间隔相等,所以
| $ {\varphi _{q1}} = q{\varphi _0} - {\varphi _1}{\text{,}} $ | (4) |
因此
| $ \begin{split} g\left( {q,t} \right) =& {A_1}\exp \left( {j2 {\text{π}} {f_1}\left( {t + \frac{{{R_0}\sin {\theta _1}\cos \left( {\frac{{2 {\text{π}} q}}{N} - {\varphi _1}} \right)}}{c}} \right)} \right)=\\ & {A_1}\exp \left( {j2 {\text{π}} \left( {{f_1}t + \frac{{{R_0}\sin {\theta _1}\cos \left( {\frac{{2 {\text{π}} q}}{N} - {\varphi _1}} \right)}}{{{\lambda _1}}}} \right)} \right){\text{。}} \end{split} $ | (5) |
用笛卡尔坐标系中的单位矢量
| $ {\hat k_1} = - (\sin {\theta _1}\cos {\varphi _1}\hat x + \sin {\theta _1}\sin {\varphi _1}\hat y + \cos {\theta _1}\hat z){\text{,}} $ | (6) |
其中,
| $ {\hat r_q} = \cos (q{\varphi _0})\hat x + \sin (q{\varphi _0})\hat y{\text{,}} $ | (7) |
因此
| $ {\hat k_1} \cdot {\hat r_q} = - \sin {\theta _1}\cos (q{\varphi _0} - {\varphi _1}){\text{,}} $ | (8) |
将此扩展为多个信号源( m= 1,2,···,M)
| $ g\left( {q,t} \right) = \sum\limits_{m = 1}^M {{A_m}\exp \left( {j2 {\text{π}} \left( {{f_m}t - \frac{{{R_0}{{\hat k}_m} \cdot {{\hat r}_q}}}{{{\lambda _m}}}} \right)} \right)} {\text{,}} $ | (9) |
则圆阵的的导向矩阵:
| $\begin{gathered} A(\theta ,\varphi ) = \left[ {\begin{array}{*{20}{c}} {\exp (j2\pi {R_0}\cos ( - {\varphi _1})\sin {\theta _1})}&{ \cdots }&{} \\ \cdots &{ \ddots }&{} \\ {\exp (j2\pi {R_0}\cos ( - {\varphi _{N1}})\sin {\theta _1})}&{ \cdots }&{} \end{array}} \right. \hfill \\ \left. {\begin{array}{*{20}{c}} &{\exp (j2\pi {R_0}\cos ( - {\varphi _1})\sin {\theta _M})} \\ &{\cdots } \\ &\;\;{\exp (j2\pi {R_0}\cos ( - {\varphi _{NM}})\sin {\theta _M})} \end{array}} \right] {\text{。}} \\ \end{gathered} $ | (10) |
其中:
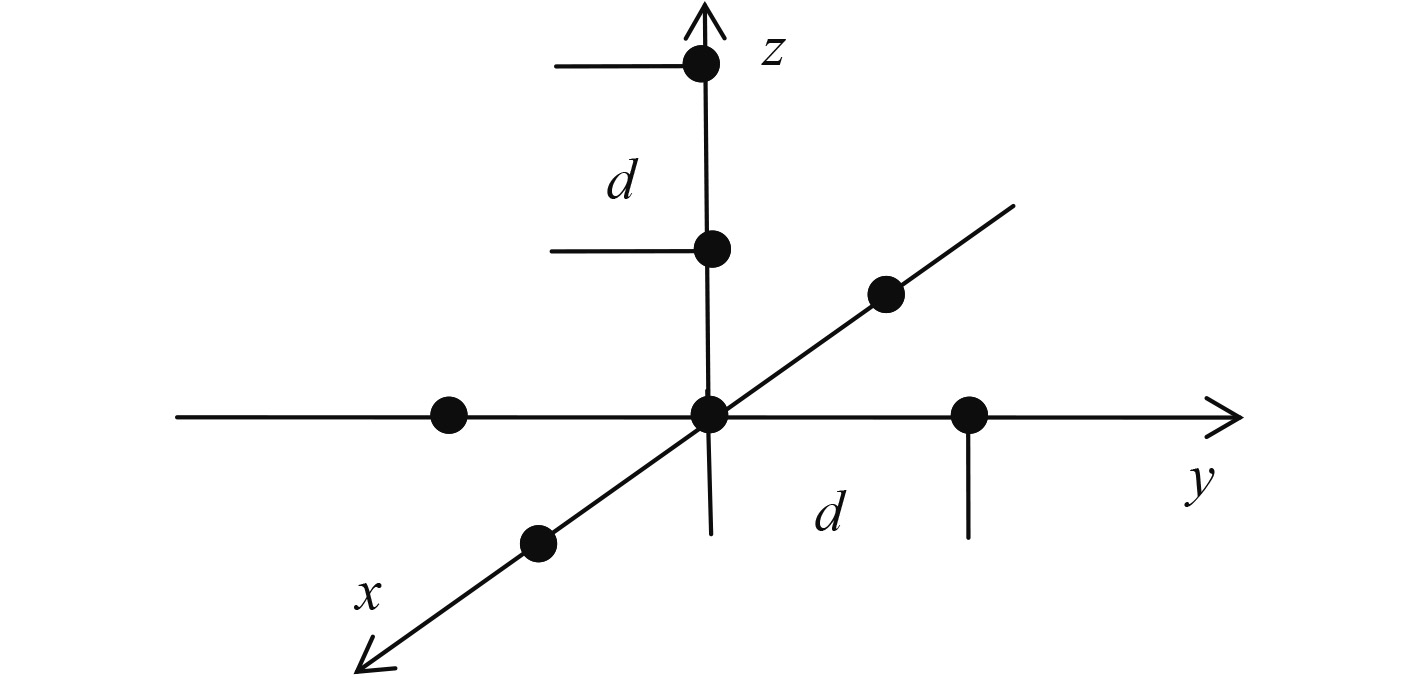
这里仅考虑由圆阵和线阵组合成三维阵列。如 图2所示,圆阵位于 X- Y平面,线阵沿 Z轴排列。在特殊情况下进行研究,圆形阵列的阵元分别在 X- Y轴上,据中心阵元的距离为 d,沿 Z轴的3个阵元间距也为 d。因此,阵列的7个阵元是等间距的。
|
图 2 线圆组合阵 Fig. 2 Combination of linear and circular arrays |
线性阵列3个阵元的位置由位置矢量给出:
| $ {\hat r_h} = (h - 1)d\hat z\text{,}\quad h=1,2,3\text{,} $ | (11) |
所以
| $ {\hat k_m} \cdot {\hat r_h} = - \cos ({\theta _m}(h - 1)d){\text{。}} $ | (12) |
如果阵列接收 M个信号,则线性阵列的第 h个阵元的输出:
| $ {g_{linear}}(h,t) = \sum\limits_{m = 1}^M {{A_M}\exp \left(j\left(2{\text{π}} {f_m}t - \frac{{2{\text{π}} {{\hat k}_m} \cdot {{\hat r}_h}}}{{{\lambda _m}}}\right)\right)} {\text{,}} $ | (13) |
由式(8)可知圆阵的阵元输出,由此可知线圆组合阵的阵元输出为:
| $ {g_{circular - linear}} = {g_{circular} \cdot g_{linear}}{\text{。}} $ | (14) |
该阵列结合线形和圆形阵列,以提供二维测向。则线圆组合阵的转向矩阵:
| $\begin{gathered} A(\theta ,\varphi ) = \left[ {\begin{array}{*{20}{c}} 1& \cdots \\ {\exp (j2{\text{π}} d\sin {\theta _1})}& \cdots \\ {\exp (j4{\text{π}} d\sin {\theta _1})}& \cdots \\ {\exp (j2{\text{π}} d\cos ( - {\varphi _1})\sin {\theta _1})}& \cdots \\ \vdots & \ddots \\ {\exp (j2{\text{π}} d\cos ( - {\varphi _{N1}})\sin {\theta _1})}& \cdots \end{array}} \right. \hfill \\ \left. {\begin{array}{*{20}{c}} &\qquad 1 \\ &\qquad {\exp (j2{\text{π}} d\sin {\theta _M})} \\ &\qquad {\exp (j4{\text{π}} d\sin {\theta _M})} \\ &\qquad {\exp (j2{\text{π}} d\cos ( - {\varphi _M})\sin {\theta _M})} \\ &\qquad \vdots \\ &\qquad {\exp (j2{\text{π}} d\cos ( - {\varphi _{NM}})\sin {\theta _M})} \end{array}} \right] \hfill \\ \end{gathered} $ | (15) |
其中
运用2种高分辨定位算法估计信号的到达角:多信号分类(MUSIC)算法;最小范数(Mini-norm)算法。
2.1 MUSIC [ 7]对于空间理想的白噪声且噪声功率为
| $ { S} = E[G{G^H}] = A{S_s}{A^H} + {S_N} = A{S_s}{A^H} + {\sigma ^2}I\text{,} $ | (16) |
对 S 进行特征分解,有
| $ { S} = { U}\Lambda {{ U}^H} = {U_S}{\Lambda _S}{U_S}^H + {U_N}{\Lambda _N}{U_N}^H {\text{。}} $ | (17) |
式中, U 为特征矢量矩阵,其中由特征值组成的对角阵
| $ {{{P}}_{{{MUSIC}}}} = \frac{1}{{{a^H}(\theta ){{\hat U}_N}\hat U_N^Ha(\theta )}}{\text{。}} $ | (18) |
这个方法和Music方法有些相似。其基本思想是在噪声子空间中找到特征向量的线性组合 D:
| $ D = {[{\varsigma _0},{\varsigma _1} \cdots {\varsigma _N}]^{\rm T}} = [1,{\varsigma _1} \cdots {\varsigma _N}]{\text{。}} $ | (19) |
式中,
| $ {\left| \varsigma \right|^2} = \sum\limits_{i = 0}^{M - 1} {\varsigma _i^2} \text{,} $ | (20) |
信号子空间
| $ {{ U}_S} = \left[ {\begin{array}{*{20}{c}} {{u_{00}}}&{{u_{00}}}& \cdots &{{u_{00}}}\\ {{u_{00}}}&{{u_{00}}}& \cdots &{{u_{00}}}\\ \vdots & \vdots & \cdots & \vdots \\ {{u_{00}}}&{{u_{00}}}& \cdots &{{u_{00}}} \end{array}} \right] = \left[\begin{array}{*{20}{c}} {{\eta ^H}}\\ {U_S'} \end{array}\right]\text{,} $ | (21) |
其中,
| $ D =\left [\begin{array}{*{20}{c}} 1\\ { - U_S'\eta /(1 - {\eta ^H}\eta )} \end{array}\right]{\text{,}} $ |
因此,最小范数 [ 7]的空间谱估计可表示为:
| $ {P_{MN}} = \frac{1}{{a(\theta )D{D^H}a{{(\theta )}^H}}}{\text{。}} $ | (22) |
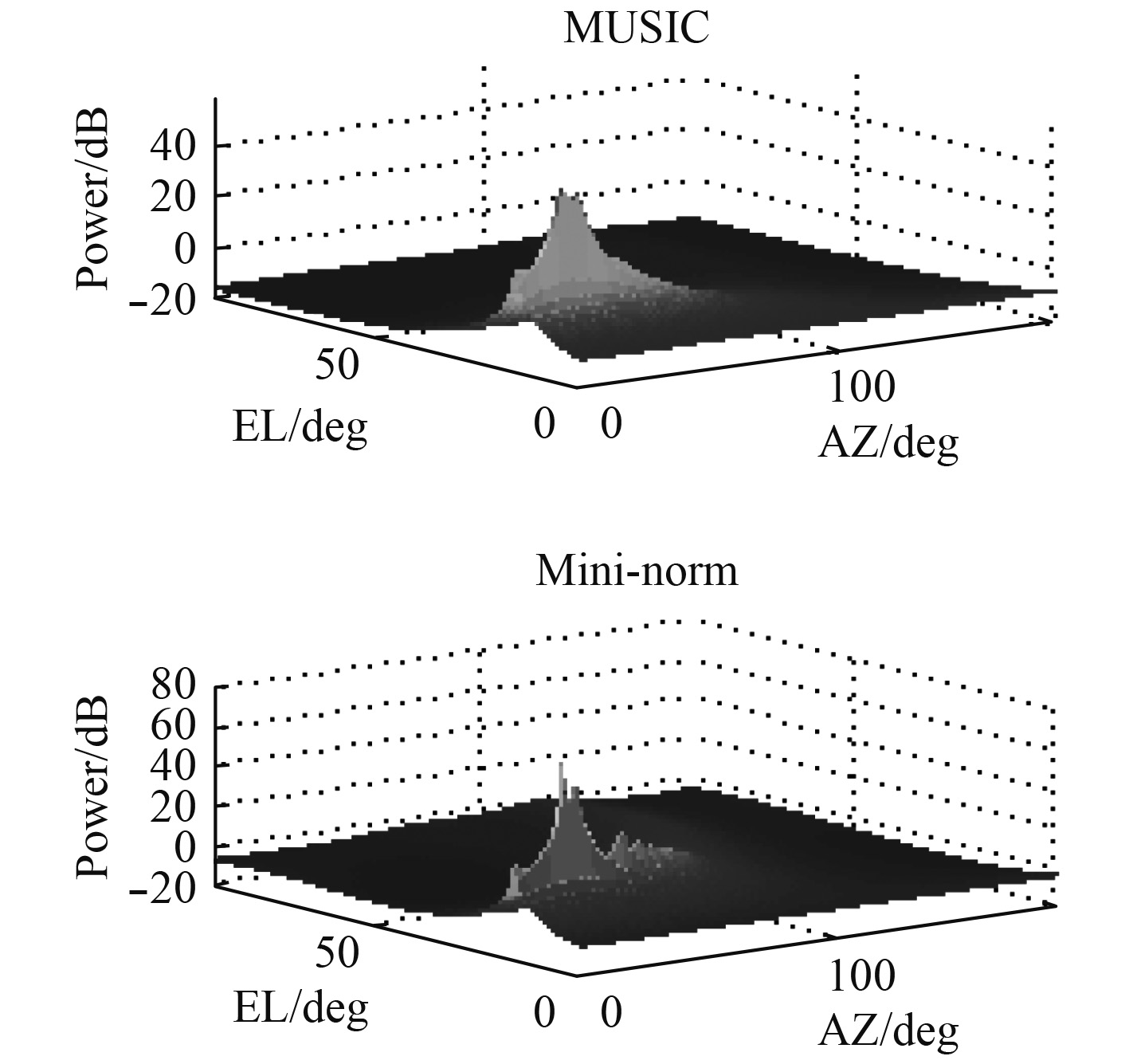
考虑7元半波长间隔均匀的圆阵和线圆组合阵,假设两等强度非相关窄带信号源分别从(16°,15°)和(21°,15°)方向入射到阵列,背景噪声与信号不相关的窄带高斯白噪声。要求分别采用Music和MIni-norm进行目标方位估计。信噪比分别为25dB,10dB,进行仿真实验,仿真结果如 图3和 图4所示。
|
图 3 线圆组合阵,SNR=25 dB Fig. 3 Circular +linear array, SNR=25 dB |
|
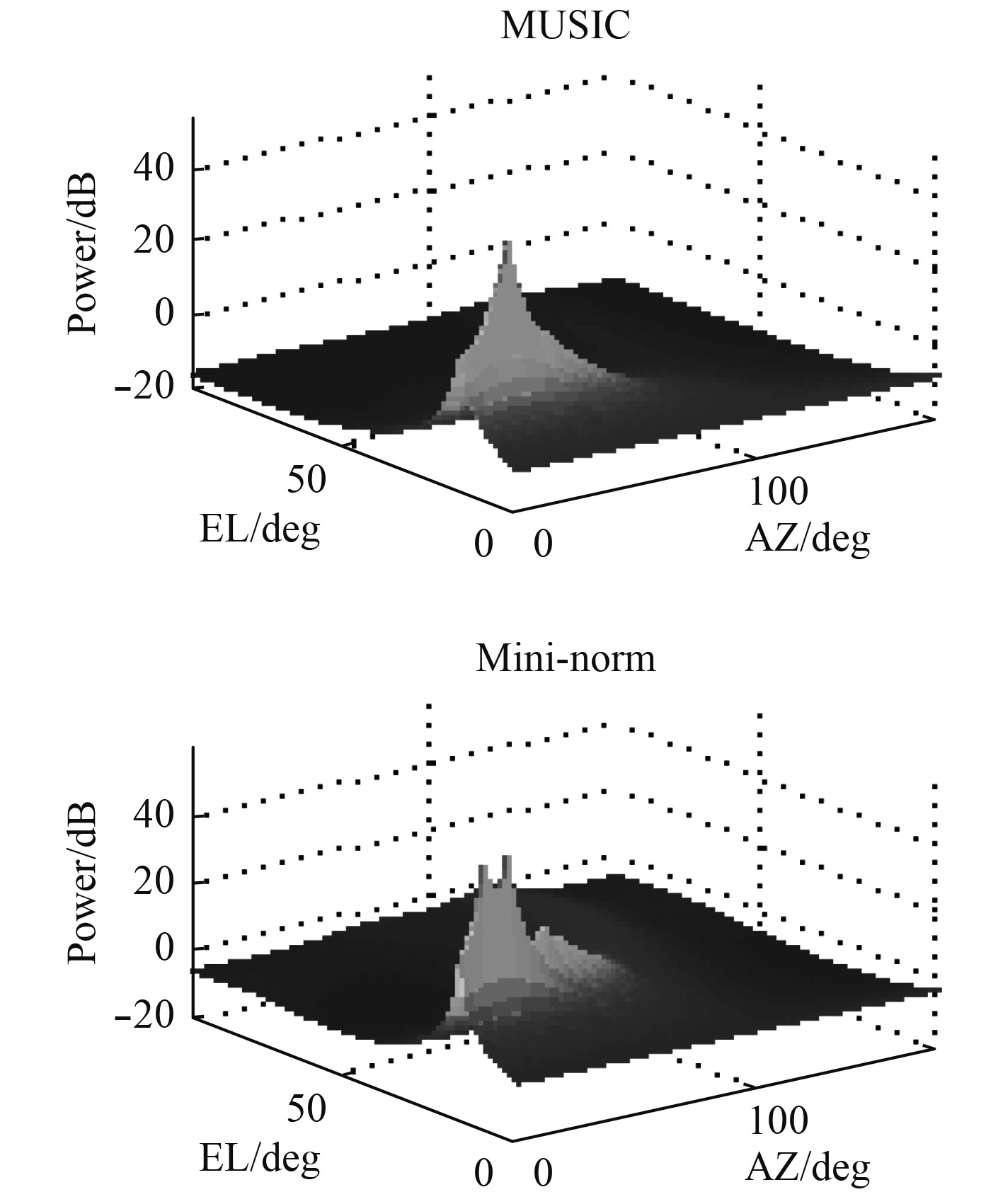
图 4 线圆组合阵,SNR=10 dB Fig. 4 Circular +linear array, SNR=10 dB |
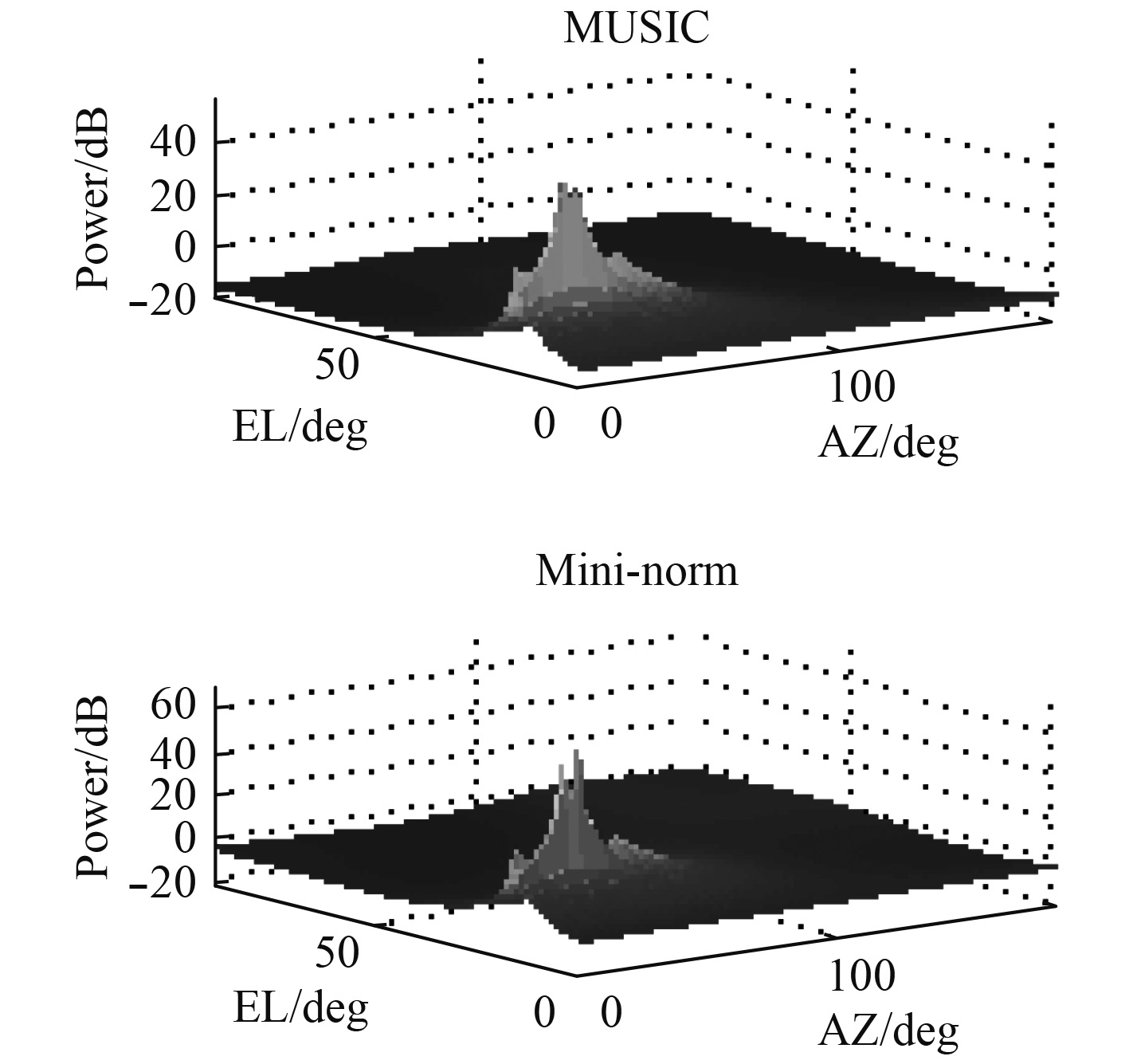
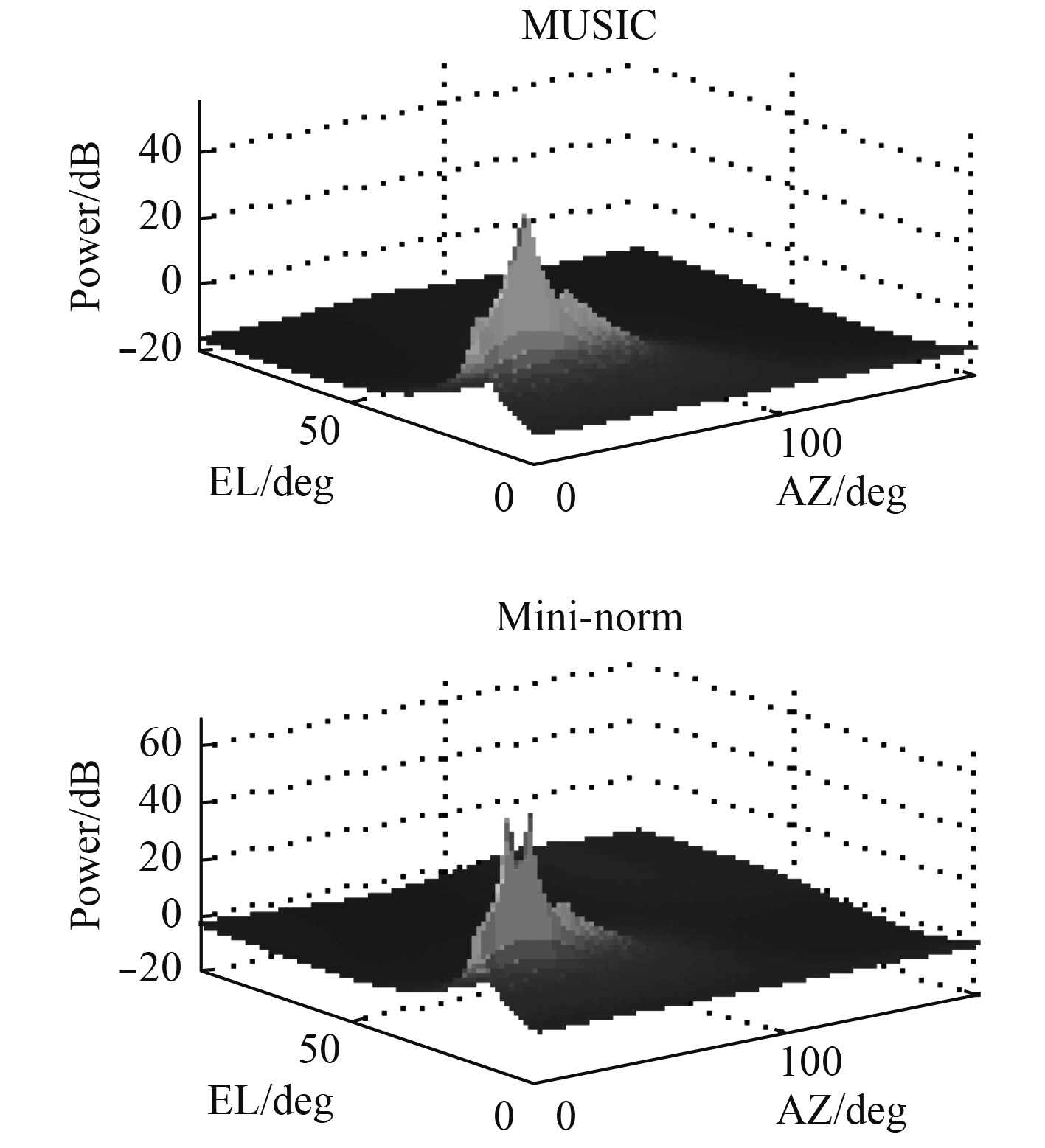
图3和 图4显示了线圆组合阵在信噪比较高时,2种算法的峰值明显,能准确定位信号源的位置。而信噪比较低时,2种算法都失效了。图5和 图6显示了圆阵在较高或较低信噪比时,都能定位信号源的位置,不过,在信噪比较低时,Mini-norm算法显示的峰值更加尖锐,准确。
|
图 5 圆阵,SNR=25 dB Fig. 5 Circular array, SNR=25 dB |
|
图 6 圆阵,SNR=10 dB Fig. 6 Circular array, SNR=10 dB |
比较 图3和 图5,得出在较高 SNR(= 25dB)时,Music和min-norm方法对于2个阵型的声源定位有相似的结果。从 图4和 图6可以看出,当 SNR较低(10dB)时,圆形阵列的效果更好。
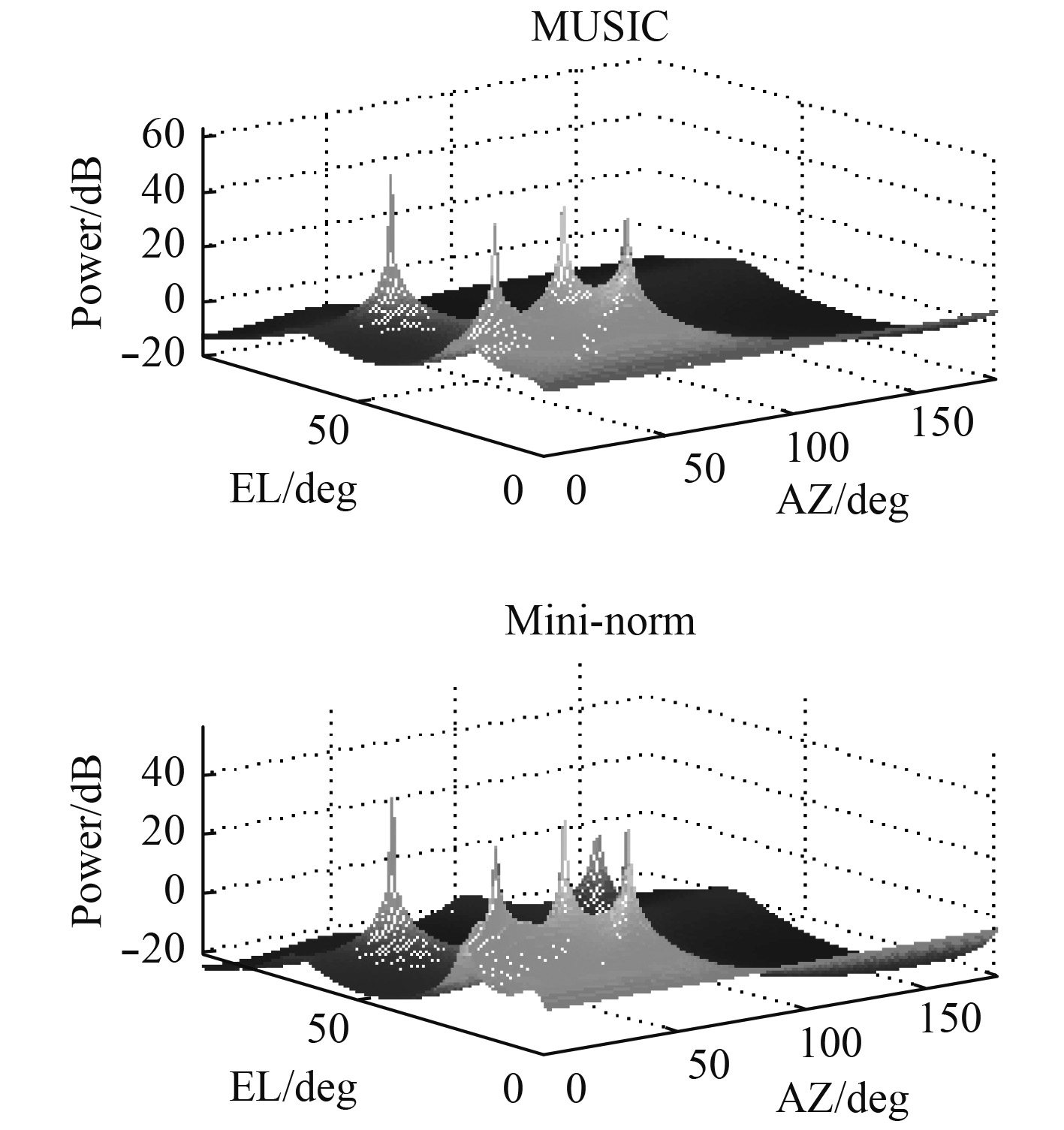
3.2 多个噪声源影响由各向同性的7元阵分别组成圆阵和线圆组合阵,快拍数为4 095,4个独立窄带远场信号,信号的方向分别为(16°,15°)、(21°,15°)、(21°,15°)(21°,15°),信噪比为25 dB,
|
图 7 线圆组合阵,SNR=25 dB Fig. 7 Circular+linear array, SNR=25 dB |
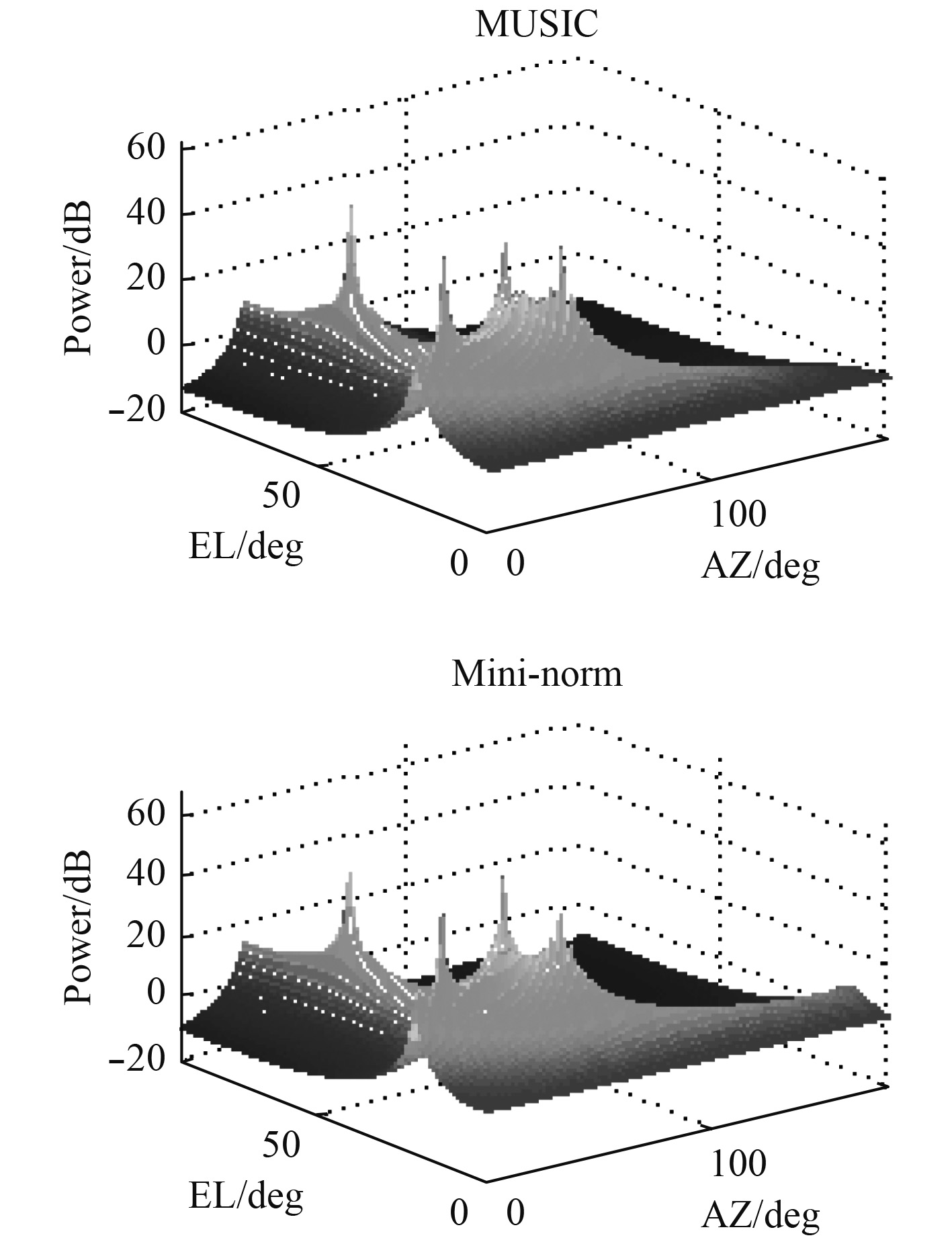
从 图7可以看出,多信号源时,线圆组合阵中2种算法都可以定位信号源,但Mini-norm算法出现了虚假峰。图8可以看出圆形阵列可以解决4个峰值,但圆形阵列具有更多的旁瓣。对比 图7和 图8可以得出在多信号源时,线圆组合阵和Music算法结合能准确定位信号源的位置,且低旁瓣。
|
图 8 圆阵,SNR=25 dB Fig. 8 Circular array, SNR=25 dB |
针对上述仿真结果,对圆阵和线圆组合阵给出以下结论:
1)在较高信噪比的情况下,2种阵型具有相似的性能;
2)在低信噪比情况下,圆阵的性能更好;
3)圆形阵列的方位角分辨率优于线圆组合阵列的。
从算法来看,MUSIC算法更稳定,几乎总是正确地显示出信号源的位置,更重要的是,低旁瓣。然而,在信噪比较低(<10 dB)的情况下,2种阵型的music算法都无法正确的提供峰值数目。
因此,可以得出在较低信噪比(<10 dB)时,圆阵和Mini-norm算法组合性能最好。在多信号源时,圆阵和线圆组合阵都能定位信号源位置,但是圆阵多旁瓣,而Mini-norm算法与线圆组合阵结合出现虚假峰。所以,在多信号源时,线圆组合阵 与Music算法结合可以更加准确的定位信号源。
由于使用子空间方法来计算AOA,因此声源的数量必须小于阵元的数目。将来,应该考虑如何突破这种限制,以及如何在低信噪比时,提高算法的性能。
| [1] |
王之程, 陈宗岐, 于沨, 等. 舰船辐射噪声测试与分析[M]. 北京:国防工业出版社, 2004, 148-160.
|
| [2] |
居太亮, 彭启宗. 麦克风阵列二维方向估计聚焦算法研究[J]. 电子科技大学学报, 2008, 37(2): 225-228. DOI:10.3969/j.issn.1001-0548.2008.02.018 |
| [3] |
KIRM H, VIBERG M. Two decades of array signal processing research; the parametric[J]. IEEE Signal Process Mag, 1996, 13: 67-94. DOI:10.1109/79.526899 |
| [4] |
TRUCCO A. Weighting and thinning wide-band arrays by simulated annealing[J]. Ultrasonics, 2002, 40(1-8): 485-489. DOI:10.1016/S0041-624X(02)00163-4 |
| [5] |
齐娜. 传声器阵列恒定束宽波束形成[J]. 电声技术, 2006(9): 23-25, 29. QI Na. Constant beamwidth beamforming based on microphone array[J]. Audio Engineering, 2006(9): 23-25, 29. DOI:10.3969/j.issn.1002-8684.2006.09.007 |
| [6] |
张卫平, 王伟策. 任意形状三阵元平面声被动目标定位分析[J]. 探测与控制学报, 2003, 25(3): 54-57. ZHANG Wei-ping, WANG Wei-ce. The analyze of passive acoustic location in plane by random shape array of three sensor[J]. Journal of Detection and Control, 2003, 25(3): 54-57. DOI:10.3969/j.issn.1008-1194.2003.03.015 |
| [7] |
SCHMIDT R O. Multiple emitter location and signal parameter esti-mation[J]. IEEE Trans, 1986, AP234(3): 276-280. |
| [8] |
KUMARESAN R.TUFTS DW. Estimation the angle of arrivel of multiple plane waves[J]. IEEE Trans AES, 1983, 19(1): 134-139. |
 2019, Vol. 41
2019, Vol. 41
