为确保无人艇的运行安全,需结合已有实践经验进行深入优化和升级,本文围绕船舶航行预测技术展开深入研究。
文献[1]基于修正卡尔曼滤波算法和AIS数据,结合最小二乘法实现了船舶运动轨迹的平滑预测;文献[2]优化了卡尔曼滤波算法的实时性,将其应用到船舶的轨迹处理中;文献[3]运用支持向量机(SVM)结合桥区水域失控船舶运动数学模型进行了航迹回归预测;文献[4]利用GPS定位系统的时序特征构建了船舶运动轨迹预测模型;文献[5]结合优化马尔科夫模型和灰度模型,提出一种短程船舶轨迹预测方法。以上研究需要以船舶运动学方程为基础,因而无法有效适应海上复杂环境。近年来随着人工神经网络研究的进步,深度学习被广泛用于此类问题。文献[6]提出一种基于3层BP神经网络的航迹预测算法,利用Sigmoid函数实现船舶位置预测,具有用时短、通用性强的特点。文献[7]利用AIS数据信息量丰富的特点,结合BP神经网络,实现了船舶航行行为预测;文献[8-9]提出了循环神经网络-长短期记忆模型,验证了LSTM神经网络回归模型的有效性。
针对研究现状,本文以AIS数据为基础,在LSTM模型的基础上引入注意力机制,提出一种基于Attention-LSTM神经网络的船舶航行预测模型,通过对隐藏层单元差异赋权突出对预测结果有关键影响的序列,从而提高预测精度。最后以成山角海域真实数据进行仿真实验,并与BP神经网络模型进行对比,验证了本文方法的优越性。
1 LSTM神经网络与注意力机制 1.1 LSTM神经网络Hochreiter等[10]在时间循环神经网络(Recurrent Neural Network,RNN)基础上进行优化,提出了长短期记忆神经网络。通过引入记忆单元和门机制,有效克服了RNN在深度学习中的梯度异常问题,同时也更易于训练。
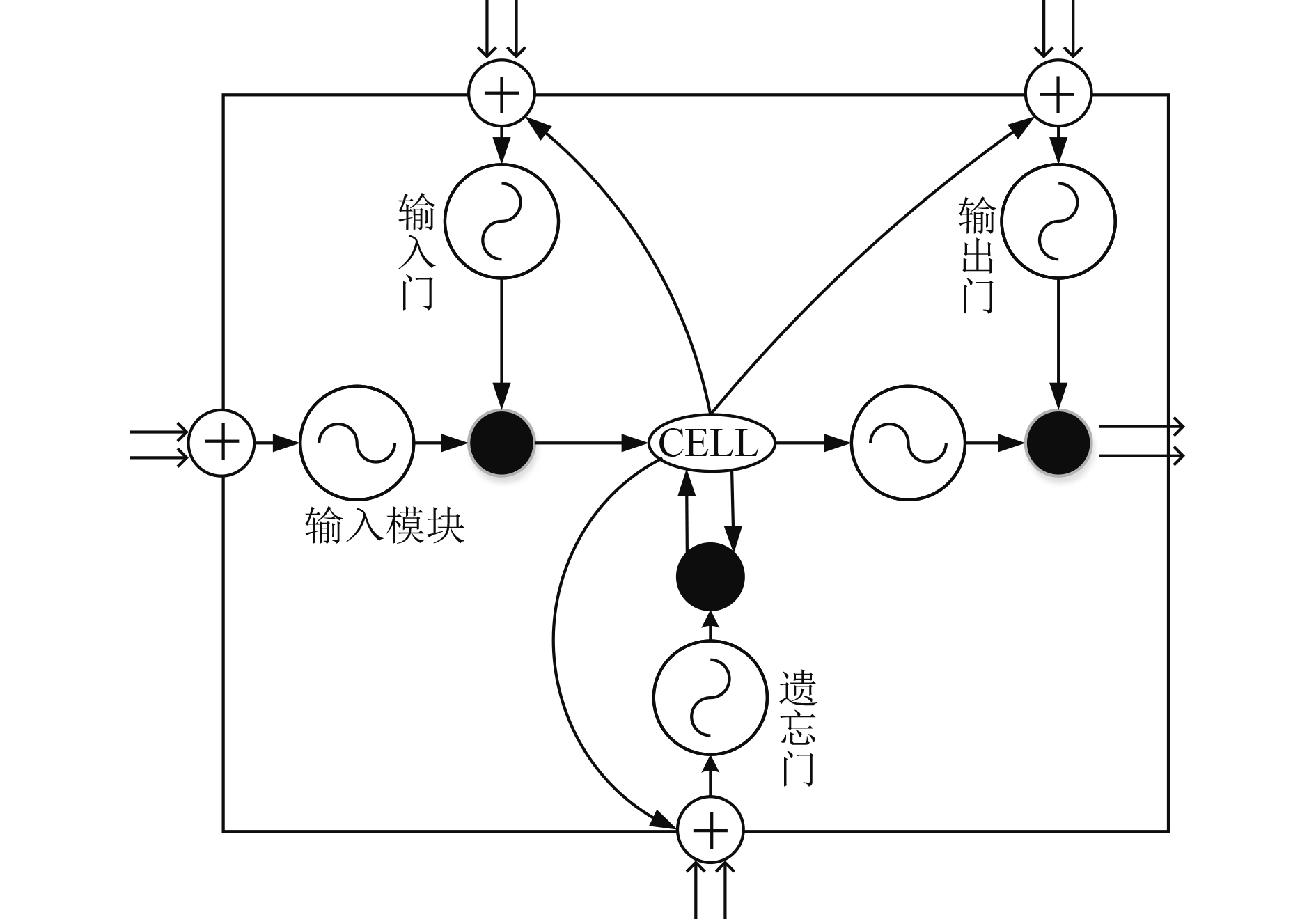
LSTM单元结构如图1所示。每个LSTM单元内部包括输入门(input gate)、遗忘门(forget gate)、输出门(output gate)和一个记忆单元结构Cell。其中,输入门用于控制记忆单元更新的信息量;遗忘门用于控制前一时刻记忆单元信息被利用的量;输出门用于控制输出到下一隐藏状态的信息量[11]。设给定输入序列xt,则输入门、遗忘门、输出门分别为it,ft,ot,记忆单元Ct则通过不同门控制数据的记忆和遗忘,具体表述如下:
|
图 1 LSTM单元结构 Fig. 1 LSTM structure |
| $\left\{ \begin{array}{l} {i_t}\; = \sigma ({W_i} * [{h_t}_{ - 1},{x_t}] + {b_i}){\text{,}}\\ {f_t} = \sigma ({W_f} * \;[{h_t}_{ - 1},{x_t}] + {b_f}){\text{,}}\\ {o_t}\; = \sigma ({W_o} * \;[{h_t}_{ - 1},{x_t}] + {b_o}){\text{,}} \end{array} \right.$ | (1) |
更新后的记忆单元Ct:
| $\left\{ \begin{array}{l} {q_t}\; = \tanh (\;{W_q} * [{h_t}_{ - 1},{x_t}] + {b_q}) {\text{,}}\\ {c_t}\; = {f_t}{C_{t - 1}} + {i_t}{q_t}{\text{,}} \end{array} \right.$ | (2) |
更新后的隐藏状态ht:
| ${h_t}\; = {o_t}\tanh (\;\;{c_t}){\text{。}}$ | (3) |
式中:σ为sigmod函数;Ct–1为现有记忆门;ht–1为当下的隐藏状态;W和b分别为对应地系数矩阵和偏差项;* 为点乘。
LSTM神经网络通过门函数控制历史数据的记忆和遗忘,适合于处理具有时间序列特性的问题。但该模型在数据输入时会将其编码为等长向量,而解码则受限于该向量,致使模型难以学到合理的向量表示。因此,引入注意力机制,更有效地提取输入序列特征。
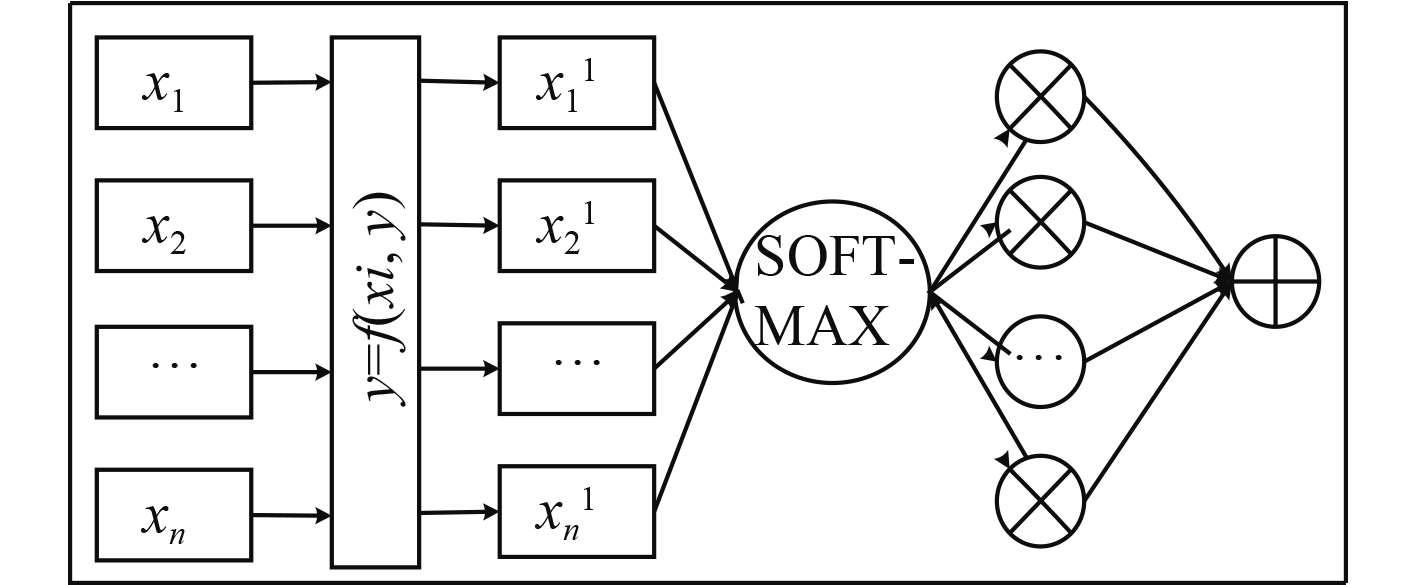
1.2 注意力机制注意力机制(Attention-based Model)发源于图像识别领域,而后也被广泛应用在回归问题中[12]。它的工作机理类似人脑,借鉴人脑中对事物各部分的注意力偏差机制,通过对输入序列内各因子赋予不同的权重,突出更关键的影响因素,帮助模型做出更准确的判断。点积注意力机制结构如图2所示。
|
图 2 Attention单元结构 Fig. 2 Attention structure |
图中,Xi为输入序列,Xi1为Xi简化计算得到的相似标量,通过归一化指数函数将其映射在[0,1]区间,即为“权重”。点积注意力则是Xi对权重的加权合。表述如下:
| $\left\{ \begin{array}{l} f\left( {{x_i},y} \right) = \left( {{W_1} * {x_i},{W_2} * y} \right){\text{,}}\\ Attention = \sum\limits_{i = 1}^n {soft\max \left( {f\left( {{x_i},y} \right)} \right)} * {x_i} {\text{。}} \end{array} \right.$ | (4) |
多维船舶航行预测是指船舶的经度、纬度、航向和航速随时间的变化预测,是对传统船舶轨迹预测的补充。其实质是对船舶航行大数据的深度挖掘,以船舶过去时刻的航行数据作为输入,未来时刻的航行数据作为输出,通过对比建立基于时间序列的航行特征映射关系,最终实现船舶航行预测。
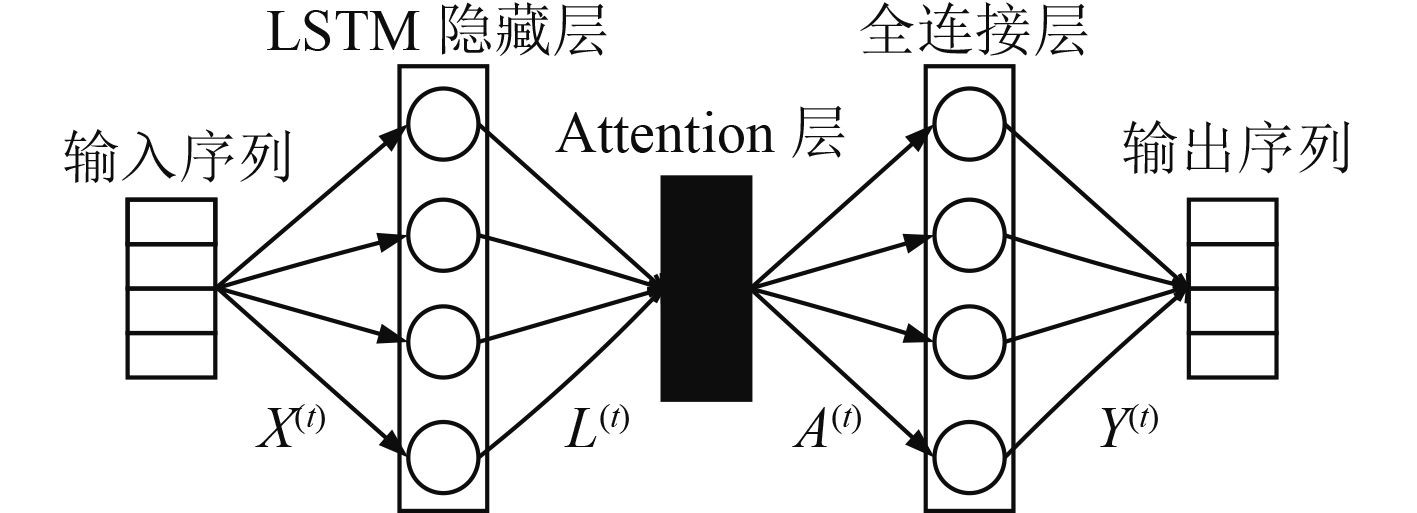
2.1 神经网络结构Attention-LSTM模型通常包括输入序列、LSTM层、Attention层、全连接层以及输出序列。其中输入序列与输出序列是模型的出入通道;LSTM层的作用是实现高层次特征学习;Attention层的作用是突出关键信息;全连接层的作用是进行局部特征整合,实现最终的预测。基于此,参考多层自适应模块化神经网络结构[13],本文将Attention层作为LSTM层和全连接层的接口,构造“LSTM层—Attention层—全连接层”结构,如图3所示。
|
图 3 Attention-LSTM网络结构 Fig. 3 Attention-LSTM structure |
图中,X(t)为输入序列数据,L(t)为X(t)的隐藏特征,A(t)为各特征的注意力权重,Y(t)为输出序列数据。
2.2 拓扑结构 2.2.1 输入、输出序列参数输入、输出序列主要是对船舶航行信息的表征,所对应的AIS信息主要有水上移动通信业务标识码(MMSI)、时间(TIME)、经度(LNG)、纬度(LAT)、航向(COG)、航速(SOG)等。输入、输出序列具体表示为:
Input :(MMSI,TIME)={LNG,LAT,COG,SOG},
Output :(MMSI,TIME)={LNG,LAT,COG,SOG}。
为减小各项数据数量级差异的影响,输入、输出序列还需要进行归一化处理,将数据集向量各元素取值转换在[0,1]内,表达式为:
| ${x^*} = {\frac{{x - {x_{\min }}}}{{{x_{\max }} - {x_{\min}}}}}{\text{。}}$ | (5) |
式中:x为原始数据;x*为归一化数据。
2.2.2 神经元节点数神经网络模型中,神经元节点数是导致“过拟合”现象的重要因素。其中,输入层和输出层节点数由训练数据的特征决定;LSTM层和全连接层神经元节点数通常取2的次方数,本文设置LSTM层和全连接层神经元节点数为α,α∈{4,8,16,32,64,128,256},初步设定α=64。
2.2.3 输入层步数船舶航行问题具有时间序列特性,因此其输入序列存在step的概念。本文设置输入层步数为β+1,β∈{2,3,4,5,6},即把Y[t–β],Y[t–(β–1)], …,Y[t]等β+1个连续时刻的船舶行为表征数据作为网络输入,t+1时刻的预测数据Y[t+1]作为网络输出,初步设定β=5。
2.2.4 模型训练方法迭代次数是影响神经网络模型精度的重要因素。本文设置迭代次数为θ,θ∈{1,500,1 000,1 500,2 000,2 500,3 000},初步设定θ=1 500。
代价函数是一种衡量系统整体误差程度的函数[14]。交叉熵损失函数可以用来评估当前训练结果与真实分布的差异状况,且不会影响模型的收敛速度,因此将其作为本网络的代价函数,如下式:
| $Loss = - \left[ {y\;\log \hat y + \left( {1 - y} \right)\log \left( {1 - \hat y} \right)} \right]{\text{。}}$ | (6) |
式中:y为参数的实际值;
传统梯度下降过程根据经验公式确定其学习率,并在训练过程中保持不变。本文针对船舶航行中的非稳态、高噪声问题,采用适应性矩估计算法代替随机梯度下降,基于训练数据和交叉熵损失函数计算梯度估计矩阵,从而为参数设定自适应学习率。
3 实验仿真分析 3.1 实验准备实验编程语言为Python3.0,开发工具为Spyder。实验数据来源于成山角水域内船舶的AIS信息,经解析后,按照MMSI,TIME,LNG,LAT,COG,SOG等字段信息进行储存。
3.2 实验设计 3.2.1 实验数据选取200组AIS作为实验数据,经清洗后其中前180组作为训练集,后20组作为测试集。为避免因数据分布差异导致的模型误差,选定数据进行标准欧式距离计算,结果如表1所示,可知训练集与测试集数据具有相似分布。
|
|
表 1 欧式距离 Tab.1 Euclidean distance |
采用均方误差(MSE)和平均绝对误差(MAE)来评估船舶航行预测的各项指标。MSE是指预测值与真实值间差值的平方期望,该值越小则模型的效果越好;MAE能够更好反映出模型误差的真实状况。表述如下:
| $MSE = \frac{1}{n}\sum\limits_{i = 1}^n {{{(y - \hat y)}^2}}{\text{,}}$ | (7) |
| $MAE = \frac{1}{n}\sum\limits_{i = 1}^n {{{\left| {y - \hat y} \right|}^2}}{\text{。}}$ | (8) |
1)神经元节点数
分别取α为{4,8,16,32,64,128,256},依次代入模型中,重复10次实验对误差汇总取平均,结果如图4所示。当隐藏层神经元节点数取128时,误差指标MSE和MAE取得最小值。

|
图 4 神经元误差分布 Fig. 4 Error of cell unit |
2)输入层步数
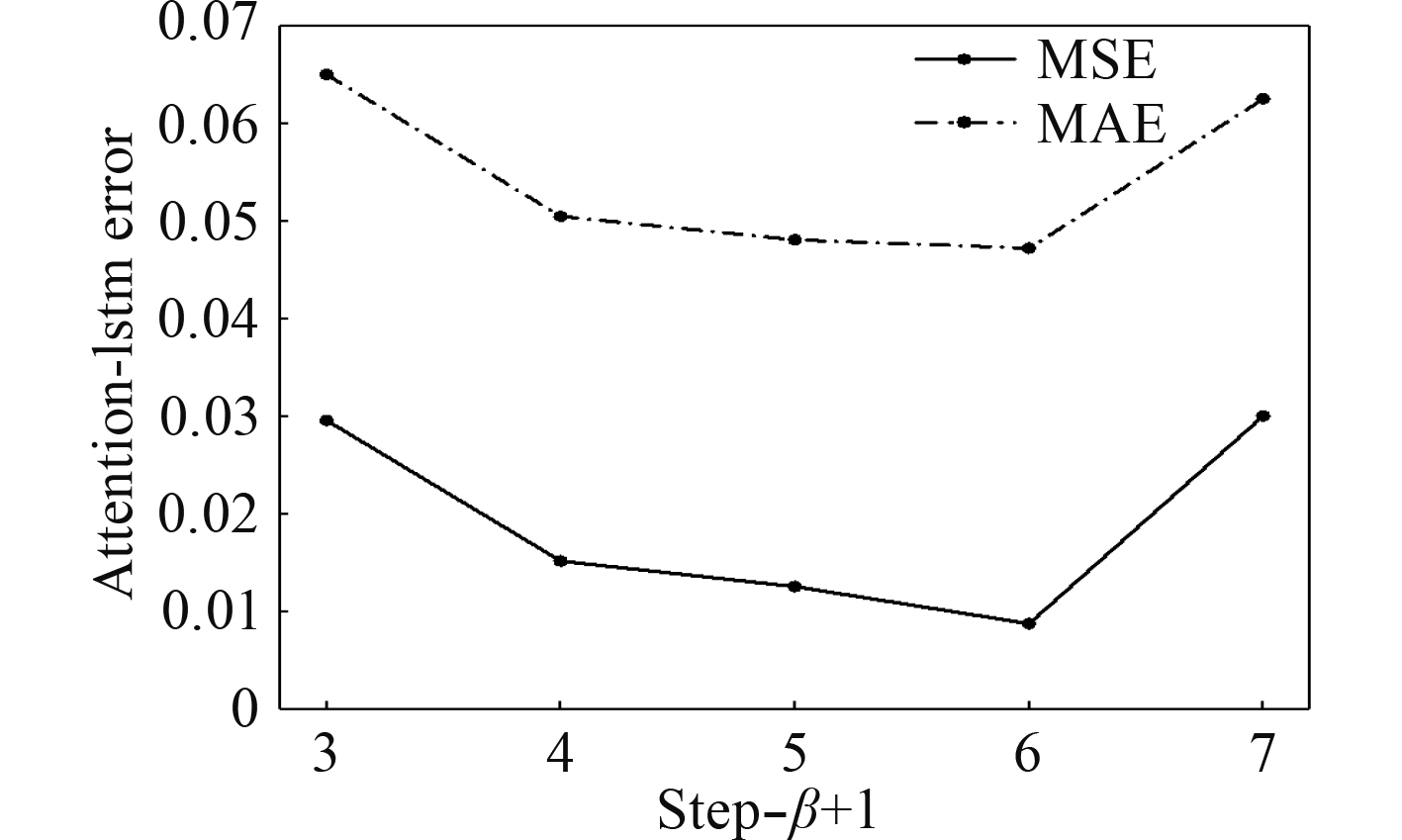
分别取β为{2,3,4,5,6,},依次代入模型中,重复10次。实验过程中不同步数对应的神经网络误差如图5所示。当β+1=6,即输入层步数为6时,模型拟合度最好。
|
图 5 输入层步数误差分布 Fig. 5 Error of step |
3)迭代次数
分别取θ为{1,500,1 000,1 500,2 000,2 500,3 000},代入模型并重复运行10次,可以得到不同迭代次数时的误差统计,如图6所示。当迭代次数为1 000时,模型效果最佳。
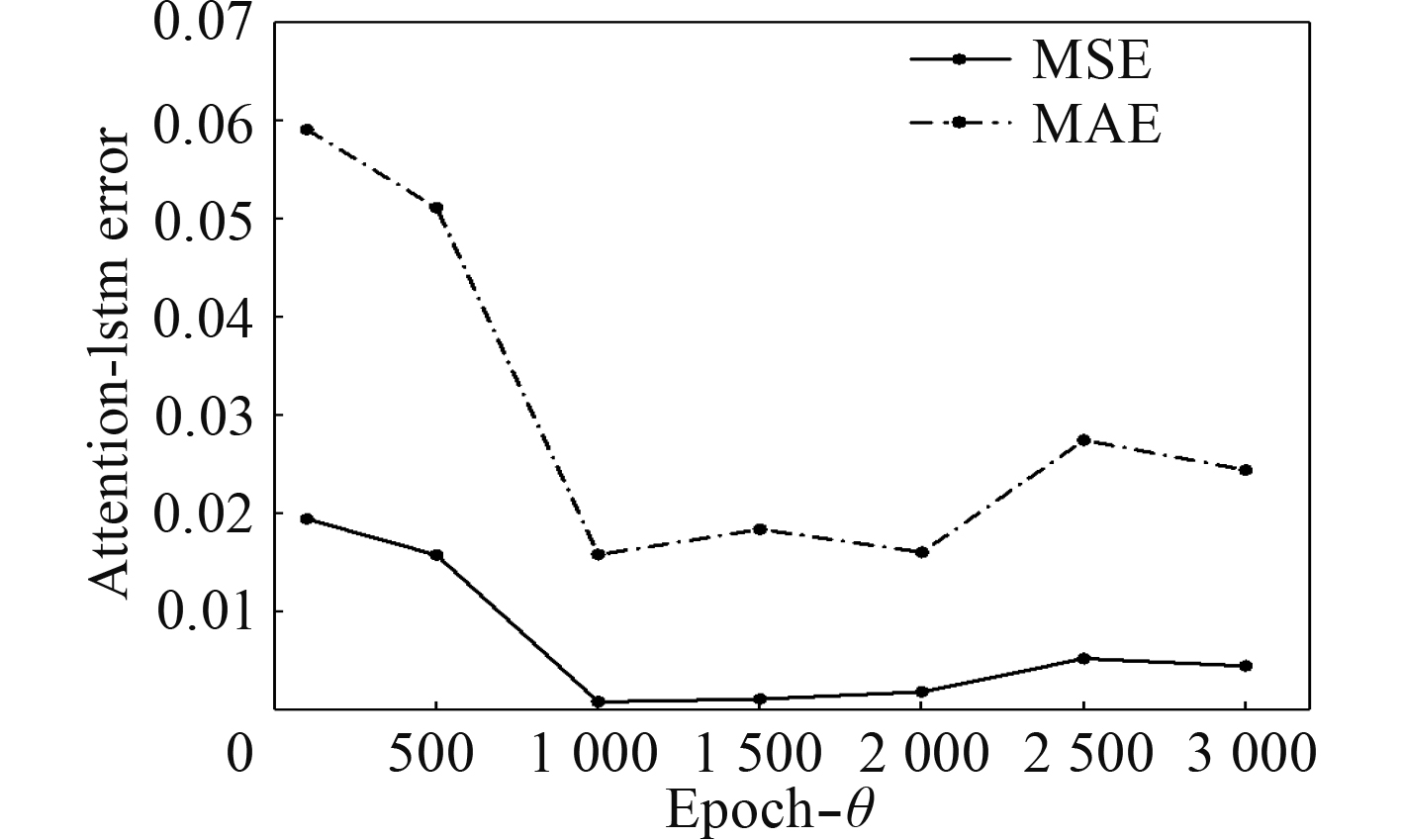
|
图 6 迭代次数误差分布 Fig. 6 Error of epoch |
使用BP神经网络进行船舶轨迹预测,效果良好。本文选用结构为4-14-4的BP神经网络与Attention-LSTM模型,对其预测效果进行对比,结果如图7所示。
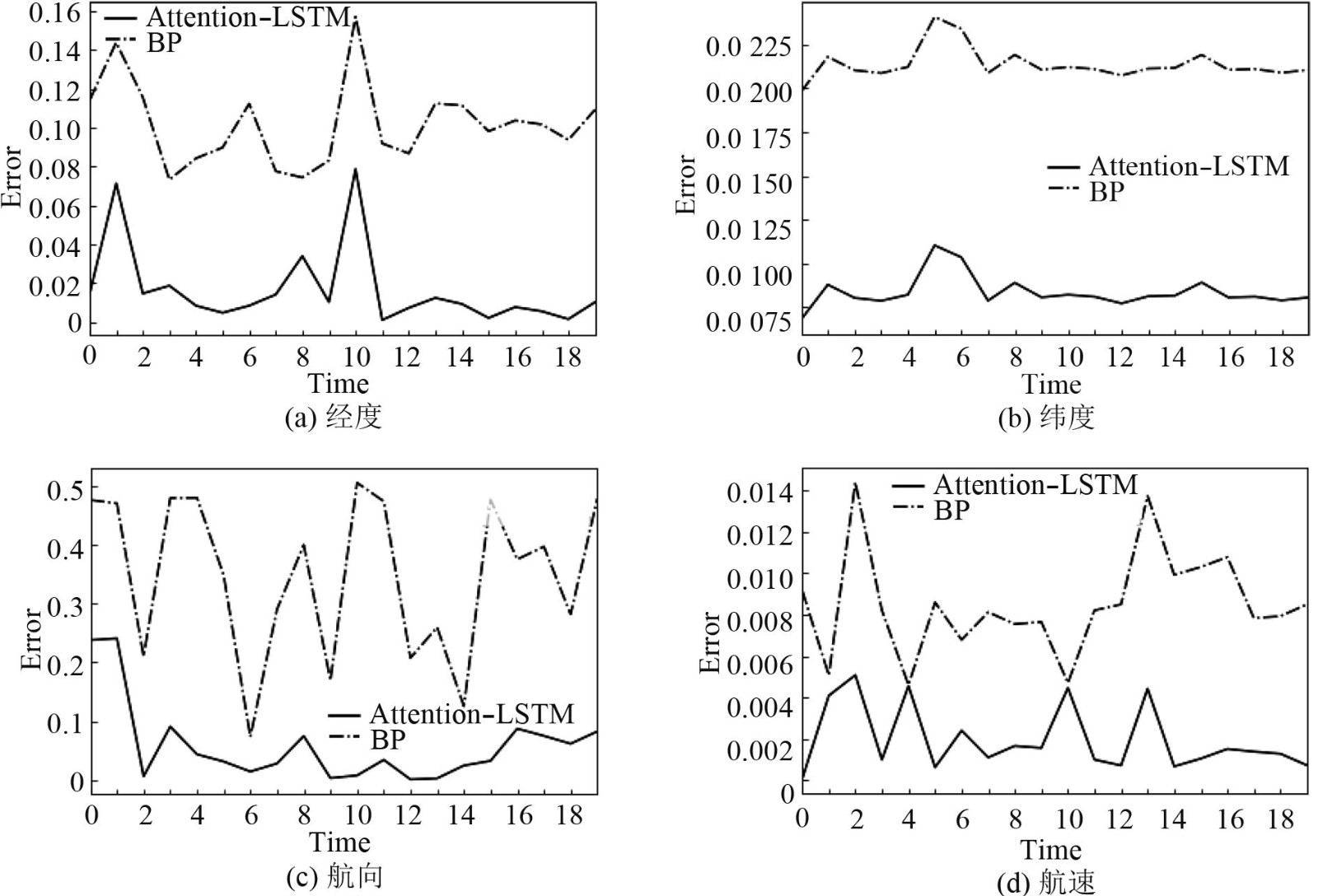
|
图 7 预测结果 Fig. 7 Prediction results |
在20次测试中,两类模型的误差曲线呈现出无规则震荡,但基于Attention-LSTM神经网络模型的预测误差均小于BP神经网络模型,即本文所提出的模型对船舶航行预测精度更高。
4 结 语本文依托船舶AIS数据,提出一种基于Attention-LSTM神经网络的多维船舶航行预测算法,实现了对船舶未来时刻经度、纬度、航向、航速的精准预测。通过仿真实验,表明本文方法的预测效果优于BP神经网络,且具有较好的鲁棒性,能够为水面无人艇自动避碰技术提供参考。
| [1] |
徐铁, 蔡奉君, 胡勤友, 等. 基于卡尔曼滤波算法船舶AIS轨迹估计研究[J]. 现代电子技术, 2014, 37(05): 97-100+104. DOI:10.3969/j.issn.1004-373X.2014.05.030 |
| [2] |
赵帅兵, 唐诚, 梁山, 等. 基于改进卡尔曼滤波的控制河段船舶航迹预测[J]. 计算机应用, 2012, 32(11): 3247-3250. |
| [3] |
王艳锋. 基于SVM的桥区水域失控船舶航迹对比分析[D]. 武汉理工大学, 2010.
|
| [4] |
刘锡铃, 阮群生, 龚子强. 船舶航行GPS定位轨迹的新预测模型[J]. 江南大学学报(自然科学版), 2014, 13(06): 686-692. DOI:10.3969/j.issn.1671-7147.2014.06.010 |
| [5] |
TONG Xiaopeng, MAO Zhe, CHEN Xu, et al.Vessel trajectory prediction in curving channel of inland river[C].//2015 International Conference on Transportation Information and Safety: 3rd International Conference on Transportation Information and Safety (ICTIS 2015), July 25-28, 2015, Wuhan, China. 2015: 706-714.
|
| [6] |
徐婷婷, 柳晓鸣, 杨鑫. 基于BP神经网络的船舶航迹实时预测[J]. 大连海事大学学报, 2012, 38(1): 9-11. DOI:10.3969/j.issn.1671-7031.2012.01.003 |
| [7] |
甄荣, 金永兴, 胡勤友, 等. 基于AIS信息和BP神经网络的船舶航行行为预测[J]. 中国航海, 2017, 40(2): 6-10. DOI:10.3969/j.issn.1000-4653.2017.02.002 |
| [8] |
权波, 杨博辰, 胡可奇, 等. 基于LSTM的船舶航迹预测模型[J]. 计算机科学, 2018, 45(S2): 126-131. |
| [9] |
杨博辰. 基于AIS的船舶轨迹分析的研究与应用[D].电子科技大学, 2018.
|
| [10] |
HOCHREITER S, SCHMIDHUBER J.Long short-term memory[M]//Supervised Sequence Labelling with Recurrent Neural Networks. Springer Berlin Heidelberg, 1997: 1735-1780.
|
| [11] |
司念文, 王衡军, 李伟, 等. 基于注意力长短时记忆网络的中文词性标注模型[J]. 计算机科学, 2018, 45(04): 66-70+82. |
| [12] |
LIU Hao, ZENG Guangping, ZHANG Qingchuan, et al. Part-of-speech and postion attention mechanism based BLSTM for question answering system[P]. Other Conferences, 2018.
|
| [13] |
张昭昭, 乔俊飞, 余文. 多层自适应模块化神经网络结构设计[J]. 计算机学报, 2017, 40(12): 2827-2838. DOI:10.11897/SP.J.1016.2017.02827 |
| [14] |
JAFARIAN Ahmad, NIA Safa Measoomy, GOLMANKHANEH Alireza Khalili, et al.. On artificial neural networks approach with new cost functions[J]. Applied Mathematics and Computation, 2018, 339. |
 2019, Vol. 41
2019, Vol. 41
