2. 上海大学 机电工程与自动化学院,上海 200444
2. School of Mechatronic Engineering and Automation, Shanghai University, Shanghai 200444, China
水面无人艇(Unmanned Surface Vehicle,USV)是一种可以自主感知环境、探测目标、智能避障,完成特定海洋任务如侦察、巡逻、监视等的小型船舶[1]。为提高无人艇执行任务的自主权,减少人工监督以降低运营成本,水面无人艇的智能避障一直是研究热点。USV的智能避障分为已知环境的全局避障和动态未知环境的局部避障。全局避障是指在已知水面环境地图上为无人艇规划出一条从起始点到终点的无障碍路径,局部避障规划是指根据无人艇的周围实时动态环境进行有效避障[2 – 3]。
基于随机采样的快速搜索树算法(Rapid-Exploring Random Tree,RRT)无需对环境空间进行预处理,已被证明可以用于各种复杂环境的路径探索,完成无人艇的全局避障规划[4 – 5]。RRT算法首先由Lavalle[6]提出用于路径规划。然而基本的RRT算法迭代次数过多,搜索节点遍布整个环境地图,浪费了大量内存资源,同时收敛速度慢,实时效果差。针对基本RRT算法存在的不足,众多学者提出了改进算法,如RRT-Connect算法、RRT*算法、B-RRT*算法、IB-RRT*算法。RRT*算法通过改变新节点连接方式以获取最低路径成本,加快了收敛速度,生成的路径渐近最优[7 – 8]。RRT-Connect算法提出起始点终点并行生成搜索树的方法,提高了路径搜索的速度[9 – 10]。B-RRT*算法则是RRT-Connect算法和RRT*算法的结合,生成一条最优路径[11]。文献[12]提出了一种基于动态步长的路径规划自适应RRT算法,并利用三次多项式曲线拟合来平滑规划路径。文献[13]采用自适应步长RRT方法进行双机器人路径规划,实现了双机器人在各自构型空间中的协同路径规划。文献[14]提出一种基于路标引导和增长采样区域的混合策略来引导RRT算法向目标搜索。文献[15]改进了RRT-Connect算法,以便设计管线最优路径,采用贪心算法去除多余节点,并采用Catmull-Rom曲线拟合关键节点处曲线。
对于无人艇的全局避障规划,这些算法仍存在一些问题:
1)在避障规划时未考虑与障碍物的安全距离。
2)随机采样带来搜索路径的不稳定性;
3)路径长度仍需优化;
4)规划的路径折点过多,仍需后续光滑处理。
为解决这些问题,本文提出一种改进的无人艇全局避障规划方法,即(Line Segment Theorem-RRT*)LT-RRT*算法。考虑到USV实际航行时应与障碍物保持一定安全距离,首先运用栅格法对环境地图进行预处理。然后再根据终点采样概率选取采样点,改善全局采样引起的路径不稳定性,节约内存资源,提高收敛速度。根据线段定理重新选取新节点和附近节点的父节点,跳过中间节点直接连接树节点,减少路径折点及路径成本,使算法最终生成相对平滑的规划路径。最后在相同水面环境下,将本文算法与现有算法进行比较,结果表明LT-RRT*算法可以为USV规划出更短的避障路径,其转折点数量大大减少,同时距离障碍物有一定安全距离,更有利于USV的安全行驶。
1 现有算法研究 1.1 问题定义假设环境空间为
基本RRT算法首先在无障碍空间

|
图 1 RRT算法示意图 Fig. 1 The diagram for RRT algorithm |
由于基本RRT算法收敛过慢,路径过长,RRT*算法改变了新节点的连接方式,以新节点
由于障碍物边缘区域为不利于无人艇安全航行的危险区域,规划的避障路径应避开障碍物一定距离。考虑无人艇航行的安全性,在算法执行过程中对路径段进行避障距离检测,虽然可以使最终生成的路径避开障碍物一定距离,但会大大增加算法计算时间,影响算法收敛速度。因此在进行无人艇全局避障规划之前,应先对环境地图进行预处理,根据障碍物位置标示出其周围不可航行区域。
运用栅格法[16 – 17],将环境地图按合适比例划分成M*N格。每个障碍物单元的8个方向上的栅格部分处理为其他颜色,定义为无人艇行驶的危险区域,避障规划时同时检测与危险区域的碰撞,可以使无人艇与障碍物保持安全距离。
2.2 改进采样点选取快速随机搜索树算法RRT在整个环境空间生成随机采样点,扩展了树节点,很好地探索了未知空间。但生成大量偏离终点的无用节点,导致迭代次数过多,占用内存过多,生成路径过长,搜索路径过慢,不能很好地满足无人艇避障规划的实时性要求。
针对此问题,引入终点采样概率p(0 ≤ p≤ 1),一次迭代以p概率直接选择终点为采样点,以1-p的概率随机选择环境空间中的点。随机采样点不再过于随机,p的值越大,避障路径的搜索更加偏向终点,大大减少无用空间的探索,有利于树节点更加快速逼近终点,提高收敛速度。
2.3 改进父节点选取RRT算法及其改进算法大多直接选取距离采样点
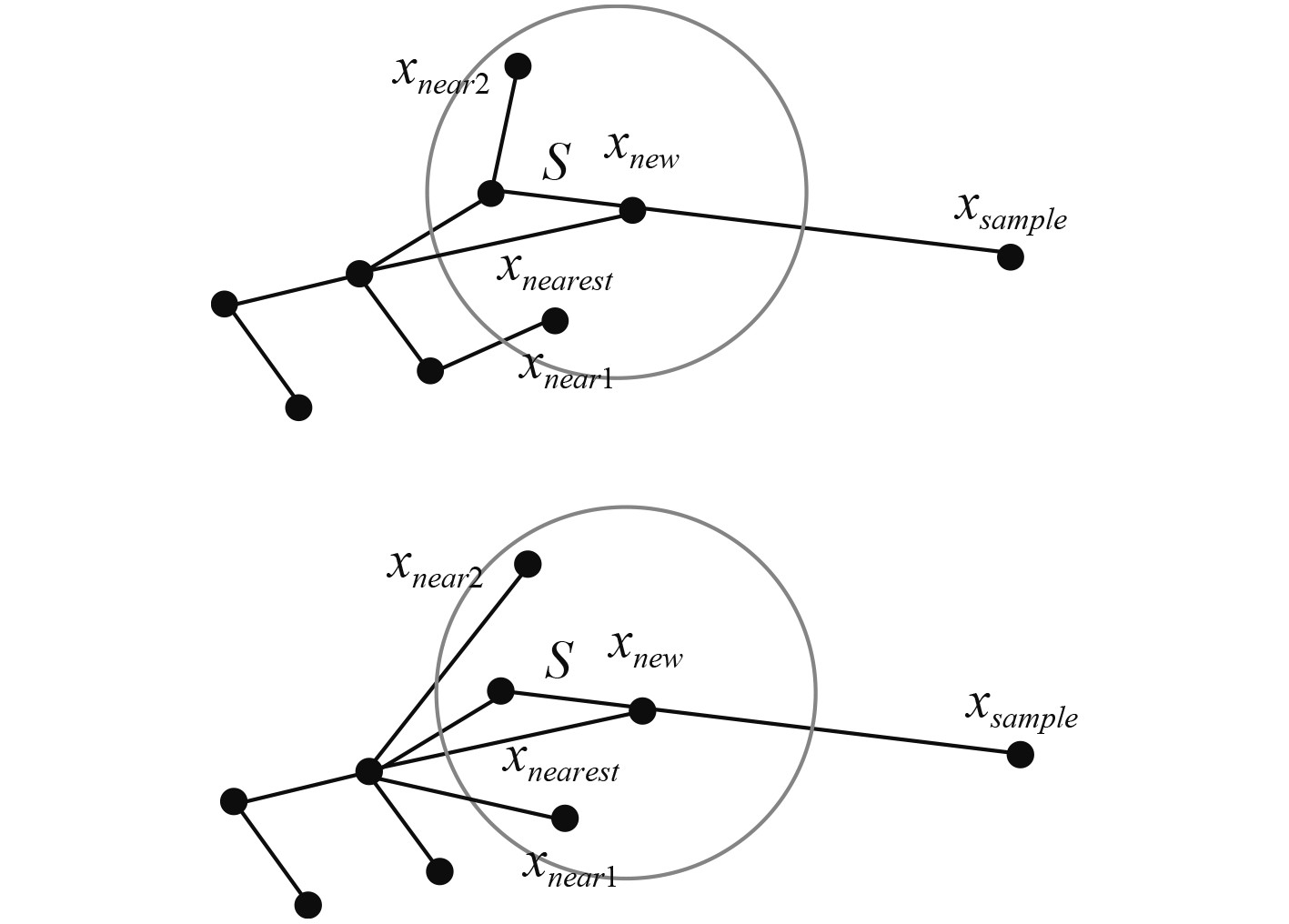
RRT*算法在添加新节点时同时考虑了新节点的周围节点,通过周围节点到达新节点的成本若低于通过最近节点到达新节点的成本,以周围节点作为新节点的父节点,从而修正航迹,提高收敛率,减少路径成本。但上述方法仍不可避免节点过多,路径过于曲折。为此,基于线段定理(两点之间直线最短),改进父节点的选择,拉直路径。每一次迭代中,选取

|
图 2 RRT*算法父节点选择和路径重连 Fig. 2 RRT* algorithm′s parent node selection and path reconnection |
|
图 3 LT-RRT*算法父节点选择和路径重连 Fig. 3 LT-RRT* algorithm′s parent node selection and path reconnection |
本文提出的LT-RRT*算法规划无人艇避障路径的步骤如下:
1)运用栅格法对环境地图进行处理,以其他颜色标示出障碍物周围的危险区域,使无人艇距离障碍物一定距离,保证其行驶的安全性。
2)以p概率(0 ≤ p ≤ 1)直接选择终点为采样点
3)在整个树T上寻找距离采样点
4)以新节点
5)删除周围节点的上一次连接,连接
6)找到路径,计算路径长度和搜索时间。
节点之间的每一次连接,都要进行避障检测,避开障碍物以及障碍物周围危险区域。
3 算法性能分析在简单障碍物环境和复杂障碍物环境下,对比现有算法和LT-RRT*算法的避障规划效果。
3.1 简单环境避开单个障碍物的水面环境是无人艇避障规划中比较简单的一种情况。图4和图5为某湖泊水面地图,地图大小为1 384 m*1 216 m,以地图左上角为原点,向右为x轴正方向,向下为y轴正方向,起始点为(600 m,600 m),终点为(720 m,260 m),无人艇起始点与终点的直线连接只有单个障碍物。为保证几种算法性能对比的有效性,本文考虑在相同环境地图上进行避障规划,且保证规划参数一致。
|
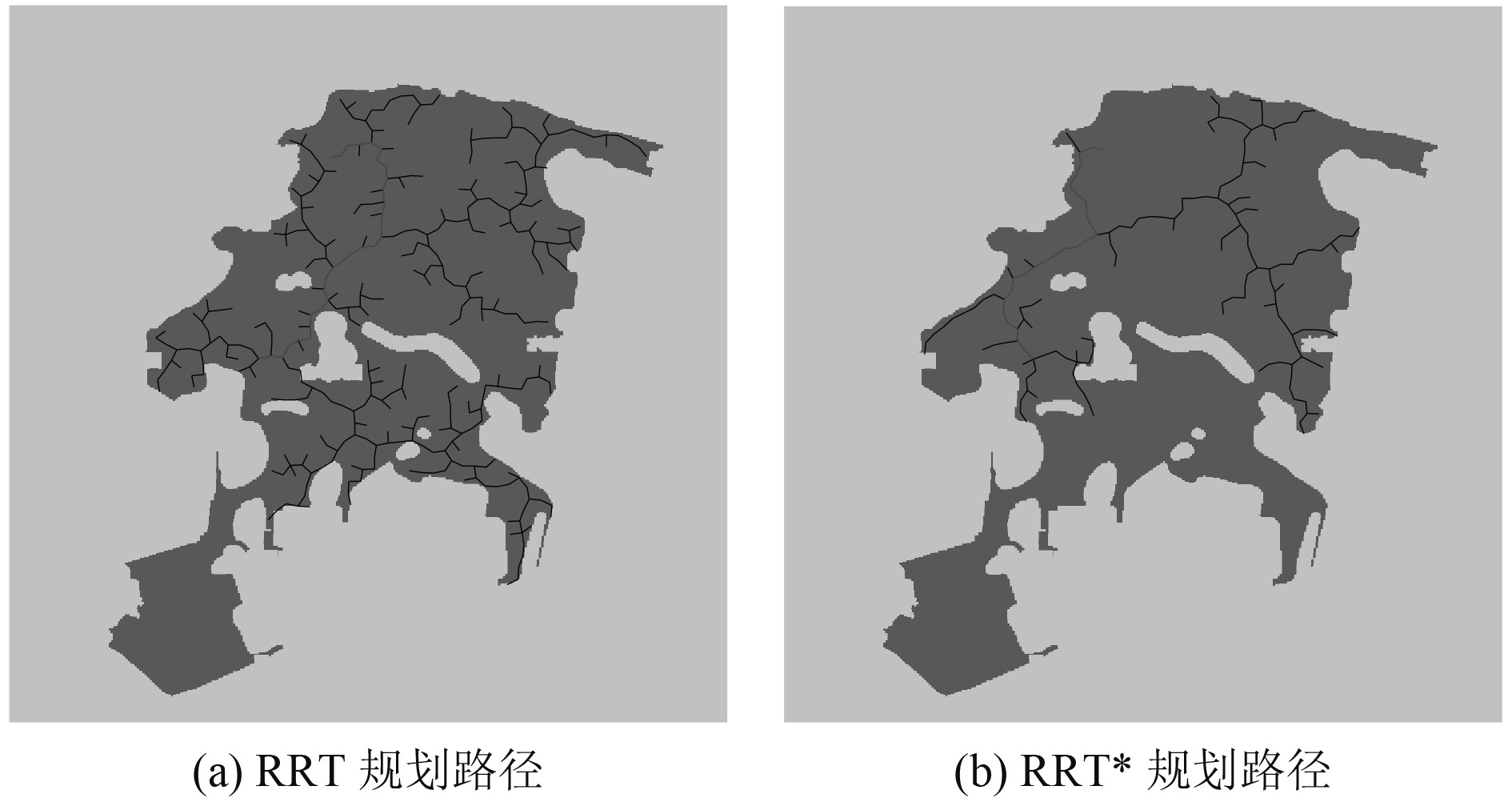
图 4 RRT规划路径和RRT*规划路径 Fig. 4 RRT algorithm′s planning path result and RRT* algorithm′s planning path result |
|
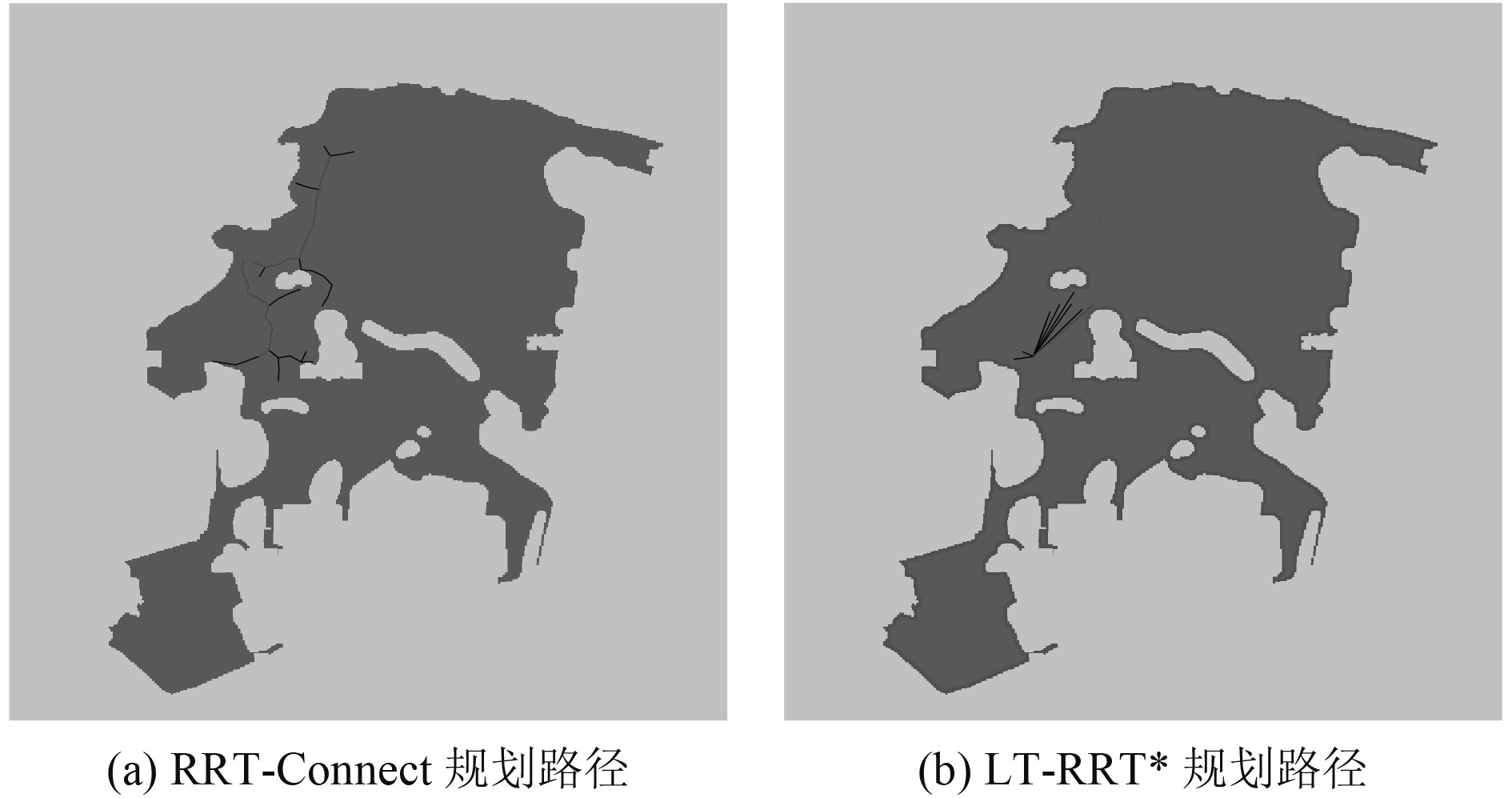
图 5 RRT-Connect规划路径和LT-RRT*规划路径 Fig. 5 RRT-Connect algorithm′s planning path result and LT-RRT* algorithm′s planning path result |
结合表1列出的几种算法规划的避障路径结果,如图4(a),可以看出经典RRT算法在整个环境空间进行采样,因而树节点遍布整个环境空间,规划时间较长,不能很好满足无人艇行驶的实时性要求,探索到的避障路径由多个树节点组成,路径比较曲折,路径长度较长。RRT*算法由于改进了新节点的连接方式,考虑了路径成本,缩短了规划时间和路径长度,但路径节点数没有大的改善。由图5(a)可知,双向搜索树算法RRT-Connect由于从起始点和终点同时向对方探索避障路径,方向性较强,减少了对环境空间中无用区域的探索,大大节约了避障规划时间,但最终搜索到的避障路径仍然较长,节点数过多,路径较曲折,不利于无人艇的行驶。
|
|
表 1 简单环境 Tab.1 Simple environment |
图5(b)中LT-RRT*算法的规划时间短,且其规划的路径被拉直,大大缩短了路径长度。经过重新选取父节点的规划路径长度缩短为RRT算法规划路径长度的64.3%,RRT*算法规划路径长度的71.4%,RRT-Connect算法规划路径长度的80.3%;路径节点数包括起始点终点只有3个,分别比RRT算法规划路径少28个,比RRT*算法规划路径少25个,比RRT-Connect算法规划路径少22个;同时与障碍物之间留有安全距离。因此可以说在简单环境下LT-RRT*算法表现优于其他算法。
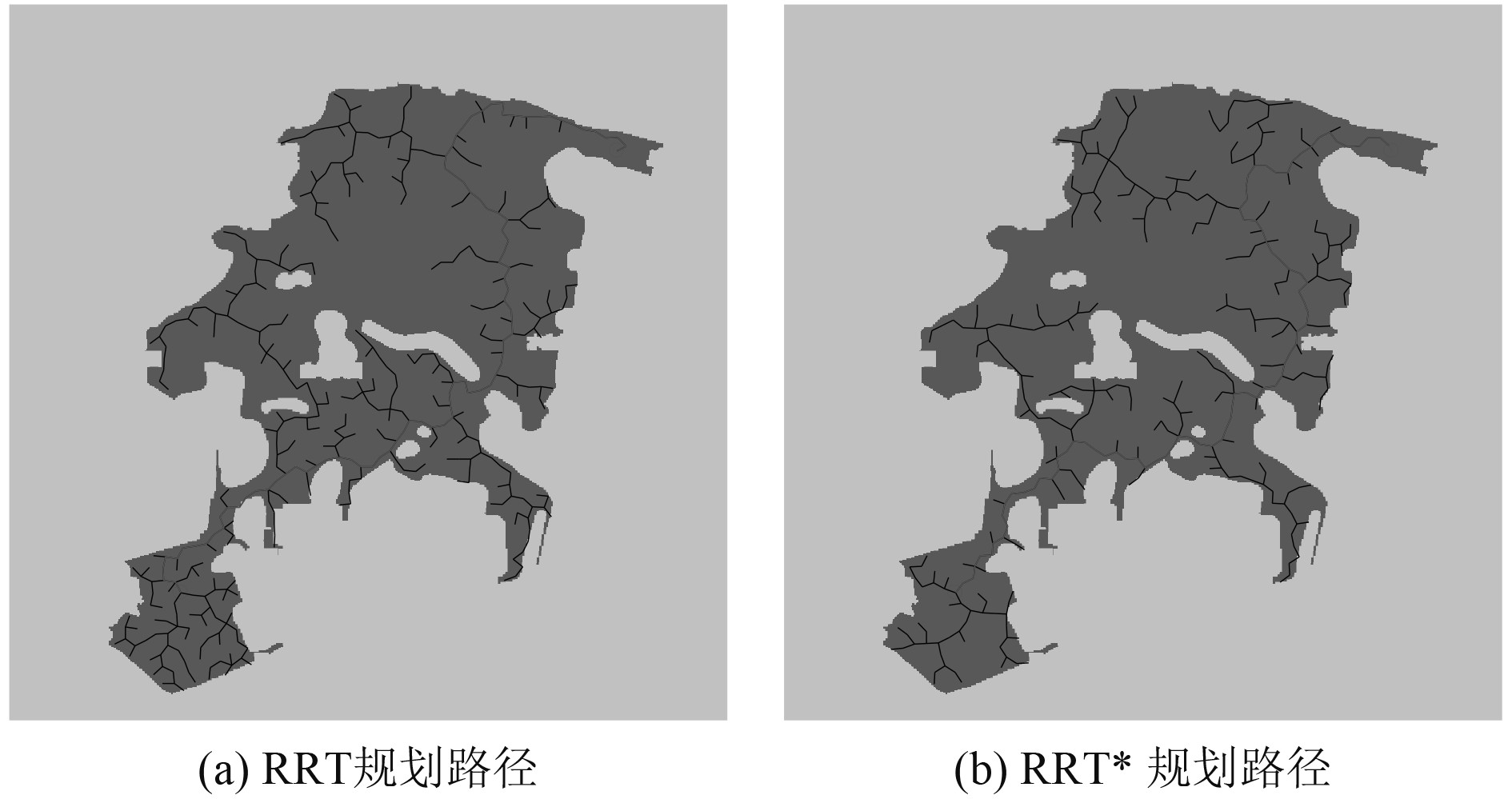
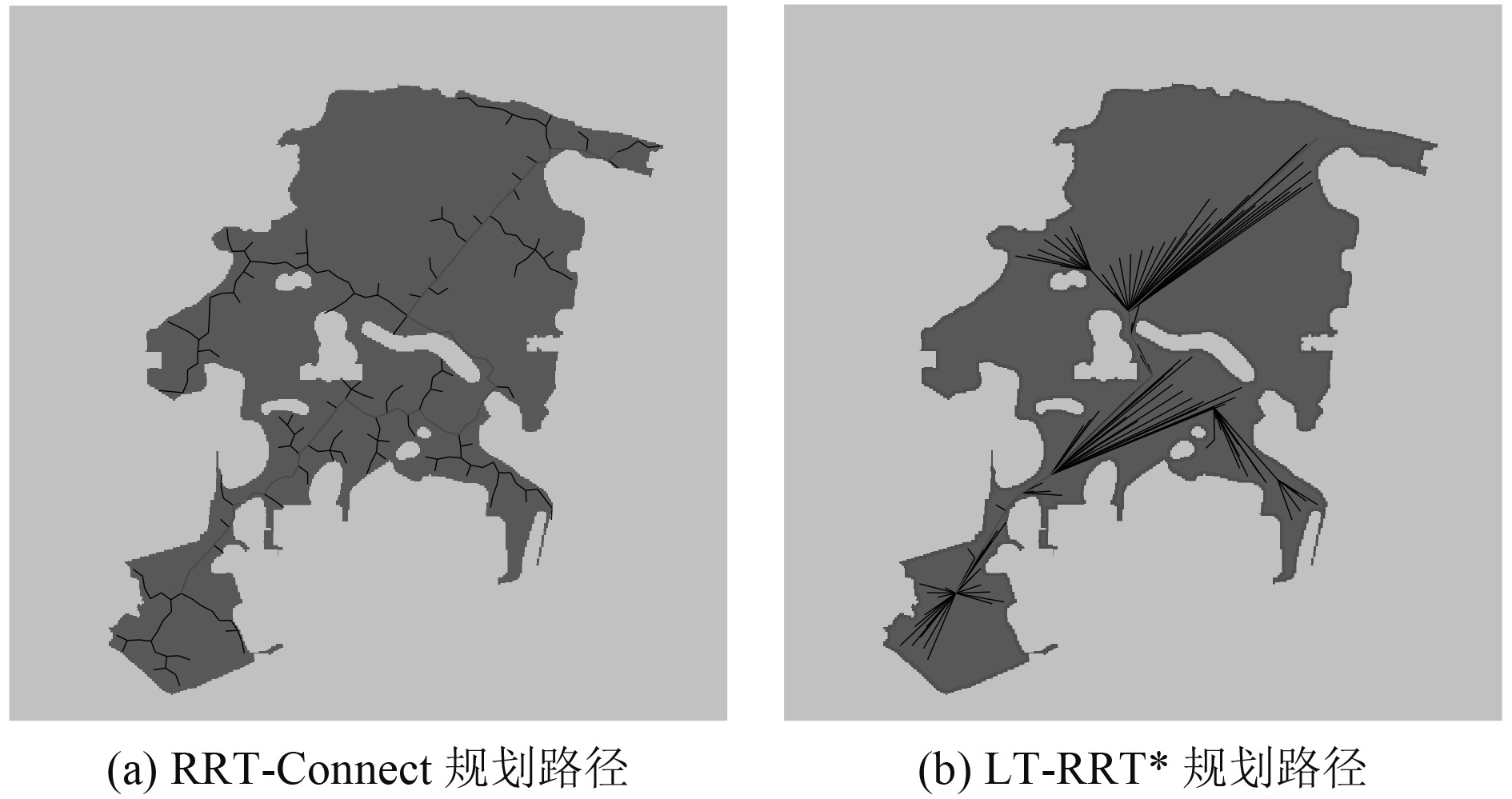
3.2 复杂环境如图6和图7所示,湖泊水面地图不变,坐标轴不变,起始点为(470 m,1 000 m),终点为(1 200 m,250 m)。无人艇起始点与终点的直线连接存在多个障碍物,在这样的复杂环境中,算法在探索新节点时增加了对避障检测程序CollisionFree的调用次数,计算时间也增长。表2列出了几种算法在该复杂环境下的避障规划结果。对比实验结果,LT-RRT*算法在时间上比RRT算法和RRT*算法短,略长于RRT-Connect算法,对全局避障规划的影响较小,但路径长度和节点数大大减小,同时与障碍物之间留有安全距离。LT-RRT*算法规划的避障路径长度为1 175.6 m,分别缩短为RRT算法规划路径长度的67.8%,RRT*算法规划路径长度的73.2%,RRT-Connect规划路径长度的77.7%,路径节点数只有10个,分别比RRT算法规划路径减少77个,比RRT*算法规划路径减少71个,比RRT-Connect规划路径减少67个。上述结果表明在复杂环境下,LT-RRT*算法规划的避障路径效果优于其他算法。
|
图 6 RRT规划路径和RRT*规划路径 Fig. 6 RRT algorithm′s planning path result and RRT* algorithm′s planning path result |
|
图 7 RRT-Connect规划路径和LT-RRT*规划路径 Fig. 7 RRT-Connect algorithm′s planning path result and LT-RRT* algorithm′s planning path result |
|
|
表 2 复杂环境 Tab.2 Complex environment |
本文在RRT*算法的基础上提出一种改进的无人艇全局避障规划方法LT-RRT*(Line Segment Theorem-RRT*)。考虑无人艇航行的安全性,首先对环境地图预先进行处理,使算法最终生成的路径避开障碍物一定距离。其次根据终点采样概率选取随机采样点,改善了全局采样引起的路径不稳定性,提高了算法收敛速度。依据线段定理重新选取新节点和附近节点的父节点,降低了规划路径节点,减少了规划路径成本,使算法最终生成相对平滑的避障路径。后续考虑加入无人艇的动力学约束,并探索不同算法规划路径对后续轨迹跟踪的影响。
| [1] |
CAMPBELL S, NAEEM W, IRWIN G W. A review on improving the autonomy of unmanned surface vehicles through intelligent collision avoidance manoeuvres[J]. Annual Reviews in Control, 2012, 36(2): 267-283. DOI:10.1016/j.arcontrol.2012.09.008 |
| [2] |
LIU Zhixiang, ZHANG Youmin, YU Xiang, et al. Unmanned surface vehicles: An overview of developments and challenges[J]. Annual Reviews in Control, 2016, 41: 71-93. DOI:10.1016/j.arcontrol.2016.04.018 |
| [3] |
庄佳园, 张磊, 孙寒冰, 等. 应用改进随机树算法的无人艇局部路径规划[J]. 哈尔滨工业大学学报, 2015, 47(1): 112-117. ZHUANG Jiayuan, ZHANG Lei, SUN Hanbing, et al. Improved rapidly-exploring random tree algorithm application[J]. Journal of Harbin Institute of Technology, 2015, 47(1): 112-117. DOI:10.3969/j.issn.1009-1971.2015.01.018 |
| [4] |
TAHIR Z, QURESHI A H, AYAZ Y, et al. Potentially guided bidirectionalized RRT* for fast optimal path planning in cluttered environments[J]. Robotics and Autonomous Systems, 2018, 108: 13-27. DOI:10.1016/j.robot.2018.06.013 |
| [5] |
JANSON L, ICHTER B, PAVONE M. Deterministic sampling-based motion planning: optimality, complexity, and performance[J]. International Journal of Robotics Research, 2018, 37(1): 46-61. DOI:10.1177/0278364917714338 |
| [6] |
LAVALLE S M. Rapidly-exploring random trees: a new tool for path planning[D]. USA: Computer Science Department, Iowa State University, 1998.
|
| [7] |
潘思宇, 徐向荣. 基于改进RRT*的移动机器人运动规划算法[J]. 山西大学学报(自然科学版), 2017, 40(2): 244-254. PAN Si-yu, XU Xiang-rong. Improved RRT*-based motion planning algorithm for mobile robot[J]. Journal of Shanxi University (Nat. Sci. Ed.), 2017, 40(2): 244-254. |
| [8] |
ADIYATOV O, VAROL H A. A novel RRT*-based algorithm for motion planning in dynamic environments [C]// IEEE International Conference on Mechatronics and Automation, Takamatsu, Japan: IEEE, 2017: 1416–1421.
|
| [9] |
LAVALLE S M, KUFFNER J J. RRT-Connect: An efficient approach to single-query path planning [C]// IEEE International Conference on Robotics and Automation. San Francisco, CA, USA: IEEE, 2002.
|
| [10] |
张亚琨, 高泽东, 曹杰, 等. 多采样寻优的双向RRT路径规划算法[J]. 计算机仿真, 2019, 36(2): 319-324. ZHANG Ya-kun, GAO Ze-dong, CAO Jie, et al. Bidirectional RRT path planning algorithm with multiple sampling optimization[J]. Computer Simulation, 2019, 36(2): 319-324. DOI:10.3969/j.issn.1006-9348.2019.02.070 |
| [11] |
王坤, 曾国辉, 鲁敦科, 等. 基于改进渐进最优的双向快速扩展随机树的移动机器人路径规划算法[J]. 计算机应用, 2019, 39(5): 1312-1317. WANG Kun, ZENG Guo-hui, LU Dun-ke, et al. Path planning of mobile robot based on improved B-RRT* algorithm[J]. Journal of Computer Applications, 2019, 39(5): 1312-1317. |
| [12] |
LIN Na, ZHANG Ya-lun. An adaptive RRT based on dynamic step for UAVs route planning [C]// Proceedings of the 5th IEEE Software Engineering and Service Science, [S. I.]: IEEE, 2014: 1111–1114.
|
| [13] |
李洋, 徐达, 周诚. 基于自适应步长RRT的双机器人协同路径规划[J]. 农业机械学报, 2019, 50(3): 358-367. LI Yang, XU Da, ZHOU Cheng. Cooperation path planning of dual-robot based on self-adaptive stepsize RRT[J]. Transactions of the Chinese Society for Agricultural Machinery, 2019, 50(3): 358-367. |
| [14] |
龙建全, 梁艳阳. 多路口环境下RRT的最优路径规划[J/OL]. 计算机工程与应用, 2019. (2019-04-02) [2019-08-02]. http://kns.cnki.net/kcms/detail/11.2127.TP.20190401.1530.002.html. LONG Jian-quan, LIANG Yan-yang. Optimal path planning of RRT in multi-intersection environment[J/OL]. Computer Engineering and Applications, 2019. (2019-04-02) [2019-08-02]. http://kns.cnki.net/kcms/detail/11.2127.TP.20190401.1530.002.html. |
| [15] |
王素琴, 王飞, 袁建平, 等. 基于双向RRT算法的管线路径规划及建模仿真[J]. 太原理工大学学报, 2018, 49(6): 839-845. WANG Su-qing, WANG Fei, YUAN Jian-ping, et al. Pipeline route planning and simulation based on bidirectional RRT algorithm[J]. Journal of Taiyuan University of Technology, 2018, 49(6): 839-845. |
| [16] |
程向红, 祁艺. 基于栅格法的室内指示路径规划算法[J]. 中国惯性技术学报, 2018, 26(2): 102-106+133. CHENG Xiang-hong, QI yi. Indoor indicator path planning algorithm based on grid method[J]. Journal of Chinese Inertial Technology, 2018, 26(2): 102-106+133. |
| [17] |
DANIEL K, NASH A, KOENIG S, et al. Theta*: Any-angle path planning on grids[J]. Journal of Artificial Intelligence Research, 2010, 39: 533-579. DOI:10.1613/jair.2994 |
 2019, Vol. 41
2019, Vol. 41
