无人艇是一种无人操作的水面舰艇,常用于危险水域搜救或人员无法到达的水域执行探测,侦察等任务。无人艇的应用极大节省了人力物力成本,并且可以高效快速执行任务。为使无人艇执行任务时可以达到较高的避碰性能以及选择最优的路径规划,本文对无人艇的航迹规划、自主避障做进一步的研究。
当前智能航行体的路径规划算法主要有遗传算法、Dijkstra算法、A*算法、人工势场法、蚁群算法等。遗传算法最早是由美国J.Holland教授提出的,遗传算法是模拟自然界中按“优胜劣汰”法则进行进化过程而设计的算法,在动态路径规划中得到广泛应用。谢玉龙等[1]针对传统遗传算法解决船舶路径规划问题的不足,提出了一种改进的遗传算法。改进算法改变了种群的编码方式,由二维编码变为基于坐标轴的一维编码;在传统遗传算法的基础上增加3个新的遗传操作:复原操作、重构操作和录优操作,使算法尽早收敛于全局最优解,录优操作保证种群朝着最优解方向进化。Dijkstra算法是一种常见的最短路径算法,由Edsger W.Dijkstra在1959年提出。传统的Dijkstra算法直接搜索全局空间而不考虑目标信息,导致路径求解时花费的时间较长,难以满足快速路径规划的需求。陈家[2]提出一种将蚁群算法和Dijkstra算法相结合的复合算法,应用于无人驾驶救助船路径规划中。该复合算法首先通过Dijkstra算法寻找出最短路径,然后利用改进的蚁群算法对所得到的最短路径进行优化,使最后得到的路径更符合实际情况。陈超等[3]提出一种改进的人工势场法,通过建立新的引力和斥力场函数来避免局部最小点问题,并应用于水面无人艇的路径规划中。余必秀等[4]提出一种改进的A*算法,在原始代价函数的基础上,新增一个与当前点到预设航线的垂直距离相关的代价值,并将改进后的算法应用于无人航道测量船的路径规划中,使无人航道测量船在避开障碍物之后更快地回到预设航线。陈立家等[5]将改进的蚁群算法应用于船舶航行路径搜索中,提出一种多约束条件下航行综合成本最低的最优航线生成算法,可以在多约束条件下规划出最优航线。王红卫等[6]提出一种平滑A*算法,能处理不同栅格规模下、障碍物随机分布的复杂环境下移动机器人的路径规划问题。
A*算法是一种启发式的搜索算法,是求解最短路径最有效的直接搜索方法,同时也适用于路径的二次规划。由于A*算法中为了处理复杂流程需要大量数学计算和理论推导,从而导致A*算法规划的路径存在折线、转折多的问题,这使得在仿真实验中,规划的路径与障碍物距离过近,极易引发碰撞,存在极大的安全隐患。针对此问题,本文以栅格法环境建模为基础,当航行体行至障碍物附近时,对障碍物尖角检测,然后进行路径平滑处理,使得航行体与障碍物始终处于安全距离的范围内。对比结果表明,改进后的A*算法规划路径优于传统的A*算法。
1 基于A*算法进行路径规划的基本原理 1.1 A*算法原理A*算法是对估价函数加上一些限制后得到的一种启发式搜索算法[7 – 8],启发式搜索可以有效地避免无效的搜索路径,提高搜索效率。A*算法路径搜索步骤如下:
新建Closed表和Open表,并进行初始化。将初始节点s添加到新建的Open表。如果Open表为空则表示失败并且退出,否则取最小节点F作为当前考察点x。从Open表中将x移入Closed表。如果x是目标节点,那么确定找到最优解并且退出,否则扩展x并生成继节点n。考察x的所有的继节点n。
1)所有的继节点n都有g(n) = g(x) + g(x, n);
2)创建一个新的指针,将n返回s;
3)如果n是Open表的旧节点,则把旧节点标记成o,并且把n加入到x的字节点表里。若f(n) < f(o),则f(o) = f(n)。如果n没在Open表,那么将判断它是否在Closed表。
4)如果n是Closed表的旧节点,则把它标记为o,把节点n加入到x的子节点表中。若f(n) < f(o),则f(o) = f(n)。否则将其加入到Open表和x的后继节点;第5步:算出F值,并返回到第3步,继续执行。
5)算出F值,并返回到第3步,继续执行。
采用A*算法无人艇的路径规划,首先需要建立A*优化函数[9]:
O为存放等待扩展节点集合;C为存放已扩展过节点集合;Ss为起点;Te为目标点;Oi为障碍物栅格;Oobs为障碍栅格的集合;g(n)为初始节点Ss到n的实际移动距离;
利用栅格地图和八邻域节点扩展法,将无人艇从当前节点k到目标点Te的Euclidean距离作为启发式函数:
| ${{h}}\left( {{k}} \right) = \sqrt {{{(kx - {T_e}x)}^2} + {{(ky - {T_e}y)}^2}} \text{。}$ |
图1为A*算法的流程图,通过下列程序的执行,得到所规划的初始路径。
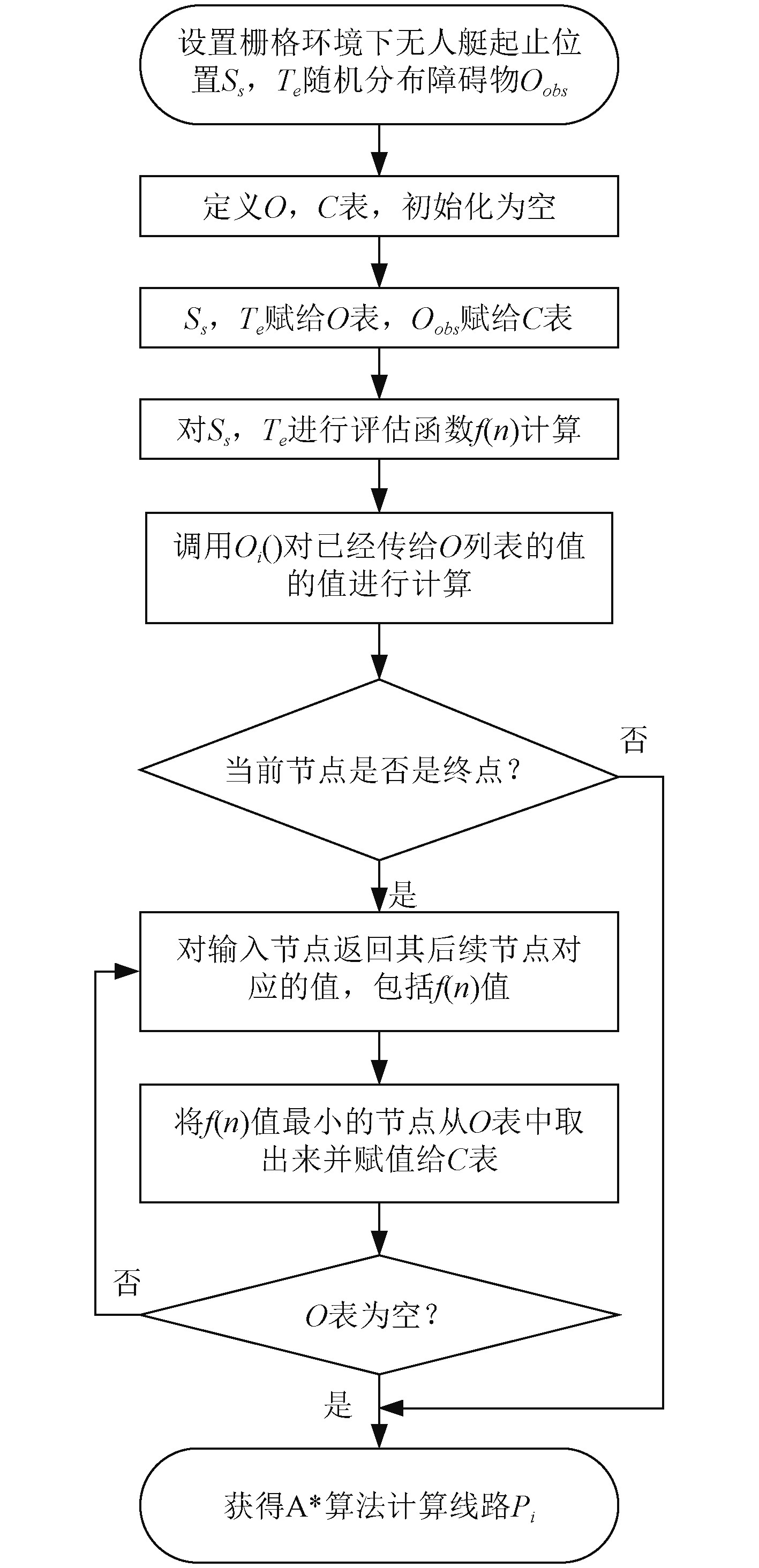
|
图 1 传统A*算法流程图 Fig. 1 Flowchart of traditional A* algorithm |
为了处理传统算法规划路径的折线多,且易穿越障碍物之间的接触地带等问题,采用改进后的算法对路径做出判断并进行平滑处理。改进算法具体步骤如下:
1)定义无人艇的原始路径为Pi,节点数为Pin,改进平滑处理后的路径为Pp。
2)判断原始路径的节点是否等于2。若大于2,则执行下一步,否则将原始路径Pi的值赋给Pp。
3)判断Pi的节点是否小于等于Pin。若是则执行下一步,否则将Pi上非N节点赋值给Pp。
4)调用线段lc()所获得节点i和i+2所在的线段
5)调用障碍物集合Ob。
6)判断线段
7)将Pi上节点i+1置为N。
8)执行i=i+1。
9)最终获得改进算法处理后所得的优化路径Pp。
在改进后的算法中,新定义2个函数Ps()和W()函数,Ps()是需要处理的路径节点,W()函数用来判断待连接节点的线段是否存在障碍物,有障碍物,则W()失败,即无通路;否则可联通。函数Ps()具体执行步骤如下:
1)定义无人艇的原始路径Pi,连接点为Pinit,改进算法处理后的路径Prp为空。
2)将连接点的下一个节点赋值给当前节点。
3)判断当前节点是否为空。若是则执行下一步,否则连接所有节点获得Prp。
4)判断连接点同当前节点的下一节点之间是否能够走通。若是则执行下一步,否则返回第2步。
5)删除当前节点,连接点的下一个节点赋值给当前节点。
函数W()具体执行步骤如下:
1)定义连接点和当前节点的下一个节点;
2)将连接点的下一个节点赋值给当前节点;
3)用线段连接连接点与当前节点的下一个节点;
4)判断当前线段上是否存在障碍物,若不存在执行下一步,若存在则不存在通路退出;
5)存在通路可行。
经过改进的A*算法用于无人艇路径规划的具体流程图,如图2所示。

|
图 2 改进A*算法水面无人艇航迹规划流程图 Fig. 2 Improved A* algorithm flowchart of route planning for surface unmanned boat |
由图3可以看出,基于传统A*算法的规划的路径为曲折的折线,这并不满足无人艇的实际航行需求。而经过改进后的算法所规划出的路径更符合实际要求。
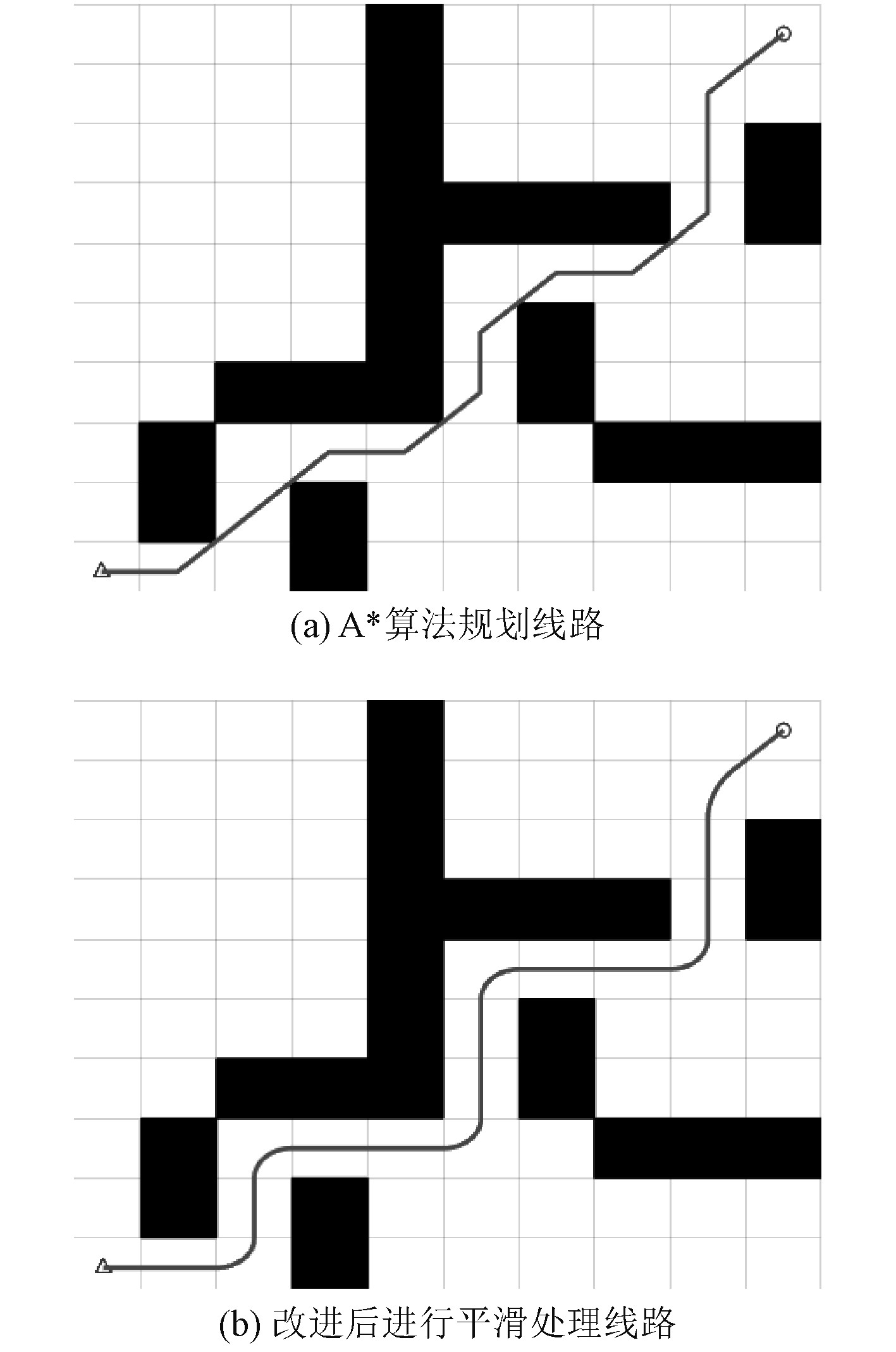
|
图 3 改进A*算法平滑处理前后的路径对比图 Fig. 3 Path comparison before and after smoothing with improved A* algorithm |
模型仿真实验在Matlab R2016b环境中进行,搭建20×20的仿真地图,通过建立直角坐标系,定义仿真环境图的左下角坐标为(1,1);右上角坐标为(20,20)。其中黑色部分表示障碍物,白色部分表示可通行区域,障碍物模拟水闸、钻井平台,抛锚船只等静态障碍物,本文的目的就是找到一条从起点到终点的无碰最优航迹。实验分别在图4中简单环境(a)和复杂环境(b)进行,分别采用传统A*算法和改进后的算法做出最优路径规划,并进行分组对比,仿真结果如图5和图6所示。
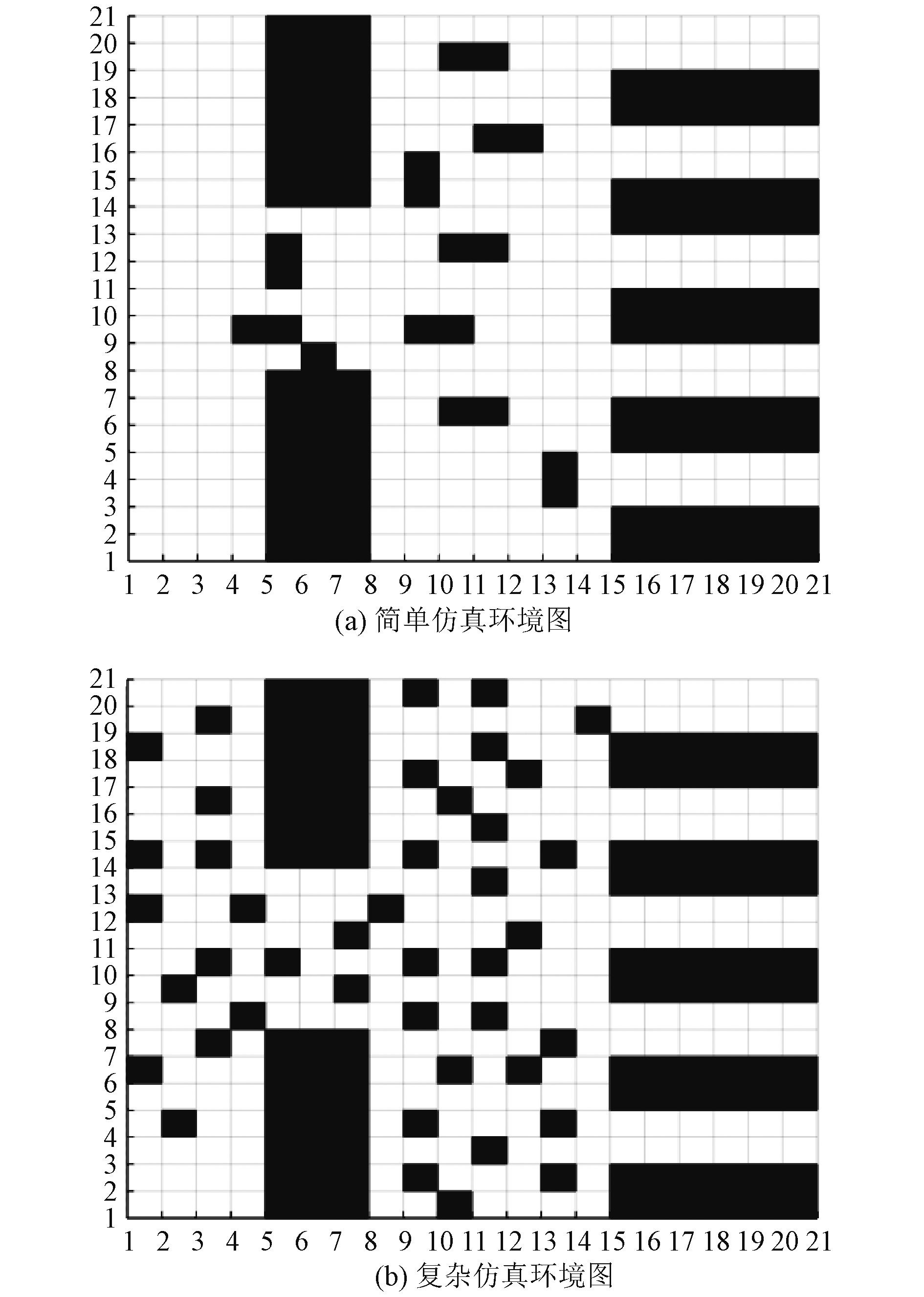
|
图 4 仿真环境图 Fig. 4 Diagram of simulation environment |

|
图 5 简单环境下的路径规划图 Fig. 5 Path planning in simple environment |

|
图 6 复杂环境下的路径规划图 Fig. 6 Path planning in complex environment |
仿真环境中无人艇起点和终点分别用三角形和圆形图标表示。分别将无人艇在仿真环境中的起点和终点设为(1,1),(20,20)。分别使用传统A*算法和改进算法对水面无人艇在简单水域仿真环境下进行仿真。由图5(a)可以看出,利用传统A*算法规划出的路径,很容易穿过障碍物的接触位置以及紧挨着障碍物边缘航行,并且在航行于障碍物水域中,规划路线折线多,这将会导致无人艇在航行期间存在极大安全隐患,很容易与障碍物的边缘发生碰撞。基于改进的A*算法所规划出的安全路径却能很好地避免上述问题,从图5(b)可以看出,在同样的仿真环境中,基于改进的A*算法所规划出的安全路径完全避开了障碍物的接触点,并且在路线拐角处进行圆弧平滑处理,使得无人艇和障碍物始终保持足够的安全距离,以保证无人艇的航行安全。
为了更好验证改进的A*算法在无人艇的路径规划中的有效性,通过建立更加复杂的水域模拟仿真环境(见图4),再次对基于传统A*算法和改进A*在无人艇的路径规划应用性能进行仿真验证。仿真结果如图6所示。结果表明,基于传统A*算法的所规划出的无人艇航行路线更加显示了其不能有效通过障碍物之间接触点和障碍物边缘的缺陷,而基于改进的A*算法在复杂模拟水域中规划路径依然高效且安全。
改变无人艇在复杂模拟水域中的起止点位置,将起点和终点改为(1,20),(20,3),仿真结果如图7所示。基于改进的A*算法在无人艇的路径规划中依然有着比传统的A*算法所规划出的路线更加科学、安全,能够更好的满足水面无人艇航行的实际需求。

|
图 7 复杂环境下的路径规划图 Fig. 7 Path planning in complex environment |
针对基于传统A*算法无人艇路径规划不能安全有效避开障碍物的问题,本文提出一种基于平滑A*算法的无人艇路径规划方法。仿真实验表明,本文提出的算法可以较好地避开障碍物,并且与障碍物保持有足够的安全距离。通过在拐点前适当位置沿着预定半径转向使得水面无人艇的规划路径更加平滑,有效避免了无人艇与障碍物接触点及边缘相碰撞的危险,最终使无人艇规划出最短路径并安全抵达目的地。
目前基于A*算法在无人艇路径规划的应用仍存在一定限制,其只适用于静态环境中的路径规划,而在水面无人艇的实际航行中,往往会遇到各种动态的障碍物,如过往船只、浮漂,水域中的大型水生物等,此时应用A*算法进行路径规划将会受到一定限制。通过继续改进A*算法使其能够针对动态障碍物实现自主避障及安全路径规划将是以后的研究方向。
| [1] |
谢玉龙, 王直. 基于改进遗传算法的船舶路径规划[J]. 计算机技术与发展, 2019(5). DOI:10.3969/j.issn.1673-629X.2019.05.037 |
| [2] |
陈家. 无人驾驶救助船路径规划算法的研究[D]. 武汉: 武汉理工大学, 2013.
|
| [3] |
陈超, 耿沛文, 张新慈. 基于改进人工势场法的水面无人艇路径规划研究[J]. 船舶工程, 2015(9): 72-75. |
| [4] |
余必秀, 初秀民, 柳晨光, 等. 利用改进A*算法进行无人航道测量船路径规划[J]. 武汉大学学报, 2019(3). |
| [5] |
陈立家, 黄立文, 崔梅. 基于改进蚁群算法的船舶多约束最优航线设计[J]. 上海海事大学学报, 2017(4). |
| [6] |
王红卫, 马勇, 谢勇, 等. 基于平滑A*算法的移动机器人路径规划[J]. 同济大学学报(自然科学版), 2010(11). DOI:10.3969/j.issn.0253-374x.2010.11.028 |
| [7] |
陈素琼, 王惠来, 向天雨. 基于改进A*算法的地图游戏寻径研究[J]. 重庆师范大学学报(自然科学版), 2017(4): 75-78. |
| [8] |
孙炜, 吕云峰, 唐宏伟, 等. 基于一种改进A*算法的移动机器人路径规划[J]. 湖南大学学报(自然科学版), 2017(4): 94-101. |
| [9] |
薛峰会, 周瑞涛. 利用Dijkstra与A*算法实现船舶导航算路[J]. 舰船科学技术, 2017(6): 81-83. |
 2019, Vol. 41
2019, Vol. 41
