0 引　言

目前，无人艇（Unmanned Surface Vessel，USV）的应用还集中在水文测量和环保领域^[1]，军事方面^[2]的应用还较少。执行水文测量和环保领域任务时，USV一般以较低速度（<10 kn）航行。而军事方面很多时候需要USV满足高速^{[3 – 4]}（>20 kn）紧急避障性能要求。庄肖波等^[5]提出基于蚁群算法（ACA）^[6]实现高速无人艇对运动目标避碰规划的方法。但蚁群算法计算量大，求解时间长，在实际应用中，由于循环次数有限，很难得到全局最优解。吉大海等^[7]提出一种基于行为的动态障碍物危险规避算法。然而该避障算法只从运动学层面上分析了动态障碍物约束，而未考虑船体动力学对避障性能的影响；该算法中避障被视为独立于控制的问题，容易出现控制无法达到路径规划期望值的问题。Bjørn-Olav Holtung Eriksen等^[8]设计并实施了基于非线性规划（Nonlinear Programming，NLP）的中层COLAV算法，可避开静态和动态障碍物。但该算法属于策略式规划控制，没有应用到反应式避障控制。

高速场景对避障的实时性有更高要求。在传统算法架构中，避障被视为独立于控制的问题，易出现控制无法达到路径规划期望值的问题。无人艇控制系统是多输入多输出系统，无人艇避障问题属于多变量约束优化问题，如采用PID控制，需要设计多个控制器，且无法兼顾多个输入输出量间的耦合关系，控制效果较差。而模型预测控制^[9]是处理多变量约束优化问题最有效的方法之一。鲁棒控制、最优控制、自适应控制等也是处理多变量约束优化问题有效的方法，但这些方法对船体模型精度要求很高。而模型预测控制采用了近似测量和计算，能在每个步长内不断滚动优化，能够补偿由于模型失配、时变、干扰等引起的不确定性，及时补偿，始终将新的优化建立在实际的基础上，使控制保持实际的最优。为此，本文设计了基于模型预测控制（Model Predictive Control，MPC）的USV速度障碍物（Velocity Obstacle，VO）避障算法（以下简称MPC_VO算法）。通过仿真实验，验证了该算法适用于高速紧急避障场景，并分析了模型不确定对该算法避障效果的影响。

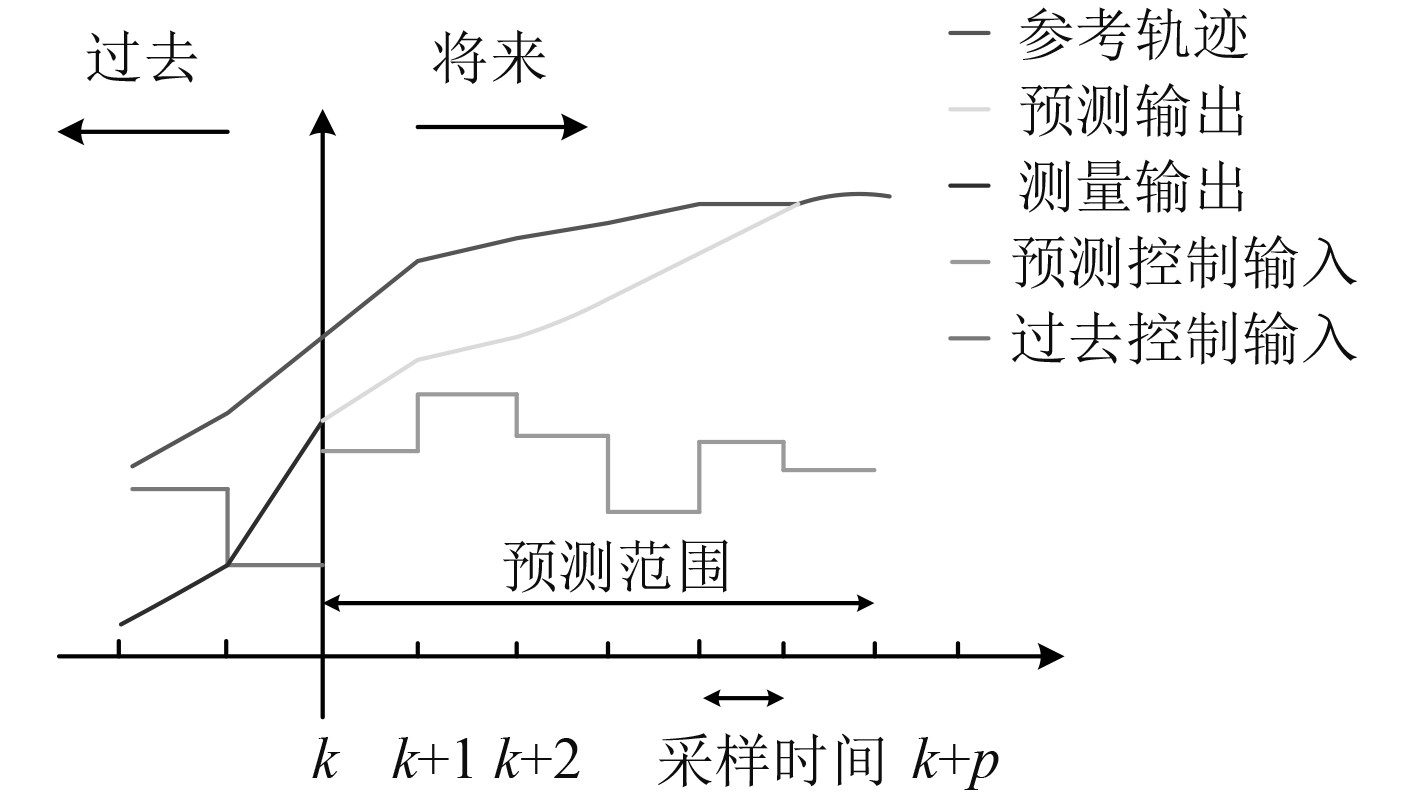
1 MPC_VO算法设计 1.1 MPC控制算法

MPC控制^[10]原理如图1所示。k轴为当前状态，左侧为过去状态，右侧为将来状态。

MPC控制算法有多种不同的表达式，但都有着相同的基本结构，如图2所示。其基本特点^[11]都是基于模型的预测、滚动优化和前馈-反馈控制结构。

其中： ${y_{sp}}$ 为系统设定输出； ${y_r}$ 为参考轨迹； $u$ 为控制量输入； $y$ 为实际输出值； ${y_m}$ 为模型输出值； ${y_c}$ 为预测输出。

本文主要用状态空间模型描述系统。状态空间的非线性离散时间模型的表达式如下：

$ x(k + 1) = f(x(k),u(k)){\text{，}} $

(1)

$ y(k) = g(x(k)){\text{。}} $

(2)

状态空间的线性连续时间模型的表达式如下：

$ x(t + {T_s}) = {{A}} \cdot x(t) + {{B}} \cdot u(t) + {{K}} \cdot e(t){\text{，}} $

(3)

$ y(t) = {{C}} \cdot x(t) + {{D}} \cdot u(t) + e(t){\text{。}} $

(4)

其中： $X(t)$ 为 $n$ 维的状态向量； $y(t)$ 为 $p$ 维的输出向量， $u(t)$ 为 $m$ 维的控制向量，是输入向量； $e(t)$ 为误差量。 ${ A},{ B},{ C},{ D},{ K}$ 为系统矩阵。

对式（3）和式（4）进行一阶欧拉离散化，得到状态空间的线性离散时间模型，其表达式如下：

$ X\left( {k + 1} \right) = {{A}} \cdot X\left( k \right) + {{B}} \cdot u\left( k \right) + {{K}} \cdot e(k){\text{，}} $

(5)

$ {\rm{y}}\left( {{\rm{k}} + 1} \right) = {{C}} \cdot {\rm{X}}\left( {\rm{k}} \right) + {{D}} \cdot u(k) + e(k){\text{。}} $

(6)

其中：X（k）为离散的n维的状态向量；y（k+1）为离散的p维的输出向量；u（k）为离散的m维控制向量，是输入向量； $e(k)$ 为误差量，A，B，C，D，K为系统矩阵。

把离散模型作为预测模型，迭代得到如下预测状态：

$ \left\{ {\begin{array}{*{20}{c}} y\left( {k + 1{\rm{|}}k} \right) = {{A}} \cdot X\left( {\rm{k}} \right) + {{B}} \cdot u\left( k \right) + {{K}} \cdot e(k){\text{，}}\\ y\left( {k + 2{\rm{|}}k} \right) = {{{A}}^2} \cdot X\left( {\rm{k}} \right) + {{AB}} \cdot u\left( {\rm{k}} \right) + {{B}} \cdot u\left( {k + 1} \right) +\\ {{AK}} \cdot e(k) + {{K}} \cdot e(k + 1){\text{，}}\\ \vdots \\ y\left( {k + {N_p}|k} \right) = {{{A}}^{{N_p}}} \cdot {\rm{X}}\left( {\rm{k}} \right) + {{{A}}^{{N_p} - 1}}({{B}} \cdot {\rm{u}}\left( {\rm{k}} \right) +\\ {{K}} \cdot e(k)) + \ldots + {{{A}}^{{N_p} - {N_c}}}({{B}} \cdot {\rm{u}}\left( {{\rm{k}} + {N_c} - 1} \right) +\\ {{K}} \cdot e({\rm{k}} + {N_c} - 1)) {\text{。}} \end{array}} \right. $

(7)

其中： ${N_p}$ 为预测时域， ${N_c}$ 为控制时域，一般 ${N_c} < {N_p}$ 。

1.2 基于VO分析的代价函数构造

在高速紧急避障场景，有效避开障碍物和减小能耗是很必要的。因此，可以构造避障和减小能耗的代价函数，把高速紧急避障问题转换为满足一定约束条件的数值优化问题，可以VO法基本原理建立VO避障评价体系。VO算法是反应式避障算法，要求计算要求低，应对环境的变化快，所以没有参考轨迹 ${\bar y}$ ，控制向量也没有参考值 ${\bar u}$ 。另外，考虑能量效率，倾向于采用小的加速度。因此，基于避障和能耗效率构造代价函数：

$ J = {\lambda _1} \cdot {J_{vo}}\; + \;{\lambda _2} \cdot {J_e}{\text{。}} $

(8)

其中： ${J_{vo}}\;$ 为避障代价函数； ${J_e}$ 为能耗代价函数； ${\lambda _1}$ 和 ${\lambda _2}$ 为权重系数。

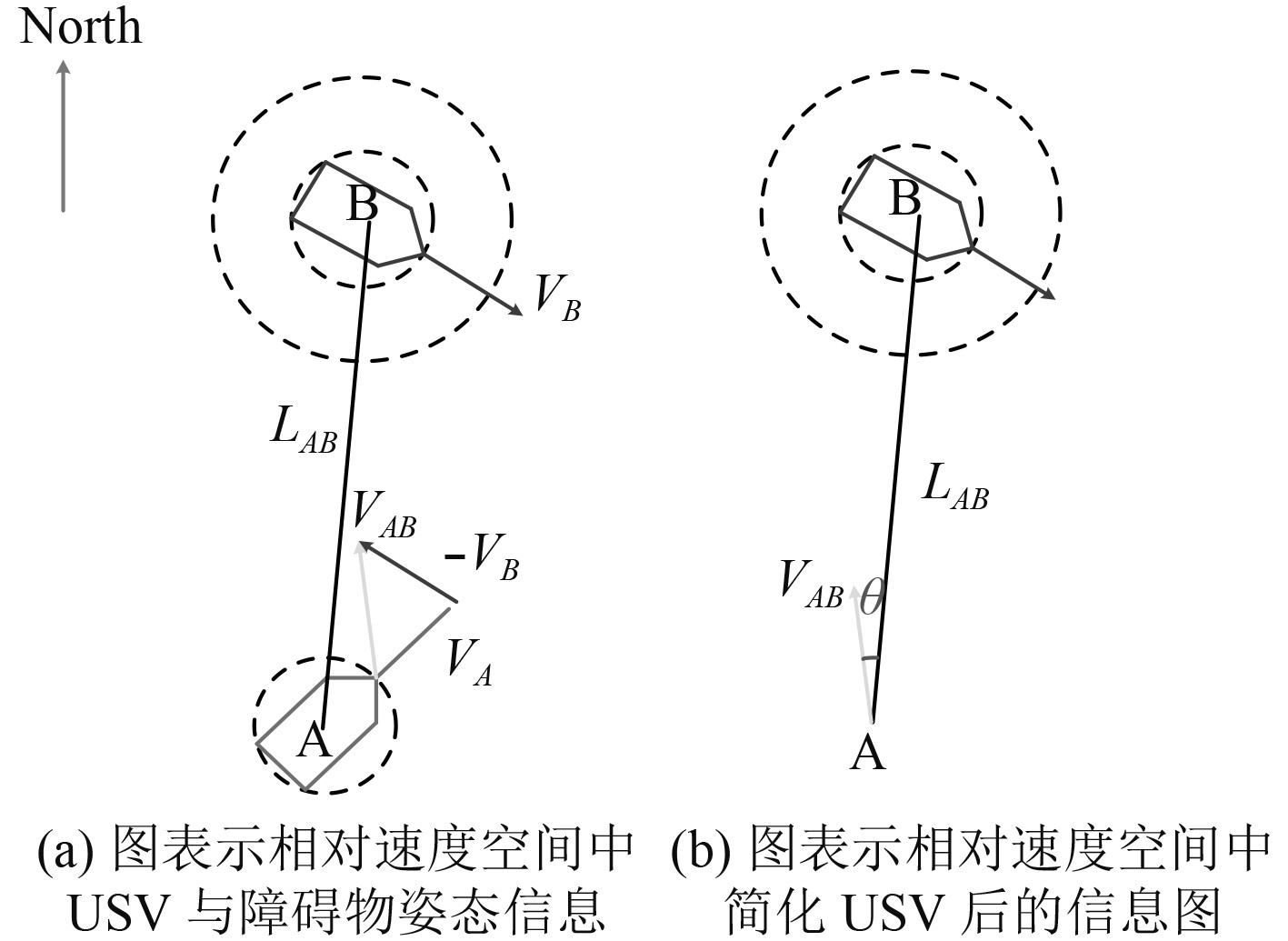
为此，可以构造状态量的代价函数，VO法原理如图3所示。

在相对空间中，以正北方向为基准，USV（A）与障碍物（B）位置的连线和正北方向的夹角为 ${\theta _{1,{t_k} + nstep}}$ ，相对速度 ${V_{AB}}$ 和正北方向的夹角为 ${{\rm{\theta }}_{2,{{\rm{t}}_{\rm{k}}} + {\rm{nstep}}}}$ 。构造避障代价函数 ${J_{vo}}$ 为：

$ {J_{vo}} = \frac{1}{{\tan |{\theta _{1,{t_k} + nstep}} - {\theta _{2,{t_k} + nstep}}|}}{\text{，}} $

(9)

${\theta _{1,{t_k} + nstep}}$ 为USV与障碍物在nstep歩位置连线与正北方向的夹角（锐角）， ${\theta _{2,{t_k} + nstep}}$ 为USV与障碍物在nstep歩合成速度方向与正北方向的夹角（锐角）。

能耗代价函数 ${J_e}$ 为：

$ {J_e} = \frac{{\sum\limits_{k = 1}^{nstep} {u_k^TQ{u_k}} }}{{nstep}}{\text{，}} $

(10)

${u_k}$ 为当前时刻的船体控制量。

权重系数是调节多项代价函数之间的权重的。由于在高速紧急避障场景中，有效避开障碍物是最重要的，能耗效率其次；又通过计算发现 ${J_e}$ 的量级是 ${J_{vo}}$ 的 ${10^6}$ 倍，为突出 ${J_{vo}}$ 的影响，选择 ${\lambda _1} = {10^8}\;\;,\;\;{\lambda _2} = 1$ 。

nstep为预测步长。MPC控制是以nstep为单位滚动优化，nstep越长，求得的解越接近于全局解，但模型失配、时变、干扰等引起的不确定性会更加明显。反之，nstep越短，求得的解将为次优解，但模型失配、时变、干扰等引起的不确定性会不明显。仿真实验取nstep=20。MPC控制采用近似测量与计算，不是实现整个控制输入序列，因为实际产生的USV状态与模型有很大差异，所以是在每个时间步不断地重新评估控制输入的最优序列。

障碍物信息可以通过USV搭载的传感器探测到，因此每个时刻障碍物的信息是已知的。 ${{\rm{\theta }}_{1,{{\rm{t}}_{\rm{k}}} + {\rm{nstep}}}}$ 和 ${{\rm{\theta }}_{2,{{\rm{t}}_{\rm{k}}} + {\rm{nstep}}}}$ 可以用USV和障碍物的位置信息来表示，因此代价函数J是关于控制向量u的函数，即

$J = f\left(u \right){\text{。}} $

(11)

其中：

$u = \left[ {\begin{array}{*{20}{c}} {F_x} \\ {F_y} \end{array}} \right]{\text{，}}$

(12)

$- 6550 \leqslant {F_x} \leqslant 13\;100{\text{，}}$

(13)

$ - 645 \leqslant {F_y} \leqslant 645{\text{。}} $

(14)

因此，可以把带有约束条件的模型预测控制问题转化为目标函数式和约束条件式的二次规划问题。

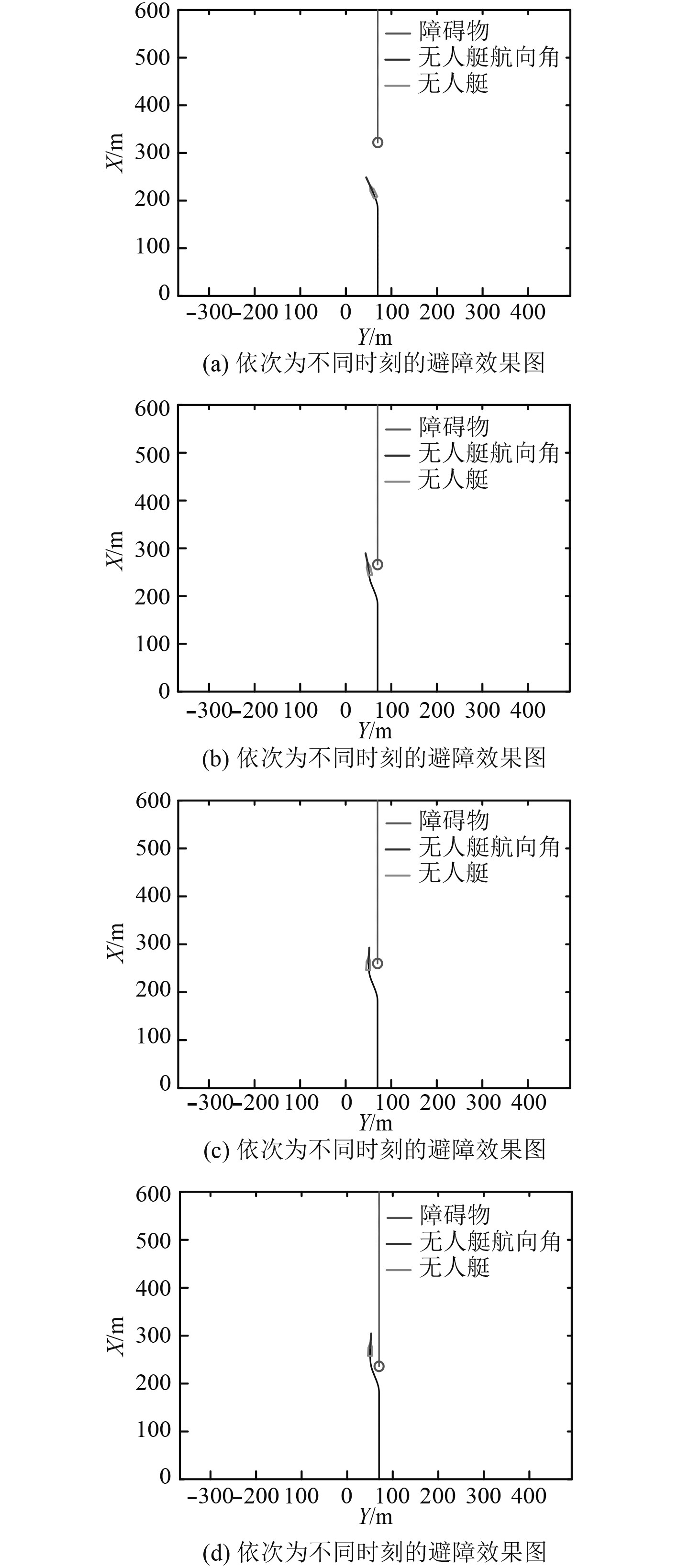
2 MPC_VO算法避障效果

在当障碍物（简称OBS.）在USV的正上方且两者对遇行驶场景（见图4）中，USV的起始速度为16 kn，OBS.的速度为20 kn。

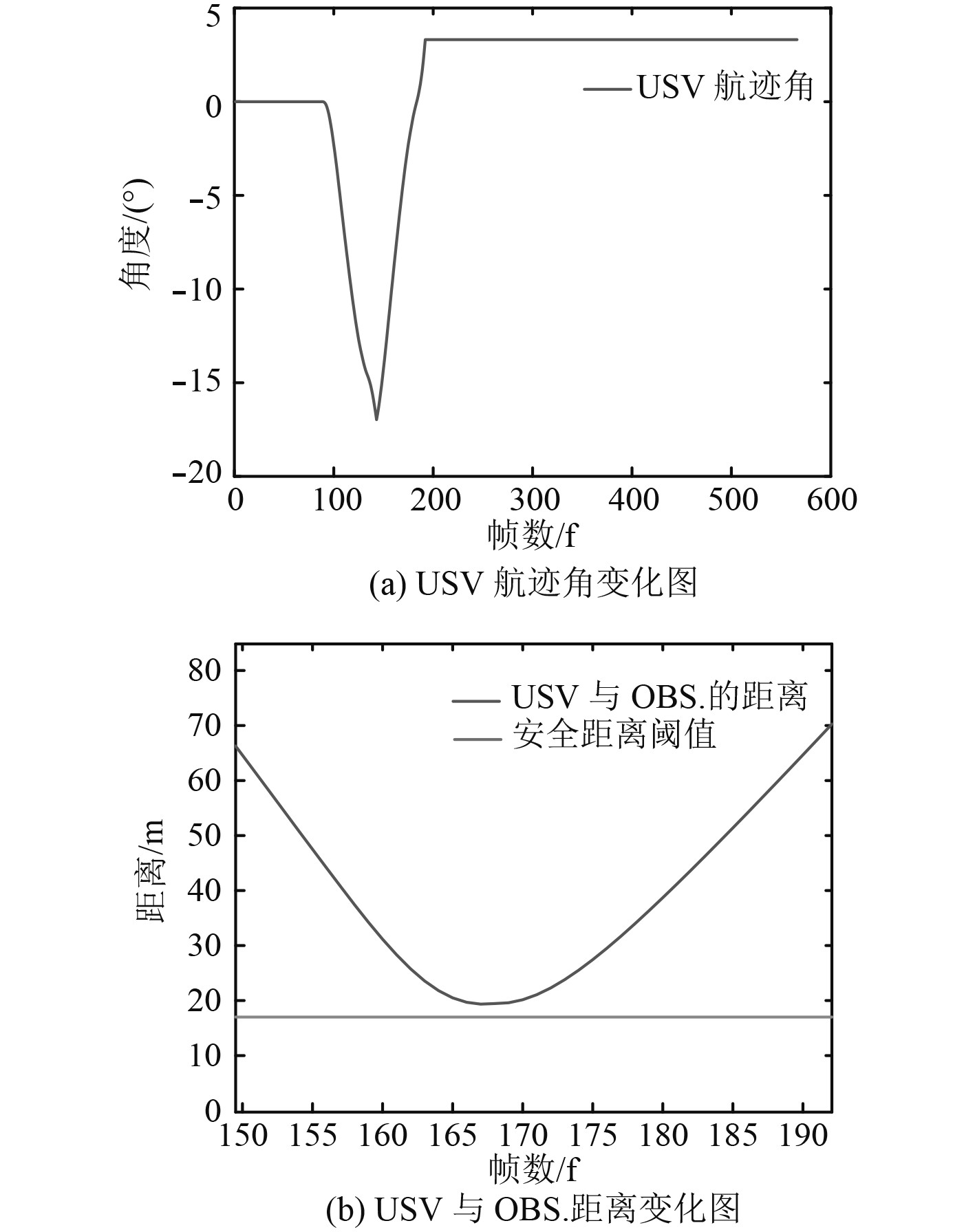
从避障效果图4和图5中USV航迹角的变化图与USV与OBS.距离的变化图可以看出，USV向左侧转向避开OBS.，距离保持在安全阈值之上，满足安全避障要求。

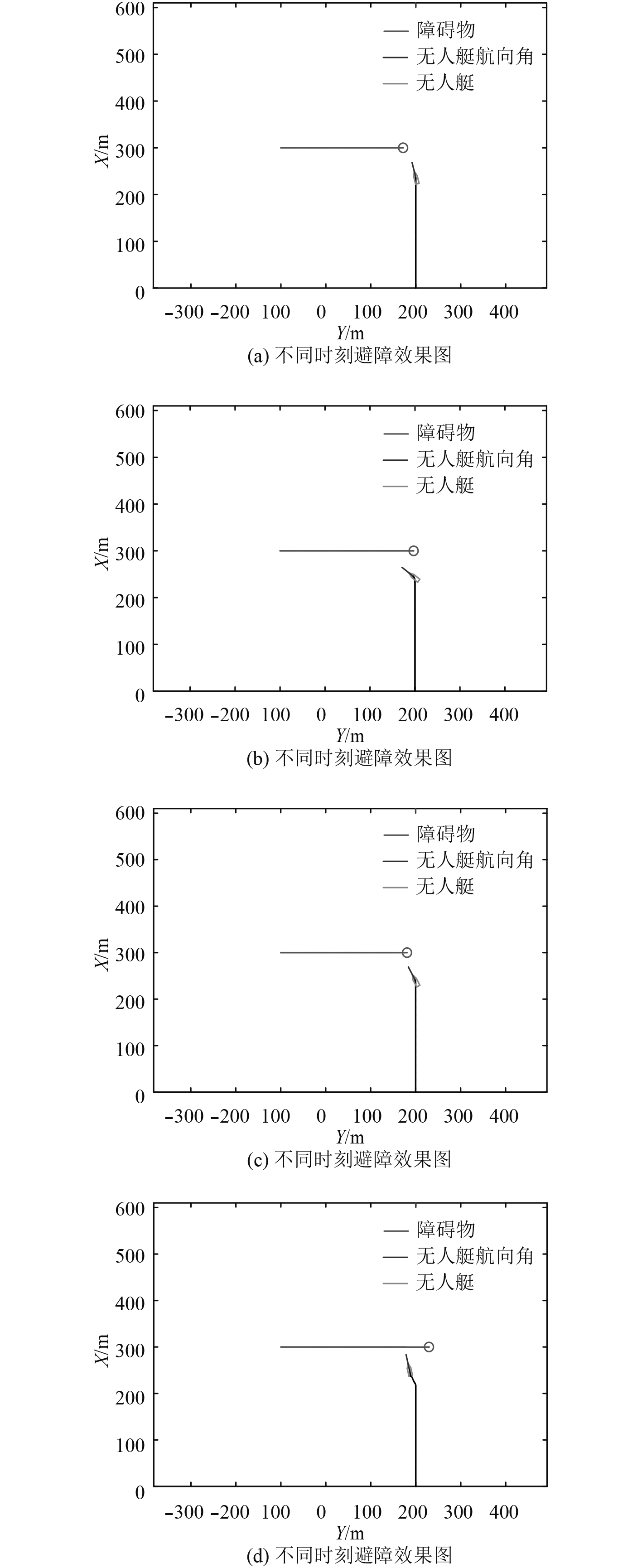
在当USV与OBS.交叉相遇的行驶场景（见图6）中，USV的起始速度为16 kn，OBS.的速度为18 kn。

从图6和图7中USV航迹角的变化图与USV与OBS.距离的变化图可以看出，USV与OBS.距离是安全距离阈值的3倍左右，满足安全避障要求，且安全系数高。航迹角变化率很大，满足迅速紧急避障要求。

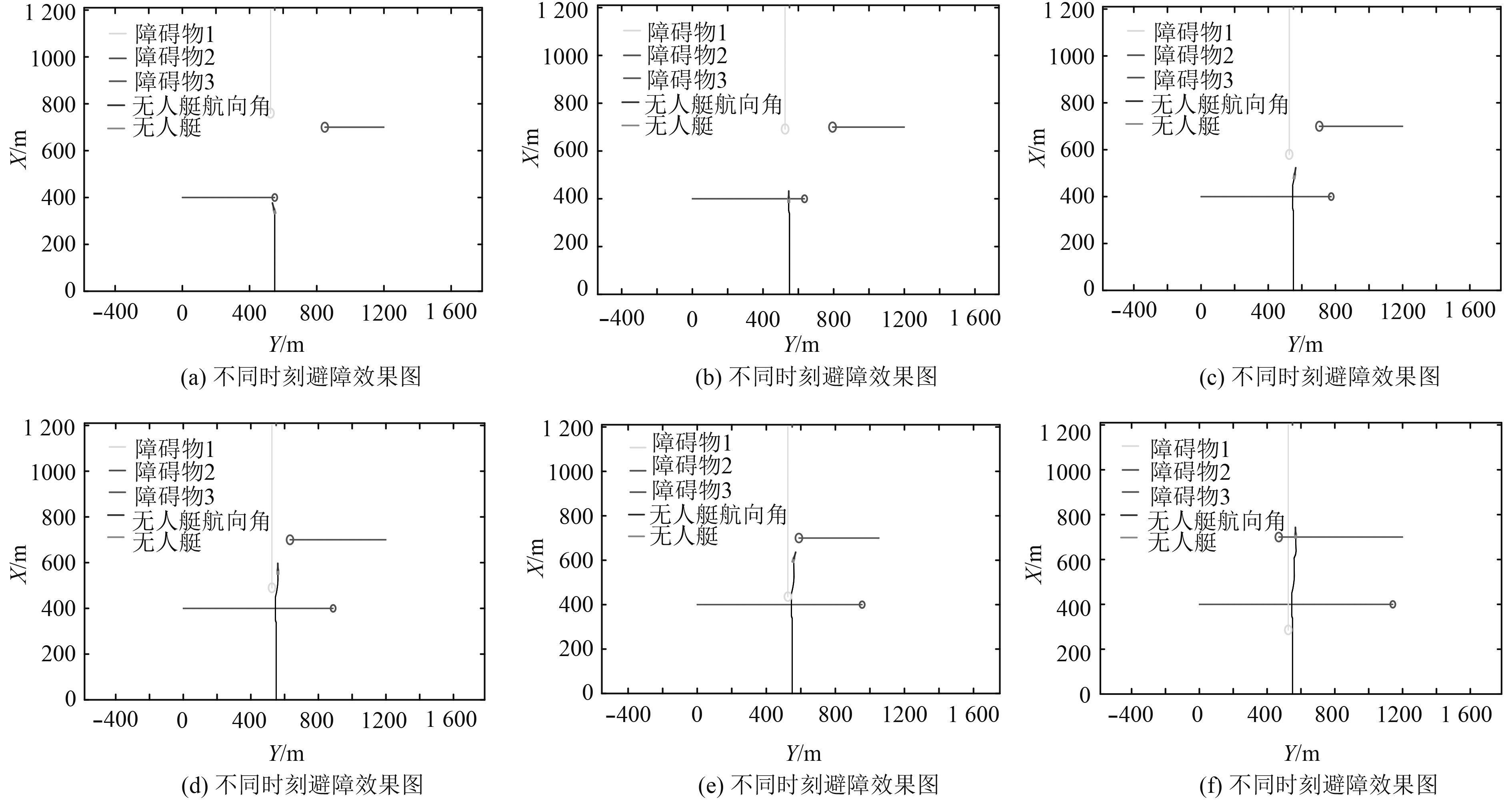
多运动障碍物避障仿真如图8所示，USV起始速度为16 kn，OBS.1速度为20 kn，OBS.2速度为25 kn，OBS.3速度为16 kn。

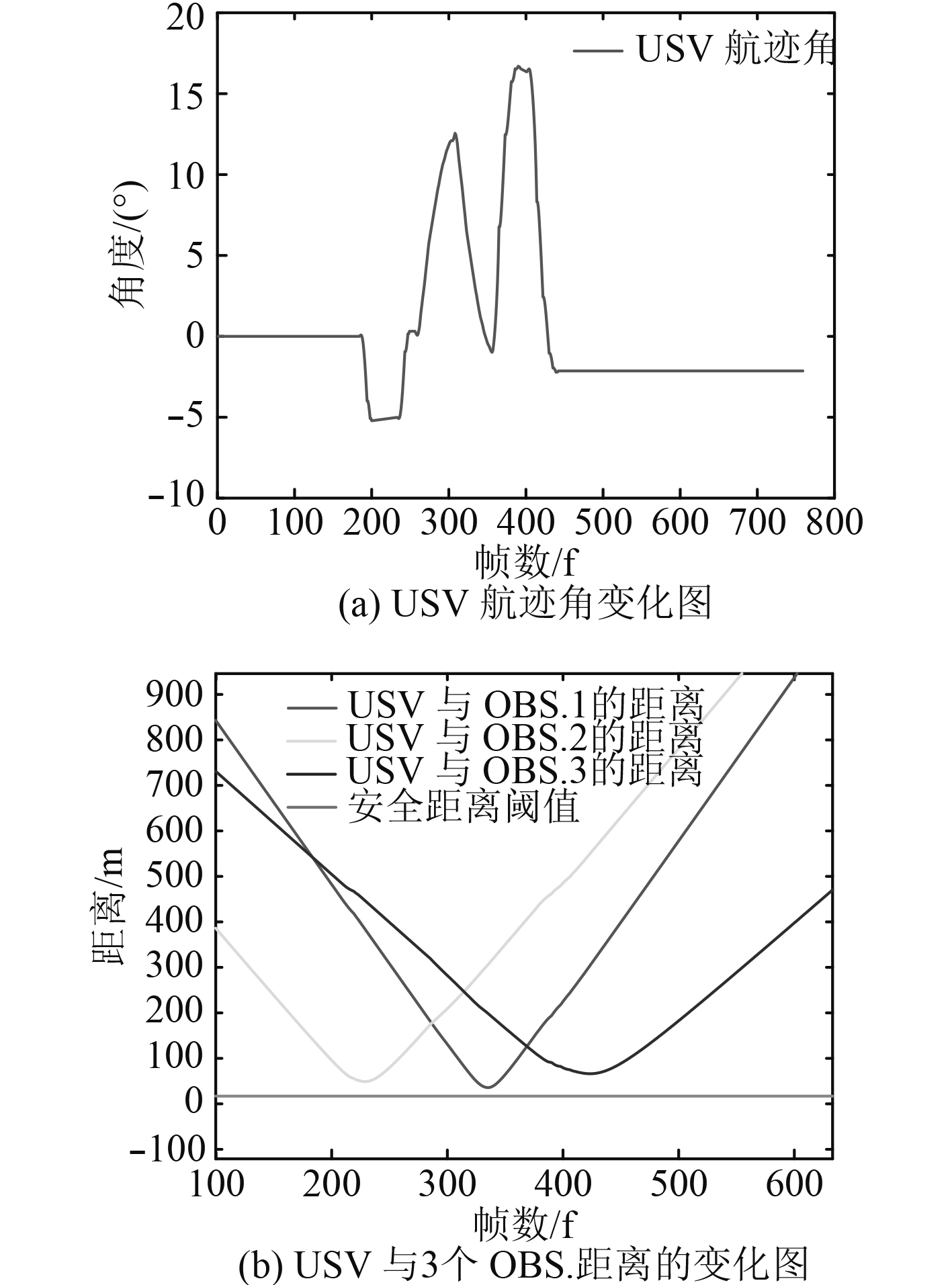
从避障效果图8和图9中USV航迹角的变化图与 USV与OBS.距离的变化图可以看出，USV与3个OBS.距离在安全距离阈值之上，满足安全避障要求。每次遇到障碍物时航迹角变化率都很大，满足迅速紧急避障要求。

3 MPC_VO算法与VO算法避障性能比较分析

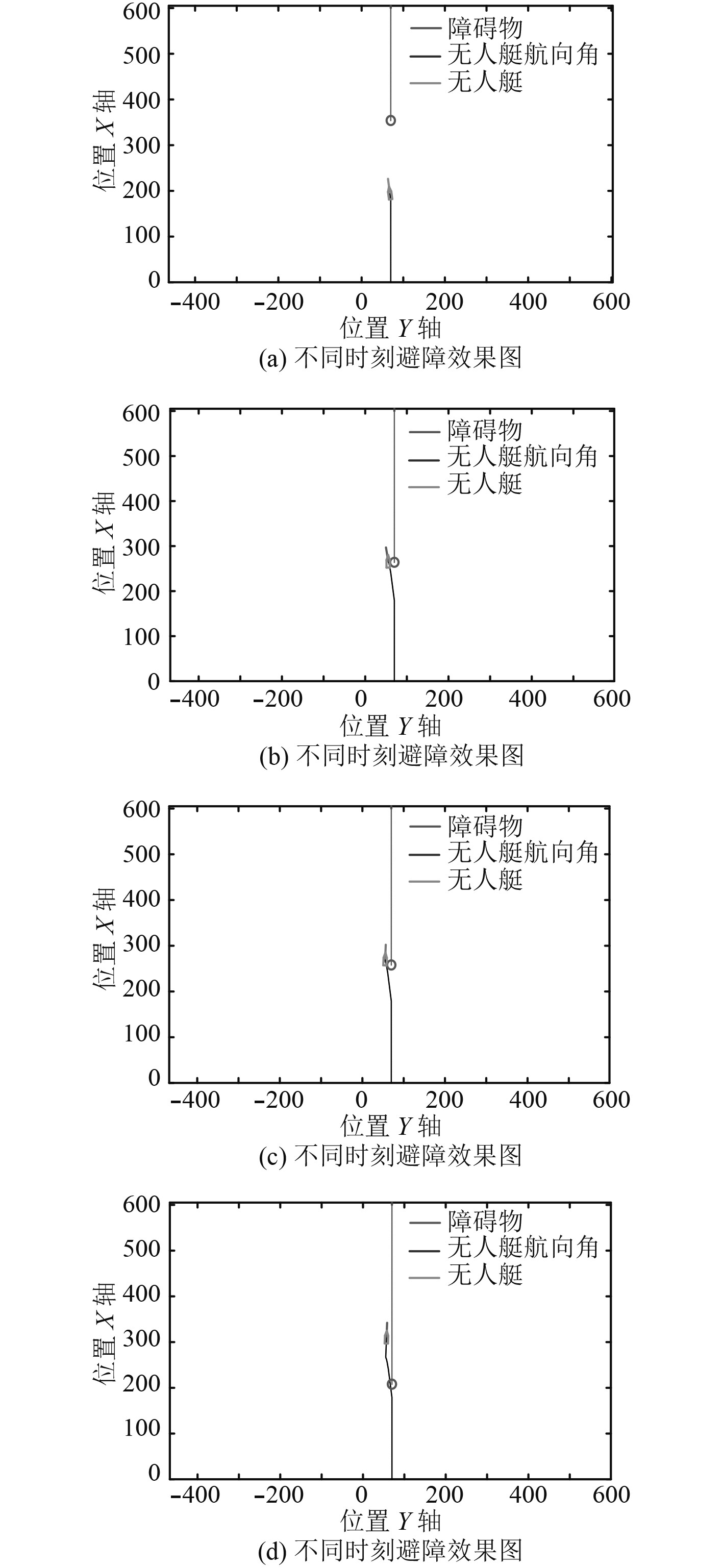
分析MPC_VO算法与传统VO算法的避障效果，在对遇场景中，设计了与图4相同的场景和初始条件。传统的VO算法避障效果如图10所示。

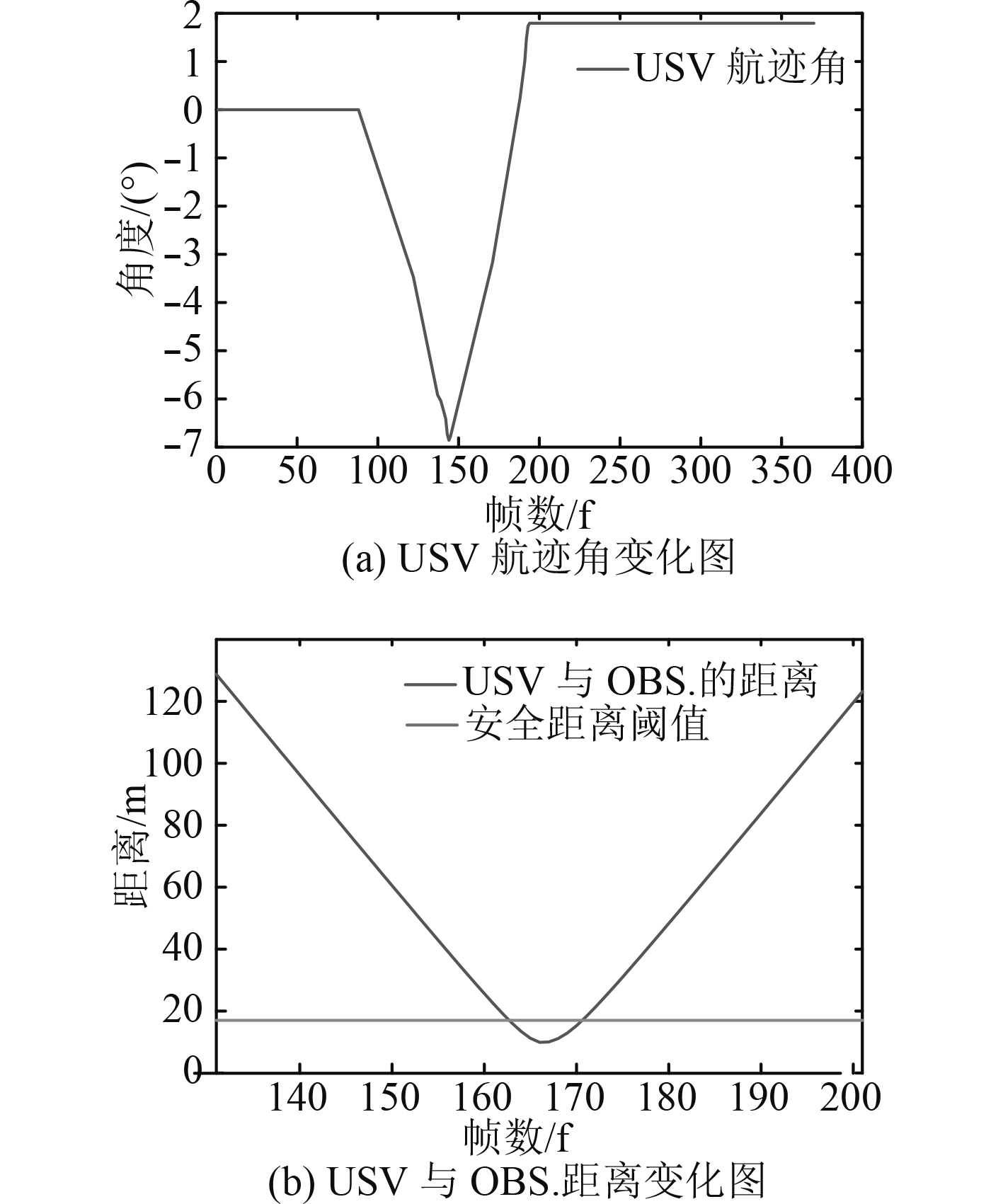
从避障效果图10（b）和图10（c）与图11（b）距离图可以看出，USV与OBS.发生碰撞。

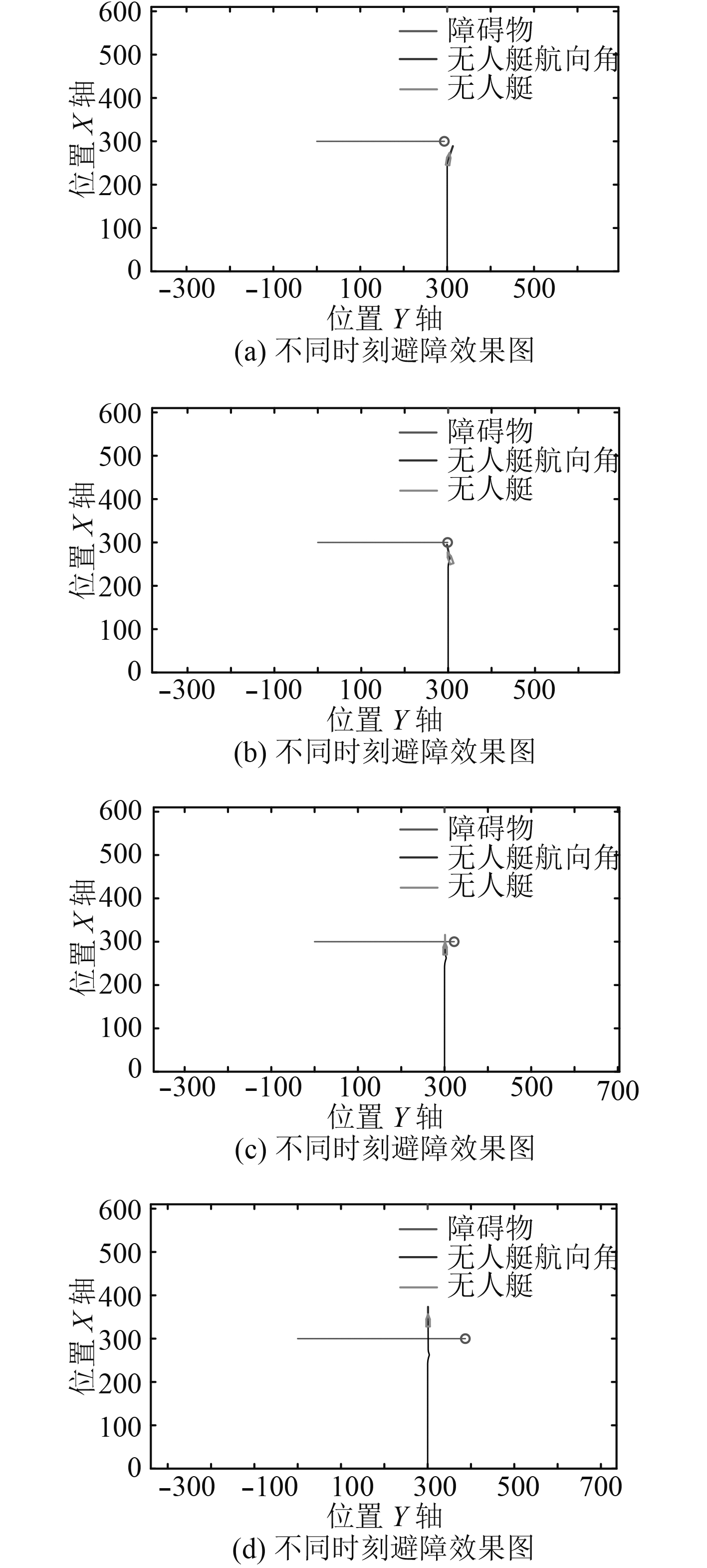
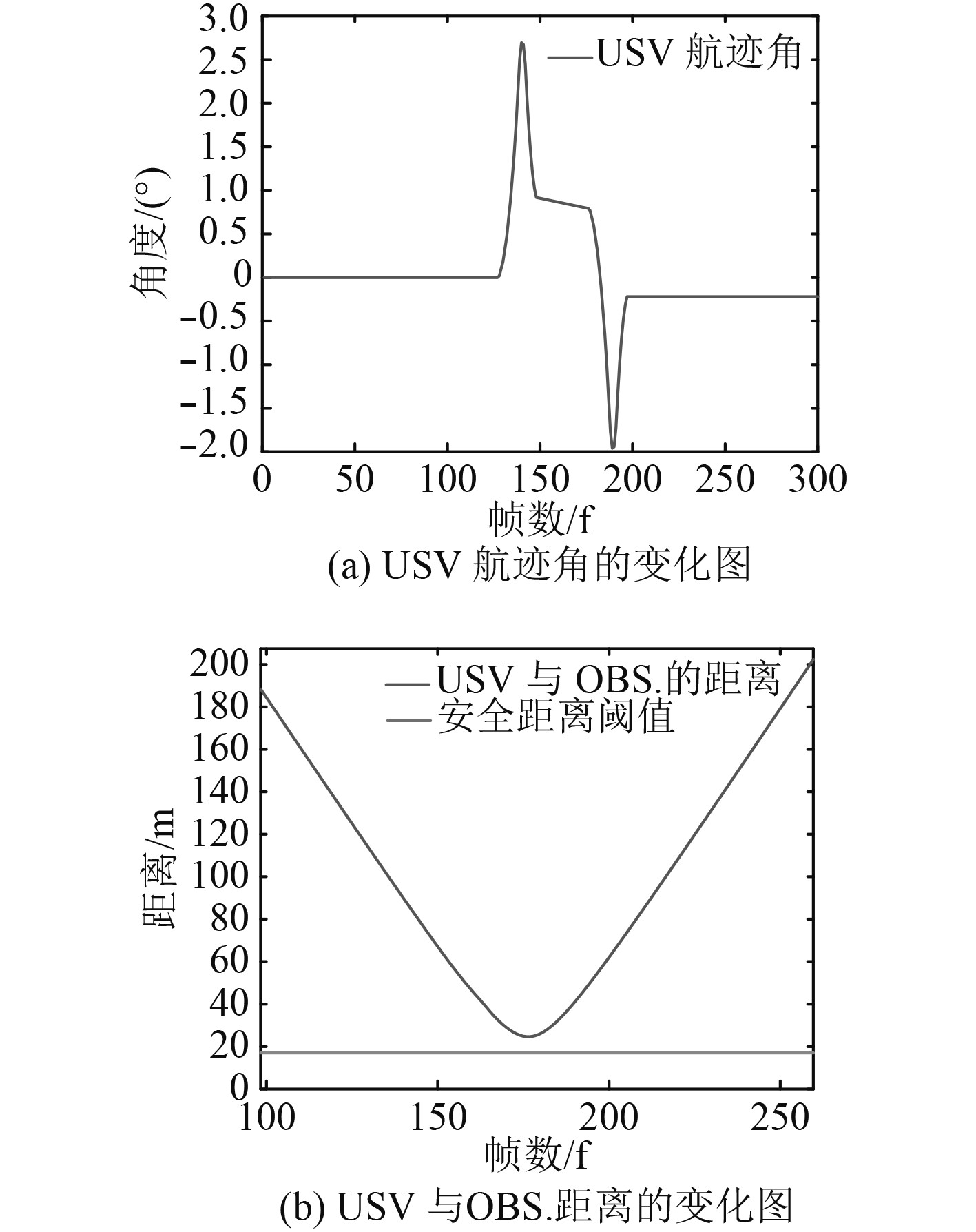
在交叉场景中，设计了与图6相同的场景与初始条件。传统的VO算法的避障效果如图12所示。可以看出，USV成功避开了OBS.。但从图13可以发现，USV在避障时航迹角左右摆动，避障效果较差，且USV到OBS.的距离较小，比同等条件下的MPC_VO算法危险。

综上所述，在高速场景中，传统的VO算法存在避不开障碍物或避障时首向摇摆不定避障效果较差的情况，而MPC_VO算法在相同场景中表现较好。

4 模型不确定性对算法的性能影响分析

为了分析模型不确定性对MPC_VO避障算法的影响，在图8多障碍物场景中分别验证船体的质量m，船体的转动惯量I_z，船体的长度L，线性阻尼项和非线性阻尼项对避障性能的影响。

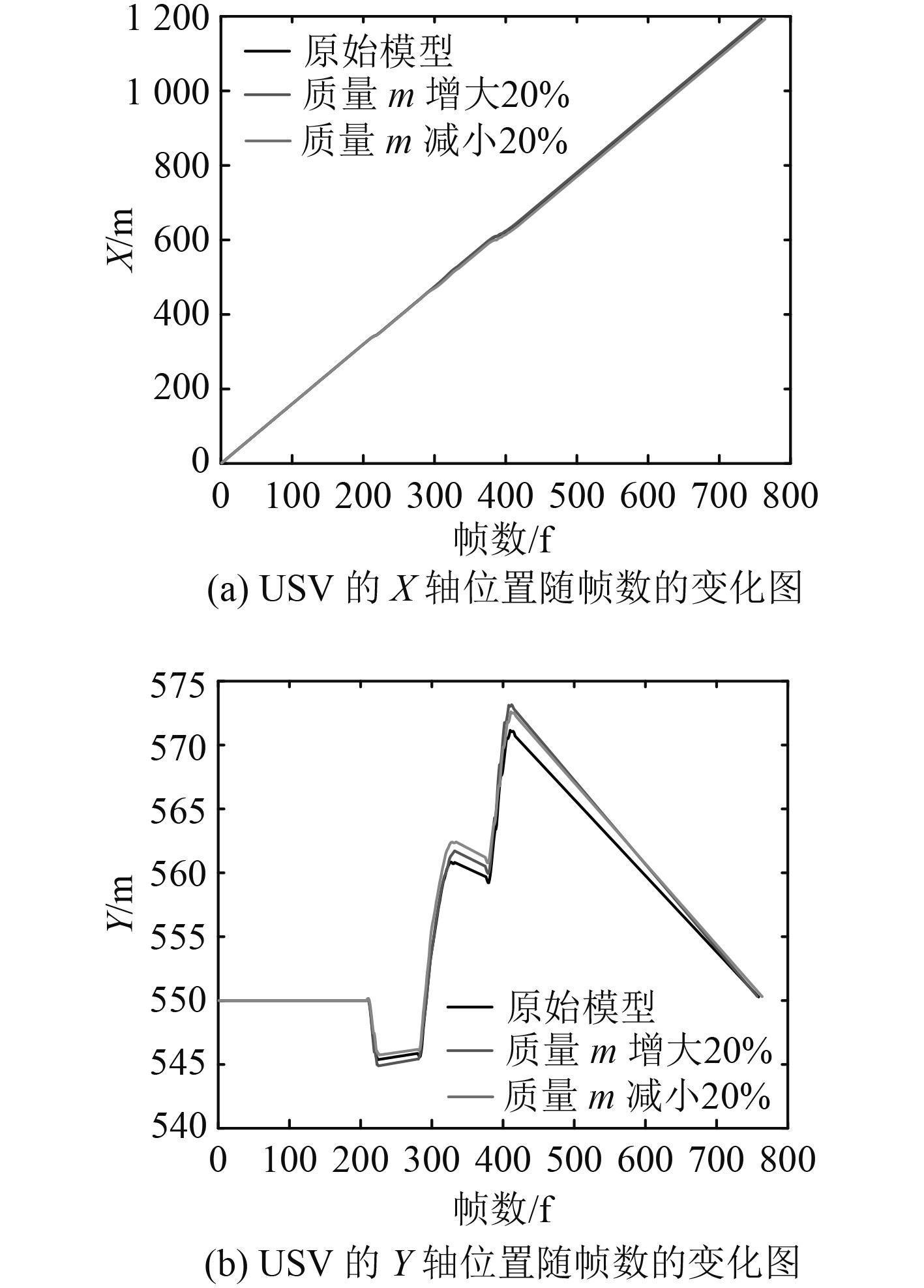
图14和图15分别是改变质量m后的模型和原始模型的避障航迹角和XY坐标。可以看出，质量 $m \pm 20\%$ 的模型避障输出和原始模型避障输出位置点和航迹角都非常接近，且从图15（a）可以看出质量m增大20%X坐标和原始模型的X坐标几乎重合。因此，船体质量m的不确定性对MPC_VO避障算法的避障效果影响不显著。

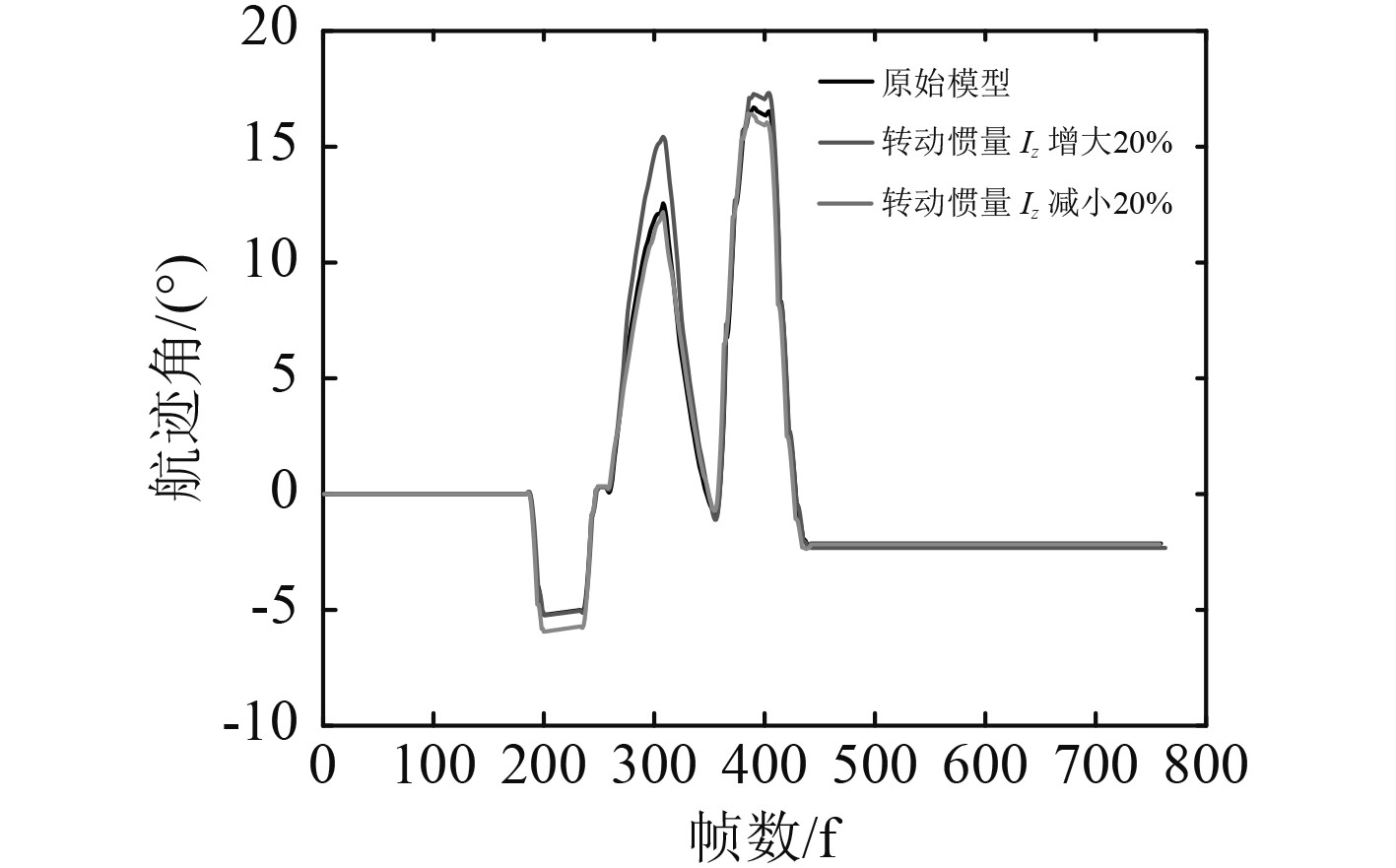
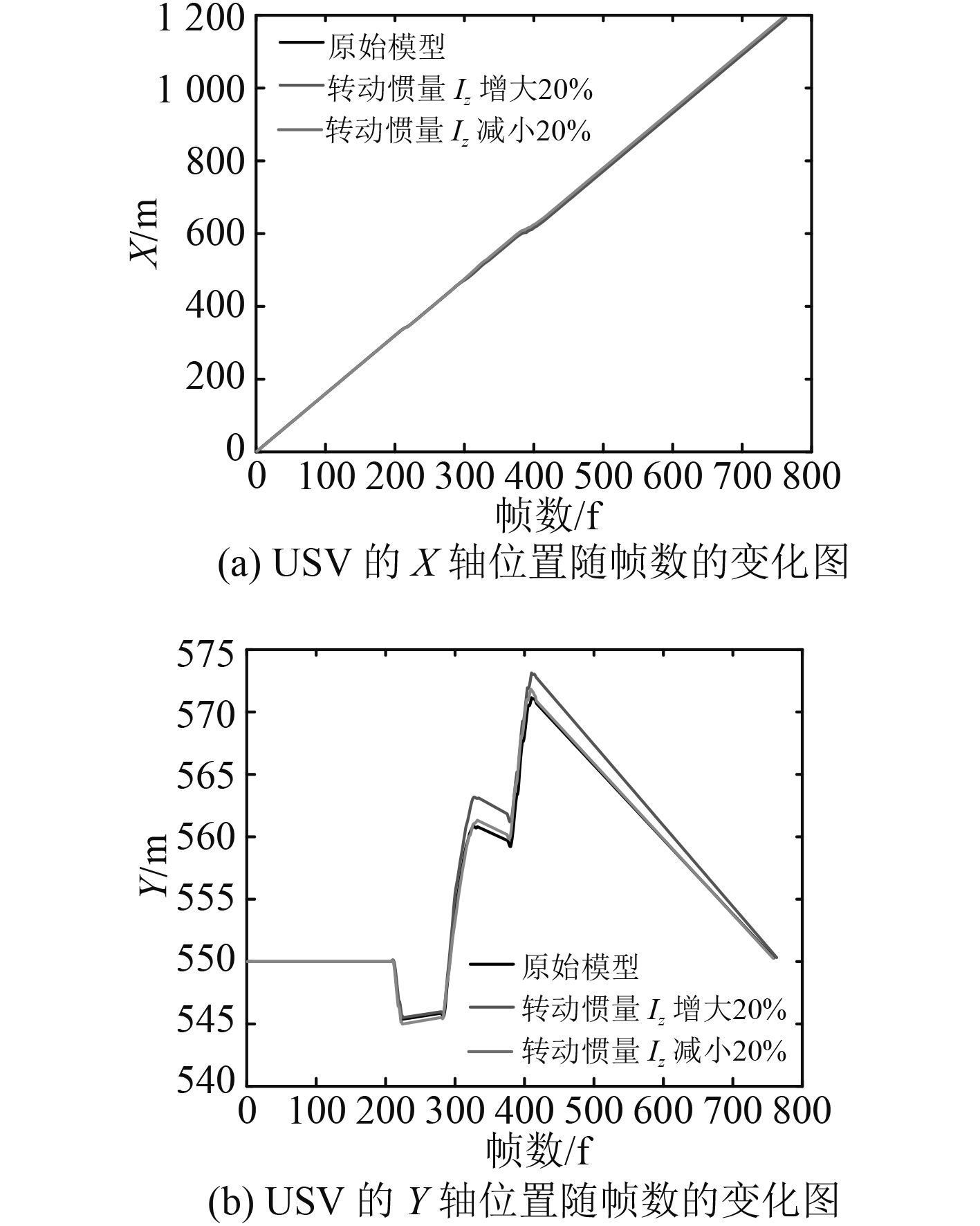
图16和图17分别是改变转动惯量I_z后的模型和原始模型的避障航迹角及XY坐标。从图17（a）可以看出转动惯量I_z减小20%的X坐标和原始模型的X坐标几乎重合。在图16中，虽然转动惯量I_z增大20%的模型在避开第2个障碍物时的航迹角和原始模型避障航迹角偏差较大，但不超过5°。因此，船体的转动惯量I_z的不确定性对MPC_VO避障算法的避障效果影响不显著。

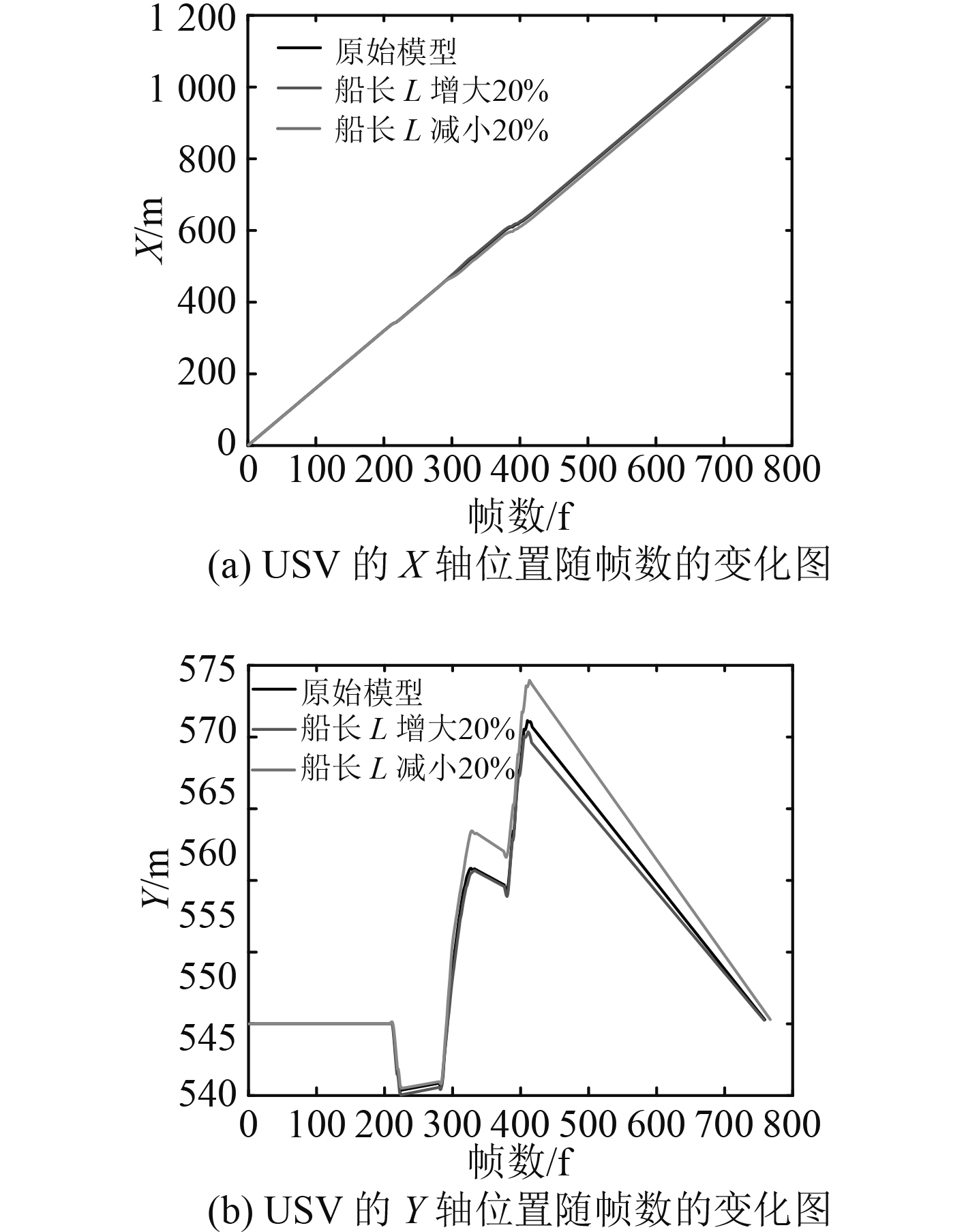
图18和图19分别是改变船长L后的模型和原始模型的避障航迹角和XY坐标。从图18改变船长L后的避障航迹图可以看出，船长L减小20%的模型在避开第2个障碍物时的航迹角和原始模型避障航迹角偏差较大，最大角度偏差为10°左右。从图19图（b）可以看出船长L减小20%的模型与原始模型的输出位置Y坐标最大偏差为4 m左右。因此，船长L的不确定性对MPC_VO避障算法的避障效果影响显著些。

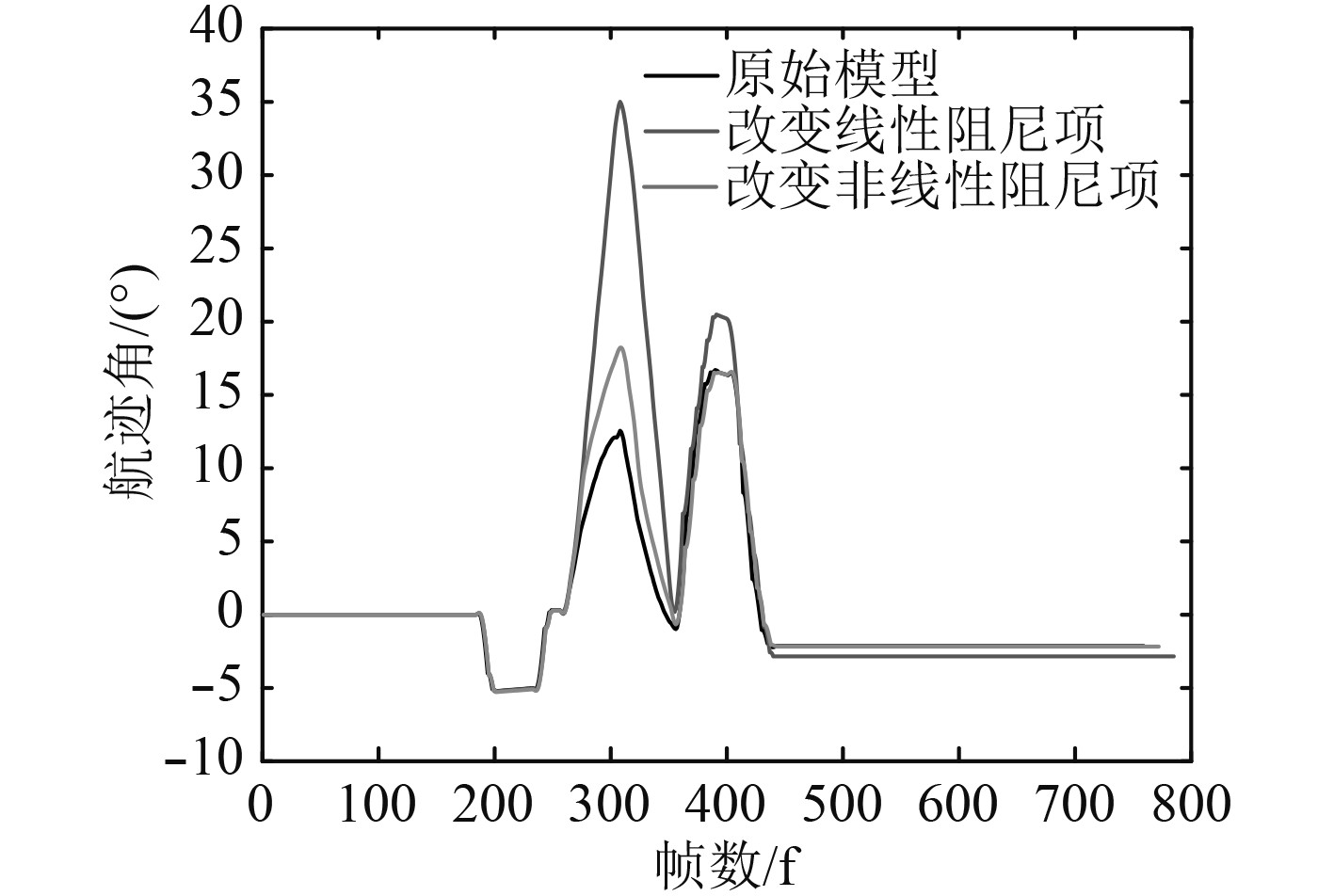
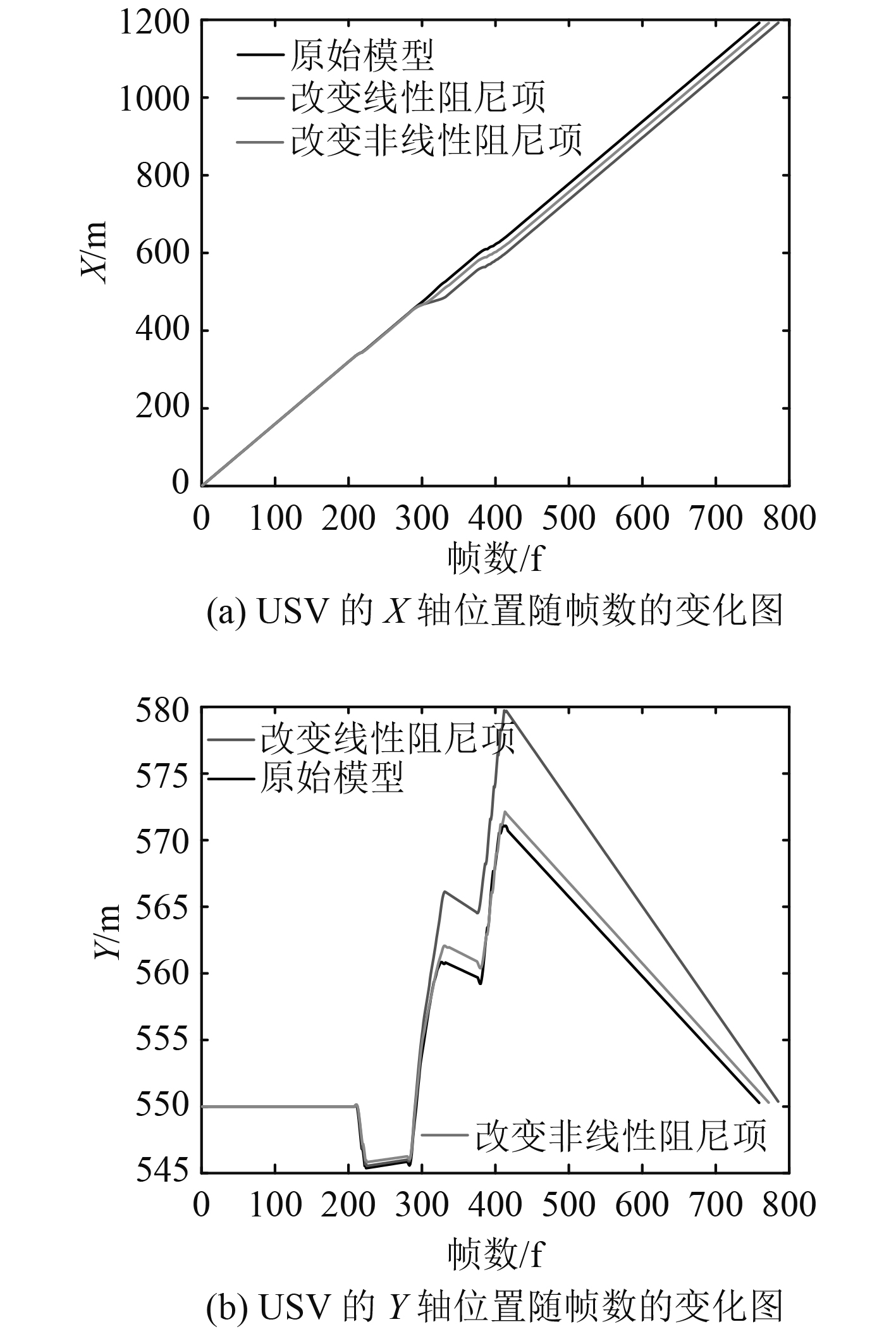
图20和21分别是改变线性阻尼项和非线性阻尼项的模型和原始模型避障航迹角及XY坐标。从图20可以看出，改变线性阻尼项的模型与原始模型避障航迹角最大偏差有25°左右，Y坐标位置偏差有10 m左右，改变非线性阻尼项后的模型与原始模型的避障航迹角最大偏差为5°左右。因此，船体的改变线性阻尼项和非线性阻尼项的不确定性对MPC_VO避障算法的避障效果影响是比较显著。

综上所述，MPC_VO算法不断滚动优化，能够补偿由于模型失配、时变、干扰等引起的不确定性，及时补偿。

5 结　语

本文针对路径规划和控制分开设计的策略容易出现控制无法达到路径规划期望值的问题，融合局部路径规划和船体控制，设计了MPC_VO算法。通过仿真实验实现了该算法的避障功能，并将该算法与传统VO算法避障效果作对比，验证了该算法的有效性。同时，通过分析模型不确定性对该避障算法性能的影响，证明了该算法的鲁棒性。