2. 武汉理工大学,湖北 武汉 430070
2. Wuhan university of technolog, Wuhan 430070, China
美国、以色列、日本、法国等国在无人艇领域的研究已经取得了相当的成果[1 – 5],其中具有代表性的如美国的Spartan、以色列的Protector等。对于无人艇的路径控制,相关学者已做出了相当多的研究。董早鹏等[6]提出了一种自适应T-S(Takagi-Sugeno)模糊神经网络控制方法,研究了欠驱动无人艇的直线航迹跟踪控制问题。庄佳园等[7]针对水面无人艇全局路径规划问题,提出一种基于电子海图的距离寻优Dijkstra算法,用以生成安全合理的航线。王常顺等[8]针对欠驱动无人艇非线性系统,设计了一种参数在线优化的路径跟踪自抗扰控制器,仿真试验表明该方法具有良好的稳定性和鲁棒性。彭艳等[9]针对无人艇设计了GPC-PID串级控制器,通过航向控制间接实现无人艇的航迹跟踪控制。
目前基于平静水域的无人艇自主航行控制技术已经逐渐成熟,但是在风浪流干扰下的水面无人艇自主航行路径控制技术尚处于起步阶段。本文以水面无人艇应用发展为需求牵引,以实现水面艇智能化、无人化航行为技术驱动,将某7米级小艇作为研究对象,通过多物理场影响下无人艇水动力学仿真建模分析技术与实船试验验证技术相结合的方式,设计水面无人艇路径控制算法,并进行实艇试验验证。
1 无人艇操纵控制系统总体架构无人艇航行控制系统的主要功能是控制和优化艇的运动姿态和状态,使无人艇在风、浪、流等环境因素影响下能够按照系统规划出的目标航向、航速及路径等指令完成各种工作使命。
本文基于无人艇的水动力学模型,考虑风、浪、流等环境因素干扰,以自主规划系统输出的最优目标值和感知系统反馈信号为输入,设计自适应控制器,生成主机、舵机的动作控制信号,从而控制艇的运动。无人船的运动控制系统主要由基于MPC预测控制算法的航向控制、基于模糊PID控制算法的航速控制和基于LOS控制算法的路径控制3个子控制模块构成,如图1所示。
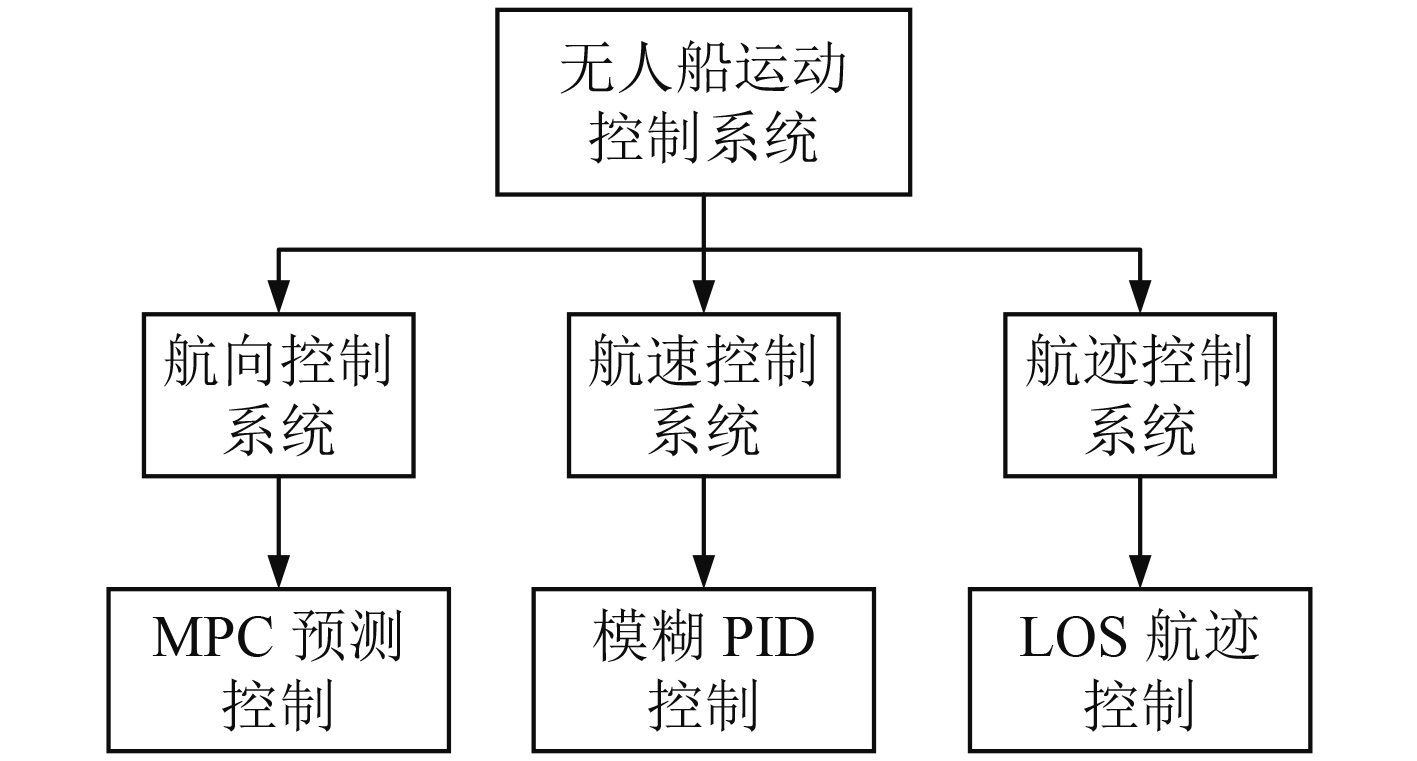
|
图 1 无人船运动控制系统总体架构 Fig. 1 The total framework of USV control system |
路径控制系统采用LOS控制算法[10],是将路径规划模块生成的轨迹曲线分解为多段小的直线路径,通过完成每一段小路径,进而实现路径控制。该方法可以减小风、浪、流等因素对无人艇航行的干扰,同时可以避免频繁操舵,适用于本文无人艇大航程航行的需求。
2 无人艇运动数学模型本文无人艇运动学数学模型采用船体结构参数法建立,该方法的时间和经济成本都比较低,适用于本文需求。船体结构参数法是根据已有的大量试验数据及经验公式,以及船体结构参数和水动力学理论,计算船舶运动的模型参数。本文无人艇采用桨-舵推进控制,所以船舶航向控制的数学模型实际上就是船舶操纵运动的数学模型。无人艇运动参数较大,因此本文预测控制系统采用的是船舶操作运动非线性模型。
2.1 无人艇空间坐标系无人艇运动的坐标系建立如图2所示。
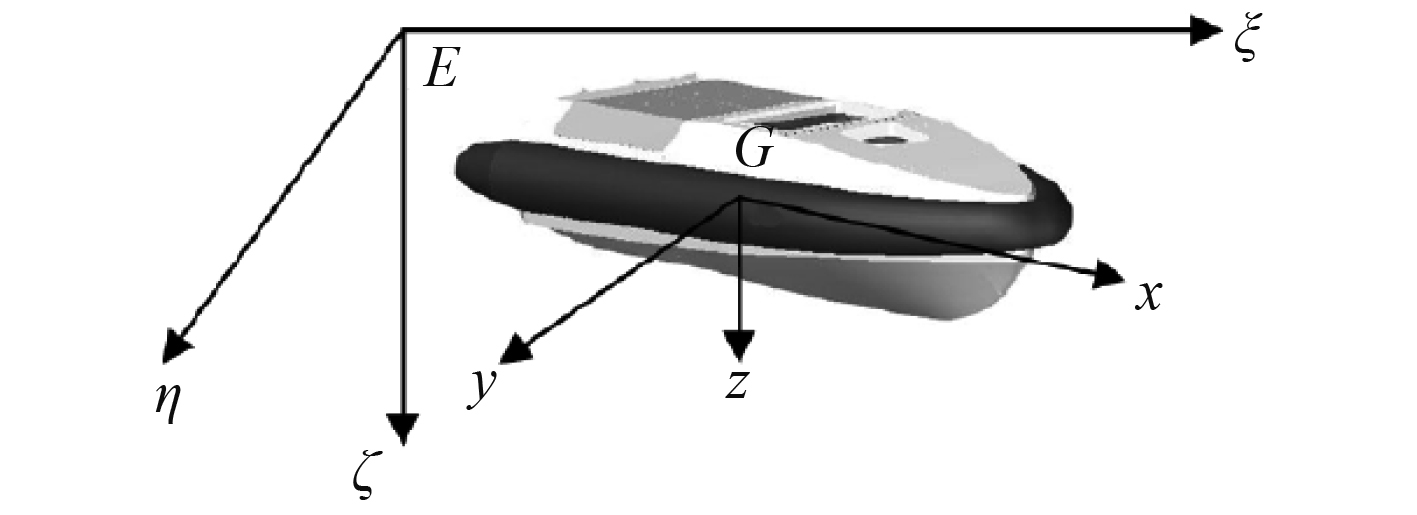
|
图 2 无人艇运动的坐标系 Fig. 2 The movement coordinate system of USV |
固定坐标系E-ξηζ,原点E固定于大地不动,一般取初始时刻(t=0)无人艇重心G所在位置;Eξ轴在海平面上,正北方向为正;Eη轴正东方向为正;Eζ轴垂直海平面,与Eξ,Eη轴构成右手坐标系。运动坐标系G-xyz,原点G在无人艇的重心处,Gx轴、Gy轴、Gz轴为无人艇艇体过G点的水线面、横剖面、纵中剖面的交线,取首部方向为Gx轴正方向,右舷为Gy轴正方向,向下为Gz轴正方向,Gx轴、Gy轴、Gz轴构成右手坐标系。同时,将Gx轴、Gy轴和Gz轴作为无人艇各方向相对应的惯性主轴。无人艇运动和受力相对各轴分解如表1所示。
|
|
表 1 无人艇参数表 Tab.1 The USV parameter list |
在上述定义的坐标系中,研究无人艇在水面操纵运动时,横摇、纵摇和升沉运动相对较小,可忽略对水平面内运动的影响。忽略惯性力和粘性流体动力的相互影响,认为船舶重心G和惯性水动力中心重合。基于上述条件,无人艇运动学方程如下:
| $\left\{ {\begin{array}{*{20}{c}} {{{\dot \zeta }_G} = u\cos \varPsi - v\sin \varPsi }\text{,} \\ {{{\dot \eta }_G} = u\sin \varPsi + v\cos \varPsi } \text{,}\\ {\dot \varPsi = r} \text{。} \end{array}} \right.$ | (1) |
综合考虑无人艇运动模型的精确性和复杂性,在保证研究精确性的前提下,对模型非关键参数进行简化,建立本研究的无人艇三自由度运动模型。将无人艇的运动学方程与运动模型结合,可以得到无人艇运动的数学模型如下:
| $ \left\{ {\begin{array}{*{20}{c}} {{{\dot \xi }_G} = u\cos \varPsi - v\sin \Psi } \text{,}\\ {{{\dot \eta }_G} = u\sin \varPsi + v\cos \varPsi } \text{,}\\ {\dot \varPsi = r} \text{,}\\ (m + {m_{11}})\dot u = (m + {m_{22}})vr + {X_0} + {X_u}u + {X_{vr}}vr +\\ {X_{vv}}{v^2} + {X_{rr}}{r^2} + {X_J} \text{,}\\ (m + {m_{22}})\dot v = - (m + {m_{11}})ur + {Y_r}r + {Y_v}v + {Y_{r\left| r \right|}}r\left| r \right| +\\ {Y_{v\left| v \right|}}v\left| v \right| + {Y_{v\left| r \right|}}v\left| r \right| + {Y_J} \text{,}\\ ({I_Z} + {m_{66}})\dot r = ({m_{11}} - {m_{22}})ur + {N_r}r + {N_v}v +\\ {N_{r\left| r \right|}}r\left| r \right| + {N_{v\left| v \right|}}v\left| v \right| + {N_{v\left| r \right|}}v\left| r \right| + {N_J} \text{。} \end{array}} \right. $ | (2) |
对无人艇运动模型进行数学模型仿真,无人艇基本参数如表2所示。
|
|
表 2 无人艇基本参数 Tab.2 The USV basic parameter |
为分析无人艇在大舵角和风、浪、流等干扰情况下的操纵特性,本文采用2阶非线性K,T方程作为船舶操纵方程:
| ${T_1}{T_2}\ddot r + ({T_1} + {T_2})\dot r + r + a{r^3} = K\delta + K{T_3}\dot \delta \text{,}$ | (3) |
| ${T_1}{T_2} = \frac{{(m + {\lambda _{22}})({I_2} + {\lambda _{66}})}}{C}\text{,}$ | (4) |
| $T = {T_1} + {T_2} - {T_3}\text{。}$ | (5) |
式中:r为首向角;δ为舵角;T为应舵指数;K为回转性指数;λ为附加质量系数。船舶首摇角速度
根据无人艇平面运动的线性化数学模型建模,得到无人艇模型的传递函数如下:
| ${G_{\Psi \delta }} = \frac{{0.42s}}{{3.6728{s^2} + 1.3636s + 0.3672}}\text{。}$ | (6) |
平均风力对水线以上无人艇建筑造成的附加干扰力和力矩为:
| $ \left\{ \begin{aligned} & {{X_{WIND}} = \dfrac{1}{2}{\rho _\alpha }{A_f}{V_R}^2{C_{X\alpha }}({\alpha _R})} \text{,}\\ & {{Y_{WIND}} = \dfrac{1}{2}{\rho _\alpha }{A_s}{V_R}^2{C_{Y\alpha }}({\alpha _R})} \text{,}\\ & {{N_{WIND}} = \dfrac{1}{2}{\rho _\alpha }{A_s}{V_R}^2{C_{N\alpha }}({\alpha _R})} \text{。} \end{aligned} \right. $ | (7) |
式中:
针对航向控制问题,主要讨论波浪漂移力。在考虑波浪对操纵性能影晌时,给出2阶波浪力和力矩的计算公式如下:
| $ \left\{ \begin{aligned} &{{{X'}_{Dwave}} = \dfrac{1}{2}\rho L{a^2}\cos \chi {C_{DX}}(\lambda )}\text{,} \\ &{{{Y'}_{Dwave}} = \dfrac{1}{2}\rho L{a^2}\sin \chi {C_{DY}}(\lambda )}\text{,} \\ &{{{N'}_{Dwave}} = \dfrac{1}{2}\rho {L^2}{a^2}\sin \chi {C_{DN}}(\lambda )} \text{。} \end{aligned} \right. $ | (8) |
式中:
| $\begin{split} \left\{ \begin{aligned} & {{C_{DX}}(\lambda ) = 0.05 - 0.2\left( {\frac{\lambda }{L}} \right) + 0.75{{\left( {\frac{\lambda }{L}} \right)}^2} - 0.51{{\left( {\frac{\lambda }{L}} \right)}^3}} \text{,}\\ & {{C_{DY}}(\lambda ) = 0.46 + 6.83\left( {\frac{\lambda }{L}} \right) - 15.65{{\left( {\frac{\lambda }{L}} \right)}^2} + 8.44{{\left( {\frac{\lambda }{L}} \right)}^3}} \text{,}\\ & {{C_{DN}}(\lambda ) = - 0.11 + 0.68\left( {\frac{\lambda }{L}} \right) - 0.79{{\left( {\frac{\lambda }{L}} \right)}^2} + 0.21{{\left( {\frac{\lambda }{L}} \right)}^3}}\text{。} \end{aligned} \right.\\[-50pt]\end{split} $ | (9) |
流对无人艇航行时产生的影响可认为是无人艇相对海水的速度发生改变而产生的附加干扰力和力矩,仿真实验时一般认为流是恒定且均匀的。对无人艇的航向运动来说,海流将引起一个绕轴的附加干扰力矩,其表达式为:
| ${N_c} = \frac{1}{2}\rho {V_c}^2{L_s}^2{C_{Nc}}(\beta )\text{。}$ | (10) |
式中:
在考虑风浪流的作用下,其干扰可等效到自动舵上的舵角干扰,可表示为:
| ${T_0}\ddot \varPsi + \dot \varPsi = {K_0}\delta + {f_a} + {f_w} + {f_l}\text{。}$ | (11) |
其中:
风浪对无人艇运动的影响可以用白噪声和1个2阶波浪传递函数来获得,流可以用一个恒值干扰来模拟,即
| $y(s) = {K_c}h(s)w(s)\text{。}$ | (12) |
其中:
| $h\left( s \right) = \frac{{{K_\omega }s}}{{{s^2} + 2\zeta {\omega _0}s + {\omega _0}^2}}\text{。}$ | (13) |
其中:
本文采用最小二乘法曲线拟合,计算无人艇的模型参数。
| ${K_{1i}}\frac{m}{{i = 1}}={a_{i0}} + {a_{i1}}{C_0} + {a_{i2}}C_0^1 + \cdot \cdot \cdot + {a_{in}}C_0^n\text{,}$ | (14) |
每个代数方程对应m条曲线,拟合成m个r次代数方程,得到一个m×n阶系数表如表3所示。
|
|
表 3 m×n阶系数表 Tab.3 The coefficient list |
将该系数表数据输入到计算机中,以待自动查找使用。同时将每条曲线所对应的参数
| $ - {10^{ - 4}} \leqslant [K(I) - \frac{L}{B}] \leqslant {10^{ - 4}}\text{,}$ | (15) |
否则按下式计算:
| $GI = \frac{{GC[K(I) - \frac{L}{B}]}}{{[K(I) - K(I - 1)]}}\text{。}$ | (16) |
式中:GC为插值因子,GI为比例因子,则有
无人艇的参数
针对无人艇进行了设计吃水状态下,
1)10°Z形试验原始数据
|
|
表 4 无人艇10°Z形试验原始数据表 Tab.4 The data log of 10/10° ZIG-ZAG test |
由K,T的无量纲公式换算出操纵指数K=1.148,T=9.548。Z操纵试验(10°/10°)的试验结果如图3所示。

|
图 3 10°/10°Z操纵试验结果 Fig. 3 The test results of 10/10° ZIG-ZAG test |
2)模型参数法数据
根据自动控制原理,对(10°/10°)Z操纵试验结果图形进行拟合,当参数为

|
图 4 10°/10°Z操纵仿真结果 Fig. 4 The simulation results of 10/10° ZIG-ZAG test |
无人艇Z形操纵实验的10°/10°Z操纵仿真结果见图4。
对比图3与图4两个图中的相关点,如表5所示。可以看出,拟合仿真结果与试验结果在超越角结果上有较大的差别。
|
|
表 5 (10°/10°)Z操纵试验与拟合仿真结果对比表 Tab.5 The comparison table between ZIG-ZAG test result and Simulation result |
3)阶跃响应
按实船试验参数进行首向角改变10°时的响应如图5所示。可以看出,系统超调量为60%,调节时间约80 s,调节时间相对较长。

|
图 5 原始参数阶跃响应 Fig. 5 The step function response of the original parameters |
按建模参数进行首向角改变10°时的响应如图6所示。可以看出,系统超调量约15.6%,调节时间约20 s,调节时间相对较短。
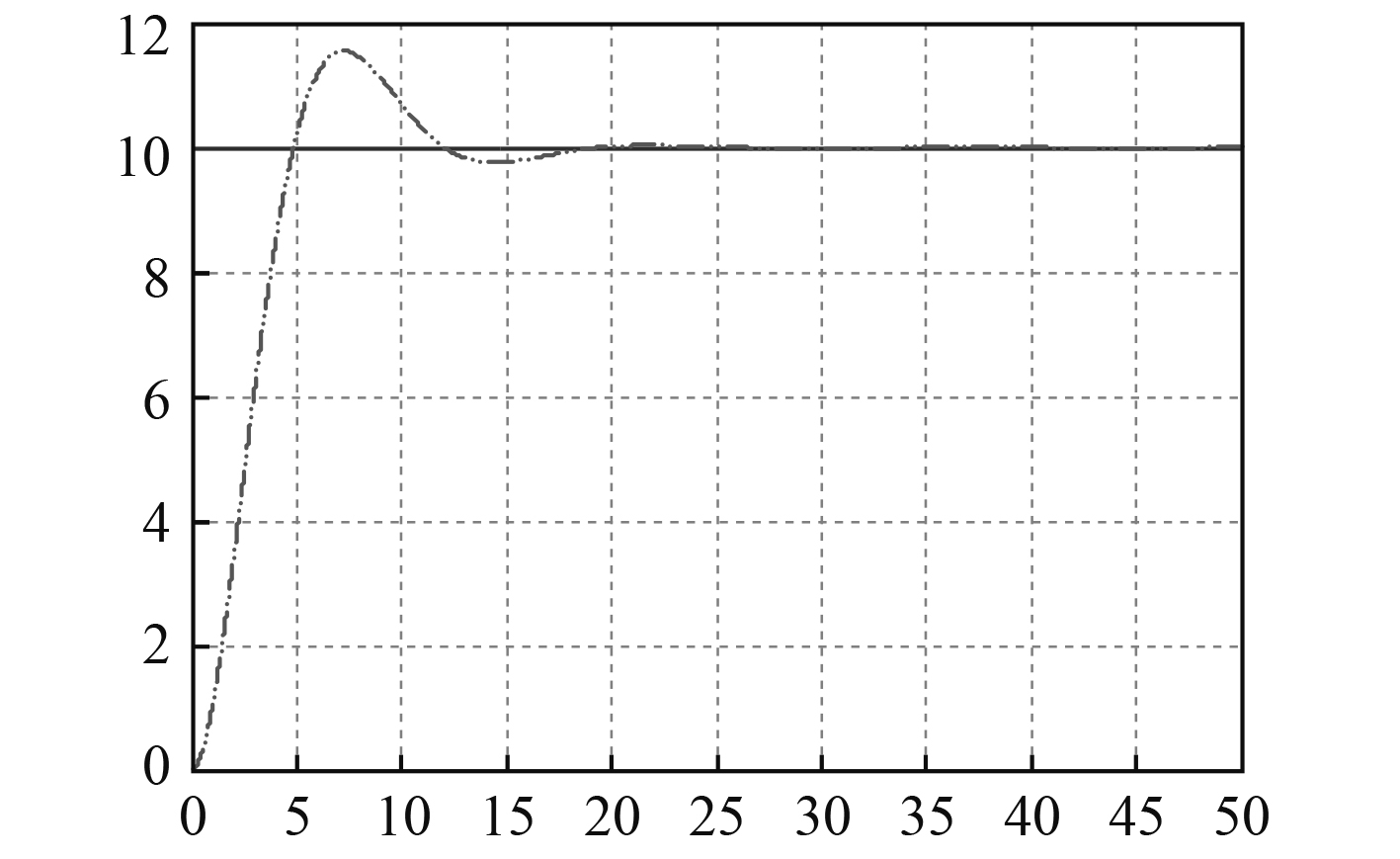
|
图 6 建模参数阶跃响应 Fig. 6 The step function response of the simulation parameters |
从图5和图6可明显看出,建模参数仿真结果超调量相对更小,调节时间相对更短,无人艇能够更快更好完成转首运动。
4 路径控制采用LOS路径控制算法,用于无人艇的路径跟踪。LOS路径控制流程图如图7所示。

|
图 7 LOS路径控制流程图 Fig. 7 The flow chart of the LOS track control method |
无人艇的路径跟踪控制系统将路径航向制导系统和航向控制系统合二为一,通过路径控制系统可以直接由航向偏差、路径偏差获得舵角指令,然后将舵角指令传送给舵角控制系统。路径跟踪控制系统是对舵角、路径偏差、偏航角以及偏航角速度等一系列耦合量进行综合考虑,而不需要解耦,因此可以获得优良的控制性能、能很好协调各变量间的耦合关系,比较适合对路径跟踪精度要求严格、性能要求较高的控制系统。
4.1 无人艇路径控制模型建立考虑无人艇航向控制系统模型中非线性的影响,在一阶线性首向响应野本方程中引入非线性项,得一阶非线性的表达式为:
| $T\ddot \varPsi + \dot \varPsi + \alpha {\dot \varPsi ^3} = K\delta\text{,} $ | (19) |
计入系统的建模误差以及不确定性外界环境的干扰,得无人艇直线路径跟踪控制的非线性运动学和动力学数学模型为:
| $\left\{ {\begin{array}{*{20}{c}} {\dot y = U\sin \phi }\text{,} \\ {\dot \phi = r} \text{,}\\ {\dot r = - \dfrac{r}{T} - \dfrac{{\alpha {r^3}}}{T} + \dfrac{{K\delta }}{T} + {\rm d}(t)} \text{。} \end{array}} \right.$ | (20) |
式中,d(t)是系统建模误差以及不确定性外界环境干扰的综合考虑。设此不确定性项的上界为D,即
无人艇路径跟踪控制,是把无人艇在水面上路径跟踪控制当作艇体航向保持和航向改变的控制问题。路径跟踪控制系统主要由舵角控制系统、航向控制系统和路径航向制导系统3部分组成。无人艇的路径跟踪控制是通过实时的循环路径航向制导、航向控制、操舵控制这一过程,通过不断的更新航向进而达到航向和路径共同趋于指定航线的航向和路径的过程。
LOS路径导航在数学上表示为如下方程式:
| ${\eta _c} = N'{V_c}\lambda \text{。}$ | (22) |
其中:Vc为闭合速度;λ为LOS角;N′为调谐参数。N′的变化可调节无人艇航行轨迹。
| $\lambda = {\tan ^{ - 1}}\left[ {\frac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}} \right]\text{。}$ | (21) |
其中:(x1,y1)是无人艇的当前位置,(x2,y2)是目标的位置。
航点指导导航方法中,2个点
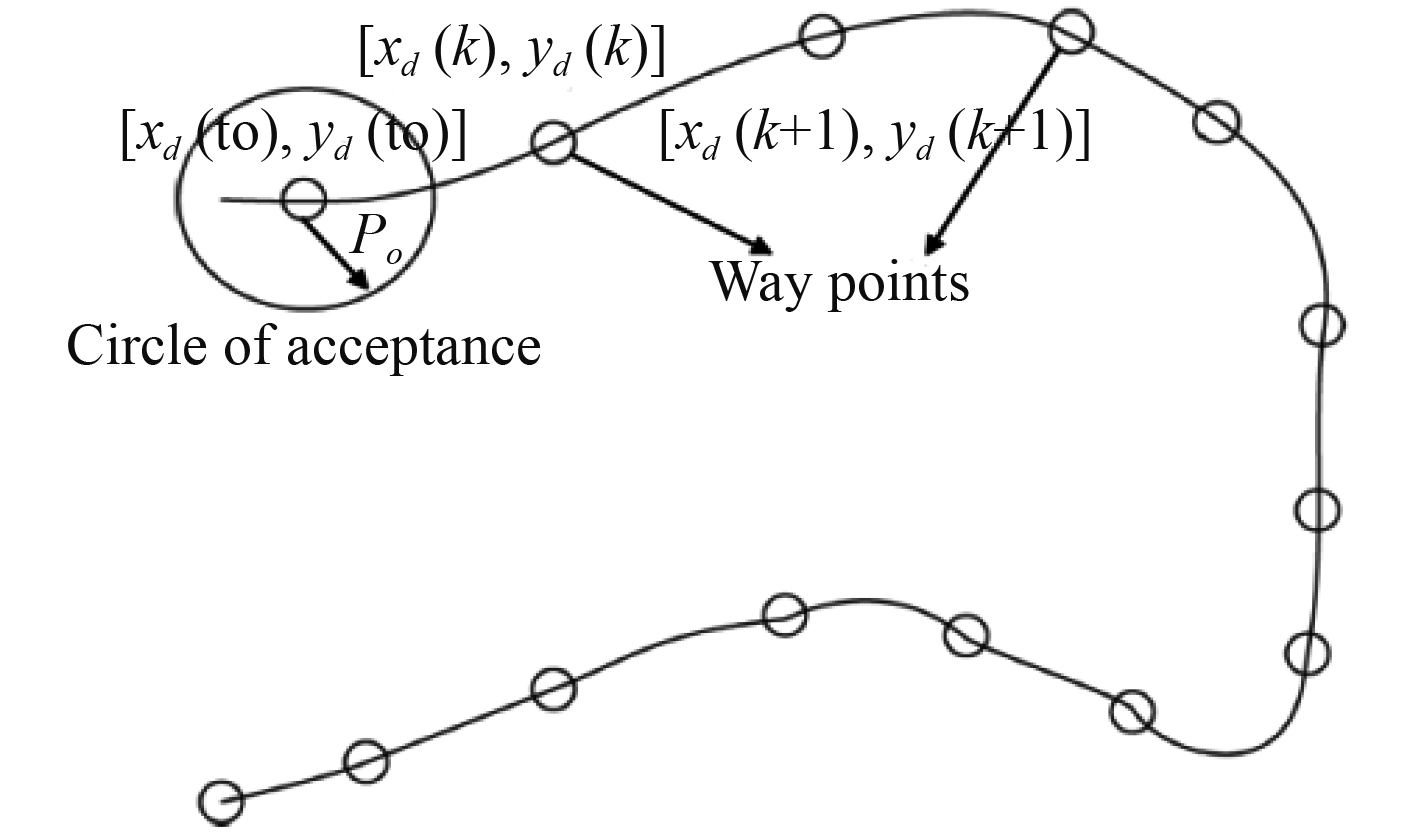
|
图 8 LOS算法路径路线控制图 Fig. 8 The path control chart of the LOS method |
导航系统不断跟踪无人艇路径,包括到达或错过的航路点以及当前目标航点,以及总数行驶距离,偏离理想轨迹等。根据无人艇位置坐标的数据更新,这些路径信息在每个时刻都会更新一次无人艇的航向。
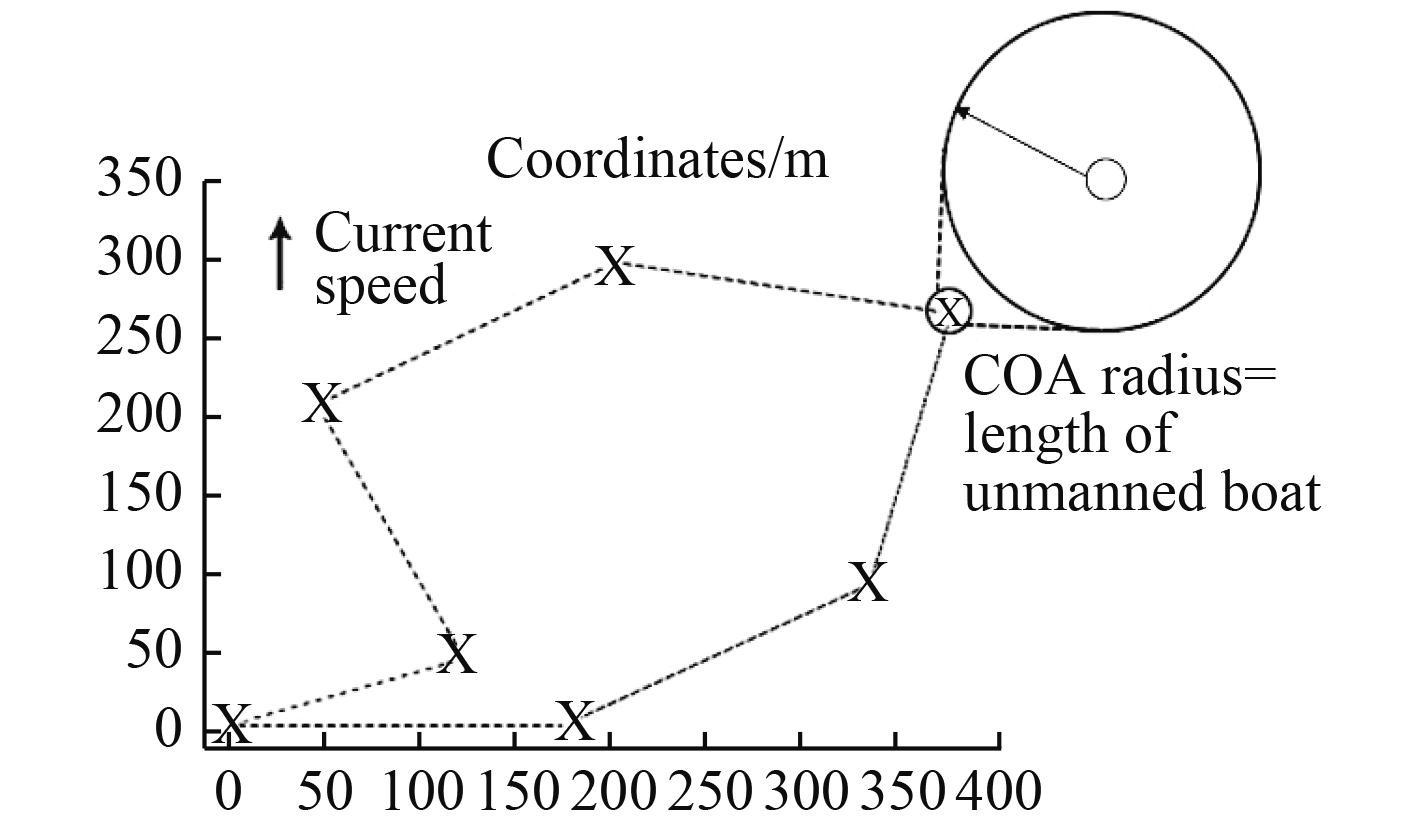
为确定航路点是否达到,指导系统在每个航点上考虑设置一个接受圈(COA),COA接受圈的直径设为无人船长度的2倍。在无人艇试验过程中,无人艇可能从各种不同的航向角度接近航点,如图9所示。
|
图 9 无人艇从不同航向角度接近航点图 Fig. 9 The different course between starting point and COA |
对于本文无人艇来说,长度为7.5 m,因此COA误差圈的直径为15 m。在每一个无人艇位置坐标采样时刻,导航系统都计算无人艇的下一个航路点。当无人艇与导航点距离小于误差圈半径时,就可判定无人艇到达航路点,导航系统会将无人艇引导到以下位置航点。
在无人艇实际航行中,可能出现测量无人艇位置坐标的时刻,无人艇已不在COA误差圈范围之内,已经进入误差圈又离开了误差圈的情况。本文设定一个到达航路点判断标准,如果无人艇2个时刻位置的连线经过COA误差圈,则判定无人艇已经到达了航路点。
在无人艇经过航路点附近而未进入目标航点情况下,位置判断过程会认定无人艇未进入误差半径圈内,错过该航点。此时,导航系统会将无人艇引导到下一个航点。
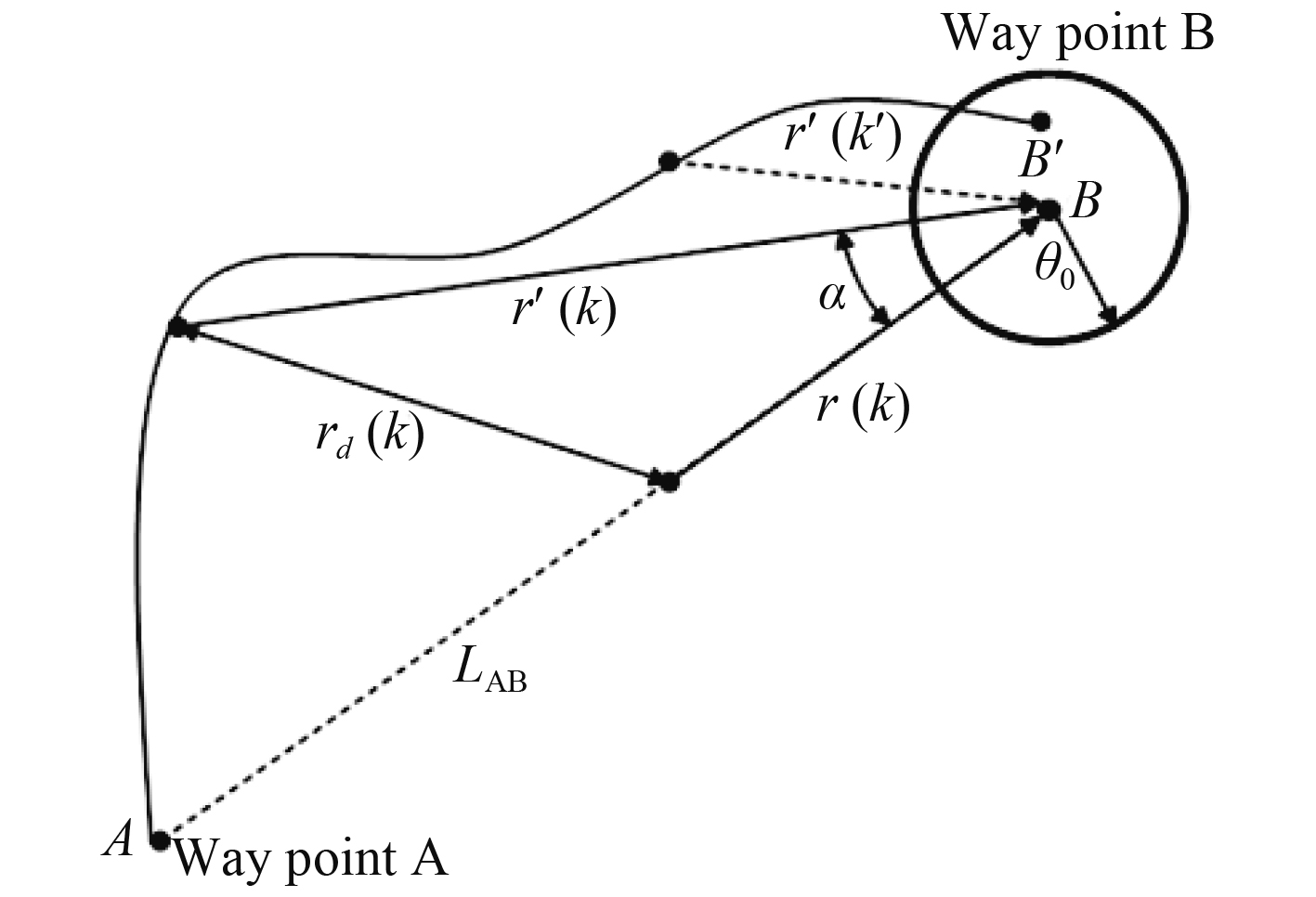
无人艇偏离理想轨迹可以通过以下等式来测量:
| ${r_d}(k) = \sqrt {{r^2}(k) + {{r'}^2}(k) - 2r(k)r'(k)\cos \alpha } \text{。}$ | (25) |
其中:r(k)为从无人艇当前位置到下一个航路点的距离;r′(k)为从实际位置到下一个航路点的距离,α是2个向量之间的角度,这些数据可以用来判断无人艇是否在理想路径上,如图10所示。
|
图 10 LOS路径控制的误差圈示意图 Fig. 10 The error circle of the LOS method |
LOS路径控制系统使无人艇能够生成参考实现所需任务所需的航行轨迹。使用该参考轨迹平均达到了5个以上的路径目标点,即使无人艇在航行过程中被风浪流等环境所影响,这7个航点可沿其参考路径方向来确定无人艇的航行轨迹。
无人艇采用LOS路径控制方法的优点是,控制系统结构相对独立,控制算法比较简单,控制指令易于实现,在当前的无人艇航海航行中经常应用于船舶的路径控制,是一种比较容易被大家理解的常见路径控制方法。
4.3 路径控制实艇试验无人艇采用本文建立的无人艇路径控制算法进行湖上实艇试验,试验当日天气晴,风力小于3级,浪高小于0.5 m。通过实艇操纵性试验与仿真试验相结合的方法,完成了无人艇路径规划控制算法。
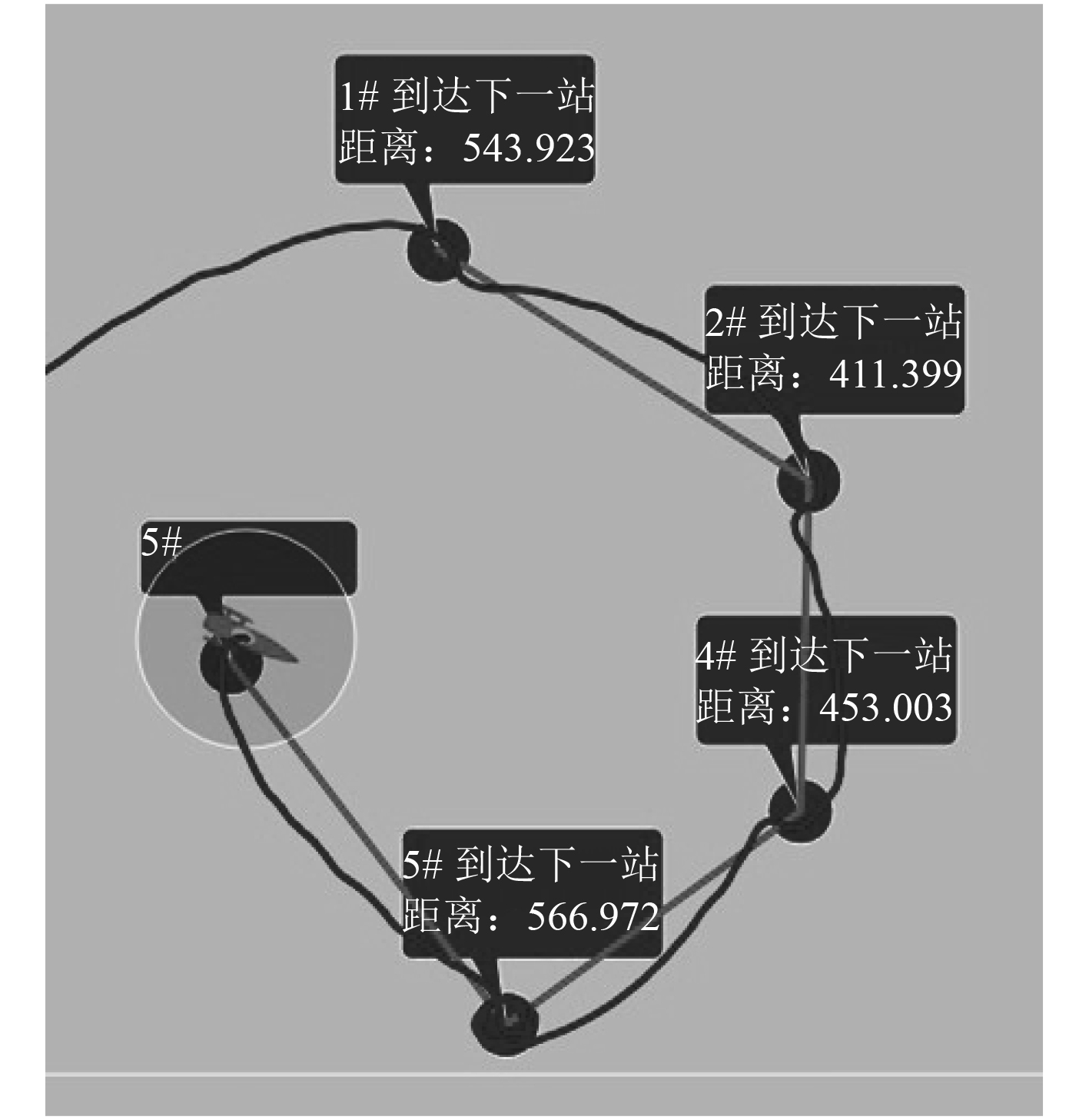
根据试验水域勘察情况,设定1-2-3-4-5号目标位置点,各位置点间距500 m左右,要求无人艇自主按照目标路径航行。试验开始时,无人艇以5.6 kn航速开始试验。
无人艇试验航行轨迹和规划路径对比如图11所示。
|
图 11 无人艇航行轨迹 Fig. 11 The USV track and plan path |
可以看出,采用本文路径控制算法的无人艇能够比较准确地执行规划路径,满足无人艇的工作需求。但由于试验水域较小,目标位置点设置的距离较近,各点之间连线的拐角较大,导致无人艇在拐角位置出现较大的操舵角,实际路径与设定路径偏差产生较大偏差。
5 结 语本文采用船体结构参数法建立了无人艇的运动模型,并根据仿真计算和实艇Z型操舵试验确定了无人艇自动控制系统的操纵系数。基于LOS控制算法建立了无人艇的路径控制系统,并对采用本文控制方法的无人艇进行了湖上试验。结果表明,在风浪流多物理场的影响下,无人艇能够比较准确地按照规划路径进行航行,满足无人艇的使用需求。但在规划路径拐角较大的位置,无人艇航迹与规划路径有较大的偏差。
| [1] |
朱炜, 张磊. 现代水面无人艇技术[J]. 造船技术, 2017(2). DOI:10.3969/j.issn.1000-3878.2017.02.013 |
| [2] |
YAN R J, PANG S, SUN H B, et al. Development and missions of unmanned surface vehicle[J]. Journal of Marine Science and Application, 2010, 9(4): 451-457. DOI:10.1007/s11804-010-1033-2 |
| [3] |
MANLEY J E. Unmanned surface vehicles, 15 years of development[C]//Oceans, Quebec City, Canada, 2008: 1-4.
|
| [4] |
李家良. 水面无人艇发展与应用[J]. 火力与指挥控制, 2012, 6: 203-207. DOI:10.3969/j.issn.1002-0640.2012.06.053 |
| [5] |
宋磊. 全球自主: 国外无人水面艇未来发展及关键技术[J]. 军事文摘, 2015, 13: 26-28. |
| [6] |
董早鹏, 刘涛, 万磊, 等. 基于Takagi-Sugeno模糊神经网络的欠驱动无人艇直线航迹跟踪控制[J]. 仪器仪表学报, 2015, 4: 863-870. |
| [7] |
庄佳园, 万磊, 等. 基于电子海图的水面无人艇全局路径规划研究[J]. 计算机科学, 2011, 9: 211-219. DOI:10.3969/j.issn.1002-137X.2011.06.050 |
| [8] |
王常顺, 肖海荣. 基于自抗扰控制的水面无人艇路径跟踪控制器[J]. 山东大学学报(工学版), 2016, 8(4): 54-59. DOI:10.6040/j.issn.1672-3961.0.2016.010 |
| [9] |
彭艳, 吴伟清, 等. 无人艇航迹跟踪GPC-PID串级控制[J]. 控制工程, 2014, 3(2): 245-248. DOI:10.3969/j.issn.1671-7848.2014.02.020 |
| [10] |
秦梓荷, 林壮, 等. 基于LOS导航的欠驱动船舶滑膜控制[J]. 中南大学学报(自然科学版), 2016, 10: 3605-3611. |
 2019, Vol. 41
2019, Vol. 41
