2. 上海大学,机电工程与自动化学院,上海 200444
2. School of Mechatronic Engineering and Automation, Shanghai University, Shanghai 200444, China
水面无人船(Unmanned Surface Vehicle,USV)是一种能够在无人操控的情况下实现自主航行的水面机器人[1]。配备传感器系统、通信系统等不同的功能模块的水面无人船可以被用于执行绘制海图、侦查以及搜救等海上作业任务[2]。船舶轨迹跟踪(Dynamic Tracking,DT)属于广义上的动力定位,具体来说,是船舶在规定的时间内通过轨迹跟踪控制系统的控制到达期望位置上[3]。实现复杂海洋环境下欠驱动水面无人船(控制输入维数小于无人船自由度)轨迹精确跟踪是保证其能够完成各项任务的重要前提,也是当前水面无人船领域研究的热点问题[4]。
由于水面无人船运动方程具有非线性特性,Fossen等[5]在非线性船舶运动模型基础上设计了反步控制律,并利用李雅普诺夫稳定性理论证明船舶位置信息的全局指数稳定,最终通过这种方法实现了船舶轨迹跟踪控制。然而,考虑到实际被控船舶模型结构的复杂性,在反步控制律设计过程中需要进行复杂的求导运算,容易出现微分爆炸问题。对此,Swaroop等[6]提出了动态面控制,其核心思想是引入滤波器避免对中间变量求导。此外,在生物神经作用机制的启发下,Yang等[7]针对机器人控制,提出了将神经动态模型与反步法相结合的方案,该方案不仅解决了反步法控制控制过程中容易出现的微分爆炸问题,还解决控制过程中存在的控制不连续的问题。在后续研究中,文献[8]将该方法应用于水面无人船的运动控制并取得了良好的效果,但该方法没有考虑到船舶运动过程中所遭受到的风、浪、流等外部干扰。为此,文献[9]为实现水面无人船在海洋干扰环境下的轨迹跟踪,设计了一种基于非线性扰动观测器与动态面控制的鲁棒控制器,在存在外界扰动的情况下实现了轨迹跟踪。文献[10]提出自适应模糊反步控制方法,该方法同样采用扰动观测器对扰动进行实时估计,并对控制量进行前馈补偿。此外,现有的航迹跟踪控制方法还常采用神经网络控制[11]以及模糊神经网络[12]等。上述方法都可以逼近外部扰动,但存在收敛速度慢、控制精度低的缺点。
根据以上研究结果,本文考虑扰动环境下水面无人船欠驱动的运动特性,并设计一种带有扰动观测器的水面无人船轨迹跟踪控制器。首先,构造扰动观测器估计未知扰动,对纵荡以及首摇2个自由度上的控制量进行补偿。然后,为增强系统的抗扰动能力与系统整体动态性能,将位置误差的积分项引入控制系统。在运用反步法设计控制器过程中结合神经网络动态模型,避免微分爆炸以及控制不连续。仿真结果表明,所设计的控制器能够实现轨迹误差的快速收敛并保证较高的控制精度。
1 问题描述水面无人船是一种能够自主航行的水面机器人,船体无法载人,其质量轻惯性小,受外界扰动影响比较大;此外,大部分水面无人船采用欠驱动设计。考虑运动特性的水面无人船模型可通过如下状态方程描述[13]
| $\dot \eta = J\left( \eta \right){\rm{v}}\text{,}$ | (1) |
| $M{\rm{\dot v}} + C\left( {\rm{v}} \right){\rm{v}} + D\left( {\rm{v}} \right){\rm{v}} = \tau + {\tau _d}\text{,}$ | (2) |
式中:
| $ {\rm J}\left( \eta \right) = \left[ {\begin{array}{*{20}{c}} {\cos \phi }&{ - \sin \phi }&0 \\ {\sin \phi }&{\cos \phi }&0 \\ 0&0&1 \end{array}} \right],\;{\rm M} = \left[ {\begin{array}{*{20}{c}} {{m_{11}}}&0&0 \\ 0&{{m_{22}}}&0 \\ 0&0&{{m_{33}}} \end{array}} \right],\; $ |
| ${\rm C}\left( {\rm{v}} \right) \!=\! \left[ {\begin{array}{*{20}{c}} 0&0&{{C_{13}}} \\ 0&0&{{C_{23}}} \\ { - {C_{13}}}&{ - {C_{23}}}&0 \end{array}} \right],\; {\rm D}\left( {\rm{v}} \right) \!=\! \left[ {\begin{array}{*{20}{c}} {{d_{11}}}&0&0 \\ 0&{{d_{22}}}&0 \\ 0&0&{{d_{33}}} \end{array}} \right]\text{。} $ |
其中,
选取水面无人船的参考轨迹为
假设1 水面无人船参考轨迹
假设2 对于任意时间
假设3 水面无人船在运动中控制输入有界,即满足
控制目标:在假设1,假设2以及假设3成立的情况下,针对水面无人船非线性模型(1)和(2),设计控制律
本文所提出的轨迹跟踪控制器设计分为两步:首先,针对无人水面船非线性模型设计扰动观测器,将观测器的输出用作控制量前馈补偿;然后,将位置误差的积分项引入系统,并把反步法与神经动态模型相结合,设计系统控制律。
神经动态模型是本节研究方法的一个重要组成部分,下面对其作简单介绍。神经动态模型是由Hodgkin和Huxley提出的细胞膜生物模型,结合细胞膜电压特性相关知识,它具有如下表达形式:
| ${\dot x_i} = - B{x_i}{\rm{ + }}\left( {C - {x_i}} \right)f\left( t \right) - \left( {D + {x_i}} \right)g\left( t \right),$ | (3) |
式中,
| $ f\left( t \right) = \left\{ {\begin{array}{*{20}{c}} {t,{\rm{ t}} \geqslant 0}\text{,} \\ {0,{\rm{ t}} < 0} \text{,} \end{array}} \right.{\rm{ }}\;\;\;g\left( t \right) = \left\{ {\begin{array}{*{20}{c}} {0,{\rm{ t}} > 0}\text{,} \\ { - t,t \leqslant 0} \text{。} \end{array}} \right. $ |
本小节将基于水面无人船非线性模型设计扰动观测器,对纵荡和首摇方向上的干扰进行在线估计,下面给出扰动观测器的设计过程:
| $\begin{split} {{{\dot{\bar{\tau }}}}_{d}}&={{K}_{0}}\left( {{\tau }_{d}}-{{{\bar{\tau }}}_{d}} \right) =\\ &{{K}_{0}}\left[ M{\rm \dot{v}}+C\left( {\rm v} \right){\rm v}+D{\rm v}-\tau \right]-{{K}_{0}}{{{\bar{\tau }}}_{d}}\text{,} \\ \end{split}$ | (4) |
式中:
考虑到实际情况下
| $\left\{ {\begin{array}{*{20}{l}} {{{\bar \tau }_d} = \beta + {K_0}M{\rm{v}}}\text{,} \\ {\dot \beta = - {K_0}\left[ { - C\left( {\rm{v}} \right){\rm{v}} - D{\rm{v}} + \tau + {K_0}M{\rm{v}}} \right] - {K_0}\beta } \text{。} \end{array}} \right.$ | (5) |
定义
| ${\tilde \tau _d} = {\tau _d} - {\bar \tau _d}\text{,}$ | (6) |
式中:
| ${{\dot{\tilde{\tau }}}_{d}}={{\dot{\tau }}_{d}}-{{K}_{0}}{{\tilde{\tau }}_{d}}\text{。}$ | (7) |
本小节将结合扰动观测器的输出设计带扰动补偿的轨迹跟踪控制器,过程中引入位置误差积分项并结合神经动态模型技术。
将上一节设计的扰动观测器输出
| $\tau = {\tau _{TD}} - {\bar \tau _d}\text{,}$ | (8) |
式中:
| $M{\rm{\dot v}} = - C\left( {\rm{v}} \right){\rm{v}} - D\left( {\rm{v}} \right){\rm{v}} + {\tau _{TD}} + {\tilde \tau _d}\text{,}$ | (9) |
根据式(1),式(9)设计控制律
在大地坐标系下,记无人水面船实际位置坐标为
定义水面无人船位置跟踪误差和角度跟踪误差分别为
| $\left\{ {\begin{array}{*{20}{l}} {{e_x} = {x_e}\cos \phi + {y_e}\sin \phi {\rm{ }}}\text{,} \\ {{e_y} = - {x_e}\sin \phi + {y_e}\cos \phi }\text{,} \\ {{e_\phi } = {\phi _e}} \text{。} \end{array}} \right.$ | (10) |
1)运动学控制律设计
引入误差积分项,定义位置误差
| $\left\{ {\begin{array}{*{20}{c}} {{e_1} = {e_x} + {K_1}\int_0^t {{e_x}{{\rm d}_T}} } \text{,}\\ {{e_2} = {e_y} + {K_2}\int_0^t {{e_y}{{\rm d}_T}} } \text{。} \end{array}} \right.$ | (11) |
为实现位置误差
| ${V_1} = \frac{1}{2}\left( {e_1^2 + e_2^2} \right)\text{,}$ | (12) |
对
| $\begin{split} {{\dot V}_1} &= {e_1}\left( {u + r{e_y} - {v_p}\cos {\phi _e} + {K_1}{e_x}} \right) +\\ & {e_2}\left( {v - r{e_x} + {v_p}\sin {\phi _e} + {K_2}{e_y}} \right) \text{,} \\ \end{split} $ | (13) |
式中,
由于欠驱动水面无人船在横荡方向上没有控制输入,所以需要用转首速率
| ${u_c} = - {A_1}{e_1} - r{e_y} + {v_p}\cos {\phi _e} - {K_1}{e_x}\text{,}$ | (14) |
| ${h_c} = - {A_2}{e_2} - v + r{e_y} - {K_2}{e_y}\text{,}$ | (15) |
式中,
| ${\dot h_f} = - {B_1}{h_f}{\rm{ + }}\left( {{C_1} - {h_f}} \right)f\left( {{h_c}} \right) - \left( {{D_1} + {h_f}} \right)g\left( {{h_c}} \right){\rm{ }}\text{,}$ | (16) |
定义误差变量
| ${V_2} = {V_1} + \frac{1}{2}\left( {e_{hc}^2 + \phi _e^2} \right)\text{。}$ | (17) |
对
| $\begin{split} {{\dot V}_2}& = - {A_1}e_1^2 - {A_2}e_2^2 + {e_{hc}}({e_2} + {{\dot v}_p}\sin {\phi _e} - {{\dot h}_f}) + \\ & \left( {r - {{\dot \phi }_d}} \right)\left( {{\phi _e} + e{}_{hc}{v_p}\cos {\phi _e}} \right) + {z_{hc}}{e_2}\text{,} \\ \end{split} $ | (18) |
根据上式,为实现辅助控制量误差
| ${r_c} = - {A_3}\left( {{\phi _e} + {e_{hc}}{v_p}\cos {\phi _e}} \right) + {\dot \phi _d}\text{。}$ | (19) |
综上,运动学控制律设计为式(14)和式(19)。
2)动力学控制律设计
为了避免动力学控制律设计过程中对
| ${\dot u_f} = - {B_2}{u_f} + \left( {{C_2} - {u_f}} \right)f\left( {{u_c}} \right) - \left( {{D_2} + {u_f}} \right)g\left( {{u_c}} \right)\text{,}$ | (20) |
| ${\dot r_f} = - {B_3}{r_f} + \left( {{C_3} - {r_f}} \right)f\left( {{r_c}} \right) - \left( {{D_3} + {r_f}} \right)g\left( {{r_c}} \right)\text{。}$ | (21) |
定义误差变量
| ${V_3} = {V_2} + \frac{1}{2}{m_{11}}e_{uc}^2 + \frac{1}{2}{m_{33}}e_{rc}^2\text{,}$ | (22) |
对式
| $\begin{split} {{\dot V}_3} &= {\rm{ }} - {A_1}e_1^2 - {A_2}e_2^2 - {A_3}{\left( {{\phi _e} + e{}_{hc}{v_p}\cos {\phi _e}} \right)^2} + \\ & {{\rm{e}}_{{\rm{uc}}}}\left( \begin{array}{l} {\tau _{TD1}} + {m_{22}}vr - {d_{11}}u + \\ {{\tilde \tau }_{d1}} - {m_{11}}{{\dot u}_f} + {e_1} \\ \end{array} \right) +\\ & {e_{rc}}\left[ \begin{array}{l} {\tau _{TD3}} + \left( {{m_{11}} - {m_{22}}} \right)uv - {d_{33}}r + {{\tilde \tau }_{d3}} -\\ {m_{33}}{{\dot r}_f} + {\phi _e} + {e_{hc}}{v_p}\cos {\phi _e} \\ \end{array} \right] + \zeta \text{。} \end{split} $ | (23) |
式中:
为实现误差
| ${\tau _{TD1}} = - {A_4}{e_{uc}} - {m_{22}}vr + {d_{11}}u + {m_{11}}{\dot u_f} - {e_1} - {\tilde \tau _{d1}}\text{,}$ | (24) |
| $\begin{split} {\tau _{TD3}} &= - {A_5}{e_{rc}} - \left( {{m_{11}} - {m_{22}}} \right)uv + {d_{33}}r + \\ & {m_{33}}{{\dot r}_f} - {\phi _e} - {e_{hc}}{v_p}\cos {\phi _e} - {{\tilde \tau }_{d3}}\text{。} \\ \end{split} $ | (25) |
结合式(8)进一步得,最终对水面无人船的控制输入为
本节将分析被控系统的稳定性,证明开始前,给出如下引理及定理:
引理1[9] Young's不等式,即对于得
定理1 对于式(1)-式(2)所表示的无人水面船系统,如果按照式(24)-式(25)进行水面无人船轨迹跟踪控制器设计,那么被控系统是稳定的,且跟踪误差收敛至零的小领域内。
构造增广Lyapunov函数
| ${V_4} = {V_3} + \frac{1}{2}\left( {z_{uc}^2 + z_{hc}^2 + z_{rc}^2} \right)\text{,}$ | (26) |
对
| ${\dot u_c} = - {A_1}{\dot e_1} - r{\dot e_y} + \dot r{e_y} + {\dot v_p}\cos {\phi _e} - {v_p}{\dot \phi _e}\sin {\phi _e} - {K_1}{\dot e_x}\text{。}$ | (27) |
当系统满足假设条件时,
| ${\dot z_{uc}} = - {B_u}{u_f} + {C_1}{u_c} - {\dot u_c}\text{,}$ | (28) |
式中,
| ${\dot z_{hc}} = - {B_h}{h_f} + {C_2}{h_c} - {\dot h_c}\text{,}$ | (29) |
| ${\dot z_{rc}} = - {B_r}{r_f} + {C_3}{r_c} - {\dot r_c}\text{。}$ | (30) |
式中,
当系统满足假设条件时,
| $\begin{split} {{\dot V}_4} &= {{\dot V}_3} - {z_{uc}}\left( {{B_u}{u_f} - {C_1}{u_c}} \right) - {z_{hc}}\left( {{B_h}{h_f} - {C_2}{h_c}} \right) - \\ & {z_{rc}}\left( {{B_r}{r_f} - {C_3}{r_c}} \right) - {z_{uc}}{{\dot u}_c} - {z_{hc}}{{\dot h}_c} - {z_{rc}}{{\dot r}_c} \text{,} \end{split} $ | (31) |
如果按照式(24)-式(25)进行水面无人船轨迹跟踪控制器设计,同时令
| $\begin{split} {{\dot V}_4}& \leqslant - {A_1}e_1^2 - {A_2}e_2^2 - {A_3}\phi _e^2 - {A_3}{\left( {e{}_{hc}{v_p}\cos {\phi _e}} \right)^2} - \\ & {A_4}{\rm{e}}_{{\rm{uc}}}^{\rm{2}} - {A_5}e_{rc}^2{\rm{ }} - {B_u}z_{uc}^2 - {B_h}z_{hc}^2 - {B_r}z_{rc}^2 + \\ & \left| {{z_{uc}}} \right|\left| {{{\dot U}_c}} \right|{\rm{ + }}\left| {{z_{hc}}} \right|\left| {{{\dot H}_c}} \right| + \left| {{z_{rc}}} \right|\left| {{{\dot R}_c}} \right| +\\ & 2{A_3}{v_p}\left| {{\phi _e}} \right|\left| {{e_{hc}}} \right| + \zeta \text{。}\\ \end{split} $ | (32) |
结合引理1,对式(32)最后5个不定项使用Young's不等式,经整理化简得式(32)可表示为具有如下形式的表达式:
| $\begin{split} {{\dot V}_4} &\leqslant - {l_1}e_1^2 - {l_2}e_2^2 - {l_3}\phi _e^2 - {A_4}{\rm{e}}_{{\rm{uc}}}^{\rm{2}} - {A_5}e_{rc}^2 -\\ & {l_4}e_{hc}^2 - {l_5}z_{uc}^2 - {l_6}z_{hc}^2 - {l_7}z_{rc}^2 + \varepsilon \text{。}\\ \end{split} $ | (33) |
式中,
| ${\dot V_4} \leqslant - 2l{V_4} + \varepsilon\text{,} $ | (34) |
| $\begin{split} {V_4}& \leqslant \left[ {{V_4}\left( 0 \right) - \frac{\varepsilon }{{2l}}} \right]{e^{ - 2lt}} + \frac{\varepsilon }{{2l}} \leqslant \\ & {V_4}\left( 0 \right){e^{ - 2lt}} + \frac{\varepsilon }{{2l}},\;\;\forall t > 0 \text{。} \end{split} $ | (35) |
综上,可以通过增大增益
为验证本文所设计的轨迹跟踪控制器的有效性,本节以具有式(1)和式(2)形式模型结构的欠驱动水面无人船为控制对象,模型参数参考文献[14],其中:
为了使仿真实验更具有代表性,期望轨迹
|
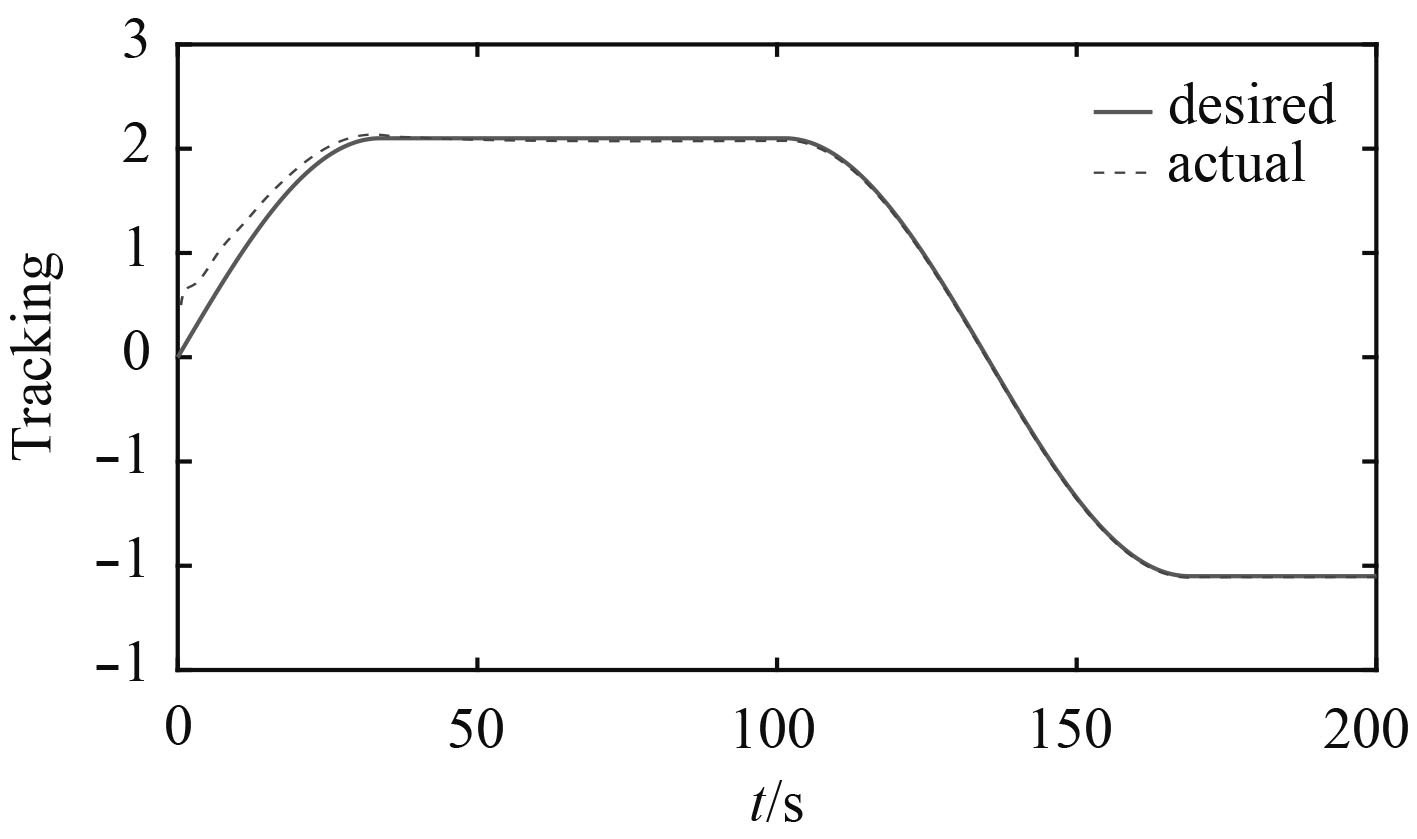
图 1 常值扰动下USV运动轨迹 Fig. 1 Motion trajectories of the USV under constant disturbance |
|
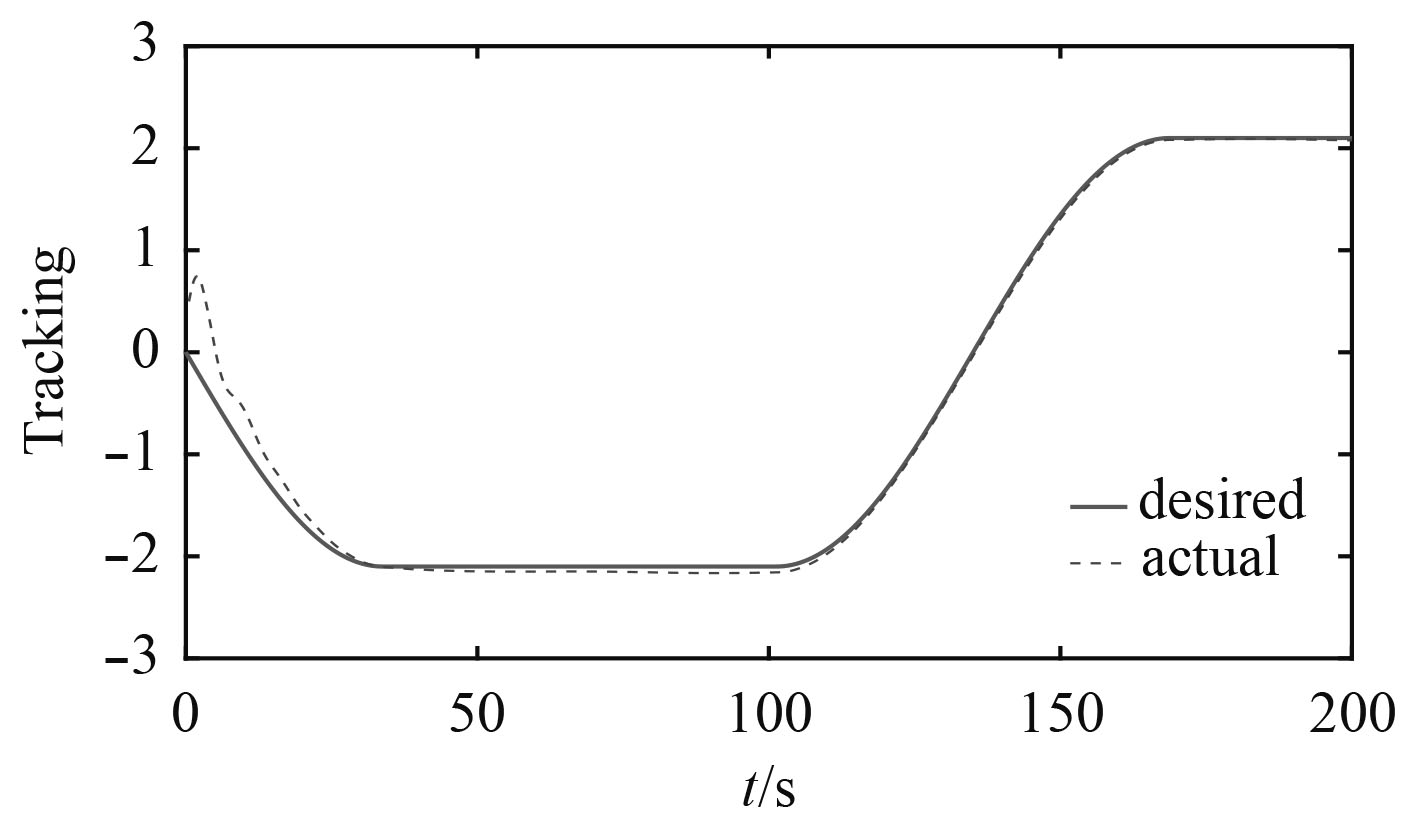
图 6 时变扰动下USV运动轨迹 Fig. 6 Motion trajectories of the USV under time-varying disturbance |
| $ {x_{d1}}{\rm{ = }}{x_{d2}} = kt{\rm{ }} \text{,} $ |
| ${y_{d1}}{\rm{ = }} - {y_{d2}}{\rm{ = }}\left\{ {\begin{array}{*{20}{c}} {A\sin (\omega t + \theta ),} \\ {{a_1},} \\ {A\sin (\omega t + \theta ),} \\ {{a_{2,}}} \end{array}} \right.\begin{array}{*{20}{c}} {0 < t < {t_1}}\text{,} \\ {t < {t_2}} \text{,}\\ {t < {t_3}} \text{,}\\ {t \geqslant {t_3}} \text{。} \end{array}$ |
式中,
水面无人船初始位置
低级海况下的扰动一般表现为常值,取常值扰动向量
|
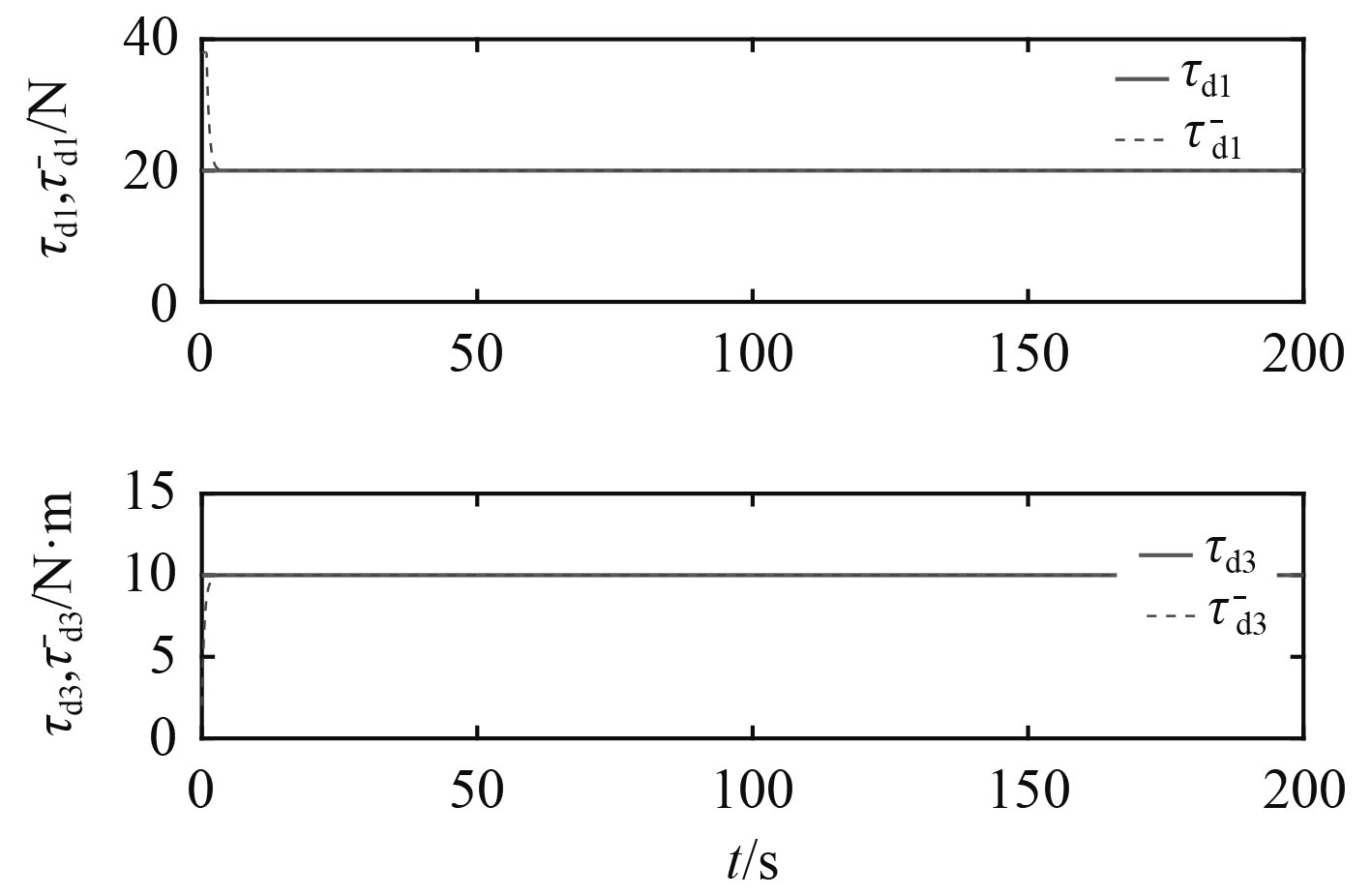
图 5 常值扰动实际值与观测值 Fig. 5 The actual and observed values of constant disturbance |
|
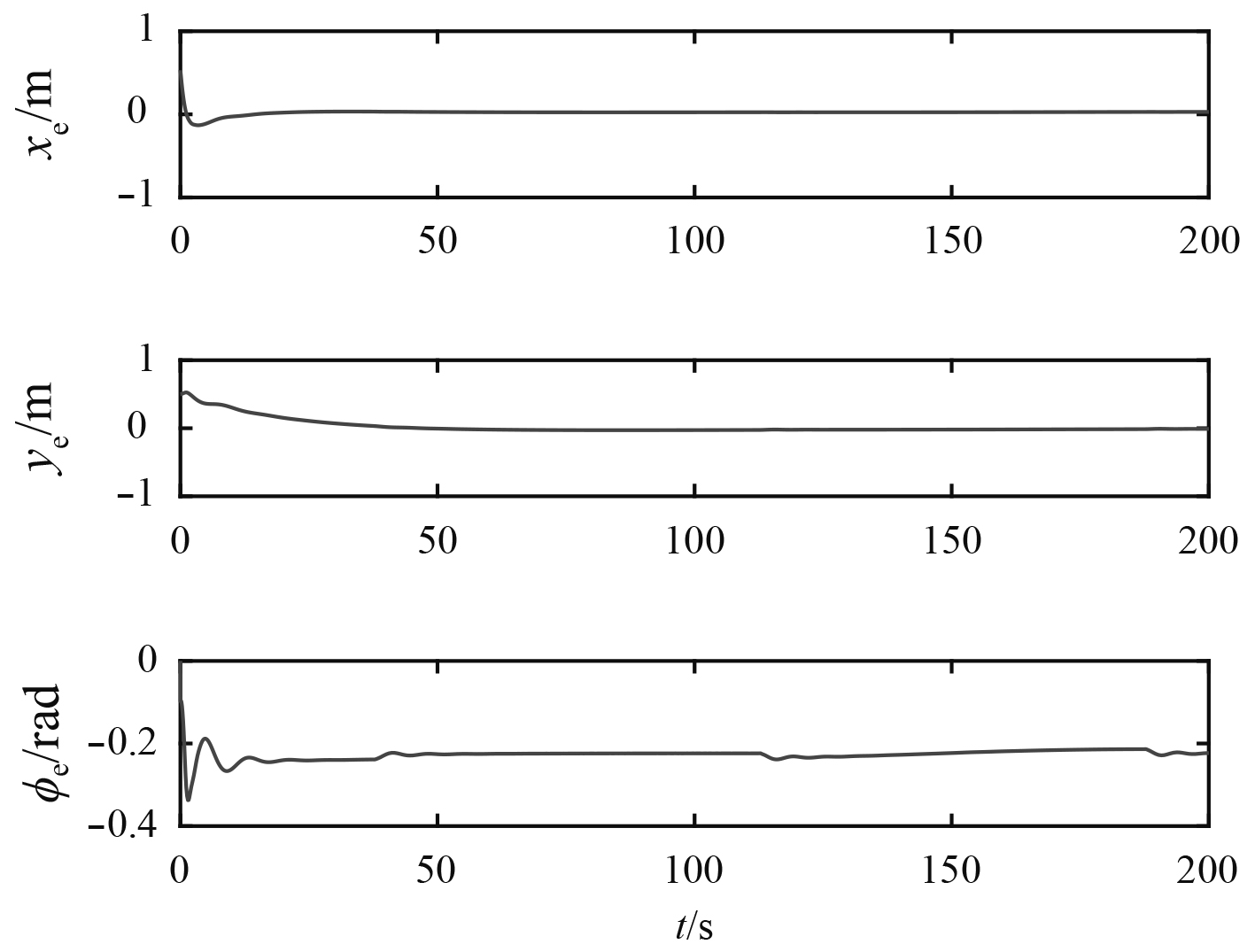
图 2 常值扰动下USV跟踪误差 Fig. 2 Tracking errors of the USV under constant disturbance |
|
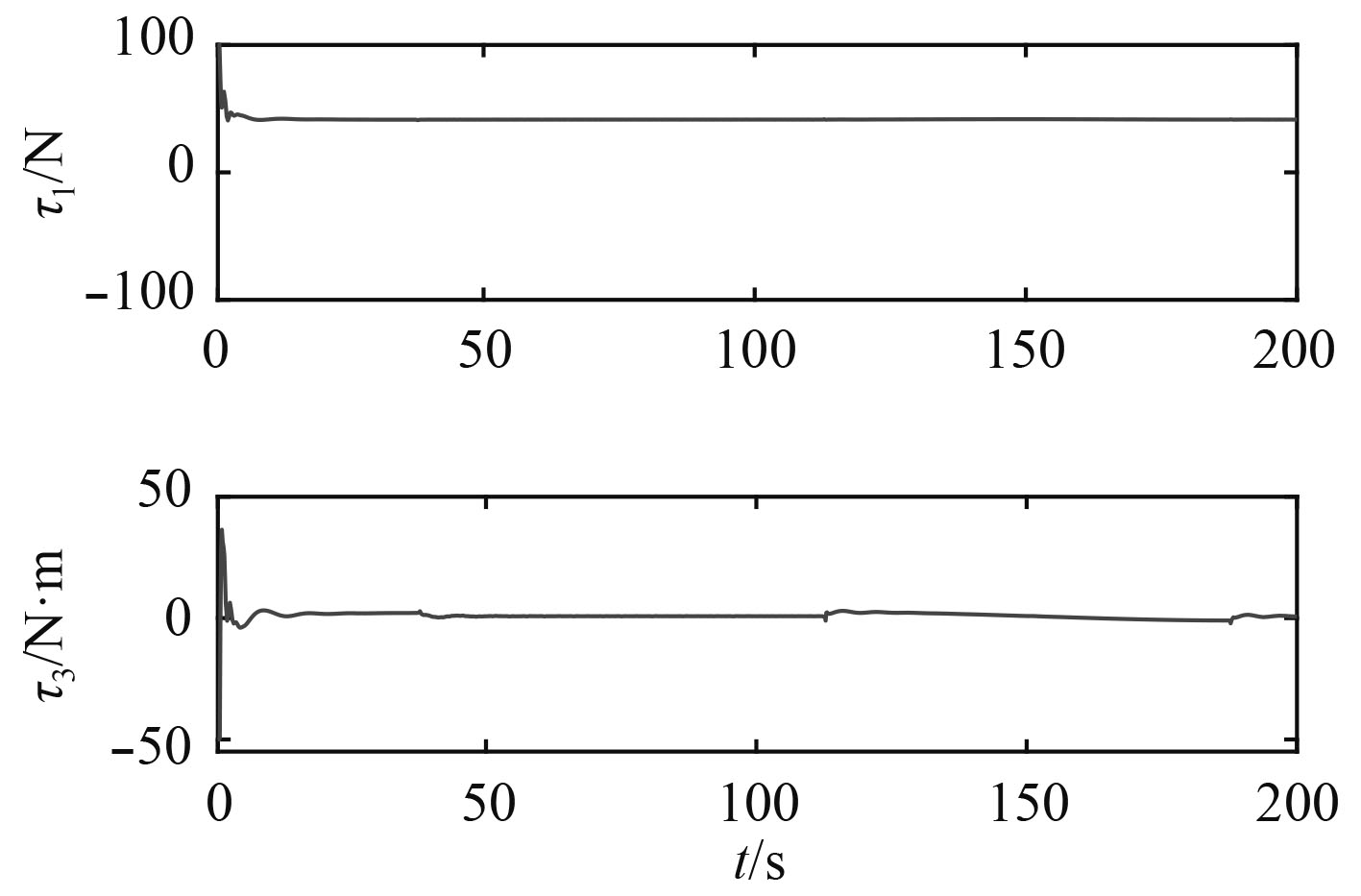
图 3 常值扰动下USV控制输入 Fig. 3 Control inputs of the USV under constant disturbance |
|
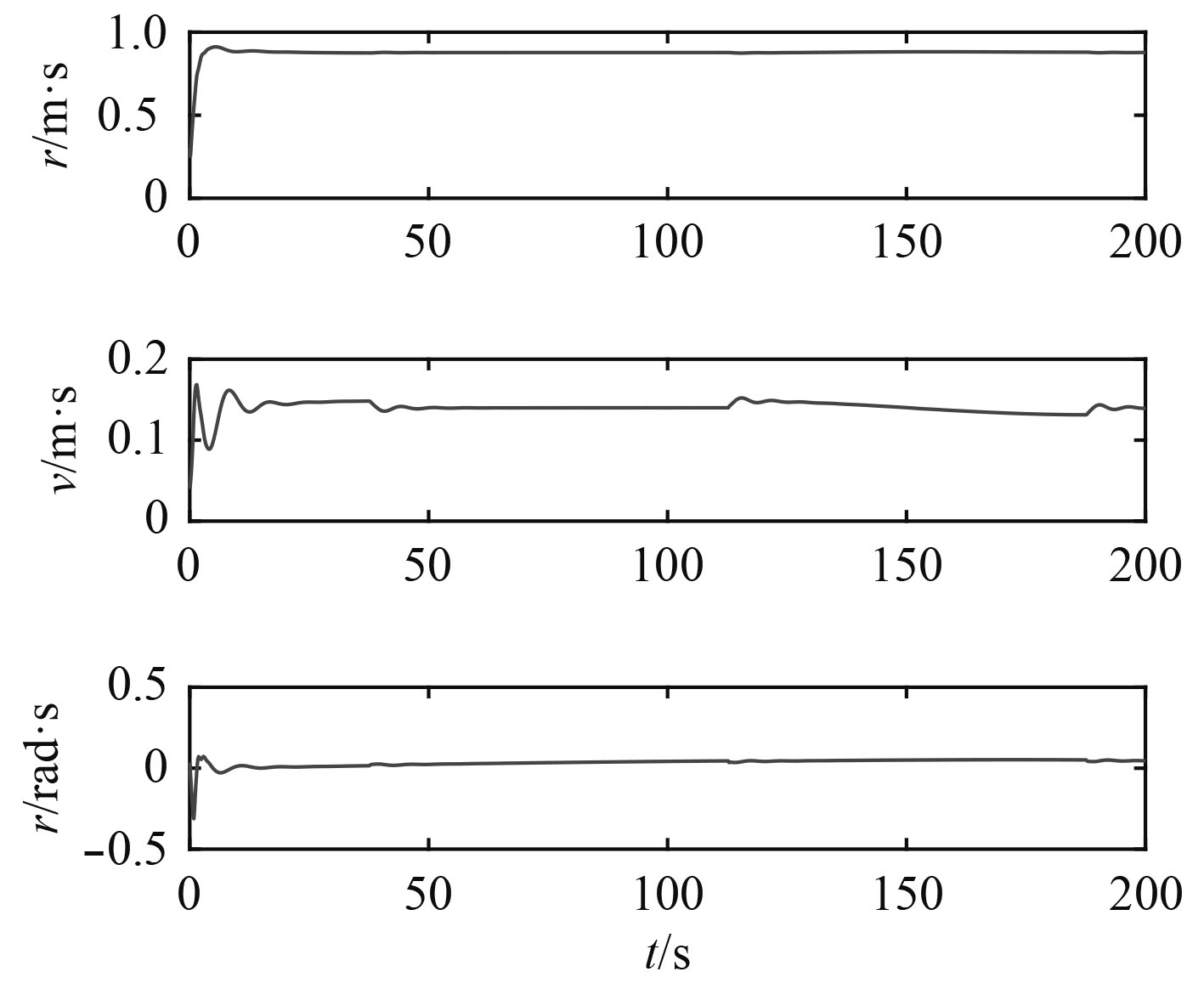
图 4 常值扰动下USV速度 Fig. 4 Velocities of the USV under constant disturbance |
高级海况下的扰动力或者力矩可以看成不同频率信号的叠加。取时变扰动向量
| $ \begin{split} {\tau _d} =& \left[ {8 + 5\sin (0.1t + {{\text{π}} / 2}) + 4\sin (0.2t + {{\text{π}} / 4})N} \right., \\ &{\rm{ 8}} + {\rm{3sin(0}}{\rm{.1t)}} + \sin (0.1t + {{\text{π}} / 6}){\rm{ N,}} \\ &{\left. {{\rm{8}} + {\rm{2sin(0}}{\rm{.1t}} + {{\text{π}} / {\rm{2}}}{\rm{)}} + {\rm{sin(0}}{\rm{.15t}} + {{\text{π}} / {\rm{4}}}{\rm{)}}N} \right]^{\rm T}} {\text{。}} \end{split} $ |
水面无人船在时变扰动下数据仿真结果如图6~图10所示。从图6和图7可看出水面无人船在时变扰动下同样能实现对期望轨迹
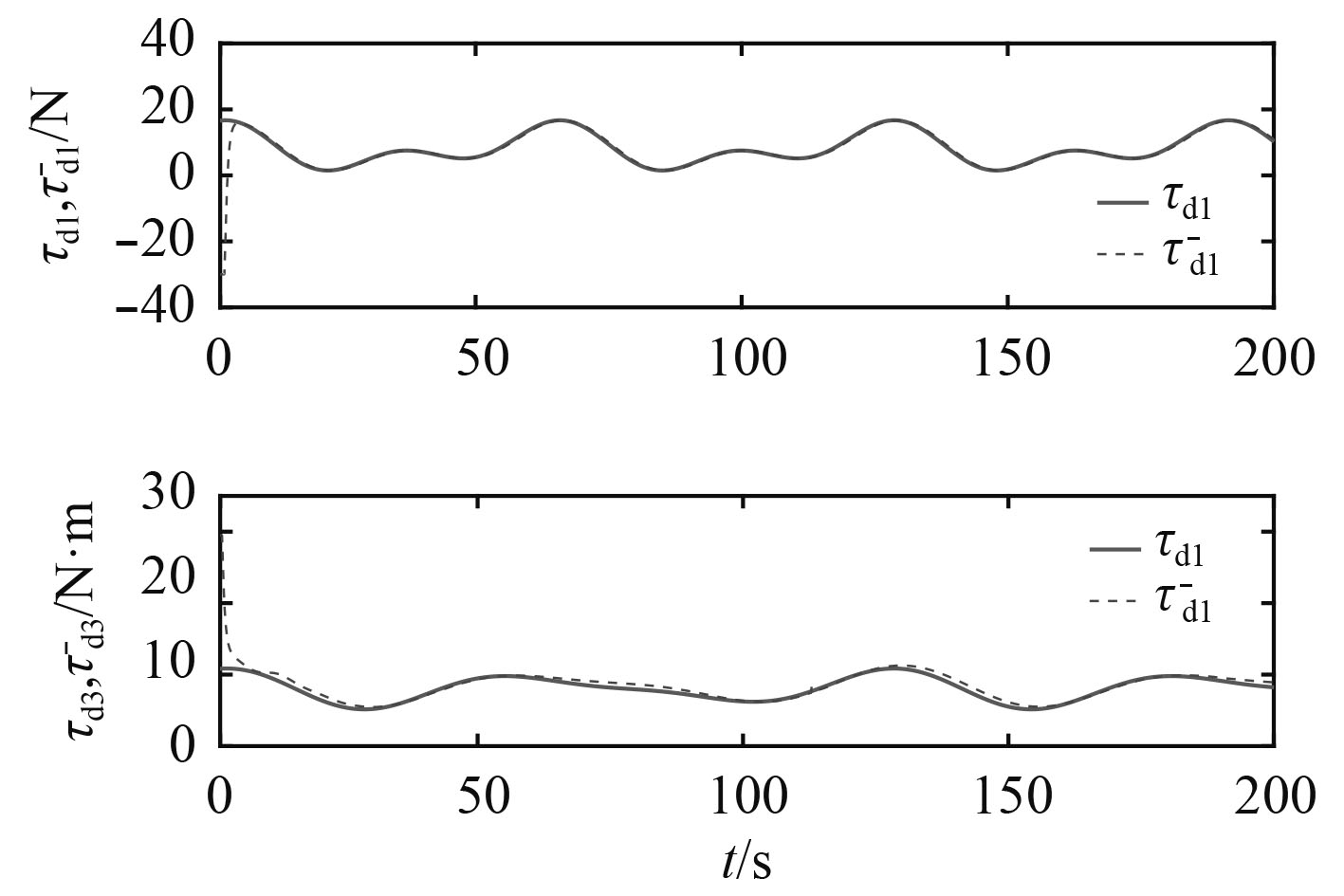
|
图 10 时变扰动实际值与观测值 Fig. 10 The actual and observed values of time-varying disturbance |
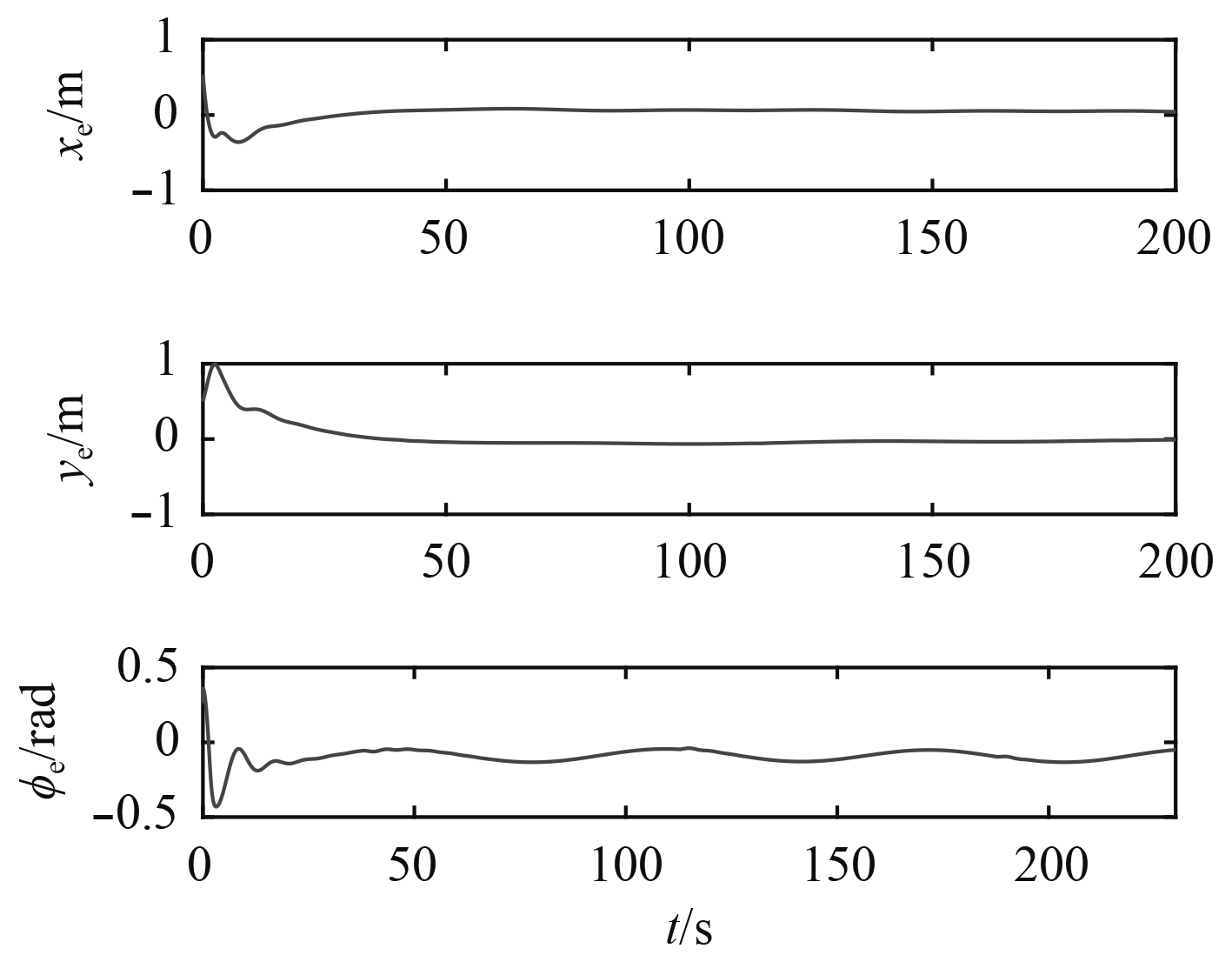
|
图 7 时变扰动下USV跟踪误差 Fig. 7 Tracking errors of the USV under time-varying disturbance |
|
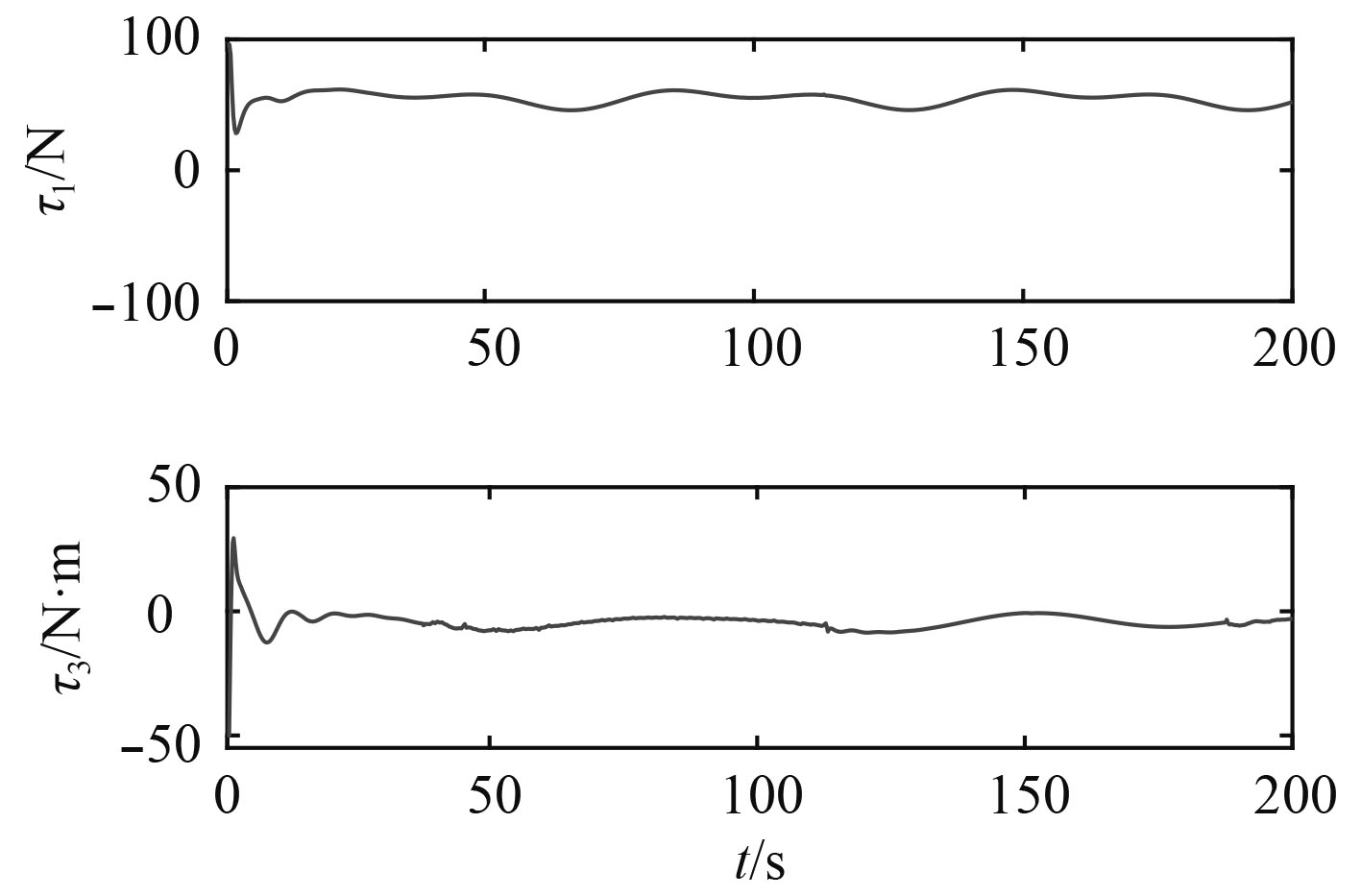
图 8 时变扰动下USV控制输入 Fig. 8 Control inputs of the USV under time-varying disturbance |
|
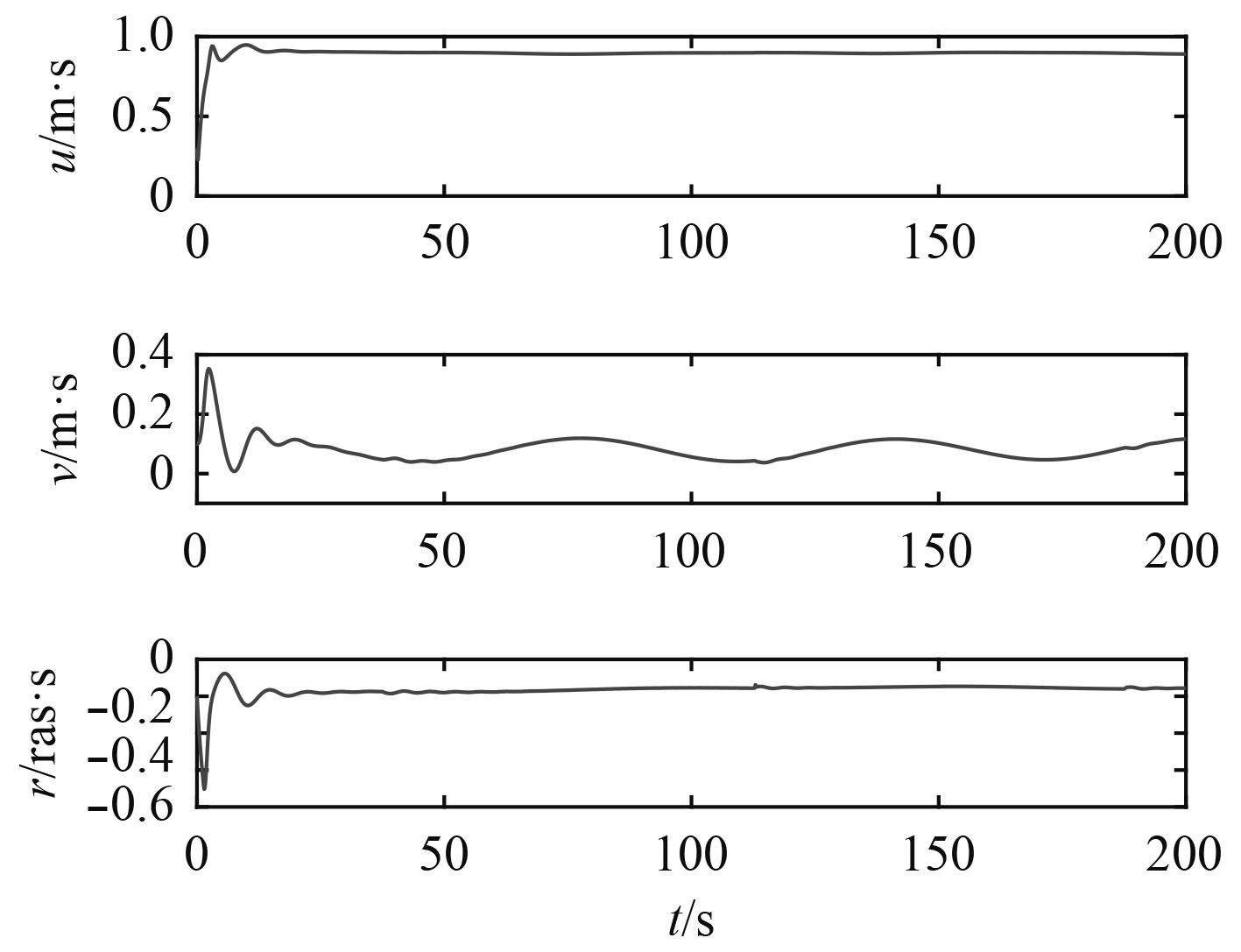
图 9 时变扰动下USV速度 Fig. 9 Velocities of the USV under time-varying disturbance |
本文考虑水面无人船欠驱动以及存在外界扰动的运动特性,构造扰动观测器估计未知扰动,对纵荡以及首摇2个自由度上的控制量进行了补偿,并通过引入位置误差积分项增强了系统抗干扰能力。在根据反步法进行控制器设计过程中结合神经动态模型,简化了控制器设计的同时有效避免了速度跳变的出现。由仿真结果可以看出,所设计控制器的各项控制输出合理,跟踪精度高,具有一定的工程应用价值。
| [1] |
FOSSEN T I. Marine control systems: guidance, navigation and control of ships, rigs and underwater vehicles[M]. 2002.
|
| [2] |
WANG N, SUN J C, ER M J. A novel extreme learning control framework of unmanned surface vehicles[J]. IEEE Transactions on Cybernetics, 2015, 46(5): 1106-1117. |
| [3] |
邱荷珍, 王磊, 王洪超. 船舶轨迹跟踪研究综述[J]. 实验室研究与探索, 2014, 33(4): 4-8. DOI:10.3969/j.issn.1006-7167.2014.04.002 |
| [4] |
PENG Y, YANG Y, CUI J, et al. Development of the USV ‘JingHai-I’ and sea trials in the Southern Yellow Sea[J]. Ocean Engineering, 2017, 131: 186-196. DOI:10.1016/j.oceaneng.2016.09.001 |
| [5] |
FOSSEN T I, BERGE S P. Nonlinear veclorial backstepping design for global exponential tracking of marine vessels in the presence of actuator dynamics[C]//Proceeding of the 36th IEEE Conference on Design and Control. IEEE, 2002.
|
| [6] |
SWAROOP D, HEDRICK J K, YIP P P, et al. Dynamic surface control for a class of nonlinear systems[J]. IEEE Transactions on Automatic Control, 2000, 45(10): 1893-1899. DOI:10.1109/TAC.2000.880994 |
| [7] |
YANG S X, MENG M. Real-time collision-free motion planning of a mobile robot using a neural dynamics-based approach[J]. IEEE Transactions on Neural Networks, 2003, 14(6): 1541-1552. DOI:10.1109/TNN.2003.820618 |
| [8] |
潘昌忠. 基于神经动态模型的自治水面艇智能跟踪控制[D]. 长沙: 中南大学, 2013.
|
| [9] |
朱齐丹, 马俊达, 刘可. 基于扰动观测器的无人水面船鲁棒轨迹跟踪[J]. 电机与控制学报, 2016, 20(12): 65-73. |
| [10] |
李冬琴, 蒋志勇, 赵欣. 多维随机不确定性下的船舶多学科稳健设计优化研究[J]. 船舶工程, 2015, 37(11): 61-66. |
| [11] |
YAN Z, WANG J. Model predictive control for tracking of underactuated vessels based on recurrent neural networks[J]. IEEE Journal of Oceanic Engineering, 2012, 37(4): 717-726. DOI:10.1109/JOE.2012.2201797 |
| [12] |
WANG N, ER M J, HAN M. Dynamic tanker steering control using generalized ellipsoidal-basis-function-based fuzzy neural networks[J]. IEEE Transactions on Fuzzy Systems, 2015, 23(5): 1414-1427. DOI:10.1109/TFUZZ.2014.2362144 |
| [13] |
FOSSEN T I. Handbook of Marine Craft Hydrodynamics and Motion Control[M]. New Jersey: John Wiley & Sons, 2011.
|
| [14] |
胡云艳. 欠驱动水面无人艇的航迹跟踪控制研究[D]. 哈尔滨: 哈尔滨工程大学, 2011.
|
 2019, Vol. 41
2019, Vol. 41
