自20世纪90年代,水面无人艇(Unmanned Surface Vehicles, USV)已被美国海军应用的战场上,它具有小型化、反应快、隐蔽性好、长航时等优点[1]。导航定位系统作为水面无人艇重要传感单元之一,决定着无人艇航行的精度,利用卫星定位技术可以实现海上精准察打一体的功能[2]。远洋地区有着丰富的自然资源和巨大航线价值,近年来世界各国对海洋权益的争夺日益激烈,随着我国北斗卫星导航系统(BDS Satellite Navigation System, BDS)的崛起,评估无人艇在远洋地区的定位性能有着重要意义。
BDS是我国正在实施的自主研发、独立运行的全球卫星导航系统,于2018年12月27日开始开放面向全球提供服务。当前BDS-3已经进入密集发射期,预计于2020年将实现35颗卫星完整星座提供全球定位能力,包括5颗地球同步卫星(Geostationary earth orbit, GEO),3颗地球倾斜轨道同步卫星(Inclined Geostationary Earth Orbit, IGSO),27颗地球中轨道卫星(Medium Earth Orbit, MEO)覆盖全球[3-5]。到目前为止,BDS星座主要包括33颗卫星组成,其中5颗GEO卫星轨道高度为35 786 km,位于赤道上方与地球同步运行;7颗IGSO,卫星运动轨迹以赤道为对称轴,绕“8”字运行;21颗MEO卫星,卫星轨道为21 500 km,为7天13圈回归周期[6]。
自2012年以来,BDS系统已具备基本的导航定位功能,实现了对我国区域性和沿线“一带一路”国家增强覆盖,BDS实际观测数据得到广泛应用,卫星信号的强度、可见性、位置精度衰减因子(Position Dilution of Precision, PDOP)值以及定位精度等多个方面已经有了大量的分析和研究工作[7-10]。BDS系统目前仍处于战略建设的最后阶段,尚未实现全球定位,特别是远洋航海区域其系统性能仍需进一步的研究和论证。基于此,本文利用BDS满星座仿真数据和GPS真实广播星历数据联合计算,从可见星数量、PDOP值以及定位精度等方面对BDS卫星导航系统及其组合的定位性能进行详细比较分析。
1 数学模型与方法当对星钟误差、电离层和对流层延迟误差进行补偿后,单个卫星修正伪距观测方程可简化为[8]:
| ${\rho ^m} = {r^m} + {b_G} + \varepsilon _\rho ^m{\text{,}}$ | (1) |
| ${\rho ^n} = {r^n} + {b_B} + \varepsilon _\rho ^n{\text{。}}$ | (2) |
式中:ρ为测量伪距;下标G和B分别表示GPS和BDS;上标m,n分别表示GPS和BDS卫星序号;
将式(1)、式(2)在接收机近似坐标
| $\begin{split} \left[ {\begin{array}{*{20}{c}} {{l^1}}\\ \vdots \\ {{l^m}}\\ {{l^{m + 1}}}\\ \vdots \\ {{l^{m + n}}} \end{array}} \right] =& \left[ {\begin{array}{*{20}{c}} {\dfrac{{{x_0} - {x^1}}}{{{{\bar r}^1}}}}&{\dfrac{{{y_0} - {y^1}}}{{{{\bar r}^1}}}}&{\dfrac{{{z_0} - {z^1}}}{{{{\bar r}^1}}}}&1&0\\ \vdots & \vdots & \vdots & \vdots & \vdots \\ {\dfrac{{{x_0} - {x^m}}}{{{{\bar r}^m}}}}&{\dfrac{{{y_0} - {y^m}}}{{{{\bar r}^m}}}}&{\dfrac{{{z_0} - {z^m}}}{{{{\bar r}^m}}}}&1&0\\ {\dfrac{{{x_0} - {x^{m + 1}}}}{{{{\bar r}^{m + 1}}}}}&{\dfrac{{{y_0} - {y^{m + 1}}}}{{{{\bar r}^{m + 1}}}}}&{\dfrac{{{z_0} - {z^{m + 1}}}}{{{{\bar r}^{m + 1}}}}}&0&1\\ \vdots & \vdots & \vdots & \vdots & \vdots \\ {\dfrac{{{x_0} - {x^{m + n}}}}{{{{\bar r}^{m + n}}}}}&{\dfrac{{{y_0} - {y^{m + n}}}}{{{{\bar r}^{m + n}}}}}&{\dfrac{{{z_0} - {z^{m + n}}}}{{{{\bar r}^{m + n}}}}}&0&1 \end{array}} \right]\times \\ &\left[ {\begin{array}{*{20}{c}} {\Delta x}\\ {\Delta y}\\ {\Delta z}\\ {\Delta {b_G}}\\ {\Delta {b_B}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {\varepsilon _\rho ^1}\\ \vdots \\ {\varepsilon _\rho ^m}\\ {\varepsilon _\rho ^{m + 1}}\\ \vdots \\ {\varepsilon _\rho ^{m + n}} \end{array}} \right]{\text{。}}\\[-55pt]\end{split} $ | (3) |
式中:
式(3)写成矩阵形式:
| $ {{L}} = {{AX}} + {{V}}{\text{。}} $ | (4) |
式中:A为观测方程的系数矩阵;X为待估计参数矩阵;L为常数项矩阵;V为残差矩阵。观测权重为高度角模型定权P,应用最小二乘法求解式,计算出未知向量为[8]:
| $ {{X}} = {\left( {{{{A}}^{\rm{T}}}{{PA}}} \right)^{ - 1}}{{{A}}^{\rm{T}}}{{PL}} = {{{A}}^{\rm{T}}}{{PL}}{\text{。}} $ | (5) |
权系数矩阵:
| $ {{H}} = {\left( {{{{A}}^{\rm{T}}}{{PA}}} \right)^{ - 1}} = \left[ {\begin{array}{*{20}{c}} {{q_{11}}}&{{q_{12}}}&{{q_{13}}}&{{q_{14}}}\\ {{q_{21}}}&{{q_{22}}}&{{q_{23}}}&{{q_{24}}}\\ {{q_{31}}}&{{q_{32}}}&{{q_{33}}}&{{q_{34}}}\\ {{q_{41}}}&{{q_{42}}}&{{q_{43}}}&{{q_{44}}} \end{array}} \right]{\text{。}}$ | (6) |
PDOP值是评价定位精度的重要参数,其值与接收机及各观测卫星间的几何结构有关,定义为[8]:
| $ PDOP = \sqrt {{q_{11}} + {q_{22}} + {q_{33}}} {\text{。}} $ | (7) |
为了评估基于GPS系统、BDS系统及其组合系统的无人艇在远洋地区的定位性能,利用4个测站进行数据仿真,分别设置为南海海域(测站1)、印度洋海域(测站2)、太平洋海域(测站3)和南极罗斯海海域(测站4),测站的坐标参数和位置分布分别如表1和图1所示。仿真过程中,采样数据长度为24 h,采样间隔为30 s,截止高度角为10°。GPS星座使用2019年3月2日0:00时-2019年3月3日0:00时的真实广播星历计算卫星位置,表2所列开普勒轨道根数用于计算BDS卫星位置,共有31颗GPS卫星和35颗BDS卫星。
|
|
表 1 测站位置坐标 Tab.1 Observation station coordinates |

|
图 1 测站位置分布图 Fig. 1 Observation station distribution |
|
|
表 2 BDS系统星座参数 Tab.2 Constellation parameters of BDS system |
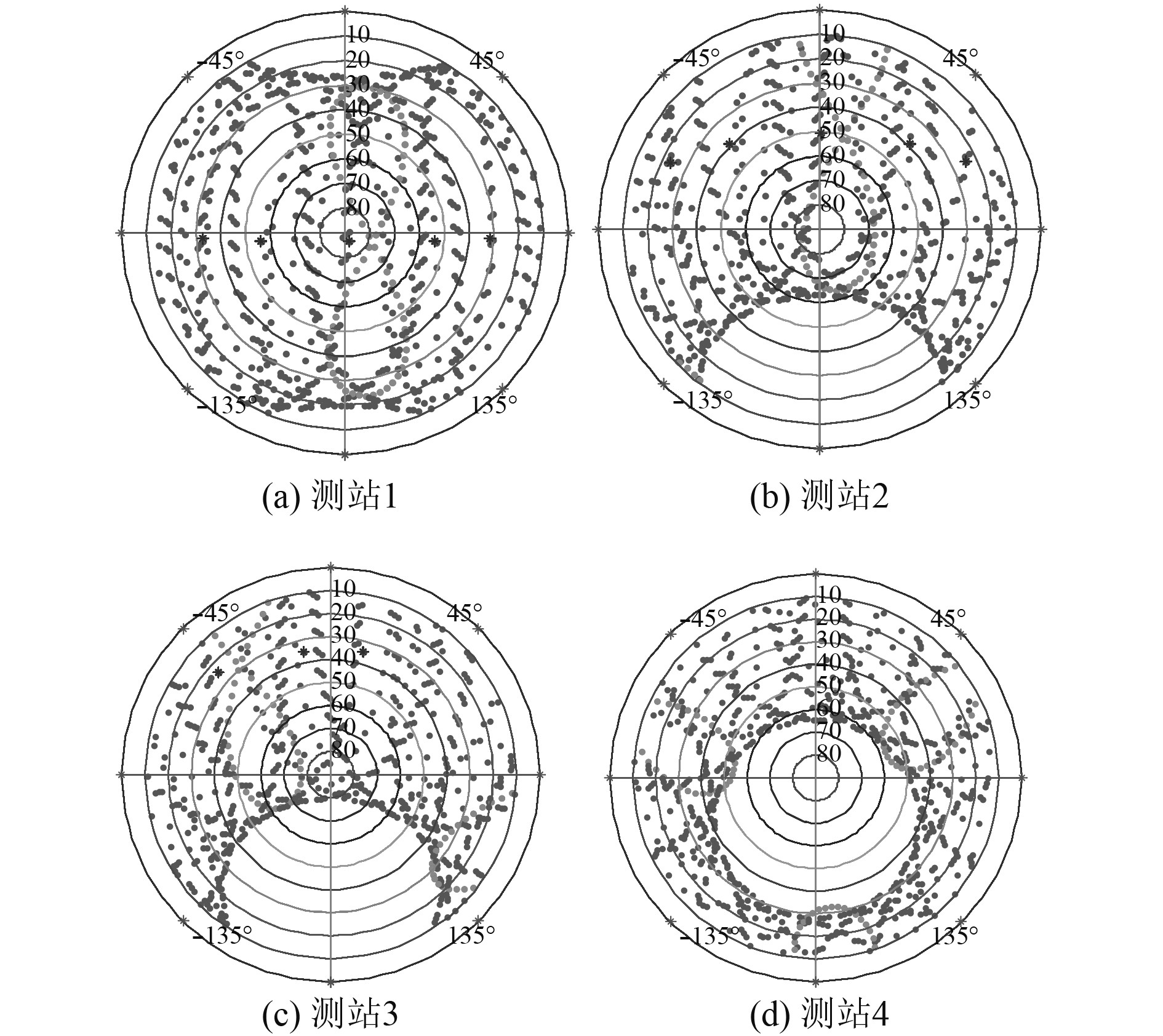
图2为4个测站上空的BDS卫星可视图,可以反映当天BDS卫星在测站上空的分布和变化情况。可见,由于BDS的GEO卫星为高轨卫星,覆盖范围为58.75°E~160°E,5颗GEO卫星在测站1和测站2长期可见,在测站3有3颗GEO卫星可见,测站2和测站3长期在[–135°,135°]方位不可见,卫星空间几何结构不强,而在测站4附近GEO卫星和高仰角卫星不可见。
|
图 2 BDS天空可视图(方位角&高度角) Fig. 2 Sky plots (azimuth vs elevation) for BDS |
可见星的数量是定位性能的重要指标,接收4颗卫星时才能进行定位解算,多余5颗卫星才有可能保证卫星定位结果的可靠性,因此有效的可视卫星数目是定位有效性的一个标志。PDOP值直接反映了卫星的空间分布情况,其取值越小,卫星的空间几何结构越强,定位精度也越高。表3为4个测站在一天内的可见星和PDOP平均值,BDS系统可见卫星数和PDOP取值整体优于GPS系统,特别在5颗GEO卫星覆盖的区域,平均值超过GPS系统可见星4颗左右,在测站4由于GEO卫星不可见,2个系统的可见星数量和PDOP取值相当。
|
|
表 3 可见卫星数和PDOP平均值 Tab.3 Mean values of visible satellites and PDOP |
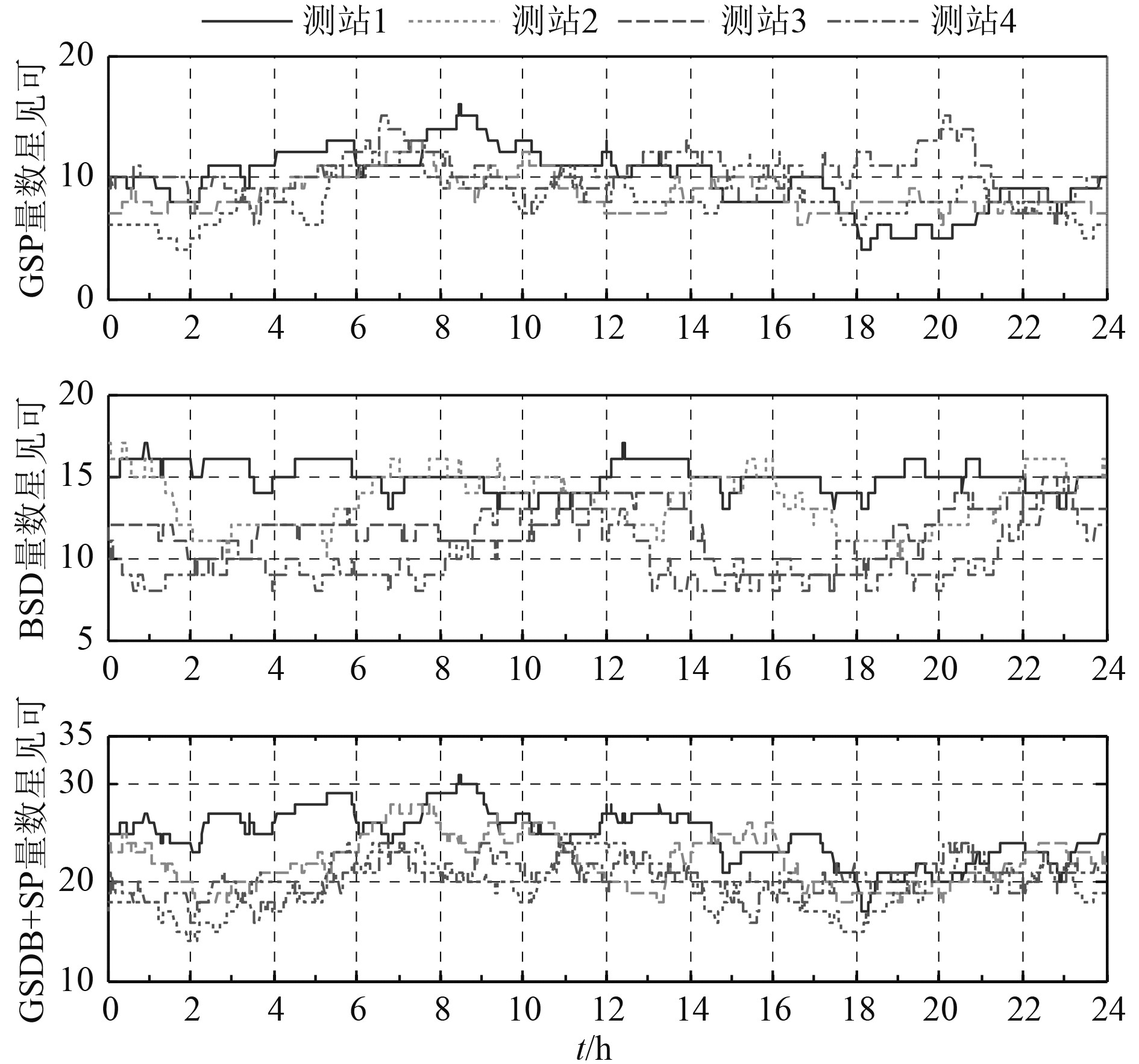
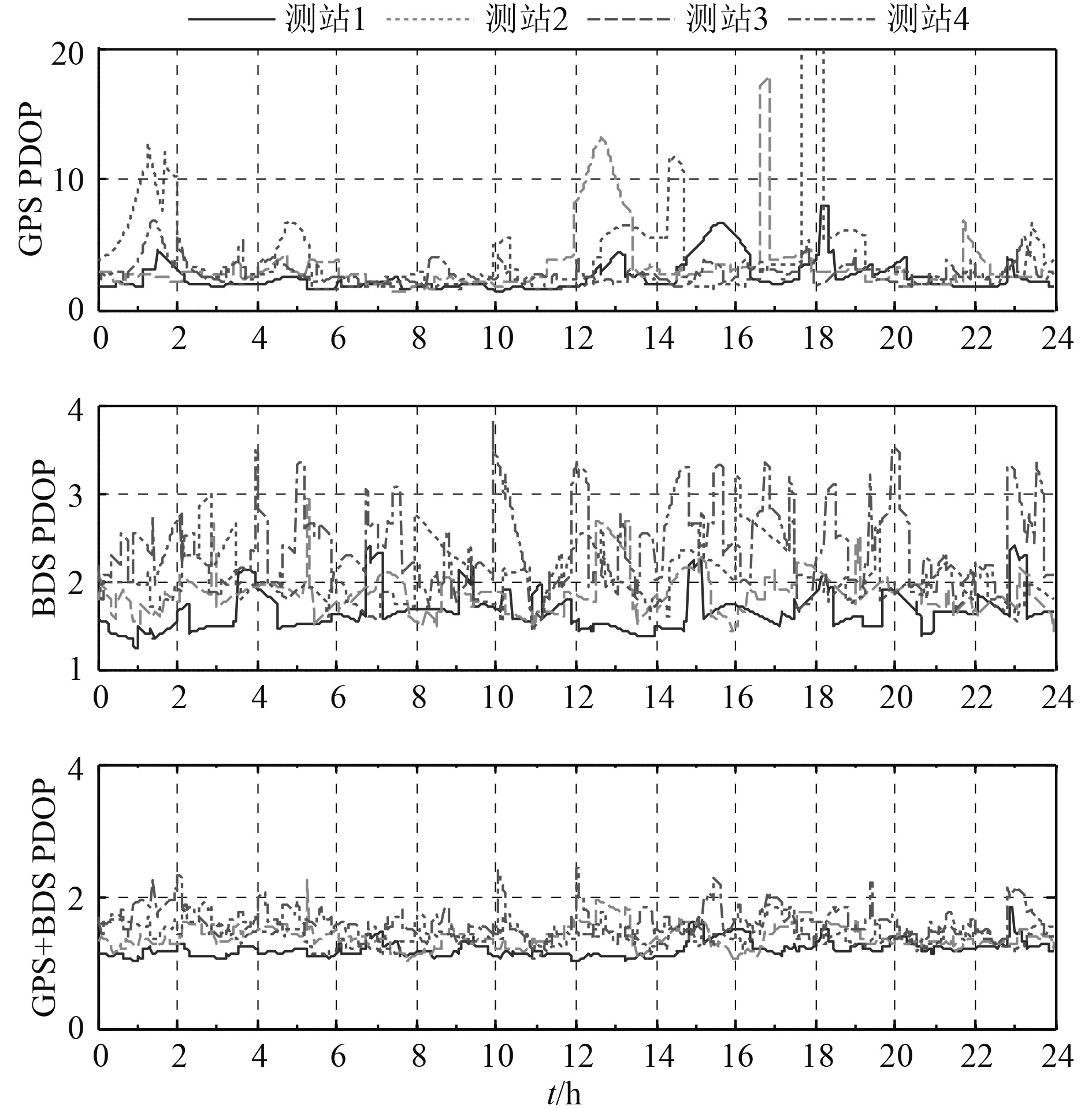
图3和图4分别描述了在4个测站GPS、BDS以及GPS+BDS组合系统可视卫星数和PDOP值变化情况。测站1中BDS可见星最多,最多可达17颗卫星,最少可见13颗卫星,PDOP值基本都在2.5以内;测站4中BDS可见星最少,保持在7~13颗之间,PDOP值在2~4之间。GPS系统在全球范围内相对均匀分布,可见星在10颗左右。部分时间段PDOP取值超过10,造成定位误差较大,这主要是由于卫星的几何结构不强造成的。GPS+BDS组合导航系统,可用卫星数大大增加,在4个测站中,最少有14颗,冗余卫星在9颗以上,可利用多余观测值提高系统的可靠性。而组合系统的PDOP值相对于GPS和BDS单系统显著降低,基本保持在2以内,能够保障导航的定位精度。
|
图 3 GPS,BDS和GPS+BDS可见星数量 Fig. 3 Number of visible satellites for GPS, BDS and GPS+BDS systems, respectively |
|
图 4 GPS,BDS和GPS+BDS系统PDOP值 Fig. 4 PDOP values for GPS, BDS and GPS+BDS systems, respectively |
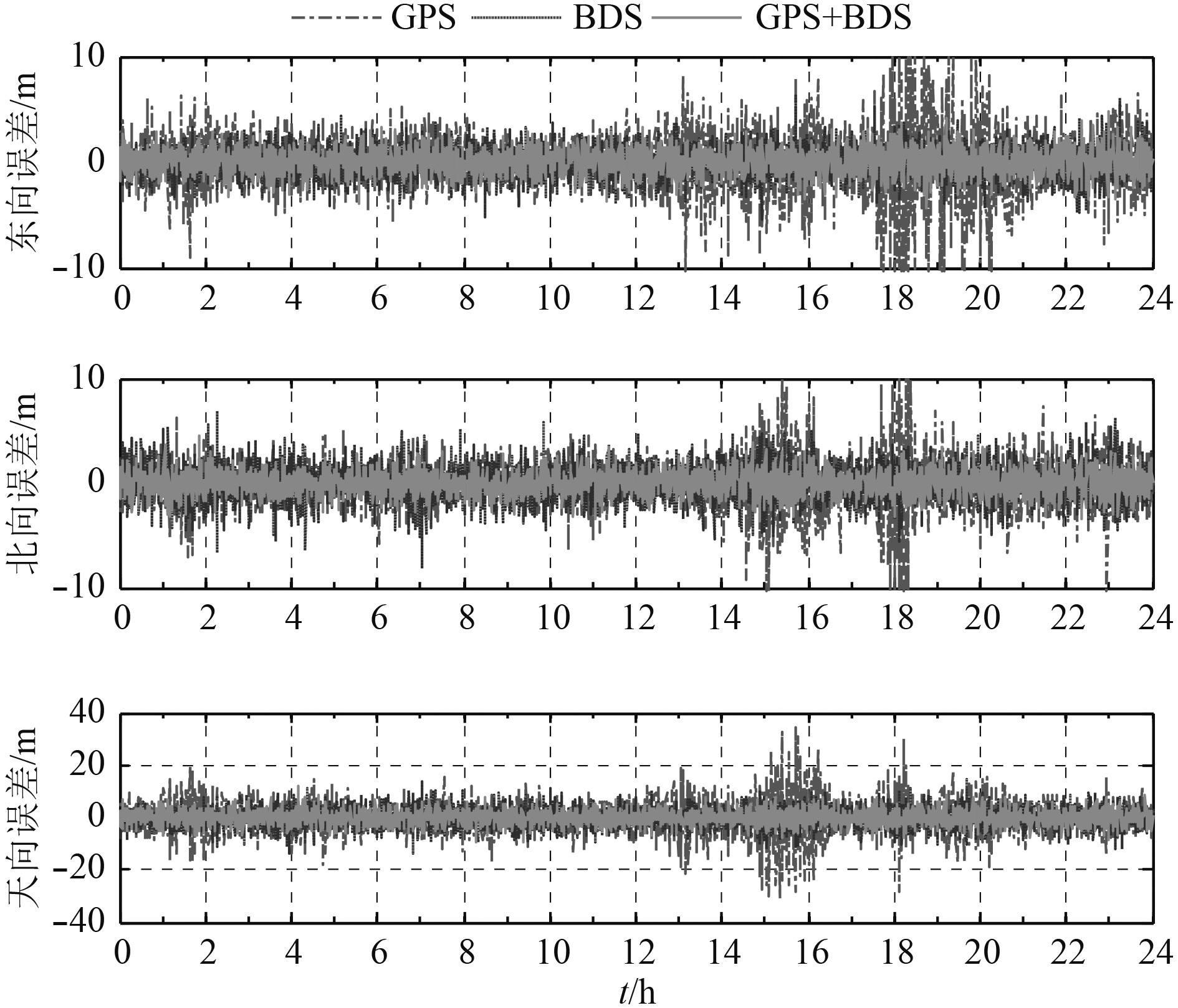
比较4个测站中,测站1一天内平均可见星最多,测站4一天内平均可见星最少,以测站1和测站4为例分析GPS、BDS以及GPS+BDS三种系统定位性能。图5和图6分别为3个导航系统在2个测站上东(E)、北(N)和天(U)三个方向上定位误差,定位统计结果的数据如表4所示。
|
图 5 测站1东北天3个方向上定位误差 Fig. 5 The position errors of E, N and U directions of station 1 |
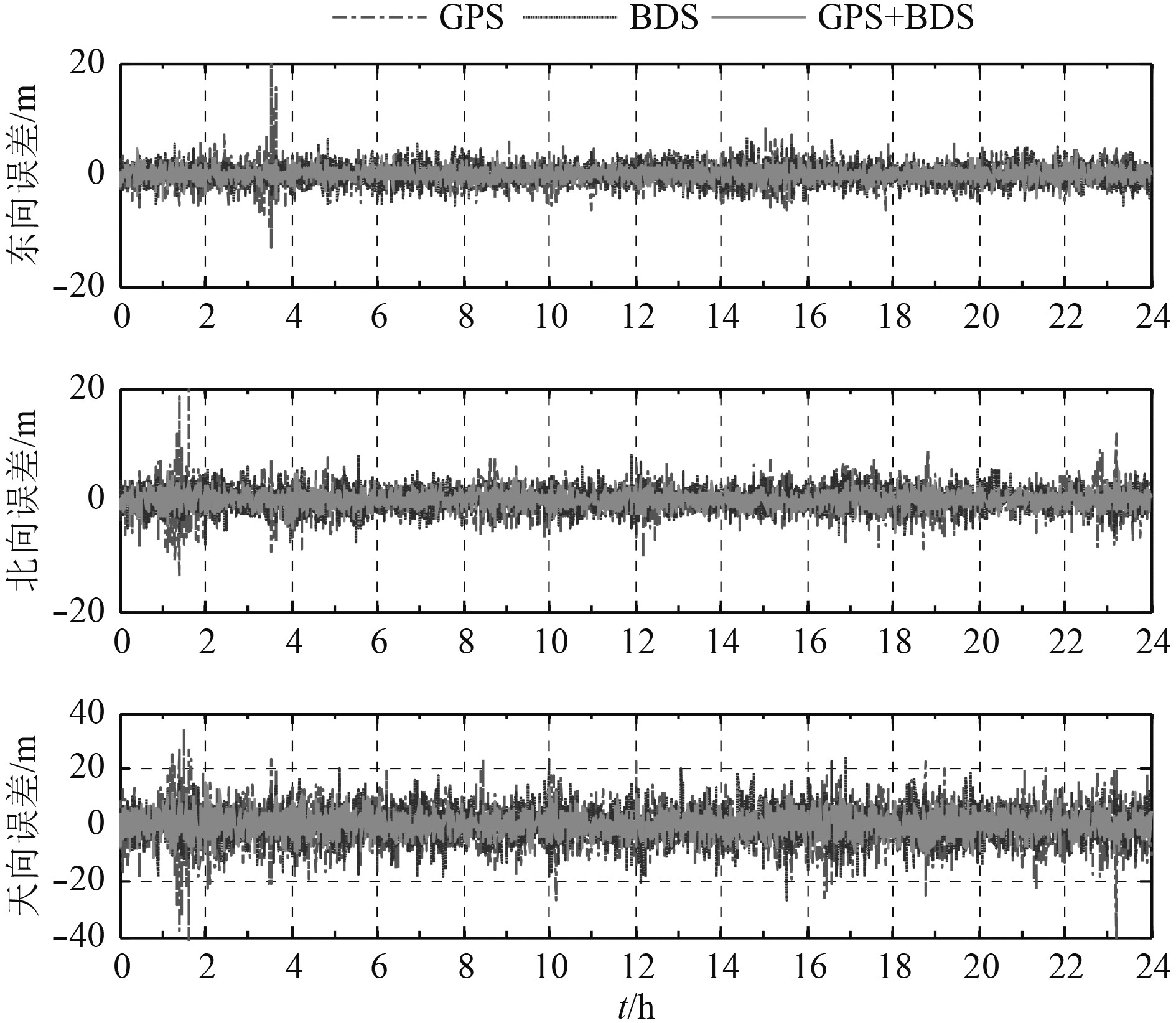
|
图 6 测站4东北天3个方向上定位误差 Fig. 6 The position errors of E, N and U directions of station 4 |
|
|
表 4 GPS,BDS以及GPS+BDS定位误差统计 Tab.4 RMS Statistics of positioning errors for GPS, BDS and GPS+BDS systems |
在测站1,单独利用GPS定位在ENU方向分别为3.00 m,2.37 m,6.28 m,BDS单系统在ENU方向分别为1.42 m,1.74 m,3.69 m,组合系统在ENU方向分别为1.17 m,1.13 m,2.76 m。可见BDS系统的定位精度显著优于GPS单系统,这是由于在测站1上5颗GEO卫星长期可见,整个观测过程中BDS系统可见星明显多于GPS可见星,GPS+BDS组合系统能够进一步提高定位精度。
测站1在18:00-20:00时间段GPS在东向和北向误差明显增大,超过10 m的误差,这是由于对应时间段可观测的卫星数量在5~7颗之间,部分时间段高程超过20 m的误差。在测站4位置上,单独利用GPS定位在ENU方向分别为2.03 m,2.55 m,7.23 m,BDS单系统在ENU方向分别为1.76 m,2.03 m,5.90 m,GPS+BDS组合系统在ENU方向分别为1.16 m,1.37 m,3.94 m。在该测站位置上,BDS系统定位精度略优于GPS系统,整个观测时间2个系统的可见星数量相当,且BDS的GEO卫星长期不可见;GPS+BDS组合系统在4个测站中,可见卫星平均值都在20颗左右,大大超过单卫星导航系统的可见星数量,并且空间几何结构强,其定位结果水平精度在2 m以内,高程精度在4 m以内。
3 结 语本文介绍GPS与BDS组合定位原理与模型,模拟BDS系统的全星座数据,分析远洋海域的4个测站位置下的可见卫星数、PDOP值以及定位精度等方面性能。具体结论如下:
1)BDS在远洋地区的整体定性能优于GPS系统,水平定位精度在2 m左右,高程在5 m左右,可见星在10颗以上。
2)BDS的GEO卫星在南海海域长期可见,可见星数量保持在13~17颗,卫星几何结构强,定位性能显著优于GPS系统。
3)在南极罗斯海海域,BDS的GEO卫星和高仰角卫星不可见,GPS系统和BDS系统可见星均在10颗左右,BDS定位性能略优于GPS系统。
4)GPS+BDS组合系统在4个测站1天内可见星在20颗左右,大大增加了系统的可靠性,改善卫星空间分布,显著降低PDOP值,提高定位精度。
| [1] |
戴海发, 卞鸿巍, 马恒, 等. 基于因子图的鲁棒性增量平滑算法的水面无人艇组合导航方法[J]. 中国惯性技术学报, 2018, 26(6): 84-92. |
| [2] |
戴海发, 卞鸿巍, 王荣颖, 等. 多航向传感器信息融合与容错联邦卡尔曼滤波器在舰艇综合导航系统中的应用[J]. 舰船科学技术, 2019, 41(4): 114-118. DOI:10.3404/j.issn.1672-7649.2019.04.022 |
| [3] |
许明. 四大导航系统在舰船作战系统中的应用[J]. 舰船科学技术, 2019, 41(1A): 137-139. |
| [4] |
PAN L, CAI C, SANTERRE R, et al. Performance evaluation of single-frequency precise point positioning with GPS, GLONASS, BDS and Galileo[J]. Survey Review, 2016, 70(3): 465-482. |
| [5] |
任晓东, 张柯柯, 李星星, 等. BDS, Galileo, GLONASS, GPS多系统融合精密单点[J]. 测绘学报, 2015, 44(12): 1307-1313. |
| [6] |
ANGRISANO A, MARATEA A, GAGLIONE S. A resampling strategy based on bootstrap to reduce the effect of large blunders in GPS absolute positioning[J]. Journal of Geodesy, 2018, 92(1): 81-92. DOI:10.1007/s00190-017-1046-6 |
| [7] |
王泽民, 杜玉军, 熊云琪, 等. 北斗系统在南极中山站地区的基本定位性能评估[J]. 武汉大学学报(信息科学版), 2017, 42(8): 1027-1034. |
| [8] |
唐卫明, 徐坤, 金蕾, 等. 北斗/GPS组合伪距单点定位性能测试和分析[J]. 武汉大学学报(信息科学版), 2015, 40(4): 529-533. |
| [9] |
PAN L, ZHANG X, FEI G. Ambiguity resolved precise point positioning with GPS and BDS[J]. Journal of Geodesy, 2017, 91(1): 25-40. DOI:10.1007/s00190-016-0935-4 |
| [10] |
MANZINO A M, DABOVE P, GOGOI N. Assessment of positioning performances in Italy from GPS, BDS and GLONASS constellations[J]. Geodesy and Geodynamics, 2018, 9(6): 19-28. |
 2019, Vol. 41
2019, Vol. 41
