0 引　言

水下机器人ROV（Remote Operated Vehicle）是深海施工作业的关键装备。在研制ROV设计过程中，需要基于任务可靠度进行各设备单元可靠度分配和评估计算，用以指导设备设计选型。常用的可靠性分配的方法主要包括等分配法、评分分配法、比例组合法、考虑复杂度和重要度的分配法等^{[1 – 4]}。其中等分配法比较简单直接，适用于产品各单元相同或者产品没有承继性且产品定义并不十分清晰的场合^[5]；评分分配法适用于可靠性数据非常缺乏的情况或者新研设备，只针对串联系统^{[6 – 7]}；比例组合法适用于继承性强、有历史故障数据的产品^[8]；基于复杂度和重要度的分配法，考虑的影响因素不够全面^[9]。ROV推进系统可靠性模型含有复杂的串并联系统和表决系统，且新研设备缺乏历史故障数据，因此不能直接利用上述常用的方法进行可靠性分配工作，亟需一种新的解决方法。拟提出一种综合运用评分分配法和比例组合法的可靠性分配计算方法，解决可靠性模型中缺乏历史故障数据，并且含有复杂串并联系统及表决系统导致无法直接分配计算的问题。以ROV推进系统为分析对象，根据作业任务需求建立推进系统的可靠性框图及数学模型，基于所提出的可靠性分配方法，对含有复杂串并联系统及表决系统的作业型ROV推进系统进行可靠性分配计算，最终获得各设备的可靠度分配值，实现所提方法的应用。

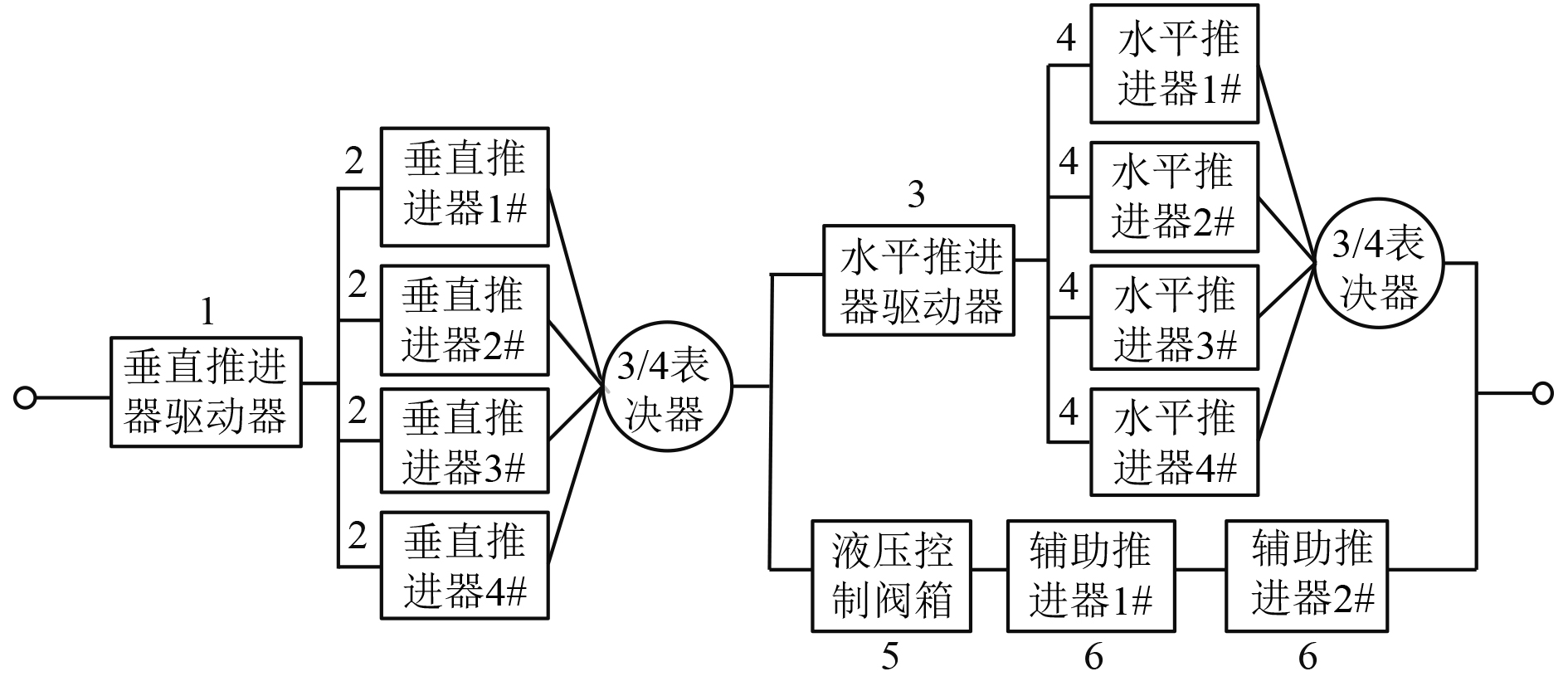
1 问题的提出

ROV推进系统可划分为垂直推进系统和水平推进系统，其中垂直推进系统由1个垂直推进器驱动罐驱动4个推进器进行上浮或者下潜运动，水平推进系统由1个水平推进器驱动罐驱动4个推进器完成前进或者后退运动并且配备2个辅助推进器作为冗余备份，2个辅助推进器由液压控制阀箱驱动。根据特定作业任务需求，ROV在水平方向和垂直方向同时调整姿态，其中4个水平推进器中至少有3个工作即可完成水平方向航行或者依靠2个辅助推进器完成水平方向航行，4个垂直推进器至少有3个工作即可完成垂直方向航行。据此工作原理，建立的可靠性模型如图1所示。

在进行可靠性分配时，推进系统突出的两大特点是：1）考虑深海使用环境因素，推进系统设备缺乏历史故障数据及相似产品的故障数据；2）该可靠性模型是一个复杂庞大的系统，不仅含有串并联结构，而且还含有表决系统结构。基于以上特点，单纯利用等分配法、评分分配方法、比例组合方法等常用的可靠性分配方法，并不能解决推进系统的可靠性模型计算问题，因此需要寻求一种新的解决方案。

2 可靠性分配计算方法

提出一种综合运用评分分配法和比例组合法的可靠性分配计算方法，其基本思路为：首先基于评分分配法获得评分系数作为设备单元的故障率基础数据，然后再根据比例组合法的基本原理设定各设备单元的比例系数，以修正后的故障率代入可靠性数学模型方程中求解计算出未知的比例系数，最后根据相对比值给每个设备分配可靠性指标。

2.1 故障基础数据建立

评分分配法一般广泛适用于缺乏具体可靠性数据的分配中，拟利用评分分配法获得的评分系数作为故障基础数据。评分分配法的基本思想是通过有经验的设计人员或专家对影响可靠性的几种因素进行评分，并对评分值进行综合分析，以获得各单元产品之间的可靠性相对比值，进而给每个分系统或设备分配可靠性指标^{[10 – 11]}。评分分配法的步骤详细如下^[6]：

1）评分因素

通常考虑的因素有产品的复杂程度、技术水平、工作时间和环境条件四大因素。

2）评分原则

各因素评分值范围为1～10分，评分数越高说明某分系统对该产品系统的可靠性影响越大。一般来说系统越复杂，可靠性程度越低，即系统最复杂的评10分，最简单的评1分；技术水平的成熟度最高评1分，最低评10分；分系统一直工作的评10分，工作时间最短评1分；环境条件越恶劣和严酷评10分，环境条件最好的评1分。

3）评分法的具体计算实施

设产品的故障率为 ${\lambda _S}$ ，分配给每个单元或者分系统的故障率为 ${\lambda _i}$ 就可表示为：

${\lambda _i} = {C_i} * {\lambda _S}\text{，}$

(1)

式中， ${c_i}$ 表示第i个单元或者分系统的评分系数。

${c_i} = {\omega _i}/\omega \text{，}$

(2)

式中： ${\omega _i}$ 表示第i个单元或者分系统的评分数； $\omega $ 表示产品的各单元或者分系统评分数之和。

${\omega _i} = \prod\limits_{j = 1}^4 {{r_{ij}}} \text{，}$

(3)

式中： ${r_{ij}}$ 为第i个单元，第j个因素的评分数。

$\omega = \sum\limits_i^4 {{\omega _i}} \text{，}$

(4)

根据可靠度与故障率之间的关系可得：

${R_i} = R_M^{{c_i}}\text{。}$

(5)

式中： ${R_i}$ 为每个单元的可靠度； ${R_M}$ 为产品的任务可靠度。按照式（5），可以将总的可靠度 ${R_M}$ 分配给串联结构的各分系统 ${R_i}$ 。

2.2 计算原理

建立各系统的可靠性数学模型，基于上述故障基础数据并设定比例系数获得修正的故障数据，然后再代入可靠性数学模型方程进行求解。

1）并联系统

并联系统是指系统中有n个单元，只有当所有单元都不能正常工作，系统才无法正常工作。并联系统的任务可靠性数学模型为：

${R_s}(t) = 1 - \prod\limits_{i = 1}^n {[1 - {R_i}(t)]} \text{。}$

(6)

式中： ${R_s}(t)$ 表示系统可靠度； ${R_i}(t)$ 表示第i个单元可靠度。

可靠性分配方法计算原理具体如下：

步骤1　根据评分法原理，对各单元进行评分，得到评分系数 ${c_i}$ 。

步骤2　将各单元的评分系数 ${c_i}$ 作为各自的故障率基础数据，即假定为老产品相似单元故障率，之所以可按如此方式处理是因为评分分配法获得评分系数是各单元故障率的比例数据值，并非实际故障率。根据比例组合的基本原则，假定各单元的分配值与老产品相似单元故障率之比相等，设比例系数为K，即^[8]

$K = {{\lambda {}_i}/{{c_i}}}\text{，}$

(7)

得到各单元故障率分配值 $\lambda {}_i$ ，视为修正后的故障率值：

$\lambda {}_i = K \cdot {c_i}\text{，}$

(8)

假设各单元的寿命仍服从指数分布，所以各单元分配的可靠度为：

${R_i} = {e^{ - K{c_i}t}}\text{，}$

(9)

而任务可靠度 ${R_M} = {e^{ - \lambda t}}$ ，故

${R_i} = R_M^{^{{c_i} \cdot {K/\lambda }}} = R_M^{^{{c_i} \cdot {K^ * }}}\text{。}$

(10)

步骤3　根据并联系统可靠性模型，可得

${R_M} = 1 - \prod\limits_{i = 1}^n {[1 - R_M^{^{{c_i} \cdot {K^ * }}}]} \text{。}$

(11)

式中： ${R_M}$ 和 ${c_i}$ 为已知量，只有 ${K^ * }$ 为未知变量，通过反解方程或者图形拟合逼近法可以很容易求解得到 ${K^ * }$ 值。

步骤4　在计算得到 ${K^ * }$ 值后，回代计算可得各单元的可靠度分配值为：

${R_i} = R_M^{^{{c_i} \cdot {K^ * }}}\text{。}$

(12)

可以看出，串联系统的可靠性分配值式（5）也可以写成式（12）的形式并且 ${K^ * }$ 值为1，而并联系统的 ${K^ * }$ 为待求值。

2）串并联系统

串并联系统是指可靠性框图中既含有串联部分，也含有并联支路部分，构成复杂的串并联系统网络，其可靠性数学模型需要根据网络的各自特点建立。由若干串联单元和一个并联模块所组成的串并联系统可靠性数学模型可表示为：

${R_s}(t) = \prod\limits_{j = 1}^m {{R_j}(t) \cdot } \left\{ {1 - \prod\limits_{i = 1}^n {[1 - {R_i}(t)]} } \right\}\text{。}$

(13)

式中： ${R_j}(t)$ 表示第1到m个串联单元的可靠度， ${R_i}(t)$ 表示并联模块中第1到n个单元的可靠度。同理，当有多个并联模块时，可将单个并联模块作为整体，与其他串联单元按照串联模型逻辑关系建立复杂串并联系统的可靠性模型。

串并联系统的可靠性分配方法参照上述并联系统可靠性分配方法，只是需要将 ${R_i} = R_M^{^{{c_i} \cdot {K^ * }}}$ 代入式（13）所示的串并联模型方程中求解未知数 ${K^ * }$ ，然后再回代计算各单元的可靠性分配值。

3）n中取r表决系统

n中取r系统是指系统中有n个单元，只要其中至少有r个单元正常，系统就能正常工作，这样的系统构成r/n表决系统。其可靠度数学模型(假定表决器可靠度为1)为：

${R_s}(t) = \sum\limits_{i = r}^n {C_n^iR{{(t)}^i}{{(1 - R(t))}^{n - i}}} \text{。}$

(14)

式中： ${R_s}(t)$ 为系统可靠度； $R(t)$ 为各单元可靠度。由于n中取r表决系统中各单元相同，因此默认各单元可靠度相同。

表决系统的可靠性分配方法参照上述并联系统可靠性分配方法，只是需要将 ${R_i} = R_M^{^{{c_i} \cdot {K^ * }}}$ 代入式（14）所示的串并联模型方程中求解未知数 ${K^ * }$ ，然后再回代计算各单元的可靠性分配值。

3 算例应用

相同设备的可靠度分配值相同，依据前述计算方法建立推进系统任务可靠性数学模型为

$ \begin{split} &R = {R_1} \cdot \left[ {C_4^3{R_2}^3(1 - {R_2}) + C_4^4{R_2}^4} \right] \times\\ & \left\{ 1 - \left\{ {1 - {R_3} \cdot \left[ {C_4^3{R_4}^3(1 - {R_4}) + C_4^4{R_4}^4} \right]} \right\}\right. \left. (1 - {R_5}{R_6}{R_6}) \right\}\text{。} \end{split} $

(15)

推进系统从一级系统分配到的可靠度 $R = 0.961$ ，将此可靠度分配到各设备单元。按照所提出的可靠性分配方法，首先由多名熟悉ROV各系统供能及工作原理并且具备丰富经验的专家给各设备打分，然后加权求平均法获得四大因素的分值，如表1所示。

然后参照第2章算法，任务可靠性数学模型可以变换为：

$ \begin{split} &R = {R^{{c_1}{K^*}}} \cdot \left[ {4{R^{3{c_2}{K^*}}}(1 - {R^{{c_2}{K^*}}}) + {R^{4{c_2}{K^*}}}} \right] \times \\ &\;\;\;\;\;\;\left\{ 1 - \left\{ {1 - {R^{{c_3}{K^*}}} \cdot \left[ {4{R^{3{c_4}{K^*}}}(1 - {R^{{c_4}{K^*}}}) + {R^{4{c_4}{K^*}}}} \right]} \right\}\right. \times\\ &\;\;\;\;\;\; \left. (1 - {R^{{c_5}{K^*}}}{R^{{c_6}{K^*}}}{R^{{c_6}{K^*}}}) \right\}\text{。} \end{split} $

用绘图逼近法求得在 $R = 0.961$ 时， ${K^ * } = 6.53$ ，再代入式（12）可以求得推进系统各组成设备的可靠度分配值（见表1）。从表1可以看出，垂直推进器和水平推进器分配的可靠度相差不大，但辅助推进器分配了最高的可靠度为0.995，这主要是由于相对于其他推进器而言辅助推进器工作时间较短的缘故，而与之配套的液压控制阀箱也获得了较高的可靠性。建议在设计选型时，提高辅助推进器及配套的液压控制阀箱的可靠性。推进器驱动器由于其设备复杂程度较高技术水平一般，而且工作时间也长，因此分配到的可靠度较低。

4 结　语

针对ROV推进系统复杂的可靠性模型特点，瞄准在可靠性分配计算过程中出现的无法直接利用常规分配方法开展工作的实际工程问题，提出了一种含复杂系统可靠性模型的分配计算方法。以含有复杂串并联系统及表决系统的ROV推进系统可靠性模型计算为例，应用所述方法进行建模计算，得到了推进系统各组成设备的可靠度分配值。结果表明，所提出的可靠性分配计算方法可以有效克服常规分配方法无法直接用于复杂串并联系统及表决系统的缺点，为ROV其他系统以及类似系统的可靠性分配工程设计提供技术支撑。