2. 武汉第二船舶设计研究所,湖北 武汉 430000
2. Wuhan Second Ship Design and Research Institute, Wuhan 430000, China
前置定子导管桨由于能够减小噪声和提高临界航速等突出优点,已成为当前国内外大力发展的水下推进器。相比于螺旋桨,前置定子导管桨由于采用了减速型导管可以使推进器转子工作在低流速环境中,从而改善了推进器的空化性能。但是,随着水下航行体航速的提高,使得前置定子导管桨发生空化的可能性大大增加。空化会降低推进器的推进性能,同时也能引起结构振动和空化噪声。因此,为了降低推进器空化噪声并提高临界航速,有必要探究带前置定子导管桨空化特性。
目前,研究推进器空化主要有数值计算方法和实验方法。由于实验成本比较高,大部分的研究都基于数值计算。随着船舶吨位和航速的提高,推进器的载荷也随之提高,使得发生空化的可能性大大增加。同时,数值计算的发展也给水下推进器的空化研究提供了很好的研究工具。在空化的数值模拟中湍流模型和空化模型的选取对数值计算结果的影响很大。因此,国内外目前在空化的数值模拟中主要针对湍流模型和空化模型进行对比计算研究,也考虑非均匀入流对空化的非定常影响。在计算中,湍流模型主要有k-ω湍流模型[1]、LES[2]、SST k-ω湍流模型[3]、PANS[4]和非线性湍流模型[5]等,而空化模型也主要有Singhal空化模型[1, 5]、Kunz空化模型[2]和Z-G-B空化模型[3-4]等。杨琼方[6-9]采用单个螺旋桨的空化数值模拟进行了大量的工作,考虑湍流对空化的影响对饱和蒸汽压力进行了修正,同时也对SST k-ω湍流模型湍流粘度进行了修正。这些数值计算研究都通过实验进行了对比验证,表明现有的方法对单桨空化模型具有较好的预测精度。
在此基础上,近些年也有一些研究人员开展了对多个转定子及导管的空化研究。王顺杰[10-11]采用Saur空化模型和RNG k-ε湍流模型,并通过动网格模型技术对对转桨进行了空化噪声特性数值分析。杨琼方[12]对对转桨的空化初生以及辐射噪声进行了预报,分别采用了SST k-ω湍流模型、SAS和DES湍流模型,并对比了3种湍流模型在空化噪声预测中适用性。施瑶[13]、鹿麟[14]分别采用标准k-ε湍流模型和SST k-ω湍流模型,并结合Z-G-B空化模型对后置定子泵喷推进器进行定常和非定常空化数值模拟。由此可见,并没有一个通用的湍流模型和空化模型可以适用于前置定子导管桨。
为了考虑计算精度,本文采用SST k-ω湍流模型和Z-G-B空化模型对前置定子导管桨进行空化数值模拟,通过DTMB4381螺旋桨的空化数值计算与试验值对比验证了数值计算精度。对前置定子导管桨不同空化数下定常空化性能进行了计算及分析,为其他种类的推进器空化流场特性研究提供一定的参考。
1 数值计算方法 1.1 流场基本控制方程在汽液混合多相流模型中,流体假定为均质多相流,因此各个部分的速度与压力相同。连续性方程和动量方程如下:
| $ \frac{{\partial {\rm{\rho }}}}{{\partial {\rm{t}}}} + \frac{{\partial \left( {{\rm{\rho }}{u_j}} \right)}}{{\partial {{\rm{x}}_j}}} = 0\text{,} $ | (1) |
| $\begin{split} \frac{{\partial \left( {{\rm{\rho }}{u_i}} \right)}}{{\partial {\rm{t}}}} +& \frac{{\partial \left( {{\rm{\rho }}{u_i}{u_j}} \right)}}{{\partial {{\rm{x}}_j}}} = {\rm{\rho }}{f_i} - \frac{{\partial p}}{{\partial {x_i}}} +\\ &\frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + {\mu _t}} \right)\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}} - \frac{2}{3}\frac{{\partial {u_k}}}{{\partial {x_k}}}{\delta _{ij}}} \right)} \right]\text{。}\end{split} $ | (2) |
其中:ui和fi分别为i方向的速度和体力;p为混合相压力;μ和μt为层流和湍流粘性系数;ρ为混合相的密度。大量文献指出SST k-ω湍流模型在空化流计算中具有较高的精确度,所以本文采用SST k-ω湍流模型进行求解。
1.2 Z-G-B空化模型Z-G-B模型应用Rayleigh-Plesset方程,在忽略汽泡表面张力和2阶导数项的情况下,得到如下的相间质量传递计算公式:
| $ \dot m_e^ + = {{{F}}_{vap}}\frac{{3{r_{nuc}}\left( {1 - {\alpha _v}} \right){\rho _v}}}{{{R_B}}}\sqrt {\frac{2}{3}\frac{{{p_v} - p}}{{{\rho _l}}}}\text{,} \;\;{{p}} < {p'_v}\text{;} $ | (3) |
| $ \dot m_c^ - = {{{F}}_{cond}}\frac{{3{\alpha _v}{\rho _v}}}{{{R_B}}}\sqrt {\frac{2}{3}\frac{{p - {p_v}}}{{{\rho _l}}}} \text{,}\;\;{{p}} > {{p'}_v}\text{。} $ | (4) |
式中:rnuc为成核区的体积分数;RB为汽泡半径;Fvap和Fcond分别为Z-G-B模型的经验蒸发系数和凝结系数。各参数取值为:RB=1 μm,rnuc=5e-4,Fvap=50和Fcond=0.01。
2 数值计算方法验证为了验证空化数值模拟的可靠性和准确性,选取DTMB4381螺旋桨作为计算对象。螺旋桨的直径为D,入口距离螺旋桨桨盘面5D,出口距离螺旋桨桨盘面10D,外流域直径为5D。静止外流域采用六面体结构化网格,旋转域采用非结构网格,并在螺旋桨叶片表面生成棱柱边界层网格。螺旋桨所在旋转区域的非结构网格总数为156万,外流域的结构化网格数为50万,螺旋桨表面计算网格如图1所示。

|
图 1 螺旋桨的网格示意图 Fig. 1 Mesh of propeller |
定义进速系数为J=U/nD,推力系数为KT=T/ρn2D4,扭转系数为KQ=Q/ρn2D5,敞水效率η=KT/KQ*J/2π,其中U为来流速度,n为螺旋桨转速,ρ为流体密度,T为推力,Q为扭矩。计算中采用的边界条件:进口和外围远场采用均匀速度入口,出口采用压力出口,定常计算中旋转域与静止域的交界面为MRF,壁面为无滑移壁面。由空化数来进行出口压力控制,空化系数定义为:
| $ \sigma = \frac{{{p_{{\rm{out}}}} - {p_v}}}{{0.5\rho {U^2}}}\text{。} $ | (5) |
式中,pout为出口压力,pv饱和蒸汽压力。
为了分析空化状态下螺旋桨的水动力性能,表1给出了螺旋桨的推力系数和扭矩系数与实验值[9]的对比。从表中可以看出计算误差基本上在5%以内,由此说明计算结果比较准确,现有的方法具有较高的模拟精度。
|
|
表 1 螺旋桨推力系数和扭矩系数随空化数的变化 Tab.1 Thrust coefficient and torque coefficient at different cavitation numbers |
为了进一步验证空化数值计算方法,给出σ=3.5时数值计算得到螺旋桨的空化形态,如图2所示。从空化形态上看,本文数值计算结果与实验空化形态吻合程度较高。

|
图 2 螺旋桨的空化形态与实验值对比 Fig. 2 Comparison of cavity pattern between calculation and experimental observation |
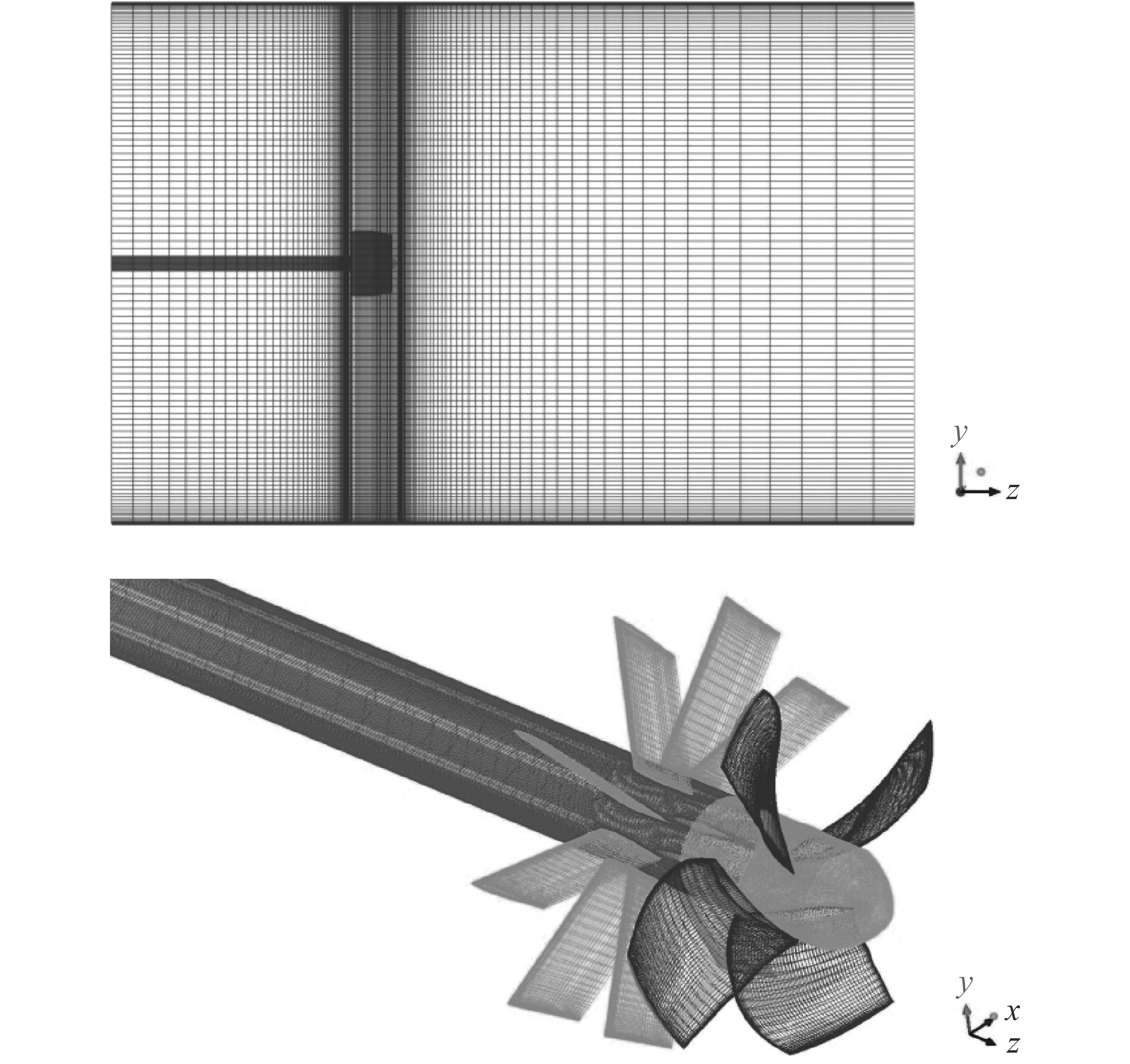
该前置定子导管桨采用4叶转子与9叶定子的组合,转子直径为0.254 m,定子安放角度为3°,几何数据取自文献[15]。计算域为圆柱体,进口位于转子盘面上游5D处,出口位于转子盘面下游10D处,圆柱直径为10D,计算域和计算网格如图3所示。
|
图 3 前置定子导管桨的网格示意图 Fig. 3 Mesh of ducted propeller with pre-swirl stators |
采用分块网格技术对各个计算域生成高质量结构化网格,在定子与外流生成H型网格,转子叶片表面生成O型网格。整个计算模型计算单元总数为461万,转子部分网格单元数为159万,定子、导管及外流域部分网格单元数为302万。
为了提高计算收敛的稳定性和收敛速度,先进行非空化数值计算,然后以非空化数值计算的结果作为空化数值计算的初始值,计算收敛精度设置为10–5。
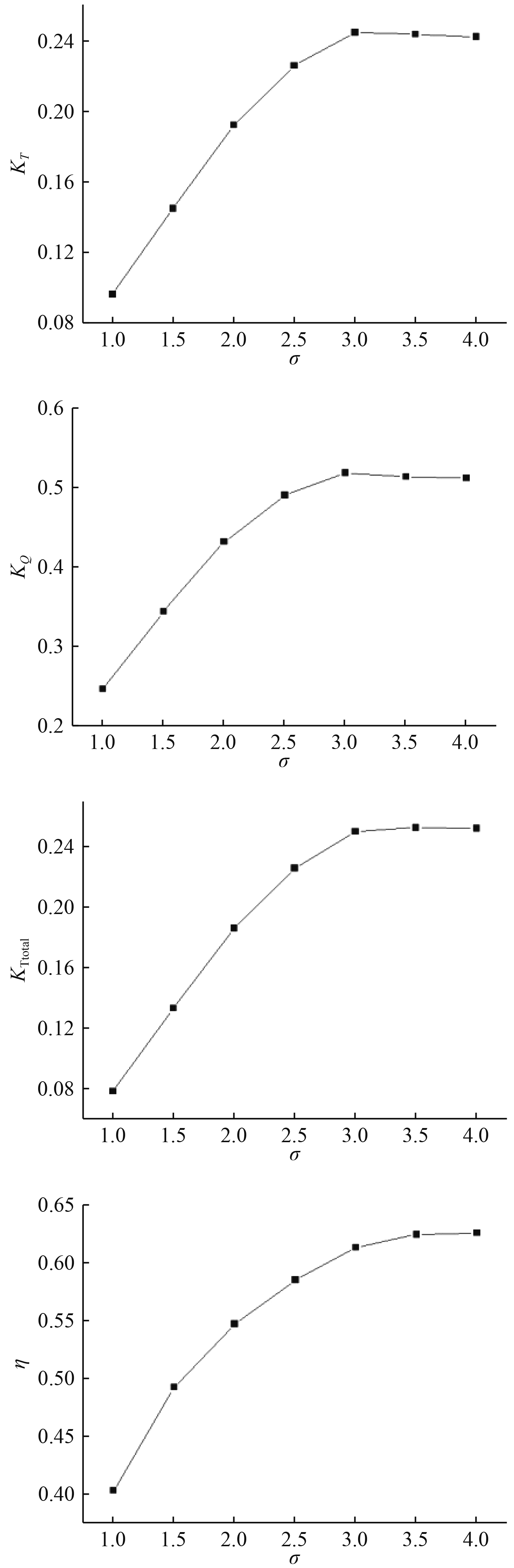
图4给出了进速系数J=0.8不同空化数时的前置定子导管桨水动力性能曲线。可以看出,随着空化数的降低(σ≤3),前置定子导管桨的推力系数、扭矩系数、总推力系数和效率都降低。在σ≥3时随着空化数的降低,推力系数和扭矩系数有略微的增大,但是前置定子导管桨的效率一直是降低的。从表2可以看出,随着空化数的降低,导管和定子原本产生正向推力,但是σ≤2.5之后推力变为负方向,而且此时导管外表面也开始出现空化。
|
图 4 不同空化数时前置定子导管桨的水动力性能曲线 Fig. 4 Hydrodynamic performance of ducted propeller |
|
|
表 2 导管螺旋桨推力系数和扭矩系数随空化数的变化 Tab.2 Performance of ducted propeller at different cavitation numbers |
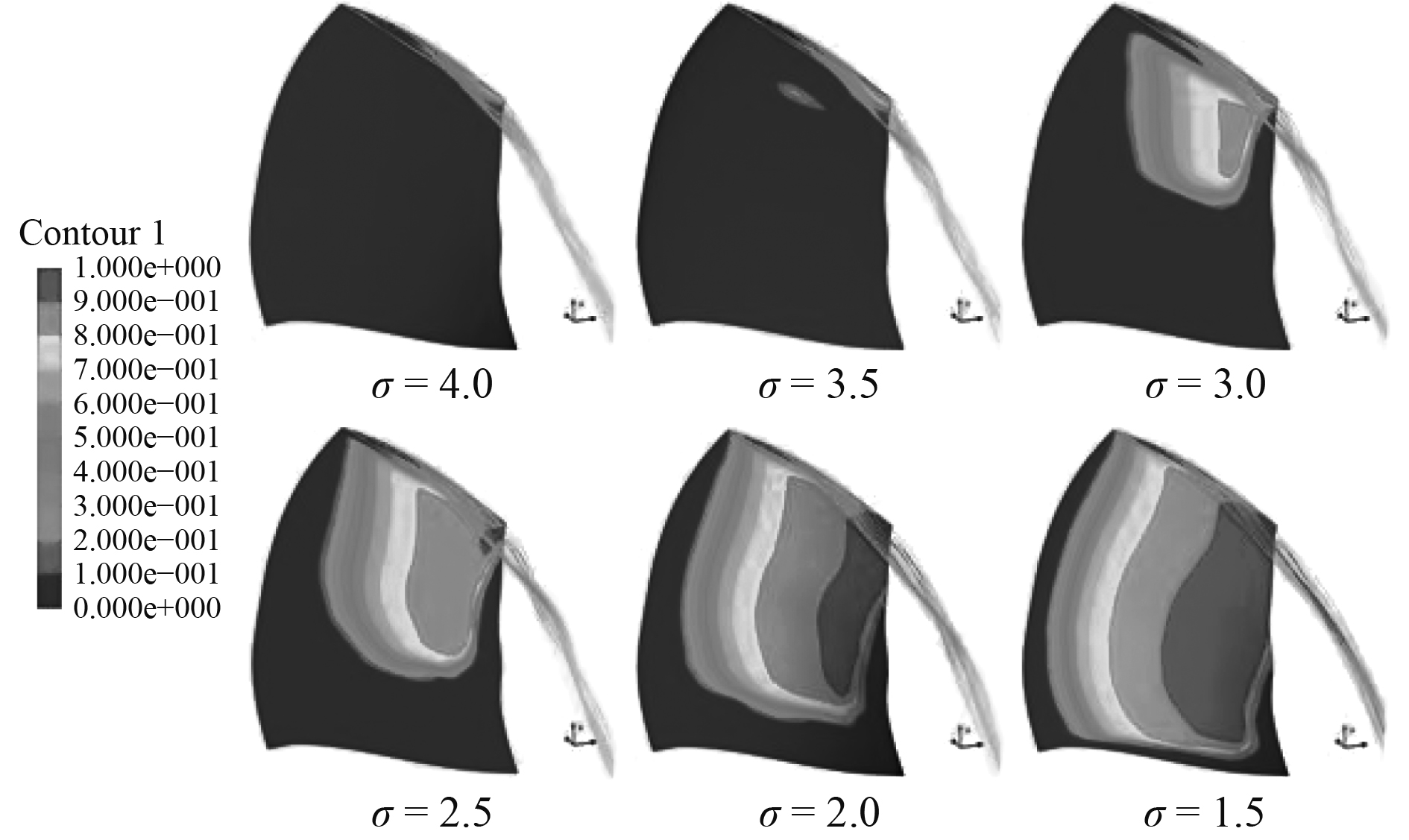
图5给出了不同空化数下前置定子导管桨的空化云图和转子叶顶流线图。云图表示为水蒸汽的体积分数αv。从图中可以看出随着空化数的降低,叶片表面空化面积逐渐增大。空化初始发生于叶顶靠近随边处,在σ=4时首先在叶顶靠近尾缘40%处产生了泄漏涡,并引起了叶顶靠近尾缘区域发生空化。随着空化数的降低σ=3.5时叶片中部开始出现空化并随着空化数的降低面积逐渐由叶顶区域向叶根区域扩散,在σ=1几乎整个吸力面都发生了空化。
|
图 5 不同空化数下前置定子导管桨的空化云图和流线图 Fig. 5 Cavitation contour and stream of ducted propeller at different rotational speeds |
图6给出了带前置定子导管桨的空化等值面图,αv为水蒸汽的体积分数。从空化等值面图可以看出,首先由于泄漏涡而在叶顶尾缘区域产生了空化;随着空化数的降低,在叶片表面也开始发生空化并随着空化数的降低空化区域逐渐变大。

|
图 6 不同空化数时推进器叶片表面的空化等值面图(αv=0.1) Fig. 6 Isosurface of cavitation on ducted propeller blades at different cavitation numbers |
叶片表面的压力系数分布如下:
| $ {{\rm{C}}_p} = \frac{{p - {p_0}}}{{0.5\rho {U^2}}}\text{。} $ | (6) |
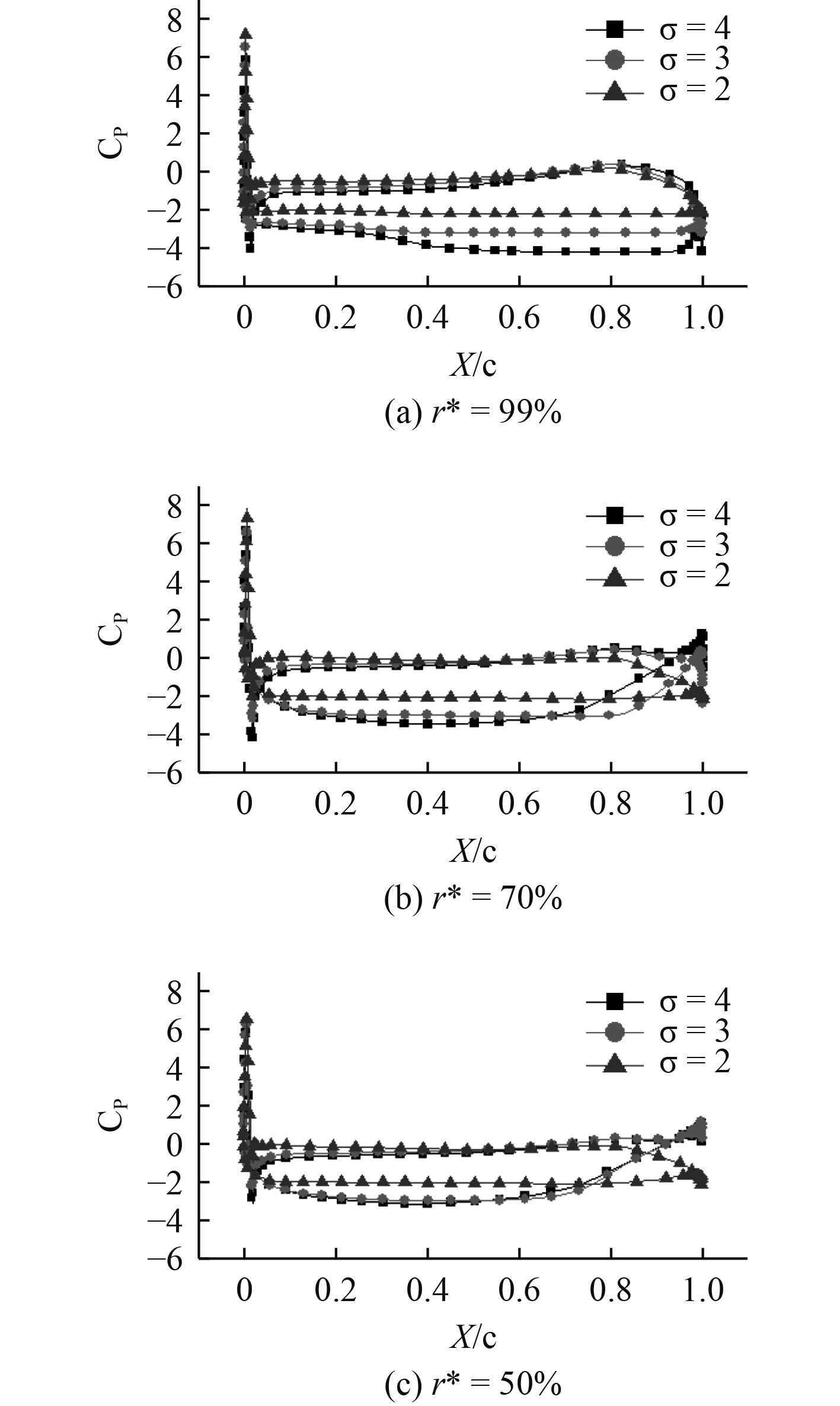
其中:p为当地压力值,p0为远场参考压力值,U为进流速度。为了更好地分析不同空化数下转子叶片载荷分布特性,图7给出了3个空化数(σ=4,3,2)下转子叶片表面不同展向位置处剖面弦向的压力系数分布。横坐标表示叶片表面点位置距离导边距离X与弦长c的比值,0表示导边,1表示随边。叶片无量纲径向系数
|
图 7 转子叶片表面的压力系数分布图 Fig. 7 Pressure coefficient distribution of rotors with different radiuses |
本文通过数值计算给出了不同空化数下前置定子导管桨水动力性能和空化特性,通过分析得到以下结论:
1)通过DTMB4381螺旋桨的空化数值模拟表明本文所采用的数值计算方法能够很好地预测空化发生现象。
2)同一进速系数下,σ≥3时前置定子导管桨的水动力性能基本上变化不大;随着空化数的进一步降低,水动力性能迅速下降。
3)空化最先出现在叶顶靠近转子叶片尾缘区域,这是转子与导管之间的间隙流和间隙泄漏涡引起。σ=3.5时叶片表面开始出现空化,随着空化数的降低,转子叶片吸力面的空化面积增大,且由转子叶顶尾缘向导边和叶根扩大。
| [1] |
RHEE S. H., KAWAMURA T., LI H. Y.. Propeller cavitation study using an unstructured grid based navier-stoker solver[J]. ASME J. Fluids Eng., 2005, 127: 986-994. DOI:10.1115/1.1989370 |
| [2] |
BENSOW R. E., BARK G.. Implicit LES predictions of the cavitating flow on a propeller[J]. ASME J. Fluids Eng., 2010, 132: 041302. DOI:10.1115/1.4001342 |
| [3] |
JI Bin, LUO Xianwu, WANG Xin, et al. Unsteady numerical simulation of cavitating turbulent flow around a highly skewed model marine propeller[J]. ASME J. Fluids Eng., 2011, 133: 011102. DOI:10.1115/1.4003355 |
| [4] |
JI Bin, LUO Xianwu, WU Yulin, et al. Partially-averaged navier-stokes method with modified k-ε model for cavitating flow around a marine propeller in a non-uniform wake[J]. International Journal of Heat and Mass Transfer, 2012, 55(23-24): 6582-6588. DOI:10.1016/j.ijheatmasstransfer.2012.06.065 |
| [5] |
KAEWKHIAW P, TIAPLE Y, DECHAUMPHAI P. Application of nonlinear turbulence models for marine propulsors[J]. ASME J. Fluids Eng., 2011, 133: 031101. DOI:10.1115/1.4003564 |
| [6] |
杨琼方, 王永生, 余亮琴, 等. 艇尾实尺桨空化初始航速和高频噪声谱的工程预报[J]. 振动与冲击, 2013, 32(15): 71-76. DOI:10.3969/j.issn.1000-3835.2013.15.013 |
| [7] |
杨琼方, 王永生, 张志宏. 非均匀进流对螺旋桨空化水动力性能的影响[J]. 水动力学研究与进展, 2011, 26(5): 538-550. YANG Qiong fang, WANG Yong sheng, ZHANG Zhi hong. Effect of non-uniform inflow on propeller cavitation hydrodynamics[J]. Chinese Journal of Hydrodynamics, 2011, 26(5): 538-550. DOI:10.3969/j.issn1000-4874.2011.05.004 |
| [8] |
杨琼方, 王永生, 张志宏. 螺旋桨空化初生的判定和空化斗的数值分析[J]. 上海交通大学学报, 2012, 46(3): 410-416. YANG Qiong fang, WANG Yong sheng, ZHANG Zhi hong. Determination of propeller cavitation initial inception and numerical analysis of the inception bucket[J]. Journal of Shanghai Jiao Tong University, 2012, 46(3): 410-416. |
| [9] |
杨琼方, 王永生, 张志宏. 螺旋桨空化崩溃性能图谱的多相流模拟[J]. 华中科技大学学报(自然科学版), 2012, 40(2): 18-22. YANG Qiong fang, WANG Yong sheng, ZHANG Zhi hong. Multiphase flow simulation and propeller cavitation breakdown performance maps[J]. Journal of Huazhong University of Science and Technology(Nature Science), 2012, 40(2): 18-22. |
| [10] |
王顺杰, 程玉胜, 高鑫. 水下对转螺旋桨空化线谱频率预报与数值模拟[J]. 兵工学报, 2013, 34(3): 310-317. |
| [11] |
王顺杰, 王易川, 戴卫国, 等. 片空化状态下对转螺旋桨噪声特性仿真分析[J]. 船舶力学, 2014, 18(7): 778-785. WANG Shun jie, WANG Yi chuan, DAI Wei guo, et al. Numerical analysis for sheet cavitation noise characteristics of contra-rotating propeller[J]. Journal of Ship Mechanics, 2014, 18(7): 778-785. DOI:10.3969/j.issn.1007-7294.2014.07.006 |
| [12] |
杨琼方, 王永生, 张志宏, 等. 伴流场中对转桨空化初生的判定与辐射噪声预报和校验[J]. 声学学报, 2014, 39(5): 589-604. YANG Qiong fang, WANG Yong sheng, ZHANG Zhi hong, et al. Numerical prediction of cavitation inception radiated noise of contra-rotating propeller with non-uniform inflow[J]. ACTA ACOUSICA, 2014, 39(5): 589-604. |
| [13] |
施瑶, 潘光, 王鹏, 等. 泵喷推进器空化特性数值分析[J]. 上海交通大学学报, 2014, 48(8): 1059-1064. |
| [14] |
鹿麟, 潘光. 泵喷推进器非定常空化性能数值模拟分析[J]. 上海交通大学学报, 2015, 49(2): 262-268. LU Lin, PAN Guang. Numerical simulation analysis of unsteady cavitation performance of a pump-jet propulsor[J]. Journal of Shanghai Jiao Tong University, 2015, 49(2): 262-268. |
| [15] |
HUGHES M J, KINNAS S A. An analysis method for a ducted propeller with pre-swirl stator blades[C]. Propellers/Shafting’ 91 Symposium, 1991.
|
 2019, Vol. 41
2019, Vol. 41
