2. 哈尔滨工程大学,黑龙江 哈尔滨 150001
2. Harbin Engineering University, Harbin 150001, China
双体船作为一种高性能船舶,相比常规单体船具有优良的横稳性、耐波性以及阻力性能。同时并列排布的片体提供了足够大的甲板面积,使得其在军民领域均具有广阔的应用前景。但是特殊的外形导致其所受的波浪载荷较为复杂,片体间较大的跨度使得其横向刚度较常规船舶偏弱。因此双体船连接桥结构的强度问题特别突出,尤其是身处横向载荷较大的工况下。
目前,对于双体船的结构设计,各主要船级社编制的规范也涉及到了设计载荷及结构尺寸方面的内容,如CCS的《海上高速船入级与建造规范》。除此之外,双体船结构强度的直接计算随着计算成本的下降逐渐成为主流手段。任慧龙[1]针对1艘5 000吨级双体船采用三维势流理论直接计算波浪载荷并对整船进行有限元分析;张清越[2]基于波浪载荷直接计算的谱分析法对1艘双体船进行疲劳评估,并给出了一种局部砰击载荷与波浪载荷联合作用下的结构应力响应计算方法;程相如[3]基于Ansys分析软件,对1艘双体船连接桥结构进行强度计算。相对于理论预报,双体船波浪载荷模型试验研究也有一定发展。汪雪良[4]对1艘穿浪双体船进行水池模型试验,测量并分析了纵向载荷和横向载荷的统计特性。
本文针对1艘小型双体船,提出采用一种桁架式结构作为其连接桥的主体。相比普通的由板材与型材组合而成的连接桥,具有造价低、自身重量低等优点。
采用三维势流理论直接计算波浪载荷并对连接桥结构进行屈服屈曲强度评估,对不满足规范要求的构件进行优化。
1 桁架式连接桥结构设计针对目标双体船体型较小,工作航速低,工作时长短,工作海况小等特点。如果采用由板材与型材的组合结构作为连接桥(见图1),其固然会很好满足强度要求,但会使建造成本偏高、连接桥自身重量偏大。本文提出采用一种由杆件组成的桁架式结构作为连接桥的承载结构,来缓解以上问题,如图2所示。

|
图 1 板架式连接桥 Fig. 1 Cross structure with grillage structure |

|
图 2 桁架式连接桥 Fig. 2 Trussed corss structure |
表1为2艘双体船的主尺度信息,其中采用桁架式设计思路的双体船在自身重量上要明显偏小。若这种船型能够同样满足作业要求,相比常规双体船,其在设计以及造价上会有不小的优势。
|
|
表 1 两艘双体船主尺度 Tab.1 Principal dimension for two boats |
构成连接桥主体的桁架结构,由不同尺寸的杆件组合而成。根据承载方式的不同,将其划分为:横向斜撑杆件、纵向斜撑杆件、水平斜撑杆件、垂向支撑杆件、强框架以及弱框架。对于这种桁架式结构的连接桥,本文将基于波浪载荷直接计算法,对其结构进行强度校核以及优化。
2 波浪载荷计算原理 2.1 双体船运动和波浪载荷预报理论研究船舶在波浪上的运动响应时,基于势流理论假设[5],认为流体无粘、不可压缩、流动无旋。通过3个坐标系来描述船波系统:大地坐标系
|
图 3 坐标系示意图 Fig. 3 Coordinate system |
在线性假设条件下,流体总的速度势可以分为:
| $ \phi \left( {x,y,z} \right) = {\phi _I}\left( {x,y,z} \right) + {\phi _D}\left( {x,y,z} \right) + \sum\limits_{j = 1}^6 {{{\dot \zeta }_j}{\phi _j}\left( {x,y,z} \right)}\text{。} $ | (1) |
其中:
计算水域为无限水深,入射波的浪向角为
| ${\Phi _I} = \frac{{ - igA}}{{{\omega _0}}}{e^{kz}}{e^{i\left( {kx\cos \beta + kx\sin \beta } \right)}}{e^{ - i\omega t}}\text{。}$ | (2) |
其中:
| $\begin{split} & \left[ F \right]\;\; - {\omega ^2}{\phi _j} + g\frac{{\partial {\phi _j}}}{{\partial z}} = 0\text{,} \\ & \left[ S \right]\;\;\left\{ \begin{array}{l} {\left. {\frac{{\partial {\phi _j}}}{{\partial n}}} \right|_{S0}} = {n_j}\;\;\left( {j = 1,2,...,6} \right) \text{,}\\ \frac{{\partial {\phi _D}}}{{\partial n}} = - \frac{{\partial {\phi _I}}}{{\partial n}}\text{,} \\ \end{array} \right. \\ & \left[ B \right]\;\;\mathop {\lim }\limits_{z \to - \infty } \nabla {\phi _j} = 0 \text{,}\\ & \left[ R \right]\;\;\mathop {\lim }\limits_{R \to \infty } \sqrt R \left( {\frac{{\partial {\phi _j}}}{{\partial R}} - ik{\phi _j}} \right) = 0 \text{。} \end{split} $ | (3) |
规则波中的船体运动可用以下方程描述:
| $\left( {{ M} + { A} } \right) \cdot {\ddot \eta (t)} + { B}\cdot {\dot \eta (t)} + { C} \cdot {\eta (t)} = {f(t)}\text{。}$ | (4) |
式中:A为附加质量阵;B为阻尼矩阵;C为恢复力矩阵;f(t)为波浪干扰力;
线性理论框架下,船舶在某海况的波浪载预报。认为短期海况为均值为0的正太平稳随机过程,船体对波浪的响应为线性时不变系统,则在海浪的作用下,船体的载荷响应也是均值为0的正太平稳随机过程。其关系可以描述为:
| ${S_M}(\omega ) = {\left| {{H_M}(\omega )} \right|^2} \cdot {S_\omega }(\omega )\text{。} $ | (5) |
式中:SM(ω)为控制载荷响应谱;|HM(ω)|2为幅频响应算子;Sω(ω)为波浪谱,选用P-M双参谱。
短期海况下控制载荷的响应服从瑞利分布,分布函数为:
| $f(x) = \frac{x}{{{\sigma ^2}}}\exp \left( { - \frac{{{x^2}}}{{2{\sigma ^2}}}} \right)\text{,}$ | (6) |
根据载荷响应谱SM(ω)计算上式中的参
| $ {\sigma ^2} = {m_0} = \int\nolimits_0^\infty {{S_M}(\omega )} \operatorname{d} \omega = \int\nolimits_0^\infty {{{\left| {{H_M}(\omega )} \right|}^2}{S_\omega }(\omega ){\rm d}\omega } \text{,} $ | (7) |
控制载荷响应的最大值表示为:
| ${R_{\max }} = 2.55\sqrt {{m_0}} \text{。}$ | (8) |
使用等效设计波法进行船体结构加载的关键需要确定设计波
| $A = \frac{{{R_{{\rm{max}}}}}}{{{A_0}}}\text{。}$ | (9) |
其中:A为设计波幅值;A0为控制载荷最大响应算子;ω,ε和β取最大响应算子对应频率、相位和浪向。
3 结构分析有限元模型处理 3.1 浮体及连接桥处模型的构建根据CCS《海上高速船入级与建造规范》的有关规定,建立有限元模型。总体结构分析的有限元模型包括船体范围内的主要横向、纵向、垂向支撑结构,以及强框架和弱框架等构件。对于需要校核的连接桥结构,真实还原桁架的布置形式。
3.2 有限元模型的重量分布用于进行结构分析的有限元模型并未包括上建,为保证模型整体的质量分布与实际情况一致,将未模型化的上建、舾装及设备的重量通过质量模型计入,并根据实际的船体质量分布特点进行布置。
3.3 边界条件对模型进行静力平衡调整后,对船体不施加任何约束,采用惯性释放的原理进行分析。
4 环境载荷 4.1 规则波响应
|
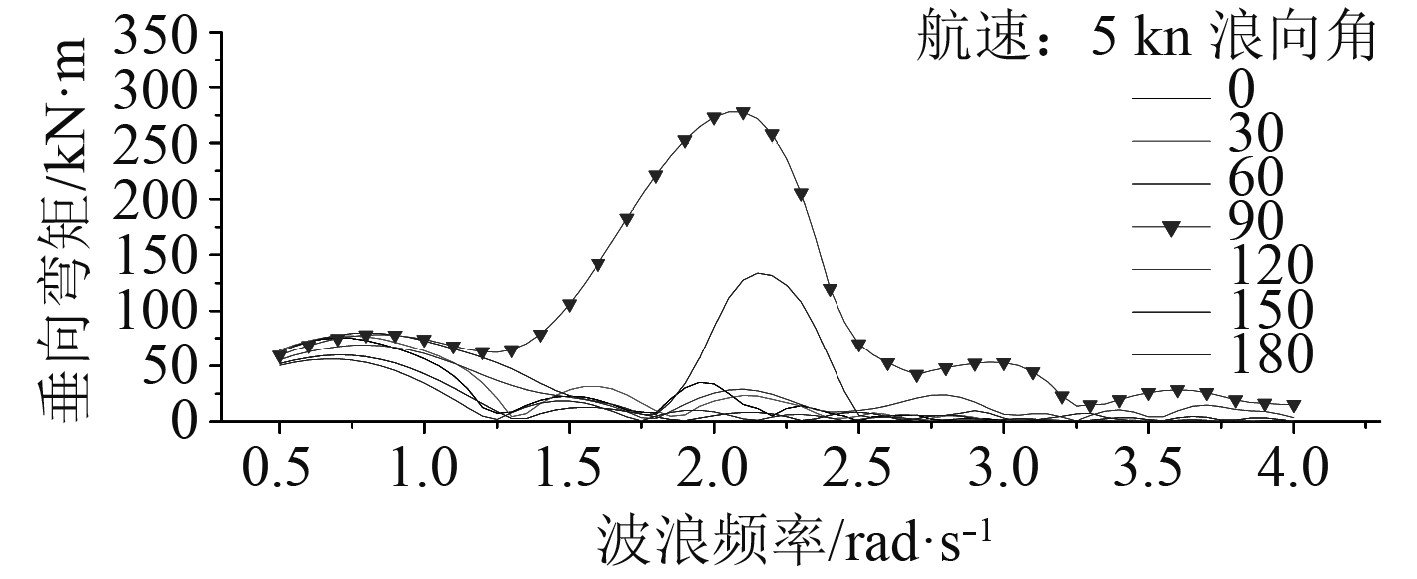
图 5 船中纵剖面对开力矩 Fig. 5 Split moment of longitudinal section |

|
图 6 船中纵剖面横向扭矩 Fig. 6 Cross torque of longitudinal section |
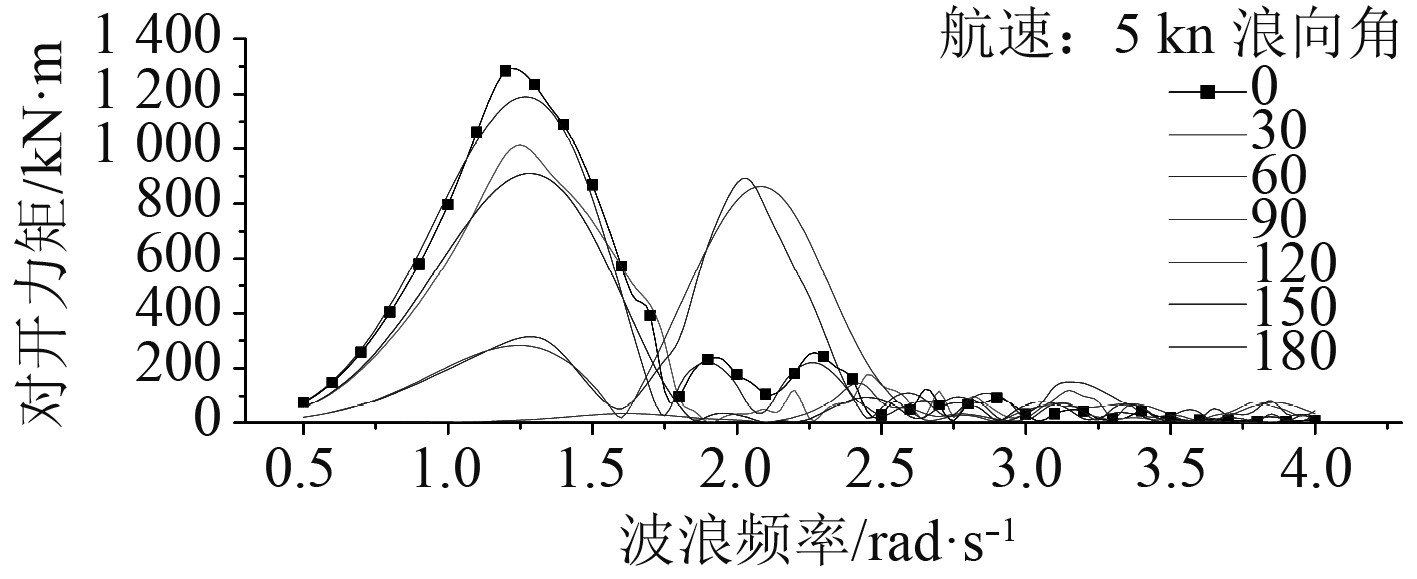
图4~图7给出连接桥处典型剖面在规则波中4种波浪载荷响应。根据规则波中的载荷计算结果,结合目标船型所处环境状态(5级海况),从而确定典型剖面所受控制载荷短期极值。
|
图 4 船舯横剖面垂向弯矩 Fig. 4 VBM of midship-section |

|
图 7 船中纵剖面水平弯矩 Fig. 7 HBM of longitudinal section |
表2为双体船控制载荷设计波参数。根据目标船型连接桥的受力特点。选取中横剖面处垂向弯矩以及中纵剖面处对开力矩、横向扭矩和水平弯矩作为主控载荷进行强度校核。根据5级海况下的短期极值采用等效设计波法进行加载。
|
|
表 2 许用应力值 Tab.2 Stress criterion |
根据CCS《海上高速船入级与建造规范》对船体结构按构件类型分类评估。校核部分采用普通钢Q235,其屈服极限为235 MPa,许用应力如表3所示。
|
|
表 3 双体船控制载荷设计波参数 Tab.3 Parameters of design wave |
对于屈曲强度的校核,船体梁的理论屈曲应力按如下公式计算:
| $\begin{array}{l} {\sigma _E} = \dfrac{{C{{\text{π}} ^2}EI}}{{A{l^2}}}\text{,} \\ \left\{ \begin{array}{l} {\sigma _C} = {\sigma _E}\text{,}\;\;\;\;\;\;\;\; \left({\sigma _E} \leqslant \dfrac{{{\sigma _y}}}{2}\right) \text{,}\\ {\sigma _C}{\rm{ = }}{\sigma _y}\left({\rm{1 - }}\dfrac{{{\sigma _y}}}{{4{\sigma _E}}}\right)\text{,}\;\;\; \left({\sigma _E} > \dfrac{{{\sigma _y}}}{2}\right) \text{。}\\ \end{array} \right.\;\; \\ \end{array} $ |
其中:
针对上述4种控制载荷,本文选取以横向扭矩为主控载荷,设计工况相对较为严重的lc3作为载荷输入,对连接桥中各种构件进行屈服、屈曲强度校核。
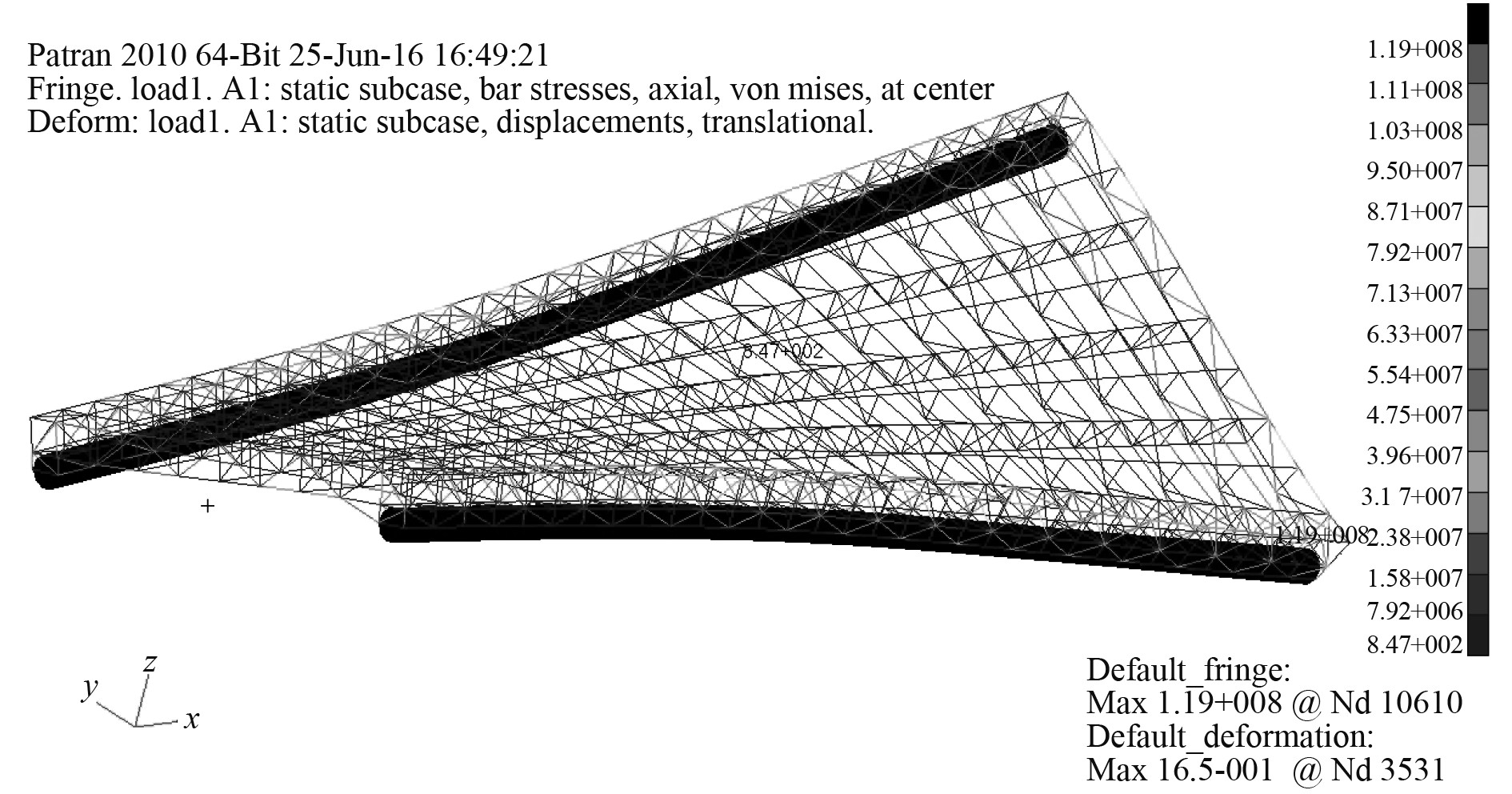
表4和表5为连接桥各构件在以横向扭矩为主控载荷的情况下的轴向拉、压应力,图8为应力云图。
|
|
表 4 连接桥构件屈服强度校核 Tab.4 Yield strength check of cross sturcture |
|
|
表 5 连接桥构件屈曲强度校核 Tab.5 buckling strength check of cross structure |
|
图 8 杆件轴向应力云图 Fig. 8 Axial stress nephogram |
由以上计算结果可知:
在5级海况下,横向支撑杆件以及强框架的拉伸应力超过许用应力的60%,需要进行优化;弱框架的轴向压应力超过临界屈服应力的60%,需要优化。
根据上述计算结果,提升相应杆件的壁厚,并进行优化后的强度校核。表6与表7为优化后的连接桥构件强度校核情况。
|
|
表 6 优化后的构件屈服强度校核 Tab.6 Yield strength check of cross sturcture after optimization |
|
|
表 7 优化后的构件屈曲强度校核 Tab.7 Buckling strength check of cross structure after optimization |
本文基于直接计算法详细校核了小型双体船的钢管桁架连接桥局部强度,并对其中不满足规范要求的构件进行优化。根据以上计算方法,有如下结论:
1)基于三维线性势流理论预报的双体船波浪载荷较为合理可信,能够有效作为后续强度校核的外部载荷;
2)基于直接计算法的对连接桥结构进行结构强度评估,在对部分结构进行优化后连接桥结构局部强度符合强度规范要求;
3)本文对于双体船连接桥的设计以及强度校核方法,可为后续类似船型结构的设计提供一定参考。
| [1] |
任慧龙, 张清越, 江雪云, 等. 大型小水线面双体船结构强度有限元分析[J]. 舰船科学技术, 2015, 37(8): 1-5. DOI:10.3404/j.issn.1672-7649.2015.08.001 |
| [2] |
张清越. 大型小水线面双体船结构强度疲劳分析[D]. 哈尔滨: 哈尔滨工程大学, 2016.
|
| [3] |
程相如. 双体船解雇强度计算[D]. 大连: 大连理工大学, 2012.
|
| [4] |
汪雪良, 顾学康. 穿浪双体船总体载荷设计研究[J]. 船舶力学, 2010, 14(1-2): 56-65. |
| [5] |
戴仰山, 沈进威, 宋竞正. 船舶波浪载荷[M], 北京: 国防工业出版社. 2005.
|
 2019, Vol. 41
2019, Vol. 41
