2. 中国船舶及海洋工程设计研究院,上海,200011
2. Marine Design and Research of China, Shanghai 200011, China
随着船舶航速、吨位以及主机功率不断增加,四桨推进船舶的应用越来越多。由于四桨船舶内外桨采用前后布置,内外桨工作的伴流场存在差异,因而内外桨负荷也会存在差异,近年多型四桨船舶在实船试验中出现内外桨负荷差异大的现象,对四桨船舶的船机桨匹配产生不利影响,主要体现在转速达不到额定值,最大航速到不到指标,主机超负荷,严重时可能会出现拉缸等问题。针对四桨船舶内外桨负荷分配问题,多家研究单位开展了船后螺旋桨和附体对伴流场和水动力性能的影响研究[1 – 3],针对内外桨负荷差异现象,提出了螺旋桨差异化设计方法[4]。
本文针对四桨船舶在拖曳水池自航模型试验中难以有效模拟内外桨负荷差的现象,建立四桨船舶自航数值计算方法,开展四桨船舶内外桨负荷数值计算和内外桨伴流场数值计算:对比不同缩尺比下四桨船舶内外桨负荷和伴流场计算结果,分析四桨船舶内外桨负荷差尺度效应影响规律。
1 数值计算方法 1.1 仿真计算前处理1)建立三维数字模型
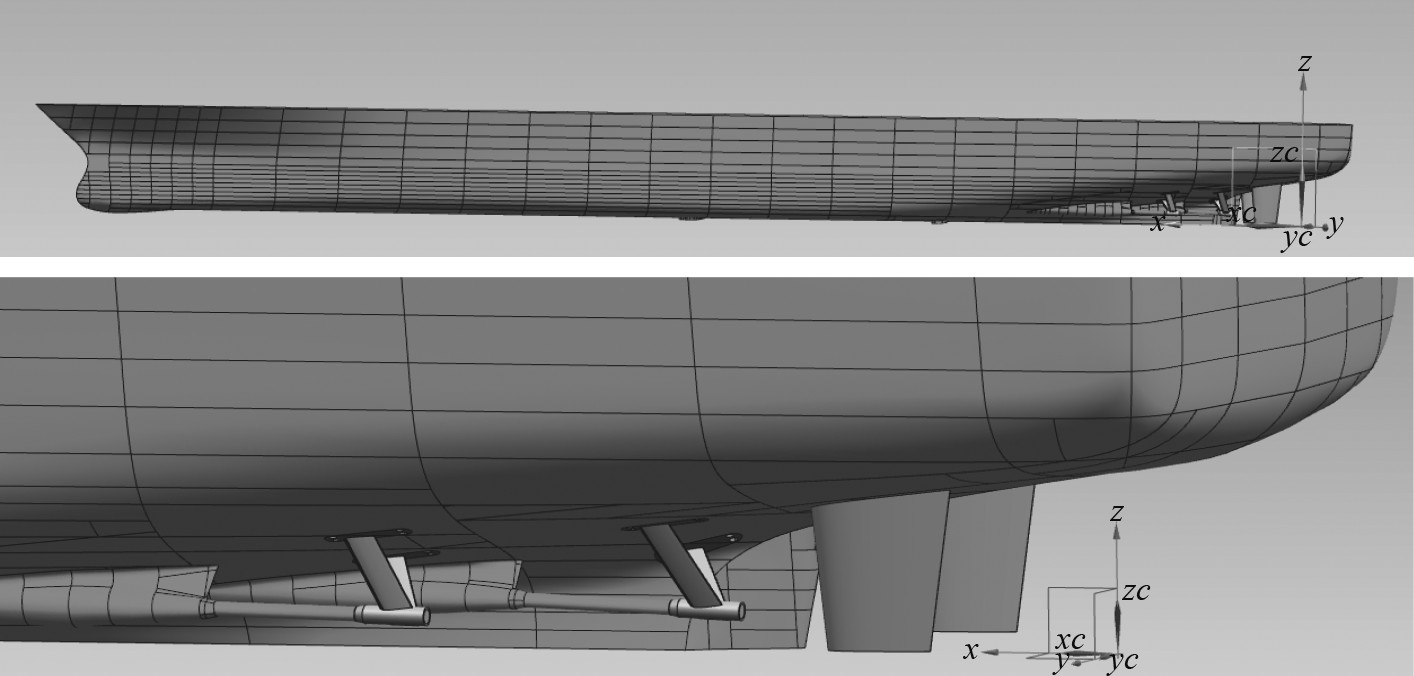
船体型线图、附体图和螺旋桨型线图为设计输入,在满足计算要求的前提下,对船体及附体(包括前机炉、后机炉、前轴包套、前支架、后轴包套、后支架、舭龙骨、呆木、舵)使用UG软件建立三维数字模型,如图1所示。
|
图 1 三维数字模型 Fig. 1 The three-dimensional digital model |
2)建立计算域
本研究计算域尺寸设置为:入口距离船首1倍船长,出口距离船尾2倍船长,左右两侧距离船舷各1倍船长,池底距离船底1倍船长。船体兴波阻力的计算考虑自由液面,在初始化设置中,将船体水线以上部分填充为空气,水线以下全部填充为水,速度入口划分为空气入口和水流入口,但二者速度大小一致,通过改变入口空气和水流的速度大小来模拟不同航速下船体的粘性绕流。
由于船体尾部型线曲率较大,且带有大量形状复杂的附体,划分结构化网格比较困难。为了网格的划分方便,将船体尾部的一部分流域单独划分出来,划分非结构化网格。
船桨一体船舶自航计算时,在桨轴后给内外螺旋桨分别创建一个圆柱形小域,小域与桨毂同轴,其直径等于3.2倍螺旋桨直径,通过MRF方法模拟螺旋桨旋转运动。
3)网格划分
采用混合形式网格方案,发挥四面体网格贴体性好和六面体网格计算效率高的优点。计算域内的大部分结构使用六面体网格,只在特别复杂的部位采用非结构化的网格划分形式,提高计算结果的精度。
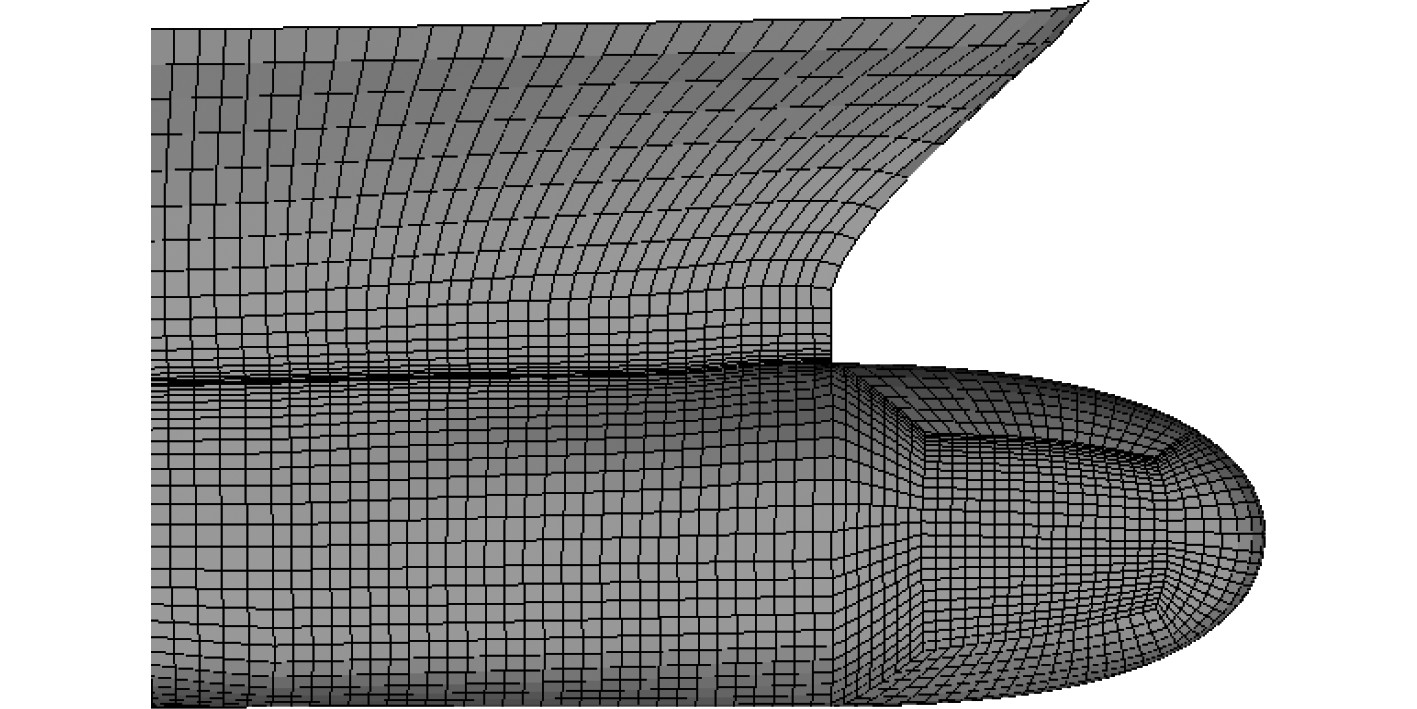
网格划分采用前处理软件ICEM完成,结构化六面体网格采取多块方式划分,在球鼻首处由于其曲面曲率大,采用O网剖分提高局部网格质量,球鼻首网格如图3所示。

|
图 3 船体表面网格 Fig. 3 The hull surface grid |
|
图 2 球首处O网划分 Fig. 2 The O type grid on Bulbous bow |
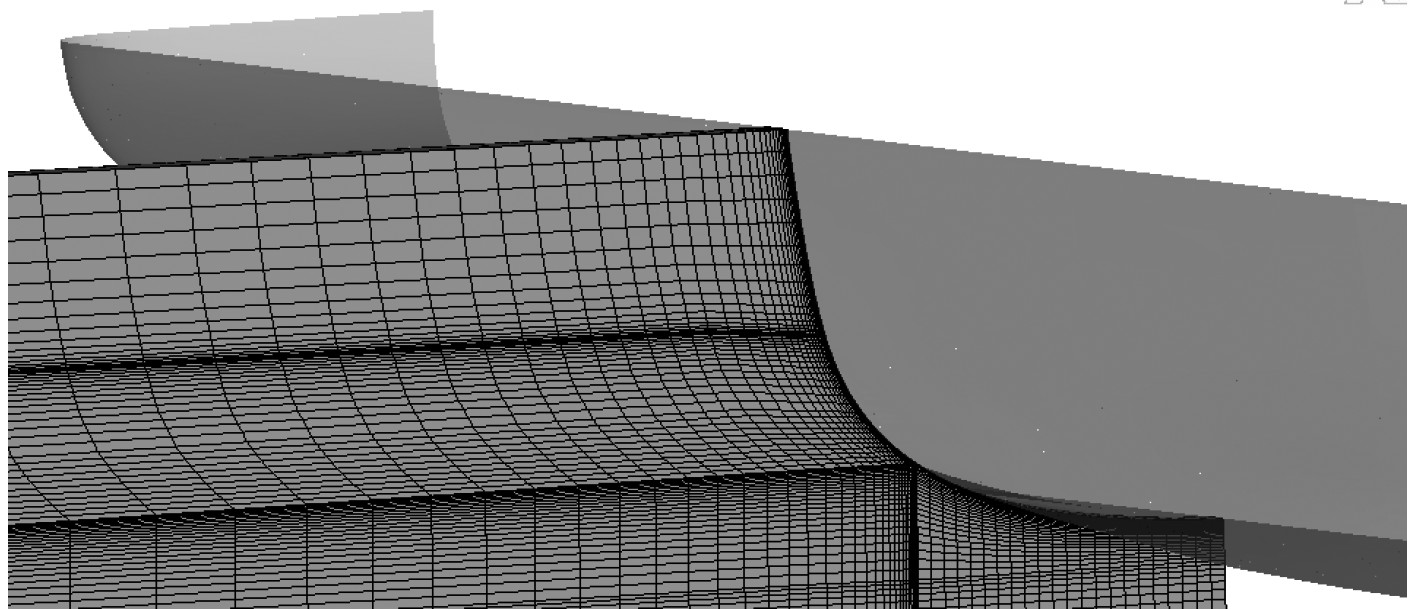
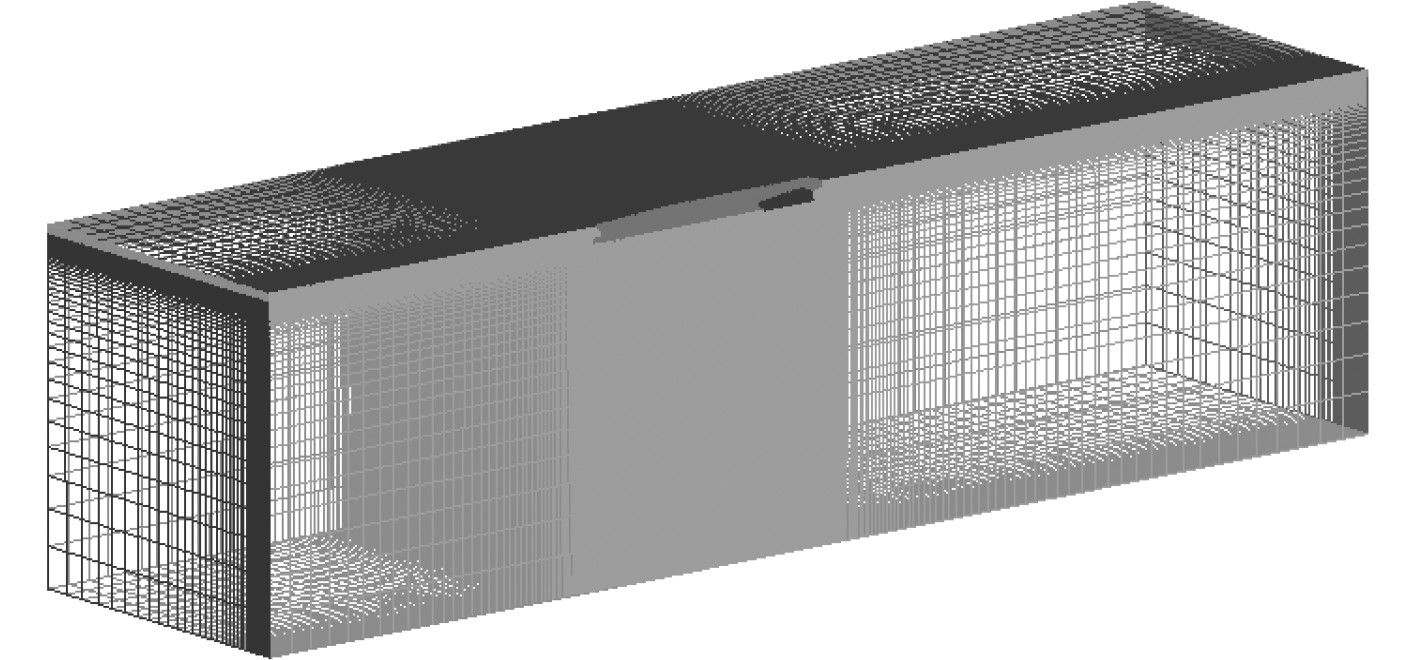
流域网格的疏密采用近船体流域网格紧密,远场流域网格稀疏的原则。为了保证粘性流场计算的准确性,Y+值控制在60左右。在模型尺度阻力计算时,为了能较好地捕捉自由液面,对靠近水线处的网格进行适当加密。网格划分如图3~图5所示。
|
图 4 网格剖面图 |
|
图 5 数值水池整体网格 |
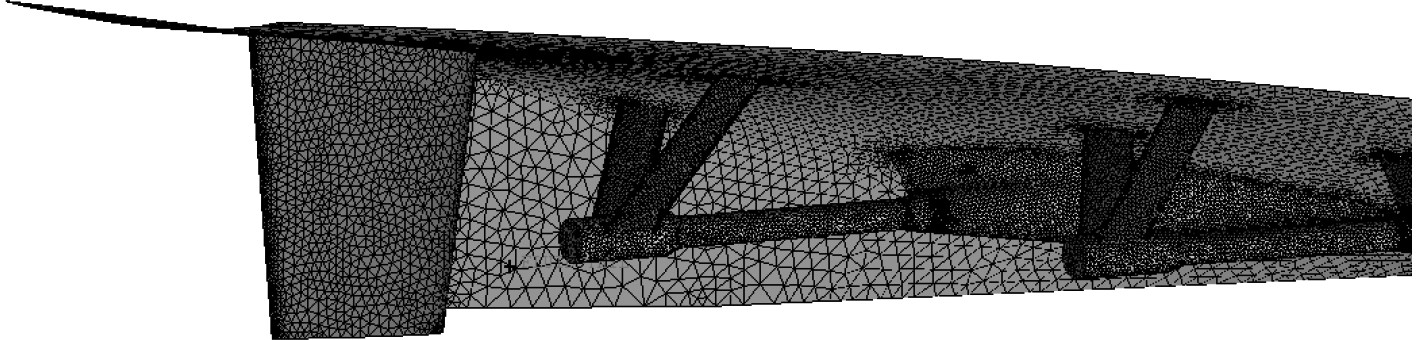
船尾非结构网格划分,对附体进行局部加密,以更好地表达其几何形状,尾部网格如图6所示。整体计算网格数目为842万。
|
图 6 附体网格示意图 Fig. 6 The appendage grid |
对于船桨一体网格划分,采用包裹螺旋桨的小域单独进行网格划分,通过interface与船尾网格连接组装。考虑到螺旋桨叶片形状复杂,对螺旋桨小域采取非结构网格划分,并对叶根和叶梢处的网格加密。螺旋桨网格如图7和图8所示。船桨一体网格如图9所示,整船网格总数为1 200万。

|
图 7 叶梢和叶根处网格示意图 |

|
图 8 螺旋桨网格 |

|
图 9 船桨一体网格 |
1)湍流模型[5]
计算采用RANS平均法,并选用SST k-ω模型来数值模拟船体周围流体流动。
SST k-ω的流动方程:
| $\frac{\partial }{{\partial t}}\left( {\rho k} \right) + \frac{\partial }{{\partial {x_i}}}\left( {\rho k{u_i}} \right) = \frac{\partial }{{\partial {x_j}}}\left( {{\varGamma _k}\frac{{\partial k}}{{\partial {x_j}}}} \right) + {G_k} - {Y_k} + {S_k}\text{,}$ | (1) |
| $\frac{\partial }{{\partial t}}\left( {\rho \omega } \right) + \frac{\partial }{{\partial {x_i}}}\left( {\rho \omega {u_i}} \right) = \frac{\partial }{{\partial {x_j}}}\left( {{\varGamma _\omega }\frac{{\partial \omega }}{{\partial {x_j}}}} \right) + {G_\omega } - {Y_\omega } + {D_\omega } + {S_\omega }\text{。}$ | (2) |
其中:Gk为湍流的动能;Gω为ω方程;Гk,Гω为k与ω的有效扩散项;Yk,Yω为k与ω的发散项;Dω为正交发散项。
2)VOF模型[6]
采用VOF方法来追踪自由液面,将整个计算区域定义为Ω,主相流体区域记为Ω1,副相流体区域记为Ω2。
| $\omega \left( {\vec x,t} \right) = \left\{ {\begin{array}{*{20}{c}} {1,\begin{array}{*{20}{c}} {}&{\vec x \in {\varOmega _1}} \text{;} \end{array}} \\ {0,\begin{array}{*{20}{c}} {}&{\vec x \in {\varOmega _2}} \text{。} \end{array}} \end{array}} \right.$ | (3) |
此外,在由2种互不相溶流体构成的流场中,流体的速度场记为
| $\frac{{\partial \omega }}{{\partial t}} + u\frac{{\partial \omega }}{{\partial x}} + v\frac{{\partial \omega }}{{\partial y}} = 0\text{。}$ | (4) |
在每个网格
| ${C_{ij}} = \frac{1}{{\Delta {V_{ij}}}}\int_{{I_{ij}}} {\omega (\vec x} ,t){\rm d}V\text{,}$ | (5) |
VOF函数也满足式(4):
| $\frac{{\partial C}}{{\partial t}} + u\frac{{\partial C}}{{\partial x}} + v\frac{{\partial C}}{{\partial y}} = 0\text{。}$ | (6) |
当C=0时,网格中全为副相流体;当C=1的时,网格充满主相流体;当0<C<1时,则是含有流体界面的网格,成为界面网格。
3)边界条件设置
边界条件设置为:上游入口采用速度入口,给定均匀来流的速度值;下游出口采用静压出口,通过UDF编写函数控制压力随水深线性变化,忽略扰动;上边界和中间面采用对称面边界条件;下边界、侧面以及船体表面定义无滑移、不可穿透的壁面边界条件。螺旋桨旋转运动通过MRF方法来模拟。
2 数值计算方法验证 2.1 船模阻力数值模拟针对某四桨船型,采用数值计算方法计算全附体船模阻力,并与模型试验结果进行比较,如表1所示。船体周围流线如图10所示。
|
|
表 1 船模阻力计算结果 Tab.1 The calculation results of ship model resistance |
|
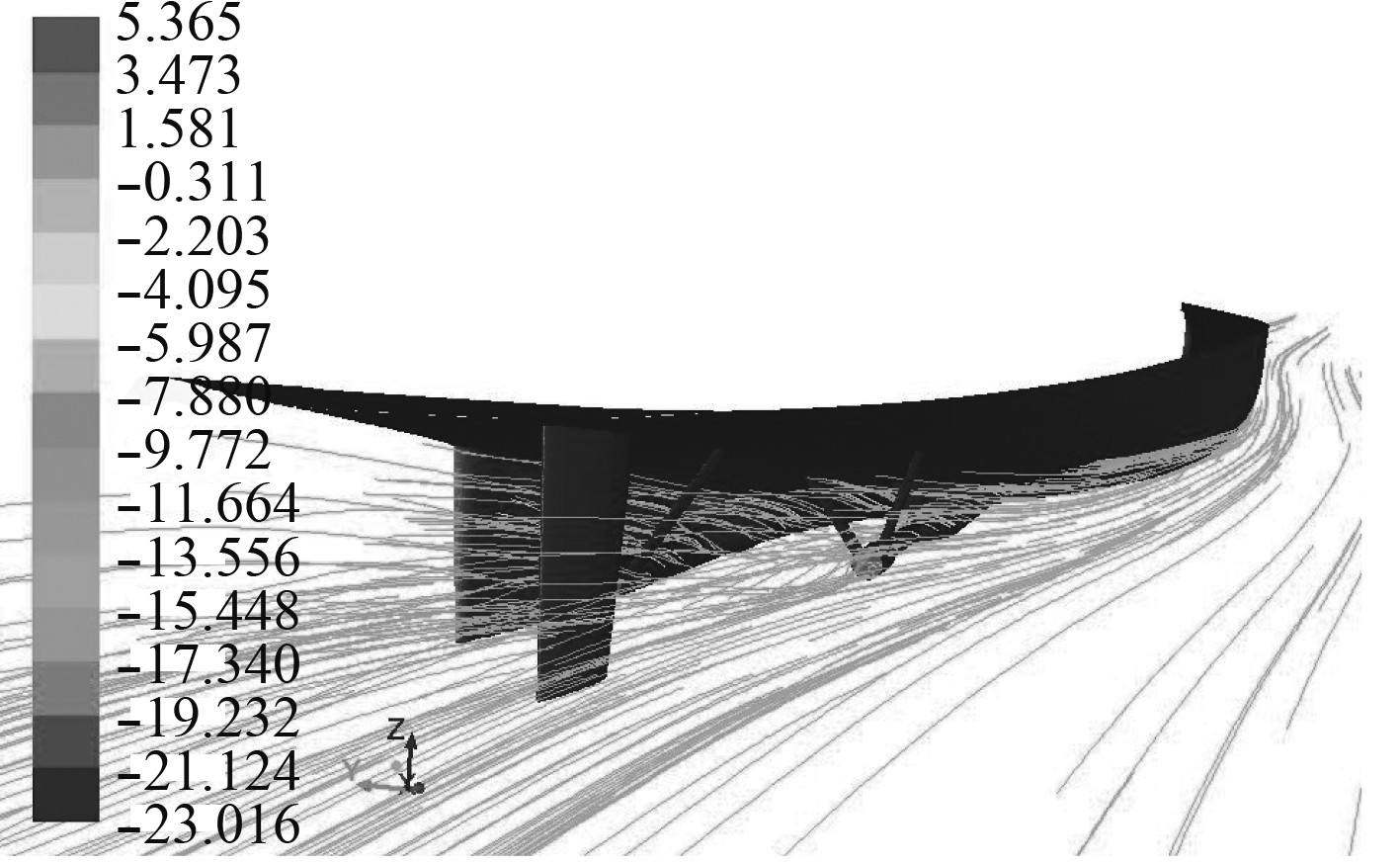
图 10 阻力计算船体周围流线图 Fig. 10 The flow line around the hull in resistance calculation |
分析表1可知,不同航速的试验值和计算值最大偏差为4.84%,随着航速的增大,偏差逐渐减小,计算值与试验值吻合良好,误差均在5%以内。因此,所采用的数值仿真方法能够较准确预报船模阻力,可用于模拟螺旋桨桨盘面伴流场。
2.2 内外桨负荷数值模拟针对某四桨船型,采用数值计算方法,开展实尺度下船桨一体自航计算,得到不同航速的内外桨负荷差,如表2所示。船体周围流线如图11所示。
|
|
表 2 内外桨负荷差 Tab.2 The load difference between inside and outside propeller |

|
图 11 自航计算船体周围流线图 Fig. 11 The flow line around the hull in self-propelled calculation |
分析表2可知,不同航速工况下的内外桨负荷差均在10%以上。随着航速增加略有减小,在进5最大航速工况下内桨负荷比外桨大约11%左右,与多型四桨船型出现的内外桨负荷差量级接近。
3 内外桨负荷差尺度效应分析为了分析四桨船型内外桨负荷差尺度效应,针对某四桨船型进5工况下,开展不同缩尺比下的内外桨负荷数值计算,计算结果如表3所示。内外桨负荷差随尺度变化(雷诺数)曲线如图12所示。
|
|
表 3 不同缩尺比下内外桨负荷差 Tab.3 The load difference between inside and outside propeller under different scaling ratios |
|
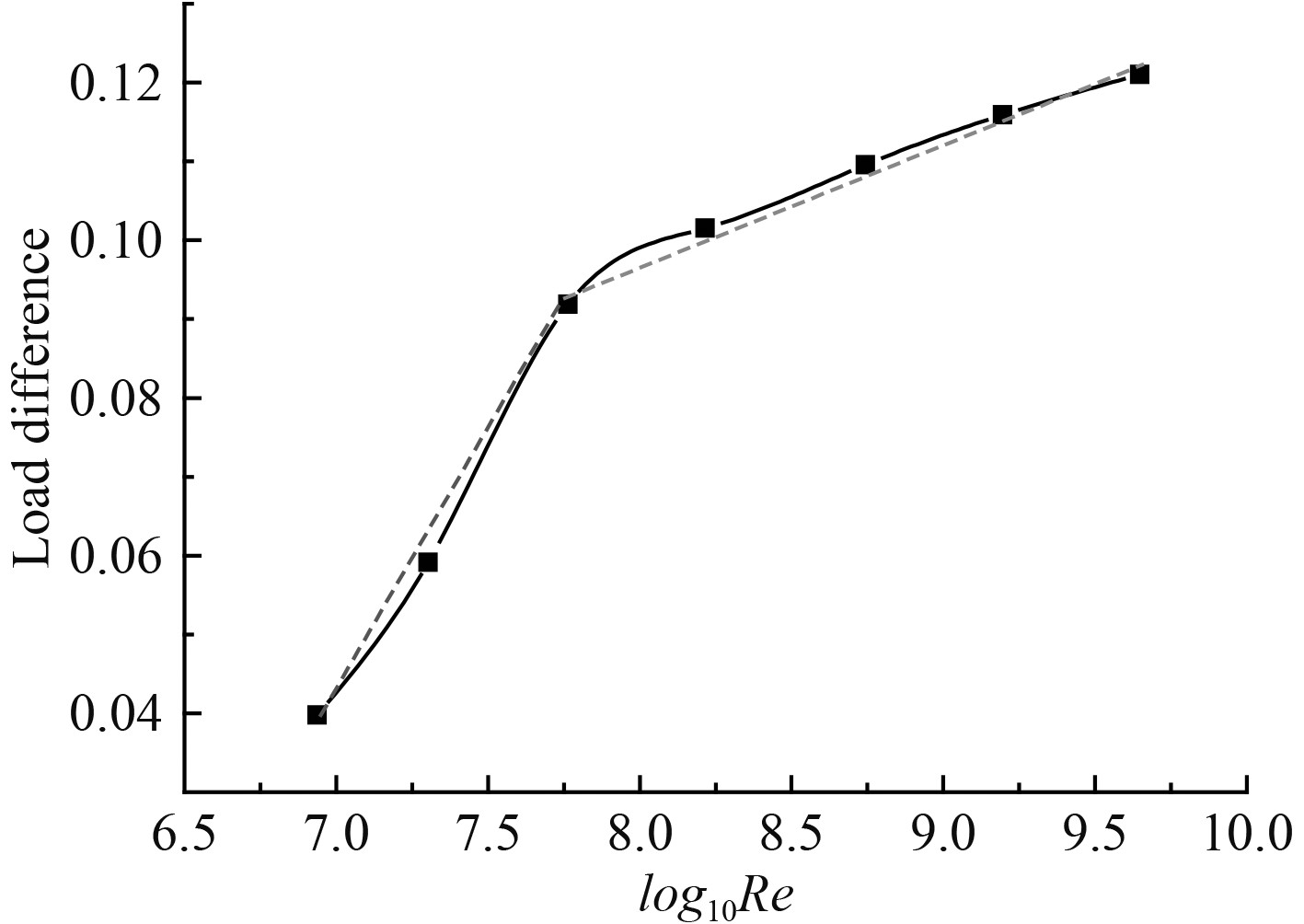
图 12 内外桨负荷差随尺度变化曲线 Fig. 12 The changing curve of load difference between inside and outside propeller under different scaling ratios |
分析表3和图12可知,随着尺度的增大,内外桨负荷差逐渐增大,在缩尺比大于16时,内外桨负荷差受船模尺度影响较大;当缩尺小于16时,内外桨负荷差受船模尺度影响较小,其中拐点在16缩尺比处。计算船体模型从1~64缩尺比下船体雷诺数均超过临界雷诺数(3×105),但在缩尺比较大时,螺旋桨雷诺数和桨近前方轴支架雷诺数则低于临界雷诺数,螺旋桨和轴支架雷诺数与负荷差关系如表4所示。
|
|
表 4 螺旋桨和轴支架雷诺数与负荷差关系 Tab.4 The relationship between the load difference and propeller, shaft bracket |
分析表4可知,在缩尺比为16时,螺旋桨雷诺数超过临界雷诺数,轴支架接近临界雷诺数,此时内外桨负荷差变化速率出现拐点,但缩尺比小于16时,内外桨负荷差量级基本相当。由于轴支架位于螺旋桨近前方对螺旋桨的进流产生较大影响,当轴支架雷诺数小于临界雷诺数时,船尾流场与实尺度存在较大差异,导致内外桨负荷差计算值与实尺度相差较大。
4 伴流场尺度效应分析为进一步分析四桨船型内外桨负荷差异的原因,开展全体附体船模不同缩尺比下桨盘面伴流场模拟,得到不同缩尺比下内外桨盘面伴流场,如图13所示。

|
图 13 不同缩尺比下内外桨盘面轴向伴流 Fig. 13 The axial wake of inside and outside propeller under different scaling ratios |
分析图13可知,横向对比来看,内桨伴流更大,伴流分布更加不均匀,主要由于内桨更靠近船体,桨盘面伴流受船体的影响更大。纵向比较来看,随着尺度增大,伴流分数等于0.1的等值线逐渐向内收缩,内外桨的伴流逐渐减小。
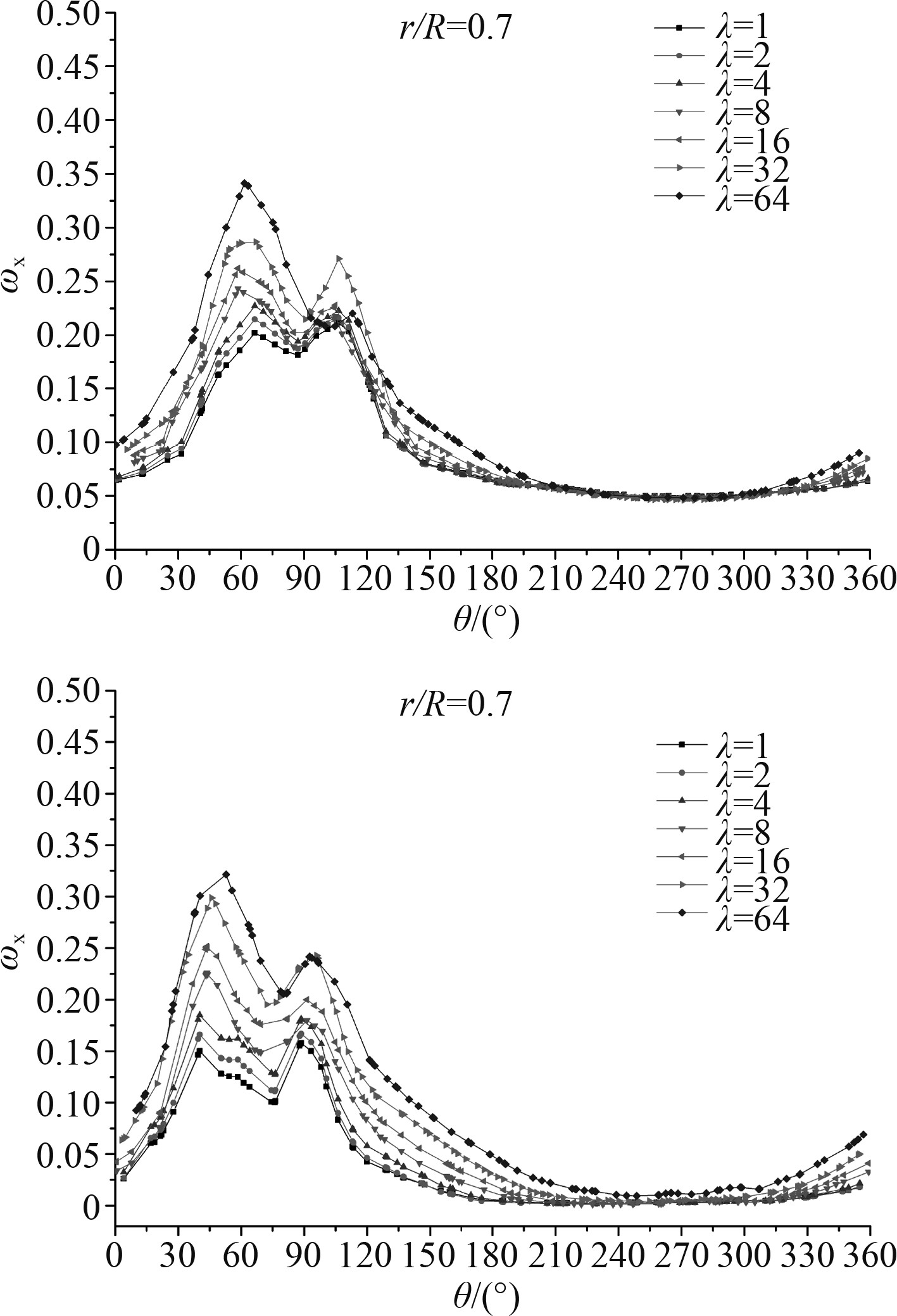
针对螺旋桨典型半径0.7R处,不同尺度下内外桨轴向伴流的周向分布如图14所示。图中更直观的体现了尺度效应对伴流的影响,尺度越大,伴流越小。
|
图 14 不同尺度0.7半径处内外桨轴向伴流的周向分布 Fig. 14 The circumferential distribution of axial wake of inside and outside propeller under different scaling ratios |
不同缩尺比下内外桨平均轴向伴流分数及伴流分数差如表5所示。从表5可知,横向对比来看,内桨伴流分数更大。纵向比较来看,随着尺度增大,平均轴向伴流逐渐减小。随着尺度的增加,内外桨的伴流分数差逐渐增大。
|
|
表 5 不同缩尺比下内外桨平均轴向伴流分数及伴流分数差 Tab.5 The average axial wake fraction and wake fraction difference of inside and outside propeller under different scaling ratios |
本文开展了四桨船型不同缩尺比下的内外桨负荷数值计算和伴流场计算,通过比较分析得到以下结论:
1)随着船模尺度增大,内外桨负荷差计算值逐渐增大,在缩尺比大于某个值时,内外桨负荷差受船模尺度影响较大,当缩尺比小于该值时,内外桨负荷差受船模尺度影响较小,其中拐点在该缩尺比处;
2)随着船模尺度增大,内外桨盘面伴流逐渐减小,但内外桨的伴流分数差逐渐增大;
3)在四桨船型自航计算中,内外桨负荷差存在较大的尺度效应,螺旋桨和轴支架雷诺数均需大于临界雷诺数,以确保内外桨负荷差计算结果满足精度要求。
| [1] |
王展智, 熊鹰, 齐万江, 等. 船后桨的布局对螺旋桨水动力性能的影响[J]. 哈尔滨工程大学学报, 2012, 33(4): 427-431. DOI:10.3969/j.issn.1006-7043.201105013 |
| [2] |
王展智, 熊鹰, 刘志华, 等. 双臂轴支架的剖面形状和安装角度对船舶伴流场的影响[J]. 中国舰船研究, 2012, 7(4): 23-29. DOI:10.3969/j.issn.1673-3185.2012.04.005 |
| [3] |
覃新川, 黄胜, 常欣. 四桨两舵推进系统的水动力干扰研究[J]. 中国造船, 2008, 49(3): 112-116. DOI:10.3969/j.issn.1000-4882.2008.03.015 |
| [4] |
叶礼裕, 常欣, 孙帅, 等. 四桨船舶螺旋桨差异化设计[J]. 哈尔滨工程大学学报, 2017, 38(5): 668-675. |
| [5] |
GIULIO D, ROBERTO M, ANDREA D M. Analysis of the performance of a marine propeller operating in oblique flow[J]. Computer & Fluid, 2013, 75: 86-102. |
| [6] |
倪崇本. 基于CFD的船舶阻力性能综合研究[D]. 上海: 上海交通大学, 2011
|
 2019, Vol. 41
2019, Vol. 41
