2. 中船重工(上海)节能技术发展有限公司,上海 210000
2. Marine Energy Saving Technology Development Company (Shanghai) of CSIC, Shanghai 210000, China
船舶阻力预报是准确预报船舶快速性的重要内容之一,目前常用的预报方法有模型试验,CFD数值模拟和一些近似估算方法。在现代船舶工程中,近似模型方法很好地解决了船舶CFD计算的复杂耗时问题[2],避免了模型试验的繁琐过程与较高成本。陈爱国等[3 – 4]基于系列60船舶试验数据,建立了最佳的BP神经网络系统,拓展了系列60的应用范围。李纳等[5]建立了基于广义回归神经网络的“船型要素—船体阻力”数学模型,并结合遗传算法完成了船型要素的优化设计,优化结果可以为玻璃钢渔船初步设计提供技术参考。肖振业等[6]采用支持向量和神经网络方法建立了国际船模KCS总阻力的近似模型,表明了支持向量机近似模型具有较好的预测精度和可推广能力。Devrim[7]在低雷诺数条件下,采用神经网络方法对双体船中心片体的形状、布置位置进行了选择优化。通过与模型试验结果的分析对比,表明了这种外形设计的有效性,可以减少波干扰所引起的阻力。Jong-hyun Lee等[8]基于遗传规划的非线性数学函数的方法,在船型设计初期对船舶附加阻力进行预报,通过预测结果与试验结果、理论结果的对比分析,表明该方法满足精度要求,具有一定的适用性。
采用近似模型方法解决船舶阻力相关问题已经受到许多学者的广泛关注,但近似模型方法有很多,为了提高船舶阻力预报的准确性,应该有针对性地选择预报模型。为此,本文以公开的泰洛系列船模试验数据为例,研究目前机器学习模型在船舶阻力预报中的应用效果。泰洛系列船模试验是以一艘军舰为母型进行系列改型[9],生成不同宽度吃水比B/T、棱形系数Cp、排水体积长度系数1 000
本文选取机器学习模型中6种经典的回归预报模型进行试验论证,即KNN近邻回归、多元线性回归、岭回归、标准支持向量回归、3层BP神经网络、回归树。
1.1 KNN近邻回归KNN近邻回归属于非参数回归方法,是通过搜索历史样本库中与新样本相似的样本数据来进行预测,需要考虑的主要因素包括:从历史样本库中选取与新样本距离较近的样本个数(K值)、近似程度度量方式、K个历史样本的权重函数和内部实现算法。本文选取比较常用的欧式距离度量方式,公式如下:
| ${d_i} = \sqrt {\sum\limits_{i = 1}^n \left({V_i} - \mathop {\mathop {V_i}\limits^\Lambda}\right)^2}\text{。}$ | (1) |
式中:
而其他3个因素在已有文献中也是针对各自的试验数据选取最优参数值[10],因此本文结合所选数据集特点,选取等比重函数和距离反比函数2种权重函数、kd树与暴力搜索2种内部实现算法、K值大小进行试验,以选出最优参数,有关权重函数与内部实现算法的具体介绍可参考文献[11]。
1.2 多元线性回归与岭回归多元线性回归是自变量多于一维时的回归形式,具体的方程形式为:
| ${y_i} = x_i^{\rm T}{ w}\text{。}$ | (2) |
式中:
多元线性回归的目标是寻找使真实值与预测值误差平方和最小的一组权值矩阵。误差平方和可写为:
| $\sum\limits_{i = 1}^m {({y_i}} - x_i^{\rm T}w{)^2}\text{,}$ | (3) |
上式对
| $\mathop {w}\limits^\Lambda = {({X^{\rm T}}X)^{ - 1}}{X^{\rm T}}y\text{,}$ | (4) |
其中
由于上式需要对矩阵求逆,当矩阵非满秩时求逆会出现问题,因此采用缩减系数法来解决这一问题,岭回归即是其中的一种。岭回归是在矩阵
支持向量回归是通过特征空间中估计内积的核隐式,实现输入变量到高维特征空间的映射,然后在高维特征空间中构建线性回归函数,对应原空间非线性问题的求解[2]。数学表达式为:
| $f(x) = {\omega ^{\rm T}}{\rm{\cdot}}\varphi (x) + b\text{。}$ | (5) |
式中:
| $\begin{split} &\min \frac{1}{2}||\omega |{|^2} + C\sum\limits_{i = 1}^l {({\xi _i}} + \xi _i^*)\text{,}\\ &\left\{ \begin{array}{l} {\rm s.t.}{y_i} - {\omega ^{\rm T}}\varphi ({x_i}) - b \leqslant \varepsilon + {\xi _i}\text{,}\\ {\omega ^{\rm T}}\varphi ({x_i}) + b - {y_i} \leqslant \varepsilon + \xi _i^*\text{,}\\ {\xi _i},\xi _i^* \geqslant 0,i = 1,2, \cdots ,l\text{。} \end{array} \right. \end{split}$ | (6) |
式中:
| $f(x) = \sum\limits_{i = 1}^l {({\alpha _i}} - \alpha _i^*) \cdot K({x_i} \cdot x) + b\text{。}$ | (7) |
因此,支持向量回归模型的设计需要选择合适的精度参数
人工神经网络基本单元如图1所示。图中
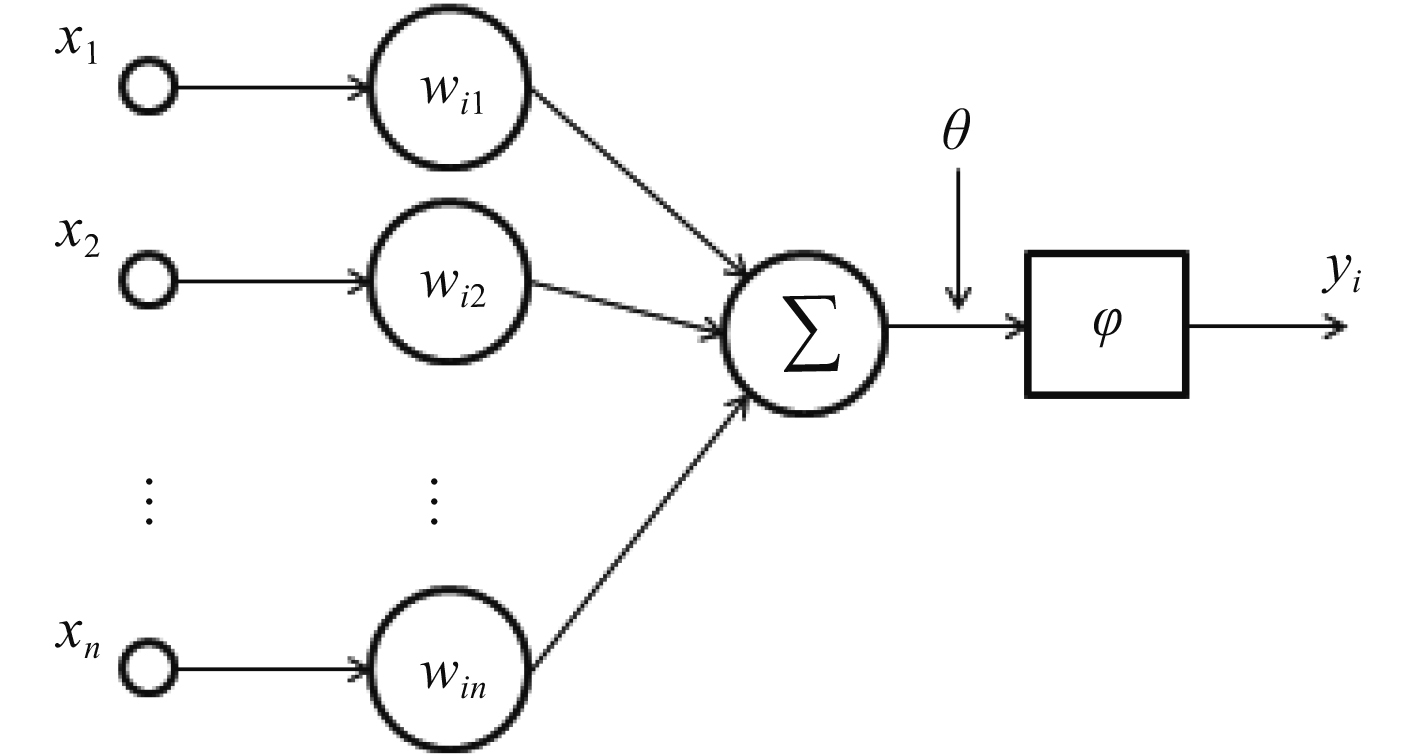
|
图 1 人工神经网络基本单元 Fig. 1 Basic unit of artificial neural network |
| ${y_i} = \phi \left(\sum\limits_{j = 1}^n {{w_{ij}}} {x_j} - \theta \right)\text{。}$ | (8) |
BP神经网络的主要思想为对于样本若干个输入向量以及与其对应的目标向量,根据网络实际输出与目标向量之间的误差,选用合适算法修改权值和阈值,使网络输出层的误差平方和达到最小[14]。
1.5 回归树回归树是一种非参数监督学习方法,基本思想是通过给定数据集的特性采用某种算法推断出简单的决策规则,进而预测目标变量的值。树构建算法中常用的是CART算法,即使用二元切分来处理连续性变量。具体算法过程如下:
在训练数据集所在的输入空间中,递归地将每个区域划分为2个子区域并决定每个子区域上的输出值,构建二叉决策树[15]。
1) 选择最佳切分变量j与切分点s,求解
| $\mathop {\min }\limits_{j,s} [\mathop {\min }\limits_{{c_1}} {\sum\limits_{{x_i} \subset {R_1}\left( {j,s} \right)} {\left( {{y_i} - {c_1}} \right)} ^2} + \mathop {\min }\limits_{{c_2}} {\sum\limits_{{x_i} \subset {R_2}(j,s)} {({y_i} - {c_2})} ^2}]\text{。}$ | (9) |
式中:
2) 遍历变量j,对固定的切分变量j寻找切分点s,找到可使式(9)达到最小值的(j,s),用选定的(j,s)划分区域并决定相应的输出值:
| $\begin{split} &{R_1}(j,s) = \{ x|{x^{(j)}} \leqslant s\} ,{R_2}(j,s) = \{ x|{x^{(j)}} > s\} \text{,}\\ &\mathop {{c_m}}\limits^\Lambda = \frac{1}{{{N_m}}}\sum\limits_{{x_i} \subset {R_m}(j,s)} {{y_i}} ,x \subset {R_m},m = 1,2\text{。} \end{split}$ | (10) |
3) 继续对2个子区域重复步骤1和步骤2,直至满足条件,
4)最终可将输入空间划分为若干区域,假定M个:R1,R2,···Rm,并生成回归树:
| $f(x) = \sum\limits_{m = 1}^M {\mathop {{c_m}}\limits^\Lambda } I(x \subset {R_m})\text{。}$ | (11) |
为选取合适的k值、权重函数和内部实现算法,开展不同组合参数的方案设计,得到均方误差与相关系数随k值数的变化曲线,如图2所示。
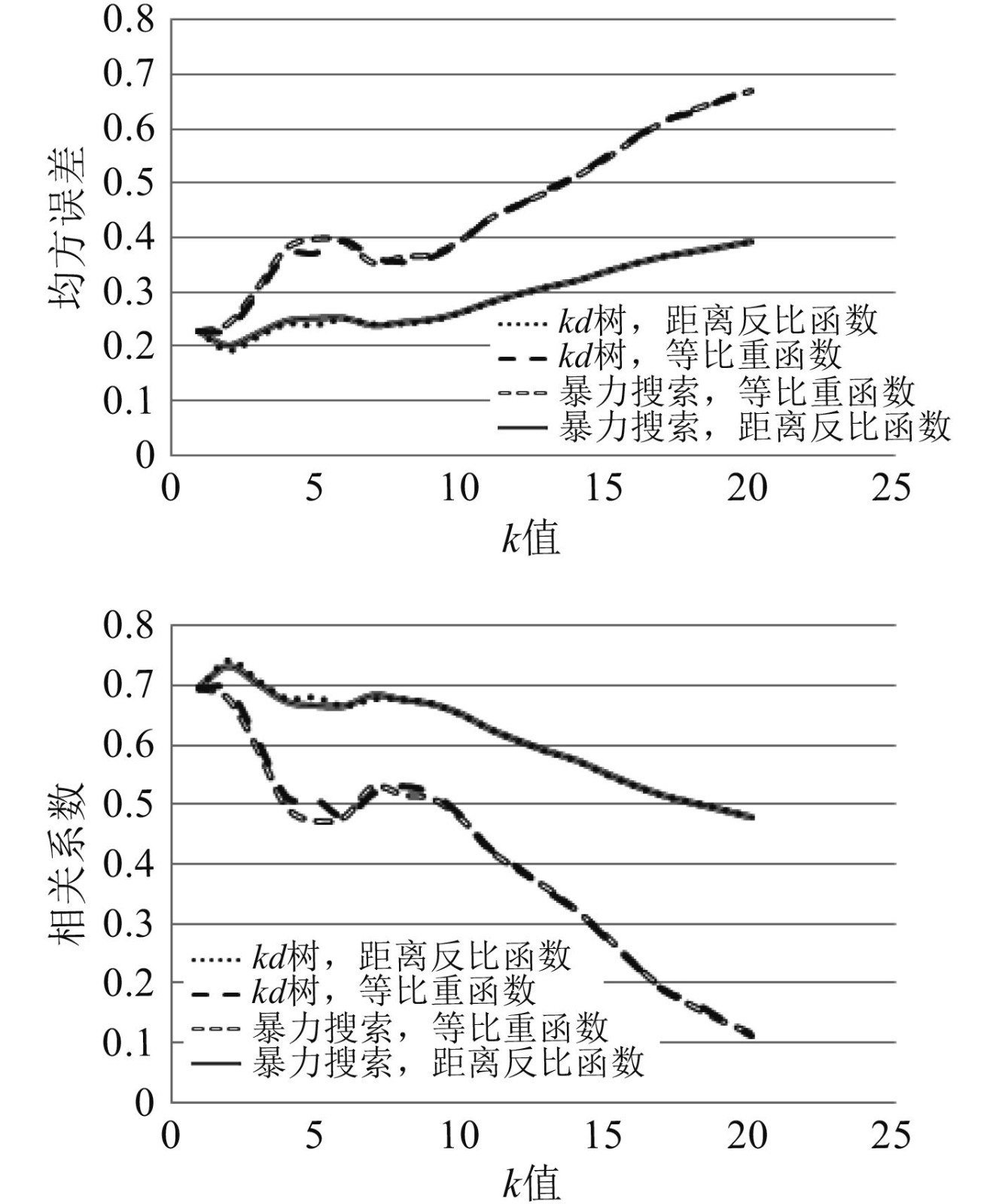
|
图 2 均方误差、相关系数随不同KNN算法参数变化曲线 Fig. 2 Variation curves of mean square error and correlation coefficient with different KNN algorithm parameters |
由图2可知,当k值为2时,相关系数出现峰值,而后随k值的增加逐渐减小,均方误差也在k值为2时出现低谷,之后随k值增加而增大;而在内部实现算法与权重函数的选择上,kd树算法与距离反比函数的组合最优。故本文选择k=2,kd树算法,距离反比函数的KNN近邻回归模型。
2.2 岭回归模型设计岭回归主要调节参数为
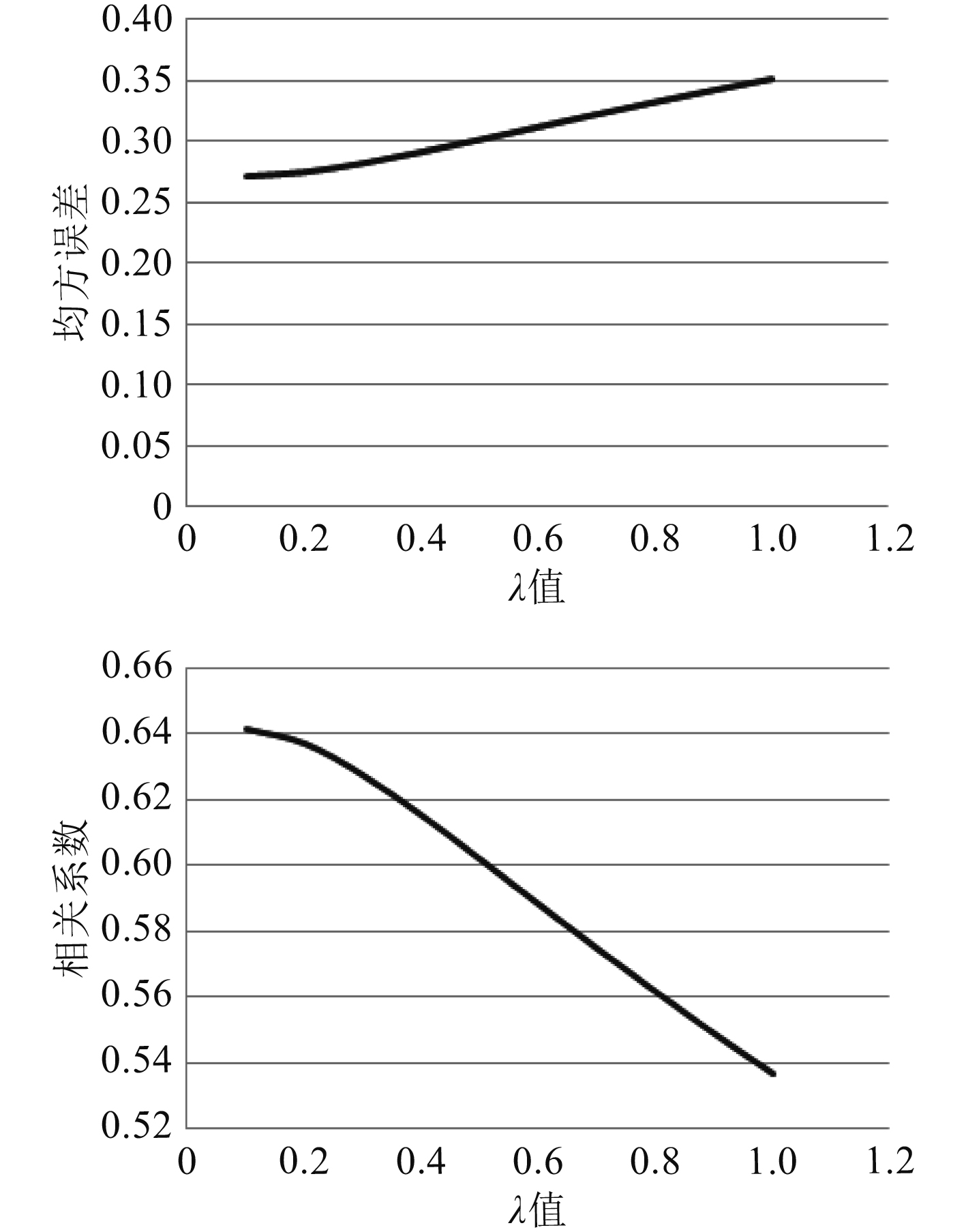
|
图 3
均方误差、相关系数随岭回归
|
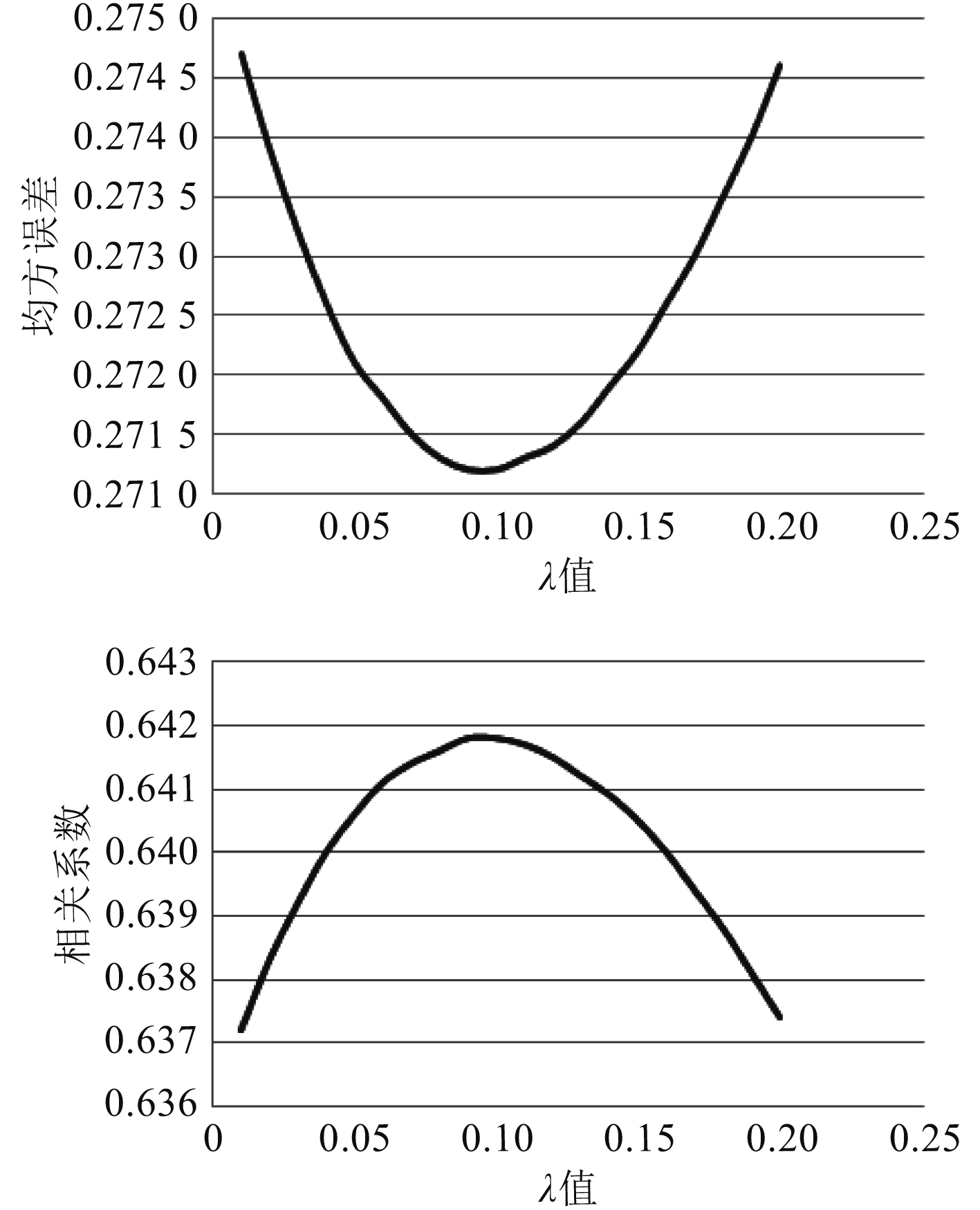
|
图 4
均方误差、相关系数随岭回归
|
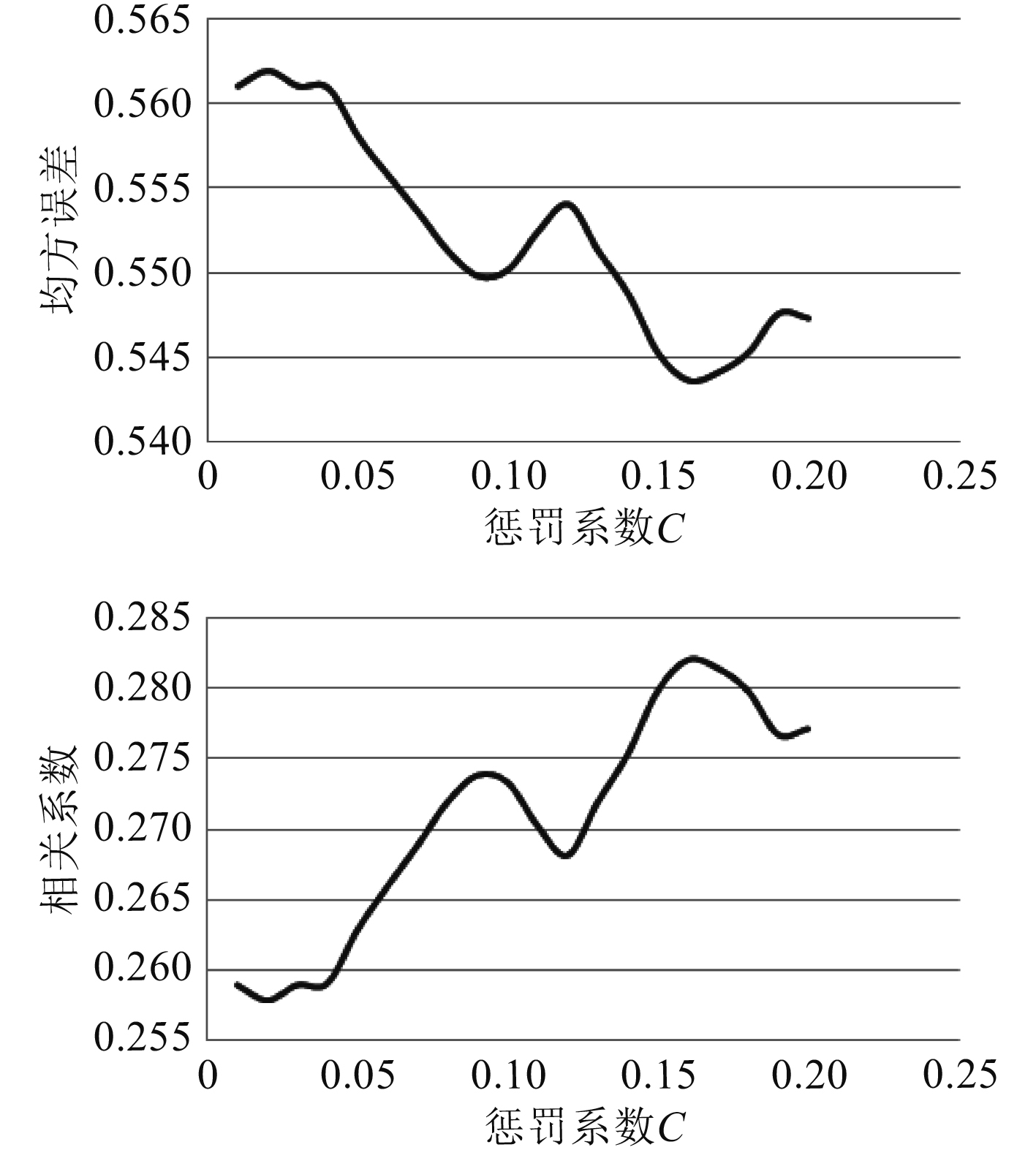
根据文献[13]可知,在预报船舶阻力时,支持向量回归模型需要考虑的参数有惩罚系数
|
|
表 1 不同核函数的相关系数与均方误差比较结果 Tab.1 Comparison results of correlation coefficients and mean square error of different kernel functions |
|
图 5
均方误差、相关系数随惩罚系数
|

|
图 6
均方误差、相关系数随拟合精度
|
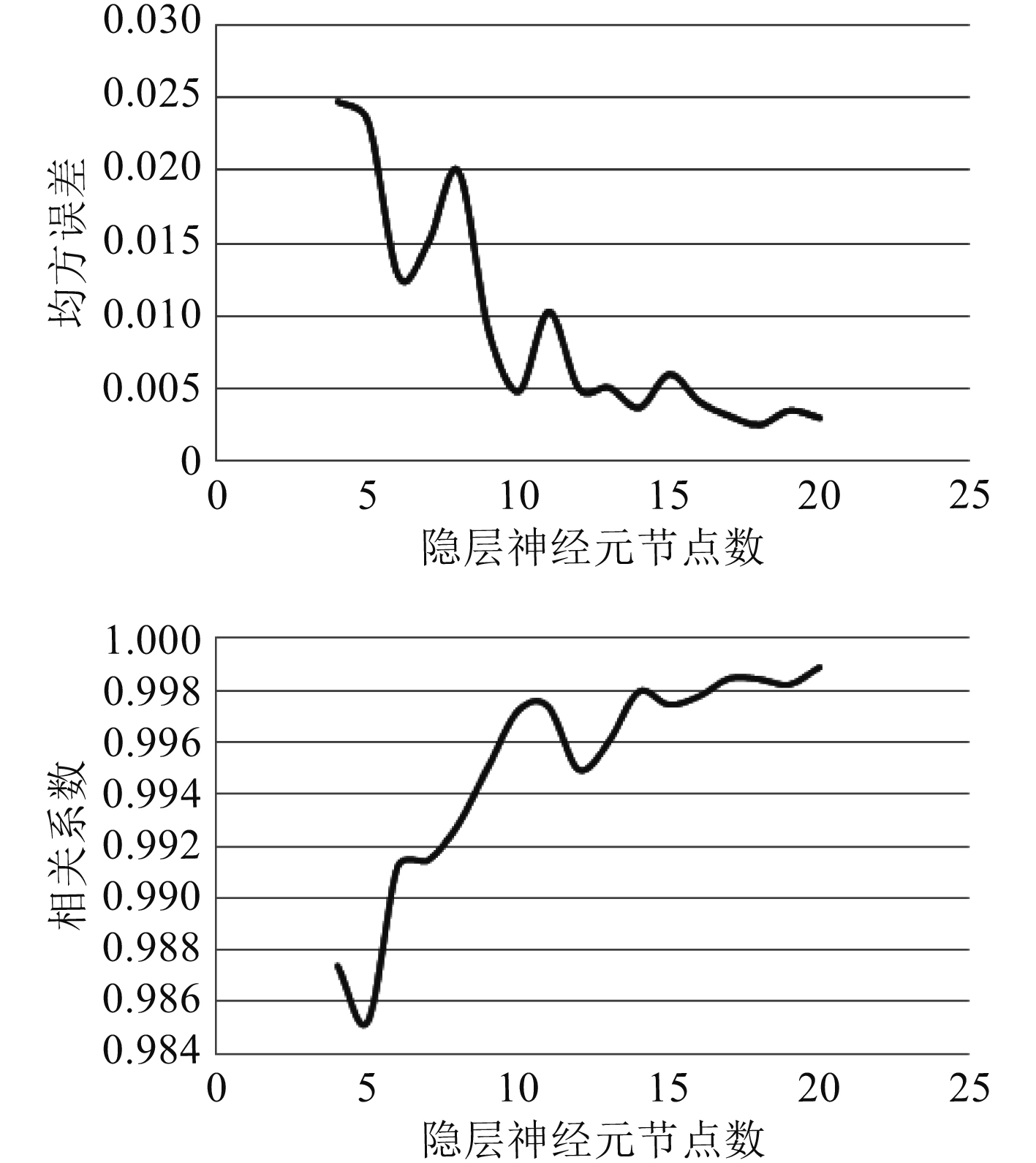
通过参考文献[3],选择贝叶斯正则化函数作为训练函数,均方误差规则化函数为性能函数,隐层传递函数为双曲正切S形函数,输出层传递函数为线性函数。而隐层神经元数则参考经验公式
|
图 7 均方误差、相关系数随隐层神经元节点数变化曲线 Fig. 7 Variation curves of mean square error and correlation coefficient with number of nodes of hidden layer neurons |
采用以上6种机器学习回归模型进行阻力预报试验,得到20组不同数据集样本排列方式的相关系数与均方误差平均值,如表2所示。由于训练和测试样本都是采用的原始数据,为了验证各模型的泛化能力,选择各模型20组中拟合效果最好的一组,对相同的Cp,1 000
|
|
表 2 机器学习模型剩余阻力系数预报结果对比 Tab.2 Comparison results of residual resistance coefficient prediction of machine learning model |
|
|
表 3 四组插值样本剩余阻力系数预报结果对比 Tab.3 Comparison results of residual resistance coefficient prediction of four sets of interpolated samples |
利用泰洛标准系列船模原始试验数据,采用6种经典机器学习回归模型,对船舶剩余阻力系数进行预报,通过每种模型预报效果对比,得到以下结论:
1)通过训练机器学习回归模型,在泰勒标准系列船模试验数据的参数范围内,可以较精确地对船舶剩余阻力系数进行预报,避免了人工查谱的的繁琐过程,且预报效率较CFD数值模拟方法要高。
2)对于机器学习近似预报模型可以进一步调整算法,以提高对船舶阻力的预报精度。
3)针对不同的船舶阻力系列数据,根据数据集的特点与分布规律,选择合适的近似模型并进行调优,从而设计出具有较高泛化能力的船舶阻力预报模型的方法切实可行。
| [1] |
盛振邦, 刘应中. 船舶原理(上册)[M]上海: 上海交通大学出版社, 2003.
|
| [2] |
肖振业, 冯佰威, 刘祖源等. 基于支持向量机的船舶阻力近似模型研究[C]//2014年MIS/S&A学术交流会议论文集; 2014年.
|
| [3] |
陈爱国, 叶家玮, 苏曙. 船舶阻力计算BP神经网络的研究[J]. 武汉理工大学学报, 2009, 34(1): 209-216. |
| [4] |
陈爱国, 叶家玮. 基于神经网络的船舶阻力计算数值实验研究[J]. 中国造船, 2010, 51(2): 21-27. DOI:10.3969/j.issn.1000-4882.2010.02.004 |
| [5] |
李纳, 陈明, 刘飞, 等. 基于广义回归神经网络与遗传算法的玻璃钢渔船船型要素优化研究[J]. 船舶工程, 2012, 34(4): 18-20, 65. |
| [6] |
肖振业, 冯佰威, 刘祖源, 等. 基于支持向量机的船舶阻力近似模型[J]. 计算机辅助工程, 2015, 24(4): 20-23. |
| [7] |
Devrim Bülent Danışman. Reduction of demi-hull waveinterference resistance in fast displacement catamarans utilizing an optimized center bulb concept[J]. Ocean Engineering, 2014, 91: 227-234. DOI:10.1016/j.oceaneng.2014.09.018 |
| [8] |
Jong-hyun Lee, Sung-soo Kim, Soon-sup Lee, et al.. Prediction of added resistance using genetic programming[J]. Ocean Engineering, 2018, 153: 104-111. DOI:10.1016/j.oceaneng.2018.01.089 |
| [9] |
张维, 王先洲. 基于改进PSO的BP神经网络在船舶设计中的应用[J]. 中国水运, 2014, 14(1): 64-67. |
| [10] |
刘钊, 杜威, 闫冬梅, 等. 基于K近邻算法和支持向量回归组合的短时交通流预测[J]. 公路交通科技, 2017, 34(5): 122-128. |
| [11] |
李航. 统计学习方法[M]. 北京: 清华大学出版社, 2012.
|
| [12] |
Peter Harrington. Machine Learning in Action[M] America: Oracle Corporation, 2012.
|
| [13] |
李冬琴, 王丽铮, 王呈方. 支持向量机回归方法在船型要素建模中的应用[J]. 中国舰船研究, 2007, 2(3): 18-21. DOI:10.3969/j.issn.1673-3185.2007.03.004 |
| [14] |
包子阳, 余继周. 智能优化算法及其MATLAB实例[M]北京: 电子工业出版社, 2016.
|
| [15] |
陈峰. 基于CART 算法的空气质量指数回归预测模型的学习[J]. 上饶师范学院学报, 2016, 6: 16-21. DOI:10.3969/j.issn.1004-2237.2016.06.004 |
| [16] |
姜次平. 重分析后之泰洛标准组阻力数据[J]. 交通大学学报, 1958, 3: 221-238. |
 2019, Vol. 41
2019, Vol. 41
