卫星通信具有通信距离远,传输容量大,覆盖范围广等优点,现已在军事、民用的各个领域得到广泛应用[1]。海上卫星通信相较于其他卫星通信而言面临更多的影响因素,其中遮挡作为限制通信的重要因素之一,会引起信号的大尺度慢衰落,甚至导致通信中断[2],在实际应用中必须加以解决。
目前已有国内外学者和机构针对遮挡问题展开研究。国际电信联盟ITU在ITU-RP.681建议中,基于生成遮蔽函数(MFK)的方法,给出了移动卫星通信房屋建筑物阻断模型[3],该模型适用于地面移动通信,但海上卫星通信障碍物会随着船体运动,不能直接利用该模型进行分析;文献[4-5]主要研究了机载卫星通信装备在旋翼和雷达的遮挡下,卫星通信的可行区域,但船舶结构相对复杂,与机载卫星通信仅受单一障碍物影响不同;文献[6]对电磁波遇到不同类型障碍物遮挡时的绕射进行研究,得出了电波绕射计算公式;文献[7]研究了船舶在卫星天线遮挡条件下的航向计算,但未考虑船体晃动的影响。由于船舶结构复杂,通信天线会受多种障碍物的影响,而且船体晃动会对遮挡情况产生影响,以上研究并不能解决实际海上卫星通信面临的遮挡问题。
当卫星通信天线受到遮挡时,只能被动地改变航向,即便是专门克服遮挡问题的双天线系统,遮挡现象也时有发生。针对上述情况,本文旨在提出一种基于遮挡区域算法的遮挡预报模型,为船载装备设计提供参考指标,预报遮挡航向,方便提前调整航向或切换天线,满足军事应用中全时通信的需求。
1 基于菲涅尔区特性的最小仰角分析 1.1 电波传播特性研究卫星通信主要应用微波波段。尽管微波频率高、波长短,绕射能力相对较弱,但是在遮挡问题中,当障碍物距离天线较近时,电磁波的绕射效果被放大,所以在计算最小仰角时,必须对电磁波的这一特性加以考虑。
电波是通过许多菲涅尔区传播的,其中最重要的是第一菲涅尔区[8]。第一菲涅尔区上的每个点到通信双方的距离和均为R+r1,比通信直线距离d大λ/2,所以第一菲涅尔区呈椭球形。第一菲涅尔区示意图如图1所示。

|
图 1 第一菲涅尔区示意图 Fig. 1 Sketch of the first Fresnel zone |
已知点N1沿通信方向与通信双方距离分别为d1,d2,信号波长为λ,则该点的第一菲涅尔区半径F1可由下式求得:
| ${F_1} = \sqrt {\frac{{{d_1}{d_2}\lambda }}{d}}\text{。} $ | (1) |
当障碍物进入第一菲涅尔椭球,会对通信产生影响。菲涅尔区的遮挡损耗模型[9]指出:1)当遮挡面积小于第一菲涅尔区面积的40%时,遮挡损耗可以忽略。2)当遮挡面积大于40%时,遮挡损耗迅速增大,当遮挡面积达到50%时,遮挡损耗可以达到6 dB。因此为保证通信的稳定性,应将遮挡面积控制在第一菲涅尔区面积的40%以下。
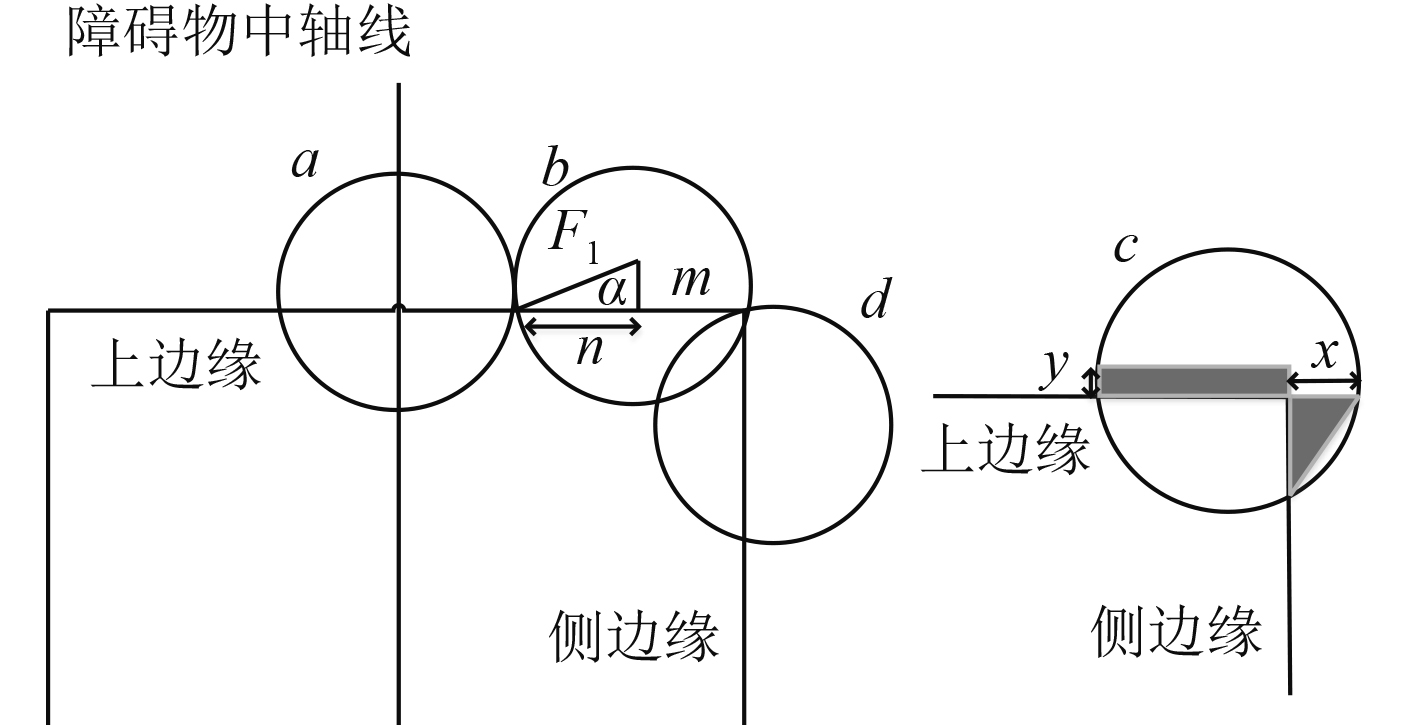
1.2 障碍物边缘遮挡对最小仰角的影响分析为保证通信稳定必须对遮挡面积加以控制。当遮挡面积占第一菲涅尔区面积的40%时,假设障碍物近似为矩形,则障碍物边缘与第一菲涅尔区横截面有如图2所示位置关系。
a状态为起始状态,此时波束中心在障碍物中轴线上。当波束与障碍物产生相对位置变化时,为保证遮挡面积占40%,波束应水平位移至b位置,此过程中只有障碍物上边缘对通信产生影响。若相对位置继续变化,则既有水平位移也有竖直位移,如c状态所示,此时障碍物上边缘与侧边缘同时遮挡第一菲涅尔区。直至移动到d位置之后,若相对位置继续变化,上边缘不再影响通信质量,可以任意调节卫星天线仰角。
设b状态时波束中心到障碍物上边缘距离为m,到侧边缘距离为n,则m,n可由以下公式求得:
| $\left\{ {\begin{array}{*{20}{c}} {m = {F_1}\cos \alpha } \text{,}\\ {n = {F_1}\sin \alpha } \text{。} \end{array}} \right.$ | (2) |
因为当遮挡面积为40%时,易求得角α为1.41,则m,n均可由菲涅尔半径F1表示。状态c相较于状态b水平平移了长度x,为了使遮挡面积保持在40%,应该再向下平移长度y,则可以依据遮挡面积不变,得到y关于x的函数关系,同时当圆心到上边缘与侧边缘距离相同,即y-m=n-x时,函数到达对称点。
本文采用近似计算方法,将水平位移后减小的面积视为三角形面积(图2中c状态三角形所示),将竖直位移补偿的面积视为矩形面积(图2中c状态矩形所示),计算公式如下:
|
图 2 障碍物边缘遮挡示意图 Fig. 2 Obstruction of the edge of the obstacle |
| $\left\{ {\begin{aligned} &{{S_{\text{三角形}}}{\rm{ = }}\frac{{x\left[ {\sqrt {{F_1}^2 - {{\left( {n - x} \right)}^2}} - m} \right]}}{2}}\text{,}\\ &{{S_{\text{矩形}}} = y\left( {2n - x} \right)}\text{。} \end{aligned}} \right.$ | (3) |
当x位于对称点左侧时,该近似方法能保证遮挡面积始终小于40%,对称点右侧函数可直接由函数对称性得到。令S三角形=S矩形,可以得到x与y在对称点左侧的函数关系:
| ${\rm{y = }}\frac{{x\left[ {\sqrt {{F_1}^2 - {{\left( {n - x} \right)}^2}} - m} \right]}}{{4n - 2x}}\text{,}$ | (4) |
根据对称性容易求出x与y在对称点右侧的函数关系,对称轴为:
| $y = m + n - x\text{。}$ | (5) |
水平调整距离x与竖直调整距离y直接关系到最小仰角与遮挡舷角的计算,最小仰角随y增大而减小,遮挡舷角随x增大而增大,具体函数关系在下文进行研究。当波束在障碍物边缘时,随着x的增大y逐渐增大,则此时最小仰角随着舷角的增大逐渐减小。此处得出x与y的函数关系,为下文研究改进最小仰角算法奠定基础。
2 基于遮挡区域算法的遮挡预报模型研究当船舶处于高纬度地区时,天线仰角较小,此时障碍物易出现在天线与卫星的通信链路上,对天线产生遮挡。为了避免遮挡的影响,本文提出一种基于遮挡区域计算的遮挡预报模型,从而预报可能出现遮挡情况的航向,以便及时做出调整。模型计算流程如图3所示。
步骤1 计算水平调整距离x与竖直调整距离y的函数关系
根据舰船实际结构,建立工程化模型。作一平面垂直于天线与障碍物轴线的连线,将障碍物在该平面上投影,得到障碍物的等效高度h(m)与1/2等效宽度w(m),并以天线位置为基准,得出障碍物轴线相对与卫星通信天线的舷角Q0(°)、距离s(m)与高度差Δh(m)。多障碍物时,每个障碍物应分别考虑,对于不规则障碍物,应视为多个障碍物的组合。
由于式(1)中的d2远远大于d1,在已知天线与障碍物轴线距离s、高度差Δh以及通信频率f的情况下,第一菲涅尔半径F1可利用如下公式近似计算:
| ${F_1} = \sqrt {\sqrt {\Delta {h^2} + {s^2}} \frac{c}{f}}\text{。} $ | (6) |
将计算得到的第一菲涅尔半径F1代入上文得出的式(2)、式(4),求出边缘的水平调整距离x与竖直调整距离y的函数关系。
步骤2 计算遮挡舷角Q与最小仰角Emin的函数关系
首先测定障碍物轴线相对于天线的舷角Q0,则遮挡的舷角Q与水平调整距离x有如下关系:
| $\left| {Q - {Q_{\rm{0}}}} \right|{\rm{ = }}\arctan \frac{{w - n + x}}{s}\text{,}\left( {0 \leqslant x \leqslant m + n} \right)\text{,}$ | (7) |
最小仰角由两部分组成,分别是障碍物造成的仰角θ1与第一菲涅尔区竖直调整后造成的仰角θ2,如图4所示。

|
图 4 第一菲涅尔区剖面图 Fig. 4 Section of the first Fresnel zone |
值得注意的是θ2可以为负,为负时即第一菲涅尔区中心处于障碍物上边缘水平面之下。
则最小仰角Emin的计算公式如下:
| $ {E_{\min }} = \left\{ {\begin{aligned} & {\arctan \frac{{\Delta h}}{s} + \arcsin \dfrac{{m - y}}{{\sqrt {{s^2} + \Delta {h^2}} }},}\\ & {\arctan \dfrac{{w - n}}{s} \leqslant \left| {Q - {Q_{\rm{0}}}} \right| \leqslant \arctan \dfrac{{w + m}}{s}}\text{;}\\ & {\arctan \dfrac{{\Delta h}}{s} + \arcsin \dfrac{m}{{\sqrt {{s^2} + \Delta {h^2}} }},}\\ & {\left| {Q - {Q_{\rm{0}}}} \right| \leqslant \arctan \dfrac{{w - n}}{s}}\text{;}\\ & {{\rm{0,}}}\\ & {\left| {Q - {Q_{\rm{0}}}} \right| \geqslant \arctan \dfrac{{w + m}}{s}}\text{。} \end{aligned}} \right. $ | (8) |
其中,由式(4)、式(7)可以得出y关于Q的关系如下:
| ${\rm{y = }}\frac{{\left( {\tan \left| {Q - {Q_0}} \right|s - w + n} \right)\left[ {\sqrt {{F_1}^2 - {{\left( {w - \tan \left| {Q - {Q_0}} \right|s} \right)}^2}} - m} \right]}}{{4n - 2\left( {\tan \left| {Q - {Q_0}} \right|s - w + n} \right)}}\text{。}$ | (9) |
将式(9)代入式(8),可以得到最小仰角Emin与遮挡舷角Q的函数关系。该函数仅与天线与障碍物的尺寸、相对位置和通信频率有关,与卫星和船舶的位置无关,因此可以提前依据舰艇结构计算得出。当存在多个障碍物时,需要分别计算遮挡舷角Q与最小仰角Emin的关系,即在不同的舷角区间内,舷角与最小仰角的关系不同。若船舶应用双天线系统,当其中一个受到遮挡时,应切换到另一侧的天线继续工作,只有二者全被遮挡时通信才会中断,此时障碍物舷角范围为两侧天线遮挡舷角的交集。
步骤3 船体晃动条件下的遮挡区域计算
船体晃动同样会引起遮挡的产生,虽然这种影响不是始终存在,但为了保证全时通信,也要加以考虑。根据海况信息对船体晃动进行量化分析,设沿天线与障碍物轴线连线方向为参考方向,将船体晃动分解为沿参考方向与垂直参考方向,晃动的最大角度分别为μ1,μ2。
分析可知,图5(a)情况下,晃动角度会直接影响天线的仰角,为保证全时通信,应预留部分仰角以对抗晃动的影响,由图形关系容易得到预留角度等于晃动角度,大小为μ1。图5(b)情况下,晃动使遮挡的舷角范围增大,此时应预留部分舷角避免遮挡,预留舷角角度计算公式如下:

|
图 5 船体晃动示意图 Fig. 5 Schematic diagram of hull shaking |
| $\Delta Q = \arctan \dfrac{{\sin \left( {{\mu _2} + \arctan \frac{w}{{\Delta h}}} \right)\sqrt {{w^2} + \Delta {h^2}} }}{s} - \arctan \frac{w}{s}\text{。}$ | (10) |
对式(8)进行如下修正:令Emin′=Emin+μ1,|Q′-Q0|=|Q-Q0|+ΔQ,从而得到船体晃动条件下最小仰角Emin,与遮挡舷角Q′的函数关系,二者所围成的区域即为可能产生遮挡的区域。
步骤4 预报遮挡航向
首先依据船舶当前航向、航速预测Δt时间后船舶位置(λ,φ),Δt可以根据实际精度要求设置,具体位置预测计算不是本文研究的重点。则预测位置船舶与定点经度λ0的卫星进行通信时的天线仰角E与方位角A的计算公式如下:
| $E = \arctan \left( {\frac{{\cos \left( {{\lambda _0} - \lambda } \right)\cos \phi - {r / R}}}{{\sqrt {1 - {{\left[ {\cos \left( {{\lambda _0} - \lambda } \right)\cos \phi } \right]}^2}} }}} \right)\text{,}$ | (11) |
| $A = \arctan \left( {\frac{{\tan \left( {{\lambda _0} - \lambda } \right)}}{{\sin \phi }}} \right)\text{。}$ | (12) |
其中:r=6 378.1 km为地球半径;R=42 164 km为卫星轨道半径。则在上文已求得遮挡舷角Q的情况下,可用如下公式计算遮挡航向:
| $C = A - Q\text{。}$ | (13) |
其中:C为遮挡航向;A为卫星方位角;Q为遮挡舷角(左舷为负值,右舷为正值)。
3 仿真结果本文以船舶与中卫10号卫星(定点经度110.5°E,通信频率12.5 GHz)[10]的通信为例,分析船载天线受障碍物A,B遮挡情况下的最小仰角与遮挡航向,并与文献[3]中传统算法得出的结果进行对比。假设经实际测量和数据处理后,得到障碍物的相关参数与预测位置的地理信息如下:
|
|
表 1 障碍物参数 Tab.1 Obstacle parameters |
|
|
表 2 预测位置坐标与海况信息 Tab.2 Predicted position coordinates and sea state information |
将已知参数代入式(2)、式(6)、式(10)计算得出如如表1 ~ 表3所示结果。
|
|
表 3 相关参数计算结果 Tab.3 Related Parameter Calculation Results |

|
图 3 遮挡预报模型流程图 Fig. 3 Blockage forecast model flow chart |
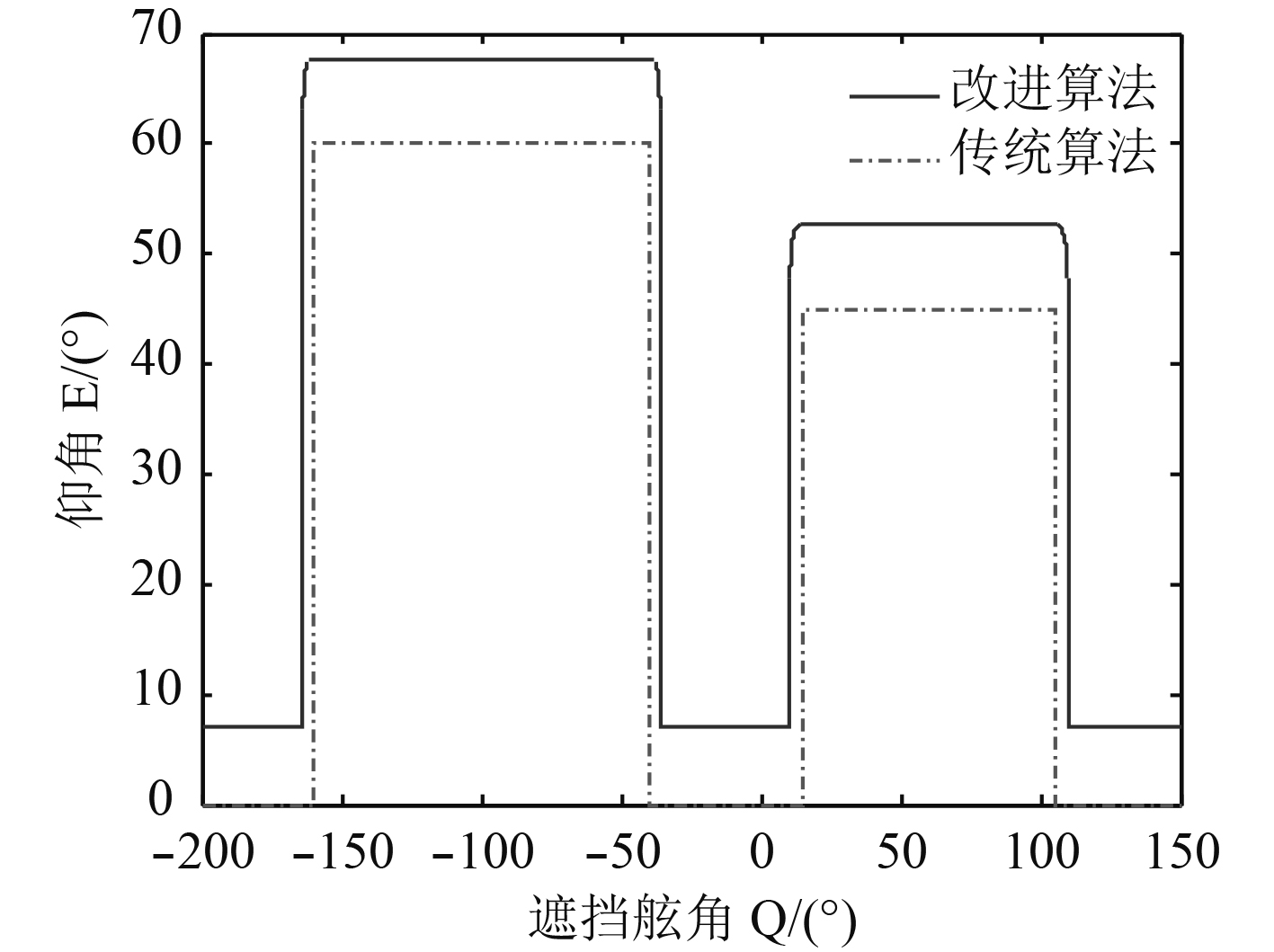
将以上计算结果与参数代入式(8)、式(9),通过计算机仿真,得出遮挡区域算法得出的遮挡区域,并与未考虑菲涅尔区特性和船体晃动的传统算法得出的遮挡区域进行对比,如图6所示。
|
图 6 遮挡区域曲线 Fig. 6 Occlusion zone curve |
由图可知,遮挡区域算法得出的遮挡舷角范围与最小仰角相较于传统算法均有不同程度的增大,而且在障碍物边缘处最小仰角的变化是渐变的,即最小仰角随着舷角的改变逐渐变化,这与传统方法中认为波束移出障碍物后最小仰角为0不同。
将预测位置信息代入式(11)和式(12),可求得预测位置的仰角和方位角分别为41°和–3.4°。通过式(15)求出基于遮挡区域算法预测遮挡航向为(–113.10°,–13.72°)∪(32.78°,160.40°),相较基于传统算法得出的遮挡航向(–108.40°,–18.40°)∪(36.6°,156.6°),范围扩大了17°
仿真结果表明,本文提出的遮挡区域算法,相较于未考虑电波绕射特性与船体晃动的传统算法,得出的最小仰角更大,障碍物的有效遮挡范围更广;本文预测的遮挡航向比传统方法范围更大。本文得出遮挡预报结果更适用于海上卫星通信实际,预留了部分航向,以防止船体晃动时通信产生中断,满足军事应用中对全时通信的需求。
4 结 语本文提出一种基于菲涅尔区特性的遮挡区域算法算法,考虑了电波传播中绕射对遮挡问题的影响,并适用于海上移动目标通信中船体晃动的情况。基于以上遮挡区域算法的研究,本文最后给出了适用于海上卫星通信的遮挡航向预报模型。通过船舶与中卫10号卫星通信的实例,验证了遮挡区域算法的可行性与遮挡预报模型的可靠性,说明本文提出的遮挡预报模型更加适用于海上卫星通信实际情况,准确预报遮挡航向,辅助工作人员提前改变航向或切换天线以规避遮挡,为船舶应对遮挡问题提供技术支持。
| [1] |
彭文标, 刘馨琼, 严朝军, 等. 卫星传输系统链路计算与分析[J]. 三峡大学学报(自然科学版), 2011, 33(3): 39-42. PENG Wen-biao, LIU Xin-qiong, YAN Chao-jun, et al. Calculation and analysis of satellite transmission system link budget[J]. Journal of China Three Gorges University(Natural Sciences), 2011, 33(3): 39-42. |
| [2] |
FENG W, GE N, LU J. Hierarchical transmission optimization formassively dense distributed antenna systems[J]. IEEE Communications Letters, 2015, 19(4): 673-676. DOI:10.1109/LCOMM.2015.2401584 |
| [3] |
ITU-R Recommendation P. 618-6, International Telecommunications Union, Geneva, April 2003.
|
| [4] |
王燕敏, 李博骁, 叶海军. 机载卫星通信波束受机身固定遮挡建模及仿真[J]. 系统工程与电子技术, 2016, 38(7): 1660-1665. WANG Yan-min, LI Bo-xiao, YE Hai-jun. Modeling and simulation for fixed blockage of airborne satellite communication beam by fuselage[J]. Systems Engineering and Electronics, 2016, 38(7): 1660-1665. |
| [5] |
苟晓刚, 邱金蕙, 江会娟. 直升机卫星通信中旋翼遮挡天线问题研究[J]. 无线电通信技术, 2013, 39(1): 55-58. GOU Xiao-gang, QIU Jin-hui, JIANG Hui-juan. Research on antenna blockage from rotor in helicopter satellite communication[J]. Radio Communications Technology, 2013, 39(1): 55-58. DOI:10.3969/j.issn.1003-3114.2013.01.017 |
| [6] |
郑灼洋. 雷达电磁波遮挡绕射仿真模型及其应用[J]. 舰船电子对抗, 2010, 33(2): 104-107+111. ZHENG Zhuo-yang. The simulative model and applications of radar electromagnetic wave diffraction over barrier[J]. Shipboard Electronic Countermeasure, 2010, 33(2): 104-107+111. DOI:10.3969/j.issn.1673-9167.2010.02.027 |
| [7] |
宋汝平, 蒋百灵. 船舶卫星通信遮挡航向的计算[J]. 舰船电子工程, 2015, 35(4): 69-71. SONG Ru-ping, JIANG Bai-ling. Course blocking calculation of satellite communications in the ship[J]. Ship Electronic Engineering, 2015, 35(4): 69-71. DOI:10.3969/j.issn.1672-9730.2015.04.018 |
| [8] |
宋铮, 张建华, 黄冶. 天线与电波传播[M]. 西安: 西安电子科技大学出版社, 2011: 222–224.
|
| [9] |
PARSONS J D. The mobile channel propagation[M]. New York: Wiley, 2000.
|
| [10] |
李朝辉, 屈晓旭, 娄景艺. 一种基于业务可通条件下的卫星通信链路最优发射功率算法[J]. 通信技术, 2017, 50(4): 714-719. LI Chao-hui, QU Xiao-xu, LOU Jinn-yi. Optimal transmit power algorithm of satellite communication link based on business connectivity[J]. Communications Technology, 2017, 50(4): 714-719. DOI:10.3969/j.issn.1002-0802.2017.04.023 |
 2019, Vol. 41
2019, Vol. 41
