2. 哈尔滨工程大学 水声工程学院,黑龙江 哈尔滨 1500011;
3. 海军大连舰艇学院,辽宁 大连 116018
2. School of Underwater Acoustic Engineering, Harbin Engineering University, Harbin 150001, China;
3. Dalian Navy Academy, Dalian 116018, China
拖曳线列阵相对于安装在平台外壳上的舰壳式声呐而言,具有不受载体平台安装尺寸限制、受本平台噪声影响相对较小、具有较大的阵列孔径和较低的工作频段等优势。对于大孔径拖曳线阵,在实际使用中受舰艇横向机动、洋流影响和水动力影响会产生一定的形变[1]。由于阵列形变,对于某θ方向上的来波信号,会导致阵元间的理论声程差和实际声程差不一致。这时,依据理论阵列流形计算出的时延差和真实时延差也会出现差距,不能实现信号的同相叠加,目标信号无法获得最大增益,减弱了波束分辨能力。针对这一问题目前常采用阵形估计算法估计各阵元的实时位置,柔性长拖曳线阵阵形估计主要有两大类:一类是安装传感器的借助硬件估计阵形方法;一类是采用水听器信号进行阵形估计的方法[2]。阵形估计算法在一定程度上还原了阵元的实时位置,对波束形成算法中计算导向矢量具有重要意义。但是阵形估计算法实时性不强、计算量大,并且阵形估计不准确时会引入新的误差。
常规时域波束形成算法存在增益低和波束分辨能力差的问题,Macdonald和和Schultheiss的研究表明分裂阵波束形成方法具有接近最优的目标估计精度,能够有效提高对目标的分辨能力[3 – 4]。分裂阵波束形成方法在线列阵精确测向中已得到了广泛应用,其中基于左右波束相位差测向的互谱法[5]和对左右波束采取和差运算的超波束形成算法[6]是2种高分辨率的分裂阵波束形成方法,但这2种算法均是在频域而非时域进行处理,无法输出听音波束信号。
针对以上问题,在无法进行阵形估计时,本文将大孔径拖曳线阵分为左右双子阵分别做波束形成,通过最大似然时延估计算法估算对应波束的时延差,再依据估算时延差对左右波束进行延时求和得到最终的波束信号。仿真和海试数据证明,相对于全阵直接做波束形成的方法,基于双子阵的时域波束形成技术有效提高了信号增益和波束分辨率。
1 阵形畸变对阵增益的影响 1.1 阵增益设均匀直线阵总阵元数为2N,阵元无指向性,阵元间距为d,目标入射角相对阵列方向夹角为θ,理想条件下,第i个阵元接收信号记为:
| $ {x_i}\left( t \right) = {s_{{\theta _i}}}\left( {t + {\tau _i}\left( \theta \right)} \right) + {n_i}\left( t \right)\text{,}\;\;\;\left( {i = 1, \cdots ,2N} \right)\text{,} $ | (1) |
| $ {D_{\text{理论}}}\left( \theta \right) = E{\left\{ {\mathop \sum _{i = 1}^{2N} {s_{{\theta _i}}}\left[ {t + {\tau _i}\left( \theta \right) - {\tau _i}\left( {{\theta _0}} \right)} \right] +\!\! \mathop \sum _{i = 1}^{2N} {n_i}\left[ {t - {\tau _i}\left( {{\theta _0}} \right)} \right]} \right\}^2}\text{。} $ | (2) |
当θ=θ0时,τi(θ)=τi(θ0),D理论(θ)=(2N)2σs2+2Nσn2,其中σs2为信号均方差、σn2为噪声均方差。可以看出信号增强了(2N)2倍,而噪声增强了2N倍。波束形成所带来的增益Gs理论为[7]:
| $ {G_{s{\text{理论}}}} = \frac{{{{\left( {2N} \right)}^2}{\sigma _s}^2}}{{2N{\sigma _n}^2}} \div \frac{{{\sigma _s}^2}}{{{\sigma _n}^2}} = 2N\text{,} $ | (3) |
通常将空间增益取对数转换为功率形式:
| ${G_{s{\text{理论}}}} = 10{\rm{*}}log{G_s} = 10{\rm{*}}\log2N\text{。} $ | (4) |
由于受阵形畸变影响,阵元位置发生偏移进而引入新的随机时延差τj(θ),第i号阵元实际接收到的信号为:
| ${x_{{\theta _i}}}\left( t \right) = {s_{{\theta _i}}}\left( {t + {\tau _i}\left( \theta \right) + {\tau _j}\left( \theta \right)} \right) + {n_i}\left( t \right)\text{,}\; \left( {i = 1, \cdots ,2N} \right)\text{。} $ | (5) |
此时波束形成输出D实际(θ)为:
| $\begin{split} {D_{\text{实际}}}\left( \theta \right) = & E\left\{ {\mathop \sum _{i,j = 1}^{2N} {s_{{\theta _i}}}\left[ {t + {\tau _i}\left( \theta \right) + {\tau _j}\left( \theta \right) - {\tau _i}\left( {{\theta _0}} \right) }\right]}\right. +\\& \left.\mathop \sum _{i = 1}^{2N} {n_i}\left[ {t - {\tau _i}\left( {{\theta _0}} \right)} \right] \right\} ^2\text{,} \end{split}$ | (6) |
τj(θ)≠0时τi(θ)+τj(θ)≠τi(θ0),波形失配使得此时的增益Gs实际<Gs理论。阵形畸变带来的时延误差τj(θ)公式为:
| $ {\tau _j}\left( \theta \right) = \alpha \left( j \right)\frac{{jd\cos\left( \theta \right)}}{c},j = 1,2 \cdots 2N\text{。} $ | (7) |
式中α(j)为取值大于零的随机畸变系数。
对于全阵,在波束形成时阵形畸变带来的误差值累积量μ为:
| $ \mu = \mathop \sum _1^{2N} \left| {{\tau _j}\left( \theta \right)} \right|\text{。} $ | (8) |
由误差累积公式可以看出,在阵元间距一定的条件下,阵形畸变带来的误差累积量同阵元数成正比例关系。
2 基于时延估计的分裂阵时域波束形成长拖曳线阵畸变会引入畸变误差,降低增益和波束分辨能力,并且在阵元间距一定的条件下,阵形畸变累积值μ将随着阵元数目的增多而非线性增大。另外,阵增益同阵元数成正比例关系,而阵元数又同阵形畸变误差累积值成反比例关系。综上,在无法进行阵形估计时,为保证阵增益的同时降低阵形畸变带来的影响,本文提出一种基于广义互相关估计时延的分裂阵时域波束形成方法。将长阵分为左右2个子阵,左右子阵分别按照各自的参考阵元进行波束形成,之后再将两左右波束合成为一个波束输出。左右子阵分别做波束形成,阵元数降为一半,畸变误差累积值被降低。对左右波束重新估计时延之后再延时累加,又利用了全阵信息,此时的阵增益理论上同全阵直接做波束形成时相同。
2.1 算法原理与技术流程设总阵元数为2N,阵元间距为d,目标入射角为θ,将均匀线阵等分为左右2个子阵,每个子阵的阵元数为N,其中1号、N/2+1号阵元分别为左右子阵的参考阵元,阵形如图1所示。
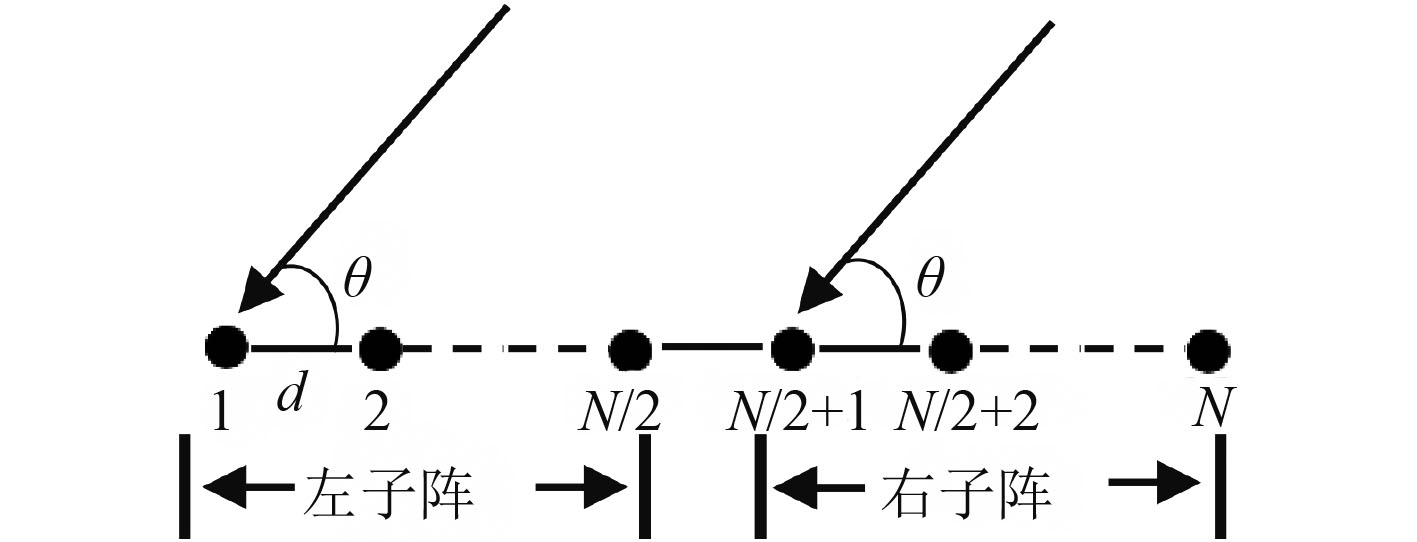
|
图 1 分裂线阵示意图 Fig. 1 Schematic diagram of split line array |
基于分裂阵时延估计时域波束形成算法计算流程如下:
1)将均匀线阵等分为左右2个子阵,采用辛格函数法进行时延的常规时域波束形成方法[8 – 9]对阵列信号
| $ \left\{ {\begin{aligned} &{{L_{{\theta _{\rm{m}}}}} = \mathop \sum _{i = 1}^{N/2} \left[ {{x_{\rm{i}}}\left( {t - {\tau _i}\left( \theta \right)} \right)} \right]}\text{,}\\ &{{R_{{\theta _{\rm{m}}}}} = \mathop \sum _{i = N/2 + 1}^N \left[ {{x_{\rm{i}}}\left( {t - {\tau _i}\left( {{\theta _{\rm{m}}}} \right)} \right)} \right]}\text{。} \end{aligned}} \right. $ | (9) |
2)左右阵元各自做时域波束形成之后,两子阵可以各自声中心等效为2个阵元,对于θ方位入射的信号,等效阵元的理论时延差为:
| $ {{\rm{\tau }}_{\text{理论}}}\left( \theta \right) = \frac{{\frac{N}{2}*d*{\rm{cos}}\left( \theta \right)}}{c}\text{。} $ | (10) |
由于阵形畸变,τ理论(θ)不等于等效阵元时延差的真实值,所以要对左右波束信号进行时延估计。另外由于阵形畸变,左右子阵对同一目标估计出的方位也会出现偏差。所以,估计左右波束时延差时,将
| $ {R_{{L_{{\theta _{\rm{m}}}}}{R_{{\theta _{\rm{I}}}}}}}\left( {{\tau _{{\theta _{\rm{m}}}}}} \right) = E\left[ {{L_{{\theta _{\rm{m}}}}}\left( t \right){R_{{\theta _{\rm{I}}}}}\left( {t + {\tau _{{\theta _{\rm{m}}}}}} \right)} \right]\text{。} $ | (11) |
此时的
| $ {{W}}\left( {{f}} \right) = \frac{{{{\left| {{\gamma _{{L_{{\theta _{\rm{m}}}}}{R_{{\theta _{\rm{I}}}}}}}\left( {{f}} \right)} \right|}^2}}}{{\left| {{G_{{L_{{\theta _{\rm{m}}}}}{R_{{\theta _{\rm{I}}}}}}}\left( {\rm{f}} \right)} \right|\left[ {1 - {{\left| {{\gamma _{{L_{{\theta _{\rm{m}}}}}{R_{{\theta _{\rm{I}}}}}}}\left( {{f}} \right)} \right|}^2}} \right]}}, $ | (12) |
其中,
最大似然加权时延估计流程图如图2所示。

|
图 2 最大似然加权时延估计流程图 Fig. 2 Maximum likelihood weighted time delay estimation flow chart |
3)将最大峰值对应的左、右波束信号
| $ {y_{{\theta _{\rm{m}}}}}\left( t \right) = {L_{{\theta _{\rm{m}}}}}\left( t \right) + {R_{{\theta _{\rm{I}}}}}\left( {t - {\tau _{{\theta _{\rm{m}}}}}} \right), $ | (13) |
通过分子阵做波束形成,再用时延估计方法而非理论公式计算左右波束的时延差,减小了阵形畸变带来的影响。
4)对M路预成波束信号
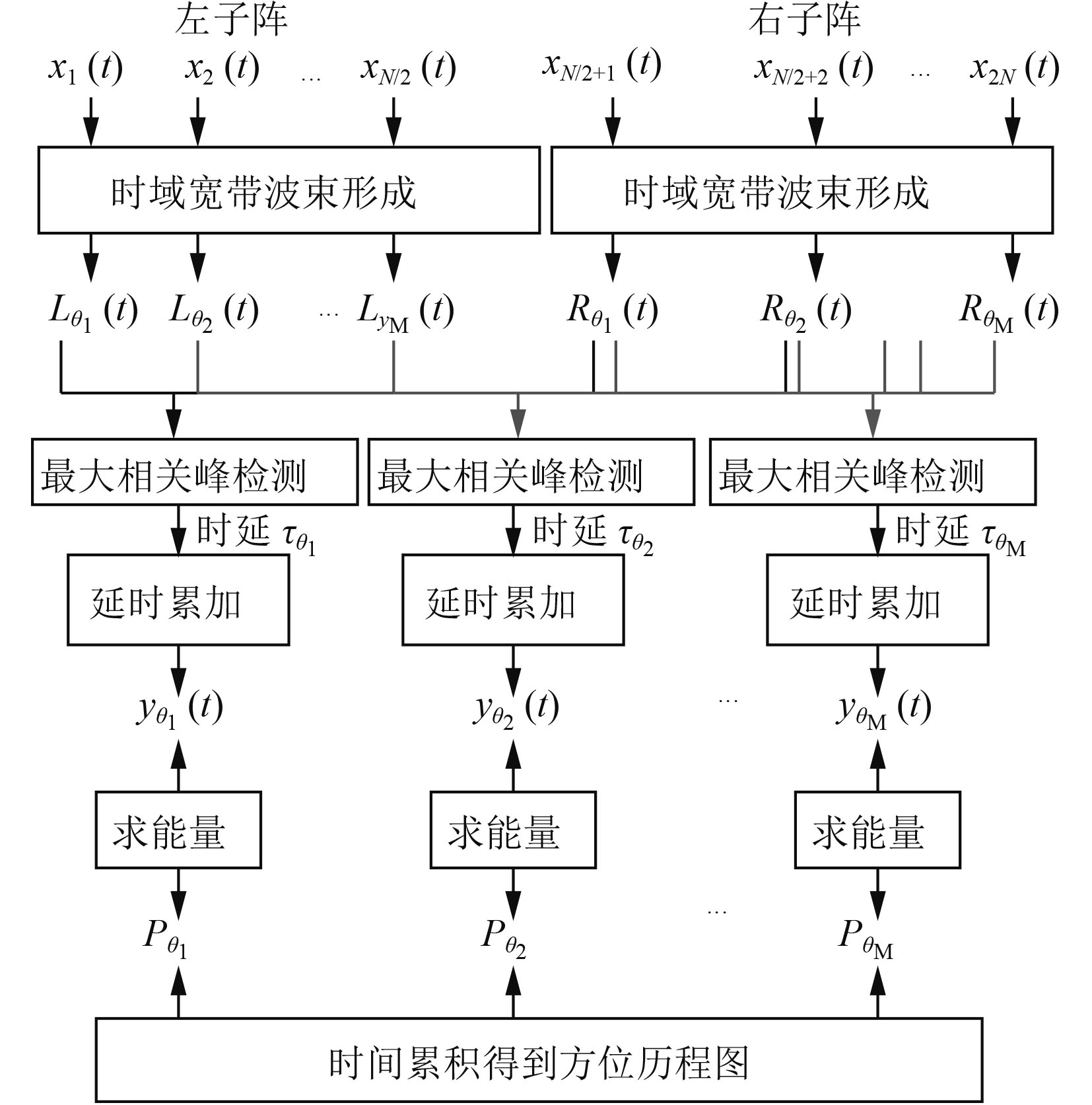
|
图 3 分裂阵算法流程图 Fig. 3 Flowchart of split matrix algorithm |
相对于全阵直接做时域波束形成方法,基于时延估计的分裂阵时域波束形成方法减小了阵形畸变带来的误差,延时后的各路信号更趋近于同相叠加。为验证本文算法的科学性和有效性,利用仿真和海试数据从对算法进行验证。
3.1 仿真验证与分析仿真阵列为均匀线阵,阵元数目512个,阵间距2.4 m,采样频率为5 000 Hz,目标源信号A和B均为海上实录的商船信号,其中目标A设置在97°方位,目标B设置在100°方位。线阵正常工作状态下应为直线阵,加入扰动后阵形畸变,扰动前后阵形示意图如图4所示。
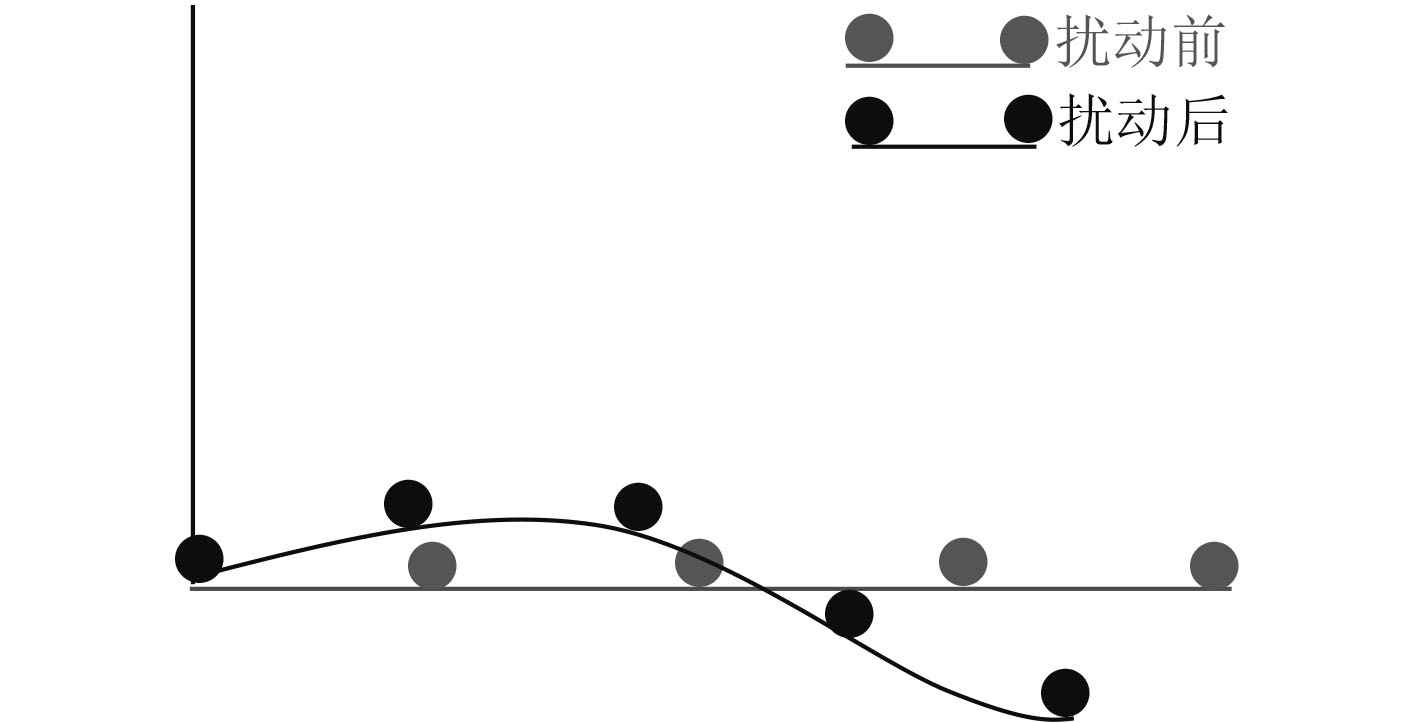
|
图 4 阵列扰动前后示意图 Fig. 4 Schematic diagram before and after array disturbance |
对比加入扰动前后,全阵直接做时域波束形成与分子阵之后时延估计做波束形成得到的空间谱,如图5和图6所示。
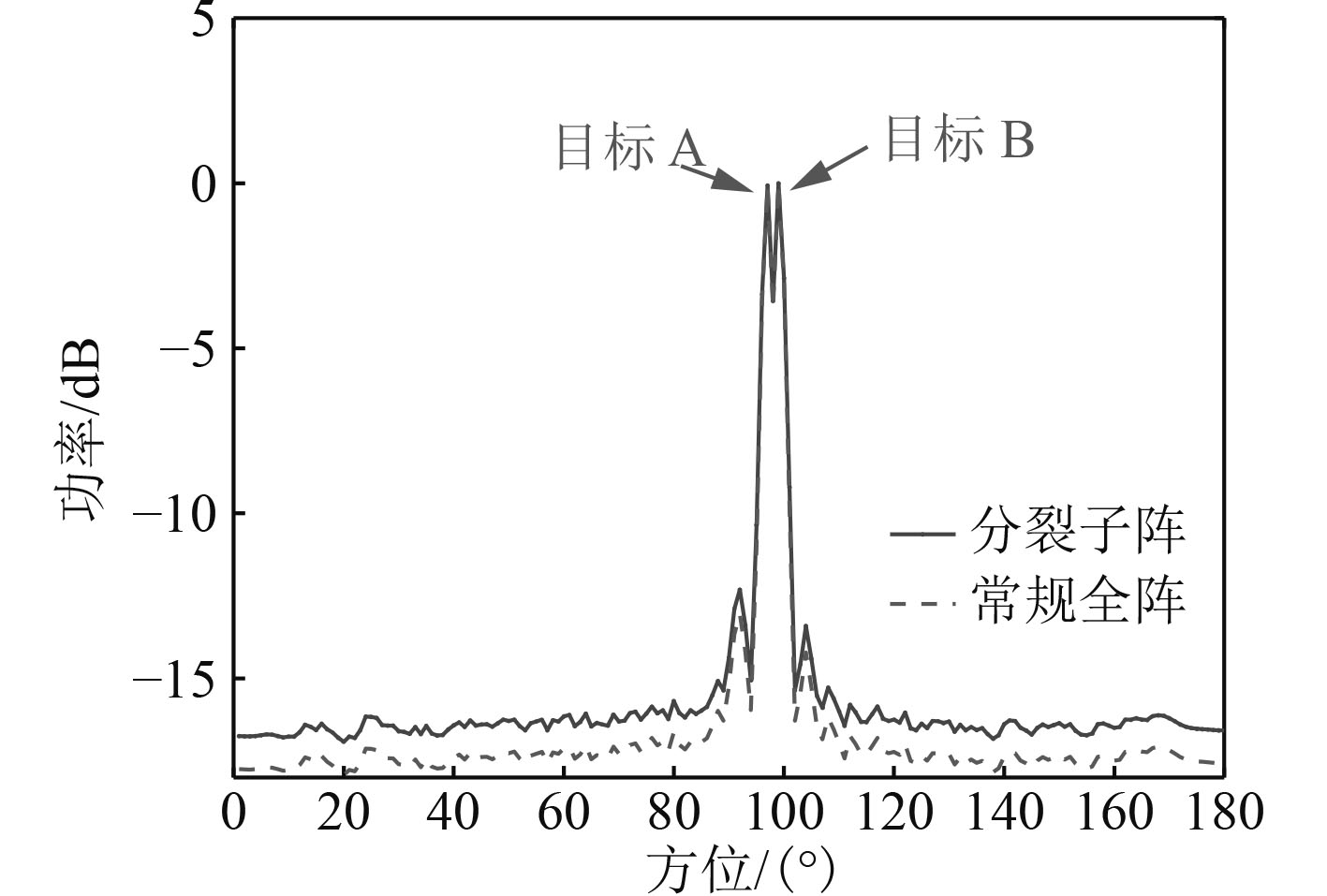
|
图 5 扰动前空间谱对比图 Fig. 5 Comparison of spatial spectrum before disturbance |

|
图 6 扰动后空间谱对比图 Fig. 6 Comparison of spatial spectrum after disturbance |
图5和图6仿真结果表明,均匀线阵加入扰动前,常规全阵做波束形成同分子阵估计时延再做波束形成均可以分开目标A,B,目标检测信噪比基本一致。加入扰动后,常规全阵波束形成算法不能有效分开目标A,B,而分子阵估计时延的方法依然可以有效检测到目标A,B,且检测信噪比相对常规全阵做法更高。
3.2 海试数据验证仿真信号验证了分裂阵方法的有效性,采用某海试数据进行验证,海试数据为某型柔性长拖曳声呐的海上实录数据。对比全阵直接做时域波束形成和分子阵波束形成方法输出的空间谱和方位历程图,如图7和图8所示。
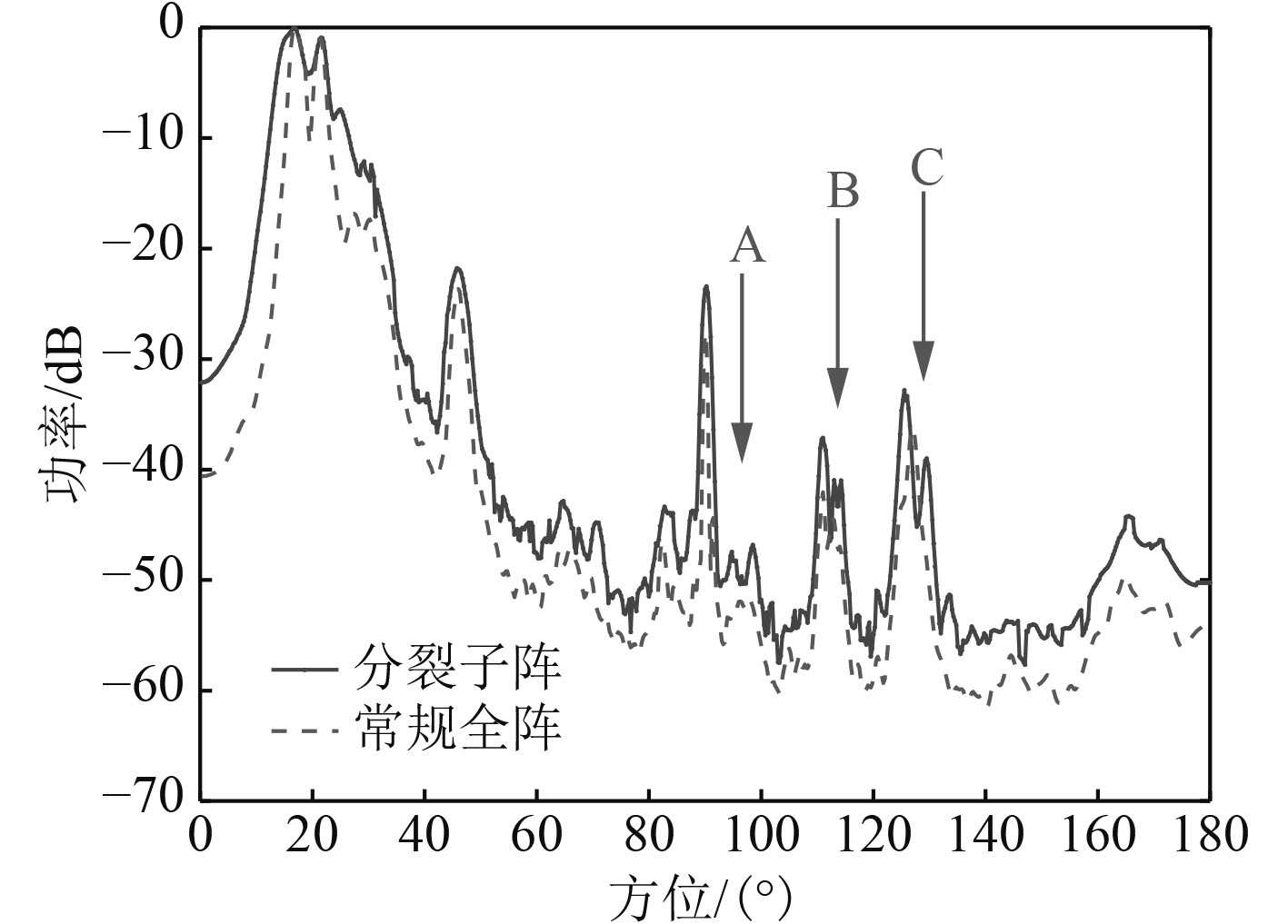
|
图 7 空间谱对比图 Fig. 7 Comparison Chart of spatial spectrum |

|
图 8 方位历程对比图 Fig. 8 Comparison of azimuth process |
对比图7和图8可以发现,图中标注的A,B,C三处,常规全阵时域波束形成算法无法有效分开临近双目标,而分裂阵算法提高了长拖曳线阵分辨率,可以有效检测到临近目标,检测信噪比更高。
4 结 语本文首先分析了柔性长拖曳线阵阵形畸变对波束形成带来的影响,之后结合频域分裂阵处理思想提出了基于时延估计的分裂阵时域波束形成算法。仿真和海试数据证明,分裂阵时域波束形成算法有效降低了阵形畸变带来的影响,提高了波束分辨率和信号增益。由于提高了信号增益,时域波束形成后输出的时域声音信号更有利于声呐兵的听音识别。在无法进行阵形估计时,可有效降低阵形畸变带来的影响。
| [1] |
WAITE A D. 王德石译. 实用声呐工程[M]. 北京: 电子工业出版社, 2004: 169.
|
| [2] |
饶伟. 水听器拖曳阵阵形估计方法研究[D]. 长沙: 国防科学技术大学, 2007.
|
| [3] |
姜楷娜, 田作喜, 翟春平, 等. 一种提高分裂阵频域波束形成测向分辨力的方法[J]. 舰船科学技术, 2016, 38(23): 138-142. |
| [4] |
STERGIOPOULOS S, ASHLEY A T. An experimental evaluation of split-beam processing as a broadband bearing estimator for line array sonar system[J]. The Journal of the Acoustical Society of America, 1997, 102(6): 3556-3563. DOI:10.1121/1.420146 |
| [5] |
李晋, 王晓庆, 陈卫东. 基于常规波束合成的分裂阵互谱定向研究[J]. 无线电工程, 2016, 46(02): 36-40+47. DOI:10.3969/j.issn.1003-3106.2016.02.09 |
| [6] |
DAVID A Miles, DAVID Kirk, TIMOTHY Clarke. A statistical analysis of the detection performance of a broadband splitbeam passive sonar[J]. IEEE Journal of Oceanic Engineering, 2006, 31(4): 986-996. DOI:10.1109/JOE.2006.880393 |
| [7] |
田坦, 刘国枝, 等. 声呐技术[M]. 哈尔滨: 哈尔滨工程大学出版社2004: 63-105 TIAN Tan, LIU Guo-zhi. etc. Technology of sonar[M]. Harbin Engineering University press. 2004: 63-105 |
| [8] |
唐建生. 时域宽带波束形成方法及实验研究[D]. 西安: 西北工业大学, 2004. TANG Jian-sheng. Studies on time domain broad-band beamforming methods and experiments[D]. Xi’an: Xi’an Northwestern Polytechnical University, 2004. |
| [9] |
翟羽佳, 胡谨贤, 黎仁刚. 宽带波束形成中小数时延滤波器设计[J]. 舰船电子对抗, 2014, 05: 110-113. ZHAI Yu-jia, HU Jin-xian, LI Ren-gang. Design of fractional time delay filter in broadband beamforming[J]. Shipboard Electronicn Countermeasure, 2014, 05: 110-113. DOI:10.3969/j.issn.1673-9167.2014.05.026 |
| [10] |
李启虎. 数字式分裂波束系统的精确定向方法[J]. 声学学报, 1984, 9(4): 225-238. LI Qi-hu. Precise bearing method of digital split beam system[J]. Acta Acustica, 1984, 9(4): 225-238. |
| [11] |
钱韬. 线阵分裂波束处理技术在水声探测中的应用[J]. 声学技术, 2015, 34(06): 551-555. |
| [12] |
游鸿, 黄建国, 史文涛. 基于宽带分裂阵列的水下远程被动多目标检测与定向[J]. 声学学报(中文版), 2009, 34(06): 527-532. |
 2019, Vol. 41
2019, Vol. 41
