均匀圆阵是声呐广泛采用的一种布阵形式,具有易实现等束宽波束形成等诸多优点。圆阵常采用常规波束形成方法(Conventional Beamforming,CBF)具有实现简单、性能稳定等优点,但存在旁瓣级高,噪声抑制能力弱的不足,通常不满足切比雪夫加权等波束形成方法应用条件[1 – 2]。最小方差信号无畸变响应方法(Minimum Variance Distortionless Response,MVDR)能有效克服上述不足,突破常规波束形成分辨率的“瑞利限”,抑制高旁瓣级。但是,阵元域MVDR方法存在计算量大、低信噪比时目标分辨率低和少快拍数信号协方差矩阵求逆易发生畸变的问题[3]。本文提出一种基于少快拍条件下均匀圆阵波束域MVDR方法,较好克服少快拍数MVDR波束形成性能严重下降问题并具有良好的低信噪比目标分辨率。
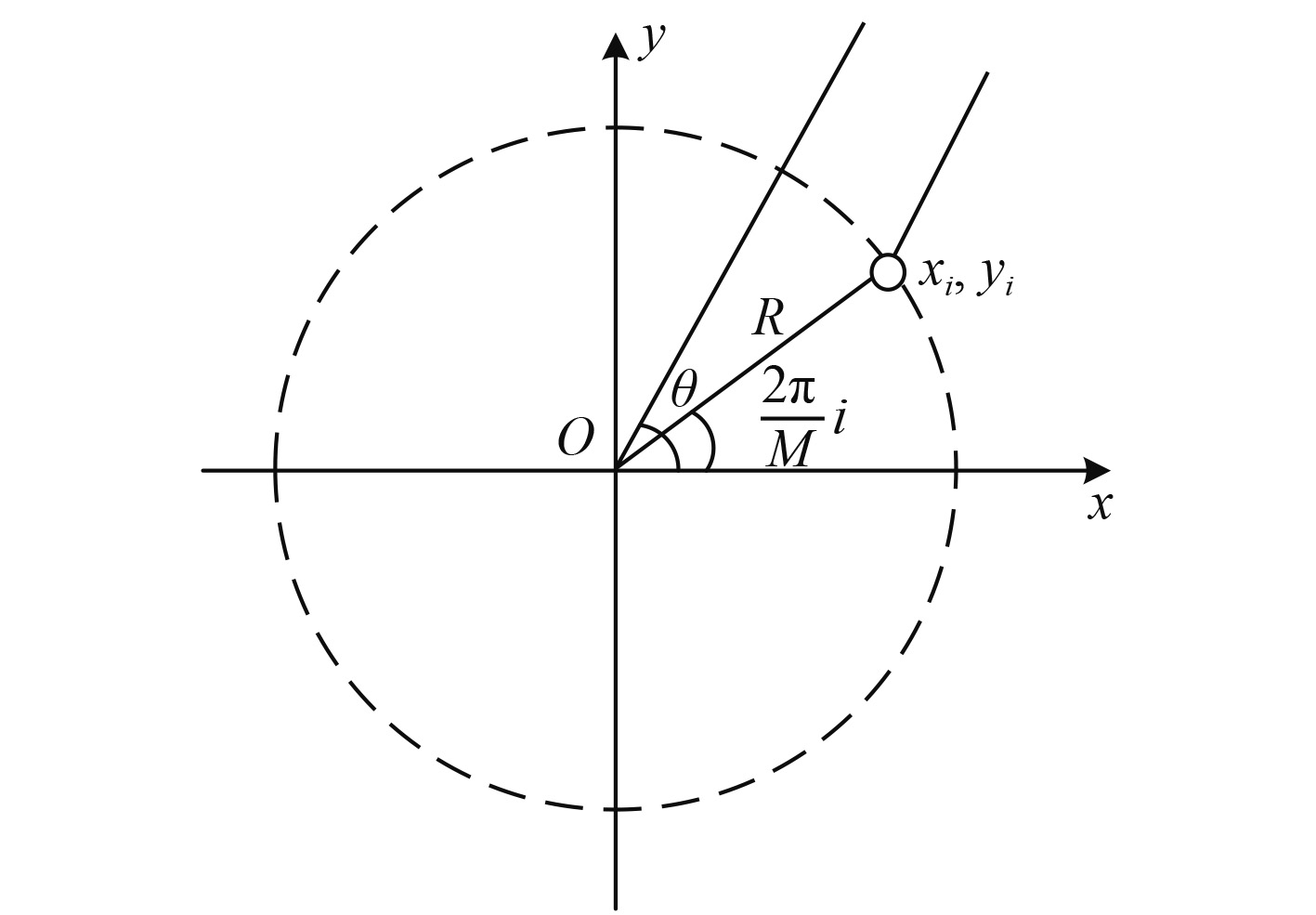
1 均匀圆阵MVDR波束形成方法及特点 1.1 均匀圆阵及信号模型如图1所示,假设圆阵的半径为
|
图 1 均匀圆阵接收信号模型图 Fig. 1 Uniform circular array received signal model |
| $ {Z_{CBF}}(t) = {A^H}(\theta )X(t) \text{。} $ | (1) |
式中:向量
| $ X(t) = S(\theta ) + N(t) \text{。} $ | (2) |
式中:
| $ {P_{CBF}}(\theta ) = E\{ Y(t) \cdot {Y^H}(t)\} = {A^H}(\theta ){{ R}_{xx}}A(\theta )\text{,} $ | (3) |
式中,
| $ {{ R}_{xx}} = E\{ X(t) \cdot {X^H}(t)\} \text{。} $ | (4) |
MVDR波束形成方法思想在于保证目标信号方向输出量不变的前提下,使阵列输出信号功率最小,可数学抽象为线性约束下求最优解的问题:
| $ \mathop {\min }\limits_a {A^H}{R_{xx}}A\;\;\;{\rm{s.t.}}\;\;\;{A^H}{{\alpha}} ({{\theta}} ) = 1\text{,} $ | (5) |
式中,
求解得,MVDR波束形成的阵列信号输出功率为:
| ${P_{MVDR}}(\theta ) = \frac{1}{{{\alpha ^H}(\theta ){{ R}^{ - 1}}\alpha (\theta )}}\text{。}$ | (6) |
由于MVDR方法中,需对协方差矩阵
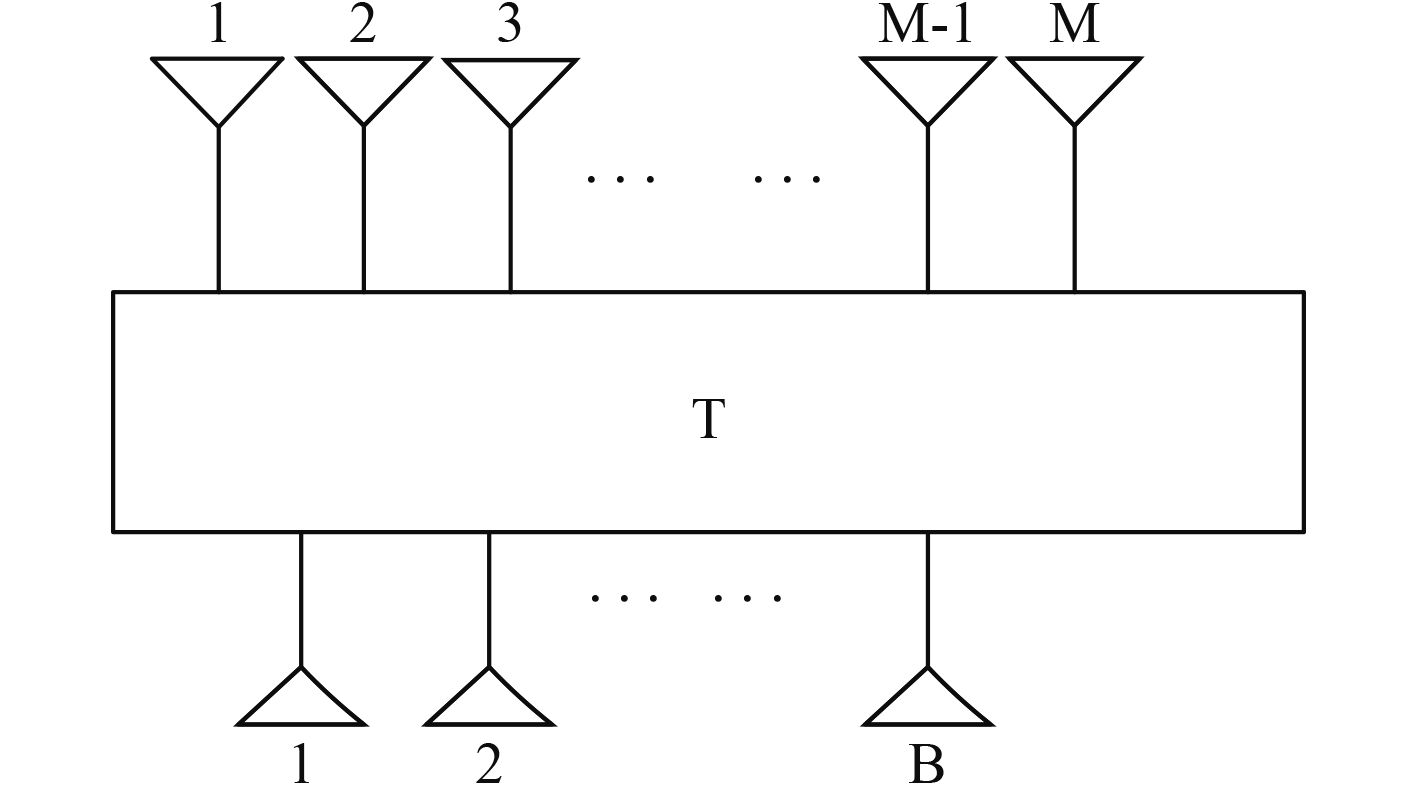
如图2所示,在波束域利用阵元域输出信息作为MVDR输入信息,将目标信号从阵元域
|
图 2 降维转换模型图 Fig. 2 Dimensional reduction transform model diagram |
基于假设的阵列构造
| $ V(u) \!=\! {[1,\exp (j{\text{π}} u),\exp (j2{\text{π}} u), \cdots ,\exp (j(M \!-\! 1){\text{π}} u)]^{\rm T}}\!\!\text{,}\!\! $ | (7) |
式中:
| $ { T} = \frac{1}{{\sqrt M }}[v(u1),v(u2), \cdots ,v(uB)]\text{,} $ | (8) |
可见,转换矩阵
| $ Z(t) = {{ T}^H}X(t) \text{,} $ | (9) |
信号实现了由阵元域
| $ {R_B} = E\{ Z(t){Z^H}(t)\} = E\{ {{ T}^H}X(t){X^H}(t)T\} \text{,} $ | (10) |
此时,波束域MVDR波束形成器的输出功率为:
| $ {P_{BMVDR}}(\theta ) = \frac{1}{{{A^H}(\theta )T{R_B}^{ - 1}{T^H}A(\theta )}} \text{。} $ | (11) |
波束域信号协方差矩阵实际工程应用是通过采样信号获得,假设信号快拍是为N,则均匀圆阵波束域信号协方差矩阵表示为:
| ${\hat { R}_B} = \frac{1}{N}\sum\limits_{i = 1}^N {Z({t_i}){Z^H}({t_i})} = \frac{1}{N}\sum\limits_{i = 1}^N {{T^H}X({t_i}){X^H}({t_i})T} \text{。}$ | (12) |
波束域信号协方差矩阵
| ${\tilde { R} _B} = {\hat { R}_B} + \xi {{ I}_B}\text{。}$ | (13) |
式中:
| $ \mathop {\min }\limits_a {A^H}T{\tilde R_B}{T^H}A\;\;\;s.t.\;\;\;{A^H}T\alpha (\theta ) = 1\text{。} $ | (14) |
对角加载后的波束域MVDR波束形成的信号输出功率为:
| $ {P_{BMVDR}}(\theta ) = \frac{1}{{{A^H}(\theta )T{{\tilde R}_B}^{ - 1}{T^H}A(\theta )}}\text{。} $ | (15) |
通过仿真实验对以上的方法进行验证:
实验1 假设均匀圆阵有48个阵元,阵元间距为半波长,波束覆盖
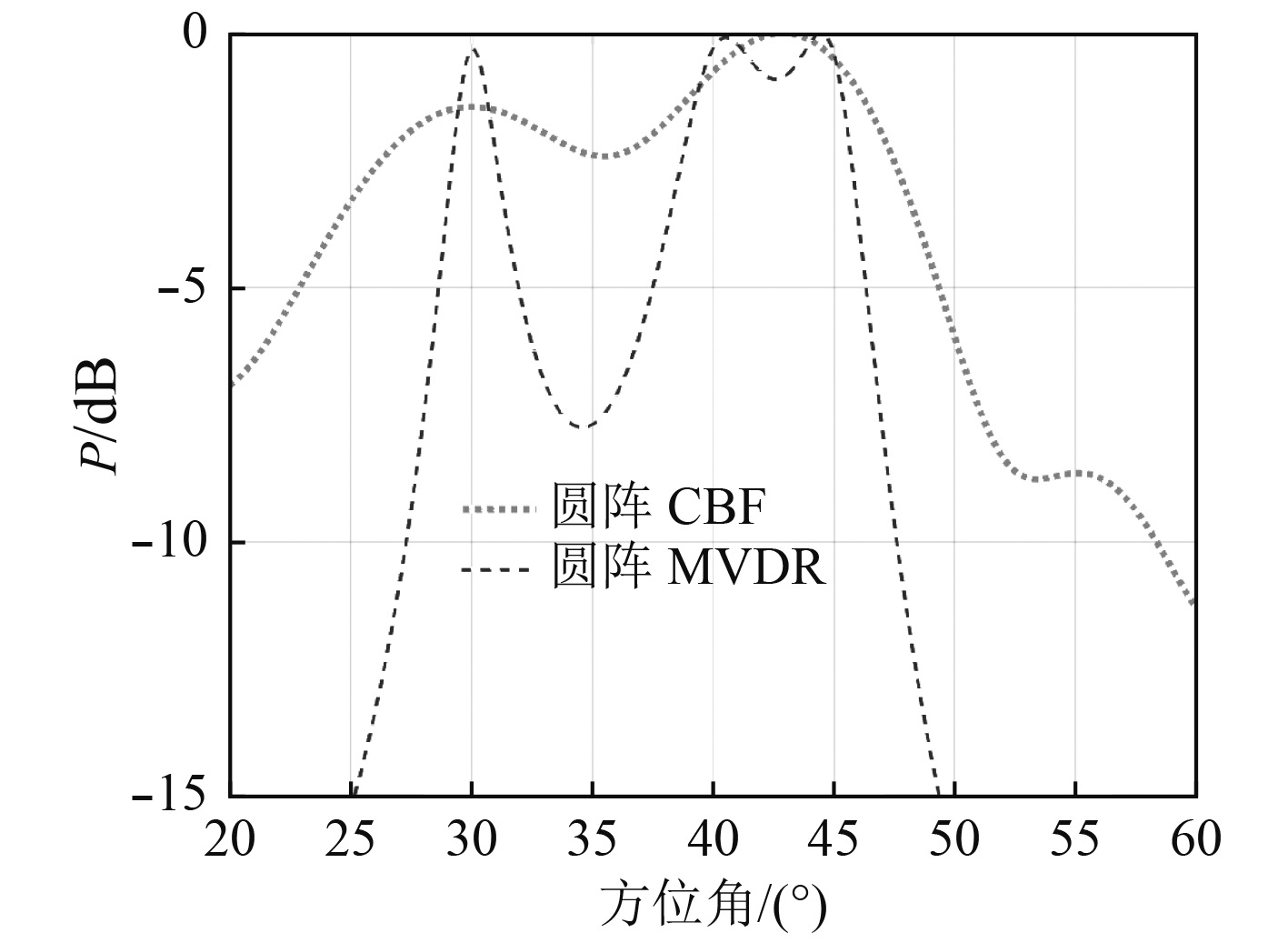
|
图 3 SNR=10 dB Fig. 3 SNR=10 dB |
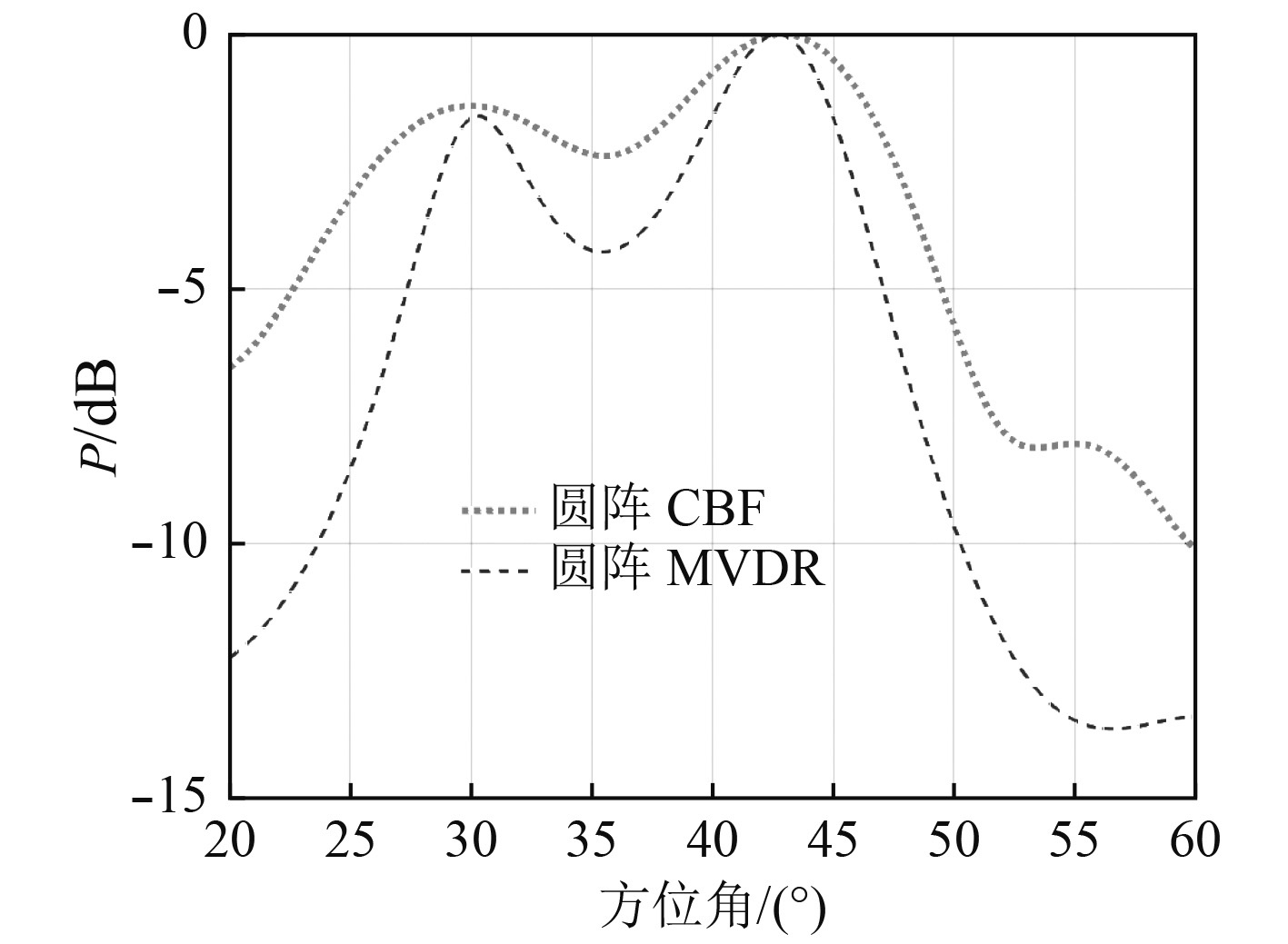
|
图 4 SNR=0 dB Fig. 4 SNR=0 dB |
在假设的仿真条件下,通过10 dB和0 dB信噪比下的仿真结果可知,阵元域MVDR波束形成在高信噪比时,具有良好的目标分辨率,能够明显区分
实验2 基于仿真实验1的条件,分别在0 dB,–5 dB和–10 dB的信噪比条件下,进行波束域MVDR波束形成方法的仿真实验。
|
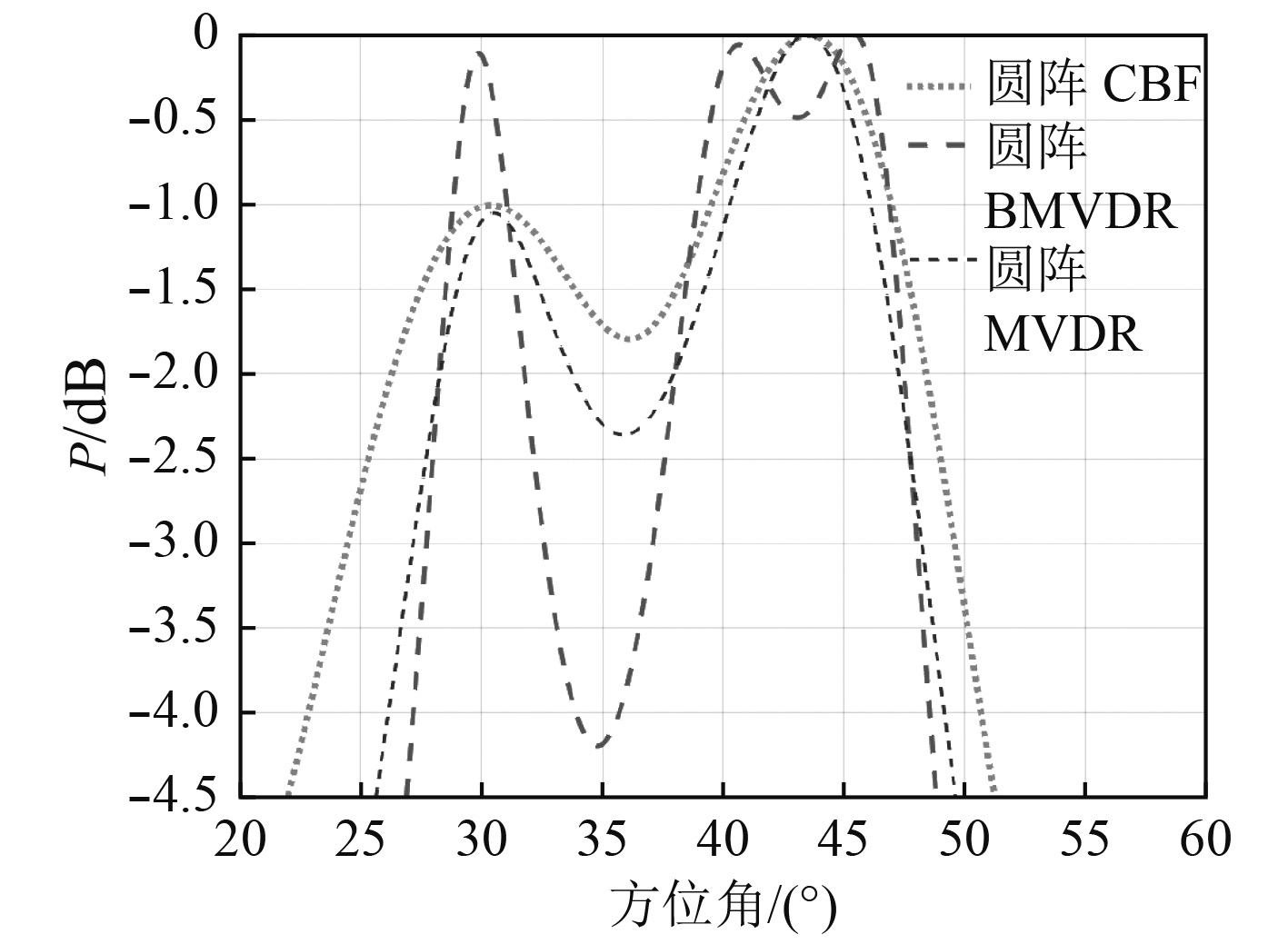
图 6 SNR=–5 dB Fig. 6 SNR=–5 dB |
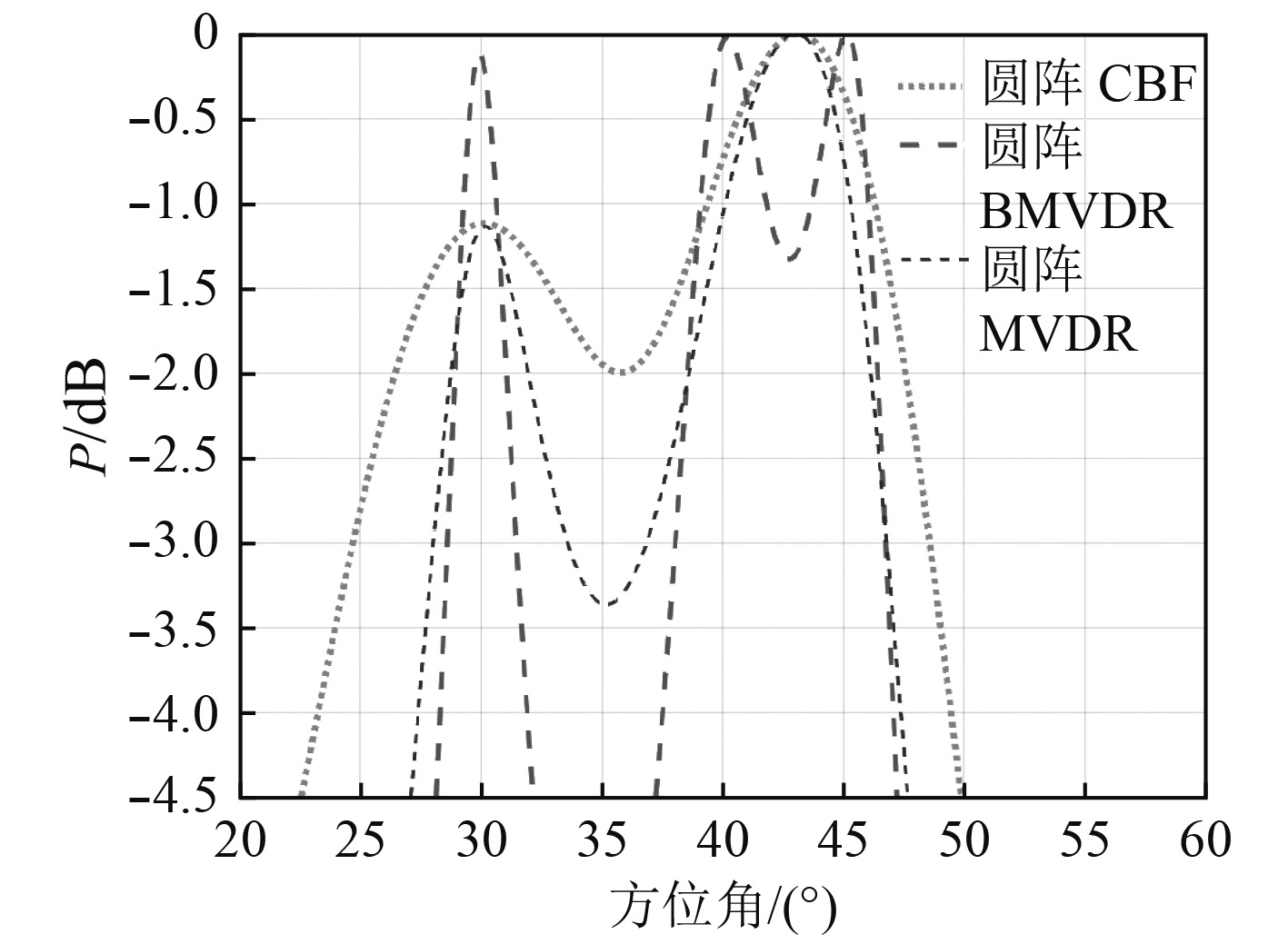
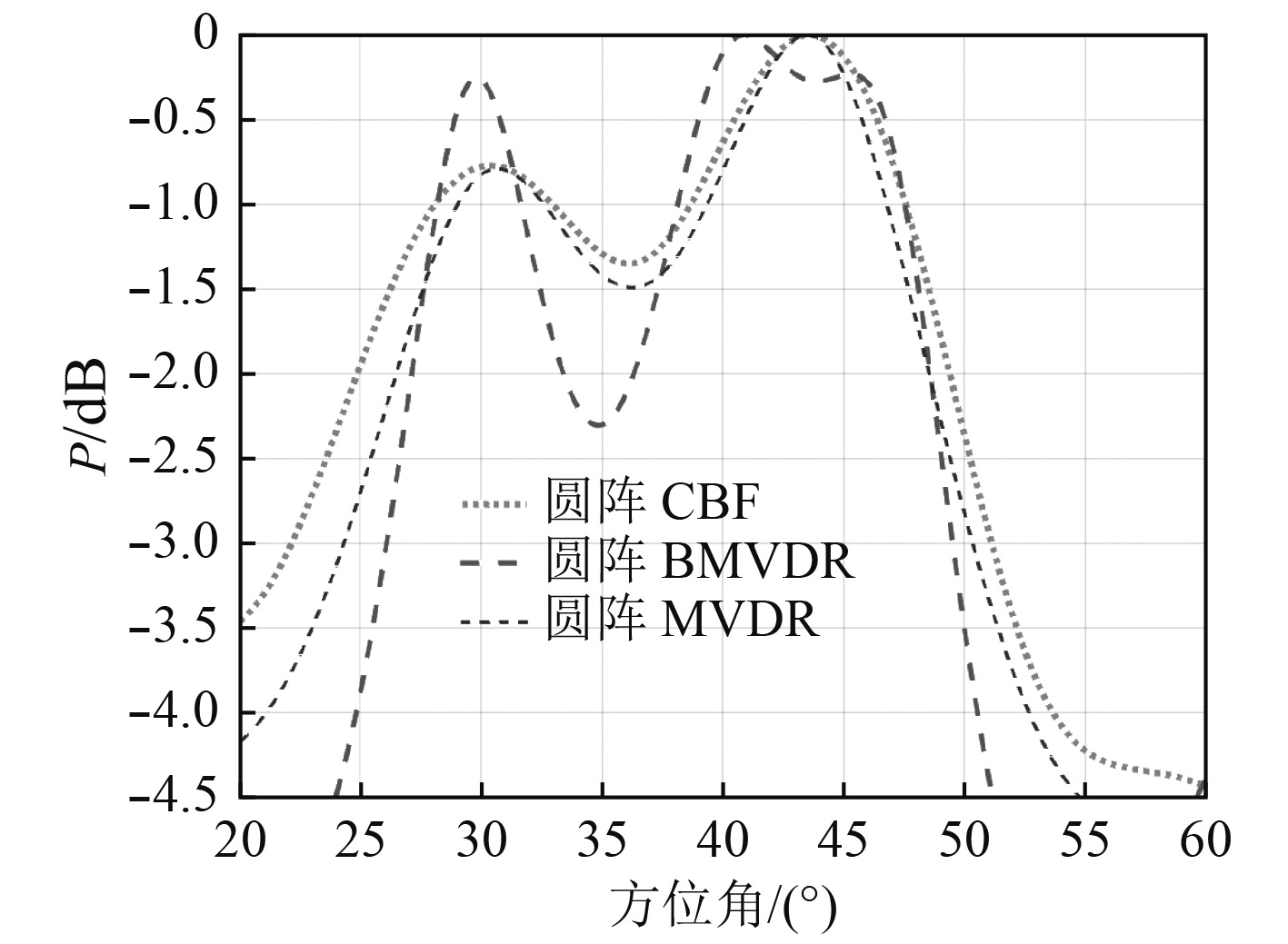
由仿真结果图5~图7可知,在3种信噪比条件下,波束域MVDR方法均可以区分
|
图 5 SNR=0 dB Fig. 5 SNR=0 dB |
|
图 7 SNR=–10 dB Fig. 7 SNR=–10 dB |
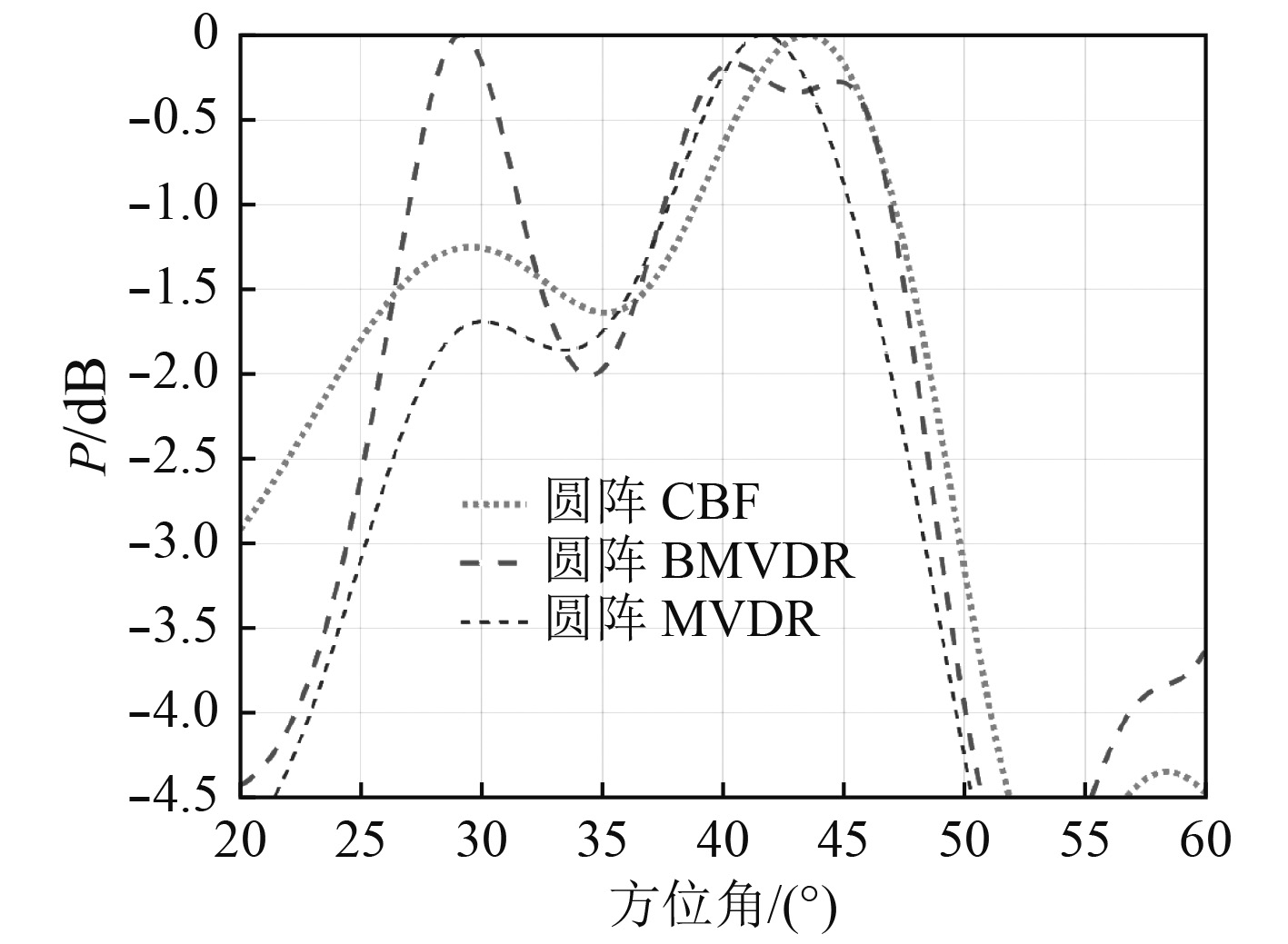
实验3 保持其他仿真条件不变,在信噪比为–10 dB,快拍数为50 pd条件下,仿真结果如图8所示。
|
图 8 快拍数50 pd Fig. 8 Snapshot number 50 pd |
由图8可知,假设仿真条件下,相较于阵元域MVDR波束形成无法区分
实验4 假设192个阵元按照半波长均匀排布在圆周上,利用相邻的48个阵元形成一个波束,在0°~360°空间上均匀产生96个波束,单个波束覆盖
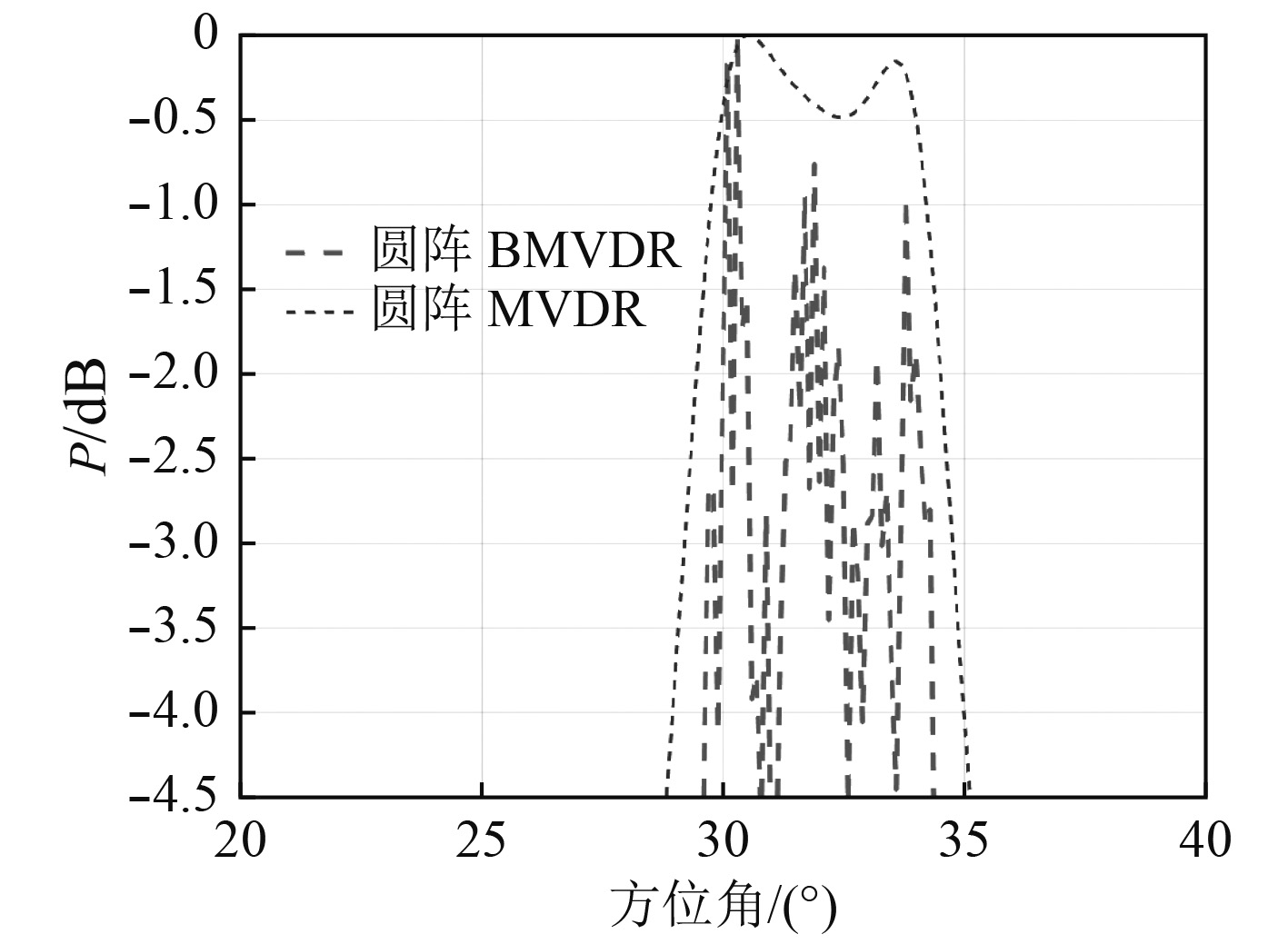
|
图 9 L<B条件下BMVDR波束形成图 Fig. 9 BMVDR beamforming under L<B condition |
由图9可知,在仿真实验4假设条件下,阵元域MVDR未发生畸变,但受到目标分辨力的限制,不能将
实验5 基于仿真实验4的条件,对信号协方差矩阵的添加
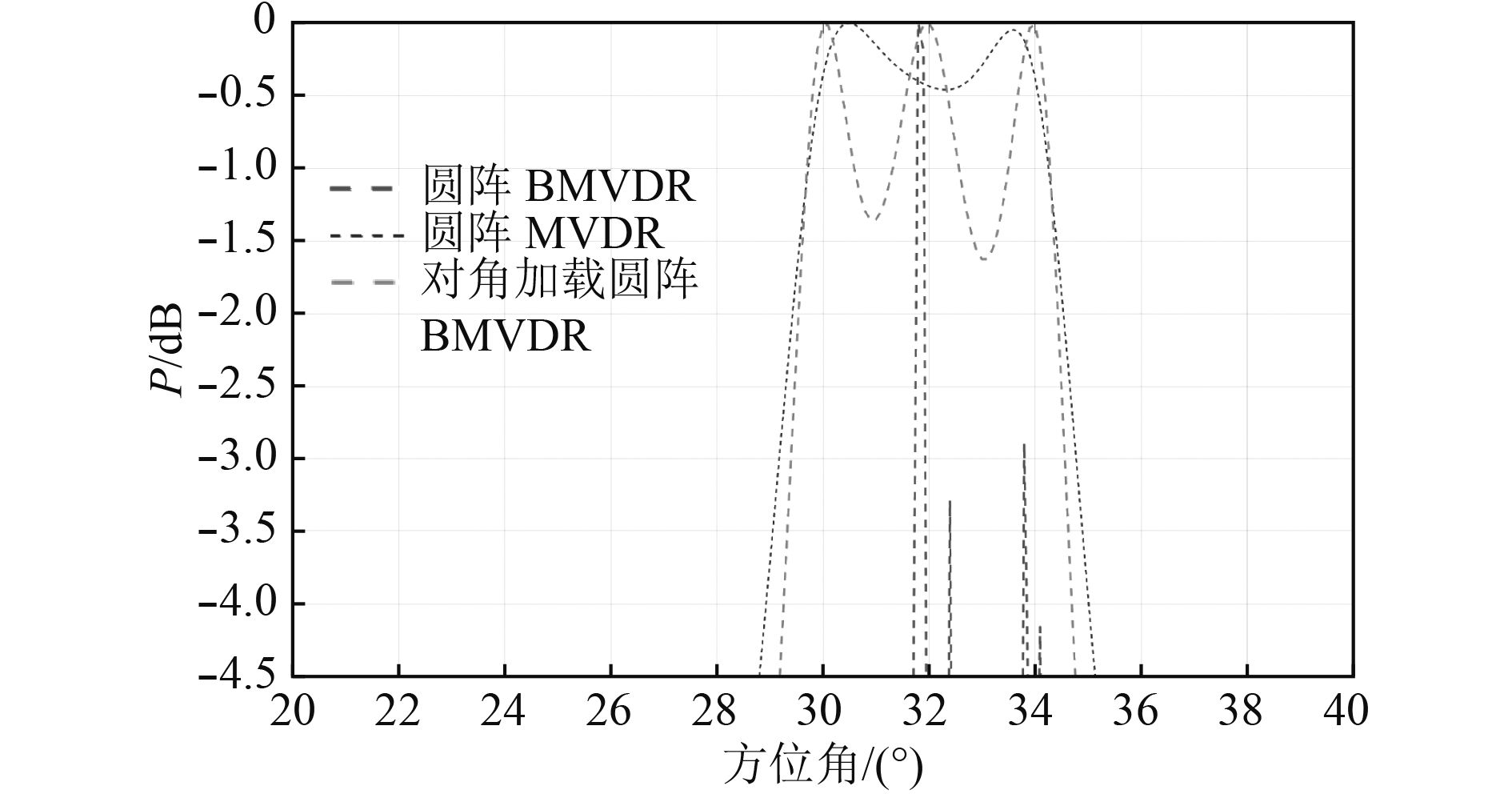
|
图 10 添加惩罚噪声后的BMVDR仿真图 Fig. 10 BMVDR simulation with penalty noise added |
由图10可知,利用对角加载技术添加惩罚噪声后,波束域MVDR形成的波束清晰区分出
引入了对角加载技术的波束域MVDR波束形成方法能够使均匀圆阵波束形成在少快拍数、低信噪比和单波束阵元的数量
| [1] |
田坦. 声呐技术[M]. 哈尔滨: 哈尔滨工程大学出版社, 2016.
|
| [2] |
李启虎.声呐信号处理引论[M]. 北京: 科学出版社, 2006.
|
| [3] |
何心怡, 黄海宁, 叶青华, 等. 波束域MVDR高分辨方位估计方法研究[J]. 武汉理工大学学报, 2003, 27(2): 201-204. HE Xin-yi, HUANG Hai-ning, YE Qing-hua. High-resolution direction of arrival estimation method of beamspace MVDR[J]. Journal of Wuhan University of Technology, 2003, 27(2): 201-204. DOI:10.3963/j.issn.2095-3844.2003.02.017 |
| [4] |
何心怡, 蒋兴舟, 李启虎. 基于子带分解的宽带波束域最小方差无畸变响应高分辨方位估计方法研究[J]. 声学学报, 2004, 29(6): 533-538. HE Xin-yi, JIANG Xing-zhou, LI Qi-hu. The research on broadband beamspace minimum variance distortionless response high resolution direction-of-arrival estimation method based on subband decomposition[J]. Acta Acustica, 2004, 29(6): 533-538. DOI:10.3321/j.issn:0371-0025.2004.06.008 |
| [5] |
张小飞, 张胜男, 徐大专. 自适应对角线加载的波束形成算法[J]. 中国空间科学技术, 2007, 2: 66-71. ZHANG Xiao-fei, ZHANG Sheng-nan, XU Da-zhuan. Adaptive diagonal loading beamforming algorithm[J]. China Space Science and Technology, 2007, 2: 66-71. DOI:10.3321/j.issn:1000-758X.2007.04.011 |
| [6] |
HARRY L. VAN TREES.最优阵列处理技术[M].汤俊译.北京 清华大学出版社, 2008 382-392.
|
| [7] |
夏麾军, 马远良, 汪勇, 等. 高增益对角减载波束形成方法研究[J]. 声学学报, 2016, 41(4): 449-455. XIA Li-jun, MA Yuan-liang, WANG Yong, et al. Study on high gain diagonally reduced carrier beamformation method[J]. Journal of Acoustics, 2016, 41(4): 449-455. |
| [8] |
KHABBAZIBASMENJ A, VOROBYOV S A, HASSANIEN A. Robust adaptive beamforming based on steering vector estimation with as little as possible prior information[J]. IEEE "Transactions on Signal Processing, 2012, 60(6): 2971-2987. |
 2019, Vol. 41
2019, Vol. 41
