在船舶机舱环境下,高压流体泄漏产生的噪声与机舱内其他动力装置、舱体振动等产生的噪声相比,其频率高、声压级低、指向性强、随传播距离衰减快,符合高频弱声源的特征。船员往往无法及时感知此种高频弱声源的出现,而通过近场声全息(Near-field Acoustical Holography,NAH)[1]的声成像技术可以获知一定空间内声场分布情况并直观地定位出噪声源,还可对相应设备、系统运行情况进行监测。
Maynard等[2]利用空间二维傅里叶变换实现声场重构,使声全息理论走向成熟。Koopmann等[3]于1989年提出用多个等效声源以波叠加方式来代替振动物体产生的声场。Jeon等[4]于2005年进一步提出等效源方法(Equivalent Source Method,ESM)来重构振动声场,并与边界元方法(Boundary Element Method,BEM)进行了比较,达到同等声辐射效果时等效源方法所需的测点数量更少,在工程上更易实现。Candes[5]和Donoho等[6]于2006年正式提出“压缩感知(Compressed Sensing,CS)”的概念。Gilles Chardon[7]于2012年将压缩感知理论首先引入平面近场声全息中,验证了该方法的可行性。Matteo Kirchner[8]将压缩感知应用于圆柱体声源的近场声全息中,相较于传统方法其在减少测量时使用传声器数目的同时,仍能得到较好的成像效果。然而,高频弱声源是噪声源识别领域的难题,直接使用传声器阵列的传统近场声全息方法测量无法获得有效的识别结果。
本文结合高频弱声源的特征与声源在平面上的分布特点,提出在船舶机舱内的低信噪比条件下,结合经验模态分解(Empirical Mode Decomposition,EMD)法与压缩感知的高频弱声源近场声全息方法。通过仿真实验,与Fourier变换方法和BEM的重构声压效果相比较,所得结果表明该方法可作为船舶机舱内低信噪比条件下的高频弱声源近场声全息方法的一种有效补充,具有较大的应用价值。
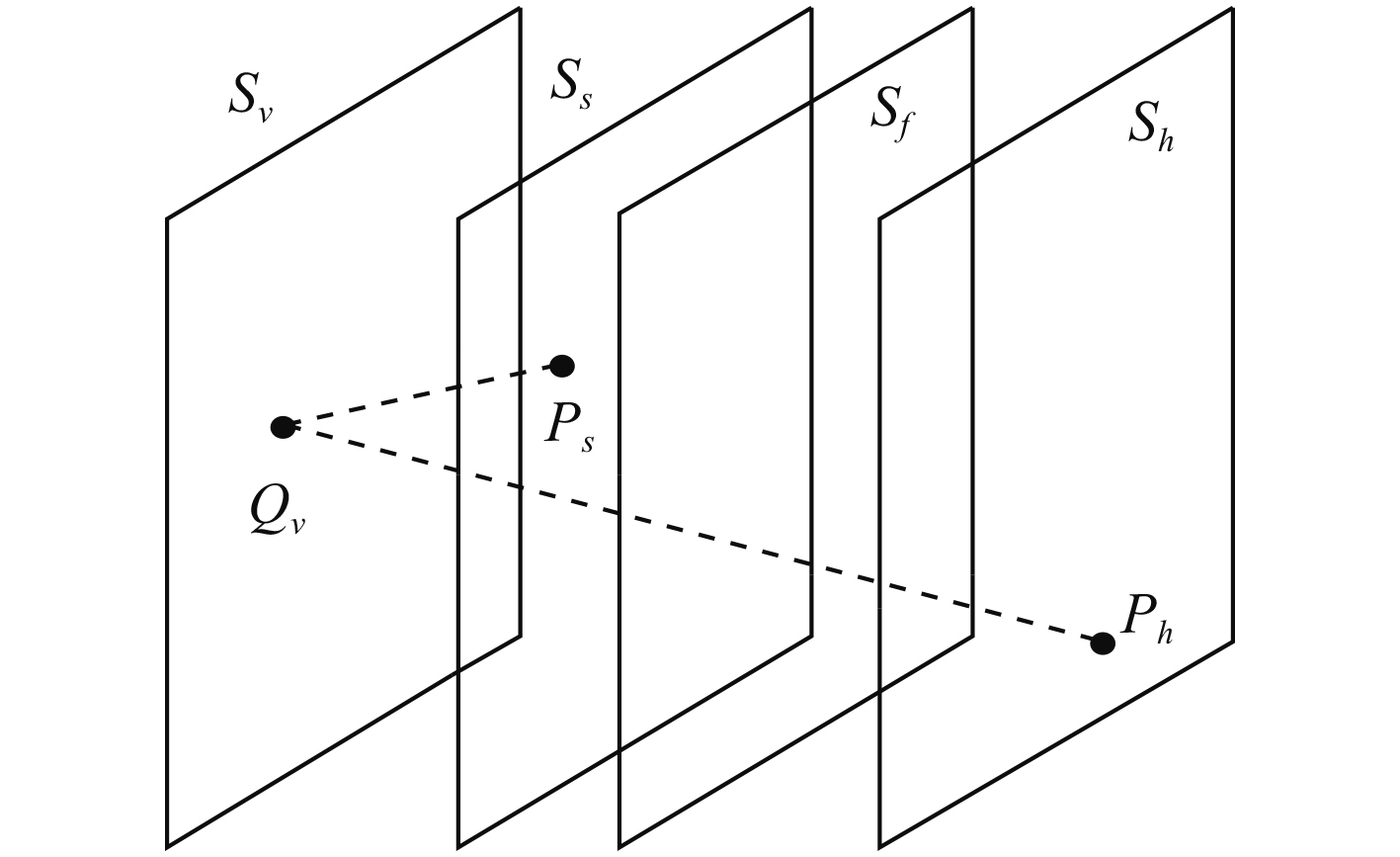
1 理论模型及算法实现 1.1 平面等效源近场声辐射计算模型将虚拟声源点设置在一个平面上,具有较好的便捷性与通用性。如图1所示,Sv为虚拟声源面,Ss为声源平面,Sf为声场中某一平面,Sh为全息面,n为声源面外法线方向,Ph为全息面上的声压分布,Ps为声源面上声压分布,Qv为虚拟声源面上声强。
|
图 1 平面等效源法近场声全息示意图 Fig. 1 A schematic diagram of plane ESM. |
全息面上声压分布可由积分方程表示如下:
| $p\left( {{r_h}} \right) = \int\limits_{{S_v}} {i\rho ckq\left( {{r_v}} \right)g\left( {{r_h},{r_v}} \right){\rm d}{S_v}} \text{。}$ | (1) |
其中:
| ${P_s} = {{ G}_{sv}}{Q_v}\text{。}$ | (2) |
式中:Ps为声源表面声压列向量;
| ${{ G}_{sv}} = i\rho ckg({r_s},{r_v})\text{。}$ | (3) |
同理,全息面上声压进行离散化处理后可表示为:
| ${P_h} = {{ G}_{hv}}{Q_v}\text{,}$ | (4) |
式中:Ph为全息面上声压列向量;Qv为等效源序列的源强列向量;Ghv为等效源序列与全息面间声压匹配矩阵:
| ${{ G}_{hv}} = i\rho ckg({r_h},{r_v})\text{,}$ | (5) |
虚拟源强的反演公式为:
| ${Q_v} = { G}_{hv}^ + {P_h}\text{,}$ | (6) |
进而将实际声源面的声压表示为:
| ${P_s} = { G}_{sv}^{}{ G}_{hv}^ + {P_h}\text{,}$ | (7) |
将声源面到全息面的声压传递矩阵表示为:
| ${ L} = {{ G}_{vs}}{ G}_{vh}^ + \text{,}$ | (8) |
得到声源面上的声压
| ${P_s} = { L}{P_h}\text{。}$ | (9) |
已知L和Ph,便可重构出近场平面上的声压分布。
1.2 阵元信号权值计算实际情况中,原信号和噪声信号往往为非平稳信号,能量或声压有效值不知,无法得到信号的信噪比。现对各阵元采样所得信号运用EMD法进行分析,该方法能使复杂信号分解为有限个本征模函数(Intrinsic Mode Function,IMF),所得各IMF分量包含了原信号不同时间尺度的局部特征信号。
已知
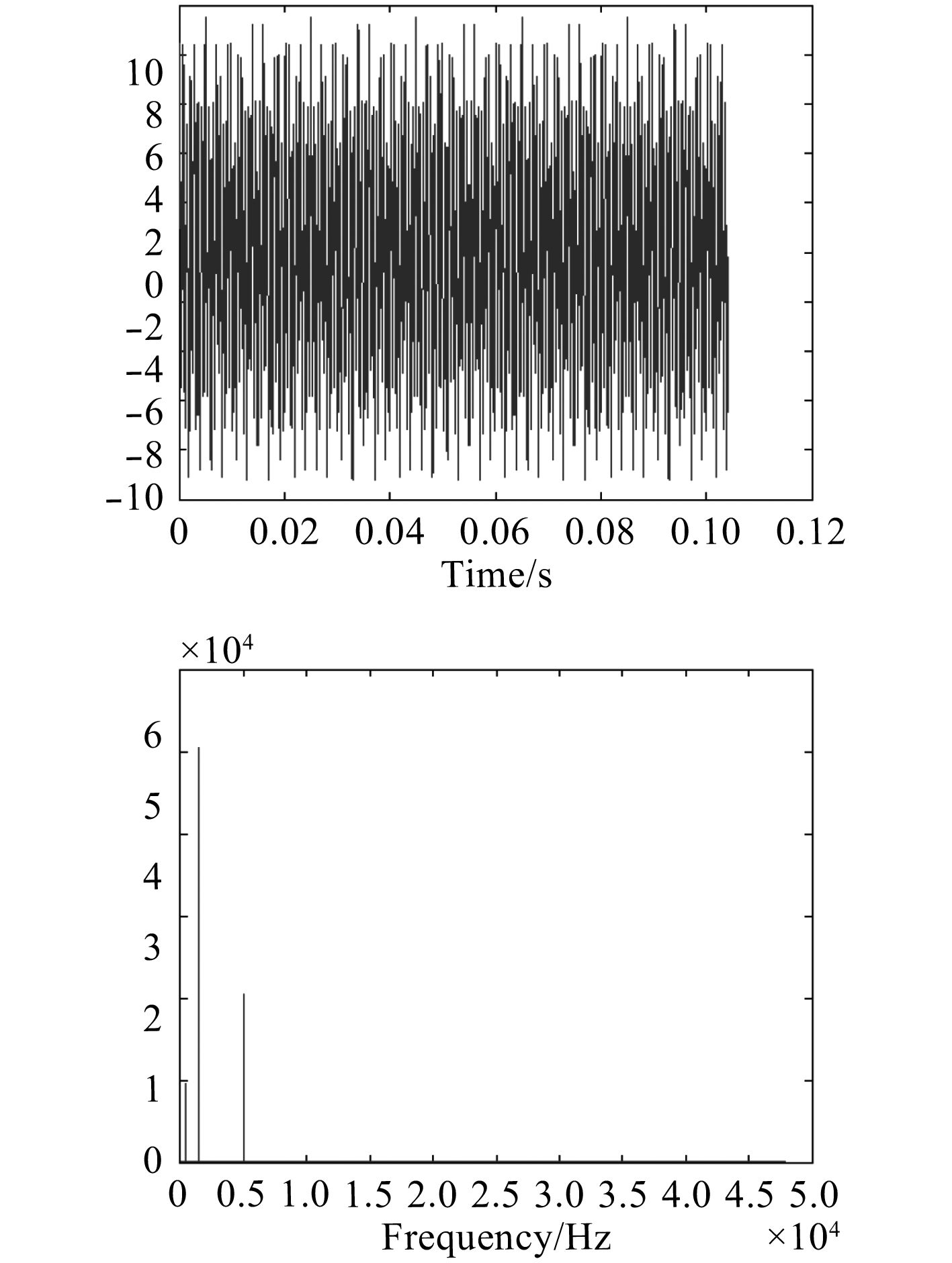
|
图 2 信号时频图 Fig. 2 Time-frequency diagrams of each signal |
该信号混有5 kHz,450 Hz和1450 Hz的3种频率信号,若将5 kHz对应的高频信号作为原信号,显然该混合信号信噪比较低。故可对该信号进行预处理,乘以一个权值α,α取值为0~1之间,对应高频部分在此信号中的占比。此过程可提高阵列分辨能力,提高对高频弱声源的定位精度。对此混合信号运用EMD法,得到有限个IMF分量,结果如图3所示。
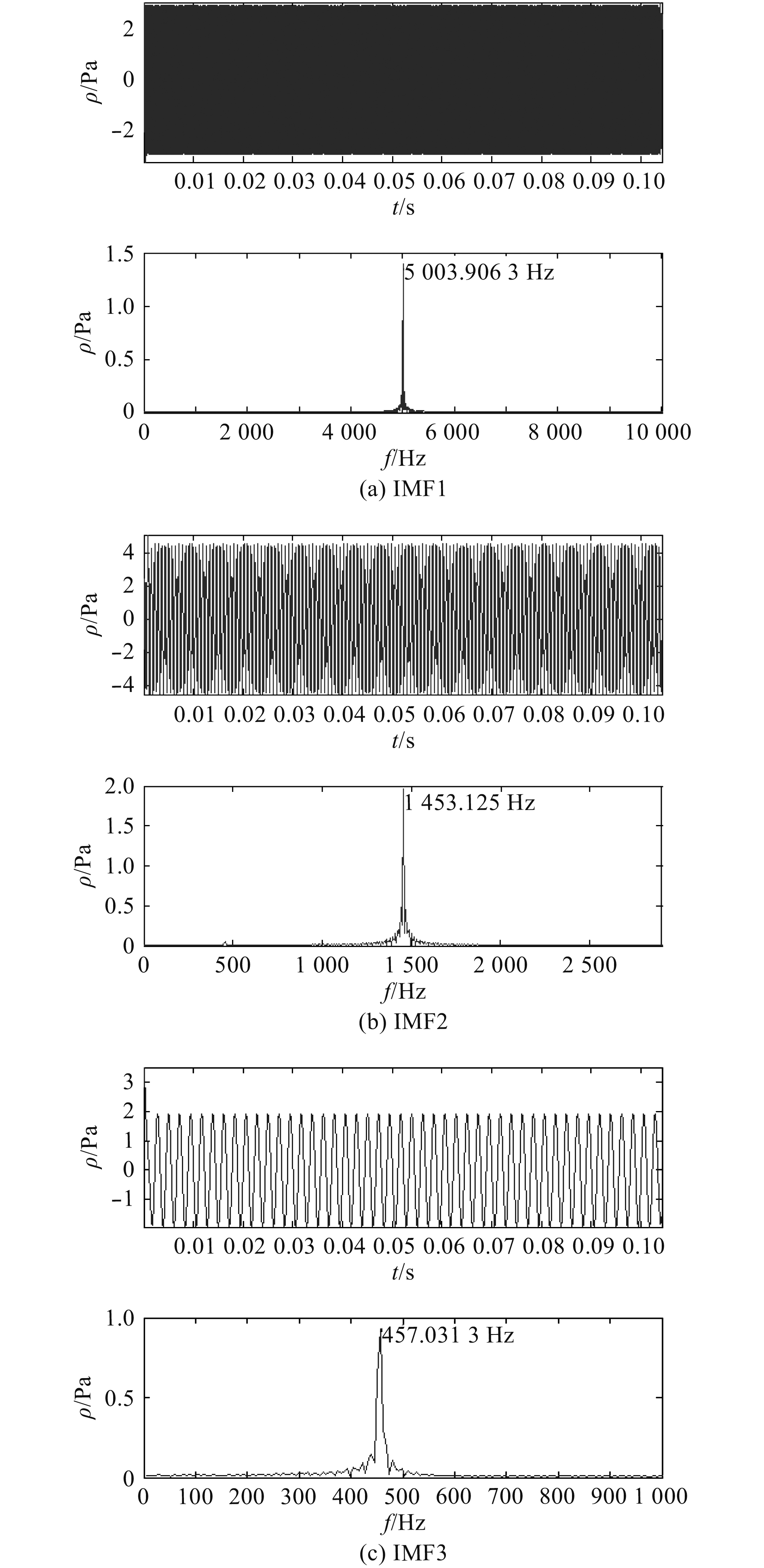
|
图 3 IMF分量时频图 Fig. 3 The time-frequency diagrams of IMF components |
可知,该混合信号的高频部分(即f=5 kHz)分布在IMF1中。频域图中,纵坐标数值越大,代表对应此频率的信号部分在该分量中的贡献越大。将每个IMF频域图上各频率点对应的幅值累加,共得3个值,再判断每个分量主要成分对应频率是否大于4.9 kHz。此信号中,IMF1的主要成分对应频率大于4.9 kHz。将所得3个值累加作为分母,IMF1对应的值累加作为分子,即得到该混合信号所需要乘的权值α=0.317,进而得到此信号中高频部分的声压值。α值与实际高频部分声压贡献值占比0.316十分接近,表明该方法可行。
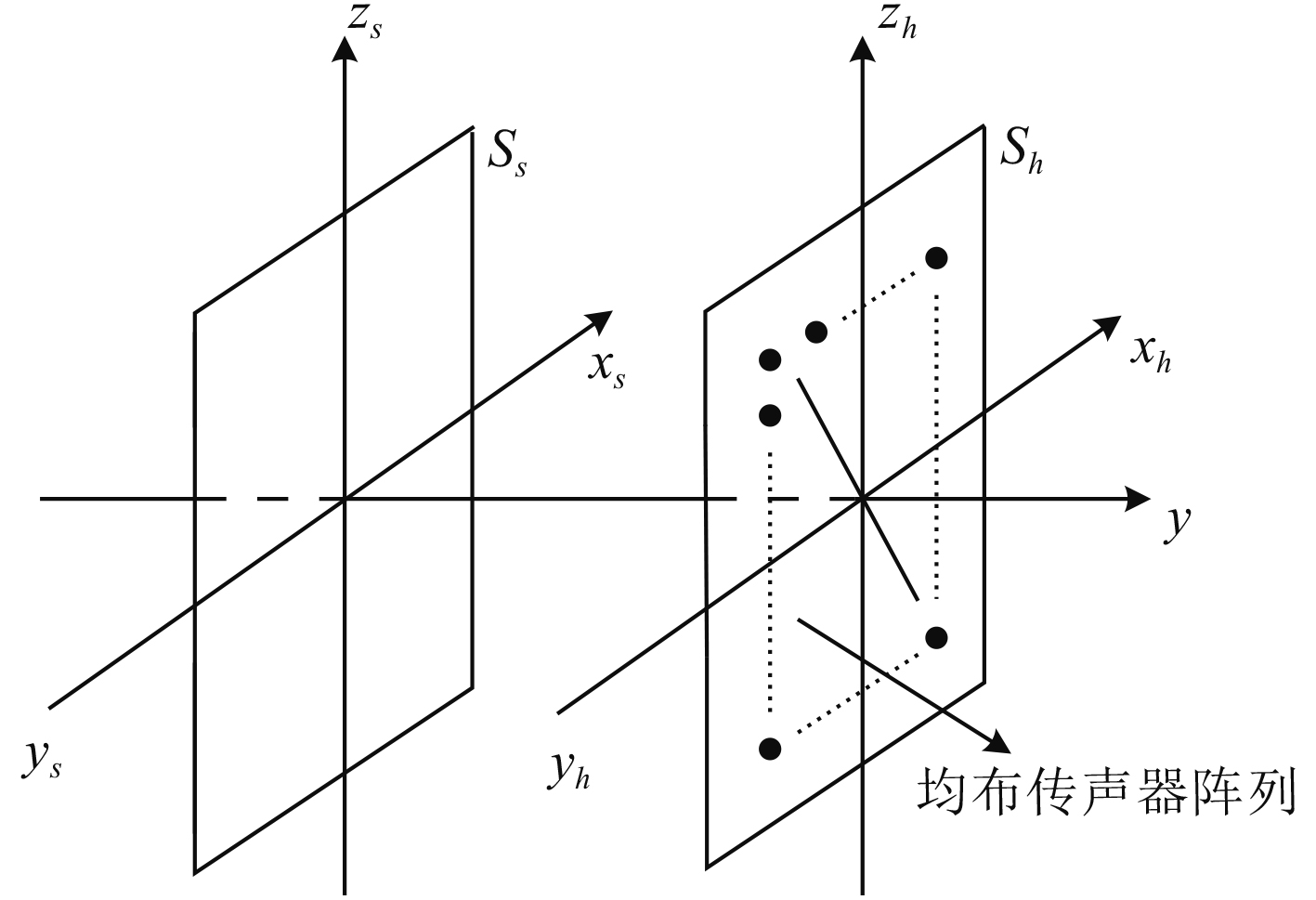
1.3 声压阵信号的稀疏表示模型图4为传声器阵列信号采集模型,在全息平面Sh上,有一个按规则排布的M元传声器阵列。声源点通常数目有限,故声源点在声源面Ss上为稀疏分布。可对声源面Ss进行均匀划分格点,使声源点位置在其上能够稀疏表示[9]。
|
图 4 传声器阵列信号采样模型 Fig. 4 Microphone array signal sampling model |
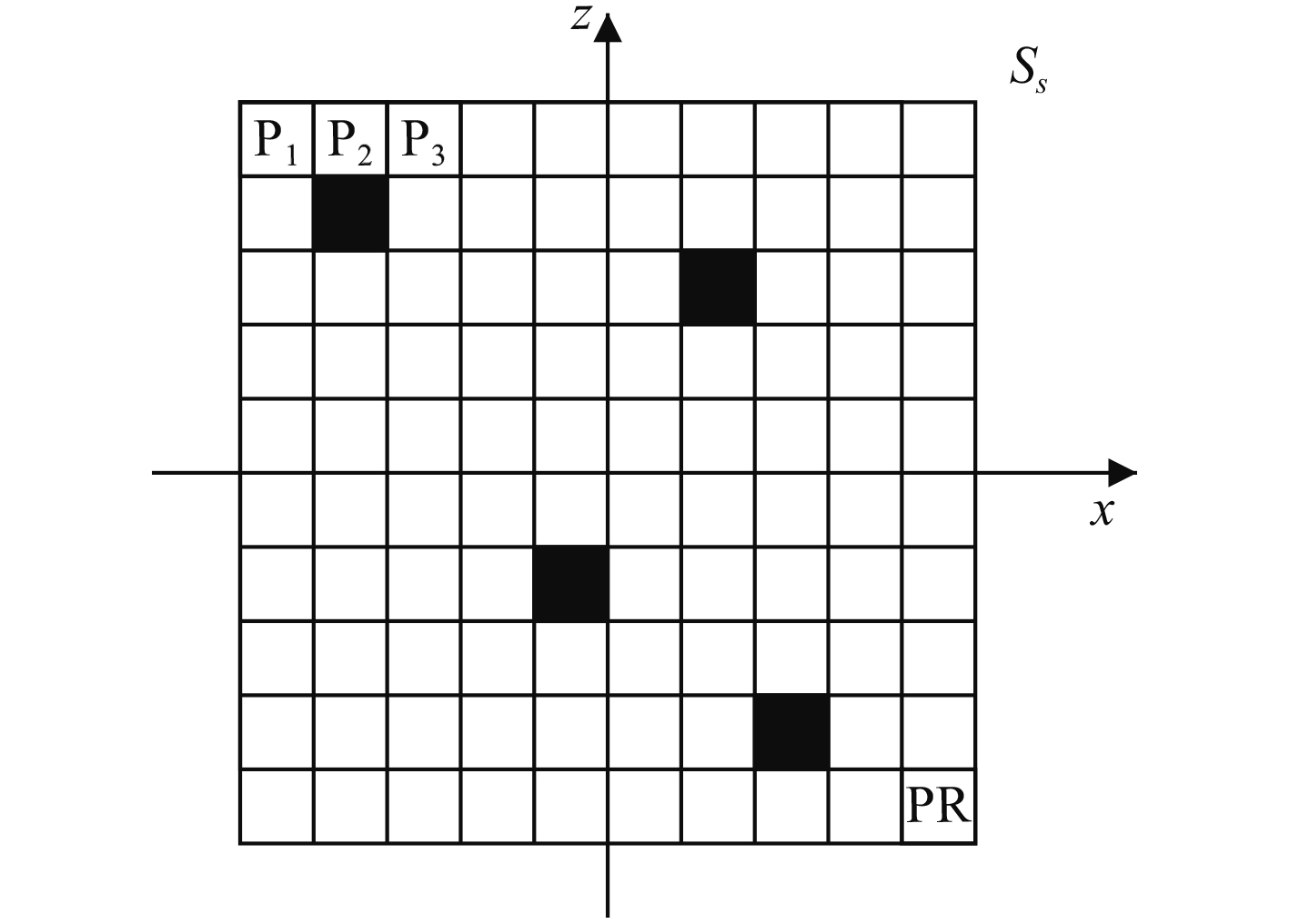
如图5所示,声源面Ss被均分为R个区域,实心区域表示该处存在声源,空心区域表示该处不存在声源。可将规则分布的M元传声器阵列接受到的声压信号稀疏表示为:
|
图 5 声源面上声源稀疏表示 Fig. 5 Sound source surface sparse representation |
| ${ y} = {{Ax}} + \theta \text{。}$ | (10) |
其中:y为M×1维矩阵,表示全息面上传声器阵列接收到的信号;A为M×R维矩阵,表示传感矩阵;x为R×1维矩阵,表示包含位置信息的声源信号,其中只有N(N<<R)个非零数值;
实际声源数量与分布相对于待测空间平面往往是稀疏的,选取适当的观测矩阵,可在少测量值情况下实现声源定位。平面等效源近场声辐射模型中,对虚拟声源面Sv进行了离散化处理。虚拟声源点在虚拟声源平面Sv上稀疏分布,将平面等效源法中的传递矩阵L直接作为传感矩阵A,此矩阵符合约束等距性条件(Restricted Isometry Property,RIP)[10]。先将虚拟声源面上的虚拟声源点位置通过压缩感知理论的正交匹配追踪(Orthogonal Matching Pursuit,OMP)算法求出,再结合已知的传递矩阵重构出近场中平面声压分布。由于非均匀网格的小面元的面积计算不方便,故一般情况下取均匀网格。
虚拟声源平面到全息面的声压传递矩阵L已由式(8)给出,此即为传感矩阵,将其代入式(10)中得:
| ${ y} = { {Lx}} + \theta \text{。} $ | (11) |
噪声信号的存在会影响声源定位的精度,式中
| ${ y} = { {Lx}}\text{,}$ | (12) |
求出带有稀疏信息的声源面信息x’后,已知传递矩阵L,可以由式(13)求得相距为d的任意近场平面的声压分布图。
| ${ {yd}} = {{Ld}}x'\text{。}$ | (13) |
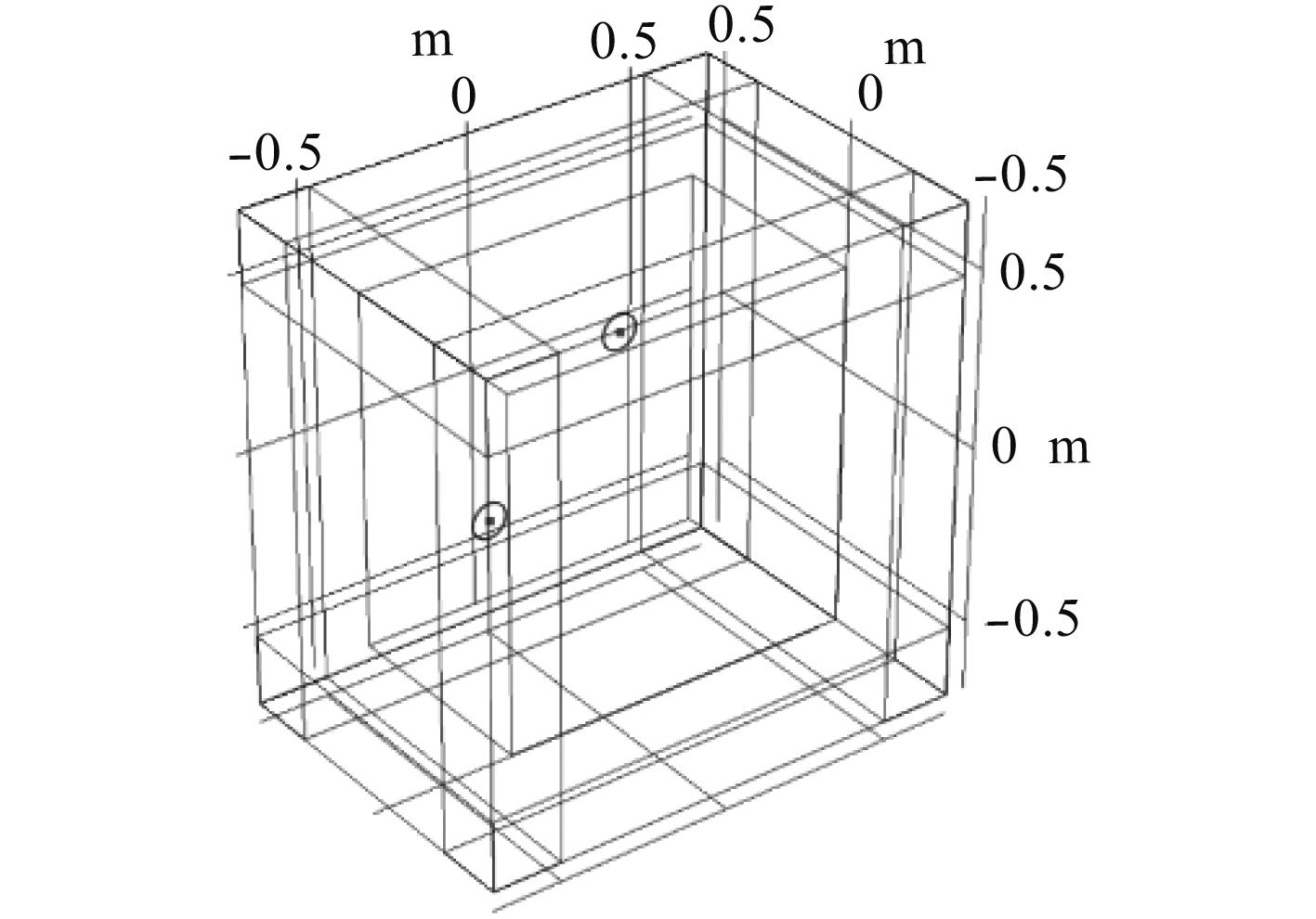
在Comsol中设置2个受到高频点激励的金属圆盘,圆盘半径均为0.05 m,厚度同为0.005 m,材料均为合金结构钢。圆盘中轴线与y轴平行,在x–z平面上分布的圆心坐标分别为(0.2,0.2)和(–0.2,–0.2),具体分布情况如图6所示。在金属圆盘四周施加固定约束,在两金属圆盘中心同时施加
|
图 6 声场三维模型 Fig. 6 Sound field three-dimensional model |
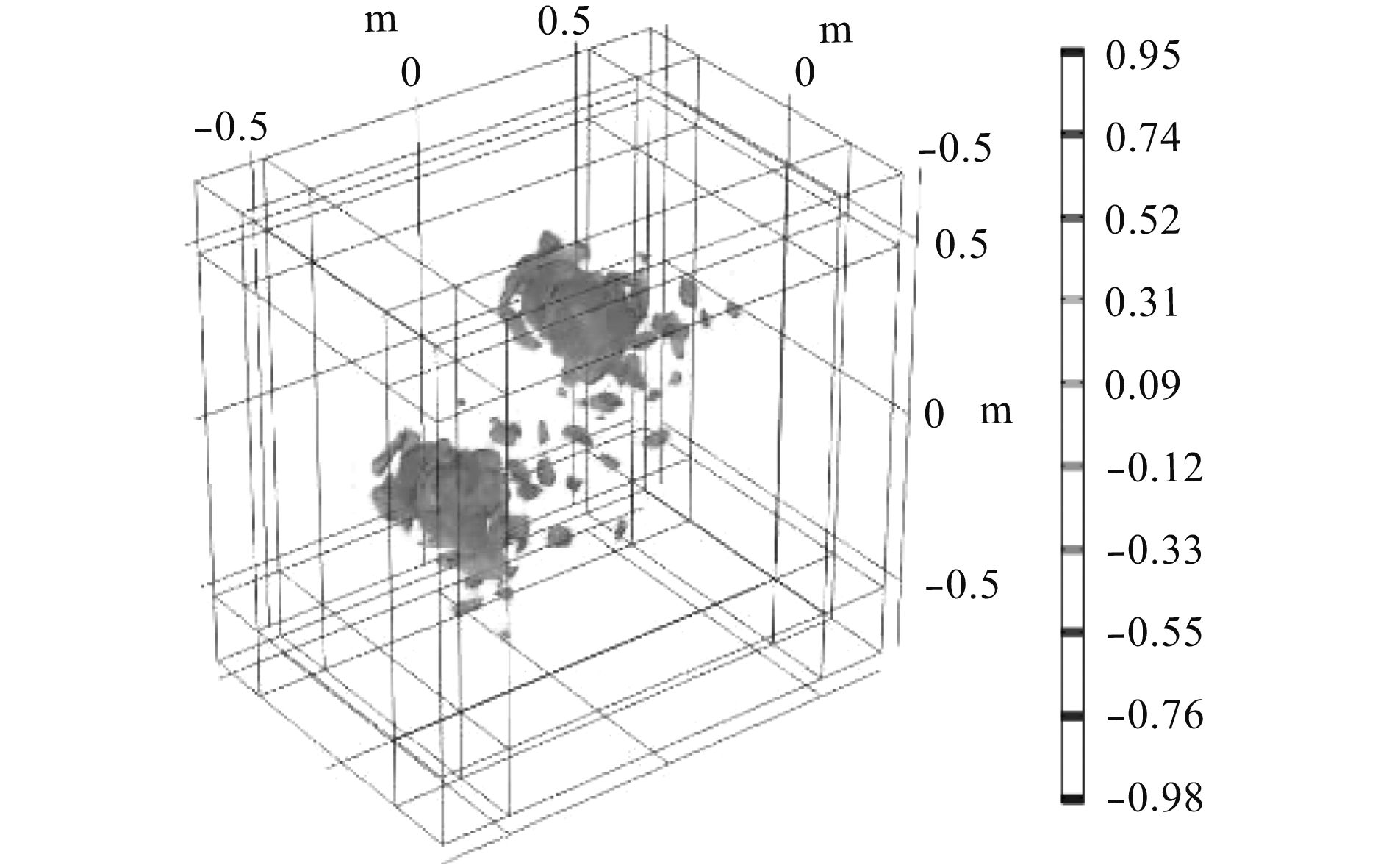
建立0.6 m×1 m×1 m的长方体自由声场空间,并在四周添加厚度为0.2 m的完美匹配层。图7为圆盘振动产生的噪声,在时间t=0.2 s时在空间中形成的声压等值面分布图。
|
图 7 声压等值面分布图(t=0.2 s) Fig. 7 Sound pressure isosurface distri-bution(t=0.2 s) |
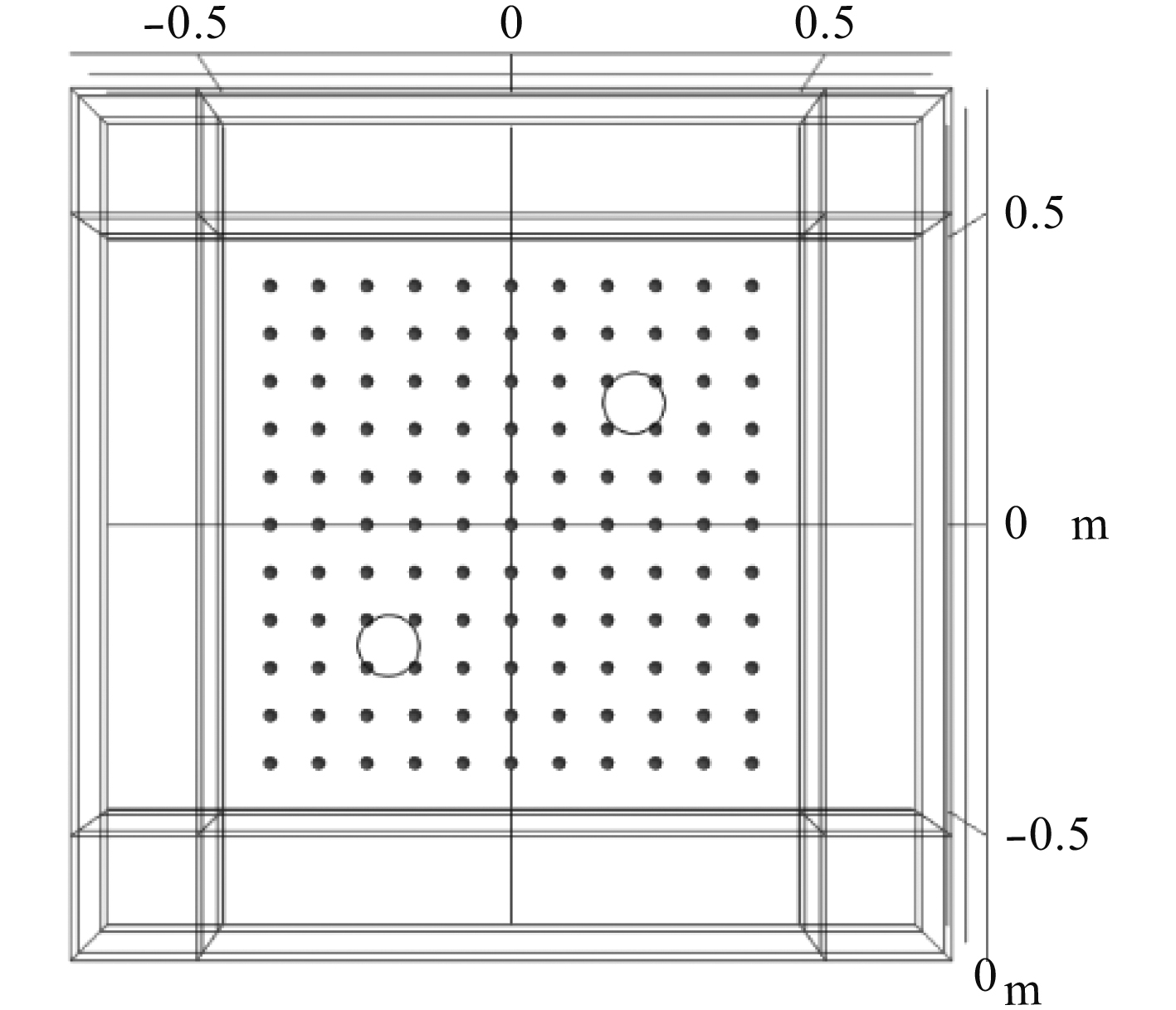
设置2个距离金属圆盘分别为0.1 m和0.2 m的平面,此2个平面理想声压分布情况分别如图8所示。采用11×11均匀排布的传声器阵列对图8(b)所示声压分布进行采样,阵列具体形式如图9所示。

|
图 8 平面声压分布图 Fig. 8 Sound pressure distribution maps |
|
图 9 传声器排布示意图 Fig. 9 Microphones arrangement diagram |
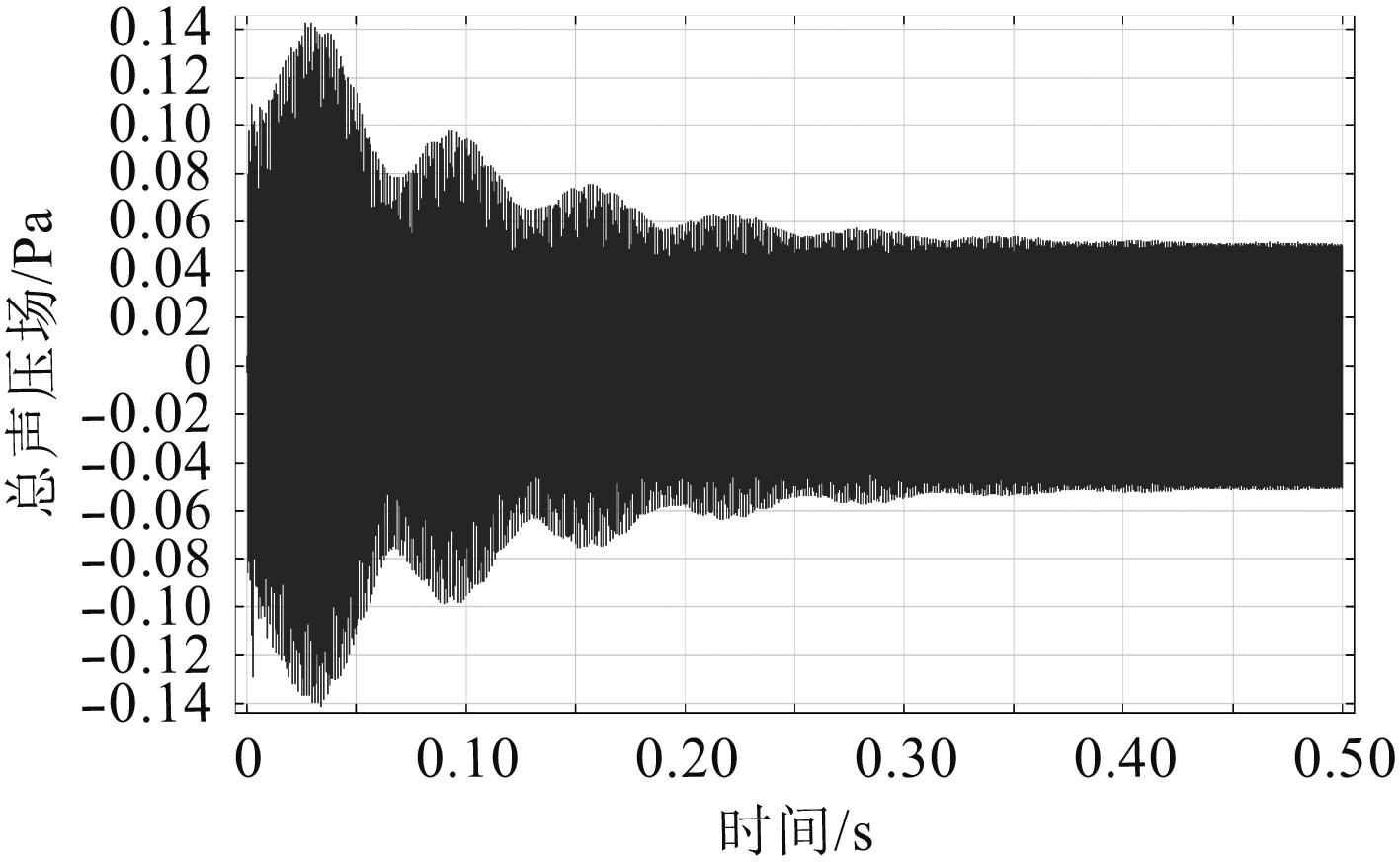
本文声阵列采样在时域内进行,选取声阵列中某一传声器,其在时域内采样所得声压变化如图10所示。可知,在0.4 s后该点声压变化趋于稳定。故均选用0.4 s后的数据进行运算。
|
图 10 阵元信号时域图 Fig. 10 Time-domain map of a single element signal |
采用声阵列对图8(b)平面上声压进行采样,各传声器采样所得时域信号时长均为0.005 s。计算得到121个点的声压值,各采样点平均声压幅值为0.038 Pa。
将虚拟声源面设置在实际声源面上,并均匀划分为16×16个网格。将声压重构面设在距离圆盘0.1 m的平面上,均匀划分为21×21个网格。声阵列在距圆盘0.2 m的全息面上,采样得到的声压分布如图11(a)所示。

|
图 11 不同噪声条件下全息面声压采样图 Fig. 11 Sound pressure sampling data with different noise in the holographic plane |
在实际船舶机舱内,各干扰噪声源距离全息面相对较远,可视为远场声源。当干扰噪声到达全息面时可近似视为平面波,故声阵列平面上的噪声可视为均匀分布在各采样点上。此处,在每个采样点的数据中增加时长同为0.005 s的干扰噪声模拟噪声干扰。
现分为3组进行实验,每组添加不同的噪声信号,具体情况为:
1)添加时长为0.005 s,表达式为
2)添加时长为0.005 s,表达式为
3)添加时长为0.005 s,表达式为
在距离圆盘0.2 m的全息面上,分别得到如图11(b)~图11(d)所示的采样声压分布图。直观比较各图差异不大,主要区别在于声压值范围不同。为方便表示,后文将本文所提方法简称为权值法。
当添加噪声信号表达式为y=0.019×

|
图 12 声压重构图 Fig. 12 Sound pressure reconstruction maps |
当添加噪声信号表达式为y=0.038×

|
图 13 声压重构图 Fig. 13 Sound pressure reconstruction maps |
当添加噪声信号表达式为y=0.19×

|
图 14 声压重构图 Fig. 14 Sound pressure reconstruction maps |
仿真实验中,各组采样所得声信号平均信噪比分别为6.02 dB,0 dB和–13.98 dB。当信噪比为零或负值时,表明此时信号功率小于噪声功率。
添加噪声信号表达式为y=0.019×
添加噪声信号表达式为y=0.038×
添加噪声信号表达式为y=0.19×
得到上述结果的原因在于,Fourier变换法和BEM均未对含强干扰噪声的信号进行处理,使得进行运算的数据包含较强噪声。而权值法针对各采样信号高频部分,计算所需乘上的权值,故在相同条件下权值法对高频弱声源的定位与声压分布重构效果优于Fourier变换法和BEM。现对添加噪声情况下,声阵列上各采样点是否乘上权值与理想值进行量化对比,具体公式如下:
| $D - value = \frac{{\sum\limits_{{\rm{i}} = 1}^{121} {\left| {\frac{{{P_h}(i) - {P_f}(i)}}{{{P_f}(i)}}} \right|} }}{{121}} \times 100{\text{%}}\text{。} $ | (14) |
其中:Ph(i)为距离声源0.2 m的全息面上各点实际测得声压值;Pf(i)为对应平面上不添加干扰噪声时的理论声压;Ph(i)和Pf(i)各有121个值。现采用式(14),对是否乘权值的差异进行量化表示,计算所得结果如表1所示。
|
|
表 1 采样点平均差值比较 Tab.1 Difference comparison |
可知,乘上权值后各采样点数据明显更接近没有干扰噪声时的理想声压值。但由重构图12(c),13(c),14(c)也可看出,权值法重构声源分布接近实际情况,但其声压分布值与实际情况存在一定的差距。出现此情形原因在于EMD法本身存在的模态混叠现象,该现象会导致无法根据特征尺度有效地分离出不同的模态成分,出现现有的IMF包含不同时间尺度组分的情况。故通过EMD法计算得到各点的权值不够精确。
3 结 语为解决船舶机舱内嘈杂环境下高压流体泄漏不易被察觉的问题,本文提出了一种高频弱声源平面近场声全息方法。并利用三维声场模型与Fourier变换法和BEM进行了比较分析,得到相关结论如下:
1)高频弱声源平面近场声全息方法,虚拟面不需要与实际声源面共形,计算过程更方便且通用性更强。其网格划分可以为均匀或非均匀,适用性较灵活。
2)在船舶机舱等低信噪比条件下,该方法对采样信号进行乘权值处理,能较好的对高频弱声源进行定位与实现近场平面声压重构,且重构效果较好。
本文提出的高频弱声源近场声全息方法,从理论到仿真实验结果表明该方法具有较强的抗噪能力,可以作为船舶机舱内信噪比较低条件下高频弱声源近场声全息方法的有效补充。
| [1] |
WILLIAMS E G, MAYNARD J D, SKUDRZYK E. Sound source reconstructions using a microphone array[J]. Journal of the Acoustical Society of America, 1980, 68(1): 340-344. DOI:10.1121/1.384602 |
| [2] |
MAYNARD J D, WILLIAMS E G, LEE Y. Nearfield acoustic holography: I. Theory of generalized holography and the development of NAH[J]. Jasa, 1985, 78(4): 1395-1413. DOI:10.1121/1.392911 |
| [3] |
KOOPMANN G H, SONG L, FAHNLINE J B. A method for computing acoustic fields based on the principle of wave superposition[J]. Journal of the Acoustical Society of America, 1989, 86(6): 2433-2438. DOI:10.1121/1.398450 |
| [4] |
JEON I Y, IH J G. On the holographic reconstruction of vibroacoustic fields using equivalent sources and inverse boundary element method[J]. Journal of the Acoustical Society of America, 2005, 118(118): 3473-3482. |
| [5] |
DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306. DOI:10.1109/TIT.2006.871582 |
| [6] |
CANDÈS E J, ROMBERG J K, TAO T. Stable signal recovery from incomplete and inaccurate measurements[J]. Communications on Pure & Applied Mathematics, 2005, 59(8): 1207-1223. |
| [7] |
CHARDON G, DAUDET L, PEILLOT A, et al. Near-field acoustic holography using sparse regularization and compressive sampling principles[J]. Journal of the Acoustical Society of America, 2012, 132(3): 1521. DOI:10.1121/1.4740476 |
| [8] |
KIRCHNER M, NIJMAN E. Nearfield acoustical holography for the characterization of cylindrical sources: practical aspects[C]// International Styrian Noise, Vibration & Harshness Congress: the European Automotive Noise Conference. 2014.
|
| [9] |
时洁, 杨德森, 时胜国, 等. 基于压缩感知的矢量阵聚焦定位方法[J]. 物理学报, 2016, 65(2): 190-200. |
| [10] |
ZHANG B, CHENG X, ZHANG N, et al. Sparse target counting and localization in sensor networks based on compressive sensing[J]. Proceedings - IEEE INFOCOM, 2011, 2(3): 2255-2263. |
 2019, Vol. 41
2019, Vol. 41
