2. 河南省水下智能装备重点实验室,河南 郑州 450015
2. Henan Key Laboratory of Underwater Intelligence Equipment, Zhengzhou 450015, China
潜射导弹具有机动性强、隐蔽性好、突防能力强等优点,是军事强国重要的武器。随着现代反潜和反导技术的发展,保持潜艇隐蔽性和提高武器系统的快速反应能力特别重要。对于水下发射潜射弹道导弹来讲,在尽可能短的时间内完成发射,缩短导弹齐射的间隔时间,在敌方来不及反应之前,迅速撤离发射区,这对保障潜艇的安全和导弹成功突防十分关键。要达到这一目的,潜射导弹必须实现大深度、大范围变深度发射。
燃气—蒸汽式发射动力系统是目前技术最为成熟的发射动力[1],发射动力组件由燃气发生器、冷却室等组成,燃气发生器使用固体推进剂,其燃烧规律靠型面设计,能够在燃烧室形成稳定的燃烧流量规律;冷却室利用液态水的相变吸热原理,可以实现发射能量调节的功能,同时降低了发射筒筒底温度,改善了发射环境,燃气—蒸汽发射动力系统可以很好的完成发射任务。随着发射能量变化范围不断加大,调节能力要求不断提高,大深度、大范围变深度发射技术对发射动力提出了新的更高的要求。
新型固-膏体燃气发生器采用膏体推进剂作为主装药,通过改变输入膏体推进剂流量进行发射能量管理,可在发射前对装药能量进行调节,装药量可调比例大,是一种具备大深度、大范围发射能量调节能力的新型发射动力系统。
1 固-膏体燃气发生器工作原理固-膏体发射动力系统技术是一种新型的高能量大范围调节的发射技术。利用固体推进剂燃烧时产生的高温、高压燃气,将膏体推进剂挤入燃烧室,挤入燃烧室的膏体推进剂燃烧,产生的燃气与固体推进剂燃烧产生的燃气一起流入发射筒底,将导弹发射出筒。
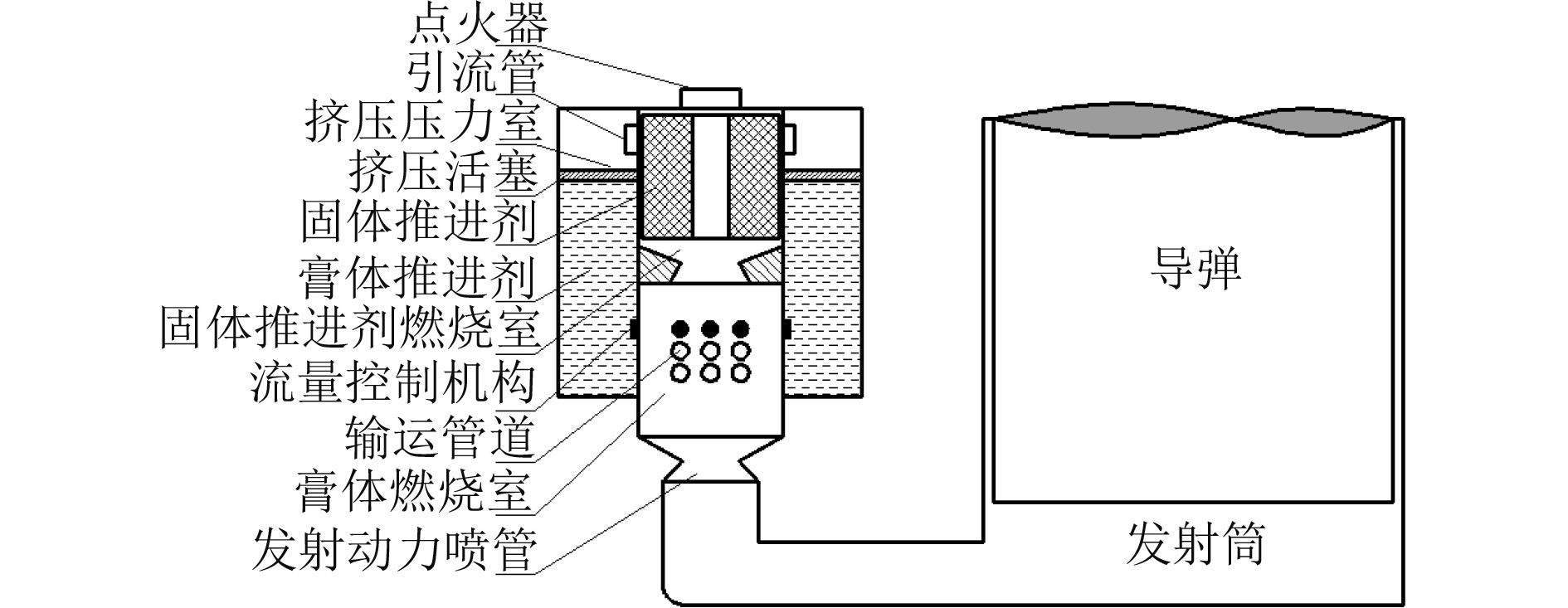
当接到指令需发射导弹时,点火器点燃固体推进剂,固体推进剂在固体燃烧室内燃烧,其燃烧的一部分燃气进入挤压活塞上部的挤压压力室形成高压,挤压压力室的高压气体挤压活塞,将膏体推进剂通过输运管道挤入膏体燃烧室,同时固体推进剂燃烧的主燃气也进入膏体燃烧室,点燃挤入膏体燃烧室的膏体推进剂,膏体推进剂燃烧生成的燃气和固体推进剂燃烧生成的燃气混合后进入发射筒底部,气体膨胀做功将导弹弹射出发射筒。
|
图 1 固-膏体推进剂发射动力系统示意图 Fig. 1 Solid-pasty propellant emission power system schematic diagram |
燃气发生器内弹道建立的基本假设[2]如下:
1)压力室燃气按完全气体处理,燃气在喷管内的流动为一维、准定常、等熵的;
2)燃气流为冻结流,固体推进剂和膏体推进剂燃烧生成的燃气成分相同,物理化学性质认为是固定不变的;
3)在压力室中推进剂的燃烧过程是绝热的。实际计算中,用热损失修正系数
4)挤压压力室燃气膨胀做功过程为绝热过程。
2.2 燃气发生器内弹道方程组 2.2.1 固体燃烧室压力计算方程固体燃烧室压力分上升段、平衡段和结束段3个阶段计算[3–4]:
| $\left\{ \begin{aligned} &{\text{上升段}}:\;{t_i} \!=\! \frac{{{V_{c0}}}}{{(1 \!-\! \nu )k{{(\frac{2}{{k \!+\! 1}})}^{\frac{{k \!+\! 1}}{{k \!-\! 1}}}}{C^*}{A_{\rm{Z}}}}}\ln \frac{{1 \!-\! {{(\frac{{{P_{ig}}}}{{{P_0}}})}^{1 \!-\! \nu }}}}{{1 \!-\! {{(\frac{{{P_i}}}{{{P_0}}})}^{1 \!-\! \nu }}}}\text{,}\\ &{\text{平衡段}}:\;{P_i} \!=\! {[{\rho _p}{U_{\rm{1}}}\varepsilon {C^*}\frac{{{A_i}}}{{\mu {\sigma _f}{A_{\rm{z}}}}}]^{\frac{1}{{1 \!-\! \nu }}}}\text{,}\\ &{\text{结束段}}:\;{p_i} \!=\! {p_{cf}}{\left[ {\frac{{2{V_{cf}}}}{{2{V_{cf}} \!+\! (k - 1)\sqrt {{R_g}{T_p}} {\varphi _2}{A_{\rm{Z}}}\Gamma {t_i}}}} \right]^{\frac{{2k}}{{k \!-\! 1}}}}\text{。} \end{aligned} \right. \!\!\!\!\!\!\!\! $ | (1) |
式中:
挤压压力室内部的压力为燃气分压力与空气分压力之和:
| ${P_l} = \frac{{{R_l}{M_a} + {R_g}{M_y}}}{{{V_0} + {V_l}}}{T_l}\text{,}$ | (2) |
| ${V_l} = \int\limits_0^t {\frac{{\mu {n_l}A\sqrt {2({P_l} - {P_S} - {P_P})} }}{\rho }{\rm d}t}\text{。} $ | (3) |
式中:
通过引流孔进入挤压压力室的燃气流量[5]可表示为:
| ${q_m} \!=\! \left\{ \begin{aligned} &A{P_{\rm{r}}}\sqrt {\frac{{2k}}{{k \!-\! 1}}\frac{1}{{{R_r}{T_r}}}{{\left[ {{{\left( {\frac{{{P_l}}}{{{P_r}}}} \right)}^{\frac{2}{k}}} \!-\! {{\left( {\frac{{{P_l}}}{{{P_r}}}} \right)}^{\frac{{k \!+\! 1}}{k}}}} \right]}^{}}} ,({P_l}/{P_r} \!\geqslant\!\beta )\text{,}\\ &A{P_r}\sqrt {\frac{{2k}}{{k \!- \!1}}\frac{1}{{{R_r}{T_r}}}{{\left( {\frac{2}{{k \!+\! 1}}} \right)}^{\frac{2}{{k \!-\! 1}}}}} \text{,}\left( {{P_l}/{P_r} < \beta } \right)\text{,} \end{aligned} \right. \!\!\!\!\!\! $ | (4) |
| $\beta = {\left( {\frac{2}{{k + 1}}} \right)^{\frac{k}{{k - 1}}}}\text{,}$ | (5) |
通过引流孔的总燃气质量:
| ${M_{\rm{y}}} = \int_0^t {{q_m}} {\rm d}t\text{。}$ |
式中:
假设膏体推进剂在挤出输运管道与燃气接触后立刻开始燃烧。根据质量守恒原理,经固体推进剂燃气发生器喷管流入的燃气质量流率
| $\frac{{d{m_r}}}{{dt}} = {\dot m_{in}} + {\dot m_{gr}} - {\dot m_{out}}\text{,}$ | (6) |
| $\frac{{d{m_r}}}{{dt}} = \bar \rho \frac{{d{V_g}}}{{dt}} + {V_g}\frac{{d\bar \rho }}{{dt}}\text{,}$ | (7) |
| $\frac{{d{V_g}}}{{dt}} = {S_g}{r_g}\text{,}$ | (8) |
| $\frac{{d\bar \rho }}{{dt}} = \frac{1}{{RT}}\frac{{d\bar p}}{{dt}}\text{,}$ | (9) |
| ${\dot m_{in}} = \frac{{{{\bar p}_c}{A_{t1}}}}{{{C_{1*}}}}\text{,}$ | (10) |
| ${\dot m_{out}} = \frac{{{{\bar p}_g}{A_{t2}}}}{{{C_{2*}}}}\text{。}$ | (11) |
式中:
整理可得:
| $\frac{{{V_g}}}{{RT}}\frac{{{\rm d}{{\bar p}_g}}}{{{\rm d}t}} = \left( {{\rho _g} - \bar \rho } \right){S_g}{r_g} + \frac{{{{\bar p}_c}{A_{t1}}}}{{{C_{1*}}}} - \frac{{{{\bar p}_g}{A_{t2}}}}{{{C_{2*}}}}\text{。}$ | (12) |
即为计算膏体推进剂燃烧室零维内弹道p-t曲线的微分方程。
3 仿真结果及分析根据上述建立的固-膏体燃气发生器内弹道数学模型,编写了仿真计算程序,运用Matlab对固-膏体燃气发生器的工作过程进行了仿真计算,计算结果如图2~图5所示。
|
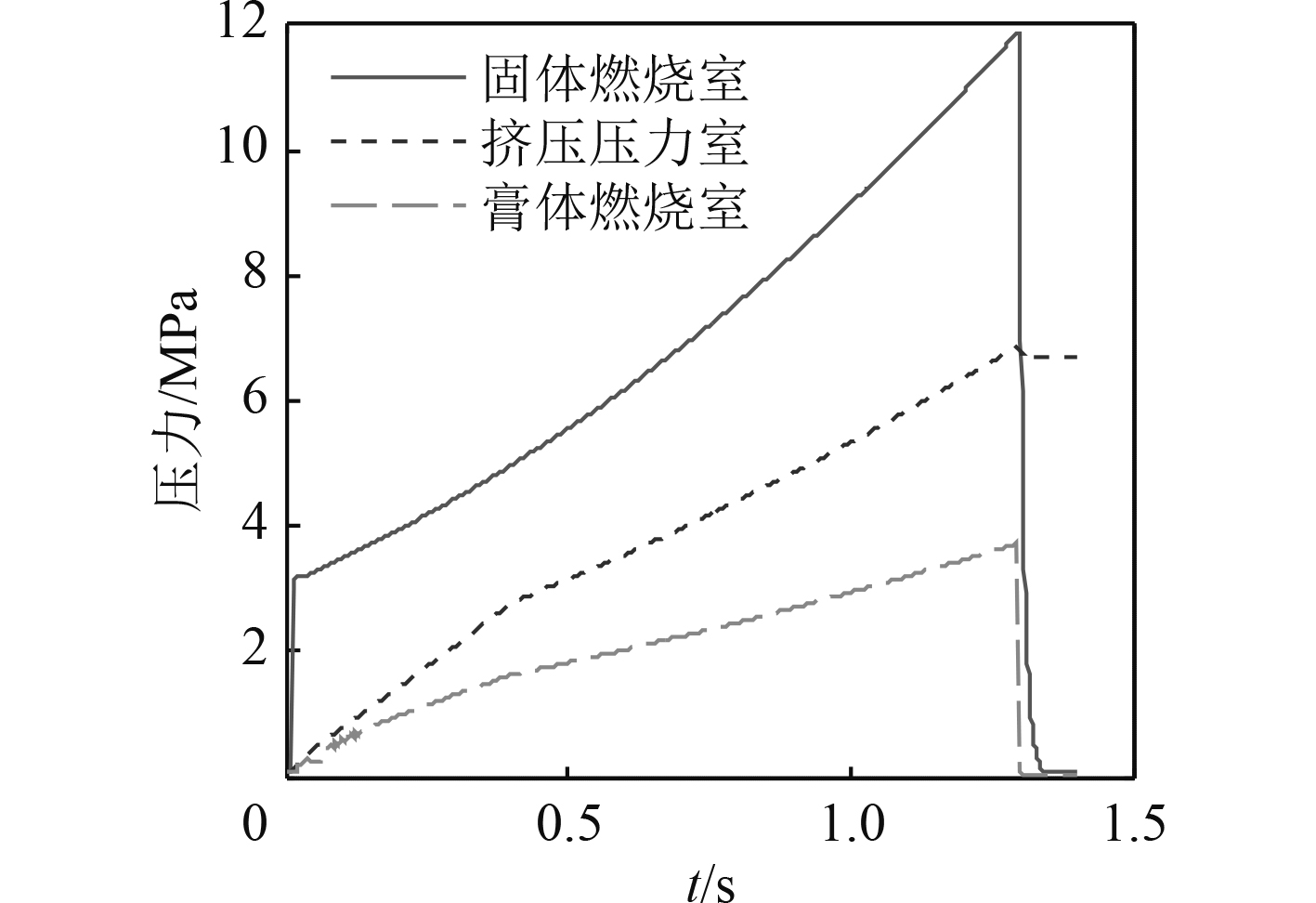
图 2 压力-时间曲线图 Fig. 2 Pressure-time graph |
|
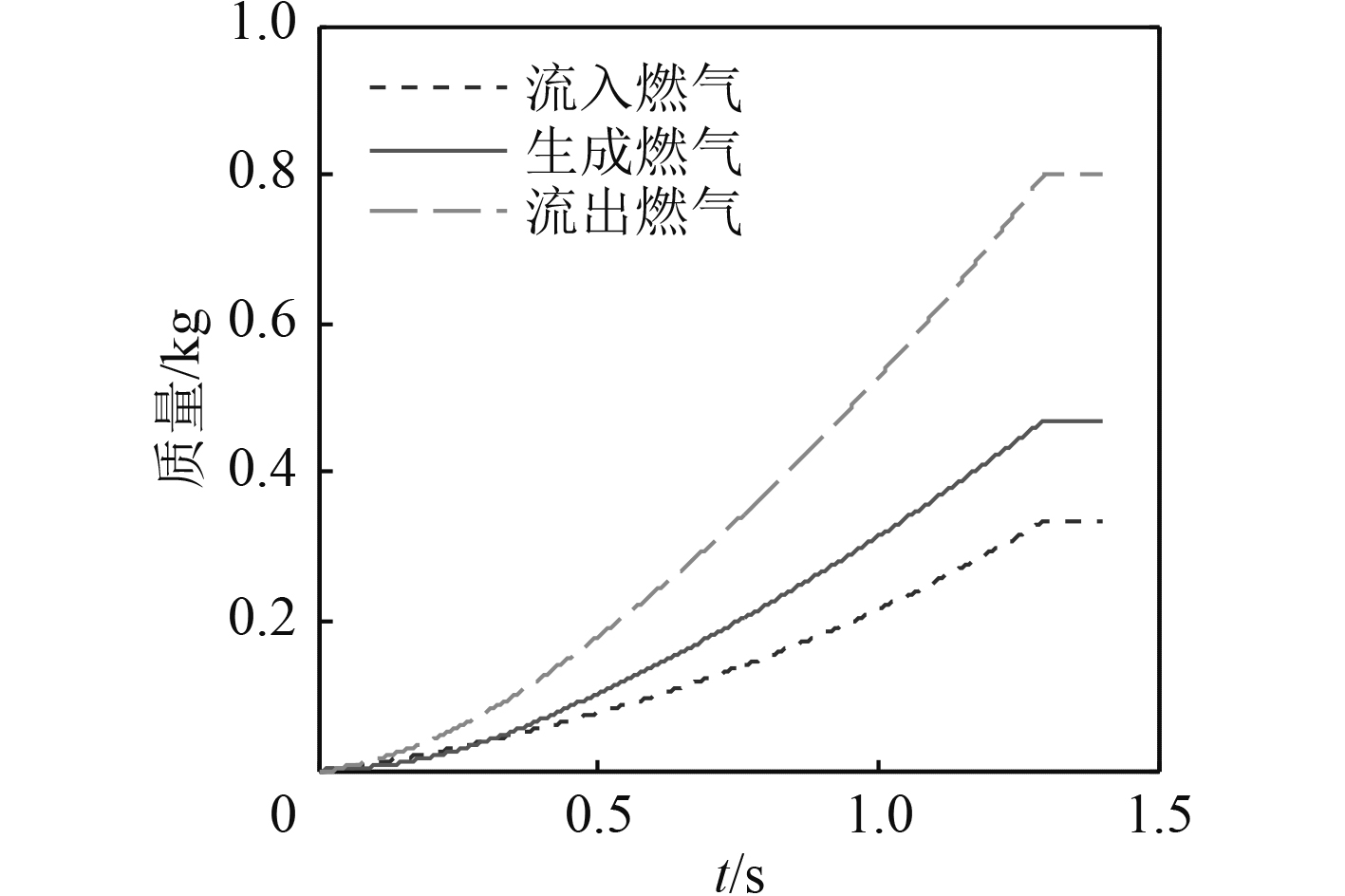
图 5 燃气质量-时间曲线图 Fig. 5 Fuel gas mass-time graph |
|
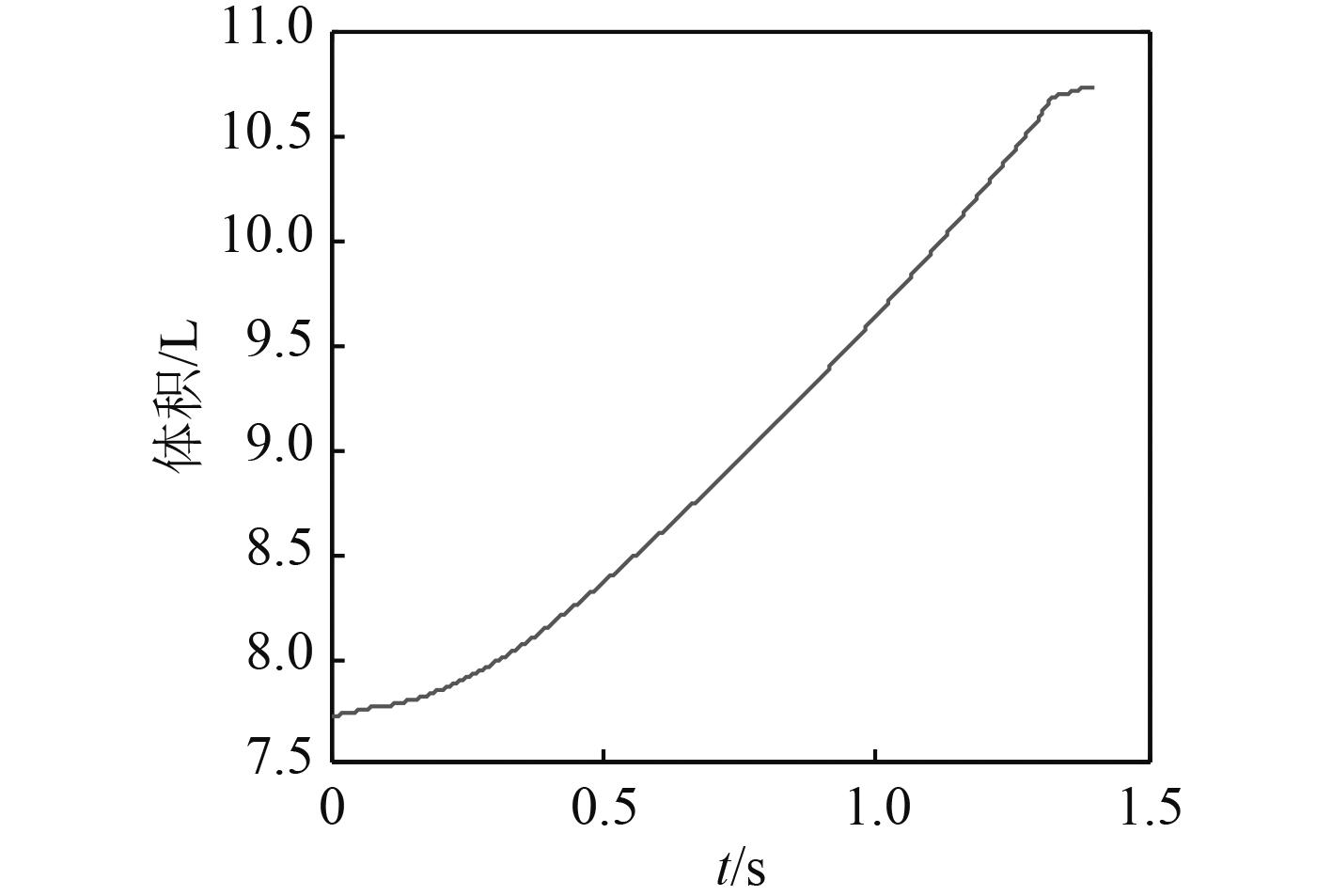
图 3 体积-时间曲线图 Fig. 3 Volume-time graph |
|
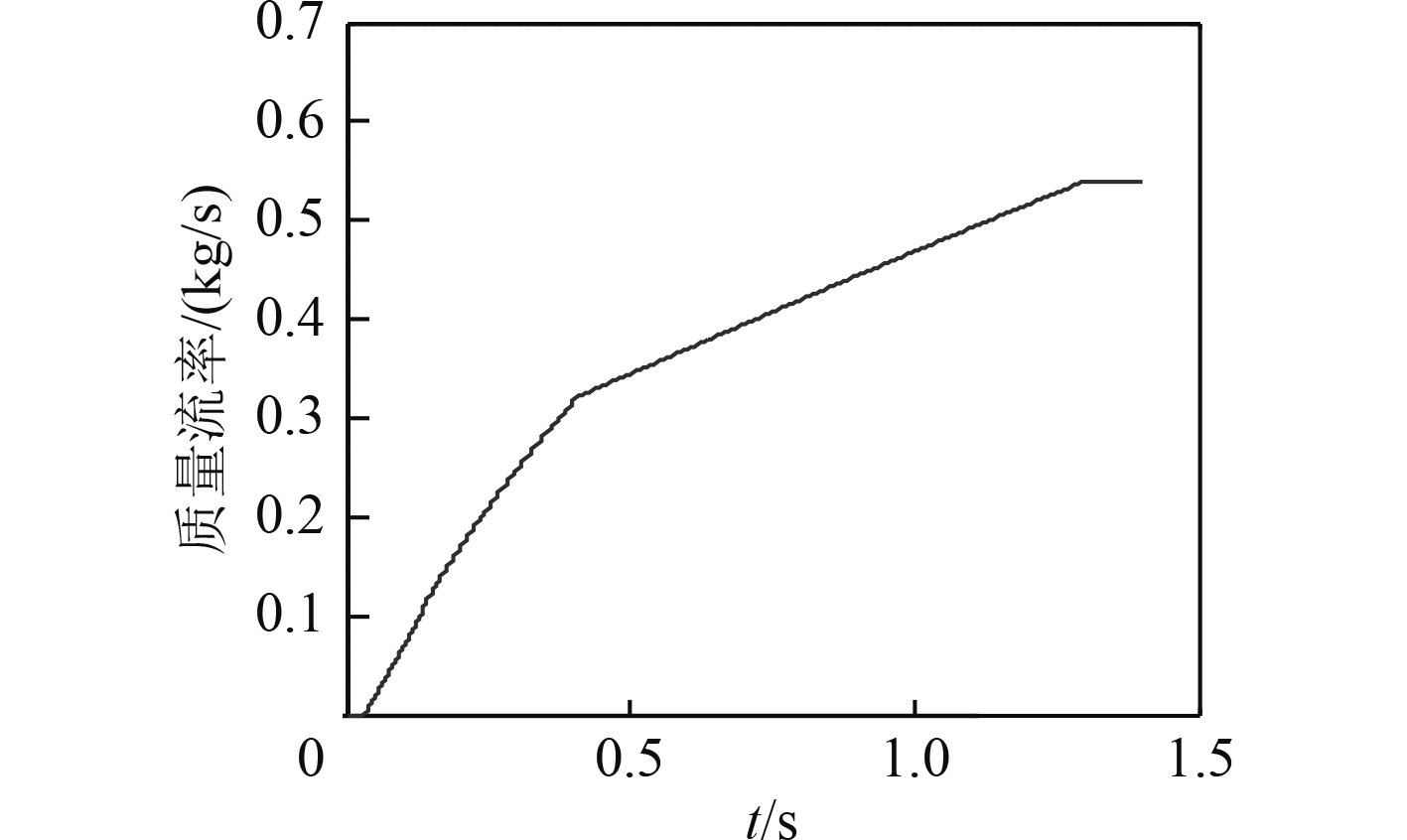
图 4 膏体推进剂挤出质量流率-时间曲线图 Fig. 4 Pasty propellant input mass flow rate-time graph |
从固-膏体燃气发生器内弹道计算结果可以得出:
1)固体燃烧室、挤压压力室和膏体燃烧室之间的压力需保持一定的压力差,以保证各压力室能够稳定工作;
2)挤压压力室的体积-时间曲线在工作起始阶段缓慢爬升,随着挤压压力室内燃气不断的流入和膏体燃烧室压力的建立,两者之间达到动态平衡,之后体积随时间的变化呈线性增加趋势;
3)膏体燃烧室中存在2种燃气的掺混,计算中按照同种燃气成分进行计算,通过改变膏体燃烧室喷管的大小,可以调节进入发射筒的燃气流量规律。
4)固-膏体燃气发生器提供的最小能量是不加入膏体推进剂时的固体推进剂能量,最大能量是将贮存的膏体推进剂全部挤出燃烧所产生的能量,从图5可以看出,固-膏体燃气发生器可提供的能量范围在0.35~0.8 kg之间,最大能量与最小能量比达到了2.3倍。
4 结 语本文建立了固-膏体推进剂燃气发生器内弹道数学模型,运用Matlab对固-膏体推进剂燃气发生器工作过程进行了仿真计算,得到了各压力室压力曲线、挤压压力室体积变化规律曲线、膏体推进剂挤出质量流率曲线和膏体燃烧室内燃气的流量规律曲线,为固-膏体燃气发生器的设计和试验验证提供了一定的理论支撑。
| [1] |
王春健, 马暄. 潜地弹道导弹发射技术现状与发展[J]. 飞航导弹, 2010. |
| [2] |
唐金兰, 刘佩进, 固体火箭发动机原理[M]北京: 国防工业出版社, 2013
|
| [3] |
李咸海, 王俊杰, 潜地导弹发射动力系统[M]哈尔滨: 哈尔滨工程大学出版社, 2000
|
| [4] |
赵险峰, 王俊杰, 潜地弹道导弹发射系统内弹道学[M]哈尔滨: 哈尔滨工程大学出版社, 2000
|
| [5] |
姜毅, 史少岩, 发射气体动力学[M]北京: 北京理工大学出版社, 2015
|
 2019, Vol. 41
2019, Vol. 41
