2. 河南省水下智能装备重点实验,河南 郑州 450015
2. Henan Key Laboratory of Underwater Intelligent Equipment, Zhengzhou 450015, China
采用高温燃气配合冷却水连续注入式调能是导弹水下弹射的主要方式之一,燃气—蒸汽式弹射动力装置主要由燃气生成器和冷却装置等部分组成,燃气生成器产生高温混合气体-燃气,是水下导弹弹射的能量源,冷却装置内装有冷却剂,一般采用水作为冷却剂,使其与高温燃气掺混,吸热相变后形成蒸汽,以降低混合气体温度,使发射环境得到改善,并通过冷却剂注入过程的流量控制来调节弹射能量,实现水下导弹变深度弹射。针对冷却水汽化过程,目前国内外已根据不同的设计理念提出了不同的计算模型。李咸海等[1]建立的蒸发汽化及分压计算模型、赵险峰等[2]的沸腾汽化及总压计算模型,但是计算精度均不够令人满意。赵世平[3]将冷却水分为预先加注水和连续喷注水并分别建立了沸腾汽化模型和饱和水蒸气模型,在此基础上将水下导弹弹射过程综合划分为4个阶段,较大地提高了导弹弹射过程计算精度。本文通过对弹射过程和冷却水汽化机理分析研究,对冷却水模型进行了改进,考虑火药燃烧产物中水蒸气的影响,将火药燃烧产物中的水和冷却水考虑为一个整体,再分为预先加注水和连续喷注水两部分,并以此为基础,依据弹射进程的不同特点,按3个不同特征阶段,建立能量平衡方程和汽化方程,构建了弹射模型基本方程组。
1 弹射过程分析导弹水下发射过程中,发控台发出点火指令后,燃气生成器装药燃烧产生工质气体-燃气,把冷却装置内处于喷水管内的预先加注水一次性全部推入弹射筒,然后在冷却装置环形水室及喷水管内建立压差,将水室内的冷却水快速喷注入燃气通道,冷却水与高速、高温燃气流混合,经过雾化、相变、掺混等一系列复杂变化过程,经弯管进一步掺混后进入发射筒内形成燃气一蒸汽混合工质,推动导弹按照设计规律运动出筒。
实际上进入弹射筒内的水并不只是冷却水,因为火药的燃烧产物中往往也包含有水蒸气,而且可能含量还比较高,通常使用的几种火药其水蒸气含量一般在10%以上。由于燃气中含有水蒸气,而且比例还比较高,所以无论是对燃气的性质还是水的相变都会产生比较大的影响。通常把燃气作为理想气体来处理,当水蒸气含量比较大时就会带来较大误差。另一方面由于这部分水的存在,不仅自身会有状态的变化,同时也会影响其他水的状态变化。本文将火药燃烧产物分为两部分进行处理,即水蒸气和其余部分,水蒸气与冷却水统一考虑,其余部分按理想气体处理。如果火药燃烧产物中固体颗粒物含量较多时,还应对固体颗粒物单独进行处理,这时火药燃烧产物可分为3部分,对此本文不作深入讨论。
将燃气中的水蒸气从燃气分出来之后,进入弹射筒内的水由3部分组成,即燃气生成器刚开始工作时一次性集中注入的冷却水、通过喷水孔连续注入的冷却水以及燃气中的冷却水,集中注入水进入弹射筒前,基本没有与高温混合气体燃气进行组分掺混以及能量交换;连续注入式冷却水在喷水孔前后压差作用下,喷出后完成一次雾化,与横向高速燃气流碰撞破碎后形成二次雾化,再通过具有一定弯曲度及长度的导入弯管,工质燃气与冷却水发生了比较充分的掺混、蒸发、热交换过程。通过对燃气及冷却水喷注射流在内通道中的衍化过程开展数值模拟,喷注射流在进入弹射筒时的汽化率大于95%[4]。这时燃气中的水蒸气与连续注入的冷却水汽化后的水蒸气状态相同,为温度相同的过热状态,因此在计算模型中可以合并在一起统一考虑。
从以上分析可以看出,进入弹射筒内的水一部分是开始时一次性集中注入的冷却水,另一部分是连续喷注水,其中包括连续注入的冷却水和燃气中的水。由于集中注水和连续注水进入弹射筒的方式不同,它们在弹射筒内的汽化过程有很大差异。一次性集中注入的水进入弹射筒时还没有与燃气掺混,不仅温度比较低,处于低温液态,而且液滴体积比较大,此后随着燃气工质的进入,弹射筒内混合气体温度不断上升,才经历加热、汽化等过程,由于此过程中冷却水量相对燃气量较大,汽化以较为缓慢的过程发生。而连续注入的水在进入弹射筒前基本上已经汽化完毕并处于高温过热状态,进入弹射筒后,这种燃气工质和过热后的水蒸气形成的高温混合气体又与弹射筒内已经存在的集中注水预先加注水、初始容积中的空气、和前期喷射入弹射筒内的低温燃气-冷却水混合物,再次在弹射筒内进行气液掺混、能量交换以及相变,形成温度介于两者之间的新的混合物,高温水蒸气温度降低后有部分甚至可能会液化。
对于集中注入的预先加注水来说,虽然也存在蒸发现象,但是蒸发速度太慢,由于蒸发而生成的水蒸气量非常少,所以在短暂的发射过程可以忽略不计。随着弹射筒内燃气不断进入和温度不断升高,预先加注水达到沸点时就会沸腾汽化,当预先加注水沸腾到全部汽化之后,随着温度继续上升进入过热阶段。从以上分析可知,预先加注水的汽化过程与沸腾比较接近,本文按沸腾来处理。
连续喷注水全部以过热水蒸汽状态进入弹射筒,在初始阶段,由于预先加注水基本上没有汽化,所以弹射筒内水蒸气的分压接近于0,而且弹射筒内导弹底部预留的初始容积比较大,初始阶段进入弹射筒气体的流量也比较小,因此弹射筒内水蒸气的分压上升比较缓慢。在这种情况下,初始进入弹射筒内的过热水蒸汽尽管温度会降低,也仍会继续以气态的形式存在,并不会发生气态向液态的相变。同时由于连续注入的高温混合气体与筒内预先加注水的掺混并不充分,所以连续喷注水的温度要比真正达到平衡状态时要高,这又进一步削弱了连续喷注水蒸气液化的倾向。随着新的高温气体的不断加入,弹射筒内的温度快速升高,所以连续喷注水基本上不存在水气共存的汽化过程,即使存在也时间极短,连续喷注水很快就可以达到过热状态,这个过程往往在弹动前后完成。由此可见,开始阶段无需考虑连续喷注水的气液相变的情况,可直接按过热水蒸气处理。该种处理方法在文献[3]处理方法基础上进行了合理简化。
在发射过程中,弹射筒内的连续喷注水经过在内通道中与燃气的掺混、热交换及相变后,为过热水蒸气状态,预先加注的冷却水进入弹射筒后会经历加热、汽化和过热3个阶段,因此可按3个阶段对弹射过程进行划分,即
1)连续喷注水过热、预先加注水加热阶段
在该阶段内预先加注水处于液态,连续喷注水为过热水蒸气状态,当燃气量增大,预先加注水开始汽化时该阶段结束。
2)连续喷注水过热、预先加注水汽化阶段
在该阶段内预先加注水开始汽化,相变后气、液两相共存,而连续喷注水继续处于过热水蒸气状态。
3)预先加注冷却水、连续喷注冷却水均处于过热阶段
预先加注冷却水此时已完成汽化,不存在液态冷却水,预先加注冷却水、连续喷注冷却水均转化为过热水蒸气。
2 模型的简化和假设工程研究中为了便于进行计算,依据气体动力学、热力学的基本理论,将水下导弹弹射进程中不平衡、不可逆、复杂的过程,简化为理想的弹射模型,研究对象为弹射筒内导弹底部空间内进入的各种燃气、冷却水工质,以及初始容积中已有的气体组成的混合工质热力系,弹射模型的简化以及假设主要有:
1)燃气工质视为冻结流。装药燃烧产生的燃气随着燃气生成器内温度、压强的变化,性质和组成会有所不同,并在经过冷却装置内通道进入弹射筒的过程中持续发生变化,在经过冷却装置的过程中由于冷却水的注入,进入弹射筒时降温效果明显,与弹射筒初始容积内的空气混合后温度在燃点以下,避免了发生二次燃烧。因燃气的有关参数变化的影响比较小,研究中视为常量。
2)燃气以及初始容积中的空气视为理想气体,冷却水相变后的水蒸气视为实际气体,各自的热力性质、化学组分一致,无摩擦、无粘性。
3)导弹水下弹射时,弹射筒内的混合气体处于准静态。各种气体在任一时刻混合均匀,处于力学平衡以及热平衡状态,流场各处的压强以及温度相同。
4)按沸腾状态考虑预先加注冷却水的汽化,沸点对应的压强为工质气体各组分的总压。
5)弹射筒内的工质不发生流动,按零维内弹道考虑,其势能和动能为0,不考虑温度、压强、密度沿长度的变化。
6)按绝热、等熵过程处理弹射过程的热力学变化。混合气体与弹射筒壁及导弹之间的热损失、做功过程中的漏气损失以及进入弹射筒前的能量损失,通过系数xe进行修正(小于1),修正后的燃气能量为
本文通过对弹射过程和冷却水汽化机理分析研究,建立了新的物理模型,考虑了火药燃烧产物中水蒸气的影响,将火药燃烧产物中的水和冷却水考虑为一个整体,再分为预先加注水和连续喷注水两部分,在此基础上把水下导弹弹射过程根据其特点,划分为3个阶段,并推导出各个阶段的质量平衡方程、能量平衡方程、状态方程、汽化方程、导弹运动方程等,建立了弹射模型基本方程组。
3.1 能量守恒方程在弹射过程中弹射筒内存在燃气(不含水蒸气)、水(含燃气中的水蒸气)以及空气3种工质气体,按照提出的的简化和假设,工质气体每个瞬时均在弹射筒内混合均匀,膨胀功为导弹提供弹射能量,将导弹加速弹射出筒,此过程中不考虑工质气体本身的动能和势能变化,依据热力学第一定律,能量平衡方程如下:
| $\frac{{{\rm{d}}U}}{{{\rm{d}}t}} = \frac{{{\rm{d}}{H_i}}}{{{\rm{d}}t}} - \frac{{{\rm{d}}W}}{{{\rm{d}}t}}\text{。}$ |
式中:
方程右边各项为:
代入上式有
| $\frac{{{\rm{d}}U}}{{{\rm{d}}t}} = {x_e}{c_{pg}}{T_1}\frac{{{\rm{d}}{m_g}}}{{{\rm{d}}t}} + {u_{l0}}\frac{{{\rm{d}}{m_w}}}{{{\rm{d}}t}} - p{S_t}v\text{。}$ | (1) |
工质气体中含有燃气(不含水蒸气)、空气、预先加注水和连续喷注水(含燃气中的水蒸气)4种工质,其质量分别为
1)连续喷注水过热、预先加注水加热阶段
| $U = {m_g}{c_{vg}}T + {m_a}{c_{va}}T + {m_y}{u_l}\left( T \right) + {m_w}{u_v}(T,p)\text{,}$ |
联合式(1)可得此热力过程的能量守恒方程:
| $\begin{split} &\left( {{m_g}{c_{vg}} + {m_a}{c_{va}} + {m_y}{c_l}} \right)\frac{{{\rm{d}}T}}{{{\rm{d}}t}} + \\ &\quad{m_w}\left[ {{c_{p0}}(T) - {R_v} + \frac{{3{C_0}}}{{{T^4}}}\left( {3p - 4 \times {{10}^4}} \right)} \right]\frac{{{\rm{d}}T}}{{{\rm{d}}t}} - \\ &\quad{m_w}\frac{{3{C_0}}}{{{T^3}}}\frac{{{\rm{d}}p}}{{{\rm{d}}t}} + {c_{vg}}T\frac{{{\rm{d}}{m_g}}}{{{\rm{d}}t}} + {u_v}(T,p)\frac{{{\rm{d}}{m_w}}}{{{\rm{d}}t}} = \\ & \quad{x_e}{c_{pg}}{T_1}\frac{{{\rm{d}}{m_g}}}{{{\rm{d}}t}} + {u_{l0}}\frac{{{\rm{d}}{m_w}}}{{{\rm{d}}t}} - p{S_t}v \text{。}\end{split} $ | (2) |
2)连续喷注水过热、预先加注水汽化阶段
| $\begin{gathered} U = {m_g}{c_{vg}}T + {m_a}{c_{va}}T + {m_w}{u_v}(T,p) + {m_y}{u_l} \\ \left( T \right) + x{m_y}\left[ {{u_v}(T,p) - {u_l}(T)} \right] \text{。} \end{gathered} $ |
联合式(1)可得此热力过程的能量守恒方程:
| $\begin{split} &\left( {{m_g}{c_{vg}} + {m_a}{c_{va}} + {m_y}{c_l} - x{m_y}{c_l}} \right)\frac{{{\rm{d}}T}}{{{\rm{d}}t}} - \\ &\quad \left( {{m_w} + x{m_y}} \right)\frac{{3{C_0}}}{{{T^3}}}\frac{{{\rm{d}}p}}{{{\rm{d}}t}} + {c_{vg}}T\frac{{{\rm{d}}{m_g}}}{{{\rm{d}}t}} + u\left( {T,p} \right)\frac{{{\rm{d}}{m_w}}}{{{\rm{d}}t}} + \\ &\quad \left( {{m_w} + x{m_y}} \right)\left[ {{c_{p0}}(T) - {R_v} + \frac{{3{C_0}}}{{{T^4}}}\left( {3p - 4 \times {{10}^4}} \right)} \right]\frac{{{\rm{d}}T}}{{{\rm{d}}t}} + \\ &\quad \left( {u\left( {T,p} \right) - {u_l}\left( T \right)} \right)\frac{{{\rm{d}}x{m_y}}}{{{\rm{d}}t}} = \\ &\quad {x_e}{c_{pg}}{T_1}\frac{{{\rm{d}}{m_g}}}{{{\rm{d}}t}} + {u_{l0}}\frac{{{\rm{d}}{m_w}}}{{{\rm{d}}t}} - p{S_t}v \text{。}\\[-15pt]\end{split} $ | (3) |
3)连续喷注水过热、预先加注水过热阶段
| $U = {m_g}{c_{vg}}T + {m_a}{c_{va}}T + \left( {{m_w} + {m_y}} \right){u_v}(T,p)\text{。}$ |
联合式(1)可得此热力过程的能量守恒方程:
| $\begin{split} & \left( {{m_g}{c_{vg}} + {m_a}{c_{va}}} \right)\frac{{{\rm{d}}T}}{{{\rm{d}}t}} + {c_{vg}}T\frac{{{\rm{d}}{m_g}}}{{{\rm{d}}t}} + u\left( {T,p} \right)\frac{{{\rm{d}}{m_w}}}{{{\rm{d}}t}} + \\ &\quad \left( {{m_w} + {m_y}} \right)\left[ {{c_{p0}}(T) - {R_v} + \frac{{3{C_0}}}{{{T^4}}}\left( {3p - 4 \times {{10}^4}} \right)} \right]\frac{{{\rm{d}}T}}{{{\rm{d}}t}} - \\ &\quad \left( {{m_w} \!+\! {m_y}} \right)\frac{{3{C_0}}}{{{T^3}}}\frac{{{\rm{d}}p}}{{{\rm{d}}t}} \!= \!{x_e}{c_{pg}}{T_1}\frac{{{\rm{d}}{m_g}}}{{{\rm{d}}t}} \!+\! {u_{l0}}\frac{{{\rm{d}}{m_w}}}{{{\rm{d}}t}} \!-\! p{S_t}v \text{。} \end{split} $ | (4) |
由于冷却水在初期的汽化阶段,弹射筒内进入的水处于液、气两相共存,应根据弹射过程冷却水喷注规律确定水蒸气的质量,温度为T时水的饱和压强为:
| ${p_s}\left( T \right) = \exp \left( {A + \frac{B}{T} + CT + D{T^2} + E\ln T} \right)\text{。}$ | (5) |
在预先加注水的汽化阶段,水蒸气饱和压强为混合气体的总压,根据阿麦加定律,此压强与预先加注冷却水的水蒸气组元容积相关,水蒸气质量可根据水蒸气状态方程获取:
| $x{m_y} = \frac{{{p_s}\left( T \right)V - \left( {{m_g}{R_g} + {m_a}{R_a}} \right)T}}{{{R_v}T - {C_0}{T^{ - 3}}{p_s}\left( T \right)}} - {m_w}\text{。}$ | (6) |
在预先加注冷却水处于加热阶段时,水蒸气质量为0,在预先冷却加注水处于过热阶段时,预先加注水的质量即为水蒸气质量。
3.3 状态方程理想气体状态方程不适用于水蒸气,应按实际气体考虑,就导弹水下弹射物理过程而言,水蒸气压强低,其参数变化有限,采用简单的状态方程来求解,计算的准确度仍较高。研究中用含有压强以及温度的分式项表征水蒸气状态方程,即
| $v = \frac{V}{m} = \frac{{RT}}{p} - \frac{{{C_0}}}{{{T^3}}}\text{。}$ | (7) |
式中:C0视为常数,C0=1.356×106。
对于由装药燃烧产生的燃气、考虑燃气中的水及加注水的水蒸气和预留空气组成的混合气体来说,其状态方程根据阿麦加定律可建立为:
| $V = \left( {{m_g}{R_g} + {m_a}{R_a} + {m_v}{R_v}} \right)\frac{T}{p} - \frac{{{C_0}{m_v}}}{{{T^3}}}\text{。}$ | (8) |
其中:mv为水蒸气的质量,
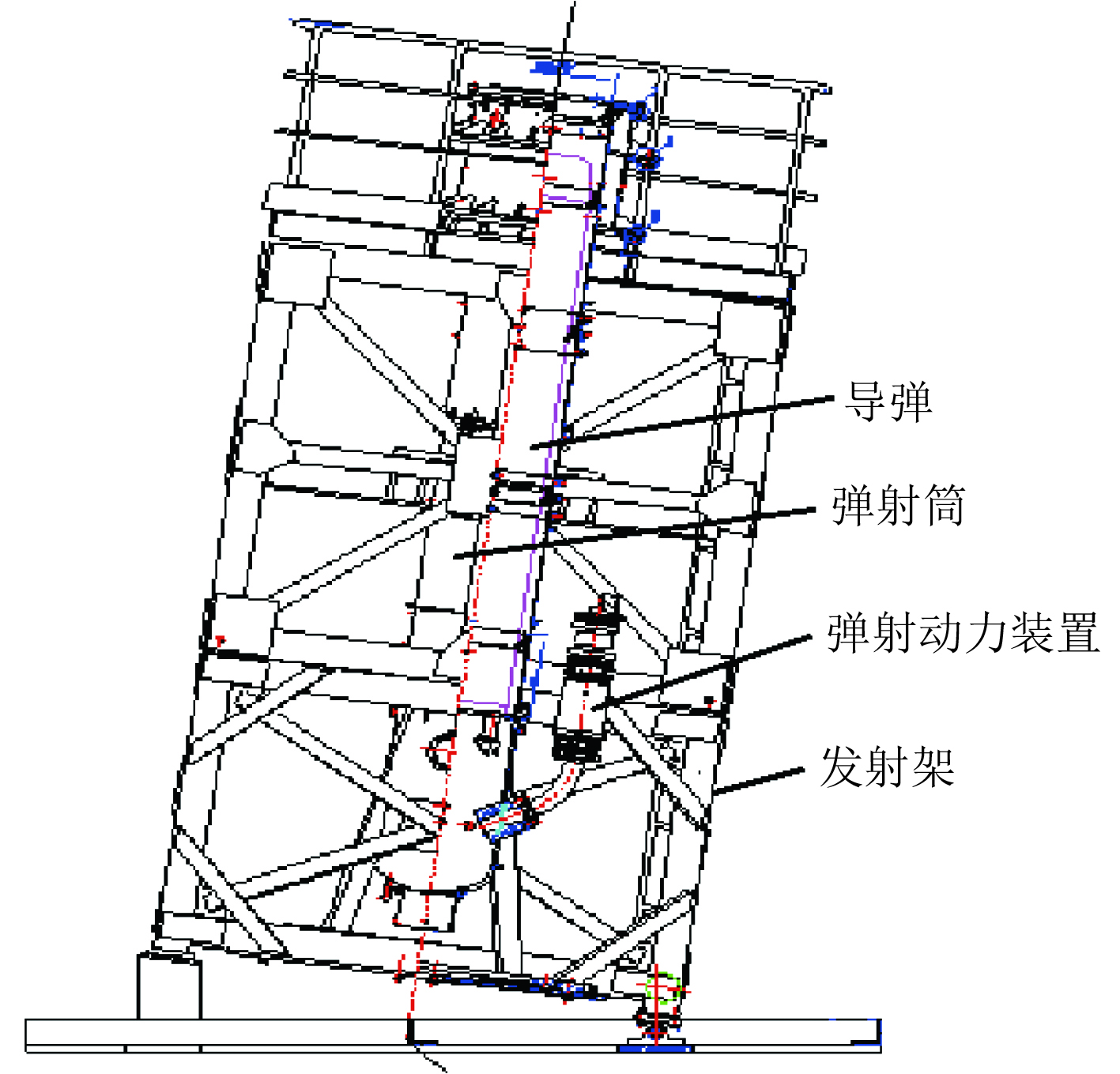
为研究考虑火药燃烧产物中水蒸气弹射模型的正确性,依据上述分析结果及方程组编制了弹射弹道计算程序,并采用发射原理试验装置,开展了发射原理试验研究。试验装置主要由弹射动力装置、弹射筒、导弹、发射架等部分组成,发射原理试验装置结构如图1所示。
|
图 1 发射装置结构示意图 Fig. 1 Diagram of the launch system |
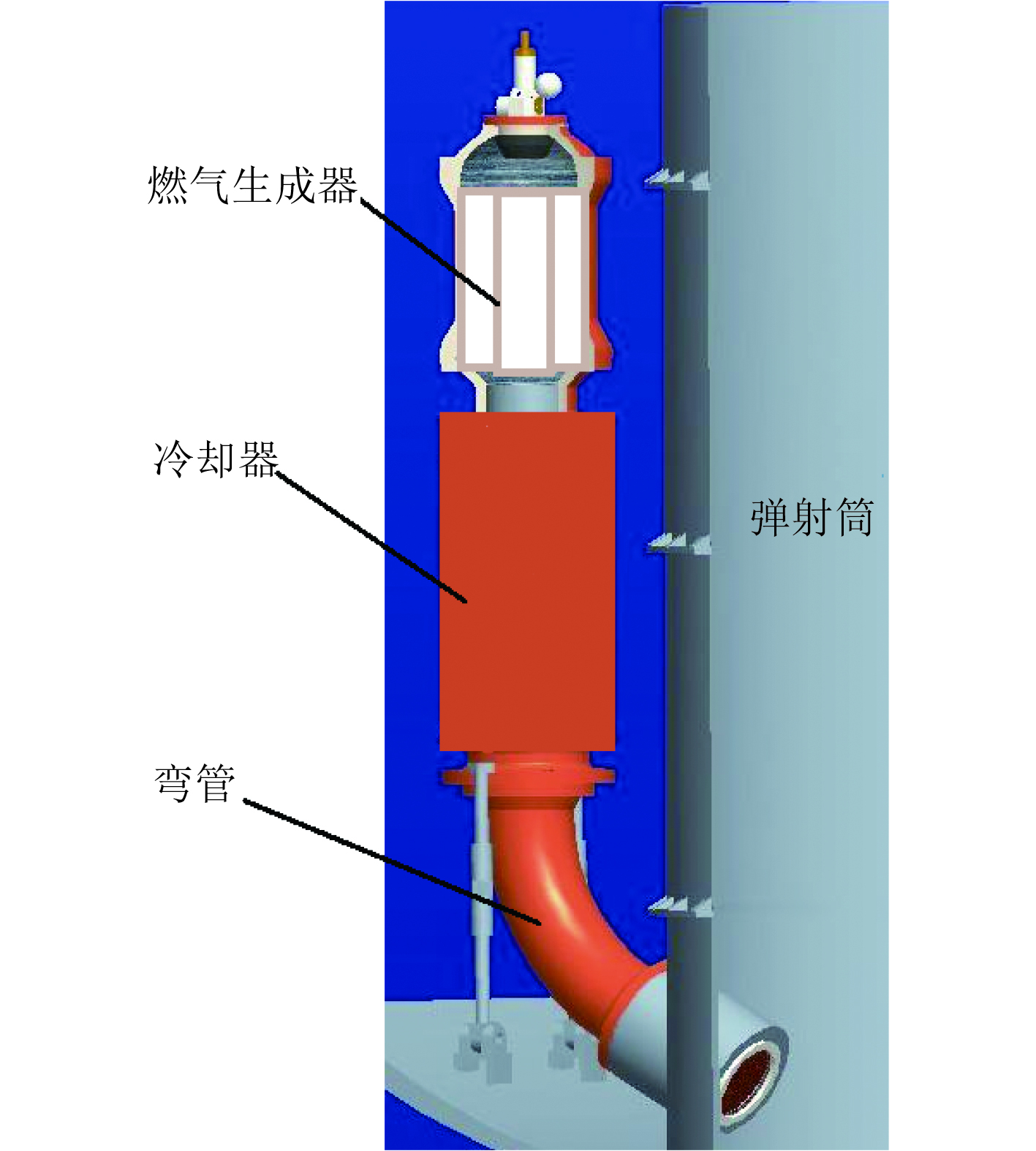
弹射动力装置主要由燃气生成器、冷却装置、弯管组成,如图2所示。导弹发射时,燃气生成器中火药燃烧生成高温高压燃气,燃气经一级喷管进入一级导流管,主燃气流继续向下沿二级喷管、喷水管、输气管流动,并将预先加注水带入弹射筒;另一部分燃气经分流进入水室,在水室和喷水管内形成喷水压差,水室内的冷却水在喷水压差作用下经喷水管进入喷水区和主燃气流混合,对燃气进行冷却,降低进入弹射筒内燃气的温度,混合后的燃气-蒸汽混合气体进入弹射筒底,依靠气体的膨胀做功推动导弹出筒。
|
图 2 弹射动力装置结构组成示意图 Fig. 2 Schematic of the ejection power system |
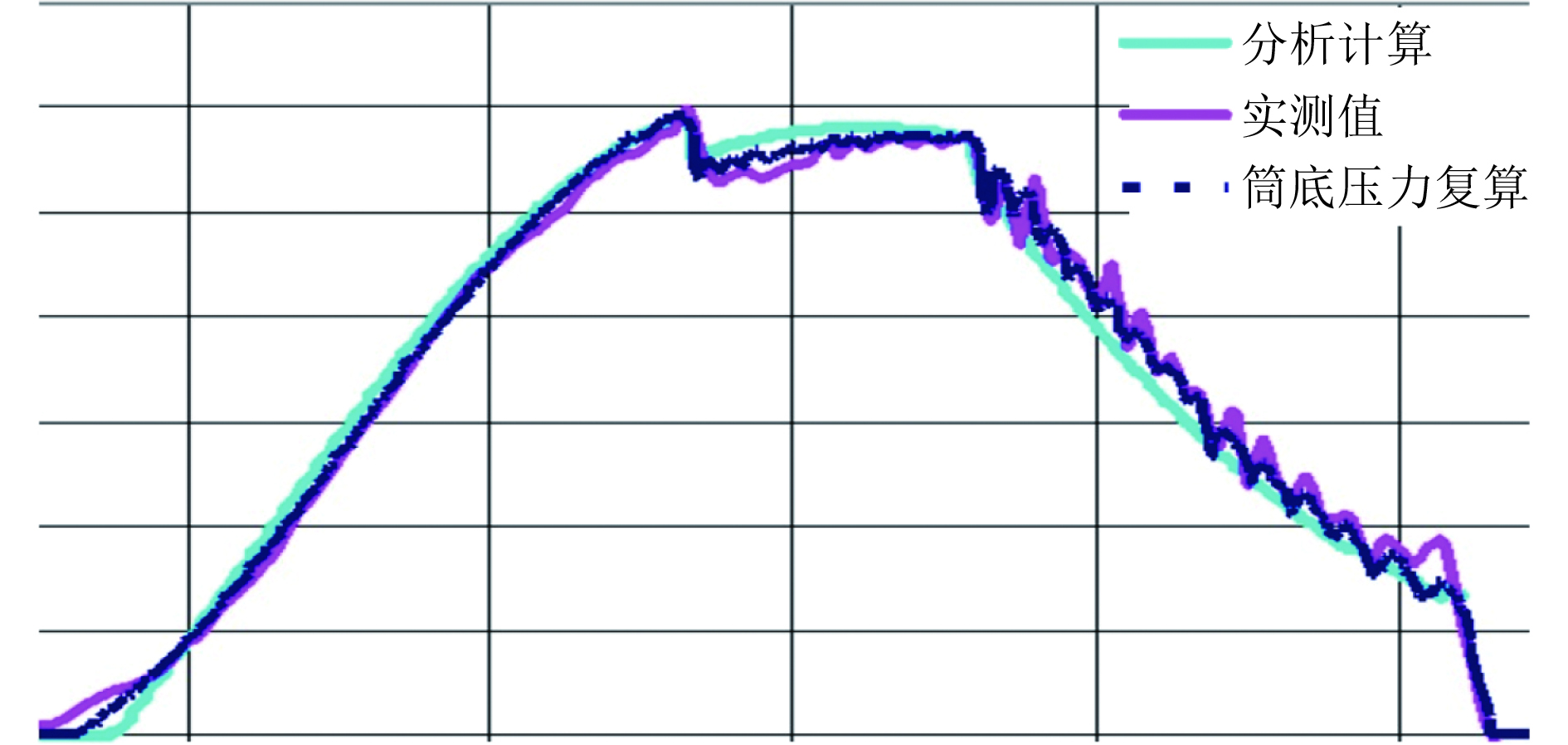
根据试验实测数据进行内弹道分析计算,得到了导弹发射过程中导弹运动加速度、速度,弹射筒内压力、温度等计算结果。根据本文所论述的冷却水汽化机理及建立的发射内弹道计算模型所得到的导弹运动时间-加速度分析计算值,与试验实测值及筒内压力复算值的对比分析情况如图3所示。可以看出,分析计算结果与实测数据、复算值一致性好,能够反映导弹运动加速度、筒内压力等变化规律,验证了燃气-蒸气式弹射动力装置冷却水汽化机理及发射内弹道计算模型的正确性。
|
图 3 导弹运动时间-加速度对比图 Fig. 3 The acceleration of the missile with time |
通过对发射过程的深入分析和汽化机理的研究,考虑了火药燃烧产物中水蒸气的影响,将燃气中的水与冷却水统一考虑,再分为预先集中注入水和连续喷注水两部分,并针对燃烧产物及不同阶段注入的水,进行了汽化机理、建压、做功过程分析,并以此为基础,依据弹射进程的不同特点,按3个不同的特征阶段,建立汽化方程和能量平衡方程,构建了考虑火药燃烧产物中水蒸气的弹射模型基本方程组,通过对试验结果和采用考虑火药燃烧产物中水蒸气的弹射模型所得的计算结果进行比较分析表明,该模型的改进提高了水下导弹弹射出筒过程的计算精度。
| [1] |
李咸海, 王俊杰编著, 潜地导弹弹射动力装置[M]. 哈尔滨: 哈尔滨工程大学出版社, 2000. 5.
|
| [2] |
赵险峰, 王俊杰编著, 潜地弹道导弹发射系统内弹道学[M]. 哈尔滨: 哈尔滨工程大学出版社, 2001. 4.
|
| [3] |
赵世平. 发射内弹道计算模型研究[J]. 舰船科学技术, 2007(S1). |
| [4] |
刘科, 赵世平. 燃气蒸汽式发射动力装置复杂内流场数值模拟[J]. 固体火箭技术, 2009(4). DOI:10.3969/j.issn.1006-2793.2009.04.013 |
 2019, Vol. 41
2019, Vol. 41
