2. 齐齐哈尔大学 计算机与控制工程学院,黑龙江 齐齐哈尔 161006
2. School of Computer and Control Engineering, Qiqihar University, Heilongjiang 161006, China
移动集群中每个节点的感知范围都十分有限,如果节点分布不合理,就会导致网络中出现感知盲区,从而无法对目标实现覆盖要求,而且由于水下节点的造价高昂,通过增加冗余节点的方法并不现实,因此研究水下节点部署问题十分重要。群体智能算法是一类新兴优化算法,并大量用于最优化求解[1]。这类算法模仿了社会性动物的群聚行为。单个动物体能够完成简单的任务,如果多个动物体间相互交流、相互协作,便能完成更加复杂的任务,这一系列过程的实现并不只是通过动物个体数量的增加得到的,更重要的是个体间的信息交互。比较经典的群体智能算法有粒子群算法、蚁群算法以及人工鱼群算法等[2-7]。这些算法均能够有效提高覆盖率,并使整个网络节点的分布更加均匀。但算法本身也存在着不足之处,均存在“早熟”收敛、局部最优解[8]等问题。
无线传感网络(Wireless sensor network,WSN)是一种将无线通信、传感器以及分布式信息处理融为一体的网络技术,它以部署灵活成本低廉等特点得到广泛的使用[9]。如何在保持网络覆盖率的条件下延长网络的生命周期,成为传感器网络研究的一个关键问题,国内外学者对无线传感网络覆盖进行了研究,文献[10]提出一种基于遗传粒子群优化算法(Particle swarm optimization,PSO)的无线传感网络覆盖优化算法,该方法能有效地实现无线传感网络覆盖优化,不足的是PSO算法易陷入局部极值点,从而限制了粒子的搜索范围。文献[11]提出将改进的蚁群算法运用到网络节点覆盖优化中,虽然增加了算法局部搜索能力,但在一定程度上没有考虑实际环境因素,影响网络覆盖优化的实时性。文献[12]提出一种运用分形理论自相似性原理进行区域划分以构建最优覆盖模型的方法,该方法有效地降低网络部署成本和能耗,但存在一定的重复覆盖比例。文献[13]提出了在无线传感网络中引入遗传算法进行节点优化,算法虽然具有较强的并行搜索能力,但在最优解附近收敛速度慢,难以满足动态节点的实时性要求。
由于水下环境的复杂,以及水下节点的造价昂贵,陆上传感网络的大规模随机部署方案在水下不可能实现。因此,国内外的研究重点都基于如何使用尽量少的节点实现网络覆盖的最优化。通过总结发现,早期国内外的很多研究基于数学模型,对于水下环境的考虑并不全面,而且大多基于静态网络的部署。而近期的研究中很多人开始使用诸如鱼群算法等智能算法,更多地考虑水下环境的复杂性以及节点的移动,不仅提高了网络的覆盖度,还增强了网络连通性,降低了能量消耗,从而保持网络稳定运行,有效防止网络空洞。
本文主要采用布尔感知模型重点研究区域覆盖,利用粒子群优化算法与人工鱼群优化算法进行混合编程,完成水下移动节点部署优化,从而实现对目标区域高覆盖度的部署目标。重点完成水下无人集群节点部署优化方案和仿真实验设计,主要利用粒子群优化算法与人工鱼群优化算法混合完成水下无人集群对水下环境的覆盖。利用粒子群算法初期收敛快的特点,进行初期寻优,再用人工鱼群算法进行后期寻优,二者优势互补,完成对集群节点部署优化。
1 网络覆盖模型 1.1 节点覆盖率现假设检测区域A为二维平面坐标,在该区域上投放参数相同的传感器节点,数目为N,每个节点的坐标均已知,且有效监测半径均为r,则传感器节点集表示为c={c1, c2, c3,
| $P\{ {r_i}\} \!=\! {P_{cov}}(x,\,y,\,{c_i}) \!=\! \left\{ {\begin{array}{*{20}{l}} {1,\;\; f{{(x - {x_i})}^2} + {{(y - {y_i})}^2} \leqslant {r^2}}\text{,}\\ {0,\;\; {\rm{else}}}\text{。} \end{array}} \right.\!\!\!\!\!\!$ | (1) |
式(1)表明,当像素点(x, y)到传感器节点i的距离小于传感器范围r时,就认为该像素点(x, y)被传感器节点i覆盖。
| $P\{ {\bar r_i}\} = 1 - P\{ {r_i}\} = 1 - {P_{\operatorname{cov} }}(x,y,{c_i})\text{,}$ | (2) |
式中,
| $P\{ {r_i} \cup {r_j}\} = 1 - P\{ {\bar r_i} \cap {\bar r_j}\} = 1 - P\{ {\bar r_i}\} \cdot P\{ {\bar r_j}\} \text{。}$ | (3) |

|
图 1 海上场景示意图 Fig. 1 Schematic diagram of the sea scene |
节点集中只要有一个节点覆盖了像素点(x, y),就认为该像素点(x, y)被节点集覆盖。因此,像素点被节点集所覆盖的概率即为ri的并集,假设所有的随机事件ri是互相独立的,则节点集C的覆盖率可以利用下式计算:
| $ \begin{split} {P_{\operatorname{cov} }}(x,y,{c_i}) = & P\{ \mathop Y\limits_{i = 1}^N {r_i}\} = 1 - P\{ \mathop I\limits_{i = 1}^N {\bar r_i}\} = \\ & 1 - \mathop \prod \limits_{i = 1}^N [1 - {P_{\operatorname{cov} }}(x,y,{c_i})]\text{。} \end{split} $ | (4) |
式(4)表明,若所有的节点都没有覆盖到像素点,则该像素点为未覆盖点,否则,便认为该像素点被节点集覆盖。
1.2 区域覆盖率监测区域A内有m×n个像素,每个像素的面积大小可表示为△x×△y(假定每个像素的面积为1),每个像素是否被覆盖用节点集覆盖率Pcov(x, y, ci)来衡量,则将节点集C的区域覆盖率Rarea定义为节点集C的覆盖率面积Aarea与监测区域A的总面积As之比,即
| ${R_{area}}(C) = \frac{{{A_{area}}(C)}}{{{A_s}}} = \frac{{\sum\limits_n^m {\sum\limits_y^n {P(x,y,C)} } }}{{m \times n}}\text{。}$ | (5) |
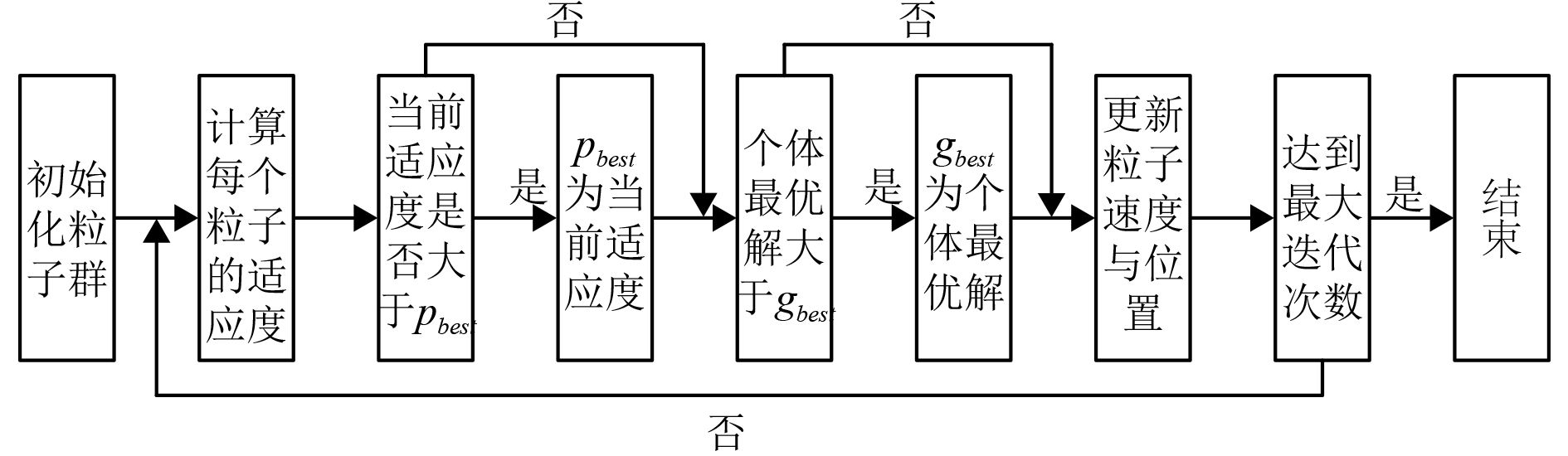
粒子是粒子群算法的基本单位,每个粒子都代表解空间的一个候选解,所有粒子构成了种群,每一个粒子都有自己的飞行状态,包括飞行速度和方向,适应度函数即算法的优化目标,决定了整个算法的搜索方向。在整个迭代过程中,每个粒子都会存在一个当前迭代值对应的最优解,被称为个体极值(Pbest),具体迭代过程如图2所示。
|
图 2 标准粒子群算法流程图 Fig. 2 Flow chart of standard particle swarm algorithm |
整个种群的当前最优解被称为全局极值(gbest)。每次迭代过程中,Pbest和gbest都会更新,如果迭代次数足够多,Pbest和gbest最终会趋于稳定,算法结束后gbest即整个算法求得的最优解。
2.2 改进粒子群算法标准粒子群算法收敛较快,但后期寻最优解效果较差,容易陷入局部最优,真实部署时不仅浪费时间,还浪费节点能量,本项目将引入线性递减惯性权重系数
| $w = {w_{\max }} - \frac{{t \times \left( {{w_{\max }} - {w_{\min }}} \right)}}{{{t_{\max }}}}{\text{。}}$ | (6) |
其中:
每次迭代过程中,粒子的速度为:
| $v_{id}^{k + 1} = w \times v_{id}^k + {c_1}rand()\left( {p_{id}^k - x_{id}^k} \right) + {c_2}rand()\left( {p_{gd}^k - x_{id}^k} \right)\text{。}$ | (7) |
每次迭代过程中,选出每个粒子中距离最近的两个节点,对这两个节点进行位置进行二次调节,使其相互远离。
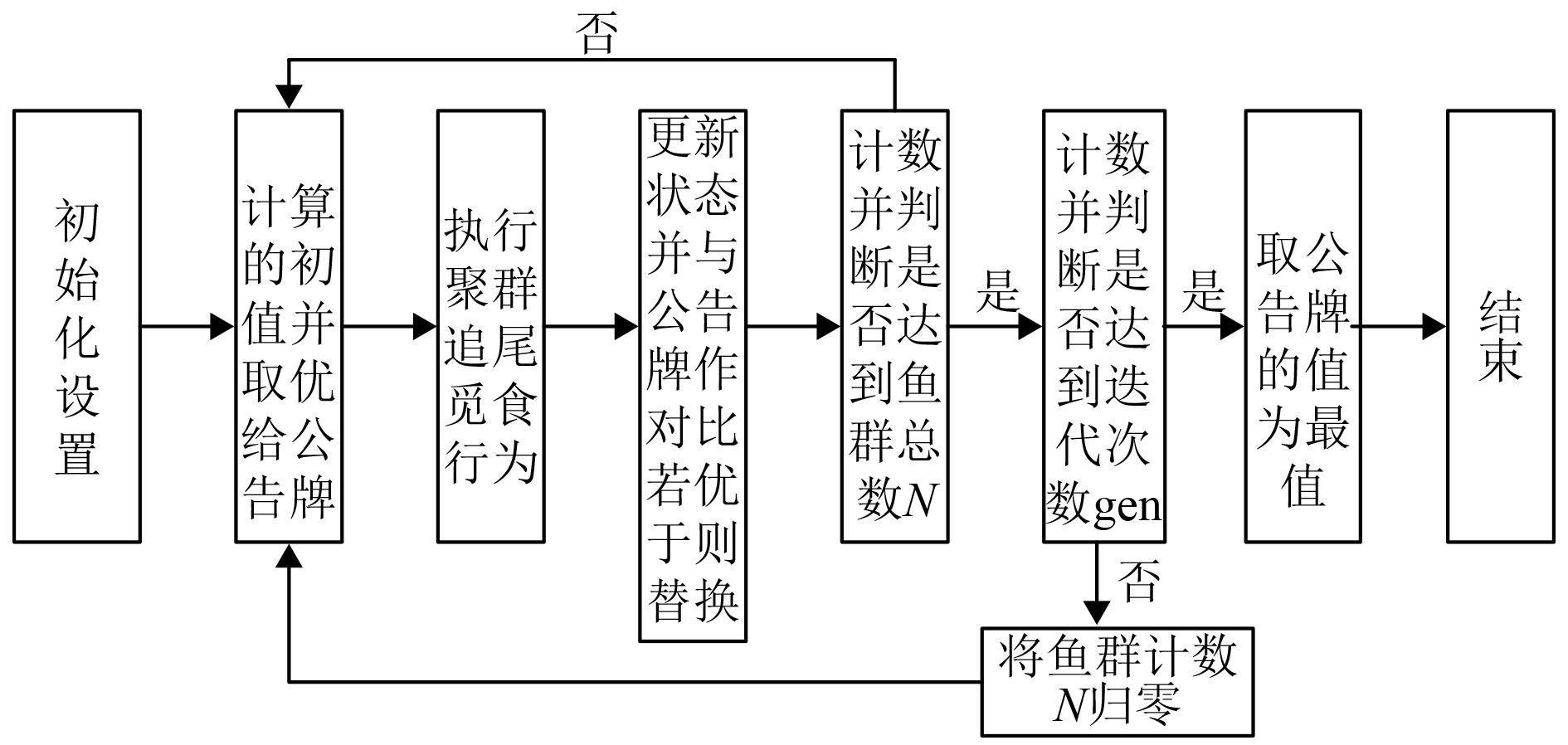
2.3 粒子群-人工鱼群算法人工鱼有觅食行为、聚群行为、追尾行为和随机行为4种,每条鱼移动之前都会进行试探,试探结束后再决定采取哪种行动,流程如图3所示。
|
图 3 人工鱼群算法流程图 Fig. 3 Flow chart of artificial fish swarm algorithm |
1)觅食行为。鱼群会根据水中的食物浓度决定游动方向,这是鱼维持生存的本能行为,鱼总会向着食物浓度高的方向游动。
假设某条人工鱼当前状态为x,鱼会在当前视野范围内选一个状态x,如果状态y优于状态x,则鱼移动到y,否则不移动。人工鱼会以此方式试探Tnum次,选出状态最好的一个为x的下一个状态。如果Tnum次试探后没有比x更好的状态,人工鱼将执行其他行为,如随机游动。
2)聚群行为。聚群行为是为了在受到攻击时寻求庇护,以保护自己,当某处食物浓度大时,也会导致群体觅食。
3)追尾行为。当鱼群中某条或几条鱼发现了食物时,会将信息传递给周围的鱼,使周围的鱼向食物游来,信息会不断传递下去。
4)随机行为。鱼会在水中自由游动,为了更好的寻找食物和同伴。以上的4种行为会在周围环境发生变化时进行转变,以更好地觅食。
5)粒子群算法初期收敛速度快,但是虽然引入了惯性权重,提升了稳定性,但是在水流的影响下,后期寻优效果并不理想,容易陷入局部最优解。相比改进粒子群算法,人工鱼群算法前期收敛速度慢,后期寻优效果好,二者可以完美的将优势互补。
3 仿真与结果分析对于区域覆盖部署问题,本文设定每条人工鱼代表一个节点,区域覆盖度为算法的适应度函数,采用 Matlab对特定场景进行了仿真分析。仿真场景设定为:部署区域为长800 m、宽700 m的长方形范围。并假设节点的通信范围大于2倍的节点感知范围,以保证网络的连通性。当节点感知半径为90 m,通信距离200 m,步长20 m,最大试探次数try number 20次,拥挤度因子0.2,节点数目20,迭代500次,初始位置为随机位置。假定部署区域存在沿X轴方向的水流,流速 1 m/s,使用人工鱼群算法,得到结果如图4~图6所示。

|
图 4 优化算法仿真图 Fig. 4 Simulation diagram of optimization algorithm |
|
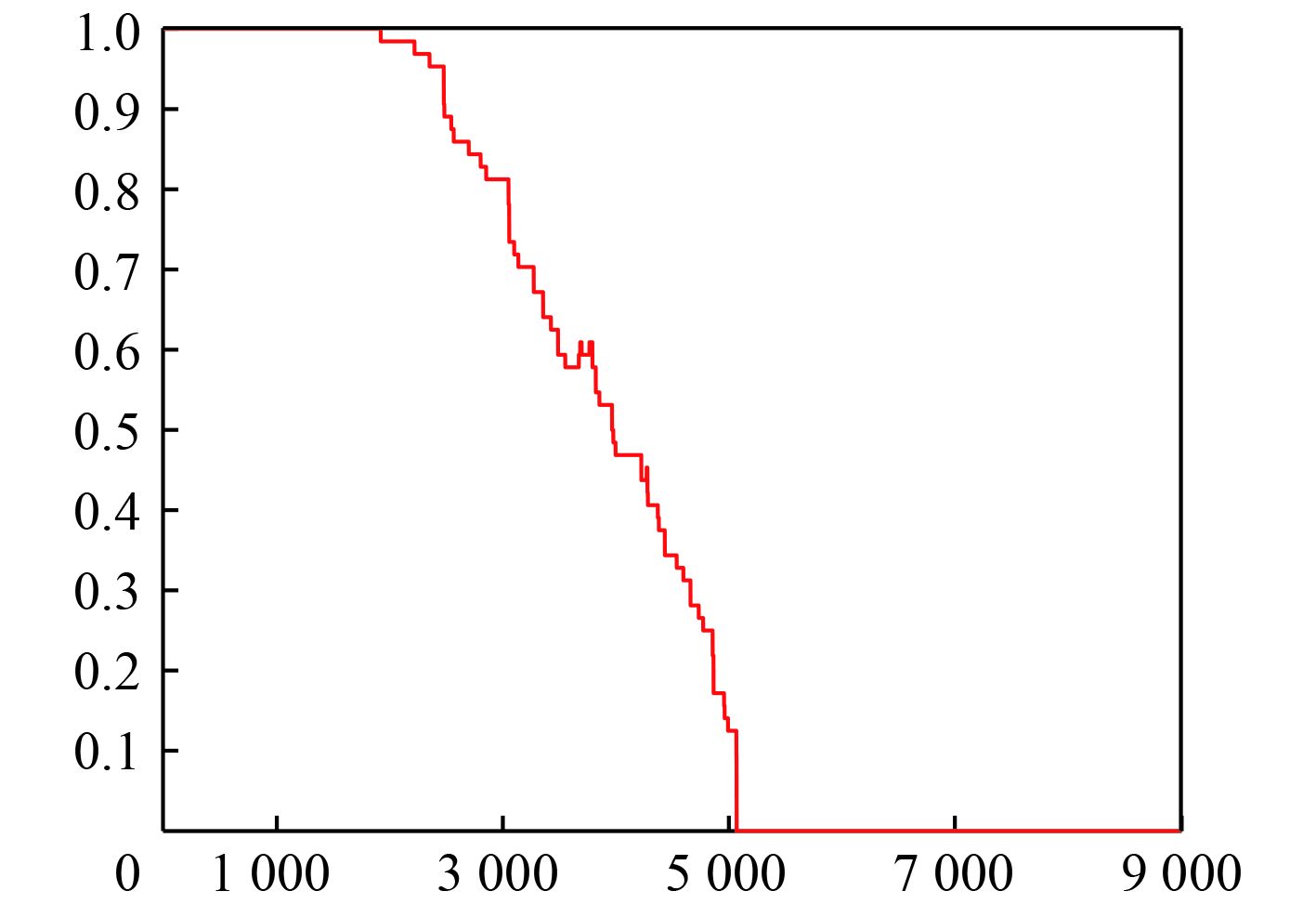
图 5 优化曲线 Fig. 5 Optimization curve |
|
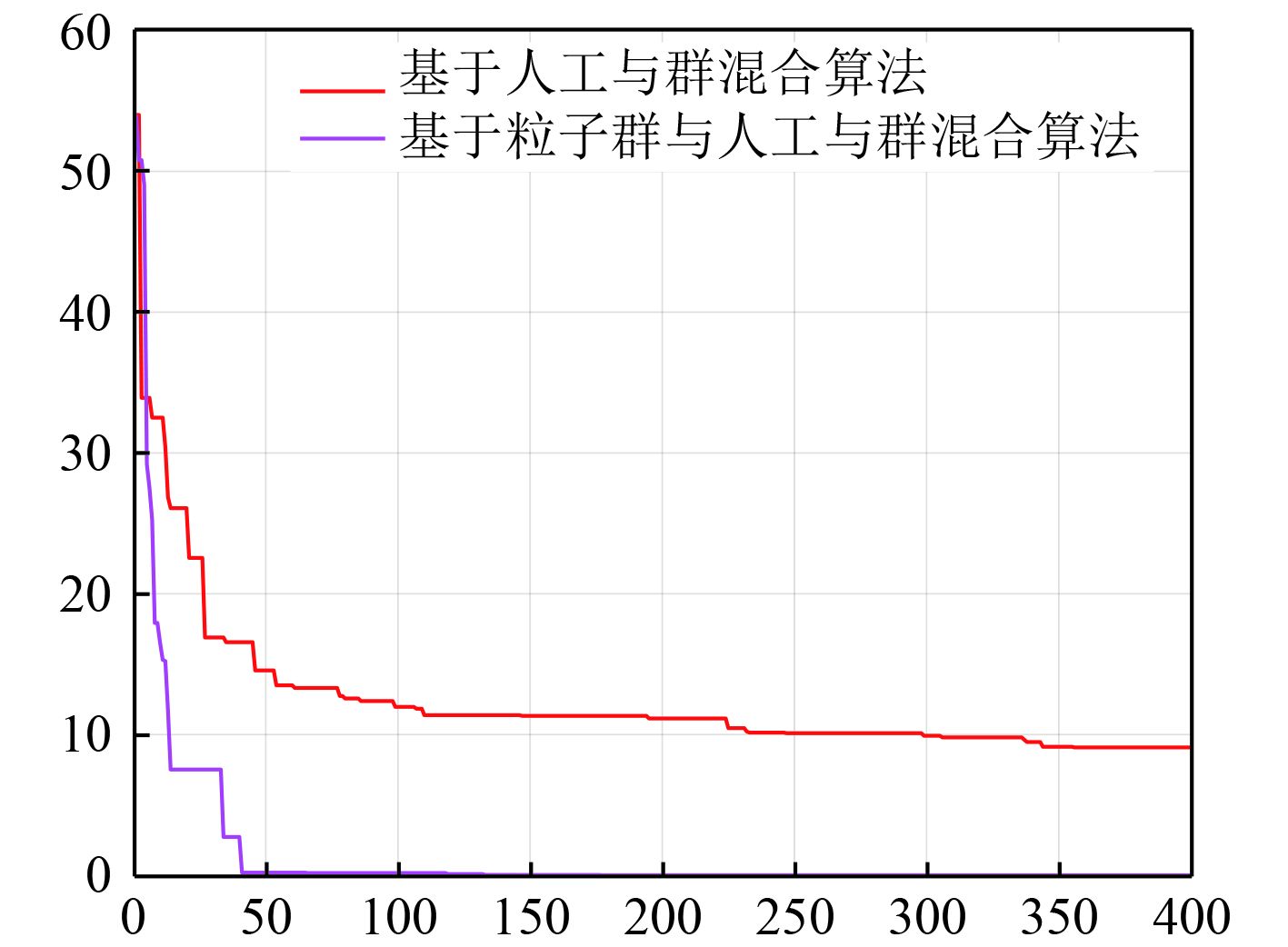
图 6 收敛速度对照图 Fig. 6 Control diagram of convergence rate |
由图可知,基于粒子群与人工鱼群混合部署优化算法的覆盖率提高了25%,且覆盖度曲线初期收敛快,后期寻优效果有明显提升,达到预期效果。
4 结 语本文主要解决水下无人集群部署的问题,采用改进粒子群算法和人工鱼群算法的混合算法进行水下无人集群的部署。这个方法克服了粒子群算法的后期寻优效果差以及人工鱼群算法前期收敛效果慢的缺点,将水下无人集群的部署达到了一个令人满意的效果。
| [1] |
詹煜, 吴冠辰. 群体智能算法在机器学习当中的应用[J]. 科技传播, 2018(1): 115-116. DOI:10.3969/j.issn.1674-6708.2018.01.066 |
| [2] |
F. R. Zaro, M. A. Abido. Multi-objective particle swarm optimization for optimal power flow in a deregulated environment of power systems[C]// International Conference on Intelligent Systems Design & Applications. 2019.
|
| [3] |
D. Gómez-Cabrero, D. N. Ranasinghe. Fine-tuning the ant colony system algorithm through particle swarm optimization[J]. 2018.
|
| [4] |
W. Qin, J. Zhang, D. Song. An improved ant colony algorithm for dynamic hybrid flow shop scheduling with uncertain processing time[J]. Journal of Intelligent Manufacturing, 2018, 1-14. |
| [5] |
Z. Yin, D. Chao, L. Jing, et al. Research on auto-disturbance-rejection control of induction motors based on ant colony optimization algorithm[J]. IEEE Transactions on Industrial Electronics, 2018, PP(99): 1-1. |
| [6] |
M.Karunanithi, N. Neethirajan, V. Padmanaban, et al. Development of dry artificial fish bait for trap fishing using tuna red meat and shrimp head wastes[J]. Journal of Aquatic Food Product Technology, 2018, 27(1): 1-14. DOI:10.1080/10498850.2018.1412696 |
| [7] |
G. Zhou, Y. Li, Y. C. He, et al. Artificial fish swarm based power allocation algorithm for MIMO-OFDM relay underwater acoustic communication[J]. Iet Communications, 2018, 12(9): 1079-1085. DOI:10.1049/iet-com.2017.0149 |
| [8] |
赫然, 王永吉, 王青, 等. 一种改进的自适应逃逸微粒群算法及实验分析[J]. 软件学报, 2005, 16(12): 2036-2044. |
| [9] |
朱永利等. 数据收集传感器网络的多模层次网络构建[J]. 计算机工程, 2011, 37(2): 111-113. DOI:10.3969/j.issn.1000-3428.2011.02.038 |
| [10] |
沈海洋. 基于遗传PSO的无线传感网络覆盖优化算法研究[J]. 微电子学与计算机, 2013, 30(3): 148-151. |
| [11] |
彭丽英. 改进的蚁群算法网络节点覆盖优化研究[J]. 计算机仿真, 2011, 28(9): 151-153. DOI:10.3969/j.issn.1006-9348.2011.09.038 |
| [12] |
顾兵. WSN中规则区域的最优覆盖研究[J]. 计算机技术与发展, 2013, 23(1): 107-111. |
| [13] |
殷卫莉等. 遗传算法在无线传感器网络覆盖中仿真研究[J]. 计算机仿真, 2010, 27(10): 120-123. DOI:10.3969/j.issn.1006-9348.2010.10.030 |
 2019, Vol. 41
2019, Vol. 41
