2. 重庆大学,重庆 400004
2. Chongqing University, Chongqing 400004, China
舰船动力传动系统是保障舰船可靠性航行和运转的重要动力系统,而滚动轴承是舰船动力传动系统的主要功能部件,当滚动轴承发生异常或故障,可能会造成船舶运行工况异常,所以对滚动轴承的寿命进行预测十分必要。滚动轴承工作异常时,可通过对振动信号采集及分析有效地进行滚动轴承寿命预测,而振动特征提取是滚动轴承性能退化状态分类与残余寿命预测的前提。振动信号中蕴含了丰富的设备状态征兆信息,如何从原始信号中全面有效地提取特征,一直是国内外学者研究的热点课题。常见的特征包括时域和频域统计特征,时域统计特征有均值,方差,有效值,峭度,波形因子,脉冲因子等。频域统计特征如平均频率,中心频率,故障特征频率等。
虽然特征越多越可以全面反映设备的状态信息,但过多的特征也会带来大量的冗余信息,对后续计算带来负担,可能会造成维数灾难。怎样从众多特征中优选出维数最少且敏感度高的最优代表性的特征子集,对提高轴承状态识别和残余寿命预测准确率及提升算法的效率都有着十分重要的意义,特征选择流程如图1所示。常用的方法有特征降维和特征选择。
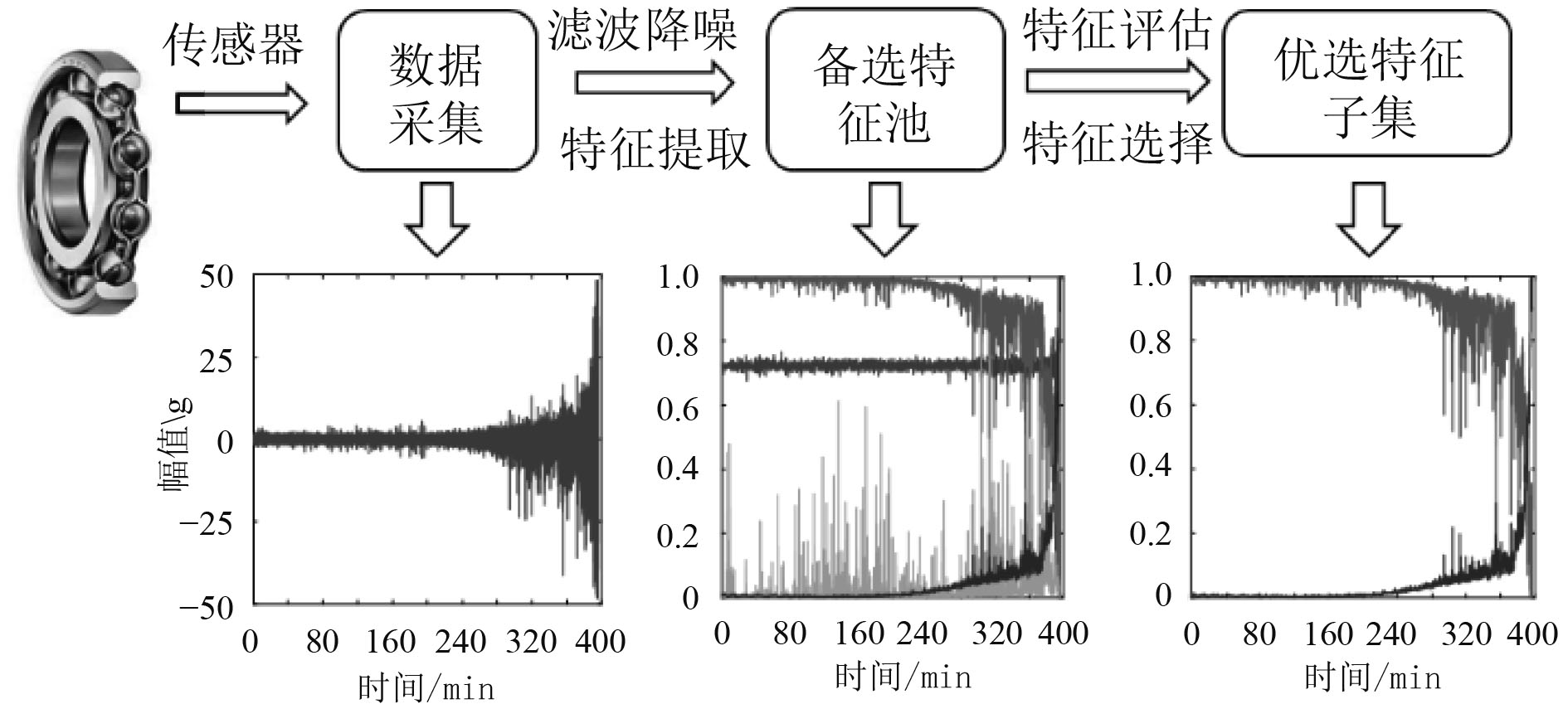
|
图 1 特征选择流程 Fig. 1 Feature selection process |
特征降维方法的思想主要是将原始的高维(多维)特征空间中的点向低维空间投影,新的特征空间维数更低,实现了特征的降维,但投影使原始特征的物理意义消失了。降维方法主要包括主成分分析(Principle Component Analysis,PCA),核主成分分析(Kernel-PCA)及线性判别分析(Linear Discriminant Analysis,LDA)等。
特征选择方法是从d个特征中选择
在滚动轴承运行过程中,如果滚动轴承出现故障或异常情况,那么在振动信号中会有相应的特征成分对其进行反应。基于数据驱动的方法对轴承进行残余寿命预测,第一步也是最重要的一步,就是从振动信号中提取出能够全面反映滚动轴承在全生命周期中性能退化趋势的特征。基于轴承振动信号处理理论,常用的统计特征包括时域特征,频域特征。单一的或者仅仅是某个域的特征难以全面准确地反映滚动轴承的运行状态以及捕捉故障信息。为了更好地反映滚动轴承的变化,引入IMF能量特征[1],希尔伯特边际谱特征和熵特征[2]。
由于滚动轴承的全生命周期振动信号通常是按固定的时间周期采集一段固定时长的信号,所以数据的特征提取也以时间段为单位进行,即在每个时间段上提取相应的特征向量
在提取出来的众多滚动轴承振动信号特征中,有一些特征相互独立,对轴承的某种特定故障比较敏感,或者对轴承退化的不同时期比较敏感,可以很好地表征轴承的退化状态,应该重点利用。但是,还有一些特征是冗余或者与轴承退化状态不相关,不敏感。如果使用这些特征,不仅会使残余寿命预测模型更复杂,增加不必要的计算量,甚至会降低预测结果的可靠性。因此,不能将所有的特征直接合成特征集,输入到残余寿命预测模型中。需要通过特征选择方法,将最具代表性,最有效的的特征筛选出来,剔除冗余,不相关的特征,进而避免维数灾难,提升计算效率,减小预测结果的误差。
2.1 特征性能评估特征评价是很多模式识别任务中的重要组成成分,目前有许多可靠,高效,实际可行的方法,如核密度估计、皮尔逊相关系数,边界宽度,Fisher判别、基于距离,基于互信息理论等,但它们多用于分类任务,适用于故障识别领域。以上方法的核心思想是:不同类别的样本在某种特征描述下具有不同的统计特征,根据可分离性明显的原则,选择出敏感的特征。以上方法是建立在样本类别已知的情况下,所以也被称为有监督算法。然而,滚动轴承残余寿命预测属于回归预测任务,滚动轴承的退化过程本质上是一个连续变化的随机过程。一个优良的健康指标应该满足下列条件:
1)特征随滚动轴承性能的退化而变化,即与残余寿命时间顺序有一定的相关性。
2)退化是一个不可逆的单调过程,所以理想特征应该具有一定的单调性。
3)对随机噪声具有良好的抗干扰能力,即具有一定的鲁棒性。
本文采用文献[2]提出的3种相关性,单调性,鲁棒性的算法作为独立评价函数,并在此基础上提出自适应顺序最优搜索算法,选择出最终的优选特征。
对于特征信号顺序
| $f\left( {{t_k}} \right) = {f_T}\left( {{t_k}} \right) + {f_R}\left( {{t_k}} \right)\text{,}$ | (1) |
EWMA的计算公式如下:
| ${f_T}\left( {{t_k}} \right) = \beta {f_T}\left( {{t_{k - 1}}} \right) + \left( {1 - \beta } \right)f\left( {{t_k}} \right)\text{。}$ | (2) |
式中,一般取
| $\begin{aligned} &\qquad Corr\left( {{{F}},{{T}}} \right) =\\& \frac{{\left| {K\sum\limits_k {{f_T}\left( k \right){t_k} - \sum\limits_k {{f_T}\left( k \right){t_k}\sum\limits_k {{t_k}} } } } \right|}}{{\sqrt {\left[ {K\sum\limits_k {{f_T}{{\left( k \right)}^2} - {{\left( {\sum\limits_k {{f_T}\left( k \right)} } \right)}^2}} } \right]\left[ {K\sum\limits_k {{{\left( {{t_k}} \right)}^2} - {{\left( {\sum\limits_k {{t_k}} } \right)}^2}} } \right]} }} \end{aligned}\text{。}$ | (3) |
F的单调性评估指标记作Mon(F)
| $\begin{split} Mon\left( {{F}} \right) =& \frac{1}{{K - 1}}\left| {\sum\limits_k {\delta \left( {{f_T}\left( {k + 1} \right) - {f_T}\left( k \right)} \right)} } \right.-\\ &\left. { \sum\limits_k {\delta \left( {{f_T}\left( k \right) - {f_T}\left( {k + 1} \right)} \right)} } \right|\text{。} \end{split}$ | (4) |
式中,
| $\delta \left( t \right) = \left\{ \begin{array}{l} 1,{\rm{ }}t \geqslant 0\text{;}\\ 0,{\rm{ }}t \leqslant 0\text{。} \end{array} \right.$ | (5) |
F的鲁棒性评估指标记为Rob(F),公式如下[3]:
| $Rob\left( F \right) = \frac{1}{K}\sum\limits_k {\exp \left( { - \left| {\frac{{{f_R}\left( k \right)}}{{f\left( k \right)}}} \right|} \right)}\text{。} $ | (6) |
以上3个特征评估指标的值域为[0,1],值越大,说明特征的得分越高。在计算3个特征评估指标之前,需要对输入数据做归一化处理,特征顺序F被规范到[0,1],时间顺序
单独的指标只能片面反映备选特征在某方面的敏感性,为了综合利用3个评估指标,可以构建一个加权的线性组合来融合3个评估指标,并作为最终的独立评价判据,具体表示如下:
| $\begin{array}{l} \mathop J\limits_{F \in \varOmega } = {\omega _1}Corr\left( {F,T} \right) + {\omega _2}Mon\left( F \right) + {\omega _3}Rob\left( F \right)\text{,}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;s = \left\{ \begin{array}{l} {\omega _i} > 0\\ \sum\nolimits_i {{\omega _i} = 1} \end{array} \right.,i = 1,2,3\text{。} \end{array}$ | (7) |
其中:J为综合判据;
假如将d个特征独立使用时的综合评价指标全部都计算一遍,然后按照综合评价指标的大小排序:
| $J\left( {{f_1}} \right) > J\left( {{f_2}} \right) > \cdots > J\left( {{f_m}} \right) > \cdots > J\left( {{f_d}} \right)\text{,}$ | (8) |
通常这种排序可以反映出单个特征的敏感程度,但对于组合特征就不一定了。文献[5]直接选择使J较大的前m个特征作为最优特征组,但是一般来说,前m个最有效的特征组合成的特征子集并非是最优的,排在前面的特征相互之间有可能是冗余的。
从d个特征中挑选m个,根据排列组合知识可知,所有可能的组合数为:
| $q = C_d^m = d!/\left( {d - m} \right)!m!\text{。}$ | (9) |
在m和d不大的情况下,可以使用穷举法把所有特征组合的J都算出来加以比较,但如果特征维数较大,则穷举法的计算量太大,显然不太合适。本文在顺序搜索算法的基础上,提出一种自适应顺序最优搜索算法来提高搜索效率,并且可以自动确定特征维数m,寻找最优特征子集。算法从空特征集开始,每一步选择一个最好的特征(即该特征与已入选的特征组合在一起时J值为最大),并将它添加到该集合中,然后用高斯白噪声取代该特征,然后继续搜索下一个特征,直到有效特征数不再增加,即最后一步新增的特征为高斯白噪声。
假设已入选了k个特征构成了一个大小为k的特征组Fk,把未入选的d-k个特征fi,j=1,2,…,d-k,和
| $J\left( {{F_k} + {f_1}} \right) > J\left( {{F_k} + {f_2}} \right) > \cdots > J\left( {{F_k} + {f_{d - k}}} \right) > J\left( {{F_k} + {\varepsilon _i}} \right)\text{,}$ | (10) |
则下一步的特征组选为
| ${F_{k + 1}} = \left[ {{F_k},{f_1}} \right]\text{。}$ | (11) |
然后用一个高斯白噪声覆盖特征f1。在式(11)中,通过下列步骤实现(Fk+f)。
计算
| $f' = f \cdot sign\left( {corr\left( {f,T} \right)} \right)\text{,}$ | (12) |
得到
| $\left( {{F_k} + f} \right) = {F_k} + f'\text{,}$ | (13) |
其流程如图2所示。
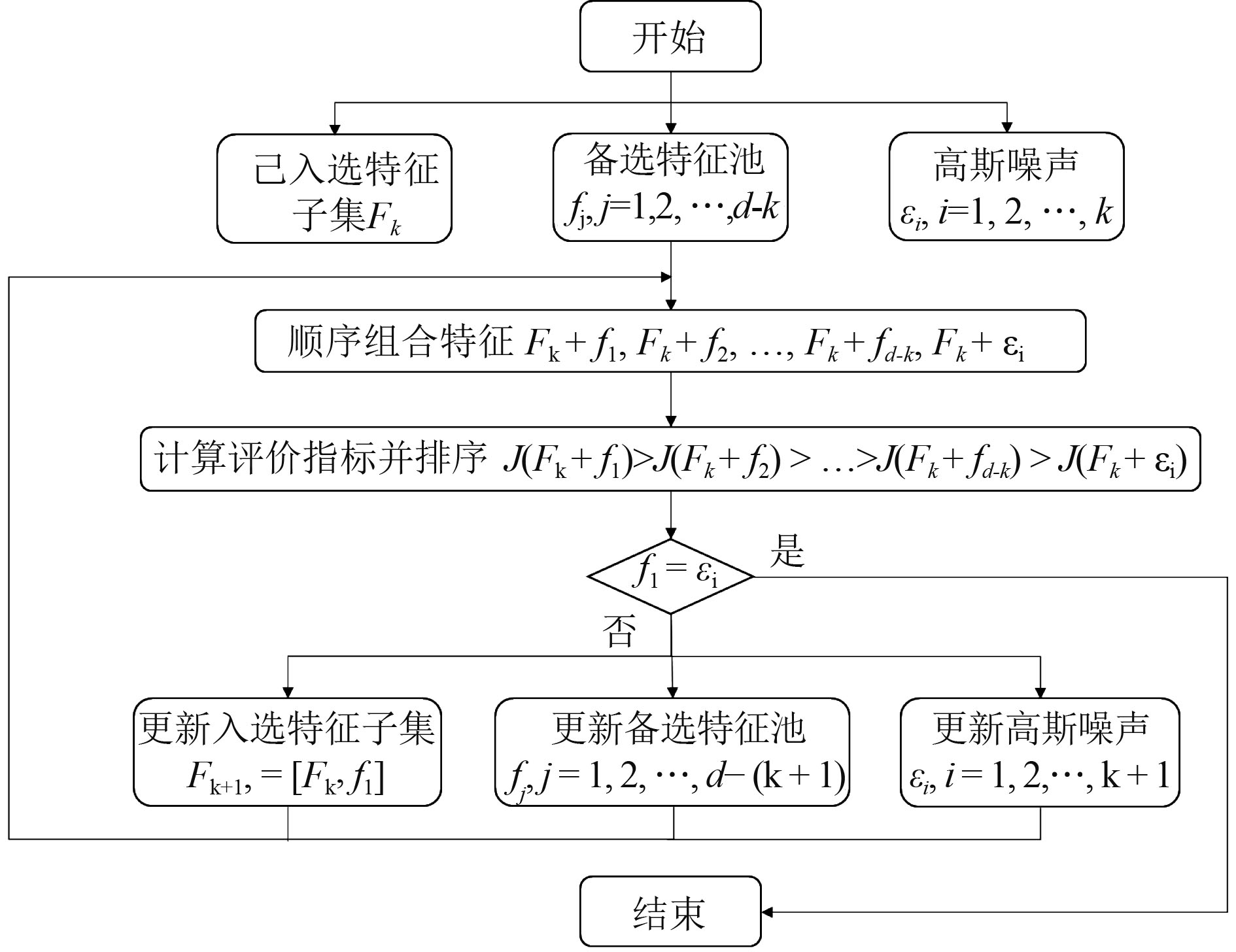
|
图 2 自适应顺序最优特征选择 Fig. 2 Adaptive sequential optimal feature selection |
综上,本节提出了一种自适应顺序最优特征选择方法,相比直接选取得分最高的m个特征,本文的方法不仅考虑了特征之间的相互影响,去除了冗余特征,还能够自动确定特征子集的维数,避免了通过试验,组合不同维数的特征,最终确定m的取值,节省了特征选择的时间。
3 基于相关向量机的轴承剩余寿命预测相关向量机(Relevance Vector Machine, RVM)是Tipping[5] 2000年提出的一种稀疏贝叶斯学习方法。它与广泛使用的支持向量机具有相似的函数形式,都可以引入核函数从而解决非线性问题。但与基于结构风险最小化原则构建学习机的SVM[6]不同,RVM是基于贝叶斯框架构建学习机,所以它不仅输出函数值,还同时输出概率值。
给定数据集
| ${t_n} = y\left( {{{{x}}_n};{{w}}} \right) + {\varepsilon _n}\text{,}$ | (14) |
其中
| $y\left( {{{x}};{{w}}} \right) = \sum\limits_{i = 1}^N {{w_i}K\left( {{{x}},{{{x}}_i}} \right) + {w_0}} \text{。}$ | (15) |
其中:
假设
| $p\left( {{{t}}\left| {{w}} \right.,{\sigma ^2}} \right) = {\left( {2{\text{π}} {\sigma ^2}} \right)^{ - N/2}}\exp \left\{ { - \frac{1}{{2{\sigma ^2}}}{{\left\| {{\bf{t}} - {\bf{\phi }}{\bf{w}}} \right\|}^2}} \right\}\text{。}$ | (16) |
其中
如果直接使用最大似然法求解
| $p\left( {{{w}}\left| {{\alpha }} \right.} \right) = \prod\limits_{i = 0}^N {N\left( {{w_i}\left| {0,\alpha _i^{ - 1}} \right.} \right)} \text{。}$ | (17) |
其中
整合模型参数后,目标值的对数边缘概率函数为:
| $\begin{gathered} \ln p\left( {{{t}}\left| {\alpha ,{\sigma ^2}} \right.} \right) = \ln \int {p\left( {{{t}}\left| {{{w}},{\sigma ^2}} \right.} \right)} p\left( {{{w}}\left| {{\alpha }} \right.} \right){\rm{d}}{{w}} {\rm{ = }} \\ - \frac{1}{2}\left[ {N\ln \left( {2{\text{π}} } \right) + \ln \left| {{C}} \right| + {{{t}}^{\rm{T}}}{{{C}}^{ - 1}}{{t}}} \right] \text{。}\\ \end{gathered} $ | (18) |
其中:
| ${{C}} = {\sigma ^2}{{I}} + {\bf{\phi }}{{\bf{A}}^{ - 1}}{{\bf{\phi }}^{\rm{T}}}\text{。}$ | (19) |
当超参数估计过程收敛,得到最优超参数值
| $\begin{split} & p\left( {{t_*}\left| {{t}} \right.,{{{\alpha }}_{MP}},{\sigma ^2}_{MP}} \right) =\\& \quad\int \!{p\left( {{t_*}\left| {{w}} \right.,{\sigma ^2}_{MP},} \right)} p( {{{w}}\left| {{t}} \right.,{{{\alpha }}_{MP}}},{\sigma ^2}_{MP} ){\rm{d}}{{w}} \!=\! N\left( {{t_*}\left| {{y_*},} \right.\sigma _*^2} \right) \text{。} \end{split} $ | (20) |
其中:
| ${y_*} = {\mu ^{\rm{T}}}{{\phi }}\left( {{{{x}}_*}} \right)\text{,}$ | (21) |
| $\sigma _*^2 = \sigma _{MP}^2 + {{\phi }}{\left( {{{{x}}_*}} \right)^{\rm{T}}}{{\Sigma }}{{\phi }}\left( {{{{x}}_*}} \right)\text{。}$ | (22) |
在超参数优化过程中,大多数
本文将使用IEEE PHM 2012数据挑战赛[3]的滚动轴承加速寿命试验数据,实验台如图3所示。2个型号为DYTRAN 3035B的单轴加速度传感器正交放置在被测轴承的轴承座上,采集被测轴承的的振动信号。一个安装在水平轴,一个安装在垂直轴。采样频率为25.6 kHz,每次采集2 560个数据点,每次采样间隔10 s。

|
图 3 PRONOSTIA滚动轴承试验台 Fig. 3 PRONOSTIA Rolling bearing test bench |
使用bearing1-1与bearing1-3分别作为训练集与测试集,其水平振动时域如图4所示。将水平方向和垂直方向的振动均用来提取特征,共计提取124维特征。其中包括36维时域特征,18维频域特征,6维熵特征,16维IMF能量特征和48维希尔伯特边际谱特征。

|
图 4 Bearing1-1和bearing1-3水平振动时域图 Fig. 4 Bearing1-1AND bearing1-3 Horizontal vibration time domain diagram |
通过自适应序列最优特征选择方法优选的特征子集共18维特征,记作FS1。从FS1中选取前10维记作FS2,选取前17维记作FS3。从特征中不重复的选择综合评价较高的特征与FS1组合为19维特征子集,分别记作FS4~FS7。
使用RVM模型预测,预测结果通过3个指标评价,均方根误差(RMSE),累积相对准确度(CRA)和耗时。评价指标的公式分别为:
| $RMSE = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {{{\left( {yi - {{\hat y}_i}} \right)}^2}} } \text{,}$ | (23) |
| $CRA = \sum\limits_{i = 1}^N {{w_i}RA\left( {{T_i}} \right)} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {w_i} = i/\sum\nolimits_{i = 1}^N i \text{。}$ | (24) |
为了直观比较各特征子集在不同指标上的表现,并且避免指标尺度的影响,将各指标归一化,如图5所示。各特征子集预测结果如图6所示。
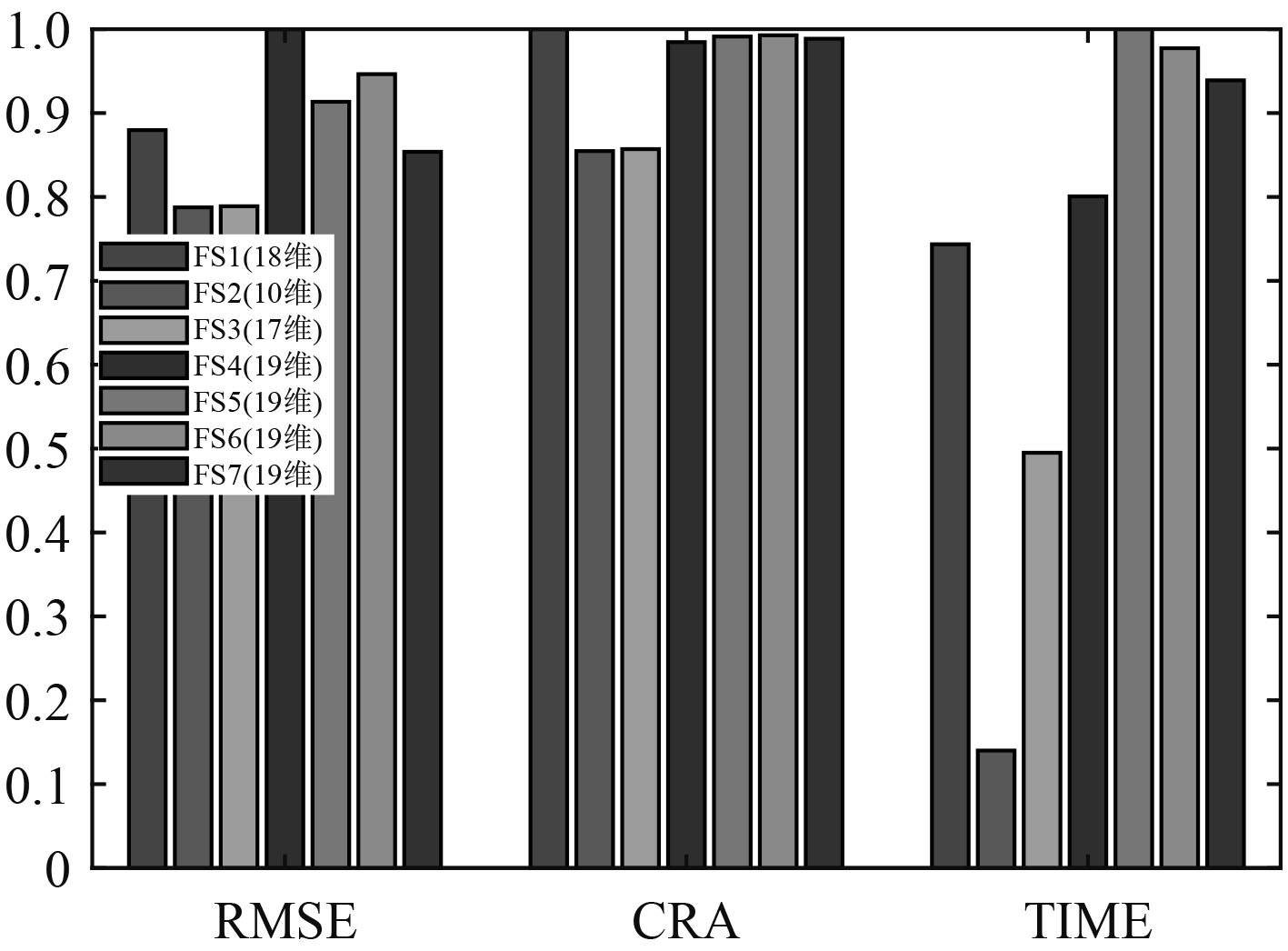
|
图 5 各特征子集预测结果指标比较 Fig. 5 Comparison of prediction indicators of each feature subset |
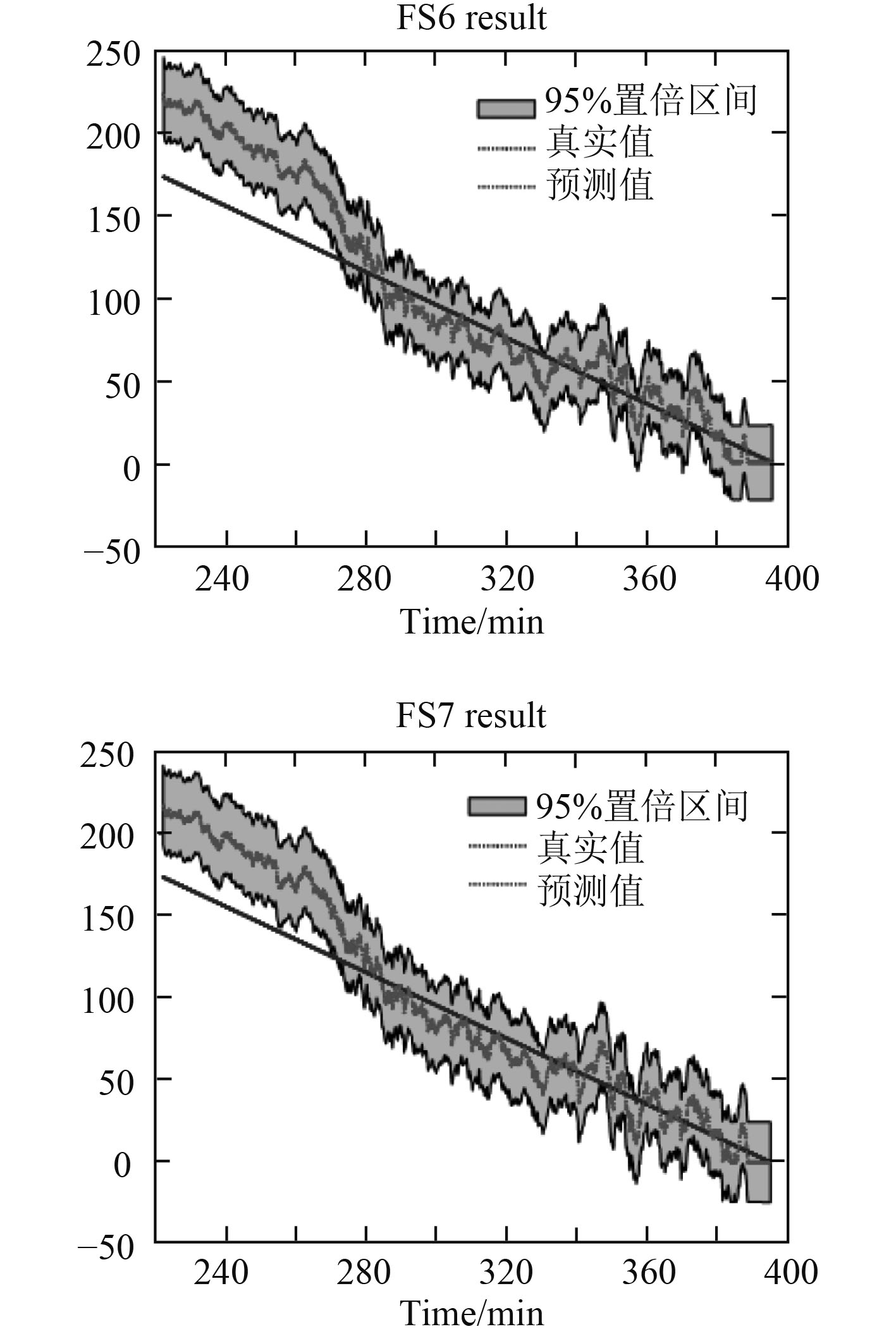
|
图 6 各特征子集预测结果 Fig. 6 Each feature subset prediction result |
从图5中可以发现,当维数少于18维时,RMSE较小,但CRA较低,耗时较少。随着特征维数增加到18维,CRA升到最高,耗时也相应增加。当特征维数为19维时,RMSE有所增大,CRA有所降低,耗时继续增加。在图6中,直线代表真实值,曲线代表预测值,区间代表95%置信区间,可以看到FS1的预测结果在中后期真实值基本都落入置信区间,预测值在真实值附近波动,由此可以说明18维确实是一个有效的最优特征维数,该算法可以自动确定最优特征子集及其维数。
5 结 语针对滚动轴承残余寿命预测特征提取与特征选择的问题,本文通过在时域,频域,时频域提取大量特征,以便全面反映轴承的状态信息。然后在序列搜索算法的基础上,提出了自适应序列最优特征选择方法,通过特征融合以及添加高斯白噪声特征,可以自动确定特征子集的维数,寻找最优特征子集,并通过实验验证了方法的有效性。
| [1] |
董绍江. 基于优化支持向量机的空间滚动轴承寿命预测方法研究[D]. 重庆: 重庆大学, 2012.
|
| [2] |
周晓君. 基于样本熵理论的进化论自适应消噪法[J]. 舰船科学技术, 2014, 36(5): 55-59. DOI:10.3404/j.issn.1672-7649.2014.05.011 |
| [3] |
ZHANG B, ZHANG L, XU J. Degradation Feature Selection for Remaining Useful Life Prediction of Rolling Element Bearings[J]. Quality and Reliability Engineering International, 2016, 32(2): 547-554. DOI:10.1002/qre.1771 |
| [4] |
N. PATRICK, G. RAFAEL, M. KAMAL, et al. PRONOSTIA: An Experimental Platform for Bearings Accelerated Life Test[C]. In Proceedings of IEEE International Conference on Prognostics and Health Management, 2012, 1–8.
|
| [5] |
TIPPING M E. The Relevance Vector Machine[C]//Advances in Neural Information Processing Systems. DBLP, 2000.
|
| [6] |
张志华, 梁胜杰, 等. 基于SVM的双层圆柱壳体机械动噪声数据特征提取方法比较[J]. 船舶力学, 2015(Z1). |
| [7] |
常飞, 乔欣, 张申, 等. 基于MFCC特征提取的故障测评与评价方法[J]. 计算机应用研究, 2015(06). DOI:10.3969/j.issn.1001-3695.2015.06.072 |
| [8] |
龚晨. 曲线的随机拟合及其自适应算法[J]. 上海交通大学学报, 2005(4). DOI:10.3321/j.issn:1006-2467.2005.04.001 |
 2019, Vol. 41
2019, Vol. 41
