2. 海军工程大学 舰船与海洋学院,湖北 武汉 430033
2. Naval University of Engineering, Wu Han, 430033, China
随着计算机技术和各种拓扑优化理论的日益成熟,结构优化设计在船舶领域的应用也越来越广泛。结构优化设计分为尺寸优化、形状优化和拓扑优化3个层次。其中,拓扑优化根据优化对象的不同可以分为离散体结构拓扑优化和连续体结构拓扑优化。离散体结构的拓扑优化理论相对计算量小,设计变量简单直观,现在国内外已发展的比较成熟[1 – 3]。连续体结构拓扑优化理论在近几十年快速发展,但仍存在很多研究难点和热点问题[4 – 5]。
拓扑优化理论从Michell桁架理论[6]提出后便开始有了逐渐的研究。随后均匀化方法,密度法,SIMP模型理论,RAMP模型理论,渐进结构优化法(ESO)等拓扑优化方法和理论模型相继出现,使拓扑优化理论不断完善。隋允康等[7]吸取了变密度法和变厚度法等方法的优点,提出了一种独立连续映射模型方法(Independent Continuous Mapping,ICM),昌俊康等[8]则针对SIMP和RAMP材料插值的不足提出了新的惩罚函数,并推导了迭代公式,还通过算例验证了新惩罚函数的效果;左孔天等[9]详细研究了基于优化准则法的变密度设计变量的迭代,并给出了相应的迭代公式,而且还深度探讨了不同优化参数对拓扑优化的影响。
船体结构优化的目标函数通常是线性的,但约束条件是非线性的,优化一般是多目标模糊优化,所以,应用在船体结构优化中的优化算法主要是准则法、数学规划法和一些新型的优化设计方法[10]。国内关于船舶结构优化的研究起步于20世纪70年代,程远胜等[11]对船舶肘板的结构型式进行了拓扑优化,解决了传统三角形肘板的应力集中问题。此类研究大多针对局部结构,如舱口形状、剖面结构等,对较为复杂的船体附体结构涉及较少。近年来,逐渐提出了模糊优化设计法[12]、遗传算法[13]和智能型优化设计方法[14]等,并逐步应用到船舶优化领域中。翟玉文[15]就某型潜艇下垂直稳定翼的钢骨架进行了优化,确定采用斜支撑板的方案,但缺乏系统的可操作性。
由于舰艇结构的固定性以及拓扑优化结构不易工程转化的缺点,利用拓扑优化对舰艇结构进行结构优化的工作较少,也没有1套完整有效的优化设计方法。现阶段,对潜艇舵翼结构的设计多为经验设计或局部优化设计,缺少针对整体舵翼结构的优化方法,对复合材料结构更是如此,因此针对这类结构系统的结构优化设计方法还需要进一步的研究。此外,结构拓扑优化的结果无法直接进行工程制造,3D打印技术虽然可以直接实现拓扑结构,但其成本太高,且误差较大,不适合在样机的制造中应用。因此,必须基于工程可实现的原则提出一种更有效的优化方法。
本文以典型的操纵面潜艇升降舵为研究对象,提出一种分步拓扑优化方法,其可以在优化过程中根据传力路径的走势限制优化结构的形式,针对其结构形式得到一种易于工程实现的结构,具有重要的研究价值和工程意义。
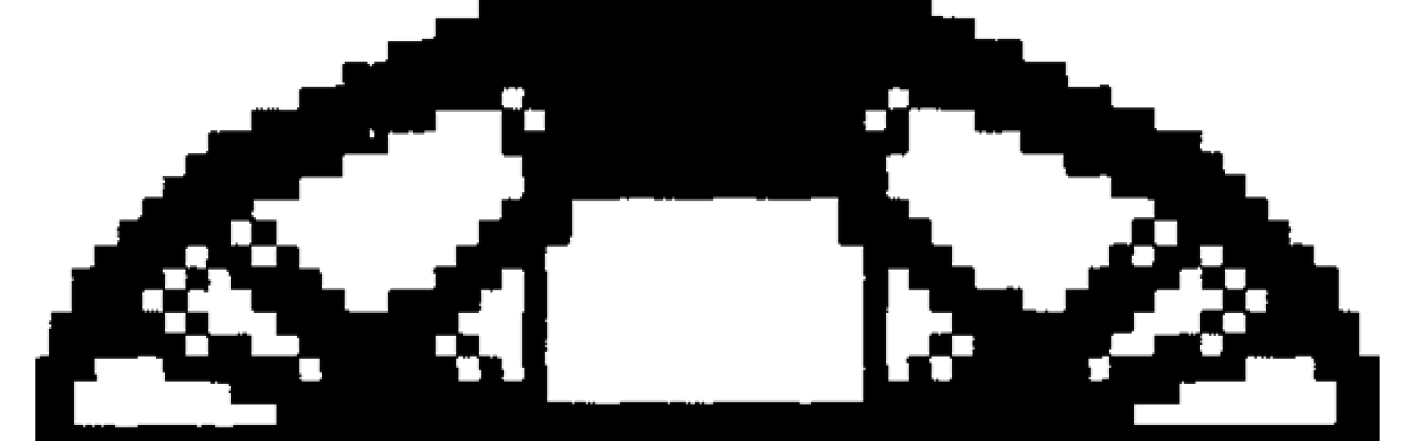
1 拓扑优化的基本原理及方法 1.1 网格依赖性的启示网格依赖性是有限元拓扑优化过程中常见的问题。所谓的网格依赖性是指由于有限单元的划分,拓扑优化后材料在某些单元上的分布并不能占据整个单元网格,从而根据算法的特点自动将单元填满或删除,使边界上出现了细小的台阶形状,不仅影响传力路径的效果,也破坏了传力路径的流顺性,如图1所示。
|
图 1 拓扑优化结果的网格依赖性 Fig. 1 Mesh dependence of topological optimization results |
但是伴随网格依赖性出现的却是每一个单元最终都是规则的六面体,如果将这些单元适当放大,成为可操作的分块,便可以使优化后的材料分布依赖于这些分块形成规则的结构,即规则的骨架形式。
1.2 Abaqus拓扑优化理论基于Abaqus中变密度法进行拓扑优化,变密度法的一般数学描述为:
| $\begin{gathered} \min c\left( x \right) = {U^{\rm{T}}}KU = {\sum\limits_{e = 1}^N {\left( {{x_e}} \right)} ^p}{u_e}^{\rm{T}}{k_0}{u_e}\text{,} \\ {\rm{s.t.}}\frac{{V\left( x \right)}}{{{V_0}}} = f \text{,}\\ KU = P\text{,} \\ 0 < {x_{\min }} \leqslant x \leqslant 1 \text{。}\\ \end{gathered} $ | (1) |
其中:
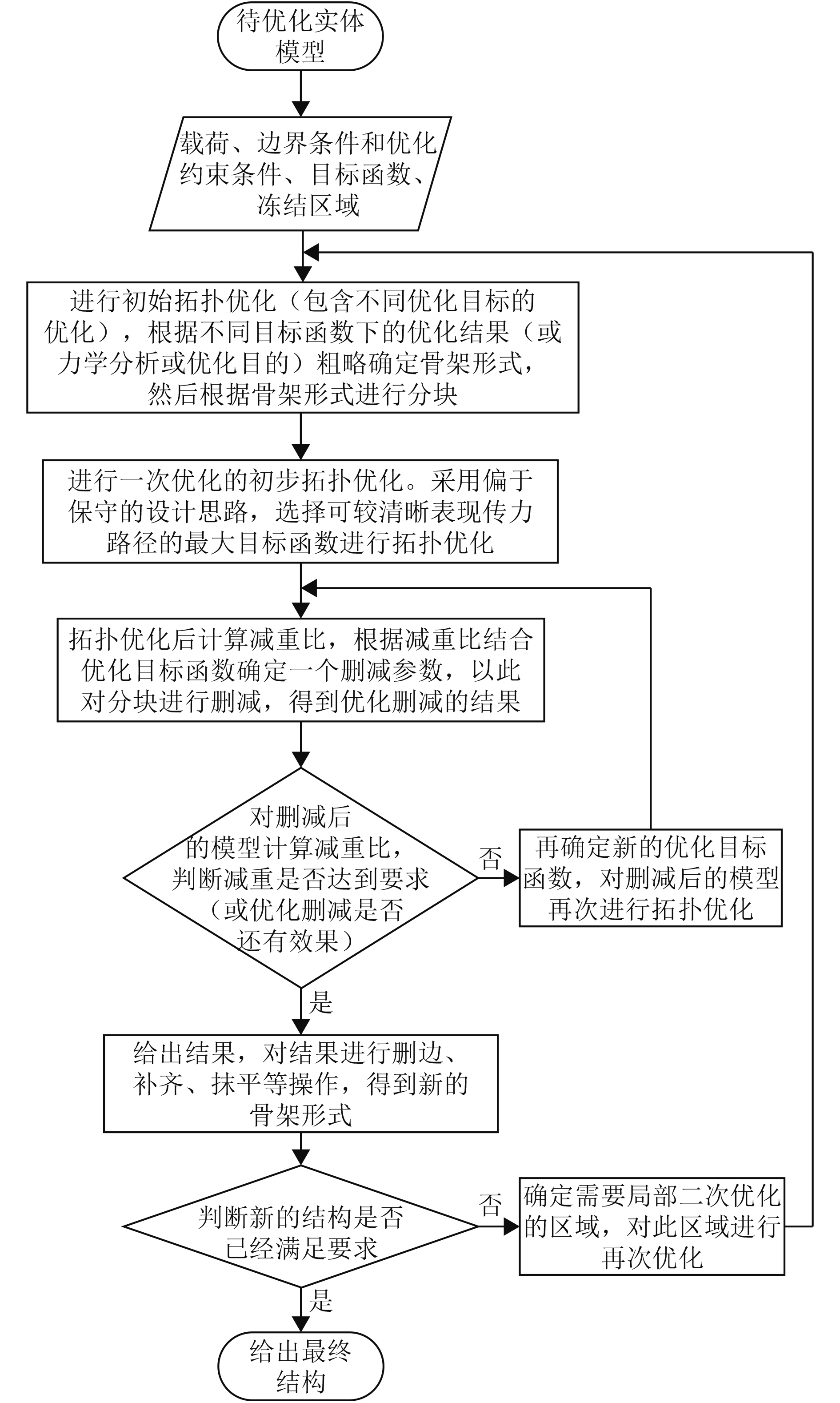
分步拓扑优化是以拓扑优化结果为基础,取不同的目标函数值,逐步趋近最终目标,将不规则的优化结果手动调整为容易实现的工程结构,优化结果与工程实际的结合提供一种思路。模型分步优化的具体流程如图2所示。
|
图 2 分步拓扑优化流程图 Fig. 2 The flow diagram of topology optimization by step |
优化过程中,首先在模型基础上,对不同目标函数的要求进行优化,根据优化结果粗略确定骨架的形式,方便对模型进行分块;确定分块后,要确定初步的优化目标,对于初步的优化目标一般采用偏于保守的设计思路,选择较大目标函数,只要优化后能出现清晰的传力路径即可;然后依据应变能、应力大小、减重比(体积)等确定分块删减参数对分块进行删减。
在对分块进行比较删减时,会出现一些边角区域的分块不满足减重条件而被保留,但在结构中却成为了独立的分块,但这些分块无法起到传力效果;还有一些传力路径存在个别区块的缺失,参差不齐等。因此需要按以下原则进行结构处理:
1)删除边角处不起传力作用的区块;
2)增加较完整的传力路径区域,将不完整的传力路径补充完整;
3)优化到最后一步时,将参差不齐的区块抹平。最终获得规则结构。
最终通过多步循环拓扑优化得到结构的优化结果。
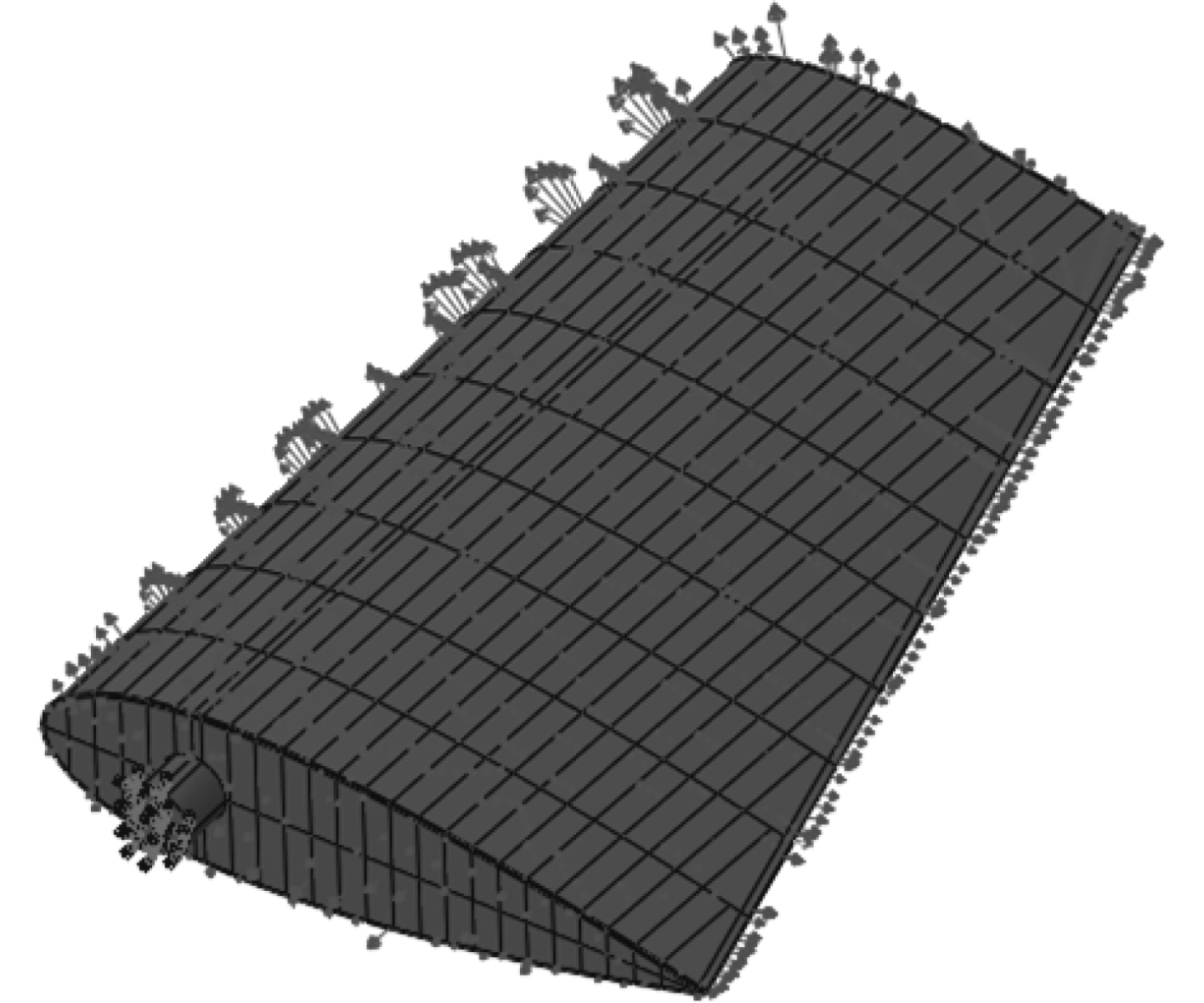
2 潜艇升降舵骨架形势的分步拓扑优化 2.1 模型介绍潜艇升降舵为悬挂舵,是典型的悬臂装置。选用17 kn航速、35°舵角(典型工况)下的操舵载荷为典型载荷对其进行结构优化设计,边界条件采用舵轴截面固支边界,通过流体仿真计算得到操舵载荷分布如图3所示。
|
图 3 模型的载荷及边界条件 Fig. 3 Load and boundary conditions of the model |
应用有限元软件Abaqus对其进行初步拓扑优化设计。以满足结构刚度要求的应变能最小化为约束,体积(减重比)为目标函数,对结构进行拓扑优化。将载荷分布区域、边界条件施加区域以及外部舵轴全部进行优化冻结,使优化结构按升降舵中面对称。
2.2 骨架形式分析及分块方案的确定在对升降舵进行初步拓扑优化时,分别以体积目标函数
|
图 4 初步优化结果 Fig. 4 Preliminary optimization results |
可以看出,优化结果以展向支撑骨架为主,其他形式的骨架结构辅助。所以,为了尽可能满足这种骨架的结构趋势,确定分块为细长型分块。
具体的分块方案如图5所示。将升降舵按展向方向均分为10等分,弦向方向则每间隔100 mm划分一次,直到随边,最后以100~200 mm终止。依此共划分出195块。
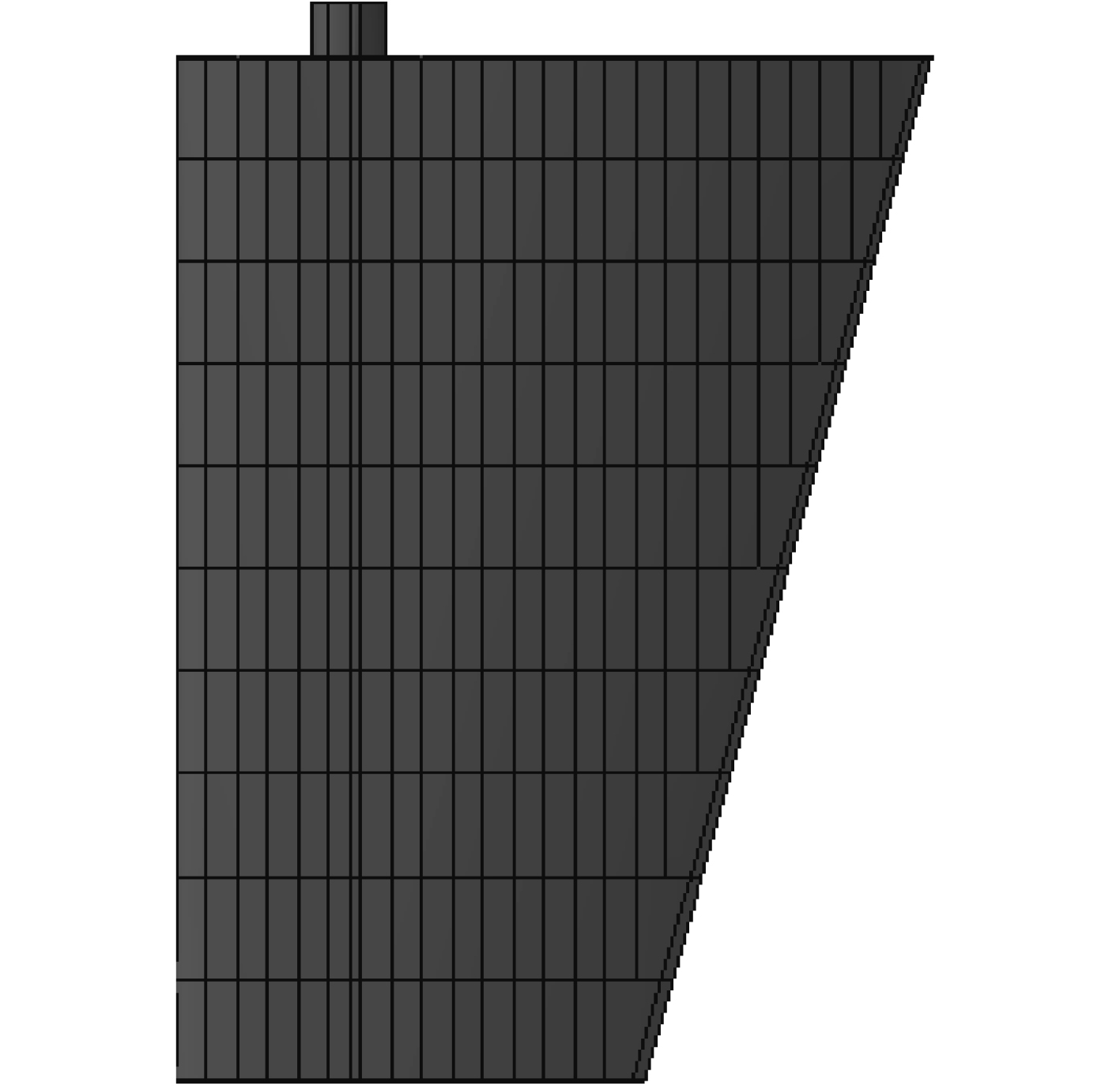
|
图 5 分块后模型 Fig. 5 Model after block |
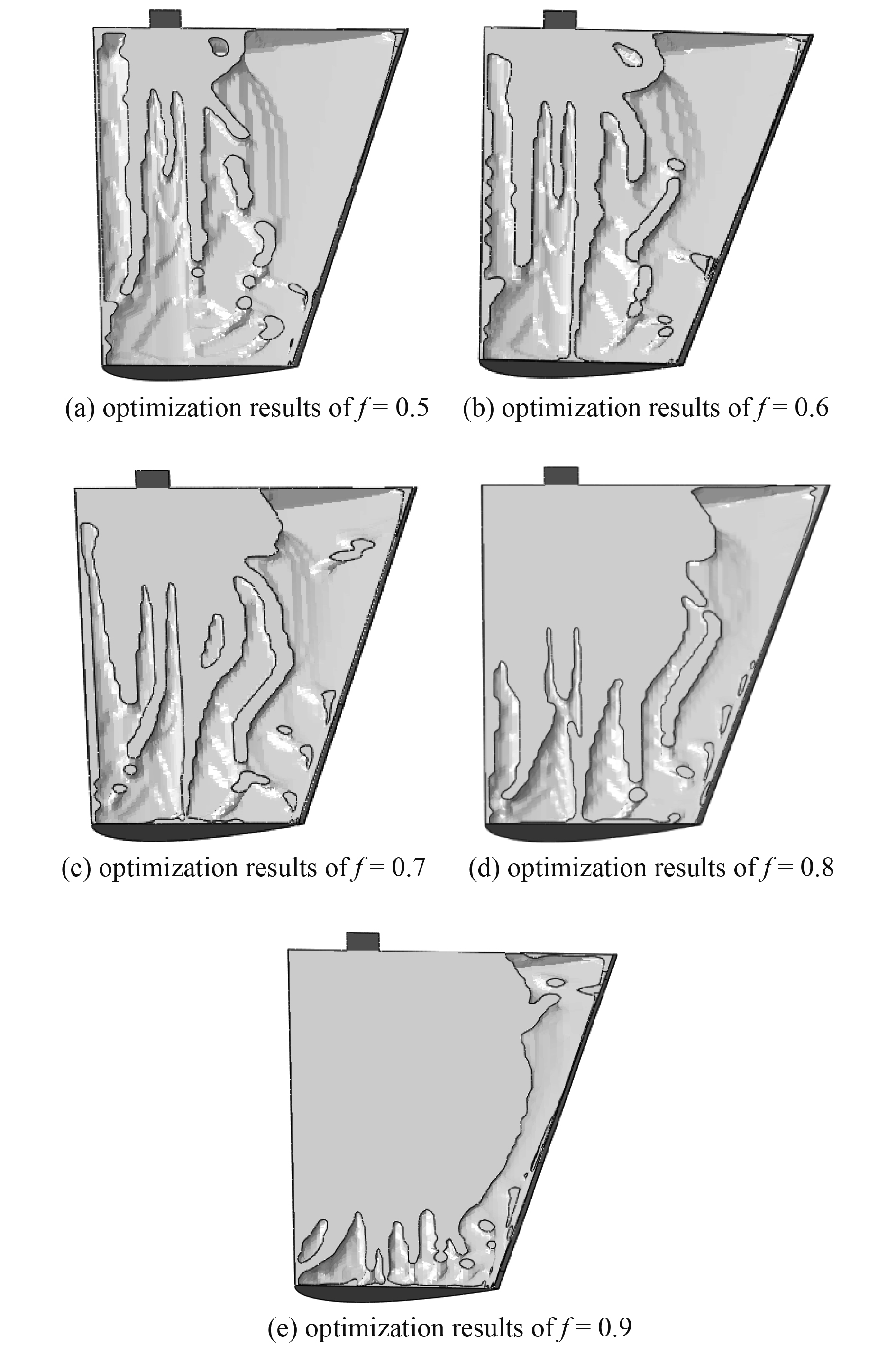
从体积目标分别为50%~90%的优化结果可以看出,当目标函数值小于80%后,优化的结果开始可以明显表现出骨架的基本形式。取偏于保守的
|
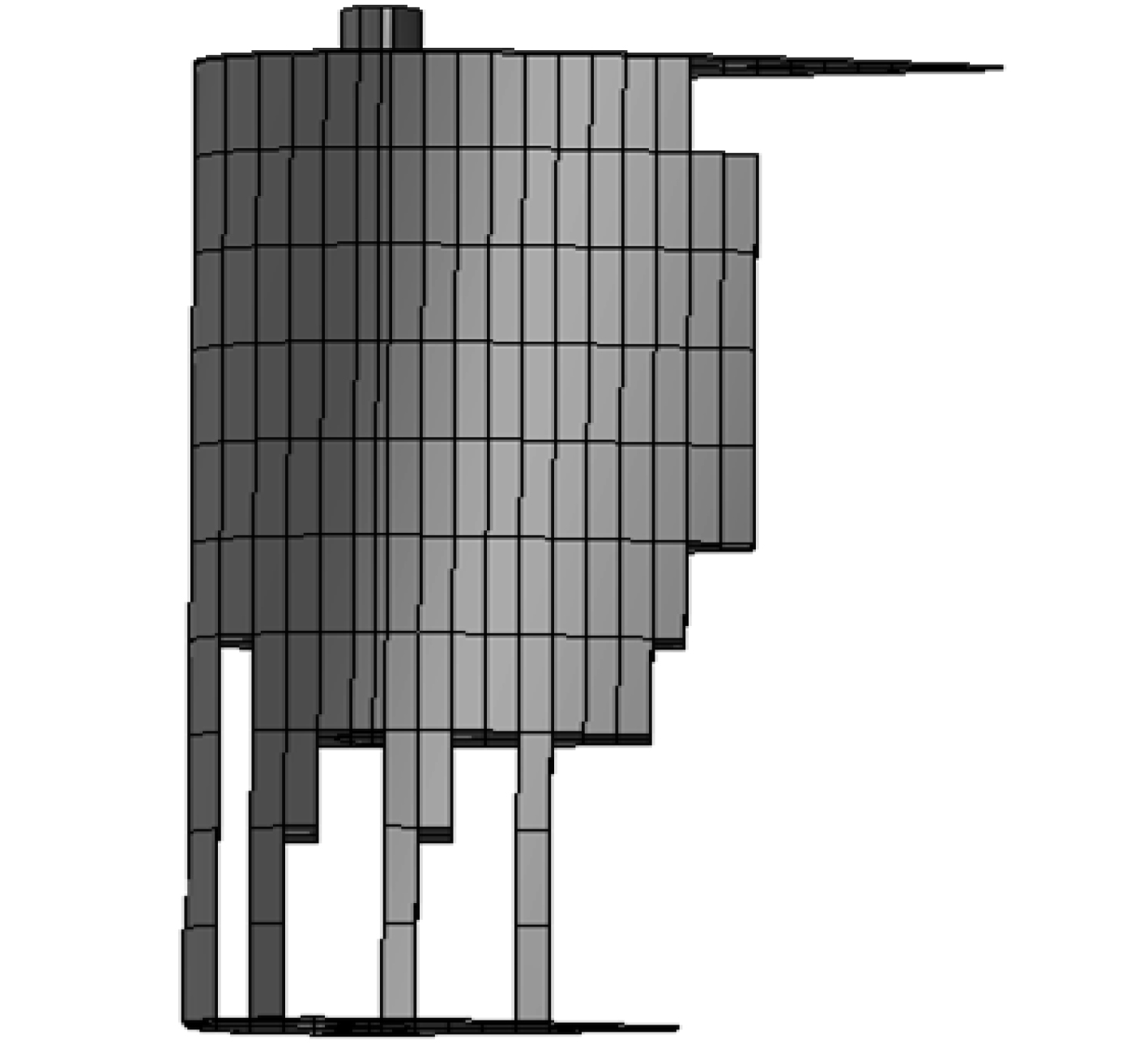
图 6 初步优化删减后材料分布结果 Fig. 6 The material distribution after preliminary deletion |
初步优化结果表明,在操舵载荷作用下,升降舵的骨架形式将以展向骨架为主要传力构件,舵轴与操纵面的连接过渡区域强度刚度要求较高,但从此时的材料分布中无法断定此区域最终的传力构件是面板还是筋板。初步确定了骨架的趋势和分布之后,接下来优化的主要目的为减轻重量,使骨架的趋势进一步明确,确定舵轴与操纵面的连接过渡区域的材料分布。因此,适当加大了体积目标的取值。
选体积目标数值分别为0.5,0.6,0.7以及0.8,对初步优化后所得的结构进行第2步拓扑优化,结果如图7所示。

|
图 7 第2次拓扑优化结果 Fig. 7 Second topological optimization results |
从图7可知,4种体积目标数值下的优化所计算的最大挠度相差不大,故选取相应的体积目标只能依靠结构本身。在体积目标为70%和80%的2次拓扑优化中,新出现的展向骨架较为复杂,不能进一步凸显骨架的趋势。当体积目标数值小于60%后,优化结果明显表示出了骨架的趋势,为了保证传力路径的连续性,选择
在变密度法的拓扑优化中,以应变能为约束条件,减重比为目标函数,能直观反映材料留存的必要性,因此,选取减重比为分步优化的删减参数。
钢舵原始质量为18 879.88 kg,按初步优化减重比为20%计算,则优化后结构质量应为15 103.9 kg,软件实际测量出的优化后结构质量为16 706 kg,减重比约为11.5%,以11.5%为初步优化删减参数,删除优化后重量减少超过11.5%的整个分块。删除相应分块后结构整体质量为15017.81 kg,为初始质量的79.5%,约等于80%,与最初设置的体积目标相符。
对优化后出现边角区域按2.3节中原则进行处理,最终得到如图8和图9所示结构。
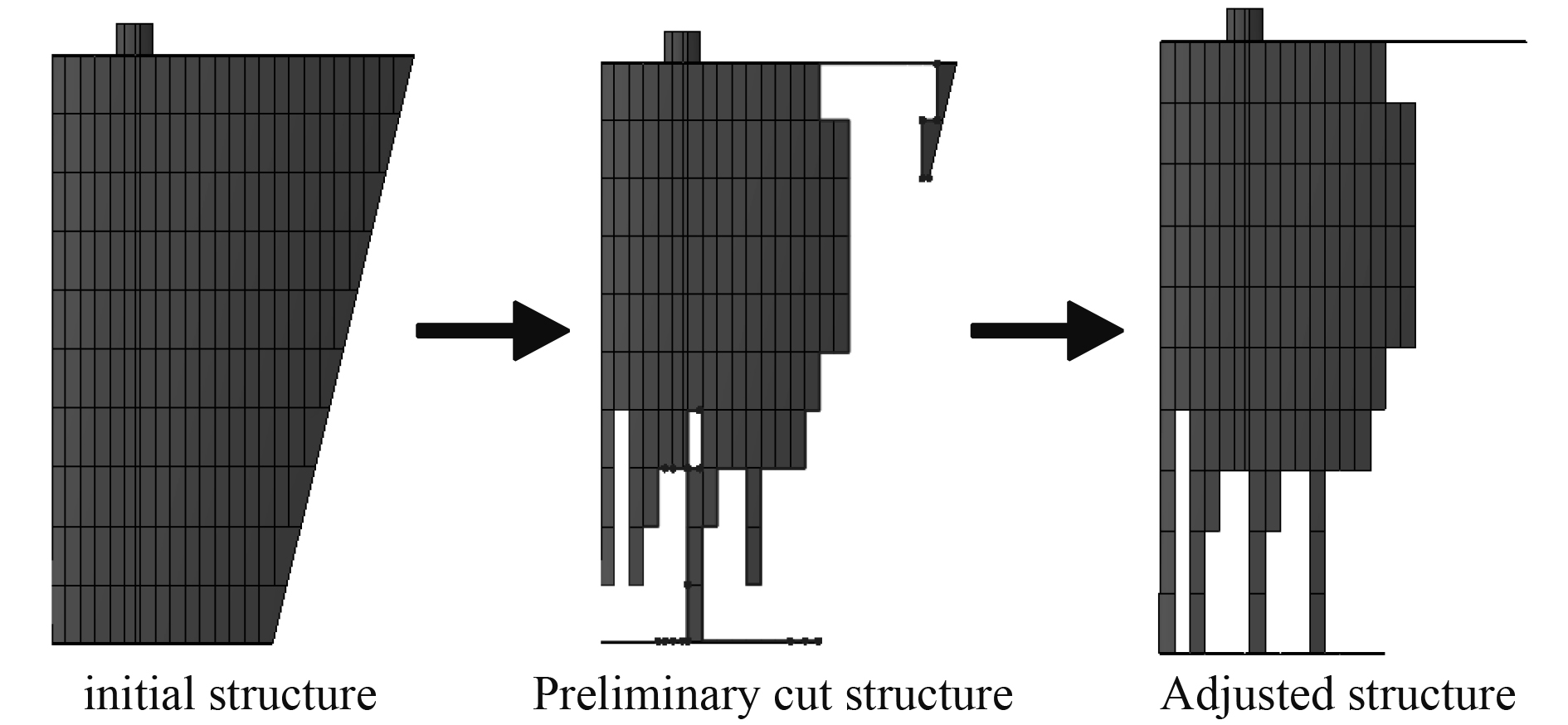
|
图 8 特殊区块的删减及调整后结果 Fig. 8 Result deletion and adjustment of special blocks |
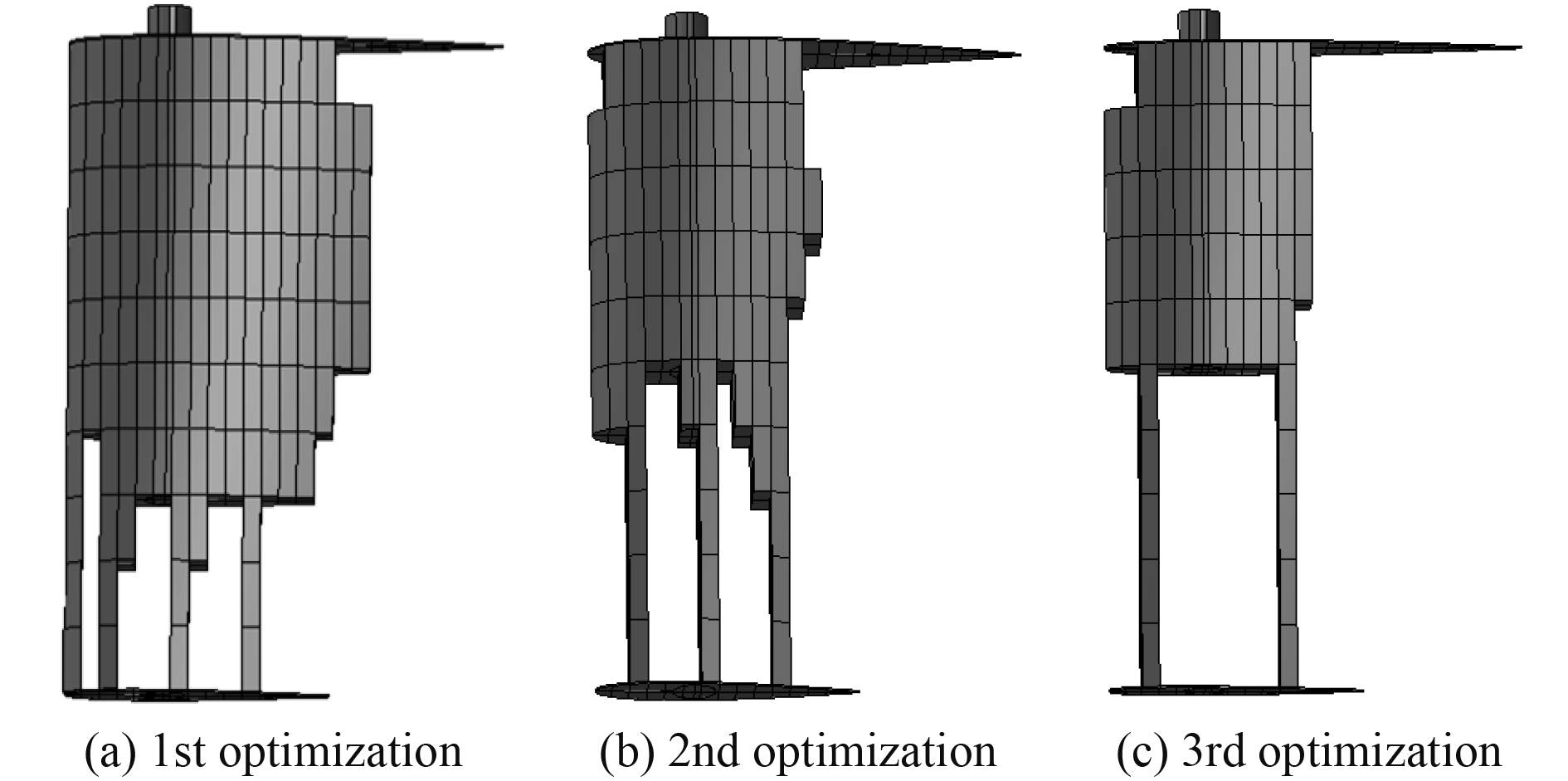
|
图 9 每步优化后结果 Fig. 9 Each step of the optimization results |
第2和第3步的删减参数分别为减重比不小于40%,50%,所以第2和第3步优化的理论预设体积目标值应为
|
|
表 1 各步优化后的质量及占比 Tab.1 The quality and proportion of each step after optimization |
从表中可以看出,优化的步数越多,优化的减重比与理论减重比越趋于一致。由图9可知,这是因为展向趋势的骨架逐渐清晰甚至确定,而舵轴与操纵面连接区域的材料仍然保留,所以继续优化效果会越来越小。
2.5 局部区域的二次优化设计在这3步的渐进优化中,基本确定了材料的分布,即舵轴与操纵面的连接应用连接板,展向方向应用展向筋板,但舵轴与操纵面连接板的厚度,连接板与轴壳的连接形式以及展向筋板的厚度等仍需要进一步的优化设计。
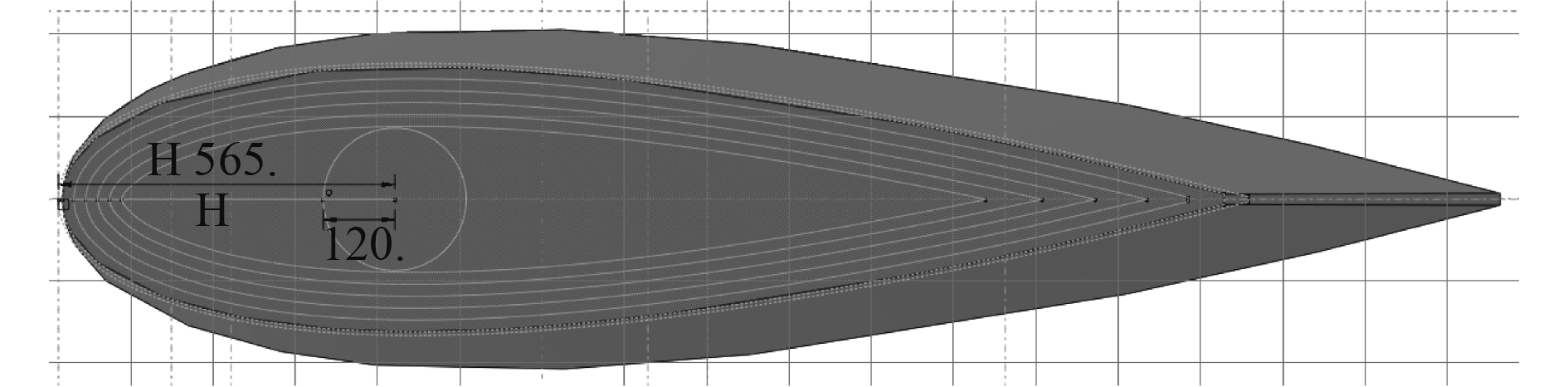
从重量、刚度,壳板厚度等各方面考虑,连接板厚度方向的区块划分定为20 mm一层。除去舵轴区域,将厚度方向划分出了5层,如图10所示。
|
图 10 厚度方向的区块划分方案 Fig. 10 Block partitioning scheme of thickness |
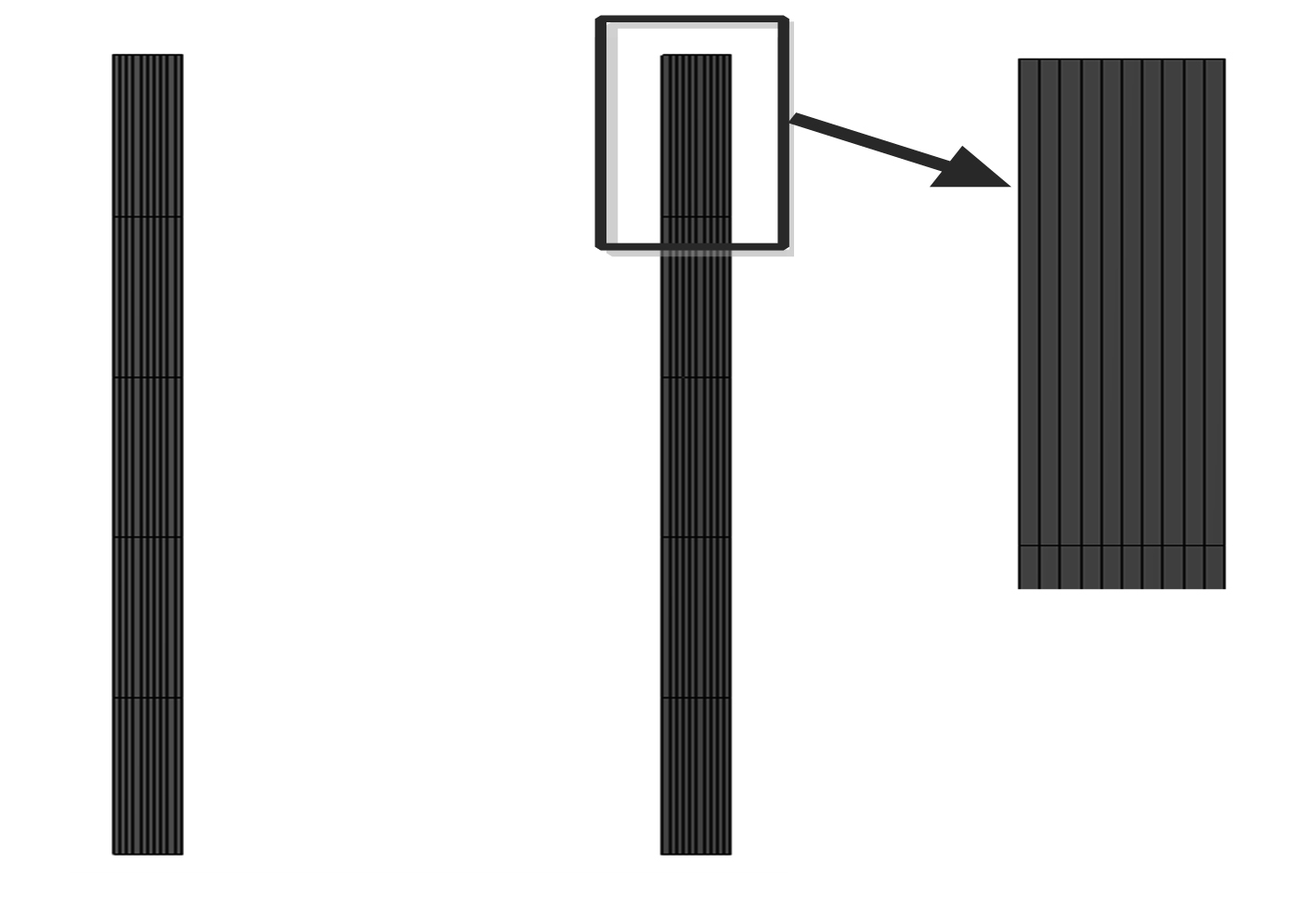
对现在100 mm厚的筋板进行再细分。在厚度方向上划分成10 mm每块,具体划分如图11所示。
|
图 11 展向筋板区块划分 Fig. 11 Block division of spanwise stiffeners |
为确定连接板的厚度,采取较大的体积优化目标函数,经过两步的拓扑优化,并结合拓扑优化的形式和删减参数的规范进行区块删减,得到如图12(a)所示的结果,其中连接板厚20 mm,在舵轴心两侧局部的加厚到40 mm。结合考虑重量的优化,已加强了舵轴的控制区域,故将连接板进行再优化时,冻结舵轴区,对保留的外两层壳板在厚度方向上划分进行优化,最终优化并删减后得到了如图12(b)所示的结构。在结构形式上优化删除掉了导边的弧形板,厚度方面整块连接板不再是变厚度,统一厚度为20 mm。

|
图 12 连接板优化结果 Fig. 12 Optimization results of the connecting plate |
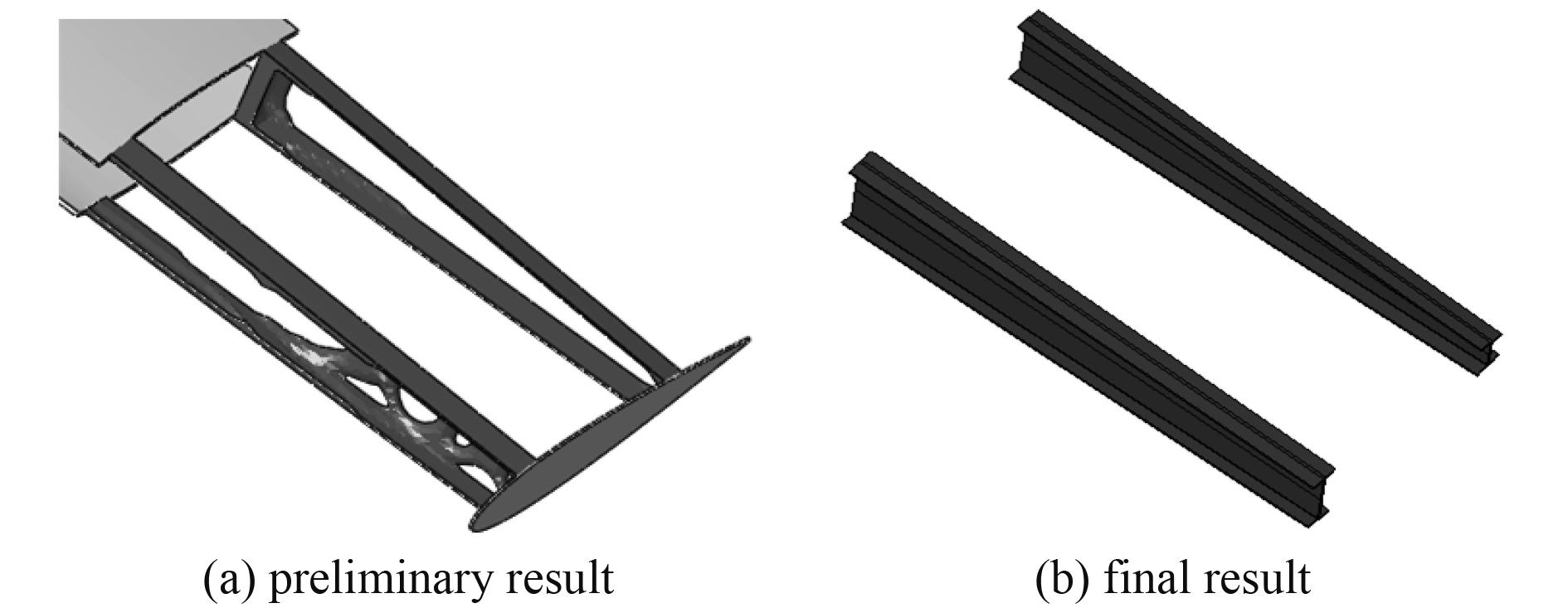
对展向筋板的再次优化经过一步优化得到如图13(a)所示的结果,经删减确定展向筋板的厚度定为10 mm。结合拓扑优化出的结果分析,采用工字钢的筋板形式,最终确定优化结果如图13(b)所示。
|
图 13 展向筋板的优化结果 Fig. 13 Optimization results of an extended stiffened plate |
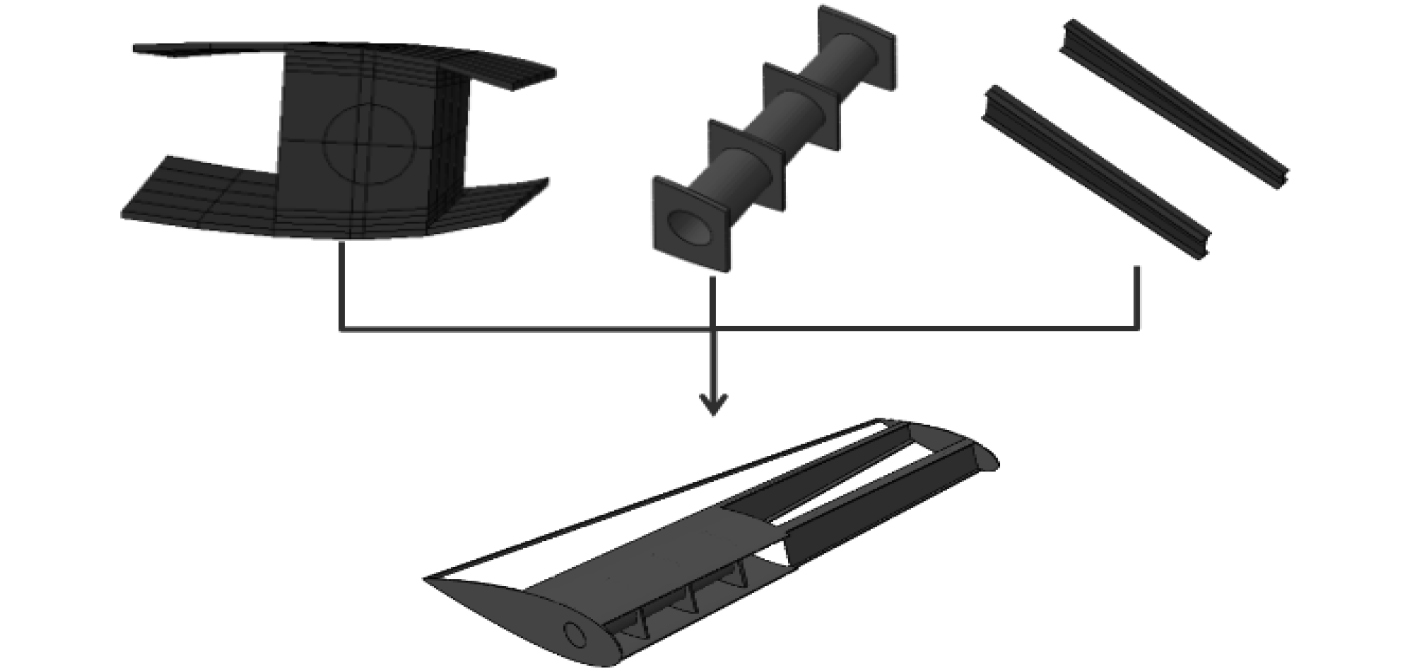
优化结束后,按照传统悬挂舵的轴壳设计方法,优化得到舵轴长度,设计出相应的轴壳,并按照优化的结构设计出悬挂舵的骨架模型,如图14所示。
|
图 14 优化设计出的骨架 Fig. 14 The skeleton is obtained by optimum design |
将优化出的骨架结构应用到复合材料舵中,表层采用10 mm的玻璃钢蒙皮,内部填充浮力芯材。载荷沿用相同的操舵载荷,边界条件为固支。将其计算结果与常规复合材料舵计算结果对比分析。2种复合材料舵选用完全相同的材料,拓扑优化复合材料舵的总质量为2 184.58 kg,常规复合材料舵总质量为2 223.96 kg。拓扑优化复合材料舵的计算结果如图15所示,与常规复合材料舵的计算结果对比如表2所示。

|
图 15 拓扑优化复合材料舵计算结果 Fig. 15 Calculation result of the composite rudder after topological optimization |
|
|
表 2 变形与应力对比表 Tab.2 Deformation and stress contrast table |
从表2可以看出,在刚度方面拓扑优化复合材料舵较常规复合材料舵有明显优势。拓扑优化复合材料舵的总质量比常规复合材料舵的总质量低39.38 kg,但拓扑优化复合材料舵的最大挠度比常规复合材料舵的最大挠度小4.99 mm,典型观测点挠度小4.6 mm,扭转角度小72.8%,扭转刚度远好于常规复合材料舵,虽然弯曲刚度比钢质舵略差,但扭转刚度却要比钢质舵好很多。在强度方面,拓扑优化复合材料舵在钢骨架上的应力略高,但却小于钢质舵的应力,且安全系数高于2,拓扑优化复合材料舵和常规复合材料舵的复合材料蒙皮的安全系数均可以取到5以上。
4 结 语本文以潜艇升降舵为例,提出了一种新的基于Abaqus变密度拓扑优化法的分步拓扑优化法。该方法利用拓扑优化的网格依赖性,灵活的提出划分大型网格,对升降舵进行了结构优化,在优化的过程中,利用提出的网格删除方法,直接将拓扑优化、形状优化和尺寸优化结合起来,使得最终优化出的结构为规范化的结构,可以直接用于工程制造。
通过拓扑优化复合材料舵与常规复合材料舵的静刚度,强度对比分析,发现优化设计出的钢骨架完全可以满足复合材料舵的刚度和强度要求,而且拓扑优化复合材料舵的总质量更低,说明拓扑优化复合材料舵的材料利用率更高,即优化设计出的钢骨架的材料利用率更高,进一步说明了优化方法的有效性。
| [1] |
RUY W S, YANG Y S. Selection strategies in a structural design support system[J]. Struct. Optim, 2001, 21: 69-79. DOI:10.1007/s001580050169 |
| [2] |
柴山, 石连栓, 孙焕纯. 包含两类变量的离散变量桁架结构拓扑优化设计[J]. 力学学报, 1999, 31(5): 574-584. |
| [3] |
BENDSOE M P, SIGMUND O. Topology optimization: theory, methods and applications[D]. New York: Springer, 2003.
|
| [4] |
袁振, 吴长春, 庄守兵. 基于杂交元和变密度法的连续体结构拓扑优化设计[J]. 中国科学技术大学学报, 2001, 31(6): 694-699. DOI:10.3969/j.issn.0253-2778.2001.06.010 |
| [5] |
董桂西, 王藏柱. 结构优化设计的现状及展望[J]. 电力情报, 2000, 1: 5-7. |
| [6] |
MICHELL A G M. The limits of economy of materials in frame structures[J]. Philosophical Magazine, 1904, 8(47): 589-597. |
| [7] |
隋允康, 彭细荣. 结构拓扑优化ICM方法的改善[J]. 力学学报, 2005, 37(2): 190-197. DOI:10.3321/j.issn:0459-1879.2005.02.010 |
| [8] |
昌俊康, 段宝岩. 连续体结构拓扑优化的一种改进变密度法及其应用[J]. 计算力学学报, 2009, 26(2): 188-192. DOI:10.7511/jslx20092007 |
| [9] |
左孔天, 陈立平, 钟毅芳, 等. 基于人工材料密度的新型拓扑优化理论和算法研究[J]. 机械工程学报, 2004, 40(12): 31-37. DOI:10.3321/j.issn:0577-6686.2004.12.007 |
| [10] |
秦洪德. 船舶结构优化设计的研究进展[A]. 中国造船工程学会船舶力学学术委员会. 2007年船舶力学学术会议暨《船舶力学》创刊十周年纪念学术会议论文集[C]. 中国造船工程学会船舶力学学术委员会, 2007: 13.
|
| [11] |
程远胜, 刘甜甜, 刘均. 船舶肘板拓扑优化设计[J/OL]. 中国舰船研究, 2015, 10(05): 53-58+70.
|
| [12] |
董海茵. 多目标模糊优化在船舶结构设计中的应用[J]. 舰船科学技术, 2017, 39(12): 6-8. DOI:10.3404/j.issn.1672-7649.2017.12.002 |
| [13] |
刘波, 林焰, 吕振望, 等. 基于量子行为遗传算法的船体局部结构优化设计[J]. 船舶力学, 2017, 21(4): 484-492. DOI:10.3969/j.issn.1007-7294.2017.04.013 |
| [14] |
邓良. 基于人工神经网络的船舶结构轻量化研究[D]. 济南: 济南大学, 2014.
|
| [15] |
翟玉文. 复合材料含筋夹层结构静动力学特性优化研究[D]. 武汉: 海军工程大学, 2013, 17-48.
|
 2019, Vol. 41
2019, Vol. 41
