船体结构建造过程中,由于焊接引起的结构变形和残余应力,不仅影响船舶外观和建造装配精度,还可能降低结构刚度、强度和稳定性等力学性能,影响结构承载能力[1 – 5]。研究焊接初始缺陷对船舶结构强度的影响,对于合理评估焊后结构承载能力,优化船舶结构设计具有理论意义[6 – 9]。
本文以典型船舶甲板板架为研究对象,基于热弹塑性有限元法[3],采用Abaqus有限元软件模拟结构焊接过程,计算具有焊接初始缺陷的甲板板架结构极限强度,并与理想状态结构进行对比,得出焊接初始缺陷对甲板板架极限强度的影响规律。
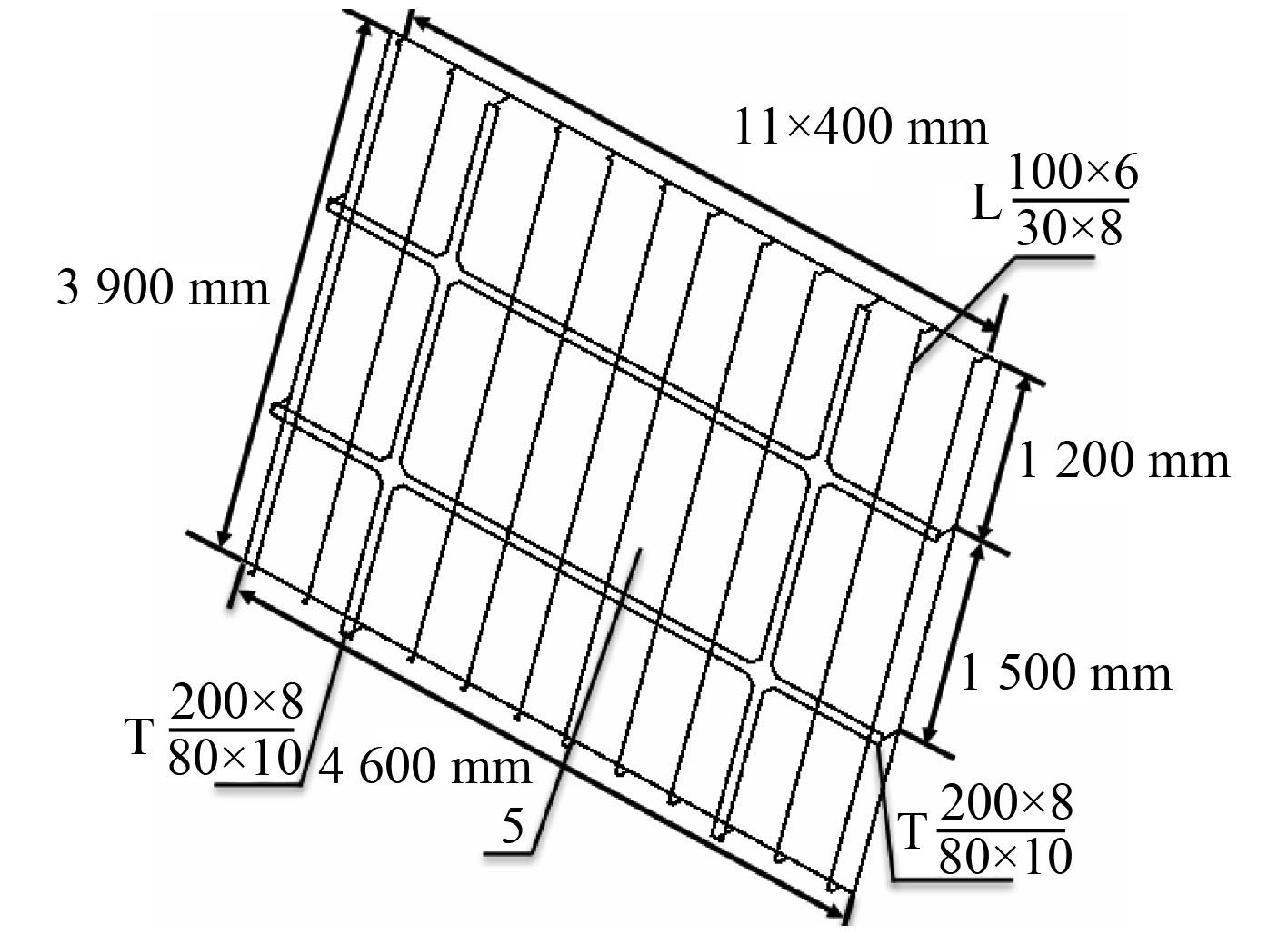
1 研究对象 1.1 甲板板架结构布置本文研究对象为某典型甲板板架,板架长4 600 mm、宽3 900 mm,沿长度方向以400 mm等间距对称布置10根纵骨、2根纵桁,沿宽度方向以1 500 mm间距布置2根横梁,纵骨采用腹板尺寸为100×6 mm、面板尺寸为30×8 mm的角钢,纵桁及横梁采用腹板尺寸为200×8 mm,面板尺寸为80×10 mm的T型钢。甲板板架布置如图1所示。
|
图 1 甲板板架结构布置 Fig. 1 Structure arrangement of deck grillage |
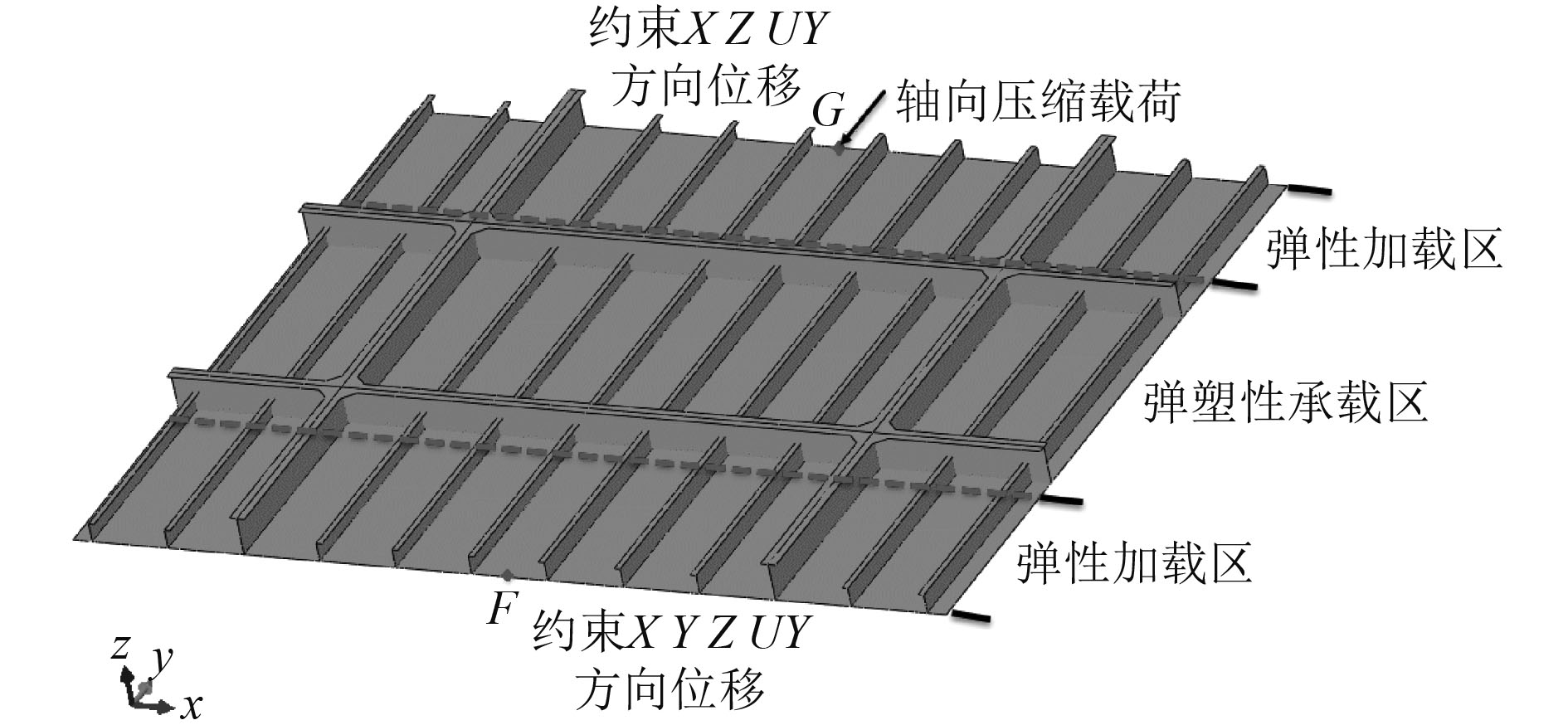
根据甲板板架结构布置形式,建立有限元模型,如图2所示。模型共包含226 329个节点,232 368个单元,单元类型为减缩积分单元S4R、板壳单元S3R。由于相邻横框架间的纵向结构为承受总纵弯曲载荷的承载结构,在有限元模型中,横梁以外结构设置为弹性加载区,横梁间结构为弹塑性承载区。计算模型整体网格大小为50×50 mm,对焊缝临近区域的网格进行细化,单元尺寸为1.5 mm×4 mm,不同尺寸网格之间进行合理过渡。
|
图 2 有限元模型 Fig. 2 FEM Model |
在模型两端对称中心的甲板板处设置主节点F,G,端面节点与相应主节点进行绑定,在进行板架极限强度计算时,主节点F设置刚体约束条件,在另一端主节点G处施加沿负Y方向位移载荷以模拟板架轴向受压过程
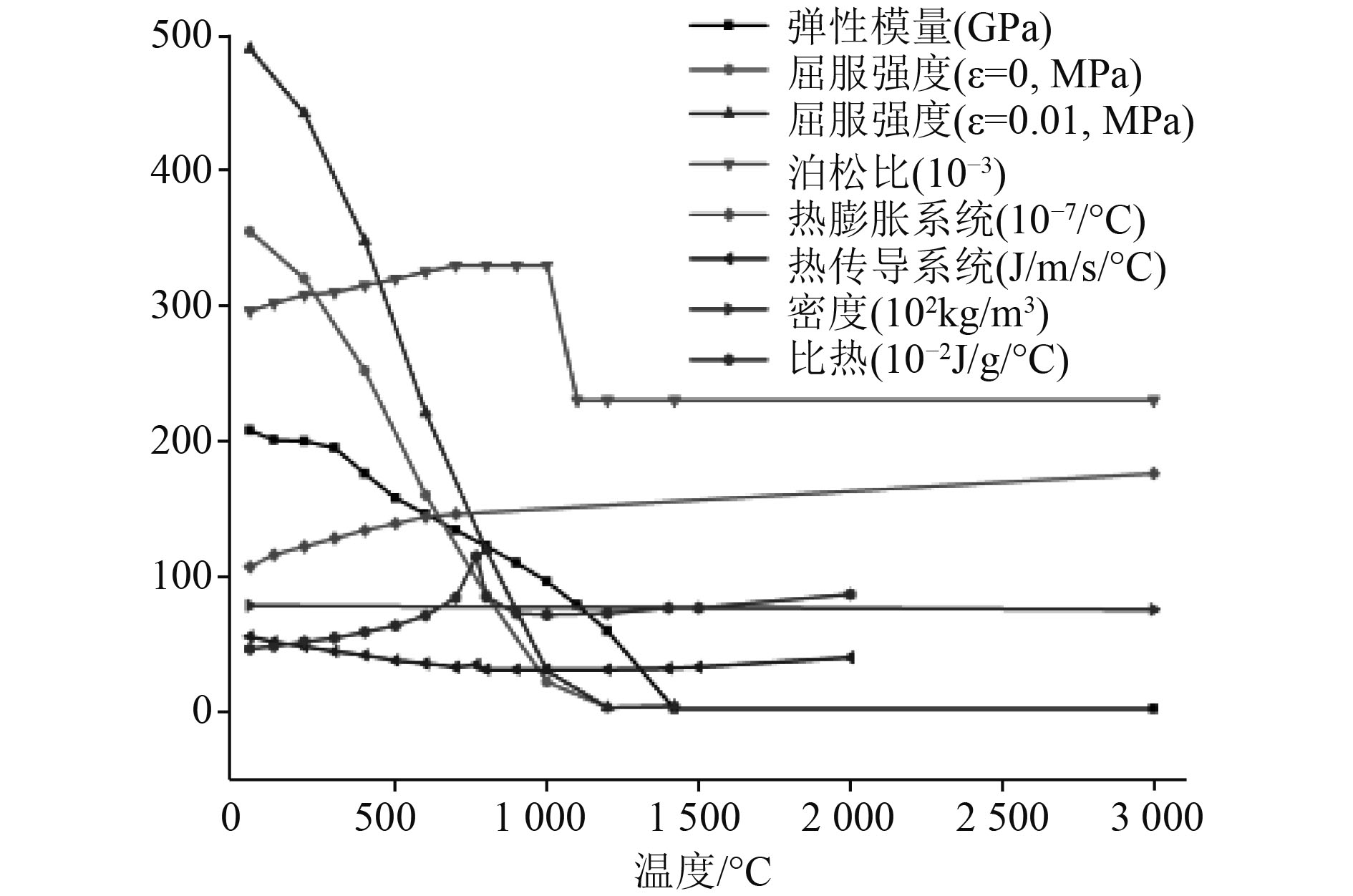
模型材料采用EH36船用高强度钢,常温下弹性模量208 GPa,屈服强度355 MPa。进行焊接数值模拟时,需考虑材料属性随温度变化情况,EH36高强度钢的弹性模型、屈服强度、泊松比、导热系数等属性随温度变化曲线如图3所示。材料为各项同性,力学性能符合线性随动强化准则及Von Mises屈服准则。
|
图 3 EH36船用高强钢材料属性图 Fig. 3 Materical property of EH36 |
本文对无焊接变形和残余应力的甲板板架极限强度进行研究,分析理想状态甲板板架的极限承载特点,为研究焊接初始缺陷对板架极限强度的影响提供基础。
2.1 极限承载能力图4为无焊接初始缺陷的理想状态板架承载曲线。如图所示,随着甲板板架压缩载荷的逐渐增大,板架结构首先进入弹性阶段(OA段),板架压缩载荷与位移之间呈线性关系,若在弹性阶段卸载,板架结构将完全恢复至初始状态;随着载荷进一步增大,板架部分构件发生屈曲,整体刚度下降(AB段),载荷位移之间呈现非线性特点;当载荷增加到一定值时,板架整体承载能力达到极值(B点),之后结构无法再继续承受更大的载荷,曲线进入卸载段,更多结构发生屈曲破坏,板架承载能力显著下降。

|
图 4 Case 0工况载荷位移曲线图 Fig. 4 Load-displacement curve of case 0 |
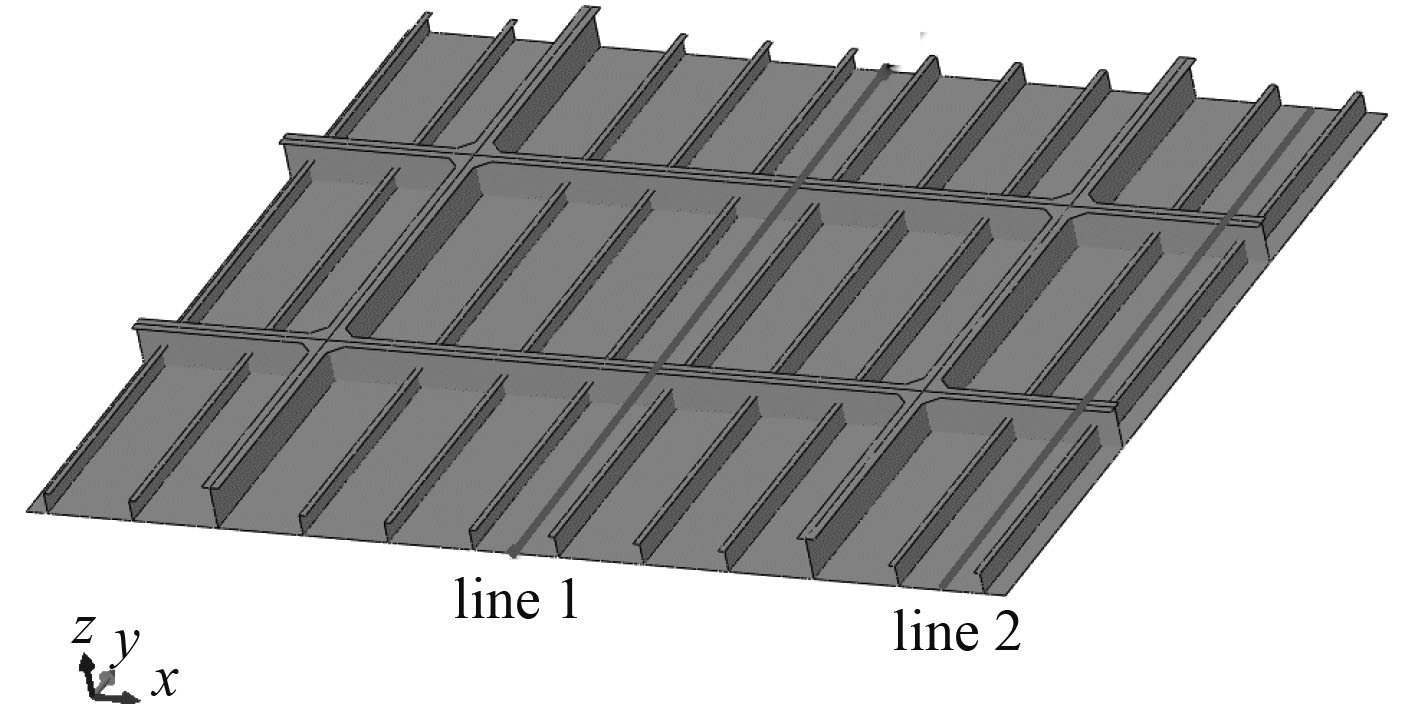
为进一步研究甲板板架各构件的失效过程,选取如图5所示典型构件截面,分析不同压缩载荷时板架各构件变形情况。其中,Line1截面为甲板板纵向中线,Line2截面为其所在板格甲板板中线。
|
图 5 截面位置示意图 Fig. 5 Location of selected sections |
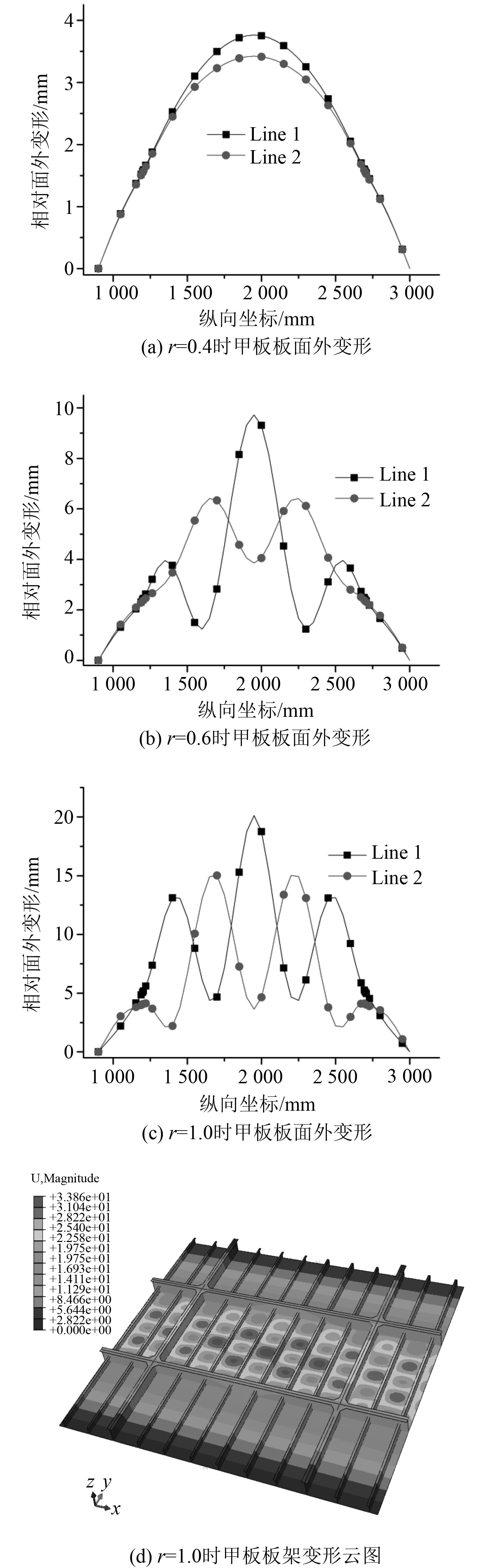
以压缩率r表示甲板板架端部压缩位移与板架承载能力极值点处对应的压缩位移的比值,不同压缩率下各典型截面的面外变形情况如图6所示。图中各曲线表示在不同压缩率下,弹塑性承载区板架截面变形与弹性加载区的差值,以体现构件变形变化情况。
|
图 6 面外变形图 Fig. 6 Out of plane deformation |
如图6(a)~图6(c)所示,当压缩率小于0.4时,2根横梁间的甲板板呈一个半波整体弯曲变形特点,中间剖面Line1处变形幅值约3.5 mm;当压缩率达到0.6时,甲板板变形半波数增加至3个,变形幅值达9 mm左右,甲板板出现局部失稳,难以继续承受更多载荷;当压缩率增大至1.0时,即达到甲板板架最大承载力时,甲板板变形半波数继续增多,板格失稳情况加剧,变形幅值达到15 mm。图6(d)为甲板板架受压时板格失稳典型云图,板格呈现多个半波弯曲变形特点。
在甲板板架受压过程中,纵桁和纵骨也逐渐发生失稳,侧向变形由1个半波变化为3个半波,变形幅值增大,失稳明显。理想状态甲板板架受轴向压缩载荷作用时,甲板板和纵向构件均发生失稳现象,使得板架整体刚度逐渐降低,直至最终失去承载能力。
3 焊接数值模拟为研究焊接变形及残余应力对甲板板架极限强度的影响,采用顺序耦合热弹塑性有限元法,对采用不同焊接顺序的板架焊接过程进行数值模拟,得到结构焊后变形及焊接残余应力。本文分别计算了3种焊接工况,Case 1为仅焊接纵向构件,Case 2为先焊接纵向构件后焊接横向构件,Case 3为先焊接横向构件后焊接纵向构件。3种工况中纵向构件焊接顺序一致,采用对称构件同时焊接、由外向内依次焊接的方式,焊接顺序及边界条件如图7所示。

|
图 7 纵向构件焊接顺序及边界条件 Fig. 7 Welding sequence of logitudinal structure and boundary conditions |
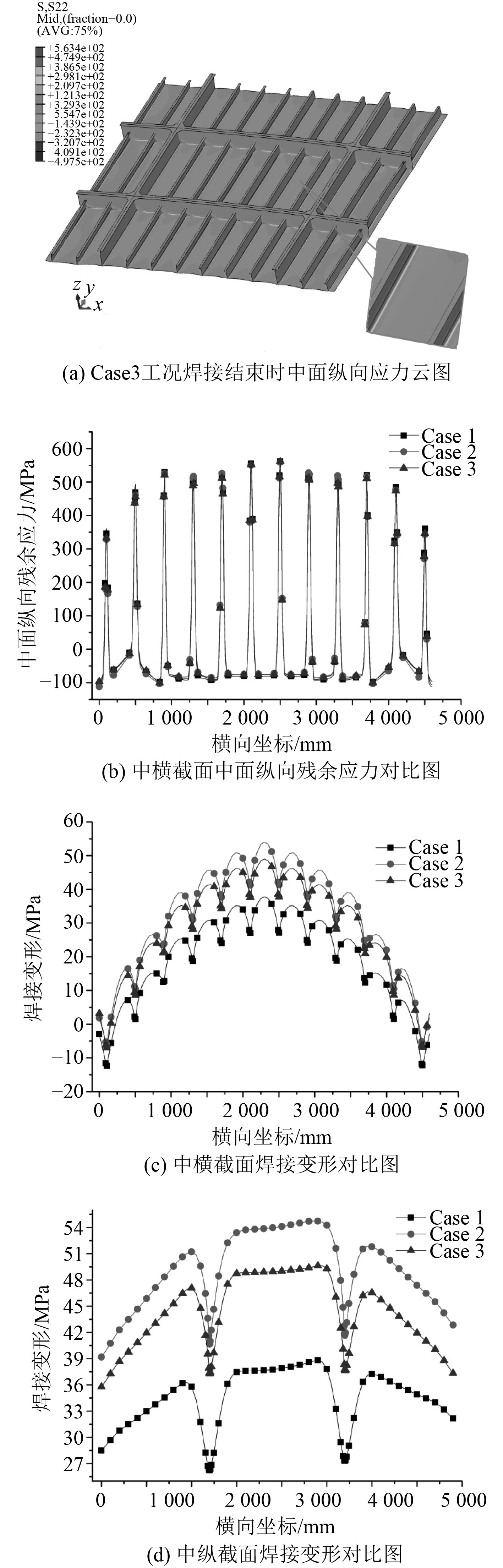
以Case 3工况为例,焊接结束时板架中面纵向残余应力云图如图8(a)所示,纵向残余拉应力集中分布于焊缝附近区域,加强筋之间的板格为压应力。3种工况焊后板架中横截面处的残余应力分布曲线如图8(b)所示,各工况的残余应力分布相近。焊后甲板板架典型横剖面和纵剖面处变形情况如图8(c)和图8(d)所示,各工况焊接变形规律一致,呈现中央区域拱起的变形特点,在变形幅值上有所差异。
|
图 8 焊接变形及中面残余应力 Fig. 8 Welding deformation and residual stress in mid-section |
在焊接数值模拟的基础上,采用非线性有限元法,对含有焊接变形和残余应力的甲板板架进行极限强度计算,分析焊接变形和残余应力对板架极限强度的影响。
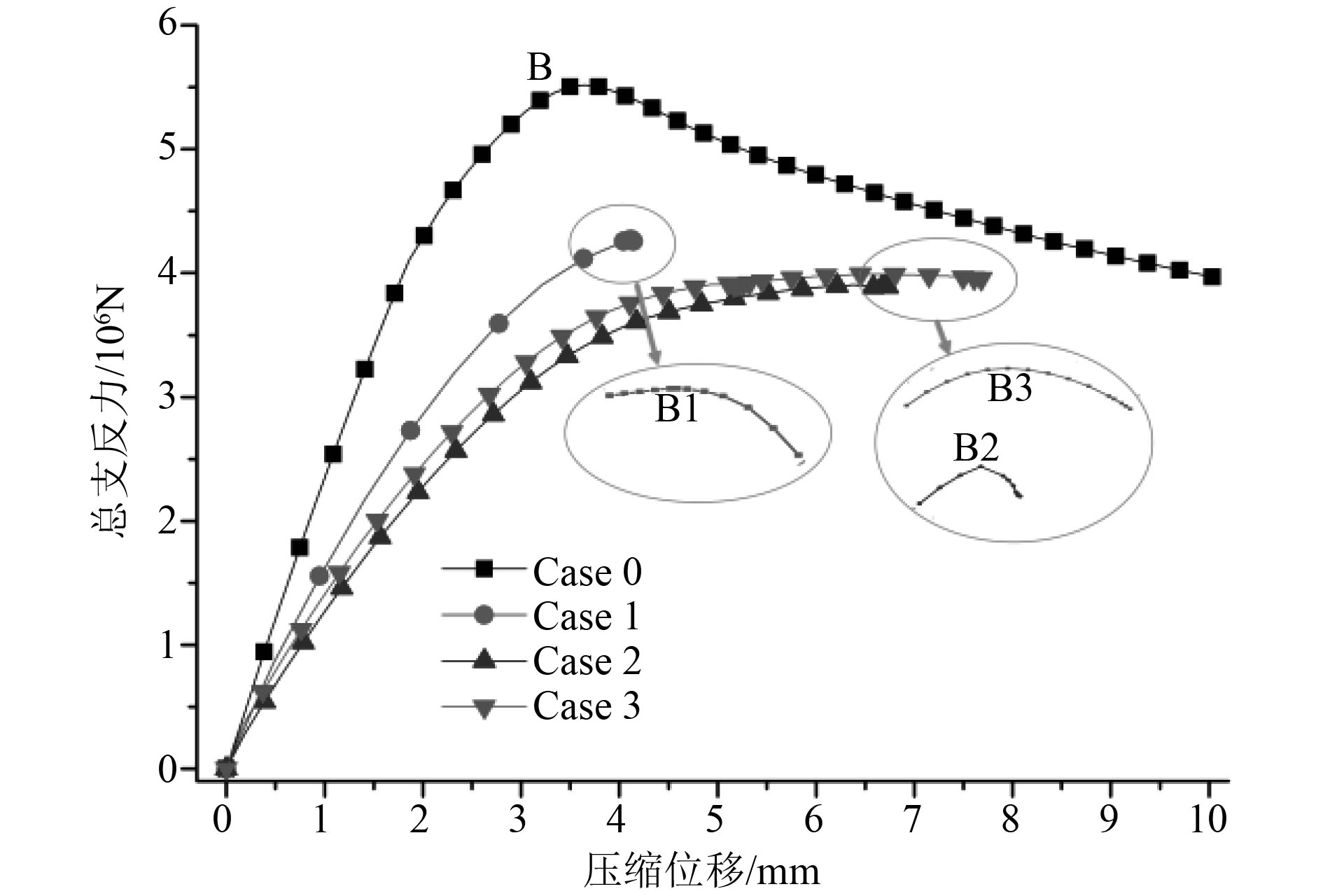
4.1 板架极限强度计算在轴向压缩载荷作用下,各焊接工况甲板板架载荷位移曲线如图9所示。由图可见,含有焊接初始缺陷的甲板板架承载曲线斜率明显低于理想状态,表明焊接变形和应力使板架结构整体刚度降低,并且具有纵横焊缝的Case 2和Case 3工况结构刚度相近,均比仅有纵向焊缝Case 1工况刚度更小。
|
图 9 载荷位移曲线图 Fig. 9 Load-displacement curve |
载荷位移曲线中的Bn点为甲板板架在轴向压缩载荷下承载能力极值点,各工况极限强度和对应的压缩位移情况列于表1。具有焊接初始缺陷时,甲板板架的极限强度较理想状态下降20%~30%,板架中焊接热输入越多,结构刚度越大,在轴向压缩载荷下的极限承载能力越低。
|
|
表 1 各工况极限强度 |
图10为板架达到极限强度时的变形情况,与理想状态相比,板架变形幅值显著增大,最大变形幅值超过50 mm,较理想状态增大约50%,过大的板格变形是导致板架整体失稳的主要因素。此外,板格主要呈现整体弯曲变形特点,几乎没有明显的半波变形形式。

|
图 10 变形云图 Fig. 10 The deformation |
为分别研究焊接变形和残余应力对甲板板架极限强度的影响,本文计算仅考虑焊接残余应力的甲板板架极限强度,并其他工况进行对比分析,得出焊接残余应力对甲板板架极限强度的影响。与Case 1~Case 3焊接工况相对应,将仅考虑焊接残余应力的计算工况分别命名为Case 1N-Case 3N。
仅考虑残余应力时各工况极限强度列于表2,此时,各计算工况的极限承载能力约为理想状态的90%,比同时考虑焊接残余应力和变形时的计算结果有明显提高,焊接变形因素较残余应力对甲板板架极限强度的影响更为明显。
|
|
表 2 仅考虑残余应力时各工况极限强度 |
板架达到极限强度时,变形情况如图11所示,仅考虑残余应力时,板架变形形式与理想状态一致,板格呈现多个半波变形的弯曲变形特点,最大变形幅值超过40 mm,较理想状态增大约20%,焊接变形因素较残余应力对甲板板架达到极限强度时变形幅值的影响更为明显。

|
图 11 变形云图 Fig. 11 The deformation |
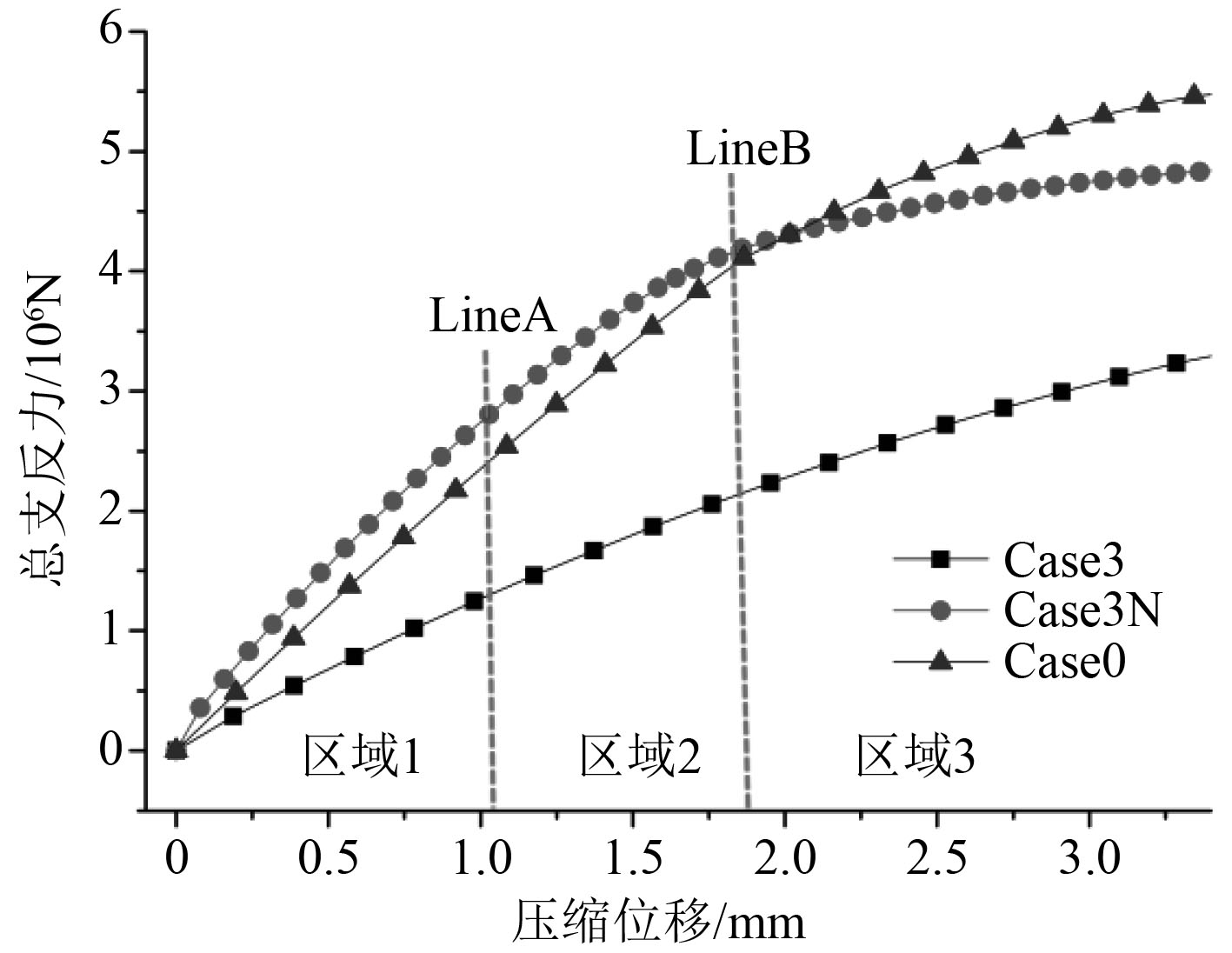
图12为Case 0,Case 3,Case 3N工况的载荷位移曲线对比图。当压缩位移小于1.02 mm时,如区域1所示,根据曲线斜率,Case 3N工况下板架刚度最大,Case 3工况下板架刚度最小;随着压缩位移增大,如区域2所示,Case 3N工况下板架刚度减小,小于理想状态,但仍大于Case 3工况;压缩位移超过1.8 mm时,如区域3所示,Case 3N工况板架刚度最小,Case 3工况次之,理想状态下板架刚度最大。以上现象表明,焊接残余应力使结构初始刚度增大。随压缩位移的增大,板格区域出现弯曲变形,集中分布于该区域的残余压应力进一步削弱了板格区域的刚度,导致结构整体刚度迅速下降、板格区域变形幅值增大。
|
图 12 载荷位移曲线图 Fig. 12 Load-displacement curve |
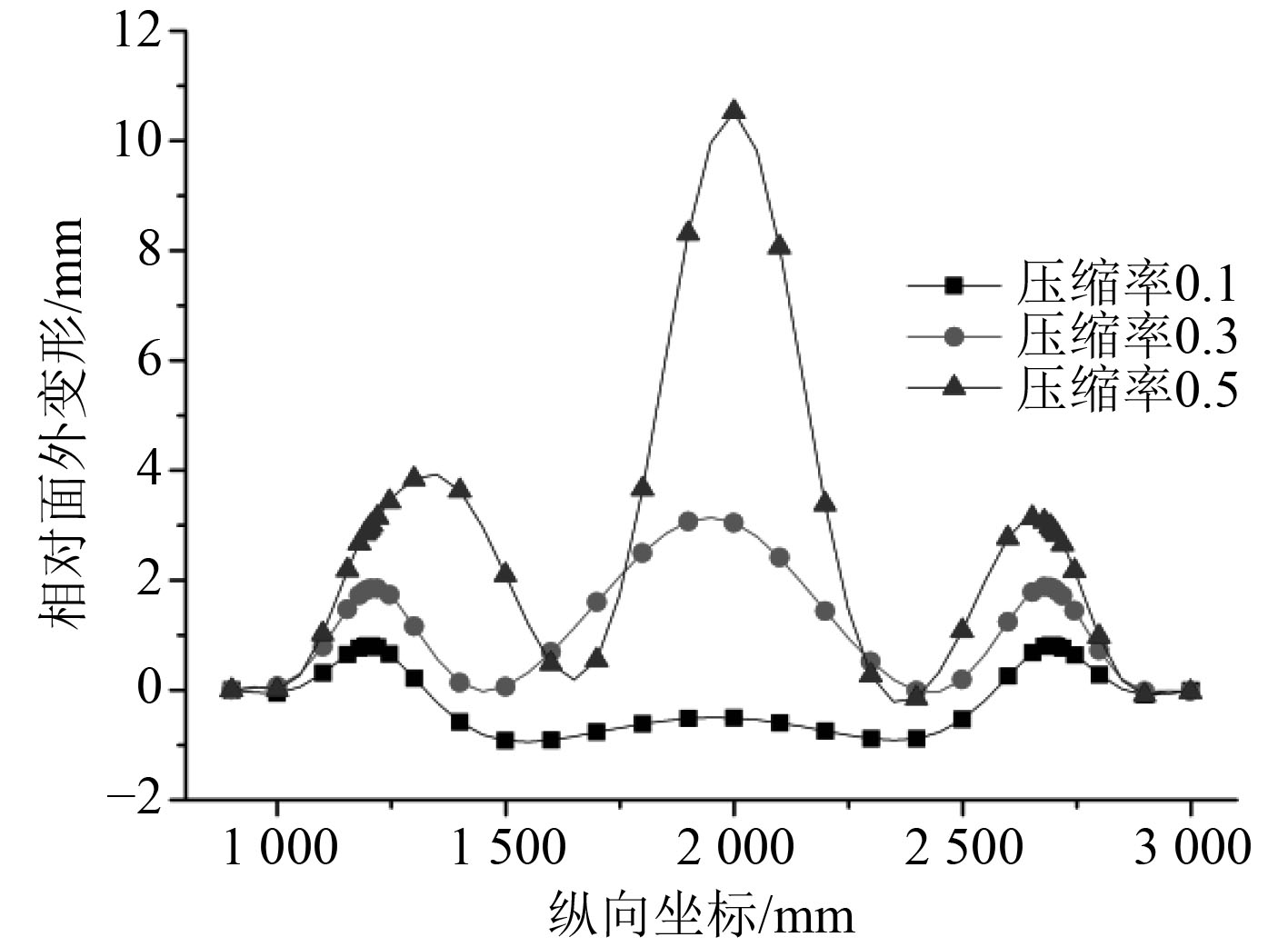
进一步研究焊接残余应力对甲板板架刚度和失效过程的影响,根据图12中Case 3N工况斜率的变化过程,分析分别对应区域1~区域3的压缩率为0.1,0.3,0.5时,Case 3N工况Line1截面面外变形情况,如图13所示。
|
图 13 Case 3N面外变形图 Fig. 13 Out of plane deformation of case 3n |
不考虑变形因素,仅考虑残余应力的影响时,板格变形形式与理想状态类似。然而,在压缩率为0.1的压缩初始阶段,不同于理想状态,此时板格面外变形方向为Z轴负向,压缩载荷进一步增大,由于加强筋及板格区域残余应力的影响(板格上表面存在残余拉应力,下表面存在残余压应力),板格变形方向发生反转,转变为Z轴正向。此外,由于中面残余压应力的影响,板格承受轴向压缩载荷能力下降,板格变形幅值大于理想状态,且随压缩载荷的增大,板格变形不断加大,直至结构失去承载能力。
5 结 语本文针对典型甲板板架,研究焊接初始缺陷对板架极限强度的影响,得出如下结论:
1)在轴向压缩载荷下,该甲板板架结构首先发生板格及纵向加强构件的局部失稳,随压缩载荷增大,构件变形幅值增大、失稳区域扩大,导致板架整体承载能力下降。
2)焊接缺陷使构件较早地出现局部失稳,进而导致甲板板架承载能力下降,显著降低板架极限强度,焊接变形因素较残余应力对甲板板架极限强度的影响更为明显。焊接热输入越多,焊接变形越大,板架承载能力越低。
3)焊接变形显著削弱板架结构刚度,同时改变板格区域变形形式;焊接残余应力使板架结构初始刚度增大,对板格区域变形形式影响较小,但会增大板架在极限强度点处变形幅值。
| [1] |
DENG D, ZHOU Y, BI T, et al. Experimental and numerical investigations of welding distortion induced by CO2 gas arc welding in thin-plate bead-on joints[J]. Materials & Design, 2013, 52(24): 720-729. |
| [2] |
李功荣, 陈震. 船底板架焊接胎架约束力分布规律分析[J]. 船海工程, 2017, 46(2): 34-37. DOI:10.3963/j.issn.1671-7953.2017.02.008 |
| [3] |
沈济超, 陈震, 罗宇. 船舶T型接头分段移动热源焊接模拟[J]. 中国造船, 2014(4): 66-73. DOI:10.3969/j.issn.1000-4882.2014.04.008 |
| [4] |
DENG D. FEM prediction of welding residual stress and distortion in carbon steel considering phase transformation effects[J]. Materials & Design, 2009, 30(2): 359-366. |
| [5] |
KNOEDEL P, GKATZOGIANNIS S, UMMENHOFER T. Practical aspects of welding residual stress simulation[J]. Journal of Constructional Steel Research, 2017, 132: 83-96. DOI:10.1016/j.jcsr.2017.01.010 |
| [6] |
赵南, 顾学康. 船体结构极限强度研究综述[J]. 舰船科学技术, 2015, 37(11): 1-7. DOI:10.3404/j.issn.1672-7649.2015.11.001 |
| [7] |
ZHEN CHEN, ZHECHAO CHEN, R. Ajit SHENOI. Influence of welding sequence on welding deformation and residual stress of a stiffened plate structure[J]. Ocean Engineering, 2015, 106: 271-280. DOI:10.1016/j.oceaneng.2015.07.013 |
| [8] |
胡杰, 刘昆, 杜训柏, 等. U型激光焊接夹层板极限强度试验研究[J]. 舰船科学技术, 2016, 38(12): 53-58. |
| [9] |
GANNON L, Yi LIU, PEGG N, et al. Effect of welding-induced residual stress and distortion on ship hull girder ultimate strength[J]. Marine Structures, 2012, 28(1): 25-49. DOI:10.1016/j.marstruc.2012.03.004 |
 2019, Vol. 41
2019, Vol. 41

