由于复杂的几何特性,船用螺旋桨在工作状态下,其周围流场为三维粘性强旋流。目前,通常通过螺旋桨敞水试验获得螺旋桨水动力性能,该方法可靠性强,但周期长,效率低,成本高[1]。传统螺旋桨经典理论,如升力线理论、升力面和面元法均建立在流体无粘假设基础上,与螺旋桨周围实际流动不相符[2]。随着计算机辅助软件的快速发展与流体力学数值模拟的进一步研究,计算流体力学(CFD)技术逐渐广泛应用于螺旋桨水动力性能预报中。基于CFD的数值模拟,投入低,效率高[3]。
近年来,国内外有众多学者开展了采用RANS方程数值求解螺旋桨敞水性能的研究,如何提高螺旋桨CFD数值模拟精度成为国际研究热点。一般而言,影响数值模拟精度主要因素有2个:一是计算域的网格划分,二是湍流模型的选择[1]。黄胜等通过比较k-ε湍流模型、k-ω湍流模型、RSM湍流模型计算结果与试验结果,认为RSM模型对于螺旋桨水动力性能计算精度更高[1-4]。叶剑平等采用k-ω湍流模型模拟,进速系数J=0.5~1.1范围水动力相关系数误差在2%左右[5]。Judyta Felicjancik,Nobuaki Sakamoto,Anirban Bhattacharyya,OBWOGI Enock Omweri,Sungwook Lee等均采用k-ω湍流模型做数值模拟,获得不同程度水动力性能精度[6-10]。由于现有湍流模型均采用不同假设和近似,因此,目前没有一种湍流模型适用于所有流体相关问题的计算和模拟。
本文选取某支线集装箱船大侧斜螺旋桨为研究对象,选取Realizable k-ε湍流模型、SST k-ω湍流模型、RSM湍流模型分别对进速系数J=0.1~0.9范围的9个速度点进行CFD数值模拟,计算得到螺旋桨推力系数、扭矩系数和效率,并与敞水试验结果比较,分析不同湍流模型在不同进速系数区间数值模拟结果的特点及适用性,为提高螺旋桨敞水性能CFD数值模拟精度提供参考。
1 理论基础任何流动问题必须满足质量守恒定律,即单位时间内流体微团中质量的增加,等于同一时间间隔内,流入该微团的净质量。因此,质量守恒方程(连续性方程)表达为:
| $ \frac{{\partial \rho }}{{\partial t}} + \nabla \cdot \left( {\rho \mathop v\limits^ \rightharpoonup}\right) = 0\text{。} $ | (1) |
式中:ρ为水密度;t为时间;
不可压缩牛顿流体动量方程(以下简称N-S方程):
| $ \frac{{{\rm d}\mathop v\limits^ \rightharpoonup }}{{{\rm d}t}} = \mathop f\limits^ \rightharpoonup - \frac{1}{\rho }\nabla p + \nu {\nabla ^2}\mathop v\limits^ \rightharpoonup \text{。} $ | (2) |
式中:
忽略质量力,湍流瞬时速度应用N-S方程(以下简称RANS)为:
| $ \frac{{\overline {\partial {u_i}} }}{{\partial t}} + \frac{{\overline {\partial \left( {{u_i}{u_j}} \right)} }}{{\partial {x_j}}} = - \frac{1}{\rho }\frac{{\overline {\partial p} }}{{\partial {x_i}}} + \nu \overline {{\nabla ^2}{u_i}} \text{。} $ | (3) |
整理后,RANS方程为:
| $ \rho \left[ {\frac{{\overline {\partial {u_i}} }}{{\partial t}} + \frac{{\overline {\partial \left( {{u_i}{u_j}} \right)} }}{{\partial {x_j}}}} \right] = - \frac{{\overline {\partial p} }}{{\partial {x_i}}} + \mu {\nabla ^2}{u_i} + \frac{{\partial \left( { - \rho \overline {{u_i}'{u_j}'} } \right)}}{{\partial {x_j}}}\text{。} $ | (4) |
式中:
RANS方程是目前求解三维湍流问题最常用方程,连续性方程与RANS方程构成了流体动力学计算的基本控制方程。Realizable k-ε湍流模型、SST k-ω湍流模型及RSM湍流模型具体公式详见参考文献[3]和参考文献[11]。
2 计算模型 2.1 主尺度某集装箱船大侧斜螺旋桨几何尺度如表1所示。
|
|
表 1 几何尺度表 |
通过三维转换公式[12],将螺旋桨桨叶二维线型转换为空间三维曲线,导入CATIA软件,建立螺旋桨三维模型,其几何模型如图1所示。

|
图 1 螺旋桨几何模型 |
采用旋转参考坐标系法(MRF)[9],将螺旋桨计算域划分为螺旋桨旋转域与计算静域,旋转域即螺旋桨旋转时带动的周界流体区域,静域为除去旋转域,剩余的计算域部分。
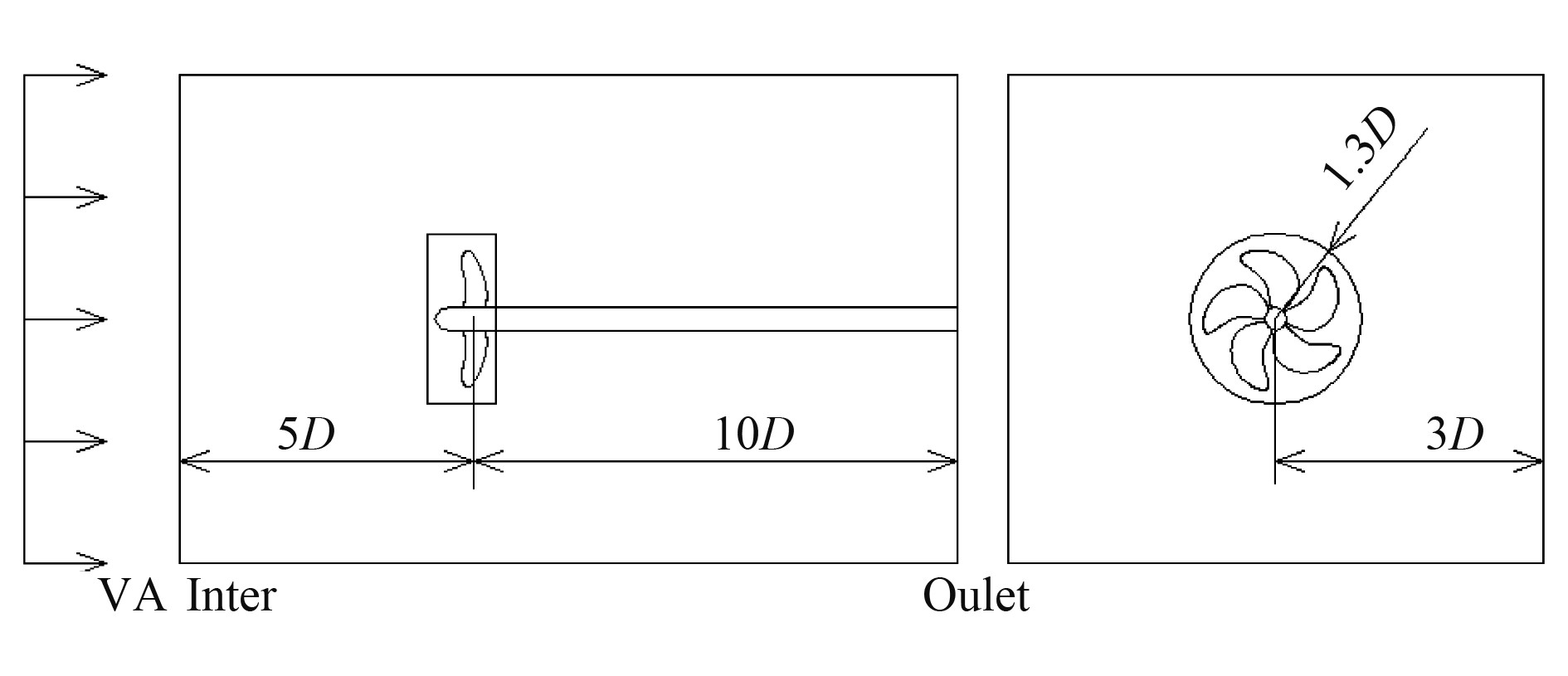
螺旋桨计算域纵向如图2所示。速度进口处距离螺旋桨原点5D,出口距离螺旋桨原点10D,各周界距离螺旋桨原点3D。螺旋桨旋转域直径为1.3D。
|
图 2 计算域范围 |
计算域网格基本网格尺寸取为8 mm,螺旋桨桨叶边界细化网格设置为5%基本网格,桨叶面细化网格25%基本网格,远场进口、出口、周界网格设置为1 500倍基本网格。螺旋桨叶面网格如图3所示,螺旋桨周界面网格如图4所示。静域网格数约为153.5万,旋转域网格数约为54.6万,总网格数约为208.1万。

|
图 3 螺旋桨桨叶细化网格 |

|
图 4 螺旋桨周界网格 |
湍流模型分别选取Realizable k-ε模型,SST k-ω模型及RSM模型进行计算与对比分析。
采用旋转参考坐标系法(MRF),保持螺旋桨不动,旋转坐标以转速18.5 r/min旋转,计算域进口速度随不同进速系数计算点设置为VA=J·n·D。计算域进口、出口、周界边界条件分别为速度进口、压力出口、对称平面。
3 水动力性能计算与分析 3.1 计算结果与分析计算不同湍流模型下,进速系数J在0.1~0.9范围,步长0.1的9个进速点螺旋桨推力系数KT、扭矩系数KQ及效率η0,不同进度系数下,螺旋桨敞水性能结果与计算误差分别如表1~表3所示。
|
|
表 2 Realizable k-ε湍流模型计算结果 |
|
|
表 3 SST k-ω湍流模型计算结果 |
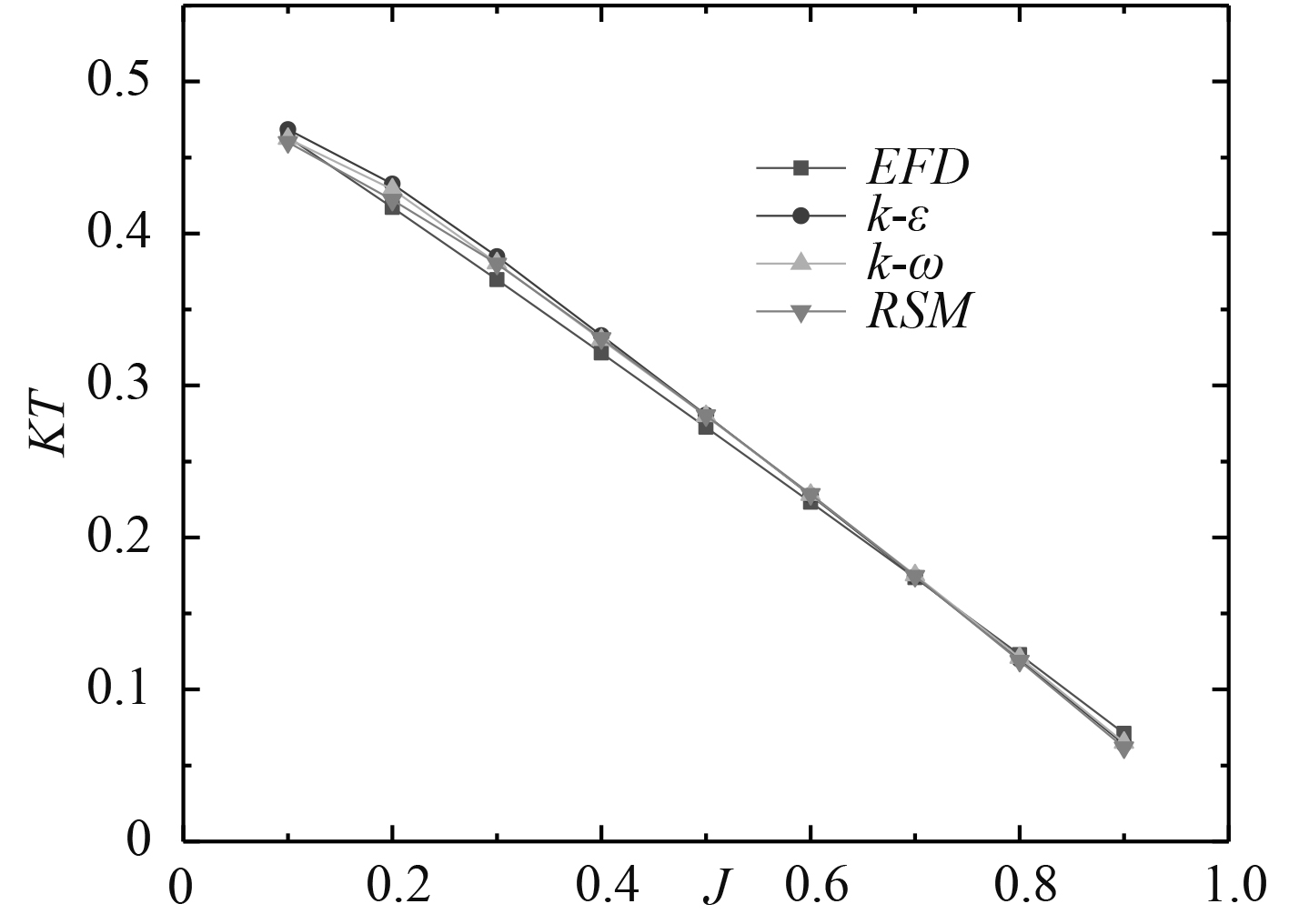
螺旋桨推力系数、扭矩系数及效率在不同湍流模型计算结果对比如图5~图7所示,图中EFD表示螺旋桨敞水试验值。
|
图 5 不同湍流模型推力系数KT计算结果 |
|
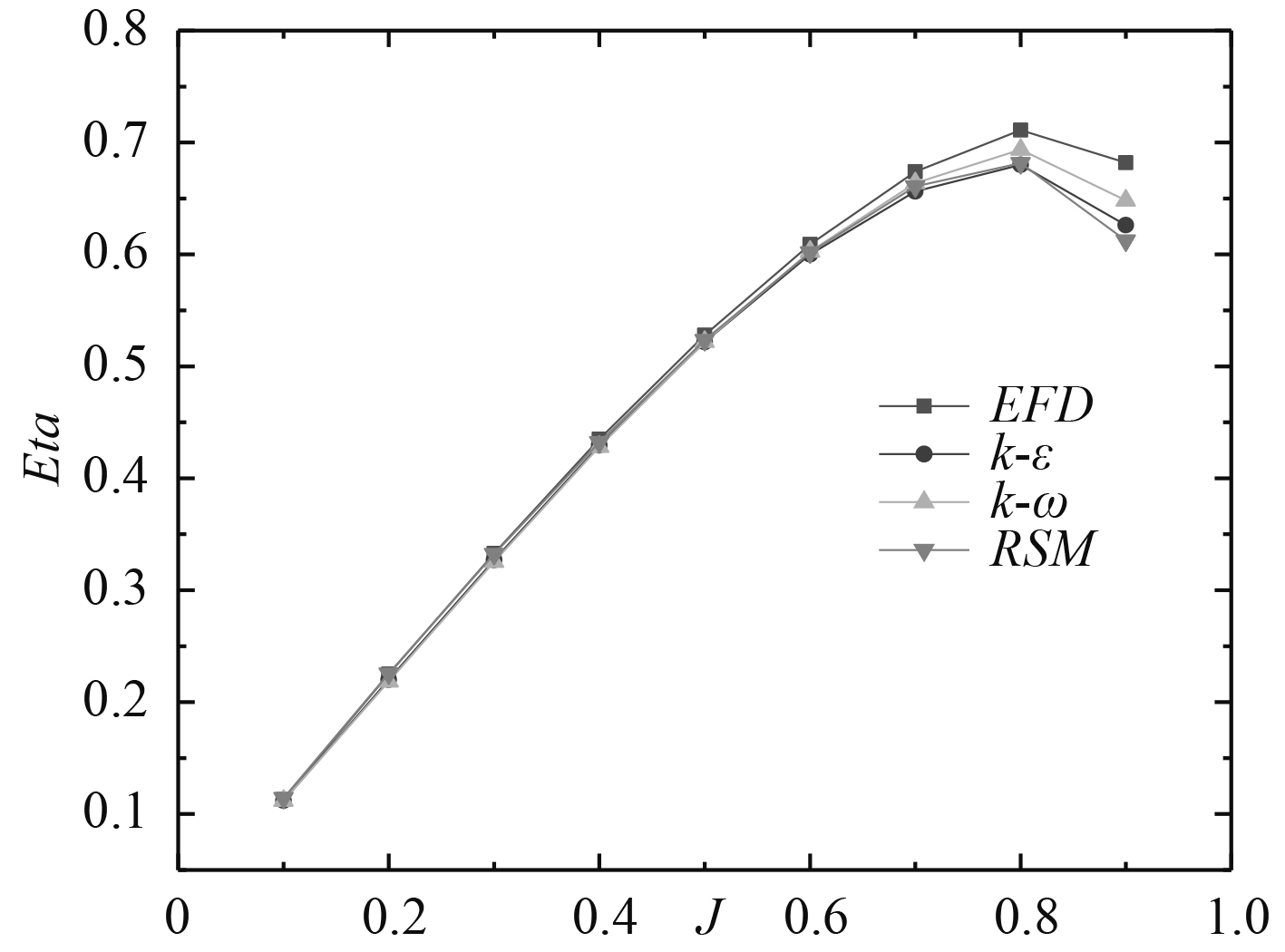
图 7 不同湍流模型效率η0计算结果 |
|
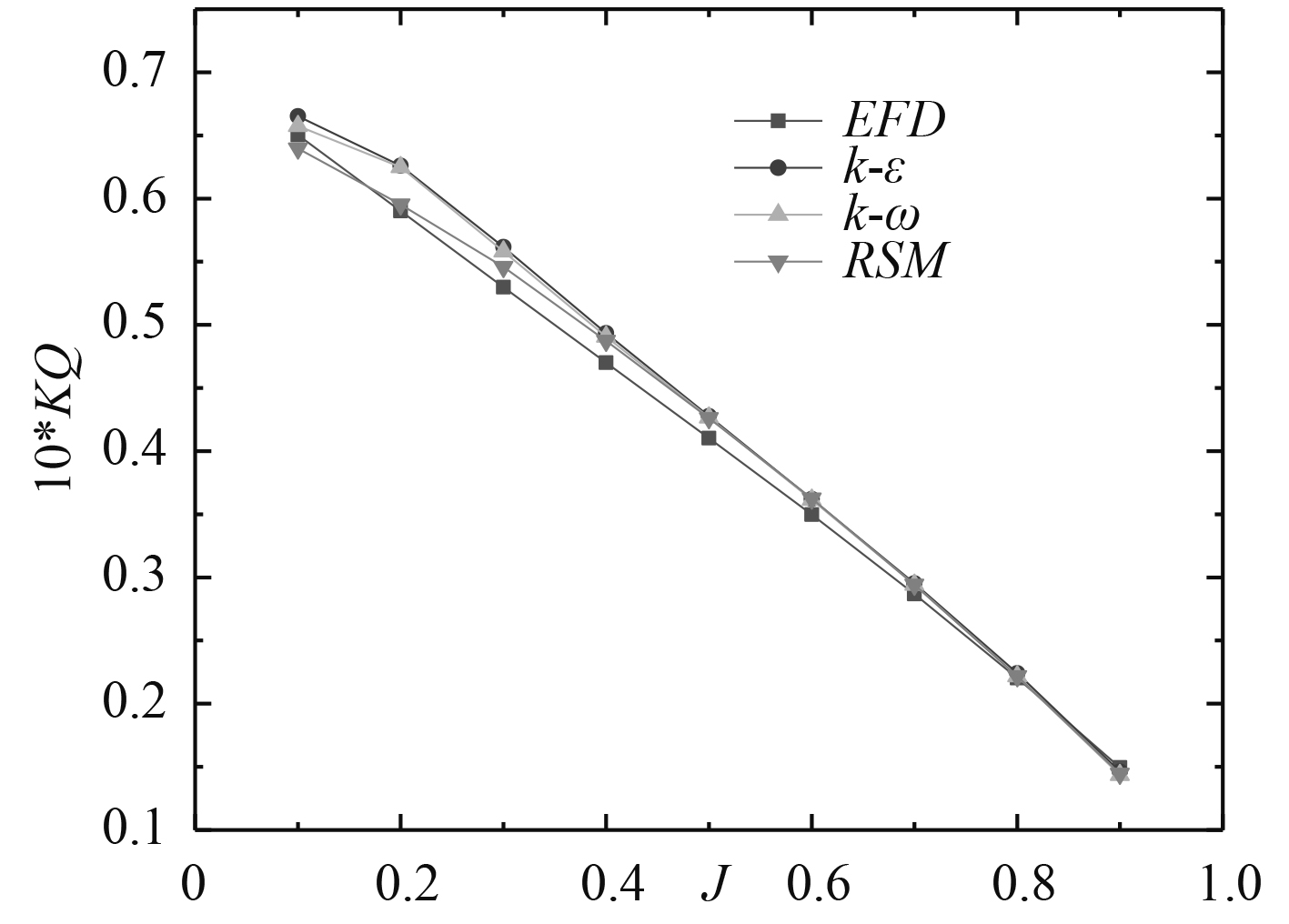
图 6 不同湍流模型推力系数10*KQ计算结果 |
由表2~表4,图5~图7可知,在进速系数0.1~0.9范围,3种湍流模型对螺旋桨推力系数、扭矩系数及效率计算结果的变化趋势均与敞水试验结果变化相同,且均在进速系数0.5~0.8范围及0.1处表现了较优的数值模拟结果,在进速系数0.9处计算结果均失真。本文螺旋桨在实船运营状态下的进速系数在0.6~0.7之间,3种湍流模型在服务进速系数点附近均有误差较优的计算结果,推力系数误差范围为0.323%~2.348%,扭矩系数误差范围2.564%~3.622%,效率误差范围–1.046%~–2.623%,即3种湍流模型的数值模拟结果均对船舶自航点处主机转速有精度较高的预报。
|
|
表 4 RSM湍流模型计算结果 |
比较Realizable k-ε与SST k-ω湍流模型,易发现2种模型在对螺旋桨推力系数、扭矩系数和效率计算结果上基本变化趋势相同,均在进速系数为0.1和0.5~0.8范围的预报结果最优,在0.2~0.4范围预报结果次之,在0.9处失真。但在0.2~0.4范围,SST k-ω模型计算精度略优于Realizable k-ε模型。2种模型相同的变化趋势,主要源于2种湍流模型均以涡粘模型假设为基础,均在湍流粘度μι的计算中引入了旋转和曲率相关项[11]。
由表4可得到,RSM模型在整个进度系数范围(0.1~0.8)在各计算工况的推力系数、扭矩系数和效率与试验值的误差变化均匀,平均误差在1.07%,2.08%,–0.94%,有很优的误差精度。比较Realizablek-ε,SST k-ω与RSM湍流模型,在整个进速系数范围,RSM湍流模型相对前两者,均有略优的数值模拟结果,尤其在0.2~0.4的低进速系数范围,因此RSM模型更适用于低进速系数范围数值模拟。以上现象主要由于,Realizable k-ε,SST k-ω湍流模型均采用涡粘模型假设且假定粘性系数μι各向同性,未考虑各向应力随几何及强旋运动引起的变化,而RSM模型放弃涡粘模型假设,直接对各向Reynolds应力输运方程进行求解,因此在局部进速系数范围计算结果表现更优。但是,由于RSM模型引入了6个Reynolds应力,相对原来的6个方程,增加了6个输运方程,求解方程达到12个,计算效率远低于Realizable k-ε、SST k-ω模型。另工程可接受误差为5%,Realizable k-ε、SST k-ω仅在0.2,0.3范围略超出,考虑几何模型调整及网格优化可改善计算误差等因素,可使计算结果落在5%以内,且2种模型在服务进速系数点附近数值模拟结果均较理想。因此,综合考虑以上各因素,Realizable k-ε与SST k-ω模型也适用于螺旋桨敞水性能预报。目前,学者也多采用SST k-ω模型计算螺旋桨水动力性能,文献[6~10]采用该计算模型均取得较优结果。
4 结 语通过比较3种不同湍流模型数值结果与敞水试验结果,得到如下结论:
1)Realizable k-ε与SST k-ω湍流模型对螺旋桨水动力性能数值模拟有相似的误差变化趋势,SST k-ω湍流模型误差结果表现略优。相较其他2种湍流模型,RSM湍流模型在低进速区间0.2~0.4范围计算更有优势,计算精度更高;
2)3种湍流模型均在进速系数点0.1,0.5~0.7计算结果相近,误差较优。在服务进速系数点0.6~0.7之间计算结果误差相近,均能较好地预报实桨工作转速;
3)RSM湍流模型在整个进速系数范围数值模拟结果相较其他2种湍流模型整体表现更优,适用于螺旋桨水动力性能计算。但RSM湍流模型计算效率低,且综合考虑在工作进速点范围计算结果精度及其他如几何模型等对计算误差的影响,Realizable k-ε与SST k-ω湍流模型同样适用于螺旋桨敞水性能数值模拟。
| [1] |
高富东, 潘存云, 蔡汶珊, 等. 基于CFD的螺旋桨敞水性能数值分析与验证[J]. 机械工程学报, 2010, 46(8): 133-139. |
| [2] |
黄胜, 王超, 王诗洋. 不同湍流模型在螺旋桨水动力性能计算中的应用与比较[J]. 哈尔滨工程大学学报, 2009, 30(5): 481-485. DOI:10.3969/j.issn.1006-7043.2009.05.002 |
| [3] |
吴建威, 尹崇宏, 万德成. 基于三种方法的螺旋桨敞水性能数值预报[J]. 水动力学研究与进展A辑, 2016, 31(2): 177-187. |
| [4] |
郑小龙, 黄胜, 王超. 基于CFD的螺旋桨定常水动力性能预报精度研究[J]. 舰船科学技术, 2014, 36(12): 11-15. DOI:10.3404/j.issn.1672-7649.2014.12.003 |
| [5] |
叶剑平, 庄光宇. 螺旋桨水动力性能计算粘性流体CFD方法的应用与研究[J]. 舰船科学技术, 2013, 35(4): 29-34. DOI:10.3404/j.issn.1672-7649.2013.04.007 |
| [6] |
JUDYTA F, SEBASTIAN K. Numberical simulation of hydrodynamic open-water characteristics of a ship propeller[J]. Polish Maritime Research, 2016(4): 16-22. |
| [7] |
NOBUAKI S, KENICHI K. Numerical towing tank procedure for JBC in self-propulsion with rotating propeller and energy saving duct[J]. 日本船舶海洋工学会论文集, 2016. |
| [8] |
ANIRBAN B, JAN C N. Influence of flow transition on open and ducted propeller characteristics[J]. Fourth International Symposium on Marine Propulsors, 2015. |
| [9] |
OBWOGI E O, AMISI J O. Performance prediction of marine propeller using steady and unsteady flow approaches[J]. Proceedings of the Sustainable Research and Innovation Conference, 2017, 126-133. |
| [10] |
SUNGWOOK L, KWANG-JUN P. URANS Simulation of a partially submerged propeller operating under the bollard condition[J]. Shipbuilding, 2018, 1(69): 107-121. |
| [11] |
王福军. 计算流体动力学分析-CFD软件原理与应用[ M]. 北京: 清华大学出版社, 2004: 113-142.
|
| [12] |
JOHN C. Marine propellersand propulsion, Carlton, [M]. Oxford: ElsevierLtd, 2007: 33-39.
|
 2019, Vol. 41
2019, Vol. 41
