0 引　言

天然气运输有许多种方式，运输船运输是其中一种。LNG（Liquefied Natural Gas，液化天然气）运输船是国际公认的“三高”产品^{[1 – 2]}。液化天然气是可燃气体，具有挥发性和易燃性，一旦在运输中发生意外，10万立方米的天然气完全燃烧会产生80万大卡，将造成巨大破坏。关于舱内爆炸的课题，国内外一般采用试验和数值分析的方法进行研究，主要分析爆炸荷载的传播规律和对舱体结构的损伤作用，以及对舱体节点结构的强度分析，主要包括峰值应力和撕裂长度^{[3 – 5]}。本文采用数值分析的方法，分析爆炸荷载作用下不同连接方式箱型船体的节点结构强度特征。

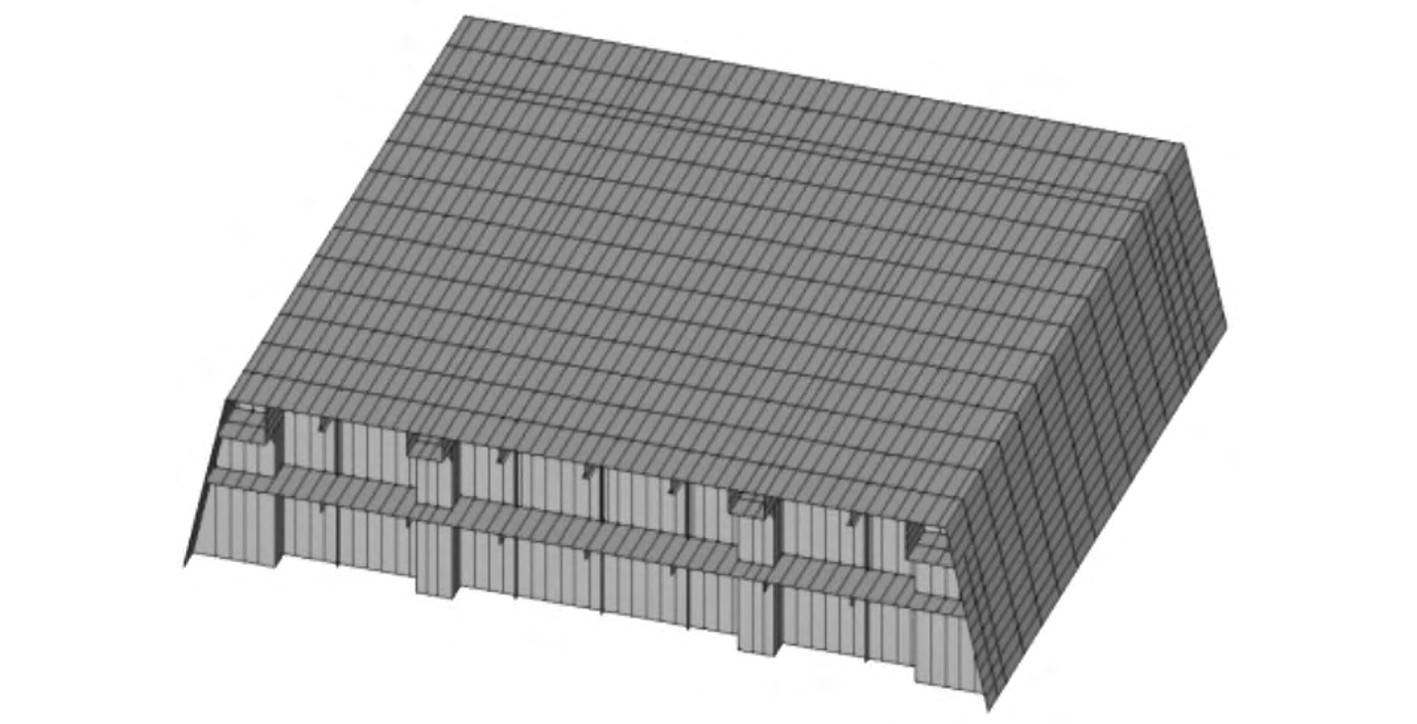
1 节点结构强度计算模型

本文以LNG运输船体的01甲板与1甲板间的舱体为研究对象，采用数值分析的方法，分析了舱体在爆炸荷载作用下中间箱型梁节点结构和舷侧箱型梁节点结构的强度特性。如图1所示，数值分析模型总尺寸为17 m×21.3 m×2.7 m，整个模型包含了舱体全部结构和筏与筏之间的舱体，这样选择是为了减少边界作用。在甲板和舱壁的水平和垂直方向分布有加强筋，梁布置在甲板上。

1.1 有限元模型及网格划分

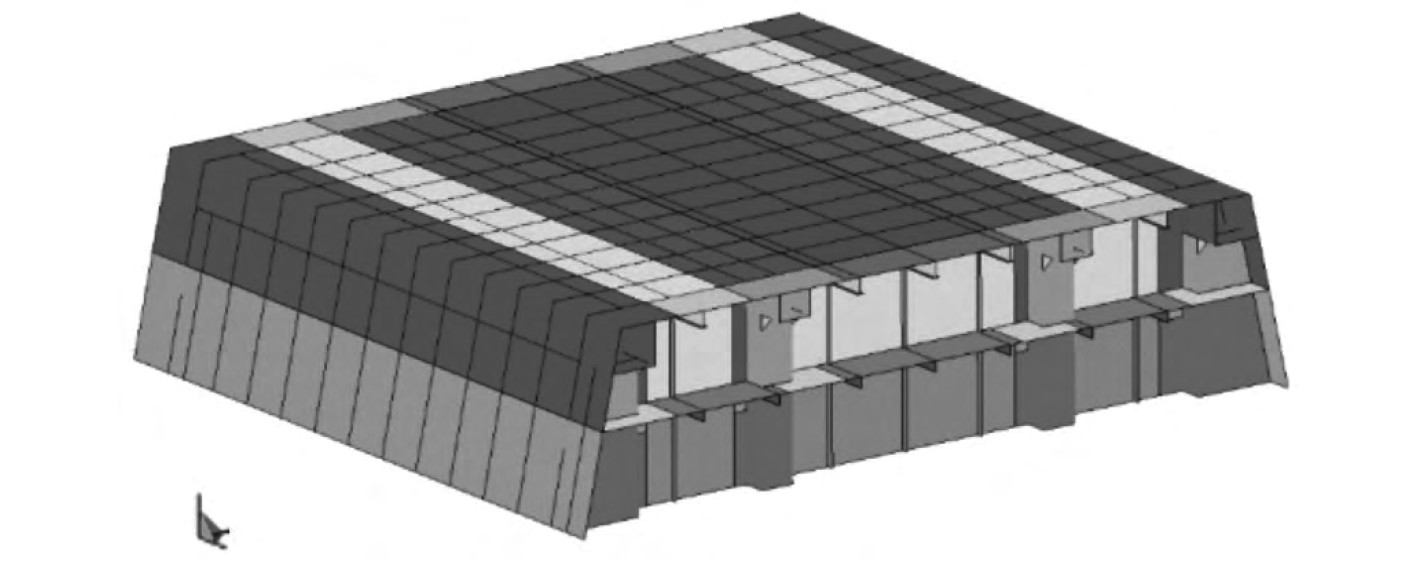
有限元模型为结构-空气-炸药组合模型，如图2所示。对模型进行网格划分，模型的甲板、舱壁、梁均采用4节点壳体单元，模型的纵骨和T型面板采用3DBeam 161单元，空气和炸药均采用164实体单元。为了使爆炸荷载作用均匀，炸药布置在模型的中心位置。所有网格尺寸一致，大小为100 mm，划分的单元网格总数约3.5×10⁵个。在计算过程中，为了考虑结构的大变形效应，计算模型的流域设置为23 m×25 m ×7.7 m，流域的网格大小均为150 mm，网格数量约5.5×10⁶个。

1.2 材料模型

船体均采用钢板，在建立有限元模型时，钢材的屈服强度模型采用*MAT_Johnson_Cook模型，采用该模型的优点在于它考虑了应变强化和温度软化效应，能够合理地描述钢材的物理力学性能，材料的屈服应力 ${{\rm{\sigma }}_{{y}}}$ 按照下式计算：

${{\rm{\sigma }}_{{y}}} = \left( {A + B_p^n} \right)\left[ {1 + {\rm{cln}}\left( {\frac{{{\varepsilon _p}}}{{{\varepsilon _0}}}} \right)} \right]\left[ {1 - {{\left( {T*} \right)}^{\rm{m}}}} \right]\text{，}$

(1)

$T* = \frac{{T - {T_T}}}{{{T_M} - {T_T}}}\text{。}$

(2)

式中参数均为Johnson-Cook材料参数。A为材料屈服应力；n为材料的硬变硬化系数；B为材料的硬化系数；m为温度系数；c为应变率系数； ${\varepsilon _0}$ 为归一化应变率因子； ${\varepsilon _{\rm{p}}}$ 为塑性应变率； $p$ 为塑性应变；T为材料的瞬时温度；T_m为材料的熔点开氏温度；T_T为室内开氏温度。本文的失效应变为0.2，采用等效应变失效准则来模拟结构的损坏和节点结构强度的变化，本文的Johnson-Cook材料参数的取值如表1所示。

采用*EOS_LINEAR_POLYNOMIAL状态方程对*MAT_Johnson_Cook模型中的*MAT_NULL材料进行表述，模型内部的压力P可以用初始内能密度E₀和模型的相对体积 $V$ 进行表述，其关系式见式（3）和式（4），它们的关系是一个多项式关系。

$P = {C_0} + {C_1}\mu + {C_2}{\mu ^2} + {C_3}{\mu ^3} + \left( {{C_4} + {C_5}\mu + {C_6}{\mu ^2}} \right){E_0}\text{，}$

(3)

$\mu = \frac{{{V_0}}}{V} - 1\text{。}$

(4)

式中：C₀～C₆都为多项式常数； $\mu $ 为模型的体积比系数。空气的密度为1.225 kg/m³，作为理想气体处理，从而不考虑高压和高温对模拟结果的影响，于是上述参数C₀～C₆的取值为C₀=C₁=C₂=C₃=C₆=0，C₄=C₅=0.4，于是式（3）和式（4）变为：

$P = \frac{{0.4{V_0}}}{V}{E_0}\text{。}$

(5)

在正常的大气压下，气体的初始内能密度E₀=253.3×10³ J/m³，初始体积V₀=1。炸药的参数设置为：1 630 kg/m³，爆炸速度为6 930 m/s，爆炸产生的气体压力为21 GPa。将*EOS_JWL状态方程和*MAT_HIGH_EXPLOSIVE_BURN材料模型结合起来表述炸药爆炸过程，产生的爆炸压力同式（3）和式（4）一样，采用内能密度E的函数和相对体积V表述，其关系式如下式：

$P = {A_1}\left( {1 - \frac{\omega }{{{R_1}V}}} \right){e^{ - {R_1}V}} + {B_{^1}}\left( {1 - \frac{\omega }{{{R_2}V}}} \right){e^{ - {R_2}V}} + \frac{{\omega E}}{V}$

(6)

式中：A₁，B₁，R₁，R₂和 $\omega $ 均为描述炸药爆炸性能的相关参数，其取值如表2所示。

1.3 边界条件与载荷定义

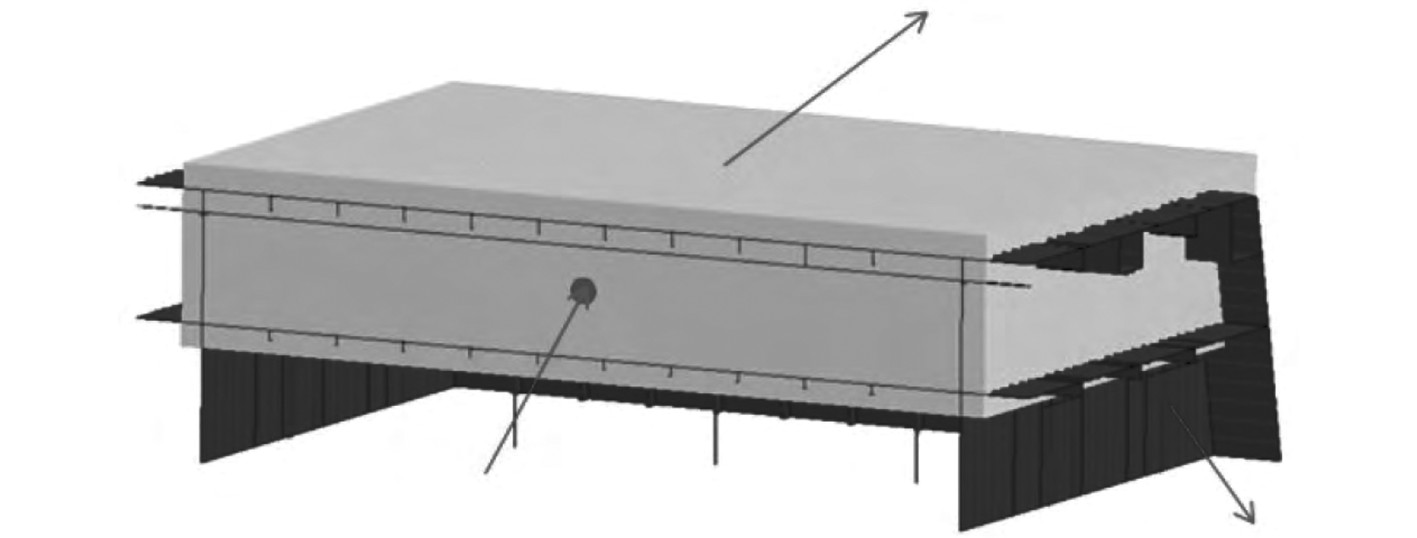
在模型长度方向上设置简单的边界条件，在模型的宽度方向上设置简单的支撑，同时考虑支撑柱的位移边界条件。流域模型的每个表面设置成无反射的边界。炸药包设置在模型额的中心位置，采用体积初始化的方法对炸药进行填充。同时，采用拉格朗日方法对爆炸物和空气进行描述分析，实现对舱体表面板和主要部件（梁、柱等）以及爆炸物、空气的组合。采用罚函数算法进行计算分析，耦合刚度为2，模型的相对位置如图3所示。

2 节点结构强度计算结果 2.1 舷侧箱型梁与强衡梁连接点结构

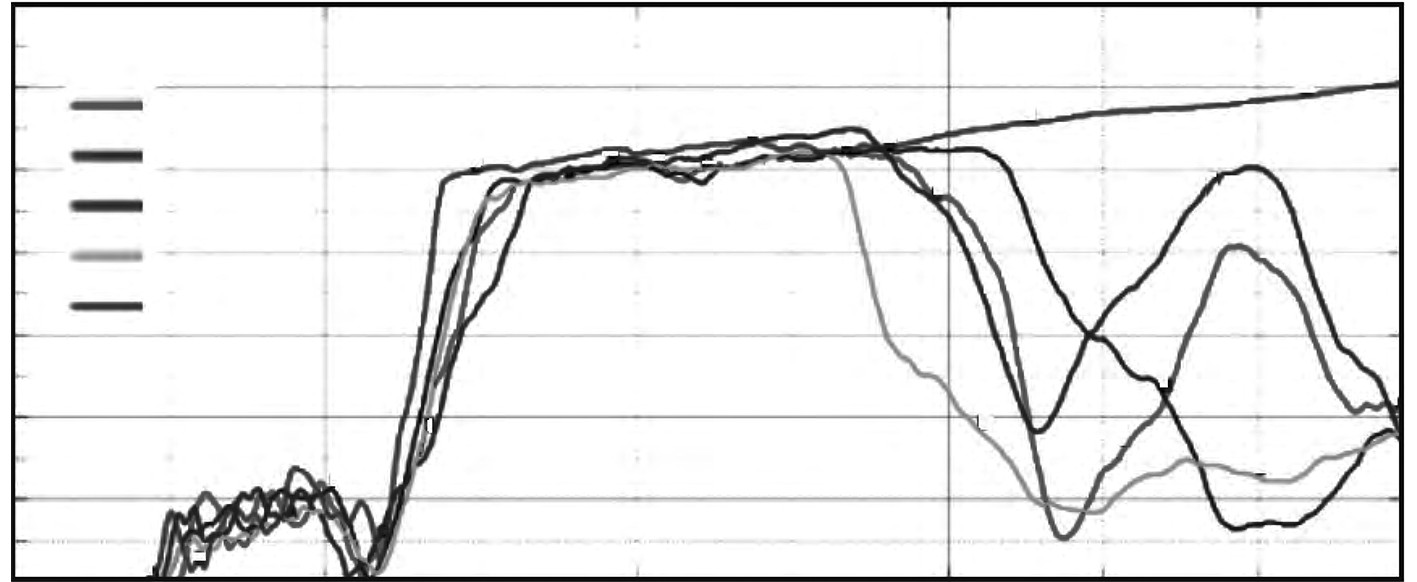
如图4所示，模型的特征点曲线，在舱内爆炸载荷作用下，应力其中出现在舱体拐角的位置，如圆弧板根部和箱形梁水平分隔壁开口边缘，应力峰值为600 MPa。如图5所示，节点结构的典型位置处的应力时程曲线，当冲击波从爆炸点传递到拐角时，应力在t = 5 ms时增加到最大值并持续一段时间，这是因为初始冲击波与上甲板和下甲板以及侧外板相互作用形成反射冲击波，反射波叠加在传播到船侧的初始冲击波上，收敛到侧面的侧角，使舷侧箱型梁节点的峰值压力持续。

2.2 中间箱型梁与强横梁连接点结构

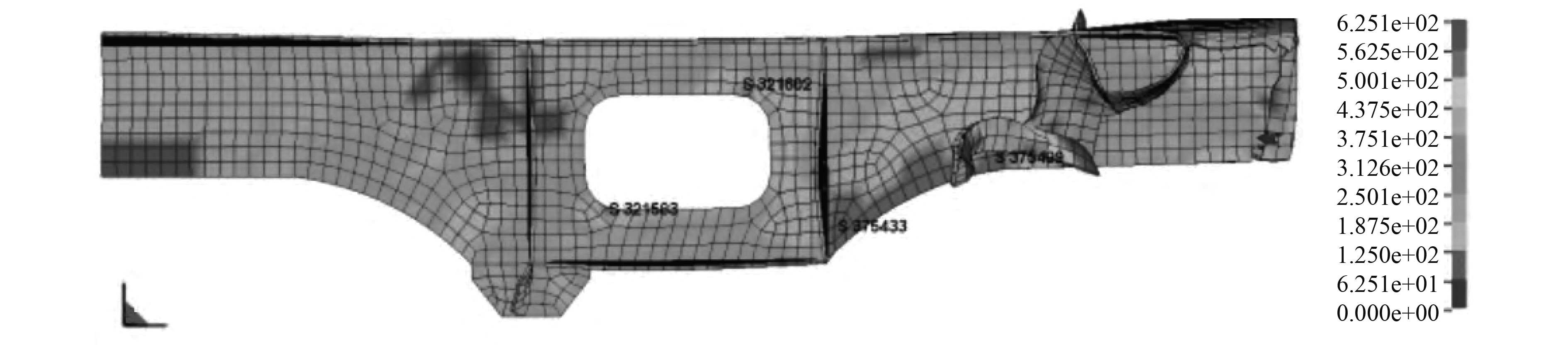
分析了中间箱梁与横梁连接节点的强度特性，计算了节点的特征点曲线和应力时程曲线。如图6所示，模型的特征点曲线，弧形连接接头结构的整体应力分布相对均匀，在强梁和箱梁之间的连接处仅发生一定的应力集中，最大值约为535 MPa，并且由于材料变形，应力集中没有达到材料的极限。如图7所示，模型的应力时程曲线，可以看出，机舱中心的空白区域表明船舶中箱梁接头的应力峰值具有较长的持续时间和更均匀的分布。

2.3 不同节点结构型式对比分析

表3和表4为不同舱体连接方式下的上和下甲板和横向舱壁的损伤的大小的关节结构的各个应力峰值的撕裂长度。具体连接方式为圆弧连接、单侧肘板连接和双侧肘板连接。

在中间箱形梁与横梁连接的节点分析过程中，圆弧连接和单侧肘板连接这2种连接方式的最大应力基本相同，分别535 MPa和550 MPa，双侧肘板连接的应力最大为625 MPa；单侧肘板连接要比圆弧连接和双侧肘板连接的破口面积要大一些。在舷侧箱梁和横梁结构节点分析过程中，圆弧式和单侧肘板这2种连接方式的破口面积和峰值应力基本相同。综上所述，圆弧连接要比单侧肘板连接要合理些，相同爆炸荷载作用下，舱体的损坏要小一些。

3 结　语

本文利用Ansys/Ls - dyna显式动力有限元软件构建了LNG船体结构的有限元模型，数值计算分析了舱体结构的动力响应强度。分析了3种连接方式下的中间箱型梁节点结构和舷侧箱型梁节点结构2种节点的应力变化规律和破坏情况。研究结果表明，2种节点结构的圆弧连接和单侧肘板连接这2种连接方式的最大应力基本相同，中间箱型梁节点结构的双侧肘板连接的峰值应力最大。相同爆炸荷载作用下，圆弧连接要比单侧肘板连接要合理些，舱体的损坏要小一些。