2. 海装装备技术合作中心,北京 100841
2. Naval Equipment Department Equipment Technology Cooperation Center, Beijing 100841, China
舰船装备可靠性近年来受到广泛关注,由于舰船装备体量庞大,设备关联程度密切,且其系统部件通常存在动态失效特征,传统的建模方式无法准确表征舰船系统的故障关联关系。动态故障树分析作为动态系统可靠性分析的重要方法,在众多领域得到广泛应用[1 – 5]。而且在舰船设计中,许多系统设备的故障状态、故障现象等存在大量的模糊不确定性。针对动态系统可靠性分析中的不确定问题,基于模糊理论的模糊动态故障树分析方法作为一种有效方法取得了一定成果[6 – 7],然而该方法需要获取大量系统部件故障数据以及其隶属度函数。在一些舰船新研系统设备中,其部件相关故障信息难以获取,且缺乏历史数据信息,通常只能依托于专家的主观判断。而且专家在对设备可靠性水平判断中,更倾向于采用高和低这样的模糊语言。文献[8 – 10]对模糊语言进行了深入研究,提供了模糊语言与模糊数之间的转化方法。为缓解模糊语言等定性评价对系统设备可靠性定量评估的困扰,本文提出一种基于专家综合评估的模糊动态故障树分析方法。该方法将专家语言信息转化为定量数据信息,并对众多专家的不同意见进行了综合,进而对系统可靠性定量评估。
1 基本概念 1.1 动态故障树分析(DFTA)随着舰船系统复杂程度的增加,系统部件通常存在动态失效特征。为解决系统的动态行为建模问题,在传统的故障树分析基础上引入动态逻辑门而构成动态故障树的方法被提出。这些动态逻辑门包括优先与门(PAND)、顺序相关门(SEQ)、功能相关门(FDEP)以及备份门(SPARE)。系统失效由部件基本事件状态以及它们的相互关系决定,这个相互关系源于系统的拓扑学。动态故障树分析依赖于与门、或门、k/n门等静态逻辑门和优先与门、顺序相关门、备份门、功能相关门等动态逻辑门。
1.2 顺序二元决策图(SBDD)二元决策图是一种布尔运算图的表现,在函数逐层展开过程中对各变量进行0或者1的赋值,直到函数的终值。二元决策图的运算基于香农分解法则,系统的故障树自下而上转化为系统的二元决策图[11]。
传统的二元决策图只适用于静态故障树,而无法处理顺序相关等动态行为。在动态故障树中,动态逻辑门输入事件的失效顺序关系对系统失效具有重大影响,因此本文采用→表示部件失效的顺序关系。例如,在温备份中,A为主件,B为备份件,A→B表示A,B均发生失效,且A先于B失效。顺序二元决策图是在二元决策图的基础上增加一些表示时序关系,其基本单元由基本事件扩展到顺序事件,弥补了传统二元决策图无法分析处理动态逻辑门的缺陷。
邢留冬等对顺序二元决策图开展了深入的研究,并成功应用工程实际[12 – 13]。
1.3 模糊数为定量刻画模糊概念和模糊现象,Zadeh[14]于1965年开创性提出模糊集合概念,其定义如下:
设给定论域U,U到[0,1]的任一映射
| $ \begin{array}{l} {\mu _{\mathop{\rm A}\nolimits} }:\;\;U \to [0,\;1]\text{,}\\ \;\;\;\;\;\;\;\;u \to {\mu _{\mathop{\rm A}\nolimits} }(u)\text{。} \end{array} $ |
所确定集合A为U上的模糊集合,
专家综合评估方法主要包括专家信息收集、专家信息模糊化、专家意见归一化以及去模糊化4个过程。
1)专家信息收集
对于系统部件失效信息严重缺乏的情形,通常选择相关专家对其进行评价。专家的选择可来自不同的领域,如设计研发、工程安装、维修保养、现场监管、系统管理等。专家根据自身的专业知识、背景以及工作经验等对系统部件的失效做出相应的判断。因此,即使对于同一系统部件,也可能表现出不同的观点和意见。对于专家信息的收集,一方面要收集专家对于系统不同部件失效信息的评价,另一方面,要收集专家的个人信息,如职业地位、工作经历、教育背景等。专家个人信息的评分用来确定专家意见之间的相对重要程度。其评分规则如表1所示。每个专家的重要度得分为职业地位、工作经历、教育背景所获得分之积。
|
|
表 1 专家重要度评分规则 Tab.1 Scoring rules of expert importance |
在征求专家对于每个基本事件失效信息的意见时,可通过语言变量来衡量专家判断的等级。语言变量对于失效定义太复杂或无法用常规定量数据进行表达的情况十分有用。本文选择7个语言变量作为专家对于基本事件失效信息的判断。基本事件的失效率可定义为7个定性语言值,即非常低、低、比较低、中、比较高、高、非常高。以上定性语言值分别对应于基本事件失效率从低到高的水平。专家对于每个基本事件,采用以上7个定性语言来确定自己对于事件失效率的判断。
2)模糊化
模糊化是指将专家对于基本事件判断的定性语言变量转化为定量的模糊数及其隶属函数。根据基本事件的失效可能性,将基本事件失效判断的语言变量转变为定量的失效率,并利用归纳推理方法得到相应的隶属函数。例如,非常低的失效率可代表基本事件的失效率低于10–7 h–1,同时非常高的失效率可表示基本事件的失效率高于10–2 h–1。当然,对于不同的系统,语言变量的应用也应有所区别,如失效率为10–3 h–1对于核电站则意味着非常高的失效率而对于自行车则意味着非常低的失效率。因此,对于失效率的定量化应依据系统实际的失效数据以及相关的专业知识。此外,采用定义在[0,1]间的模糊集隶属函数来表示基本事件的失效率。横坐标表示基本事件的失效率,其中越接近于原点意味着失效率越低,纵坐标则表示基本事件失效率的隶属度。Yu和Park指出失效率的定量化是一个主观性问题。对于基本事件失效率的模糊区间以及隶属度函数的确定可根据直觉、推论、排序、神经网络、遗传算法和归纳推理等方法。通过选择合适的方法,不同的语言变量即可转变为对应的模糊集隶属函数。
3)专家意见归一化
由于每个专家在相关领域的经验、特长的差异,对于同一事件失效的判断可能存在不同的见解。为获得专家相冲突意见的一致性,不同专家语言值所对应的模糊数应综合为单一模糊数。传统的一致性聚合方法由Hsu 和 Chen提出,然而该方法必须要求专家意见所对应的模糊集合存在交集。为克服传统方法的局限性,本文提出了一种新的一致性聚合方法,其具体流程如下:
1)计算任2位专家间的认可度
假设对于某一基本事件的失效参数判断,专家
| ${S_{ij}} = S({\tilde A_i},{\tilde A_j}) = 1 - \frac{1}{4}\sum\limits_{k = 1}^4 {|{a_{ik}} - {a_{jk}}|}\text{。} $ | (1) |
显然,当
2)计算所有专家的认可矩阵M和每位专家的平均认可度
由专家两两间认可度可得所有专家的认可矩阵为
| ${ M} = \left[ {\begin{array}{*{20}{c}} {{s_{11}}}&{\;{s_{12}}}& \ldots &{{s_{1n}}} \\ {{s_{21}}}&{{s_{22}}}& \cdots &{{s_{2n}}} \\ \vdots & \vdots & \ddots & \vdots \\ {{s_{n1}}}&{{s_{n2}}}& \cdots &{{s_{nn}}} \end{array}} \right]\text{。}$ | (2) |
专家认可矩阵为对称矩阵。
每位专家的平均认可度为:
| $A({E_i}) = \frac{1}{{n - 1}}\sum\limits_{j = 1,j \ne i}^n {{S_{ij}}}\text{。} $ | (3) |
3)计算专家的相对认可度
| $ R({E_i}) = A({E_i})/\sum\limits_{i = 1}^n {A({E_i})} \text{。} $ | (4) |
4)计算专家的重要度
| $IM({E_i}) = \frac{{score(i)}}{{\sum\limits_{i = 1}^n {score(i)} }}\text{。}$ | (5) |
式中:
5)计算专家的权重系数
专家的权重系数为其重要度与相对认可度的综合,其表达式为:
| $w({E_i}) = \alpha IM({E_i}) + (1 - \alpha )R({E_i})\text{。}$ | (6) |
式中:
6)专家意见归一化结果
| ${\tilde \lambda _j} = \sum\limits_{i = 1}^n {{w_i} \cdot } {\tilde \lambda _{ij}},\;\;j = 1,2, \cdots m\text{。}$ | (7) |
式中:
4)去模糊化
去模糊化的目的是将专家意见归一化得到的模糊数变为近似的失效率。
COG是一种基于隶属函数重心的去模糊化方法,是目前使用最广泛的方法,其表达式为:
| ${{COG}} (A) = \frac{{\int_{ - \infty }^{ + \infty } {x{\mu _A}(x){\rm d}x} }}{{\int_{ - \infty }^{ + \infty } {{\mu _A}(x){\rm d}x} }}\text{。}$ | (8) |
对于三角模糊数
| ${{COG}} (A) = \frac{{\int_a^b {x \cdot \frac{{x - a}}{{b - a}}dx + \int_b^c {x \cdot \frac{{c - x}}{{c - b}}dx} } }}{{\int_a^b {\frac{{x - a}}{{b - a}}dx + \int_b^c {\frac{{c - x}}{{c - b}}dx} } }} = \frac{{a + b + c}}{3}\text{。}$ | (9) |
去模糊化后得到的近似失效率得分可通过以下经验公式转化为近似概率失效率值。
| $PV = \left\{ {\begin{array}{*{20}{c}} {\frac{1}{{{{10}^{{{(1 - CPS)}^{1/3}} \times 2.301}}}},\;\;CPS \ne 0} ;\\ {\;\;\;\;\;\;\;\;0 ,\;\;\;\;\;\;\;\;\;\;\;\;\;CPS = 0} \text{。} \end{array}} \right.$ | (10) |
式中:CPS为去模糊化值,如COG(A)等,PV为近似失效率。
3 基于专家综合评估的系统模糊动态故障树分析针对系统失效定量数据严重缺乏的情形,提出一种基于专家综合评估的系统模糊动态故障树分析方法,该方法假定各系统部件寿命分布类型为指数分布。其可靠性定量分析主要包括系统可靠性评估和系统重要度分析。
1)顶事件发生概率计算
顶事件发生概率计算是系统可靠性分析的核心,是系统能否满足可靠性定量要求的重要判据。专家综合评估的目的是将专家的主观判断转化为系统部件失效数据定量值。其顶事件发生概率计算采用顺序二元决策图模型。具体步骤为动态逻辑门的转化、二元决策图模型的建立以及顺序二元决策图的分析评估,详细内容可参考文献[12–13]。在顺序二元决策图的分析评估中,失效路径发生概率的计算依赖于专家综合评估方法得到的部件失效率近似值。
2)系统重要度分析
系统重要度分析也是系统可靠性分析的重要环节,其意义是确定各部件对系统可靠性影响的显著程度,为系统可靠性的改进提高提供一定的依据和建议。系统部件的重要度得分可采用以下公式进行计算。
| $IM(i) = {P_T}(t) - {P_{T/i}}(t)\text{。}$ | (11) |
式中:
对于部件
以某型舰船弹药控制系统为例,由于系统部件是全新的,其失效数据不够充分,难以定量描述其失效率,因此其失效信息必须依靠相关专家进行主观判断。采用本文提出的基于专家综合评估的模糊动态故障树分析对其进行可靠性分析。分析弹药控制系统结构功能,其主要失效模式如下:
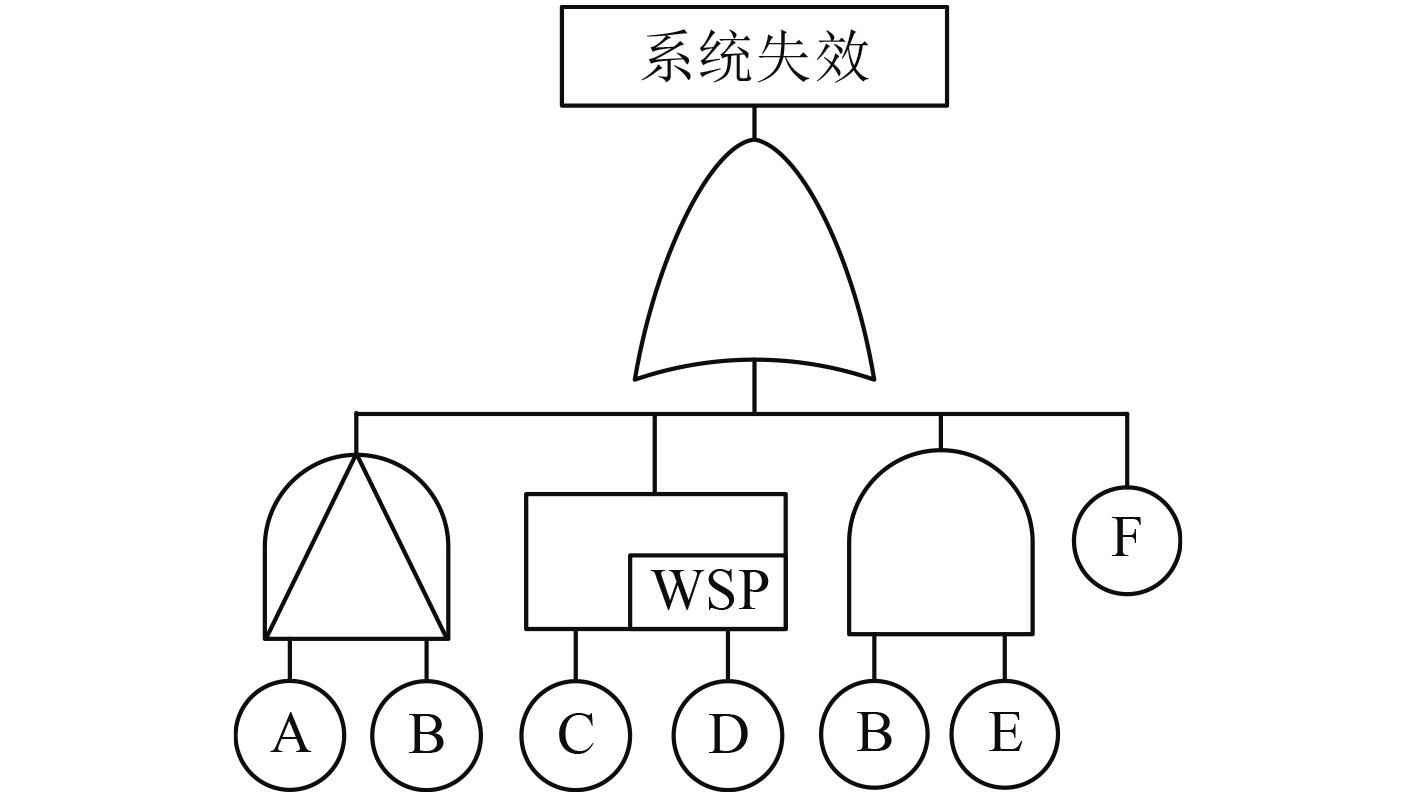
A,密封件失效;B,火工品失效;C,关键电子器件失效;D,关键备用电子器件失效;E,陀螺仪驱动装置失效;F,激光探测器失效。考虑各种失效模式之间的时间相关、功能相关,建立了弹药控制系统的动态故障树,如图1所示。
|
图 1 弹药控制系统动态故障树 Fig. 1 Dynamic fault tree of ammunition control system |
1)专家信息收集
为获取弹药控制系统的密封件、火工品、关键电子器件、关键备用电子器件、陀螺仪驱动装置以及激光探测器的失效信息,邀请5位相关专家对其进行判断。对4位专家的个人信息进行收集,参考重要度得分规则确定各位专家的重要度得分,相关数据如表2所示。
|
|
表 2 专家重要度得分 Tab.2 The scores of expert importance |
采用语言变量来描述系统部件的失效信息,将各部件失效率由低到高分成7个等级,分别为非常低、低、比较低、中、比较高、高、非常高。各专家根据各自的专业知识和经验,采用以上语言变量对弹药控制系统的密封件、火工品、关键电子器件、关键备用电子器件、陀螺仪驱动装置以及激光探测器进行主观判断,其意见如表3所示。
|
|
表 3 专家对于各部件的失效判断 Tab.3 Expert failure judgments toeach component |
2)模糊化
三角模糊数和梯形模糊数能很好处理语言变量的模糊化,因此采用三角模糊数与梯形模糊数相结合的方法来处理语言变量。对于弹药控制系统部件而言,其失效率一般不会低于10–6 h–1,也不会高于10–2 h–1。因此采用“非常低”来表示失效率低于10–6 h–1,“非常高”来表示失效率高于10–2 h–1。参考文献[8 – 10],所有语言变量对应的模糊数如表4所示。
|
|
表 4 语言变量对应模糊数 Tab.4 Fuzzy numbers corresponding to language variables |
3)专家意见归一化
以火工品为例,详细介绍专家意见归一化方法。
根据专家对火工品失效判断以及语言变量的量化方法,5位专家的意见可分别转化为模糊数(0.07,0.13,0.19),(0.35,0.50,0.65),(0.17,0.27,0.37),(0.35,0.50,0.65),(0.07,0.13,0.19)。三角模糊数可视为梯形模糊数的一种特例,即梯形模糊数隶属度为1对应的区间左右边界相等,如三角模糊数(0.07,0.13,0.19)可转化为梯形模糊数(0.07,0.13,0.13,0.19),根据式(1)专家的认可矩阵为:
| $ { M} = \left[ {\begin{array}{*{20}{c}} 1&{0.63}&{0.86}&{0.63}&1 \\ {0.63}&1&{0.77}&1&{0.63} \\ {0.86}&{0.77}&1&{0.77}&{0.86} \\ {0.63}&1&{0.77}&1&{0.63} \\ 1&{0.63}&{0.86}&{0.63}&1 \end{array}} \right]\text{。}$ |
专家重要度相比于相对认可度的松弛因子
|
|
表 5 每个专家的平均认可度、相对认可度、重要度以及权重系数 Tab.5 Average recognition,relative recognition,importance,and weight coefficient of each expert |
根据式(7),可得到专家对所有部件失效判断归一化的结果,如表6所示。
|
|
表 6 专家对部件失效判断归一化结果 Tab.6 Normalization results of expertsfailure judgement toeach component |
采用COG法进行去模糊化,根据式(9)和式(10)可得各部件去模糊化得分以及失效率,如表7所示。
|
|
表 7 部件去模糊化得分以及失效率 Tab.7 Defuzzification score and failure rate ofeachcomponent |
1)系统可靠性评估
参考文献[12–14]采用顺序二元决策图的方法对系统动态故障树进行建模分析,并利用扩展的布尔运算化简失效路径,每条路径的发生概率如下:
| $ \begin{array}{l} {P_1} = P({\rm{A}} \to {\rm{B}})\text{,}\\ {P_2} = [1 - P({\rm{A}} \to {\rm{B}})] \cdot P({\rm{C}} \to {\rm{D}})\text{,}\\ {P_3} = [1 - P({\rm{A}} \to {\rm{B}})] \cdot P({\rm{D}} \to {\rm{C}})\text{,}\\ {P_4} = [1 - P({\rm{A}} \to {\rm{B}})] \cdot [1 - P({\rm{C}} \to {\rm{D}}) - P({\rm{D}} \to {\rm{C}})] \cdot P({\rm{F}})\text{,}\\ {P_5} = \{ [1 - P({\rm{A}})] \cdot P({\rm{B}}) + P({\rm{B}} \to {\rm{A}})\} \cdot \\ \;\;\;\;\;\;\;[1 - P({\rm{C}} \to {\rm{D}}) - P({\rm{D}} \to {\rm{C}})] \cdot [1 - P({\rm{F}})] \cdot P({\rm{E}})\text{。} \end{array} $ |
因此,顶事件的发生概率为:
| $ {P_T} = {P_1} + {P_2} + {P_3} + {P_4} + {P_5}\text{。} $ |
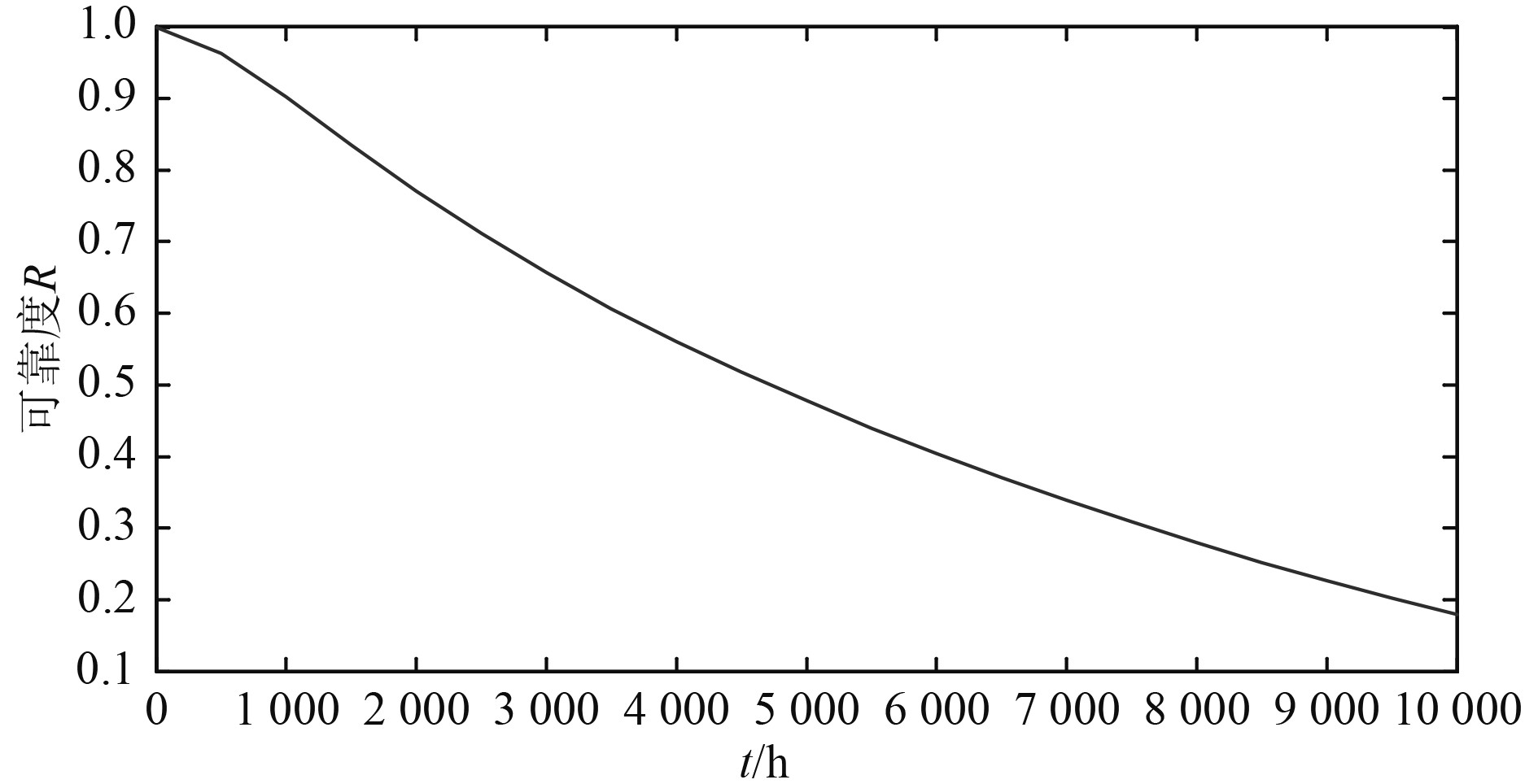
将表数据代入可得到系统可靠性随时间变化曲线,如图2所示。
|
图 2 系统可靠性随时间变化曲线 Fig. 2 System reliability curve with time |
2)系统重要度分析
假定任务时间t=2000 h,采用式(11)的重要度分析方法,得到系统部件的重要度及其排名,结果如表8所示。
|
|
表 8 部件重要度及其排名 Tab.8 Importance andranking of Components |
可知,火工品是对系统可靠性影响最显著的部件,同时陀螺仪驱动装置以及密封件也对系统有较大的影响,因此,若要提高系统可靠性,应首先针对火工品开展改进措施,提高其可靠性水平。
5 结 语针对舰船系统部件失效信息难以定量描述,更多依靠相关专家主观判断情形,提出了一种基于专家综合评估的模糊动态故障树分析方法。该方法给出了语言变量的设置规则以及语言变量转化为模糊变量的方法,同时针对不同专家对于舰船同一部件的不同意见,提出了一种专家意见归一化方法,采用去模糊化方法将归一化的模糊数转化为近似值,并结合基于顺序二元决策图的动态故障树建模方法,对动态系统进行了可靠性评估与重要度分析,最后以某型舰船弹药控制系统战备状态为例,采用本文提出的方法进行可靠性分析评估,结果表明文方法合理可行,对于模糊不确定状态下的复杂舰船系统可靠性分析提供了新思路。
| [1] |
AMARI S, DILL G, HOWALD E. A new approach to solve dynamic fault trees[C]. Reliability and Maintainability Symposium, 2003. Annual. IEEE, 2003: 374-379.
|
| [2] |
TANG Z, DUGAN J B. Minimal cut set/sequence generation for dynamic fault trees[C]. Reliability and Maintainability, 2004 Annual Symposium-RAMS. IEEE, 2004: 207-213.
|
| [3] |
BOUDALIH, DUGAN J B.A new Bayesian network approach to solvedynamic fault trees[C]. Reliability and Maintainability Symposium, 2005. Piscataway, NJ: IEEE Press, 2005: 451-456.
|
| [4] |
BOUDALI H, CROUZEN P, STOELINGA M. Dynamic fault tree analysis using input/output interactive markov chains[C]. IEEE Computer Society, 2007: 708-717.
|
| [5] |
RAO K D, GOPIKA V, RAO V V S S, et al. Dynamic fault tree analysisusing Monte Carlo simulation in probabilistic safetyassessment[J]. Reliability Engineering and System Safety, 2009, 94(4): 872-883. DOI:10.1016/j.ress.2008.09.007 |
| [6] |
JIANG G, YUAN H J, LI P C, LI P. A new approach to fuzzy dynamic fault tree analysisusing the weakest n-dimensional t-norm arithmetic[J]. Chinese Journal of Aeronautics, 2018, 31(7): 1506-1514. DOI:10.1016/j.cja.2018.04.014 |
| [7] |
LI Y F, HUANG H Z, LIU Y, XIAO N, LI H. A new fault tree analysis method: fuzzy dynamic fault tree analysis[J]. Maintenance and Reliability, 2012, 14(3): 208-214. |
| [8] |
KARIMI I, LLERMEIER E. Risk assessment system of natural hazards: A new approach based on fuzzy probability[J]. Fuzzy Sets and Systems, 2007, 158(9): 987-999. DOI:10.1016/j.fss.2006.12.013 |
| [9] |
RAJAKARUNAKARAN S, KUMAR. A M, PRABHU V A. Applications of fuzzy faulty tree analysis and expert elicitation for evaluation of risks in LPG refuelling station[J]. Journal of Loss Prevention in the Process Industries, 2014, 33: 109-123. |
| [10] |
LIU J, YANG J B, DA R, et al. Self-tuning of fuzzy belief rule bases for engineering system safety analysis[J]. Annals of Operations Research, 2008, 163(1): 143-168. DOI:10.1007/s10479-008-0327-0 |
| [11] |
BRYANT R E. Graph-Based algorithms for boolean function manipulation[J]. IEEE Transactions on Computers, 1986, c-35(8): 677-691. DOI:10.1109/TC.1986.1676819 |
| [12] |
XING L, SHRESTHA A, DAI Y. Exact combinatorial reliability analysis of dynamic systems with sequence-dependent failures[J]. Reliability Engineering and System Safety, 2011, 96(10): 1375-1385. DOI:10.1016/j.ress.2011.05.007 |
| [13] |
XING L, TANNOUS O, DUGAN J B. Reliability analysis of nonrepairable cold-standby systems using sequential binary decision diagrams[J]. Systems, Man and Cybernetics, Part A: Systems and Humans, IEEE Transactions on, 2012, 42(3): 715-726. DOI:10.1109/TSMCA.2011.2170415 |
| [14] |
ZADEH L A. Fuzzy sets[J]. Information and Control, 1965, 8(65): 338-353. |
| [15] |
ONISAWA T. Fuzzy theory in reliability analysis[J]. Fuzzy Sets and Systems, 1989, 30(3): 361-363. |
 2019, Vol. 41
2019, Vol. 41
