2. 海军航空大学 青岛校区,山东 青岛 266041
2. Qingdao Branch of China Naval Aviation University, Qingdao 266041, China
舰载机在航母甲板上的起降一般分波次循环进行,按循环方式分单周期、双周期等,循环间隔受舰载机制空时间影响,美军历次演习证明,航母航空保障作业中,双周期循环出动能够提高舰载机的出动强度,而双周期连续出动的制约因素主要在于舰载机制空时间和舰载机再次出动准备时间的匹配。在循环出动模型下,留给舰载机进行再次出动准备的时间非常有限,美国海军1997年对尼米兹级航母进行高强度出动演习表明,当循环周期为1 h 45 min时,平均可用甲板作业时间仅为57 min。因此,在舰载机和航母设计定型后,如何优化配置和合理安排批次舰载机的再次出动保障工作对于提高航母舰载机出动强度的提高具有非常重要的意义。
受作业完成时间的不确定性、舰载机及保障装设备故障的随机性、作业环节的多态性等因素的影响,涉及多架舰载机、多种保障资源的舰载机再次出动作业的调度问题属于典型的动态调度问题。近年来,国内学者在该领域进行了大量的研究工作,针对该问题常用的方法是建模仿真方法[1 − 2,6]、最优化方法[3],以及基于专家方案的逆向强化学习方法等[4]。但多数文献中仍以静态调度为研究基础[5,7],通过提高调度结果的鲁棒性和自适应性来增强调度系统(算法)对动态、随机环境的响应能力,避免频繁重调度。基于仿真的研究方法计算时间偏长,对于实时重调度的适应能力较弱。
针对航母舰载机甲板航空保障作业的调度问题,本文在对调度作业指挥人员实际需求分析的基础上,重点研究了双周期出动模式下舰载机再次出动准备的调度问题,建立了舰载机再次出动准备的优化计算模型,并设计一种适用于动态甲板环境的基于启发式禁忌搜索的快速求解算法,最后以库兹涅佐夫航母上8机双周期再次出动准备作业为例进行验证。
1 舰载机再次出动保障任务调度模型 1.1 舰载机甲板作业描述俄罗斯“库兹涅佐夫”航母是一种采用滑跃方式起飞的中型航母,通常搭载苏-35飞机作为主战舰载机。航母设计阶段,通常将飞行甲板分为若干功能区域,并在各区域设置多个站位,受空间及站位配置资源的限制,“库兹涅佐夫”航母上,舰载机着舰后必须先滑行至临时停机位,而在起飞前则必须牵引至暖机位进行惯导对准、暖机、飞控系统自检等作业,随后依次滑行至起飞位起飞。舰载机再次出动准备的作业流程如图1所示。

|
图 1 舰载机再次出动准备作业时序 Fig. 1 The sequence diagram of carrier aircraft turnaround operations |
对于任一架舰载机,图中作业集
上述诸多作业中按照对甲板资源的需求类型可分为特定甲板资源、不定甲板资源和无需资源作业。对于加油作业,每一停机区能够同时加油的舰载机数量受该区加油站数量的限制;对于挂弹作业,受甲板配置的挂弹小组数约束;对于转运作业,除了受转运小组数量约束外,还受空间路径约束;机务保障受机务保障小组数量约束,因机务作业可与加油挂弹并行作业,此处忽略该约束;惯导对准、暖机等作业受甲板可用暖机位数量的约束;滑行作业可视为不需甲板资源作业类型;起飞作业受起飞站位数量的约束,对于库兹涅佐夫航母,每一时刻只能起飞1架舰载机。
1.2 舰载机甲板作业调度的数学模型模型中以一波次舰载机全部着舰滑行至临时停机位为甲板航空保障作业调度起始点,不考虑再次出动机务检修工作所需资源和用时。相关参数定义如下:舰载机
调度模型的目标函数取为最小化本波次舰载机的再次出动准备时间:
| $F = \min {C_{\max }}{\text{,}}$ | (1) |
约束条件为:
| $ \sum\limits_{k = 1}^K {{y_{i{j_i}k}}} = 1,\ \ \forall i {\text{和}}{j_i} \in {V_i} \cap \left( {{V_{nr}} \cup {V_{ra}}} \right){\text{,}} $ | (2) |
| $ \sum\limits_{{j_i} \in {E_{{j_i}}}} {\sum\limits_{k = 1}^K {{y_{i{j_i}k}} = 1} } ,\ \ \forall i{\text{和}}{j_i} \in {V_i} \cap {V_{rs}}{\text{,}} $ | (3) |
| $ \sum\limits_{s = k}^K {{y_{i{m_i}s}}} + \sum\limits_{s = 1}^{k + {d_{{m_i}{n_i}}} - 1} {{y_{i{n_i}s}}} \leqslant 1,\\ \ \ \ \ \ \ \ \ \forall i,j{\text{和}}\left( {{m_i},{n_i}} \right) \in {A_i}{\text{,}} $ | (4) |
| $ \sum\limits_{i = 1}^I {{y_{ijk}}} \leqslant {N_{jk}},\ \ \forall k{\text{和}}j \in {V_{rs}} \cup {V_{ra}}{\text{,}} $ | (5) |
| $ \sum\limits_{k = 1}^K {\left( {{y_{i{j_l}k}} + {y_{i{j_m}k}}} \right)} \leqslant 1,\ \ \forall i{\text{和}}\left( {{j_l},{j_m}} \right) \in {V_s}{\text{,}} $ | (6) |
| $\begin{array}{l} s{t_{i1{j_{zy}}}} \leqslant s{t_{i2{j_{zy}}}},\\ \ \ \ \ \ \ \ \ \ \forall Z{W_{i1,i2}} \in {H_s}, {X_{zwi1}} \geqslant {X_{zwi2}}\end{array} {\text{。}}$ | (7) |
式(2)和式(3)联合确保每一作业必须只被每一架飞机启动一次,带有仅单一资源的特定性任务需要额外执行要求的作业通过式(3)强调。不等式(4)确保作业期间的时序优先级条件,该不等式主要针对作业集
若将待保障的舰载机视为工件,将保障资源视为加工机器,则舰载机循环出动的再次出动准备作业调度模型可视为具有工序顺序不定、加工时间不确定的柔性车间作业调度问题,该问题属于一类NP-难解问题,时间复杂度为
迭代禁忌搜索算法从某一局部极小值开始,重复地使用摄动策略使之逃离该局部极小值,并基于禁忌搜索算法去寻找另一局部极小,直到满足停止条件。解的接受标准决定新的局部极小值是否被接受,还是继续从一些以前访问过的解继续搜索。迭代禁忌搜索算法的总体框架如下:
步骤1 function ITS(),
步骤2 基于启发式规则的初始解→s,
步骤3 s←tabuSearch(s),
步骤4 for ii = 1,…,maxIT do,
步骤5
步骤6 s←tabuSearch
步骤7 以概率1-
步骤8 end for,
步骤9 返回搜索中发现的最优解
步骤10 end function。
在该算法中,在第
初始解的生成规则基于优先级索引策略、先到先服务和舰首区舰载机优先原则生成,具体规则如下:
1)对于挂弹、转运作业类受限保障资源,优先分配给甲板首区停机位上待保障的舰载机;
2)对于加油作业,按照区域,首先进入该区域停机位的舰载机优先接受加油服务;
3)对于转运作业,每一区域需要转运的舰载机,按照后进先出的顺序依次转运;
4)在满足相关约束条件的前提下,尽量避免长时间占用着舰跑道;
5)在甲板范围内,尽可能保持各类保障资源的负担均匀。
2.3 约束条件的处理舰载机再次出动作业调度问题的约束条件比起一般的车间作业调度问题更为复杂,主要体现在
步骤1 function
步骤2 记录没架飞机第j到作业工序为挂弹作业的飞机数为tgd,自增;
步骤3 取当前舰载机作业工序j的上一工序结束时间→
步骤4 若当前为所有飞机的第一道作业工序,且
步骤5 当前已安排挂弹作业的飞机数量
步骤6 若当前非第一道作业工序,且
领域结构是对初始解进行一次移动操作而获得另一个解的机制。在禁忌搜索算法中,领域结构直接影响禁忌搜索算法的搜索效率[9 – 11]。因舰载机再次出动甲板作业中,对于每架飞机集
以库兹涅佐夫航母为实例,对8机双周期连续出动模式下的舰载机再次出动保障进行调度仿真。甲板初始停机数设为16架,假设连续出动过程中所有舰载机均无故障,舰载机各作业工序的时间取值如下:加油时间
|
|
表 1 算法性能对比 Tab.1 Performance evaluation of algorithms |
|
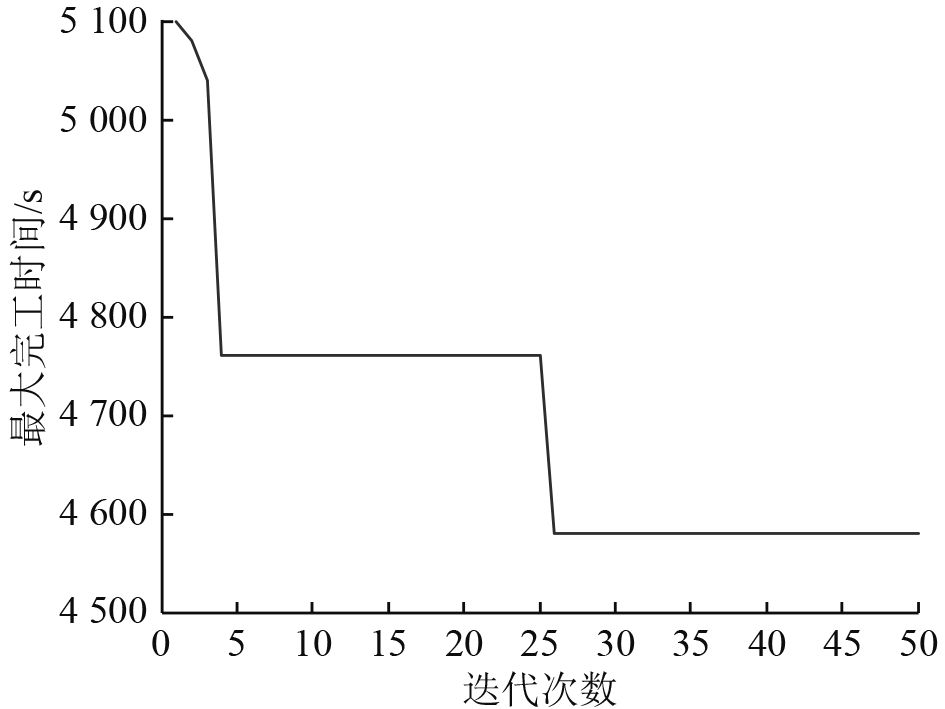
图 2 I-TB算法收敛曲线 Fig. 2 Convergence curve of I-TB algorithm |
|
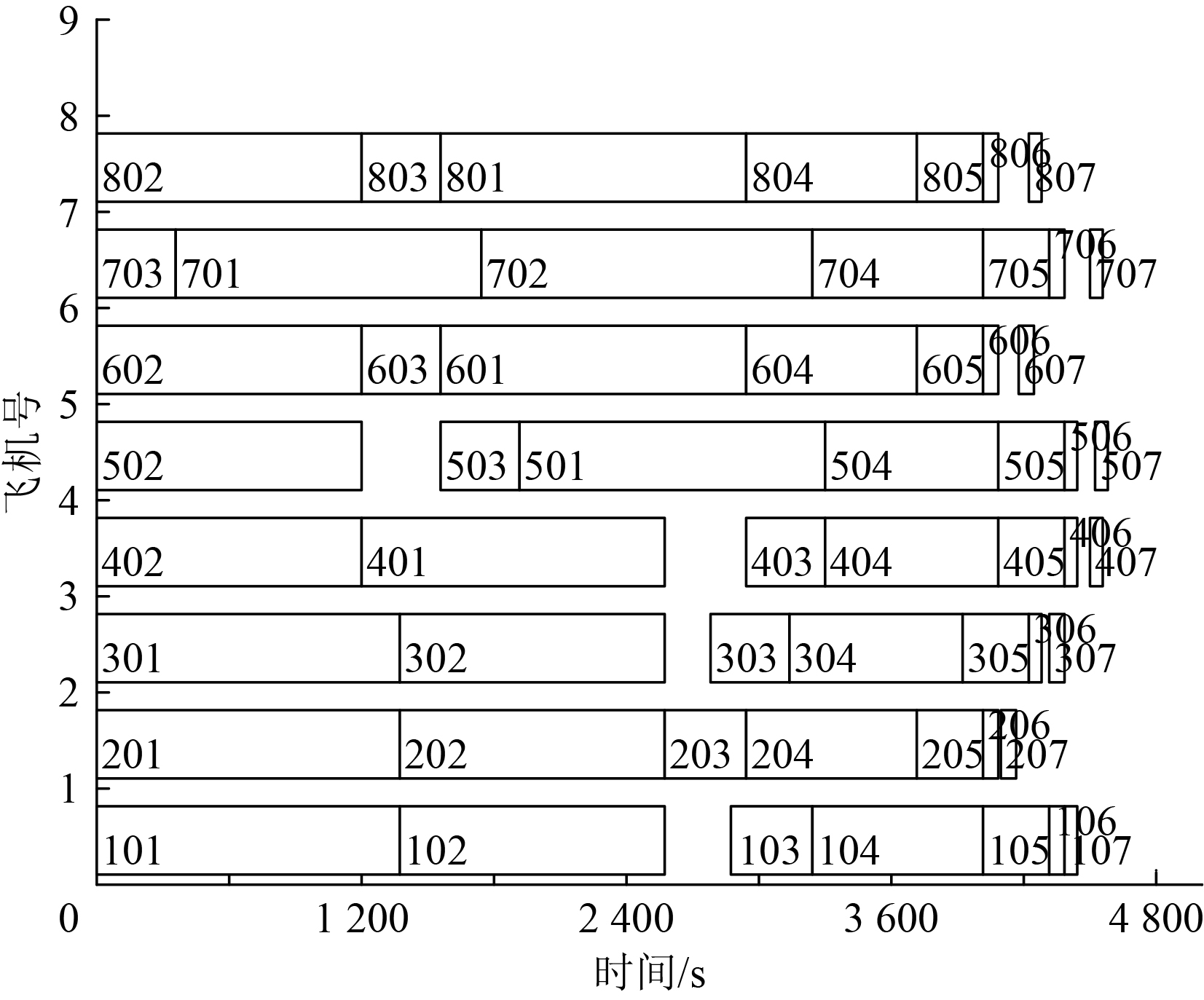
图 3 8机再次出动准备调度时序图 Fig. 3 Turnaround operations scheduling diagram for 8 carrier aircrafts |
从仿真结果可以看出,I-TB算法、SA算法、TB算法较全局搜索算法的搜索效率均有非常显著的提高,其中I-TB算法搜索时间最短;在解的质量方面,全局搜索算法可获得全局最优解,其他3种算法均无法保证获得全局最优解,但I-TB算法与TB和SA相比解的质量更高。从调度算法输出的甘特图上看,算法结果能够获得调度专家的认可。
4 结 语本文针对双周期连续出动模式下的舰载机舰面保障作业调度问题,通过分析作业流程和资源约束条件,以优化批次飞机最短再次出动准备时间为目标,建立了优化计算模型。在此基础上,采用迭代禁忌搜索算法框架设计了一种基于启发式初始解的快速求解算法,并给搜素过程中的约束条件处理测量和领域构造策略。通过以库兹涅佐夫航母为背景的仿真计算验证了算法的有效性,且算法获得的调度结果能够被甲板调度专家接受。
| [1] |
苏析超, 韩维, 等. 基于Memetic算法的舰载机舰面一站式保障调度[J]. 系统工程与电子技术, 2016, 38(38): 2303-2309. SU Xi-chao, HAN Wei, et al. Pit-stop support scheduling on deck of carrier plane based on Memetic algorithm[J]. Systems Engineering and Electronics, 2016, 38(38): 2303-2309. |
| [2] |
冯强, 等. 基于MAS的舰载机动态调度模型[J]. 航空学报, 2009, 30(11): 2119-2125. FENG Q, ZENG S k, KANG R. A MAS-based model for dynamic scheduling of carrier aircraft[J]. Acta Aeronautica et Astronautica sinica, 2009, 30(11): 2119-2125. DOI:10.3321/j.issn:1000-6893.2009.11.017 |
| [3] |
魏昌全, 陈春良, 等. 基于任务的连续出动舰载机航空保障重调度研究[J]. 指挥控制与仿真, 2012, 34(3): 23-26, 34. WEI Chang-quan, CHEN Chun-liang, WANG Bao-ru. Rescheduling study of aircraft support of running launch aircraft on carrier based on mission[J], Command Control & Simulation 2012, 34(3): 23-26, 34. |
| [4] |
李耀宇, 朱一凡, 等. 基于逆向强化学习的舰载机甲板调度优化方案生成方法[J]. 国防科技大学学报, 2013, 35(4): 171-175. LI Yao-yu, ZHU Yi-fan, et al. Inverse reinforcement learning based optimal schedule generation approach for carrier aircraft on flight deck[J]. Journal on National University of Defense Technology, 2013, 35(4): 171-175. DOI:10.3969/j.issn.1001-2486.2013.04.030 |
| [5] |
RYANA, et al. Designing an interactive local and global decision support system for aircraft carrier deck scheduling[C]// AIAA Infotech@Aerospace St. Louis, 2011.
|
| [6] |
林骥鹏. 基于离散事件的舰载机出动架次计算方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2011. 12. LIN Ji-peng. Research on aircraft sortie generation rate based on discrete event[D]. Harbin Engineering University master thesis, 2012. 12. |
| [7] |
RAJARSHI. A queueing network based approach to distributed aircraft carrier deck scheduling[C]// AIAA Infotech@Aerospace St. Louis, 2011.
|
| [8] |
VERONIQUE Sels, JOSé Coelho, et al. Hybrid tabu search and a truncated branch-and-bound for the unrelated parallel machine scheduling problem[J]. Computers & Operations Research, 2015(53): 107-117. |
| [9] |
ZHOU Yang-ming, HAO Jin-kao. An iterated local search algorithm for the minimum differential dispersion problem[J]. Knowle dge-Base d Systems, 2017(125): 26-38. |
| [10] |
张超勇, 等. 基于进化禁忌算法的Job-Shop调度问题研究[J]. 华中科技大学学报, 2009, 37(8): 80-84. ZHANG Chao-yong, etal. Solving Job-Shop scheduling problem using genetic tabu algorithm[J]. Journal of Huazhong University of science and technology (Natural science edition), 2009, 37(8): 80-84. DOI:10.3321/j.issn:1671-4512.2009.08.022 |
| [11] |
SLIM Belhaiza, et al. A hybrid variable neighborhood tabu search heuristic for the vehicle routing problem with multiple time windows[J]. Computers & Operations Research, 2014(52): 269-281. |
 2019, Vol. 41
2019, Vol. 41

